Abstract
Flavonoids provide potential health benefits due to their antioxidant properties. The antioxidant activity of natural flavonoids is primarily exerted by phenolic hydroxyl groups; however, C–H bonds also contribute to these properties. In this study, the contributions of phenolic groups and C–H bonds to the antioxidant properties of 13 flavonoids were investigated by using the (RO)B3LYP/6-311++G(2df,2p)//B3LYP/6-311G(d,p) model chemistry in the gas phase and water and ethanol solvents. It was found that the C–H bonds have lower bond dissociation energies than O–H bonds in the 4-carbonyl and/or 3-hydroxyl group containing flavonoids and hence define antioxidant activity. The HOO· radical scavenging of the selected flavonoids is also investigated in detail through the potential energy surface, natural bond orbitals, and kinetic calculations. It was found that the favored radical scavenging mechanism of the flavonoids is hydrogen atom transfer, with the gas phase rate constants in the range of 7.23 × 103–2.07 × 109 L·mol–1·s–1. The results suggest that the flavonoids, isomelacacidin, isoteracacidin, melacacidin, and teracacidin, have antioxidant properties as high as typical phenolic compounds such as quercetin, trans-resveratrol, trolox, and ascorbic acid.
1. Introduction
Flavonoids are common phytochemicals recognized for their potential health benefits. Up to now, more than 9000 flavonoids have been identified.1 Many studies demonstrated that flavonoids exhibit a broad spectrum of biological activity, including vasodilating, anti-allergenic, antiviral, and anti-inflammatory actions.2−4 The antioxidant activity of flavonoids attracted the most interest: they can not only scavenge free radicals but also reduce free radical formation. The Acacia and Populus genera were found to be good sources of natural phenolic antioxidants.5 It was shown that the knotwood and bark extracts from waste materials of these species display strong antioxidant properties due to the high flavonoid content, including, for example, kaempferol, dihydrokaempferol, dihydromyricetin, naringenin, pinobanksin, catechin, taxifolin, melacacidin, teracacidin, isomelacacidin, isoteracacidin, and keto-teracacidin.5−7
The chemical structure plays a fundamental role in the antioxidant activity of flavonoids. Previous studies suggested that the existence of a certain hydroxylation pattern, particularly, in the ring B of the flavonoid structure and/or a C2=C3 double bond in conjugation with a C4-carbonyl group, methoxyl groups, and O3–H groups increases antioxidant properties while the presence of saccharide groups reduces antioxidant activity.2,3,8 However, it is very challenging to clearly link the structural characteristics to the antioxidant activity. It is known that flavonoids owe their radical scavenging activity to the presence of phenolic hydroxyl groups, acting via the hydrogen atom transfer (HAT) or the single electron transfer followed by proton transfer (SETPT) mechanisms.9−12 Therefore, the bond dissociation energy (BDE) of the O–H moiety is a key factor in the comparison and the explanation of the antioxidant properties. However, in some cases, it is difficult to explain the empirically confirmed antioxidant properties of compounds based solely on the lowest BDE(O–H) values. In the case of dihydrokaempferol, the lowest BDE(O–H) and the trolox equivalent antioxidant capacity (TEAC) values are 87.5 kcal·mol–1 and 1.39 mM, respectively, whereas the lowest BDE(O–H) of kaempferol is 85.2 kcal·mol–1; however, the antioxidant capacity of kaempferol is less than that of dihydrokaempferol (the TEAC value of kaempferol was 1.34 mM).13,14 Moreover, the experimental vitamin C equivalent antioxidant capacity (VCEAC) test of kaempferol and naringenin indicated that the latter exhibits higher antioxidant activity (VCEAC = 135.1 mg/mL vs kaempferol VCEAC = 114.6 mg/mL), but the lowest BDE(O–H) of naringenin (88.0 kcal·mol–1) is higher than that of kaempferol (85.2 kcal·mol–1).13,15 Recent studies in lignans highlighted that C–H (benzylic) bonds can also play a fundamental role in antioxidant activity.16 Therefore, it is possible that contribution from C–H bonds can explain the seemingly anomalous antioxidant properties of flavonoids. This possibility has never been explored before.
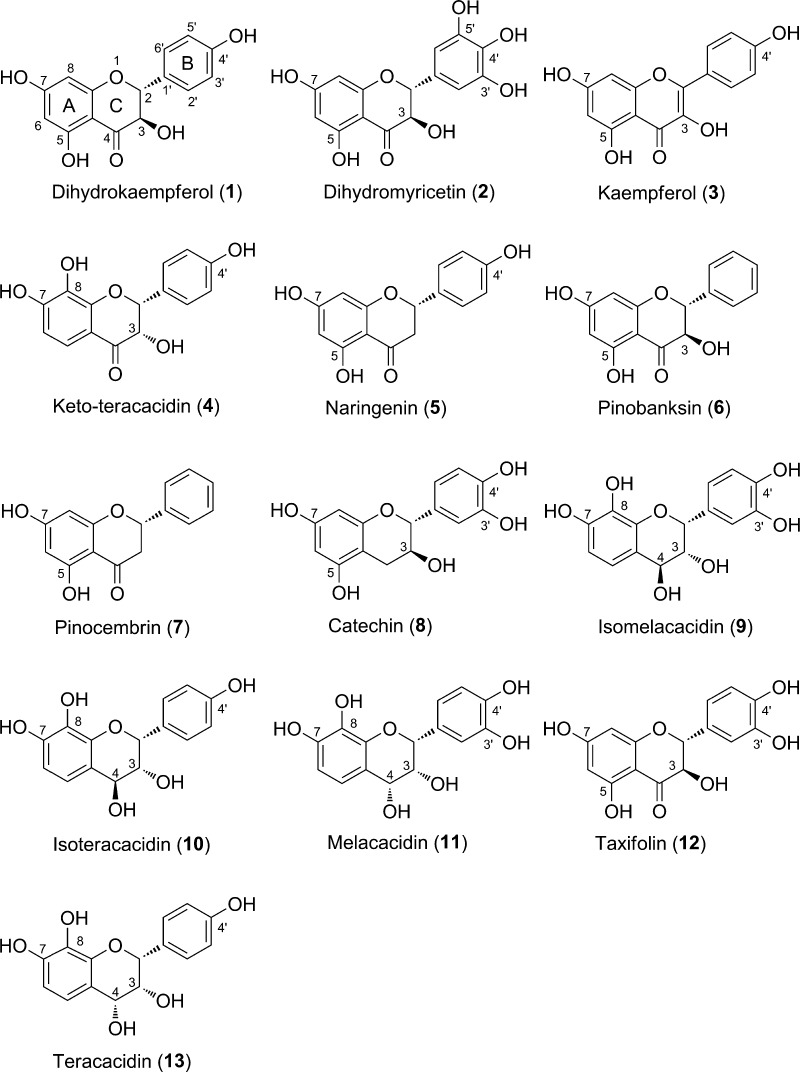
This study is aimed at evaluating the antioxidant properties of 13 flavonoids (Figure 1) identified from the extracts of the Acacia and Populus genera. The compounds can be divided into four classes: flavanones (compounds 5 and 7), flavonols (compound 3), flavanols (compounds 8, 9, 10, 11, and 13), and flavanonols (compounds 1, 2, 4, 6, and 12).6 In this work, antioxidant activity is defined by the ability of H-donation and/or electron transfer to the free radicals, an approach that was validated before.17,18 The calculation of thermodynamic parameters will be applied to study the antioxidant properties of these compounds following three typical mechanisms: HAT, SETPT, and the sequential proton loss electron transfer (SPLET).9,19 The potential energy surface (PES), kinetics, and natural bond orbitals (NBOs) will be calculated for investigating the mechanism of reactions of the most potential antioxidants with the hydroperoxyl radical (HOO·).
Figure 1.
Structures of the studied flavonoids (1–13).
2. Results and Discussion
2.1. Hydrogen Atom Transfer (HAT) Mechanism
The BDE value is a deciding factor in the evaluation of the antioxidant properties of compounds that follow the HAT mechanism.9,19 The B3LYP/3-21G level of theory was used first to calculate the BDEs of all possible X–H (X = C, O) bonds in the flavonoids; the results are presented in Table S1 (Supporting Information). The lowest BDEs of X–H (X = C, O) were then recalculated with higher accuracy at the ROB3LYP/6-311++G(2df,2p)//B3LYP/6-311G(d,p) level of theory in the gas phase as well as in two different solvents: water and ethanol (Table 1). As shown in Table 1, although the O–H bonds have the lowest BDE values in compounds 3, 8, 9, 10, 11, and 13 in a range of 77.0–85.4 kcal·mol–1, the lowest BDE values are for the C–H bonds in flavonoids 1, 2, 4, 5, 6, 7, and 12 in a range of 73.0–82.5 kcal·mol–1. The lowest BDE(C–H) (73.0 kcal·mol–1) belongs to the C3–H bond of the compound 1, whereas the lowest BDE(O–H) is found at the position O7 of the compound 9 (77.0 kcal·mol–1). In general, the lowest BDE(C–H) values are found at the C3–H bonds of the flavanonols (compounds 1, 2, 4, 6, and 12) and at the C2–H bonds of the flavanones (compounds 5 and 7). The optimized geometries of the radicals at the position C3 of compounds 1, 2, 4, 6, and 12 suggest that the single electron at the C3 atom is released to the O–C3–C4–O system (Figure S1, Supporting Information). Furthermore, the AIM analysis (Figure S2, Supporting Information) of the radicals formed by the dissociation of C3–H bonds revealed that there are intermolecular bonds between H atoms of the 3-hydroxyl group and O atoms of the 4-carbonyl group; hence, the radicals are stabilized. By contrast, in flavanones, the aromatic ring B is responsible for the electron delocalization from the C2 atom of the radicals that is not found in the radicals formed by the dissociation of the C3–H bonds (Figure S1, Supporting Information). The results also show that the lowest BDE is found at the C–H bond only in the flavanone and flavanonol families and never in the flavanols. Thus, the 4-carbonyl and 3-hydroxyl groups have a determining effect on the BDEs of the C–H bonds. Previous studies concluded that the presence of 4-carbonyl and/or 3-hydroxyl groups increases the antioxidant activity of the flavonoids because the single electron at the O atom in the ring A of radicals is released to these groups.2,14 However, the optimized geometries of the radicals of 1–O7–H, 2–O7–H, 4–O7–H, 6–O7–H, and 12–O7–H (Figure S1, Supporting Information) show that there is no electron release from the O atom of the radicals to the O atoms of the 4-carbonyl and 3-hydroxyl groups. Thus, the results suggest that the increase in antioxidant activity of flavanonols is due to the dissociation of the C3-H bond rather than O–H bonds. On the basis of the calculated BDE values in the gas phase, the H-donation ability of the C–H bonds of the studied compounds follows the sequence 1 < 2 < 6 < 12 < 4 < 5 < 7. The highest H-donation ability of the O–H bonds is observed at O7–H and/or O4′–H of the compounds 8, 9, 10, 11, and 13 with BDE(O–H) at ∼77–78 kcal·mol–1. It suggests that these compounds may exhibit antioxidant activities as high as typical phenolic compounds such as quercetin, trans-resveratrol, and vitamin C (the lowest BDE(O–H) values: 75.2, 77.2, and 77.5 kcal·mol–1, respectively20,21). It was found that the S configuration of the O4 position (compounds 9 and 10) can reduce the BDEs of O7–H and C–H by 0.7–2.1 kcal·mol–1, compared with the R configuration (compounds 11 and 13). Thus, the isoflavandiols 9 and 10 must have higher antioxidant properties than the isoflavandiols 11 and 13.
Table 1. Calculated BDEs in Gas Phase and Water and Ethanol Solvents at the Weakest X–H (X = C, O) Bonds of the Studied Compounds (in kcal·mol–1).
| BDEs (X–H) |
|||||
|---|---|---|---|---|---|
| compounds | name | X–H position | gas phase | water | ethanol |
| 1 | dihydrokaempferol | C3–H | 73.0 | 75.9 | 75.2 |
| O4′–H | 87.5 | 88.6 | 88.0 | ||
| 2 | dihydromyricetin | O4′–H | 79.0 | 80.6 | 78.7 |
| C3–H | 73.4 | 77.2 | 76.6 | ||
| 3 | kaempferol | O3–H | 85.2 | 84.2 | 83.3 |
| O4′–H | 85.4 | 86.9 | 86.3 | ||
| 4 | keto-teracacidin | O7–H | 79.3 | 84.3 | 83.6 |
| C3–H | 76.1 | 79.2 | 78.6 | ||
| 5 | naringenin | O4′–H | 88.0 | 89.3 | 88.7 |
| C2–H | 80.5 | 84.1 | 83.5 | ||
| 6 | pinobanksin | O7–H | 94.0 | 96.7 | 96.1 |
| C3–H | 73.5 | 77.6 | 76.9 | ||
| 7 | pinocembrin | O7–H | 93.5 | 96.1 | 95.5 |
| C2–H | 82.9 | 86.4 | 85.8 | ||
| 8 | catechin | O4′–H | 77.2 | 81.0 | 80.4 |
| C2–H | 81.3 | 85.1 | 84.4 | ||
| 9 | isomelacacidin | O7–H | 77.0 | 81.0 | 80.3 |
| O4′–H | 77.8 | 81.6 | 80.9 | ||
| C4–H | 80.3 | 83.8 | 83.2 | ||
| 10 | isoteracacidin | O7–H | 77.1 | 81.0 | 80.3 |
| C4–H | 80.1 | 83.7 | 83.0 | ||
| 11 | melacacidin | O7–H | 77.7 | 81.7 | 81.1 |
| O4′–H | 77.3 | 81.1 | 80.5 | ||
| C2–H | 82.6 | 85.5 | 84.9 | ||
| 12 | taxifolin | O4′–H | 78.2 | 81.9 | 81.2 |
| C3–H | 73.7 | 78.0 | 77.3 | ||
| 13 | teracacidin | O7–H | 77.8 | 81.7 | 81.1 |
| C2–H | 82.2 | 85.3 | 84.7 | ||
Following the gas phase calculations, the BDE values were calculated in ethanol and water solvents to investigate the effects of the dielectric environment on the H-donating ability of the studied compounds.5,6,16,22 The results show that, in ethanol and water, the BDE(X–H, X = O, C) values increase slightly in the range of 0.7 to 4.6 kcal·mol–1 apart from the compound 3 (O3–H) that decreased in the polar solvents. The lowest BDE(C–H) values of compounds 1 and 5 are lower than that of the compound 3 in all of the studied environments (Table 1). The results explain the higher empirical antioxidant activity of compounds 1 and 5 compared with compound 3,13−15 despite the fact that the lowest BDE(O–H) values of the compound 3 (85.2, 84.2, and 83.3 kcal·mol–1 in gas phase, water, and ethanol, respectively) are lower than those of compounds 1 and 5 (86.5, 88.6, and 88.0 kcal·mol–1 and 87.6, 88.9, and 88.3 kcal·mol–1 in gas phase, water, and ethanol, respectively). Therefore, the C–H bonds play a fundamental role in the antioxidant activity of these compounds. However, similar to the gas phase, the compound 9 has the lowest BDE(O–H) values in the flavonoid family with 81.0 kcal·mol–1 in water and 80.3 kcal·mol–1 in ethanol, whereas the lowest BDE(C–H) values are observed at the C3–H bond in the compound 1 with 75.5 and 75.2 kcal·mol–1 in water and ethanol, respectively. It is important to note that in the solvent environments, the easiest bonds to dissociate are still the C–H bonds in compounds 1, 2, 4, 5, 6, 7, and 12. On the basis of these calculated values, compounds 1, 2, 9, and 12 are the most powerful antioxidants.
2.2. Sequential Electron Transfer Proton Transfer (SETPT) Mechanism
The SETPT mechanism, which is characterized by the ionization energy (IE) and the proton dissociation energy (PDE), is also investigated to evaluate antioxidant properties of the studied compounds and compare it to the order obtained based on the HAT mechanism.16,23,24 The first step (the sequential electron transfer (SET)) plays a key role in the antioxidant activity in the SETPT mechanism.9,25 Thus, the adiabatic IE values were first calculated in gas and solution phases by using the B3LYP/6-311++G(2df,2p)//B3LYP/6-311G(d,p) method; results are presented in Table 2. The sequence of adiabatic IE values in the gas phase is 3 < 9 < 8 < 10 < 11 < 13 < 4 ≈ 2 ≈ 12 < 1 < 5 < 6 < 7 (Table 2). The compound 3 has the lowest IE because the presence of the C2=C3 double bond reduces ionization energy through electron delocalization from the B ring. The number of O–H groups in the B ring also has a significant influence on the ionization energy of the flavonoid compounds. For example, in the case of flavanol, IE values decrease in the order to 6 > 1 > 12 > 2 corresponding to an increase of the number of OH groups. In the water and ethanol solvents, the IE values decreased by approximately 50–60 kcal·mol–1 compared with those for the gas phase (Table 2). This suggests that the studied compounds can lose an electron much easier in the solute phase, for example, in water or ethanol, than in the gas phase. However, the calculated IE values in the range of 108.0 to 126.9 kcal·mol–1 are still higher than the respective BDE values, making the SET mechanism less likely to occur than the HAT mechanism. Consistently, the SET reactions between the studied compounds and a typical radical (HOO·) are endothermic with the (calculated) ΔH and ΔG values in the ranges of 142.9–157.8 kcal·mol–1 in the gas phase and 35.5–48.5 and 38.6–51.6 kcal·mol–1 in the water and ethanol solvents, respectively. Hence, the results suggest that the SET mechanism is not favored in any of the studied environments.
Table 2. Calculated IEs, ΔH, and ΔG Values of the Reaction with HOO· Radical via the SET Mechanism in Gas Phase and Water and Ethanol Solvents of the Studied Compounds (in kcal·mol–1).
| |
thermodynamic
properties of reaction
between the studied compounds with HOO· radical via
the SET mechanism |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| IEs |
gas phase |
water |
ethanol |
||||||
| compounds | gas phase | water | ethanol | ΔH | ΔG | ΔH | ΔG | ΔH | ΔG |
| 1 | 177.9 | 124.7 | 118.6 | 154.0 | 153.5 | 46.2 | 45.7 | 49.2 | 48.7 |
| 2 | 176.4 | 120.7 | 114.9 | 151.5 | 151.2 | 42.2 | 41.9 | 45.5 | 45.1 |
| 3 | 167.8 | 114.0 | 108.0 | 143.0 | 142.9 | 35.6 | 35.5 | 38.6 | 38.6 |
| 4 | 176.0 | 122.4 | 116.5 | 151.2 | 150.8 | 44.0 | 43.7 | 47.1 | 46.8 |
| 5 | 178.2 | 124.3 | 118.3 | 153.3 | 153.0 | 45.9 | 45.7 | 48.9 | 48.7 |
| 6 | 182.7 | 126.9 | 121.0 | 157.8 | 157.3 | 48.5 | 47.9 | 51.6 | 51.1 |
| 7 | 183.5 | 125.4 | 119.6 | 158.6 | 158.0 | 47.0 | 46.3 | 50.2 | 49.5 |
| 8 | 168.2 | 117.1 | 110.9 | 143.3 | 143.9 | 38.7 | 39.3 | 41.5 | 42.2 |
| 9 | 167.9 | 115.8 | 109.8 | 143.0 | 143.2 | 37.4 | 37.6 | 40.4 | 40.6 |
| 10 | 169.6 | 115.8 | 109.8 | 144.7 | 144.7 | 37.4 | 37.3 | 40.4 | 40.4 |
| 11 | 170.2 | 117.5 | 111.5 | 145.3 | 145.3 | 39.1 | 39.1 | 42.1 | 42.1 |
| 12 | 176.5 | 122.1 | 116.2 | 151.7 | 151.3 | 43.7 | 43.3 | 46.8 | 46.4 |
| 13 | 172.6 | 117.8 | 112 | 147.7 | 147.6 | 39.4 | 39.3 | 42.6 | 42.4 |
In general, the antioxidant mechanism follows the HAT mechanism if the ΔBDEs are approximately −10 kcal·mol–1 and the ΔIEs are higher than −36 kcal·mol–1 (compared with phenol: BDE(O–H) = 87.7 kcal·mol–1 and IE(adiabatic) = 193.8 kcal·mol–1 at the B3LYP/6-311++G(2df,2p)//B3LYP/6-311G(d,p) model chemistry).17 For the studied compounds, the calculated ΔBDEs and ΔIEs in the gas phase are in the ranges of −14.7 to −2.3 and −8.5 to −25.8 kcal·mol–1, respectively. Therefore, the HAT mechanism appears to be the main radical scavenging pathway for the flavonoids.
2.3. Sequential Proton Loss Electron Transfer (SPLET) Mechanism
The potential for the SPLET mechanism was also assessed; SPLET is defined by the proton affinity (PA) and the electron transfer enthalpies (ETEs).26,27 As before, the B3LYP/3-21G level of theory was first applied to calculate the PAs for all of possible X–H (X = C, O) bonds (Table S2, Supporting Information); then, the lowest PAs of X–H (X = C, O) were calculated using the (RO)B3LYP/6-311++G(2df,2p)//B3LYP/6-311G(d,p) model chemistry. Results shown in Table 3 demonstrate that the PA values in the gas phase of the C–H bonds (from 338.8 to 364.6 kcal·mol–1) are higher than those of O–H bonds (in the range of 318.6–337.0 kcal·mol–1), whereas ETEs of the C–H bonds are lower than those of O–H bonds. Therefore, the C–H bonds are not favored in the first step in the SPLET mechanism. With increasing the solvent polarization, PA values decrease by 282.0–299.6 kcal·mol–1, whereas ETE values increase slightly by around 15.2–30.6 kcal·mol–1 (Table 3). This suggests that the deprotonation process is more preferable than the single electron transfer process in the strong dielectric environments. The thermochemical properties of the first step of the SPLET reaction between the studied compounds and HOO· radical are endothermic with positive ΔH and ΔG values in all studied media (Table S3, Supporting Information). Thus, the SPLET pathway is not favored for the flavonoids.
Table 3. Calculated PAs and ETEs of the Studied Compounds (in kcal·mol–1).
| PAs |
ETEs |
||||||
|---|---|---|---|---|---|---|---|
| compounds | O–H position | gas phase | water | ethanol | gas phase | water | ethanol |
| 1 | O7–H | 326.0 | 40.7 | 36.3 | 82.4 | 96.4 | 102.1 |
| C3–H | 339.0 | 53.0 | 48.8 | 48.5 | 63.4 | 69.1 | |
| 2 | O4′–H | 323.4 | 39.7 | 35.4 | 70.1 | 80.7 | 85.3 |
| C3–H | 338.8 | 53.8 | 49.5 | 48.5 | 61.6 | 67.6 | |
| 3 | O4′–H | 327.2 | 43.5 | 39.2 | 72.6 | 83.2 | 89.1 |
| 4 | O7–H | 318.6 | 36.2 | 31.7 | 75.1 | 87.9 | 93.7 |
| C3–H | 349.2 | 58.7 | 54.7 | 41.3 | 60.4 | 65.8 | |
| 5 | O7–H | 330.0 | 41.4 | 37.2 | 77.6 | 94.2 | 99.9 |
| C2–H | 361.5 | 79.8 | 75.4 | 33.5 | 44.2 | 49.9 | |
| 6 | O7–H | 320.0 | 36.6 | 32.2 | 88.5 | 99.9 | 105.8 |
| C3–H | 339.5 | 53.5 | 49.2 | 48.5 | 64.0 | 69.6 | |
| 7 | O7–H | 329.4 | 41.3 | 37.0 | 78.6 | 94.6 | 100.3 |
| C2–H | 360.3 | 78.2 | 73.8 | 37.1 | 48.0 | 53.8 | |
| 8 | O4′–H | 333.4 | 44.3 | 40.1 | 58.3 | 76.6 | 82.1 |
| 9 | O4′–H | 328.8 | 43.2 | 38.9 | 63.5 | 78.2 | 83.9 |
| O7–H | 335.0 | 44.7 | 40.6 | 56.5 | 76.1 | 81.6 | |
| 10 | O7–H | 334.6 | 44.6 | 40.5 | 68.1 | 87.4 | 92.8 |
| 11 | O7–H | 330.5 | 44.0 | 39.7 | 61.7 | 77.6 | 83.3 |
| 12 | O4′–H | 328.1 | 42.7 | 38.4 | 64.6 | 79.1 | 84.7 |
| C3–H | 364.6 | 68.7 | 65.0 | 23.6 | 49.2 | 54.2 | |
| 13 | O7–H | 330.1 | 43.8 | 39.6 | 62.2 | 77.7 | 83.4 |
2.4. HAT Mechanism Reaction of HOO· Radical with the Selected Studied Compounds
2.4.1. Potential Energy Surface (PES)
The comparison of the potential antioxidant reaction mechanisms of the studied flavonoids confirmed that the HAT mechanism is the main pathway for their antioxidant activity. Thus, the reactions of compounds 1 and 9, characterized by the lowest BDE(X–H) (X = C, O) values, with a HOO· radical were studied to gain further insights into the antioxidant capacity of the flavonoids. In this study, the (RO)B3LYP/6-311++G(2df,2p)//B3LYP/6-311G(d,p) model chemistry was used to calculate the energies of the reactants (R), the transition states (TS), the intermediates (Int), and the products (P). To ensure that there is a connection between each TS and its reactant and product, the intrinsic coordinate calculations (IRCs) were calculated and are shown in Figure S3 (Supporting Information). The PESs are displayed in Figure 2, and all optimized TS structures are shown in Figure S4 (Supporting Information).
Figure 2.
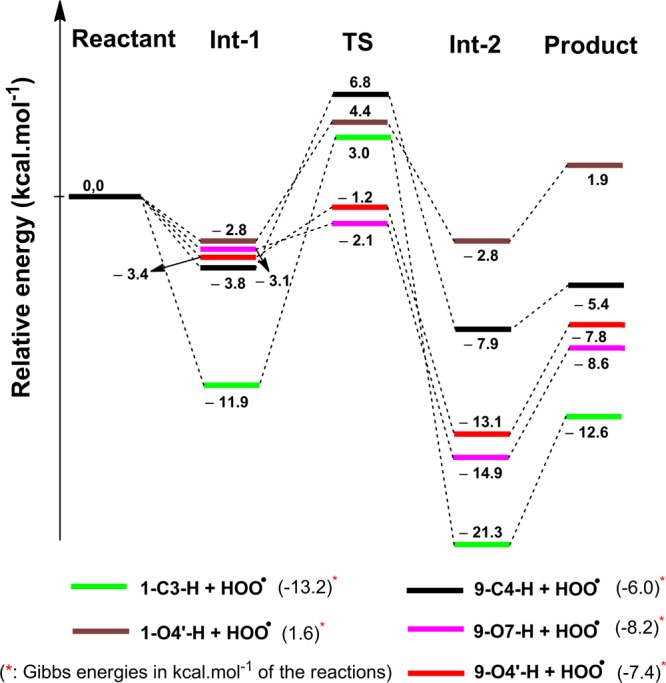
PES of reaction between the selected compounds and HOO· radical.
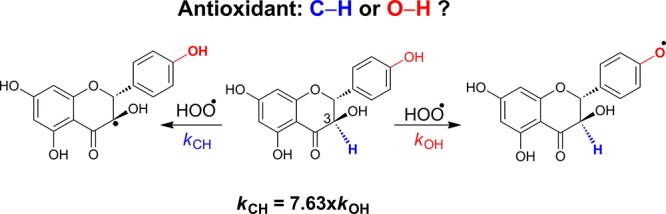
Examination of the structures of the TSs reveals that the H···OOH and X···H (X = C, O) distances are in the ranges of 1.2612–1.9906 and 1.0989–1.3012 Å, respectively. The X···H···O (X = C, O) angles are in the range of 167.2–171.9° (Figure S4, Supporting Information). It is clear from Figure 2 that the energies of the studied TSs are in the range of −2.1 to 6.8 kcal·mol–1. These data suggest that compounds 1 and 9 can easily transfer the hydrogens of the C–H groups or phenyl hydroxyl groups to a HOO· radical to form H2O2 and an unreactive radical (ArX·). The compound 9 is expected to have the highest antioxidant activity because of the lowest energy of its transition states (−2.1 and −1.2 kcal·mol–1 for 9–O7–H–OOH and 9–O4′–H–OOH TSs, respectively) in a good agreement with the conclusions of the analysis presented above. On the basis of the calculated Gibbs free energies (Figure 2), these hydrogen abstraction reactions will be spontaneous apart from 1–O4′–H–OOH (ΔG = 1.6 kcal·mol–1). The hydrogen abstraction reaction of 1–C3–H has a higher priority than that of 1–O4′–H due to the lower Gibbs free energies of the reactions of the C–H bond (−13.2 kcal·mol–1) compared with the O–H bond (+1.6 kcal·mol–1). Additionally, the energy of the TS of 1–C3–H–OOH (3.0 kcal·mol–1) is lower than that of 1–O4′–H–OOH (4.4 kcal·mol–1). As a result, the C3–H bond plays a deciding factor in the radical scavenging activity of the compound 1.
2.4.2. Kinetic Study
For further insights into the radical scavenging activity of the C–H and O–H bonds of the selected flavonoids, calculations of the kinetics of the reactions were also performed. The Gibbs free energy of activation (ΔG≠) and rate constants (k) were calculated at the B3LYP/6-311G(d,p) level at 298.15 K for the gas phase reactions between compounds 1 and 9 with the HOO· radical, and are presented in Table 4. To obtain realistic data, the correction for diffusion-controlled rates was applied for the highest rate constant values, that is, for the reaction of 9–O7–H and 9–O4′–H with HOO· radicals.25 The apparent rate constants (kapp) were calculated following the Collins–Kimball theory in water at 298.15K;28 the steady-state Smoluchowski29 rate constant (kD) for an irreversible bimolecular diffusion-controlled reaction between compounds 1 or 9 with the hydroperoxyl radical was 2.50 × 109 (or 2.60 × 109 L·mol–1·s–1).
Table 4. Calculated ΔG≠ and k at the B3LYP/6-311G(d,p) Level of Theory at 298.15 K in the Gas Phasea.
| reactions | ΔG≠ (kcal·mol–1) | k (L·mol–1·s–1) |
|---|---|---|
| 1–C3–H + HOO· | 9.6 | 3.13 × 107 |
| 1–O4′–H + HOO· | 10.4 | 4.10 × 106 |
| 9–C4–H + HOO· | 13.9 | 7.23 × 103 |
| 9–O7–H + HOO· | 4.4 | 1.02 × 1010 (2.07 × 109)* |
| 9–O4′–H + HOO· | 5.2 | 5.12 × 109 (1.72 × 109)* |
Asterisk (*): the apparent rate constants kapp.
As can be seen from the Table 4, the rate constants are in the range of 7.23 × 103–2.07 × 109 L·mol–1·s–1. It is also worth noting that the 1–C3–H + HOO· reaction has a lower energy barrier and proceeds faster than 1–O4′–H (ΔG≠ = 9.6 kcal·mol–1, k = 3.13 × 107 L·mol–1·s–1 compared to ΔG≠ = 10.4 kcal·mol–1, k = 4.10 × 106 L·mol–1·s–1 for the 1–O4′–H + HOO· reaction). This result strongly affirms that the C3–H bond decides the radical scavenging activity of the compound 1 along with the O–H bonds. It was found that the compound 9 has the highest rate constants with kapp = 2.07 × 109 and 1.72 × 109 L·mol–1·s–1 for the 9–O7–H + HOO· and 9–O4′–H + HOO· reactions, respectively. These reactions are much faster than the HOO· radical scavenging of trolox or ascorbic acid (kTrolox= 5.30 × 105 L·mol–1·s–1, kAsc = 2.65 × 105 L·mol–1·s–1).26,30 To validate these results, the M05-2X/6-311G(d,p) level of theory was applied to calculate the kinetics of the reactions in the gas phase. The results are shown in Table S6 (Supporting Information). It is apparent that the order of the HOO· radical scavenging capacity at the M05-2X/6–311G(d,p) level reproduces the trend predicted by the B3LYP/6-311G(d,p) method, with the known difference of higher rate constants in the B3LYP method compared to the M05-2X method. The highest rate constant was observed for the 9–O7–H + HOO· reaction at k = 1.75 × 107 L·mol–1·s–1. This result again suggests that the compound 9 is the most powerful antioxidant.
2.4.3. Natural Bond Orbital (NBO)
NBO analysis was also applied to the antioxidant mechanism of compounds 1 and 9.(16,31) In this approach, singly occupied molecular orbitals (SOMO) and atomic spin densities (ASDs) of the TSs of the studied compounds were determined; the results are presented in Table 5 and Figure 3. In case of TSs of 1–C3–H–OOH and 9–C4–H–OOH, the three electron lone pairs on the O1 atom, LP(1,2,3)O1, are donated to the antibonding orbital on the H·, LP*(1)H, with stabilization energies (E(2)) of 160.9 and 152.0 kcal·mol–1, respectively. Moreover, the interaction between two unoccupied orbitals on C3/C4, LP*(1)C3/C4, and on the H atom, LP*(1)H, leads to form a new O1–H bond on H2O2 with E(2) values at 324.1 and 346.0 kcal·mol–1, respectively. Notice that the stabilization energy values for LP(3)O1 to σ*(1)X–H, which were found in the transition states of 1–C3–H–OOH and 9–C4–H–OOH (54.3 and 49.8 kcal·mol–1, respectively (Table 5)), are not observed for the TSs of 1–O4′–H–OOH, 9–O7–H–OOH, and 9–O4′–H–OOH. In the 1–O4′–H–OOH, 9–O7–H–OOH, and 9–O4′–H–OOH TSs, the high stabilization energy is found for the donor LP(3)O1 and the acceptor LP*(1)H (X–H) at 114.1, 76.7, and 86.9 kcal·mol–1, respectively, and for the donor LP(3)O(O–H) and the acceptor LP*(1)H (O–H) at 118.3, 154.8, and 154.2 kcal·mol–1, respectively (Table 5). It is worth noticing that in the TSs of 1–C3–H–OOH and 9–C4–H–OOH, the significant atomic orbital density is oriented along the O1···H···X (X = C, O) transition vector while that was not observed in the TSs of 1–O4′–H–OOH, 9–O7–H–OOH, and 9–O4′–H–OOH (SOMO, Figure 3). Instead, the atomic orbital densities of 1–O4′–H–OOH, 9–O7–H–OOH, and 9–O4′–H–OOH TSs are distributed on both sides of the transition vector and are close to being planar. These results also again support for the HAT mechanism of the radical scavenging of the X–H bonds.32,33
Table 5. Natural Bond Analysis of Transition States of the Reactions at the B3LYP/6-311G(d,p) Level of Theory.
| reactions | donor NBO (i) | acceptor NBO (j) | E(2) (kcal·mol–1) |
|---|---|---|---|
| 1–C3–H + HOO· | LP(3)O1 | σ*(1)C3–H | 54.3 |
| LP*(1)(C3) | LP*(1)(H) | 324.1 | |
| LP(1,2,3)(O1) | LP*(1)(H) | 160.6 | |
| 1–O4′–H + HOO· | LP(3)O1 | LP*(1)H | 114.1 |
| LP(3)O4′ | LP*(1)H | 118.3 | |
| 9–C4–H + HOO· | LP(3)O1 | σ*(1)C4–H | 49.8 |
| LP*(1)(C4) | LP*(1)(H) | 346.0 | |
| LP(1,2,3)(O1) | LP*(1)(H) | 152.0 | |
| 9–O7–H + HOO· | LP(3)O1 | LP*(1)H | 76.7 |
| LP(3)O7 | LP*(1)H | 154.8 | |
| 9–O4′–H + HOO· | LP(3)O1 | LP*(1)H | 86.9 |
| LP(3)O4′ | LP*(1)H | 154.2 |
Figure 3.
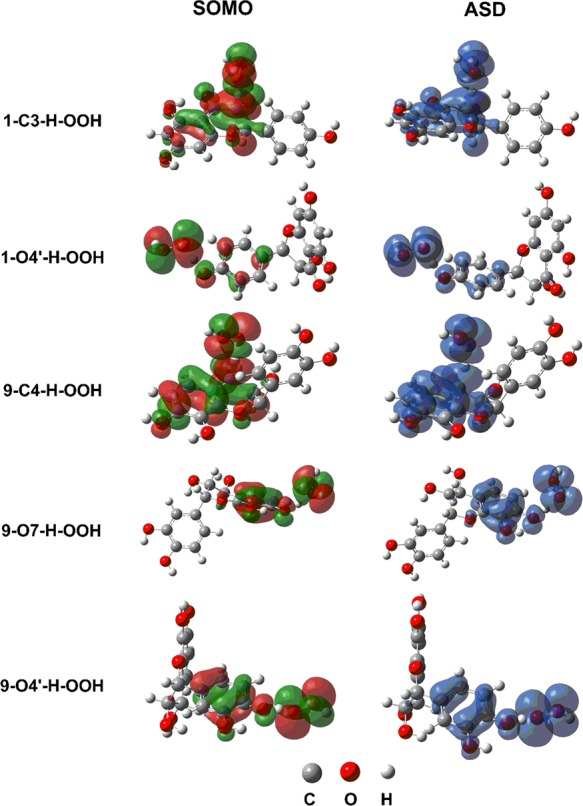
SOMO density surface and ASD of the transition states of the reactions.
It should be noted that in aqueous solutions, phenolic compounds are involved in acid–base equilibria. The anionic species have been implicated before in radical scavenging activity, and they may have higher activities than the neutral species.25 Therefore, the results shown here may underestimate the activity of some of the compounds, further emphasizing the high potential of flavonoids as therapeutic antioxidants.
3. Conclusions
The antioxidant activity of 13 natural phenolic compounds of the flavonoid family was evaluated by using the (RO)B3LYP/6-311++G(2df,2p)//B3LYP/6-311G(d,p) model chemistry in the gas phase and two typical solvents: water and ethanol. It was found that the C–H bonds (C3–H of the flavonoid backbone structures) play a fundamental role in antioxidant properties of flavonoids containing 4-carbonyl and/or 3-hydroxyl groups. These groups release the single electron on the C3 radical (the C3–H bond) into the O–C3–C4–O system and form intermolecular bonds to stabilize the radicals, yielding reduced BDE(C3–H) and increased antioxidant activity of the flavonoids. Among the studied compounds, keto-teracacidin 4, isomelacacidin 9, isoteracacidin 10, melacacidin 11, and teracacidin 13 were theoretically evaluated for antioxidant activity for the first time. The results show that these compounds may have antioxidant properties as high as typical phenolic compounds such as quercetin, trans-resveratrol, trolox, and ascorbic acid, particularly in isomelacacidin 9. The analysis of PES and kinetics on the reactions of the lowest BDE(X–H) (X = C, O) compounds with the typical HOO· radical shows that the HAT mechanism is the main pathway for antioxidant activity of the flavonoids, with the rate constants in the gas phase are in the range of 7.23 × 103–2.07 × 109 L·mol–1·s–1.
4. Computational Methods
The thermochemical properties of the compounds were obtained following methodologies well established in the literature16,34 by using the Gaussian 09 suite of programs.35 All of the compounds and related radicals, cationic radicals, anions, transition states, intermediates, and products were optimized, and their vibrational frequencies were determined at the B3LYP/6-311G(d,p) level of theory.31,34 The single point electronic energies were then calculated by the ROB3LYP/6-311++G(2df,2p) method.9,36 The lowest electronic energy conformer that contains possible intermolecular hydrogen bonds were used for further analysis.16,37−39 The integral equation formalism of the polarizable continuum model (IEF-PCM) was used to treat implicitly the solvents at the same level of theory as in the gas phase.40,41 The antioxidant mechanisms were investigated following the previously described methods.9,16,19 The reaction enthalpies of the individual steps in the above described mechanisms of antioxidant activity in the gas phase (at 298.15 K and 1 atm) were also calculated according to the literature.19,42,43
In the gas phase, the enthalpy of the hydrogen atom was −0.5 hartree and for other environments, the enthalpy of the hydrogen atom was calculated by the same method. The (calculated) enthalpies of the electron (e–) and proton (H+) were taken from the literature.19,44−46 Vibrational frequencies obtained at the B3LYP/6-311G(d,p) level were scaled by a factor of 0.9669.47,48
The rate constant (k) was calculated in the gas phase by using the conventional transition state theory (TST) as49−51
where kB and h are the Boltzmann and Planck constants, respectively, —G≠ is the Gibbs free energy of activation of the studied reaction, σ is the reaction symmetry number that represents reaction path degeneracy, the number of possible difference but equivalent reaction pathways, and κ accounts for tunneling corrections that were calculated using the Eckart barrier.52 Kinetics were calculated at the B3LYP/6-311G(d,p) level using the Eyringpy program.25,53,54
Atom-in-molecule (AIM) analysis55 was performed at the B3LYP/6-311G(d,p) level by using AIM2000 software.56
Acknowledgments
The research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 104.06-2018.308.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.9b00677.
BDE and PA values for X–H bonds, the reaction thermal properties, the Cartesian coordinates, and the optimized geometries of the radicals and transition states of all of the studied flavonoids (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Wang Y.; Chen S.; Yu O. Metabolic engineering of flavonoids in plants and microorganisms. Appl. Microbiol. Biotechnol. 2011, 91, 949. 10.1007/s00253-011-3449-2. [DOI] [PubMed] [Google Scholar]
- Wang T.-y.; Li Q.; Bi K.-s. Bioactive flavonoids in medicinal plants: Structure, activity and biological fate. Asian J. Pharm. Sci. 2018, 13, 12–23. 10.1016/j.ajps.2017.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heim K. E.; Tagliaferro A. R.; Bobilya D. J. Flavonoid antioxidants: chemistry, metabolism and structure-activity relationships. J. Nutr. Biochem. 2002, 13, 572–584. 10.1016/S0955-2863(02)00208-5. [DOI] [PubMed] [Google Scholar]
- Harborne J. B.; Williams C. A. Advances in flavonoid research since 1992. Phytochemistry 2000, 55, 481–504. 10.1016/S0031-9422(00)00235-1. [DOI] [PubMed] [Google Scholar]
- Willför S. M.; Ahotupa M. O.; Hemming J. E.; Reunanen M. H.; Eklund P. C.; Sjöholm R. E.; Eckerman C. S.; Pohjamo S. P.; Holmbom B. R. Antioxidant activity of knotwood extractives and phenolic compounds of selected tree species. J. Agric. Food Chem. 2003, 51, 7600–7606. 10.1021/jf030445h. [DOI] [PubMed] [Google Scholar]
- Pietarinen S. P.; Willför S. M.; Ahotupa M. O.; Hemming J. E.; Holmbom B. R. Knotwood and bark extracts: strong antioxidants from waste materials. J. Wood Sci. 2006, 52, 436–444. 10.1007/s10086-005-0780-1. [DOI] [Google Scholar]
- Kyselka J.; Rabiej D.; Dragoun M.; Kreps F.; Burc̆ová Z.; Nĕmec̆ková I.; Smolová J.; Bjelková M.; Szydłowska-Czerniak A.; Schmidt S̆. Antioxidant and antimicrobial activity of linseed lignans and phenolic acids. Eur. Food Res. Technol. 2017, 243, 1633–1644. 10.1007/s00217-017-2871-9. [DOI] [Google Scholar]
- Cai Y.-Z.; Sun M.; Xing J.; Luo Q.; Corke H. Structure–radical scavenging activity relationships of phenolic compounds from traditional Chinese medicinal plants. Life Sci. 2006, 78, 2872–2888. 10.1016/j.lfs.2005.11.004. [DOI] [PubMed] [Google Scholar]
- Wright J. S.; Johnson E. R.; DiLabio G. A. Predicting the activity of phenolic antioxidants: theoretical method, analysis of substituent effects, and application to major families of antioxidants. J. Am. Chem. Soc. 2001, 123, 1173–1183. 10.1021/ja002455u. [DOI] [PubMed] [Google Scholar]
- Janeiro P.; Brett A. M. O. Catechin electrochemical oxidation mechanisms. Anal. Chim. Acta 2004, 518, 109–115. 10.1016/j.aca.2004.05.038. [DOI] [Google Scholar]
- Nakanishi I.; Miyazaki K.; Shimada T.; Ohkubo K.; Urano S.; Ikota N.; Ozawa T.; Fukuzumi S.; Fukuhara K. Effects of metal ions distinguishing between one-step hydrogen-and electron-transfer mechanisms for the radical-scavenging reaction of (+)-catechin. J. Phys. Chem. A 2002, 106, 11123–11126. 10.1021/jp026190c. [DOI] [Google Scholar]
- Mahmoud M. A. A.; Chedea V. S.; Detsi A.; Kefalas P. Ascorbic acid modifies the free radical scavenging behaviour of catechin: An insight into the mechanism. Food Res. Inter. 2013, 51, 907–913. 10.1016/j.foodres.2013.02.023. [DOI] [Google Scholar]
- Amić D.; Luc̆ić B. Reliability of bond dissociation enthalpy calculated by the PM6 method and experimental TEAC values in antiradical QSAR of flavonoids. Bioorganic Med. Chem. 2010, 18, 28–35. 10.1016/j.bmc.2009.11.015. [DOI] [PubMed] [Google Scholar]
- Rice-Evans C. A.; Miller N. J.; Paganga G. Structure-antioxidant activity relationships of flavonoids and phenolic acids. Free Radical Biol. Med. 1996, 20, 933–956. 10.1016/0891-5849(95)02227-9. [DOI] [PubMed] [Google Scholar]
- Amić D.; Davidović-Amić D.; Bes̆lo D.; Trinajstić N. Structure-radical scavenging activity relationships of flavonoids. Croat. Chem. Acta 2006, 76, 55–61. 10.1016/j.phytochem.2006.07.002. [DOI] [Google Scholar]
- Vo Q. V.; Nam P. C.; Bay M. V.; Thong N. M.; Cuong N. D.; Mechler A. Density functional theory study of the role of benzylic hydrogen atoms in the antioxidant properties of lignans. Sci. Rep. 2018, 8, 12361. 10.1038/s41598-018-30860-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prior R. L.; Wu X.; Schaich K. Standardized methods for the determination of antioxidant capacity and phenolics in foods and dietary supplements. J. Agric. Food Chem. 2005, 53, 4290–4302. 10.1021/jf0502698. [DOI] [PubMed] [Google Scholar]
- Galano A.; Mazzone G.; Alvarez-Diduk R.; Marino T.; Alvarez-Idaboy J. R.; Russo N. Food antioxidants: chemical insights at the molecular level. Annu. Rev. Food Sci. Technol. 2016, 7, 335–352. 10.1146/annurev-food-041715-033206. [DOI] [PubMed] [Google Scholar]
- Rimarc̆ík J.; Lukes̆ V.; Klein E.; Ilc̆in M. Study of the solvent effect on the enthalpies of homolytic and heterolytic N–H bond cleavage in p-phenylenediamine and tetracyano-p-phenylenediamine. J. Mol. Struct.: THEOCHEM 2010, 952, 25–30. 10.1016/j.theochem.2010.04.002. [DOI] [Google Scholar]
- Lu L.; Qiang M.; Li F.; Zhang H.; Zhang S. Theoretical investigation on the antioxidative activity of anthocyanidins: A DFT/B3LYP study. Dyes Pigm. 2014, 103, 175–182. 10.1016/j.dyepig.2013.12.015. [DOI] [Google Scholar]
- Jabeen H.; Saleemi S.; Razzaq H.; Yaqub A.; Shakoor S.; Qureshi R. Investigating the scavenging of reactive oxygen species by antioxidants via theoretical and experimental methods. J. Photochem. Photobiol., B 2018, 180, 268–275. 10.1016/j.jphotobiol.2018.02.006. [DOI] [PubMed] [Google Scholar]
- Willfor S.; Eklund P.; Sjoholm R.; Reunanen M.; Sillanpaa R.; von Schoultz S.; Hemming J.; Nisula L.; Holmbom B. Bioactive phenolic substances in industrially important tree species. Part 4: Identification of two new 7-hydroxy divanillyl butyrolactol lignans in some spruce, fir, and pine species. Holzforschung 2005, 59, 413–417. 10.1515/HF.2005.067. [DOI] [Google Scholar]
- Nakanishi I.; Kawashima T.; Ohkubo K.; Kanazawa H.; Inami K.; Mochizuki M.; Fukuhara K.; Okuda H.; Ozawa T.; Itoh S.; Fukuzumi S.; Ikota N. Electron-transfer mechanism in radical-scavenging reactions by a vitamin E model in a protic medium. Org. Biomol. Chem. 2005, 3, 626–629. 10.1039/b416572a. [DOI] [PubMed] [Google Scholar]
- Markovic̆ Z.; Amic̆ D.; Milenkovic̆ D.; Dimitrić-Marković J. M.; Marković S. Examination of the chemical behavior of the quercetin radical cation towards some bases. Phys. Chem. Chem. Phys. 2013, 15, 7370–7378. 10.1039/c3cp44605k. [DOI] [PubMed] [Google Scholar]
- Galano A.; Alvarez-Idaboy J. R. A computational methodology for accurate predictions of rate constants in solution: Application to the assessment of primary antioxidant activity. J. Comput. Chem. 2013, 34, 2430–2445. 10.1002/jcc.23409. [DOI] [PubMed] [Google Scholar]
- Alberto M. E.; Russo N.; Grand A.; Galano A. A physicochemical examination of the free radical scavenging activity of Trolox: mechanism, kinetics and influence of the environment. Phys. Chem. Chem. Phys. 2013, 15, 4642–4650. 10.1039/c3cp43319f. [DOI] [PubMed] [Google Scholar]
- Litwinienko G.; Ingold K. U. Abnormal solvent effects on hydrogen atom abstractions. 1. The reactions of phenols with 2, 2-diphenyl-1-picrylhydrazyl (dpph•) in alcohols. J. Org. Chem. 2003, 68, 3433–3438. 10.1021/jo026917t. [DOI] [PubMed] [Google Scholar]
- Collins F. C.; Kimball G. E. Diffusion-controlled reaction rates. J. Colloid Sci. 1949, 4, 425–437. 10.1016/0095-8522(49)90023-9. [DOI] [Google Scholar]
- Smoluchowski M. V. Mathematical theory of the kinetics of the coagulation of colloidal solutions. Z. Phys. Chem 1917, 92, 129–168. [Google Scholar]
- Ngo T. C.; Thi Hau N.; Dao D. Q. Radical Scavenging Activity of Natural-based Cassaine Diterpenoid Amides and Amines. J. Chem. Inf. Model. 2018, 59, 766. 10.1021/acs.jcim.8b00847. [DOI] [PubMed] [Google Scholar]
- Ngo T. C.; Dao D. Q.; Nguyen M. T.; Nam P. C. A DFT analysis on the radical scavenging activity of oxygenated terpenoids present in the extract of the buds of Cleistocalyx operculatus. RSC Adv. 2017, 7, 39686–39698. 10.1039/C7RA04798C. [DOI] [Google Scholar]
- Mayer J. M.; Hrovat D. A.; Thomas J. L.; Borden W. T. Proton-coupled electron transfer versus hydrogen atom transfer in benzyl/toluene, methoxyl/methanol, and phenoxyl/phenol self-exchange reactions. J. Am. Chem. Soc. 2002, 124, 11142–11147. 10.1021/ja012732c. [DOI] [PubMed] [Google Scholar]
- Sirjoosingh A.; Hammes-Schiffer S. Proton-coupled electron transfer versus hydrogen atom transfer: generation of charge-localized diabatic states. J. Phys. Chem. A 2011, 115, 2367–2377. 10.1021/jp111210c. [DOI] [PubMed] [Google Scholar]
- Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; Nakatsuji H.; Caricato M.; Li X.; Hratchian H. P.; Izmaylov A. F.; Bloino J.; Zheng G.; Sonnenberg J. L.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Montgomery J. A. Jr; Peralta J. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Rega N.; Millam J. M.; Klene M.; Knox J. E.; Cross J. B.; Bakken V.; Adamo C.; Jaramillo J.; Gomperts R.; Stratmann R. E.; Yazyev O.; Austin A. J.; Cammi R.; Pomelli C.; Ochterski J. W.; Martin R. L.; Morokuma K.; Zakrzewski V. G.; Voth G. A.; Salvador P.; Dannenberg J. J.; Dapprich S.; Daniels A. D.; Farkas Ö.; Foresman J. B., Ortiz J. V.; Cioslowski J.; Fox D. J.. Gaussian 09; Gaussian, Inc.: Wallingford, CT, 2009. [Google Scholar]
- Nam P.-C.; Nguyen M. T.; Chandra A. K. The C– H and α (C– X) Bond Dissociation Enthalpies of Toluene, C6H5-CH2X (X= F, Cl), and Their Substituted Derivatives: A DFT Study. J. Phys. Chem. A 2005, 109, 10342–10347. 10.1021/jp0534030. [DOI] [PubMed] [Google Scholar]
- Baschieri A.; Pulvirenti L.; Muccilli V.; Amorati R.; Tringali C. Chain-breaking antioxidant activity of hydroxylated and methoxylated magnolol derivatives: the role of H-bonds. Org. Biomol. Chem. 2017, 15, 6177–6184. 10.1039/C7OB01195D. [DOI] [PubMed] [Google Scholar]
- Thavasi V.; Leong L. P.; Bettens R. P. A. Investigation of the influence of hydroxy groups on the radical scavenging ability of polyphenols. J. Phys. Chem. A 2006, 110, 4918–4923. 10.1021/jp057315r. [DOI] [PubMed] [Google Scholar]
- Lucarini M.; Pedulli G. F.; Guerra M. A Critical Evaluation of the Factors Determining the Effect of Intramolecular Hydrogen Bonding on the O-H Bond Dissociation Enthalpy of Catechol and of Flavonoid Antioxidants. Chem. – Eur. J. 2004, 10, 933–939. 10.1002/chem.200305311. [DOI] [PubMed] [Google Scholar]
- Cancès E.; Mennucci B.; Tomasi J. A new integral equation formalism for the polarizable continuum model: Theoretical background and applications to isotropic and anisotropic dielectrics. J. Chem. Phys. 1997, 107, 3032–3041. 10.1063/1.474659. [DOI] [Google Scholar]
- Tomasi J.; Mennucci B.; Cancès E. The IEF version of the PCM solvation method: an overview of a new method addressed to study molecular solutes at the QM ab initio level. J. Mol. Struct.: THEOCHEM 1999, 464, 211–226. 10.1016/S0166-1280(98)00553-3. [DOI] [Google Scholar]
- Thong N. M.; Duong T.; Pham L. T.; Nam P. C. Theoretical investigation on the bond dissociation enthalpies of phenolic compounds extracted from Artocarpus altilis using ONIOM (ROB3LYP/6-311++ G (2df, 2p): PM6) method. Chem. Phys. Lett. 2014, 613, 139–145. 10.1016/j.cplett.2014.08.067. [DOI] [Google Scholar]
- Thong N. M.; Quang D. T.; Bui N. H. T.; Dao D. Q.; Nam P. C. Antioxidant properties of xanthones extracted from the pericarp of Garcinia mangostana (Mangosteen): a theoretical study. Chem. Phys. Lett. 2015, 625, 30–35. 10.1016/j.cplett.2015.02.033. [DOI] [Google Scholar]
- Bartmess J. E. Thermodynamics of the electron and the proton. J. Phys. Chem. 1994, 98, 6420–6424. 10.1021/j100076a029. [DOI] [Google Scholar]
- Urbaniak A.; Szeląg M.; Molski M. Theoretical investigation of stereochemistry and solvent influence on antioxidant activity of ferulic acid. Comput. Theor. Chem. 2013, 1012, 33–40. 10.1016/j.comptc.2013.02.018. [DOI] [Google Scholar]
- Donald W. A.; Demireva M.; Leib R. D.; Aiken M. J.; Williams E. R. Electron Hydration and Ion– Electron Pairs in Water Clusters Containing Trivalent Metal Ions. J. Am. Chem. Soc. 2010, 132, 4633–4640. 10.1021/ja9079385. [DOI] [PubMed] [Google Scholar]
- Irikura K. K.; Johnson R. D.; Kacker R. N. Uncertainties in scaling factors for ab initio vibrational frequencies. J. Phys. Chem. A 2005, 109, 8430–8437. 10.1021/jp052793n. [DOI] [PubMed] [Google Scholar]
- Alecu I. M.; Zheng J.; Zhao Y.; Truhlar D. G. Computational thermochemistry: scale factor databases and scale factors for vibrational frequencies obtained from electronic model chemistries. J. Chem. Theory Comput. 2010, 6, 2872–2887. 10.1021/ct100326h. [DOI] [PubMed] [Google Scholar]
- Evans M. G.; Polanyi M. Some applications of the transition state method to the calculation of reaction velocities, especially in solution. Trans. Faraday Soc. 1935, 31, 875–894. 10.1039/tf9353100875. [DOI] [Google Scholar]
- Eyring H. The activated complex in chemical reactions. J. Chem. Phys. 1935, 3, 107–115. 10.1063/1.1749604. [DOI] [Google Scholar]
- Truhlar D. G.; Hase W. L.; Hynes J. T. Current status of transition-state theory. J. Phys. Chem. 1983, 87, 2664–2682. 10.1021/j100238a003. [DOI] [Google Scholar]
- Eckart C. The penetration of a potential barrier by electrons. Phys. Rev. 1930, 35, 1303–1309. 10.1103/PhysRev.35.1303. [DOI] [Google Scholar]
- Dzib E.; Cabellos J. L.; Ortíz-Chi F.; Pan S.; Galano A.; Merino G. Eyringpy: A program for computing rate constants in the gas phase and in solution. Int. J. Quantum Chem. 2018, 119, e25686 10.1002/qua.25686. [DOI] [Google Scholar]
- Dzib E.; Cabellos J. L.; Ortiz-Chi F.; Pan S.; Galano A.; Merino G.. Eyringpy 1.0.2; Cinvestav Mérida: Yucatán, Mexico, 2018.
- Bader R. F. W. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. 10.1021/cr00005a013. [DOI] [Google Scholar]
- Biegler-König F.AIM 2000; University of Applied Sciences: Bielefeld, Germany, 2000. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.