Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2019 Jun 4;4(6):9769–9777. doi: 10.1021/acsomega.9b01276

MS-CASPT2 Studies on the Photophysics of Selenium-Substituted Guanine Nucleobase

Ye-Guang Fang 1, Qin Peng 1, Qiu Fang 1,*, Weihai Fang 1, Ganglong Cui 1,*
PMCID: PMC6649137  PMID: 31460068

Abstract

graphic file with name ao-2019-012765_0011.jpg

The MS-CASPT2 method has been employed to optimize minimum-energy structures of 6-selenoguanine (6SeGua) and related two- and three-state intersection structures in and between the lowest five electronic states, i.e., S2(1ππ*), S1(1nπ*), T2(3nπ*), T1(3ππ*), and S0. In combination with MS-CASPT2 calculated linearly interpolated internal coordinate paths, the photophysical mechanism of 6SeGua has been proposed. The initially populated S2(1ππ*) state decays to either S1(1nπ*) or T2(3nπ*) states through a three-state S2/S1/T2 intersection point. The large S2/T2 spin–orbit coupling of 435 cm–1, according to the classical El-Sayed rule, benefits the S2 → T2 intersystem crossing process. The S1(1nπ*) state that stems from the S2 → S1 internal conversion process at the S2/S1/T2 intersection point can further jump to the T2(3nπ*) state through the S1 → T2 intersystem crossing process. This process does not comply with the El-Sayed rule, but it is still related to a comparatively large spin–orbit coupling of 39 cm–1 and is expected to occur relatively fast. Finally, the T2(3nπ*) state, which is populated from the above S2 → T2 and S1 → T2 intersystem crossing processes, decays to the T1(3ππ*) state via an internal conversion process. Because there is merely a small energy barrier of 0.11 eV separating the T1(3ππ*) minimum and an energetically allowed two-state T1/S0 intersection point, the T1(3ππ*) state still can decay to the S0 state quickly, which is also enhanced by a large T1/S0 spin–orbit coupling of 252 cm–1. Our proposed mechanism explains experimentally observed ultrafast intersystem crossing processes in 6SeGua and its 835-fold acceleration of the T1 state decay to the S0 state compared with 6tGua. Finally, we have found that the ground-state electronic structure of 6SeGua has more apparent multireference character.

Introduction

Nucleobases are the basic chromophores in deoxyribonucleic acid (DNA) and ribonucleic acid (RNA). They have important properties shared by all these nucleobases, namely their photostability when interaction with ultraviolet light, which prevents photodamages.1,2 Time-resolved experiments and high-level theoretical studies have shown that nucleobases in the gas phase and in solution adopt similar ultrafast radiationless decay processes via energetically efficient conical intersections, which finally deactivate nucleobases from their initially populated excited singlet to ground states before harmful photoreactions take place.3−19

In stark contrast, thio-substituted nucleobases have distinctly different photophysics. A simple O-to-S substitution in these natural nucleobases largely suppresses internal conversion to the ground state and instead allows efficient intersystem crossing to the lowest triplet state.20−30 This is qualitatively different from excited-state behaviors of natural nucleobases in which internal conversion to the ground state is a predominant deactivation channel that protects them from harmful photodamages. To rationalize these intriguing photophysical phenomena and figure out the underlying physical origins, a lot of high-level electronic structure calculations and nonadiabatic dynamics simulations have been carried out in the past several years, and several efficient intersystem crossing channels have been proposed to explain such ultrahigh quantum yields for the formation of triplet states in experiments.31−40

In addition to natural and thio-substituted nucleobases, experimental scientists have recently focused on seleno-substituted nucleobases due to their potential applications as photosensitizers in photodynamic therapy.41−44 Recently, Farrell and co-workers have used time-resolved absorption spectroscopies to explore the excited-state relaxation dynamics of 6-selenoguanine (6SeGua).45 Compared with its thio-substituted analogue, selenium substitution remarkably enhances relevant intersystem crossing rates to and from triplet manifolds and meanwhile leads to a short-lived triplet state. Given the similarities between theoretical and experimental results for 6SeGua and 6tGua, they suggest that the initially populated S2(1ππ*) state will first convert to the dark S1(1nπ*) state, which is followed by intersystem crossing to the T2(3nπ*) and/or T1(3ππ*) state. Furthermore, the triplet state deactivation has been suggested to increase by 835-fold in comparison with that of 6-thioguanine (6tGua). Farrell et al. have ascribed this acceleration of 1.7 vs 1420 ns, in addition to the stronger T1/S0 spin–orbit coupling in 6SeGua, to a smaller energy barrier to access the T1(1ππ*) potential energy region where the T1 → S0 intersystem crossing process takes place. As a consequence, the short triplet-state lifetime of 6SeGua makes it less efficient to sensitize molecular oxygen to generate singlet oxygen than 6tGua. To shed light on the clear and detailed photophysical mechanism of 6SeGua behind these spectroscopic phenomena, a highly accurate electronic structure calculations are useful.

Computationally, to the best of our knowledge, local spectroscopic and excited-state properties of selenium-substituted thymidine and deoxyguanosine have been studied with density functional theory (DFT) and time-dependent (TD)-DFT methods.46−48 For selenium-substituted deoxyguanosine, possible excited-state relaxation pathways have been proposed based on TD-DFT optimized excited-state minima and related energies.48 Nonetheless, besides these excited-state geometries and energies, it is also necessary to investigate their accessibility from the initially populated singlet states. In addition, intersection structures and energies among involved excited states are also very important and not explored before. The determination of quasi-degenerate structures could not be accurate enough with single-reference methods and thus calls for multiconfigurational electronic structure methods. Taken together, we have, in this work, employed a highly accurate MS-CASPT2 method to optimize equilibrium geometries in the lowest five electronic states, i.e., S0, S2(1ππ*), S1(1nπ*), T2(3nπ*), and T1(1ππ*), and to calculate linear interpolation internal coordinate (LIIC) paths connecting these minima and crossing points. On the basis of the present results, a possible excited-state relaxation mechanism is proposed to explain recent experimental studies.

Results and Discussion

Local Spectroscopic Properties

Figure 1 shows the MS-CASPT2-optimized minimum-energy structure in the S0 state. It is clear that the structure is totally planar and the C2=Se1 bond length is calculated to be 1.821 Å, much longer than the typical C=O and C=S double bonds but a little shorter than 1.839 Å predicted by the DFT method for selenium-substituted deoxyguanosine. Our MS-CASPT2 predicted C9–N10 bond length, 1.322 Å, is longer than 1.310 Å estimated by the DFT method. Interestingly, the S0 state has a very remarkable multireference character in that electronic structure analysis at the MS-CASPT2 level shows that in addition to the closed-shell electronic configuration, i.e., 2222220000 with 0.77 weight, there is a comparable open-shell electronic configuration, i.e., 22222ud000 with 0.11 weight. This multireference ground-state property also makes its C7–C11 bond length much longer than those predicted for natural Gua and 6tGua by the CASPT2 method (1.410 Å vs 1.369 Å vs 1.367 Å).11,31

Figure 1.

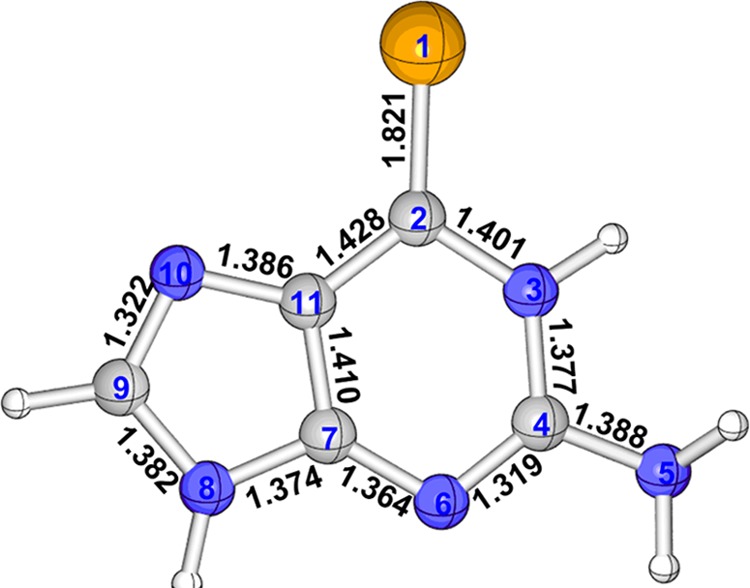
Figure 1

Open in a new tab

MS-CASPT2-optimized ground-state equilibrium structure of 6SeGua. Also shown are selected bond lengths (in Å) and atomic numbering.

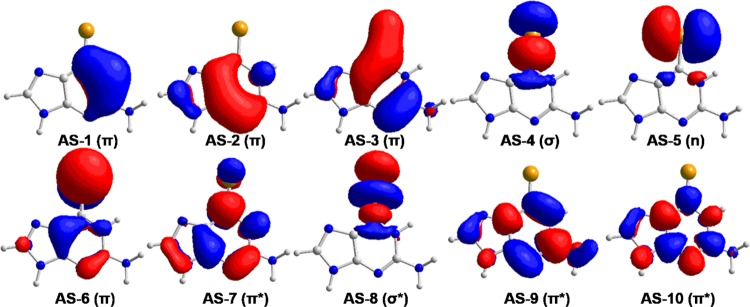
Vertical excitation energies and associated electronic structures at the Franck–Condon point are very important for us to understand the excited-state relaxation mechanism and we have thus explored these local spectroscopic properties at the above MS-CASPT2-optimized S0 minimum. At this Franck–Condon point, the spectroscopically “bright” electronically excited singlet state is the second excited singlet state, i.e., S2 (oscillator strength: ca. 0.24). The electronic configuration that is mainly responsible for this S0 → S2 electronic transition corresponds to an electron excited from AS-6 to AS-7 (i.e., 22222ud000; weight: 0.628). The AS-6 and AS-7 orbitals are of π character. The former one has a large contribution from the C2–Se1 moiety; in contrast, the latter is more delocalized than AS-6 (see Figure 2). Its vertical excitation energy is calculated to be 3.39 eV (366 nm), which is close to experimentally measured 3.47 eV (357 nm). Previous TD-B3LYP calculations predict 3.60 eV (341 nm).48 This good agreement demonstrates that our chosen electronic structure method is accurate enough for the description of excited states of our studied system.

Figure 2.

Figure 2

Open in a new tab

Molecular orbitals are used as the active space (AS-X) in all of the MS-CASPT2 calculations in this work. Also, shown are the character of these molecular orbitals.

There exists a spectroscopically “dark” excited singlet state that is lower than the above S2 state in energy. This S1 state is mainly caused by the electronic transition of an electron from AS-5 to AS-7 as shown in Figure 2 and thus is of 1nπ* character. Its vertical excitation energy is predicted to be 2.61 eV at the MS-CASPT2 level, 0.78 eV lower than the S2 state at the Franck–Condon point. However, the predicted TD-B3LYP calculations merely give 3.10 eV (400 nm), which is 0.49 eV higher than the MS-CASPT2 predicted one.48

Furthermore, there are two triplet states below both S2 and S1 states in energy, which are referred to as T1 and T2. The T1 and T2 states have similar electronic configurations to those of S2 and S1 (see Table 1) and therefore are of 3ππ* and 3nπ* characters, respectively. The vertical excitation energies of these two triplet states are calculated to be 2.40 and 2.56 eV, respectively, which are lower than the TD-B3LYP estimated to be 2.50 and 2.90 eV, respectively.48 It is meaningful to see that both T1 and T2 states are close to 2.61 eV of the S1 state, which is important for the excited-state relaxation among these three excited states.

Table 1. MS-CASPT2 Calculated Vertical Excitation Energies at the MS-CASPT2-Optimized S0 Minimum (in eV, nm) and Associated Electronic Characters and Main Electronic Configurations (2: Doubly Occupied Orbitals; u and d: Singly Occupied Orbitals in “up” and “down” Spins; 0: Empty Orbital).

state eV nm character main config.
S1 2.61 476 1nπ* 2222u2d000
S2 3.39 366 1ππ* 22222ud000
T1 2.40 517 3ππ* 22222uu000
T2 2.56 484 3nπ* 2222u2u000
Open in a new tab

Excited-State Minima

Figure 3 shows the MS-CASPT2-optimized minimum-energy structures in the lowest excited singlet and triplet states, i.e., S1, S2, T1, and T2. As discussed above, the S2 state is mainly caused by the electronic configuration from AS-6 to AS-7 as shown in Figure 2; it is thus natural to expect an elongation of the C2–Se1 bond because there is an antibonding character between the C2 and Se1 atoms in the AS-7 orbital involved in the electronic transition leading to the S0 → S2 electronic transition. This bond length is increased to 2.032 Å at the S2 minimum from 1.821 Å at the S0 minimum, which is a little longer than 1.999 Å predicted by the TD-B3LYP level. In addition, the C7–C11, N6–C7, and C4–N6 bond lengths have some changes from the S0 to S2 minima. Similarly, the C2-Se1 bond length is also elongated to 1.935 Å in the S1 minimum because the AS-7 orbital is also involved in the corresponding electronic transition (from AS-5 to AS-7 in Table 1). The TD-B3LYP method also gives a similar bond length of 1.917 Å for the C2–Se1. The other bond lengths, e.g., C2–N3 and N6–C7, are also increased to some extent. The T2 state is also caused by the electronic configuration from AS-5 to AS-7 and the T2 minimum is more or less similar to the S1 minimum. The C2–Se1 bond length is also increased to 1.951 Å at the T2 minimum (1.940 Å by TD-B3LYP) as well as its C2–N3 bond length. The T1 minimum is structurally different from the S2 one, although both share similar electronic transitions. The C2–Se1 bond length also becomes longer in the T1 minimum compared with that in the S0 state (1.944 Å vs 1.821 Å). In contrast, the TD-B3LYP method predicts a shorter C2–Se1 bond length of 1.851 Å at the T1 minimum. In addition, the C2–N3 bond length is also elongated in the T1 minimum, which is not so remarkable in the S2 minimum. To sum up, the main bond length changes in these S1, S2, T1, and T2 minima in comparison with the S0 minimum are related to the C2–Se1 bond, which is more than 0.12 Å, even 0.211 in the S2 minimum. By contrast, the others change less than 0.025 Å (see Figure 4).

Figure 3.

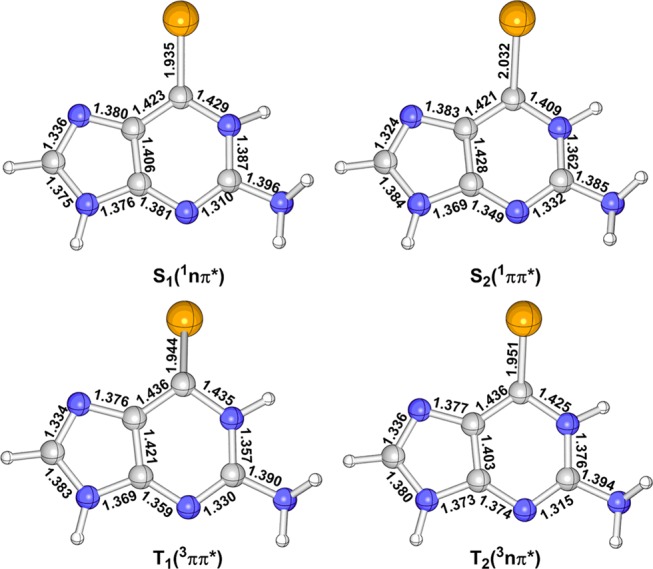
Figure 3

Open in a new tab

MS-CASPT2-optimized minimum-energy structure of 6SeGua in the S2 (1ππ*), S1 (1nπ*), T2 (3nπ*), and T1 (3ππ*) excited states. Also, shown are selected bond lengths (in Å).

Figure 4.

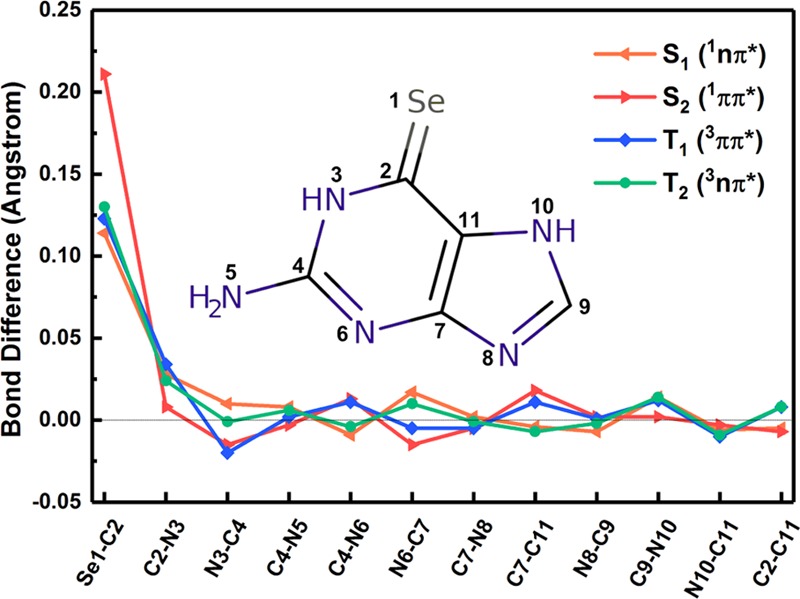
Figure 4

Open in a new tab

Corresponding bond-length variation (in Å) of the excited-state S2 (1ππ*), S1 (1nπ*), T2 (3nπ*), and T1 (3ππ*) minimum-energy structures relative to those of the S0 structure. Please see Figure 1 for the specific atomistic numbering.

On the energetical side, the MS-CASPT2 energies of the S1, S2, T1, and T2 minima relative to that of the S0 minimum, i.e., adiabatic excitation energies, are collected in Table 2. Their adiabatic excitation energies are calculated to be 2.46, 3.04 2.24, and 2.36 eV, respectively, which are lower than their vertical excitation energies, i.e., 2.61, 3.39, 2.40, and 2.56 eV at the same computational level (see Table 1). In comparison, previous TD-DFT method gives 2.90, 3.40, 2.40, 2.70 eV for S1, S2, T1, and T2, respectively.48

Table 2. Energies (in eV) of MS-CASPT2-Optimized Minima Relative to the S0 Minimum (see Figures 3–5).

S1 S2 T1 T2 S2/S1/T1 T2/T1/S0 T1/S0
2.46 3.04 2.24 2.36 3.23/3.21/3.21 3.27/3.17/3.11 2.35/2.22
Open in a new tab

Intersection Structures

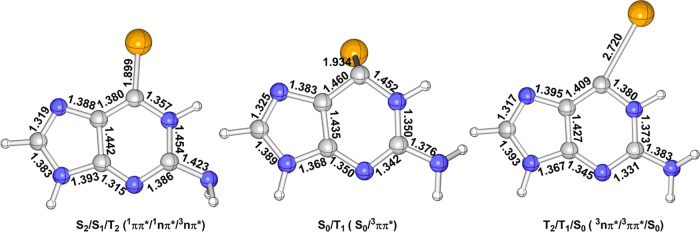
In addition to minima, three mechanistically relevant quasi-degenerate three- and two-state intersection structures have been identified at the MS-CASPT2 level and are referred to as S2/S1/T2, T2/T1/S0, and T1/S0 in Figure 5. It is worth to notify that these two three-state crossing points S2/S1/T2 and T2/T1/S0 are not obtained by direct three-state optimization. Instead, the two-state crossing points S2/S1 and T1/S0 are first optimized and additional single point calculations reveal that these two-state crossing points S2/S1 and T1/S0 are actually three-state crossing points. In S2/S1/T2, the C2–Se1 bond is also elongated compared with that in the S0 minimum, 1.899 Å vs 1.821 Å at the MS-CASPT2 level; however, it is a little shortened in comparison with those in the S1, S2, T1, and T2 minima (see Figures 3–5). Structurally, the most remarkable change of S2/S1/T1 in comparison with the S1, S2, T1, and T2 minima is related to the NH2 group attached to the C4 atom, which is overall perpendicular to the molecular plane (the minima are essentially planar, see Figure 3). The other bond lengths are also shown in the left panel of Figure 5. Energetically, at this three-state intersection structure, the S2, S1, and T2 states are highly degenerate in energy at the MS-CASPT2 level, whose energies are estimated to be 3.23, 3.21, and 3.21 eV, respectively. These energies are lower than the S2 energy at the Franck–Condon point, 3.39 eV. Therefore, this S2/S1/T2 intersection should play an important role in the excited-state relaxation mechanism starting from the initially populated S2 state (vide infra).

Figure 5.

Figure 5

Open in a new tab

MS-CASPT2 determined three- and two-state intersection structures, which are referred to as S2/S1/T2, T2/T1/S0, and T1/S0 (characters of involved electronic states are in parentheses).

Moreover, in T2/T1/S0, the C2–Se1 bond length is significantly elongated up to 2.720 Å, which is much longer than those in all of the minima and the S2/S1/T2 intersection structure. Different from S2/S1/T2, the NH2 group is not rotated visibly in T2/T1/S0 (see other bond lengths in the right panel of Figure 5). Energetically, this T2/T1/S0 intersection structure is estimated to be 3.27/3.17/3.11 eV at the MS-CASPT2 level, which is much higher than those related to their relevant excited-state minima, 2.36 and 2.24 eV. Since this T2/T1/S0 intersection structure has really high energies, the intersystem crossing channel through this T2/T1/S0 intersection structure to the S0 state could become inefficient from either T2 or T1 (see below).

We have also optimized another two-state T1/S0 intersection structure, which is overall different from the above two intersection structures. Its Se atom is already out of the molecular plane as shown in Figure 5. The C2–Se1 bond length is calculated to be 1.934 Å at the MS-CASPT2 level, which is much shorter than 2.720 Å that in T2/T1/S0. The other bond lengths are depicted in Figure 5. Importantly, this two-state T1/S0 intersection has much smaller adiabatic excitation energy compared with that of T2/T1/S0. The T1 and S0 states’ energies are calculated to be 2.35 and 2.22 eV at the MS-CASPT2 level (T2/T1/S0: 3.27/3.17/3.11 eV; see above), respectively. This comparison could imply that the two-state intersection could play a more vital role in the decay of the lowest T1 triplet state.

Excited-State Relaxation Paths

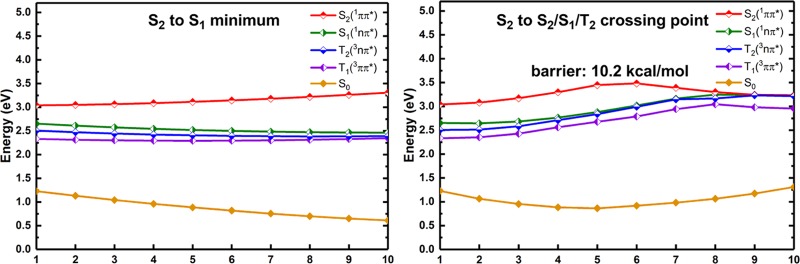
As mentioned in the preceding discussion, the S2 state is first populated at the Franck–Condon point with large probability due to its comparably larger oscillator strength. After this, the system will relax smoothly to its S2 minimum without crossing any other relevant electronic state as demonstrated by the MS-CASPT2 calculated linearly interpolated internal path (LIIC) as shown in Figure 6. At the S2 minimum, the S2 state is still a little far away from the other S1, T2, and T1 states as evidenced by the calculated LIIC path connecting both the S2 and S1 minima (see the left panel of Figure 7); thus, the vibronically assisted internal conversion and intersystem crossing processes to S1, T2, and T1 could be inefficient considering the comparable energy gaps among these excited states. Instead, because of the existence of an energetically approachable three-state S2/S1/T2 intersection structure, both internal conversion to S1 and intersystem crossing to T2 become efficient at this intersection point. Importantly, this three-state intersection structure is also energetically and structurally accessible. The right panel of Figure 7 shows the MS-CASPT2 calculated LIIC path connecting both the S2 minimum and the S2/S1/T2 intersection structure. There is a barrier of 0.44 eV, which is 0.09 eV higher than the S2 energy at the Franck–Condon point. Nonetheless, it should be stressed that the LIIC path is not a minimum-energy reaction path, and the estimated barrier therefrom is a top limit. At this three-state intersection, the internal conversion process to the S1 state takes place efficiently. The intersystem crossing process to the T2(3nπ*) state from the S2(1ππ*) state is also enhanced by the large S2/T2 spin–orbit coupling of 435 cm–1, which also complies with the classical El-Sayed rule.

Figure 6.

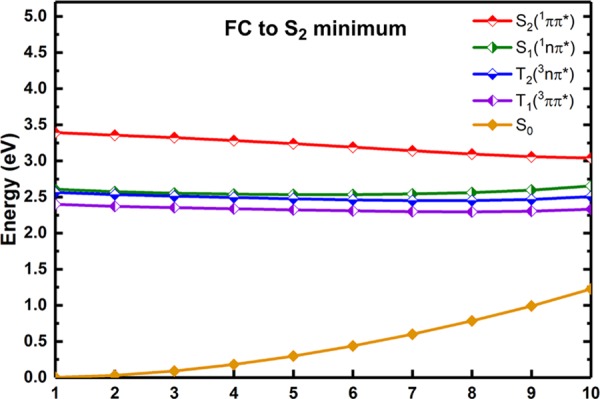
Figure 6

Open in a new tab

LIIC path connecting the Franck–Condon point, i.e., the S0 minimum and the S2 minimum calculated at the MS-CASPT2 level (in eV).

Figure 7.

Figure 7

Open in a new tab

MS-CASPT2 calculated LIIC paths connecting (left) the S2 and S1 minima; (right) the S2 minimum and the S2/S1/T2 three-state intersection structure (in eV).

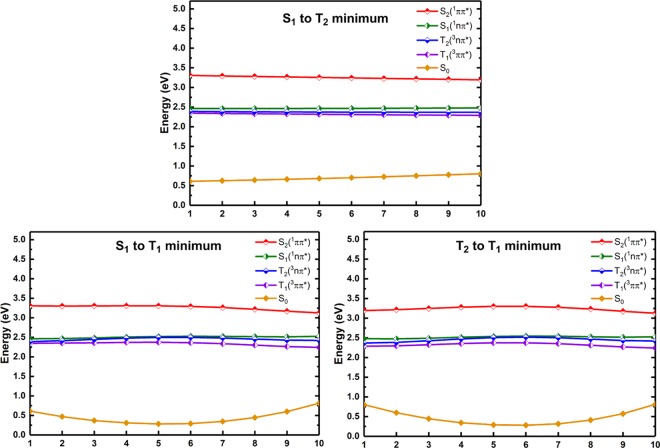
Once one of both S1 and T2 states are populated through both internal conversion and intersystem crossing processes via the above discussed S2/S1/T2 intersection structure, these two excited states will become highly quasi-degenerate with the T1 state in energy in an extended region. This viewpoint can be seconded by our MS-CASPT2 calculated LIIC paths, which separately connect the S1, T2, and T1 minima as shown in Figure 8. Therefore, there will exist two different relaxation paths that finally populate the lowest triplet state, i.e., T1. In the first one, the S1(1nπ*) state that is from the S2 state via the S2/S1/T2 intersection will further hop to the T1(3ππ*) state through the more efficient intersystem crossing process than that to the T2(3nπ*) state (still because of the El-Sayed rule). The spin–orbit coupling is calculated at the MS-CASPT2 level to be 437 cm–1 for S1/T1 and 39 cm–1 for S1/T2. In the second one, the T2(3nπ*) state that is also generated from the S2/S1/T2 intersection will jump to the T1 state through the fast internal conversion process. In the third one, the S1(1nπ*) state is first decayed to the T2(3nπ*) state followed by the internal conversion to the T1(3ππ*) state, which should not be as efficient as the former two, however, because the intersystem crossing process from S1(1nπ*) to T2(3nπ*) is not favorable due to the classical El-Sayed rule.

Figure 8.

Figure 8

Open in a new tab

MS-CASPT2 calculated LIIC paths connecting (top) the S1 and T2 minima; (bottom-left) the S1 and T1 minima; (bottom-right) the T2 and T1 minima (in eV).

Finally, the T1 decay channel to the S0 state is also explored at the MS-CASPT2 level. Figure 9 depicts the calculated LIIC path connecting both the T1 minimum and the T2/T1/S0 intersection structure. It can be found that the latter demands a large energy change of more than 0.87 eV relative to the T1 minimum although there is a large T1/S0 spin–orbit coupling at the three-state T2/T1/S0 intersection structure (508 cm–1). Hence, the S0 state’s repopulation from the lowest T1 state via T2/T1/S0 should be unimportant. In comparison, the T1 state can more efficiently decay to the S0 state via the two-state T1/S0 intersection structure because this process only demands 0.11 eV in terms of the flat T1 potential energy surface as demonstrated by the LIIC path connecting the T1 minimum and the T1/S0 intersection structure. This radiationless process to the ground state is also accelerated by the large T1/S0 spin–orbit coupling at the two-state T1/S0 intersection structure (252 cm–1 at the MS-CASPT2 level). This is also consistent with recently observed 835-fold enhancement of the T1 decay of 6SeGua compared with that of 6tGua in experiments.

Figure 9.

Figure 9

Open in a new tab

MS-CASPT2 calculated LIIC paths connecting (left) the T1 minimum and the two-state T1/S0 intersection structure; (right) the T1 minimum and the three-state T2/T1/S0 intersection structure (in eV).

Correlation with Previous Works

Figure 10 shows our suggested photophysical mechanism of 6SeGua when its S2(1ππ*) state is populated in the Franck–Condon region. This initial excited singlet state, after the FC relaxation, will decay to either S1(1nπ*) or T2(3nπ*) states via the three-state intersection point S2/S1/T2. Both the internal conversion from the S2(1ππ*) to S1(1nπ*) state and the intersystem crossing from the S2(1ππ*) to T2(3nπ*) state should be efficient. The latter is also enhanced by its large S2/T2 spin–orbit coupling according to the classical El-Sayed rule (435 cm–1 at the MS-CASPT2 level). The resultant S1(1nπ*) state can further hop to either the T2(3nπ*) state or the T1(3ππ*) state via the second intersystem crossing process. In spite of the fact that the S1(1nπ*) → T1(3ππ*) intersystem crossing is more efficient than the S1(1nπ*) → T2(3nπ*) one due to the El-Sayed rule, the latter cannot be excluded due to its comparably large S1/T2 spin–orbit coupling of 39 cm–1, which still cannot compete with the latter, however (S1/T1: 437 cm–1). The T2 state that is populated from either the initial S2(1ππ*) state or the intermediate S1(1nπ*) state will further hop to the T1 state through the subsequent internal conversion process, which should be very fast concerning that both states are nearly quasi-degenerate in an extended region of involved potential energy surfaces. Finally, the generated T1 state can also decay to the ground state via the energetically allowed two-state T1/S0 intersection point, which is merely 0.11 eV higher than the T1 minimum. This process is also expedited by the large spin–orbit coupling (see above).

Figure 10.

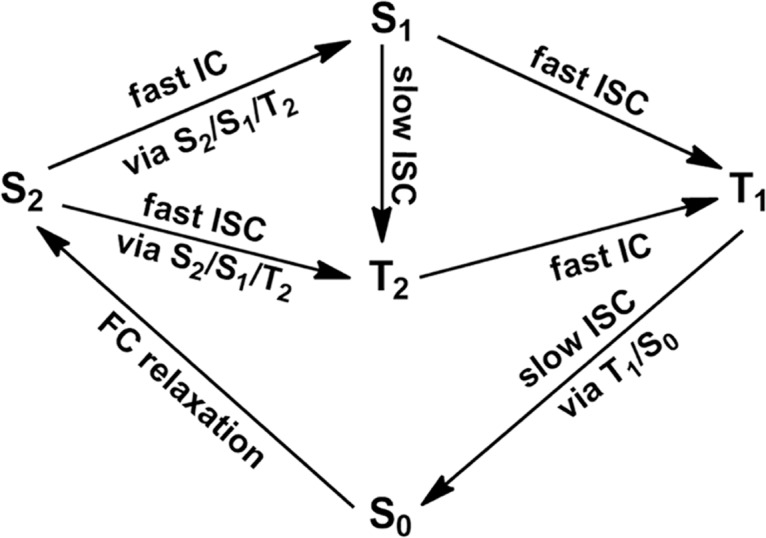
Figure 10

Open in a new tab

Suggested photophysical mechanism for 6SeGua based on our present MS-CASPT2 calculations.

Our suggested excited-state relaxation paths are qualitatively similar to that reported by Pirillo et al. predicted by the TD-DFT method.48 The S2(1ππ*) → S1(1nπ*) → T1(3ππ*) path should be the most favorable one, followed by the S2(1ππ*) → S1(1nπ*) → T2(3nπ*) → T1(3ππ*) path, as shown in Figure 10. However, our present work provides more accurate excited-state structures and energies because the TD-DFT method overestimates all adiabatic excitation energies for the involved S2(1ππ*), S1(1nπ*), T2(3nπ*), and T1(3ππ*) states, as discussed above (more than 0.43 eV for S1). This situation is also seen for the vertical excitation energies (see above, 2.61 eV at MS-CASPT2 vs 3.10 eV at TD-B3LYP to the S1(1nπ*) state). Moreover, the MS-CASPT2 optimization also gives a little different geometric parameter, for example, 1.944 Å at MS-CASPT2 vs 1.851 Å at TD-B3LYP for the C2–Se1 bond length of the T1(3ππ*) minimum. Finally, it should be stressed that previous works merely determined the stationary points in the ground- and excited-states but did not explore the accessibilities of these stationary points from the initially populated singlet state. In addition, intersection structures responsible for the radiationless transition between different potential energy surfaces were also not studied. In the present work, the accessibilities of the excited-state minima are all explored using the MS-CASPT2 calculated LIIC paths and the related three- and two-state intersection structures and their roles in the excited-state relaxation are scrutinized as well at the same computational level.

Experimentally, it is suggested that the 835-fold acceleration of the T1 decay to the S0 state in 6SeGua compared with that in 6tGua, 1.7 vs 1420 ns, is ascribed to a stronger spin–orbit coupling and a smaller energy barrier to the T1/S0 intersection region. In terms of the present and previous calculations, one can find that the energy barriers to the related T1/S0 intersection points are more or less close to each other, 0.11 eV in 6SeGua vs 0.16 eV in 6tGua.34 Therefore, we infer that the large difference of the T1 decay rates should primarily stem from the significantly increased T1/S0 spin–orbit coupling of 6SeGua relative to that of 6tGua.

Finally, we have found that the ground-state electronic structure of 6SeGua has a much obvious multireference character. MS-CASPT2 electronic structure analysis shows that the weight of the closed-shell electronic configuration, i.e., 2222220000 is only 0.77; in contrast, there is a comparable open-shell electronic configuration, i.e., 22222ud000 with 0.11 weight. This multireference ground-state property could make the C7–C11 bond length of 6SeGua much longer than those of natural Gua and 6tGua (1.410 Å vs 1.369 Å vs 1.367 Å). This peculiar electronic structure could be employed in certain applications.

Conclusions

We have employed the highly accurate MS-CASPT2 method to study the photophysical mechanism of 6-selenium-substituted guanine (6SeGua). The MS-CASPT2 calculated vertical excitation energies are consistent with experimentally measured adsorption peaks very well and show that the S2(1ππ*) singlet state is first populated in the Franck–Condon region. In comparison with the TD-DFT method, the MS-CASPT2 method provides more accurate structures and energies. In terms of our MS-CASPT2-optimized stationary and intersection points and computed LIIC paths, there exists two possible excited-state relaxation paths from the electronically excited S2(1ππ*) singlet state and they are the S2(1ππ*) → S1(1nπ*) → T1(3ππ*) and S2(1ππ*) → S1(1nπ*) → T2(3nπ*) → T1(3ππ*) paths, respectively. In addition, we suggest that the large difference of the T1 decay rates to the S0 state, 1.7 ns for 6SeGua vs 1420 ns for 6tGua in experiments, should primarily stem from the significantly increased T1/S0 spin–orbit coupling of 6SeGua in that the energy barriers to the related T1/S0 intersection points are more or less close to each other, 0.11 eV in 6SeGua vs 0.16 eV in 6tGua. Finally, we have found that the electronic structure of 6SeGua in the S0 state is of much obvious multireference character with significant contribution from the open-shell electronic configuration, which rationalizes its much longer C7–C11 bond length compared with those of natural Gua and 6tGua. This intriguing finding could be employed in certain applications. The present computational work also enriches our knowledge of the photophysics of seleno-substituted nucleobases and could motivate the following experimental studies on other nucleobase variants.

Computational Methods

Minima and intersection structural optimization are carried out directly using the multistate complete active space second-order perturbation approach (MS-CASPT2).49,50 Three and five roots are used in the MS-CASPT2 optimizations and single point energy refinements in which equal roots are used. All MS-CASPT2 calculations use an active space of 12 electrons in 10 orbitals, which includes 7 π and π* orbitals, 2 σ and σ* orbitals, and 1 n orbital of the selenium atom. The ionization potential-electron affinity (IPEA) is set to zero51 because our tests show that such setting gives better agreement with experiments for the vertical excitation energy of the S2 state (3.39 vs exp. 3.47 eV). This has been noticed by González and co-workers in their recent work.52 An imaginary shift value of 0.2 is employed to avoid the intruder-state issue;53 the Cholesky decomposition approach with on-the-fly unbiased auxiliary basis sets is used to deal with two-electron integrals.54 The cc-pVDZ and cc-pVTZ basis sets are used for geometry optimizations and energy refinements on the C, N, and H atoms; whereas for selenium atom, aug-cc-pVDZ and aug-cc-pVTZ basis sets are employed for geometry optimizations and single point calculations, respectively.55 Spin–orbit coupling calculations use the same basis sets as single point refinements, in which the atomic mean-field approximation is adopted.56−58 The effective spin–orbit couplings reported in this work are expressed

graphic file with name ao-2019-012765_m001.jpg

in which ΨI and ΨJ are electronic wavefunctions of involved singlet and triplet states; Hxso, Hy, and Hzso are spin–orbit operators of x, y, and z components. All of the computations are performed using MOLCAS8.0.59,60

Acknowledgments

This work has been supported by the National Natural Science Foundation of China (21522302, 21520102005, and 21421003); G.C. is also grateful for financial support from the “Fundamental Research Funds for Central Universities”.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.9b01276.

  • Active orbitals in MS-CASPT2 computations, additional figures and tables, and Cartesian coordinates of all optimized structures (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao9b01276_si_001.pdf (1MB, pdf)

References

  1. Crespo-Hernández C. E.; Cohen B.; Hare P. M.; Kohler B. Ultrafast Excited-state Dynamics in Nucleic Acids. Chem. Rev. 2004, 104, 1977–2019. 10.1021/cr0206770. [DOI] [PubMed] [Google Scholar]
  2. Middleton C. T.; de La Harpe K.; Su C.; Law Y. K.; Crespo-Hernández C. E.; Kohler B. DNA Excited-State Dynamics: From Single Bases to the Double Helix. Annu. Rev. Phys. Chem. 2009, 60, 217–239. 10.1146/annurev.physchem.59.032607.093719. [DOI] [PubMed] [Google Scholar]
  3. Kang H.; Lee K. T.; Jung B.; Ko Y. J.; Kim S. K. Intrinsic Lifetimes of the Excited State of DNA and RNA Bases. J. Am. Chem. Soc. 2002, 124, 12958–12959. 10.1021/ja027627x. [DOI] [PubMed] [Google Scholar]
  4. Merchán M.; Serrano-Andrés L. Ultrafast Internal Conversion of Excited Cytosine via the Lowest ππ* Electronic Singlet State. J. Am. Chem. Soc. 2003, 125, 8108–8109. 10.1021/ja0351600. [DOI] [PubMed] [Google Scholar]
  5. Ullrich S.; Schultz T.; Zgierski M. Z.; Stolow A. Direct Observation of Electronic Relaxation Dynamics in Adenine via Time-Resolved Photoelectron Spectroscopy. J. Am. Chem. Soc. 2004, 126, 2262–2263. 10.1021/ja030532q. [DOI] [PubMed] [Google Scholar]
  6. Ullrich S.; Schultz T.; Zgierski M. Z.; Stolow A. Electronic Relaxation Dynamics in DNA and RNA Bases Studied by Time-Resolved Photoelectron Spectroscopy. Phys. Chem. Chem. Phys. 2004, 6, 2796–2801. 10.1039/b316324e. [DOI] [PubMed] [Google Scholar]
  7. Canuel C.; Mons M.; Piuzzi F.; Tardivel B.; Dimicoli I.; Elhanine M. Excited States Dynamics of DNA and RNA Bases: Characterization of a Stepwise Deactivation Pathway in the Gas Phase. J. Chem. Phys. 2005, 122, 074316 10.1063/1.1850469. [DOI] [PubMed] [Google Scholar]
  8. Perun S.; Sobolewski A. L.; Domcke W. Ab Initio Studies on the Radiationless Decay Mechanisms of the Lowest Excited Singlet States of 9H-adenine. J. Am. Chem. Soc. 2005, 127, 6257–6265. 10.1021/ja044321c. [DOI] [PubMed] [Google Scholar]
  9. Gustavsson T.; Bányász A.; Lazzarotto E.; Markovitsi D.; Scalmani G.; Frisch M. J.; Barone V.; Improta R. Singlet Excited-State Behavior of Uracil and Thymine in Aqueous Solution: A Combined Experimental and Computational Study of 11 Uracil Derivatives. J. Am. Chem. Soc. 2006, 128, 607–619. 10.1021/ja056181s. [DOI] [PubMed] [Google Scholar]
  10. Chen H.; Li S. H. Ab Initio Study on Deactivation Pathways of Excited 9H-Guanine. J. Chem. Phys. 2006, 124, 154315 10.1063/1.2186998. [DOI] [PubMed] [Google Scholar]
  11. Serrano-Andrés L.; Merchan M.; Borin A. C. A Three-State Model for the Photophysics of Guanine. J. Am. Chem. Soc. 2008, 130, 2473–2484. 10.1021/ja0744450. [DOI] [PubMed] [Google Scholar]
  12. Conti I.; Garavelli M.; Orlandi G. Deciphering Low Energy Deactivation Channels in Adenine. J. Am. Chem. Soc. 2009, 131, 16108–16118. 10.1021/ja902311y. [DOI] [PubMed] [Google Scholar]
  13. Hassan W. M. I.; Chung W. C.; Shimakura N.; Koseki S.; Kono H.; Fujimura Y. Ultrafast Radiationless Transition Pathways Through Conical Intersections in Photo-excited 9H-Adenine. Phys. Chem. Chem. Phys. 2010, 12, 5317–5328. 10.1039/b926102h. [DOI] [PubMed] [Google Scholar]
  14. Barbatti M.; Aquino A. J. A.; Szymczak J. J.; Nachtigallova D.; Hobza P.; Lischka H. Relaxation Mechanisms of UV-Photoexcited DNA and RNA Nucleobases. Proc. Natl. Acad. Sci. U.S.A. 2010, 107, 21453–21458. 10.1073/pnas.1014982107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Picconi D.; Barone V.; Lami A.; Santoro F.; Improta R. The Interplay Between ππ*/nπ* Excited States in Gas-Phase Thymine: A Quantum Dynamical Study. ChemPhysChem 2011, 12, 1957–1968. 10.1002/cphc.201001080. [DOI] [PubMed] [Google Scholar]
  16. Heggen B.; Lan Z.; Thiel W. Nonadiabatic Decay Dynamics of 9H-Guanine in Aqueous Solution. Phys. Chem. Chem. Phys. 2012, 14, 8137–8146. 10.1039/c2cp40300e. [DOI] [PubMed] [Google Scholar]
  17. Nakayama A.; Arai G.; Yamazaki S.; Taketsugu T. Solvent Effects on the Ultrafast Nonradiative Deactivation Mechanisms of Thymine in Aqueous Solution: Excited-State QM/MM Molecular Dynamics Simulations. J. Chem. Phys. 2013, 139, 214304 10.1063/1.4833563. [DOI] [PubMed] [Google Scholar]
  18. Improta R.; Santoro F.; Blancafort L. Quantum Mechanical Studies on the Photophysics and the Photochemistry of Nucleic Acids and Nucleobases. Chem. Rev. 2016, 116, 3540–3593. 10.1021/acs.chemrev.5b00444. [DOI] [PubMed] [Google Scholar]
  19. Guo W.-W.; Fang Y.-G.; Fang Q.; Cui G.-L. Mechanistic Insights into the Photophysics of Ortho-hydroxyl GFP Core Chromophores. Chin. J. Chem. Phys. 2017, 30, 696–704. 10.1063/1674-0068/30/cjcp1709179. [DOI] [Google Scholar]
  20. Harada Y.; Suzuki T.; Ichimura T.; Xu Y.-Z. Triplet Formation of 4-Thiothymidine and its Photosensitization to Oxygen Studied by Time-Resolved Thermal Lensing Technique. J. Phys. Chem. B 2007, 111, 5518–5524. 10.1021/jp0678094. [DOI] [PubMed] [Google Scholar]
  21. Harada Y.; Okabe C.; Kobayashi T.; Suzuki T.; Ichimura T.; Nishi N.; Xu Y.-Z. Ultrafast Intersystem Crossing of 4-Thiothymidine in Aqueous Solution. J. Phys. Chem. Lett. 2010, 1, 480–484. 10.1021/jz900276x. [DOI] [Google Scholar]
  22. Reichardt C.; Crespo-Hernández C. E. Ultrafast Spin Crossover in 4-Thiothymidine in an Ionic Liquid. Chem. Commun. 2010, 46, 5963–5965. 10.1039/c0cc01181a. [DOI] [PubMed] [Google Scholar]
  23. Reichardt C.; Crespo-Hernández C. E. Room-Temperature Phosphorescence of the DNA Monomer Analogue 4-Thiothymidine in Aqueous Solutions after UVA Excitation. J. Phys. Chem. Lett. 2010, 1, 2239–2243. 10.1021/jz100729w. [DOI] [Google Scholar]
  24. Kuramochi H.; Kobayashi T.; Suzuki T.; Ichimura T. Excited-State Dynamics of 6-Aza-2-thiothymine and 2-Thiothymine: Highly Efficient Intersystem Crossing and Singlet Oxygen Photosensitization. J. Phys. Chem. B 2010, 114, 8782–8789. 10.1021/jp102067t. [DOI] [PubMed] [Google Scholar]
  25. Reichardt C.; Guo C.; Crespo-Hernández C. E. Excited-State Dynamics in 6-Thioguanosine from the Femtosecond to Microsecond Time Scale. J. Phys. Chem. B 2011, 115, 3263–3270. 10.1021/jp112018u. [DOI] [PubMed] [Google Scholar]
  26. Zhang Y.; Zhu X.; Smith J.; Haygood M. T.; Gao R. Direct Observation and Quantitative Characterization of Singlet Oxygen in Aqueous Solution upon UVA Excitation of 6-Thioguanines. J. Phys. Chem. B 2011, 115, 1889–1894. 10.1021/jp109590t. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Pollum M.; Crespo-Hernńndez C. E. Communication: the Dark Singlet State as a Doorway State in the Ultrafast and Efficient Intersystem Crossing Dynamics in 2-Thiothymine and 2-Thiouracil. J. Chem. Phys. 2014, 140, 071101 10.1063/1.4866447. [DOI] [PubMed] [Google Scholar]
  28. Sánchez-Rodríguez J. A.; Mohamadzade A.; Mai S.; Ashwood B.; Pollum M.; Marquetand P.; González L.; Crespo-Hernández C. E.; Ullrich S. 2-Thiouracil Intersystem Crossing Photodynamics Studied by Wavelength-Dependent Photoelectron and Transient Absorption Spectroscopies. Phys. Chem. Chem. Phys. 2017, 19, 19756–19766. 10.1039/C7CP02258A. [DOI] [PubMed] [Google Scholar]
  29. Siouri F. M.; Boldissar S.; Berenbeim J. A.; de Vries M. S. Excited State Dynamics of 6-Thioguanine. J. Phys. Chem. A 2017, 121, 5257–5266. 10.1021/acs.jpca.7b03036. [DOI] [PubMed] [Google Scholar]
  30. Ashwood B.; Pollum M.; Crespo-Hernández C. E. Photochemical and Photodynamical Properties of Sulfur-Substituted Nucleic Acid Bases. Photochem. Photobiol. 2019, 95, 33–58. 10.1111/php.12975. [DOI] [PubMed] [Google Scholar]
  31. Martínez-Fernández L.; González L.; Corral I. An ab Initio Mechanism for Efficient Population of Triplet States in Cytotoxic Sulfur Substituted DNA Bases: the Case of 6-Thioguanine. Chem. Commun. 2012, 48, 2134–2136. 10.1039/c2cc15775f. [DOI] [PubMed] [Google Scholar]
  32. Cui G. L.; Fang W.-H. State-Specific Heavy-Atom Effect on Intersystem Crossing Processes in 2-Thiothymine: A Potential Photodynamic Therapy Photosensitizer. J. Chem. Phys. 2013, 138, 044315 10.1063/1.4776261. [DOI] [PubMed] [Google Scholar]
  33. Cui G.; Thiel W. Intersystem Crossing Enables 4-Thiothymidine to Act as a Photosensitizer in Photodynamic Therapy: An Ab Initio QM/MM Study. J. Phys. Chem. Lett. 2014, 5, 2682–2687. 10.1021/jz501159j. [DOI] [PubMed] [Google Scholar]
  34. Martínez-Fernández L.; Corral I.; Granucci G.; Persico M. Competing Ultrafast Intersystem Crossing and Internal Conversion: a Time Resolved Picture for the Deactivation of 6-Thioguanine. Chem. Sci. 2014, 5, 1336–1347. 10.1039/c3sc52856a. [DOI] [Google Scholar]
  35. Mai S.; Marquetand P.; González L. A Static Picture of the Relaxation and Intersystem Crossing Mechanisms of Photoexcited 2-Thiouracil. J. Phys. Chem. A 2015, 119, 9524–9533. 10.1021/acs.jpca.5b06639. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Mai S.; Marquetand P.; González L. Intersystem Crossing Pathways in the Noncanonical Nucleobase 2-Thiouracil: A Time-Dependent Picture. J. Phys. Chem. Lett. 2016, 7, 1978–1983. 10.1021/acs.jpclett.6b00616. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Mai S.; Pollum M.; Martínez-Fernández L.; Dunn N.; Marquetand P.; Corral I.; Crespo-Hernández C. E.; González L. The Origin of Efficient Triplet State Population in Sulfur-Substituted Nucleobases. Nat. Commun. 2016, 7, 13077 10.1038/ncomms13077. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Xie B.-B.; Wang Q.; Guo W.-W.; Cui G. L. The Excited-State Decay Mechanism of 2,4-Dithiothymine in the Gas Phase, Microsolvated Surroundings, and Aqueous Solution. Phys. Chem. Chem. Phys. 2017, 19, 7689–7698. 10.1039/C7CP00478H. [DOI] [PubMed] [Google Scholar]
  39. Bai S.; Barbatti M. On the Decay of the Triplet State of Thionucleobases. Phys. Chem. Chem. Phys. 2017, 19, 12674–12682. 10.1039/C7CP02050C. [DOI] [PubMed] [Google Scholar]
  40. Martínez-Fernández L.; Granucci G.; Pollum M.; Crespo-Hernández C. E.; Persico M.; Corral I. Decoding the Molecular Basis for the Population Mechanism of the Triplet Phototoxic Precursors in UVA Light-Activated Pyrimidine Anticancer Drugs. Chem. - Eur. J. 2017, 23, 2619–2627. 10.1002/chem.201604543. [DOI] [PubMed] [Google Scholar]
  41. Salon J.; Sheng J.; Jiang J.; Chen G.; Caton-Williams J.; Huang Z. Oxygen Replacement with Selenium at the Thymidine 4-position for the Se Base Pairing and Crystal Structure Studies. J. Am. Chem. Soc. 2007, 129, 4862–4863. 10.1021/ja0680919. [DOI] [PubMed] [Google Scholar]
  42. Salon J.; Jiang J.; Sheng J.; Gerlits O. O.; Huang Z. Derivatization of DNAs with Selenium at 6-position of Guanine for Function and Crystal Structure Studies. Nucleic Acids Res. 2008, 36, 7009–7018. 10.1093/nar/gkn843. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Hassan A. E. A.; Sheng J.; Zhang W.; Huang Z. High Fidelity of Base Pairing by 2-Selenothymidine in DNA. J. Am. Chem. Soc. 2010, 132, 2120–2121. 10.1021/ja909330m. [DOI] [PubMed] [Google Scholar]
  44. Salon J.; Gan J. H.; Abdur R.; Liu H. H.; Huang Z. Synthesis of 6-Se-Guanosine RNAs for Structural Study. Org. Lett. 2013, 15, 3934–3937. 10.1021/ol401698n. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Farrell K. M.; Brister M. M.; Pittelkow M.; Sϕlling T. I.; Crespo-Hernández C. E. Heavy-Atom-Substituted Nucleobases in Photodynamic Applications: Substitution of Sulfur with Selenium in 6-Thioguanine Induces a Remarkable Increase in the Rate of Triplet Decay in 6-Selenoguanine. J. Am. Chem. Soc. 2018, 140, 11214–11218. 10.1021/jacs.8b07665. [DOI] [PubMed] [Google Scholar]
  46. Wang J.; Gu J.; Leszczynski J. The Electronic Spectra and the H-Bonding Pattern of the Sulfur and Selenium Substituted Guanines. J. Comput. Chem. 2012, 33, 1587–1593. 10.1002/jcc.22991. [DOI] [PubMed] [Google Scholar]
  47. Pirillo J.; De Simone B. C.; Russo N. Photophysical Properties Prediction of Selenium- and Tellurium-Substituted Thymidine as Potential UVA Chemotherapeutic Agents. Theor. Chem. Acc. 2015, 135, 1–5. 10.1007/s00214-015-1744-1. [DOI] [Google Scholar]
  48. Pirillo J.; Mazzone G.; Russo N.; Bertinil L. Photophysical Properties of S, Se and Te-Substituted Deoxyguanosines: Insight into Their Ability To Act as Chemotherapeutic Agents. J. Chem. Inf. Model. 2017, 57, 234–242. 10.1021/acs.jcim.6b00486. [DOI] [PubMed] [Google Scholar]
  49. Andersson K.; Malmqvist P.-Å.; Roos B. O.; Sadlej A. J.; Wolinski K. Second-Order Perturbation Theory with a CASSCF Reference Function. J. Phys. Chem. 1990, 94, 5483–5488. 10.1021/j100377a012. [DOI] [Google Scholar]
  50. Andersson K.; Malmqvist P.-Å.; Roos B. O. Second-Order Perturbation Theory with a Complete Active Space Self-Consistent Field Reference Function. J. Chem. Phys. 1992, 96, 1218–1226. 10.1063/1.462209. [DOI] [Google Scholar]
  51. Ghigo G.; Roos B. O.; Malmqvist P.-Å. A Modified Definition of the Zeroth-Order Hamiltonian in Multiconfigurational Perturbation Theory (CASPT2). Chem. Phys. Lett. 2004, 396, 142–149. 10.1016/j.cplett.2004.08.032. [DOI] [Google Scholar]
  52. Zobel J. P.; Nogueira J. J.; González L. The IPEA dilemma in CASPT2. Chem. Sci. 2017, 8, 1482–1499. 10.1039/C6SC03759C. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Försberg N.; Malmqvist P.-Å. Multiconfiguration Perturbation Theory with Imaginary Level Shift. Chem. Phys. Lett. 1997, 274, 196–204. 10.1016/S0009-2614(97)00669-6. [DOI] [Google Scholar]
  54. Aquilante F.; Lindh R.; Pedersen T. B. Unbiased Auxiliary Basis Sets for Accurate Two-Electron Integral Approximations. J. Chem. Phys. 2007, 127, 114107–114713. 10.1063/1.2777146. [DOI] [PubMed] [Google Scholar]
  55. Dunning T. H. Jr. Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. 10.1063/1.456153. [DOI] [Google Scholar]
  56. Heß B. A.; Marian C. M.; Wahlgren U.; Gropen O. A Mean-Field Spin-Orbit Method Applicable to Correlated Wavefunctions. Chem. Phys. Lett. 1996, 251, 365–371. 10.1016/0009-2614(96)00119-4. [DOI] [Google Scholar]
  57. Marian C. M.; Wahlgren U. A New Mean-Field and ECP-Based Spin-Orbit Method. Applications to Pt and PtH. Chem. Phys. Lett. 1996, 251, 357–364. 10.1016/0009-2614(95)01386-5. [DOI] [Google Scholar]
  58. Marian C. M. Spin-Orbit Coupling and Intersystem Crossing in Molecules. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012, 2, 187–203. 10.1002/wcms.83. [DOI] [Google Scholar]
  59. Karlström G.; Lindh R.; Malmqvist P.-Å.; Roos B. O.; Ryde U.; Veryazov V.; Widmark P. O.; Cossi M.; Schimmelpfennig B.; Neogrady P.; Seijo L. MOLCAS: A Program Package for Computational Chemistry. Comput. Mater. Sci. 2003, 28, 222–229. 10.1016/S0927-0256(03)00109-5. [DOI] [Google Scholar]
  60. Aquilante F.; De Vico L.; Ferré N.; Ghigo G.; Malmqvist P.-Å.; Neogrády P.; Pedersen T. B.; Pitoňák M.; Reiher M.; Roos B. O.; Serrano-Andrés L.; Urban M.; Veryazov V.; Lindh R. MOLCAS 7: The Next Generation. J. Comput. Chem. 2010, 31, 224–247. 10.1002/jcc.21318. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao9b01276_si_001.pdf (1MB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES