Abstract
Optical fluorescence imaging is capable of measuring both the translational and rotational dynamics of single molecules. However, unavoidable measurement noise will result in inaccurate estimates of rotational dynamics, causing a molecule to appear to be more rotationally constrained than it actually is. We report a mathematical framework to compute the fundamental limit of accuracy in measuring the rotational mobility of dipole-like emitters. By applying our framework to both in-plane and three-dimensional methods, we provide a means to choose the optimal orientation-measurement technique based on experimental conditions.
Fluorescence microscopy has been widely utilized to study the rotational dynamics of single molecules (SMs), revealing new insights into DNA organization [1–3] and the movement of molecular motors [4–8]. Orientation measurements are also critical for ensuring the accuracy of SM localization microscopy [9–12], since changes in orientation can be mistakenly perceived as changes in molecular position. To sensitively measure dipole orientation, a fluorescence microscope is typically augmented either by measuring fluorescence emission under varying pumping polarization, by manipulating the polarization and/or angular spectrum of the fluorescence emission, or both [13]. Analyzing an SM’s fluorescence signal thereby yields its average orientation and/or its rotational mobility or “wobble” during some integration time.
One intuitive method to measure SM orientation is to quantify linear dichroism (LD) [14–17], i.e., the ratio of the difference over the sum of the intensity of the x- and y-polarized emission from a single emitter. A rotationally-fixed SM will yield a certain LD value depending upon its orientation, but due to symmetry, a rotationally-unconstrained SM will give an LD of zero. However, measurement noise, e.g., photon shot noise, will almost certainly produce a nonzero LD and therefore reduce the apparent molecular wobble. This phenomenon is similar to the effect of finite localization precision in single-particle tracking [18–22], where a translationally-fixed particle appears to have a nonzero diffusion coefficient due to shot noise. However, in the case of rotational dynamics, the non-zero estimates of LD cause the measurement of rotational mobility to be biased; the molecule will appear to be more constrained than it actually is. To our knowledge, the effects of noise and measurement sensitivity and the impact of 2D versus 3D measurements on the accuracy of quantifying SM rotational dynamics remain unexplored.
Here, we present a mathematical framework to compute the distribution, accuracy, and precision of measuring the rotational constraint (inversely proportional to rotational mobility) of dipole-like emitters in both 2D and 3D. For a given imaging scenario with a certain number of signal and background photons detected, we derive a lower bound on the apparent rotational constraint, that is, the expectation of estimated rotational constraint for a freely-rotating molecule; it is impossible to detect a constraint smaller than this limit. Further, we derive a relation between the measured in (xy)-plane and 3D rotational constraints, which reveals how 2D and 3D methods perceive the same 3D rotational diffusion differently. We then analyze the accuracy and precision of various commonly-used and state-of-the-art 2D and 3D orientation measurement techniques.
We model a fluorescent molecule as a radiating dipole [23] with orientation , where µz is the out-of-plane component, i.e., the projection of µ along the optical axis. Since fluorescence intensity and not electric field is detected, both excitation and emission modulation methods are limited to measuring the even-order moments of µ. The recorded image , where the dimension n is the number of pixels or groupings thereof, can then be represented using the second moments of µ, given by
| (1) |
for a 3D measurement and
| (2) |
for an in-plane (2D) measurement, where are termed the basis images of the imaging system. The image produced by an emitter will be a mixture of these images weighted by the orientational second moments . The prefactor s and image represent the integrated signal photons and background photons, respectively, for each measurement g. The second moment vector is the normalized projection of molecular orientation µ into the xy plane, and the angle brackets denote the temporal average taken over one camera frame or the equivalent average over the orientation domain. The basis images can be computed for any excitation-modulation method by computing the SM’s response to varying excitation polarization [3] and for any emission-modulation technique using vectorial diffraction models [24–28].
The accuracy and precision with which the rotational constraint of a single molecule can be estimated depend on three factors: 1) the detected photons from the emitter, i.e., its signal, 2) background fluorescence, and 3) most importantly, the basis-image matrix that describes the sensitivity of the imaging system to each orientational second moment . To illustrate these effects, we evaluate a simple 2D method where we pump an SM using three distinct in-plane excitation polarizations Ei and observe the corresponding emission intensities [29] (Fig. S1(b)).
The normalized second moments are computed by inverting the basis matrix: Rearranging them into a 2-by-2 Hermitian matrix M2D and decomposing it as
| (3) |
we obtain the in-plane rotational constraint (Fig. S3). The scalars λi and vectors νi represent the ith eigenvalue and eigenvector of M2D, respectively. The matrix M2D can be interpreted as a mixture of a fixed dipole with orientation ν1 and intensity fraction γ2D and an isotropic emitter with intensity fraction 1 − γ2D. The rotational constraint γ2D = 1 represents a completely immobile emitter, and γ2D = 0 represents a freely-rotating molecule. Further, since rotational correlation times are typically 1–30 ns for fluorophores in liquids [11, 30] and practical camera integration times are 1 ms or longer, rotational constraint measurements are typically indicative of the full range orientations explored by each molecule [29].
We assume that the measured second-order moments follow unbiased Gaussian distributions with precision achieving the Cramér-Rao lower bound (CRLB) [31]. Therefore, for a simplified case where the three excitation polarizations are symmetric and linear and the average orientation of the emitter lies within the xz plane , the probability density function (PDF) of measurements of rotational constraint is given by [29]
| (4) |
The measurement precision of the second moments is is the true rotational constraint of the SM, and Ik(·) is the modified Bessel function of the first kind. This PDF matches simulated measurements using realistic noise (Fig. S4). The expectation of (Fig. 1(b)) is given by [32]
| (5) |
where is the generalized Laguerre function. Critically, this expectation does not equal the true constraint γ2D for any nonzero measurement precision σ.
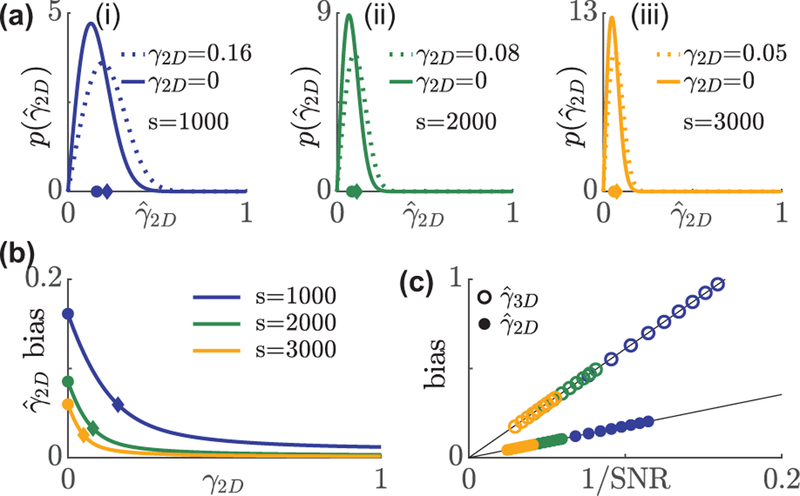
FIG. 1.
Distribution and bias of rotational constraint measurements using in-plane excitation polarization modulation. (a) A non-central chi PDF describes the distribution of under s = (i) 1000, (ii) 2000, and (iii) 3000 signal photons with 1†b = 7290 background photons per 526.5 × 526.5 nm2 (3.5× FWHM of a diffraction-limited spot) region. Solid line: isotropic emitters, dashed line: emitter whose bias is smaller by 1/e compared to an isotropic emitter. Circles and diamonds on the x axis represent the mean of the aforementioned two distributions, respectively. (b) Average bias in versus the ground truth γ2D. Blue, green, and orange represent 1000, 2000, and 3000 signal photons, respectively. Circles and diamonds correspond to the same data points in (a). (c) Bias in the measured rotational constraint of isotropic emitters scales linearly with the inverse of SNR, . Solid circles: , open circles:.
For a typical background of 30 photons per 58.5 × 58.5 nm2 (one camera pixel in object space), the expected biases for an isotropic emitter when 1000, 2000, 3000 signal photons are detected are 0.16, 0.09, and 0.06, respectively. To provide physical intuition, these biases correspond to half-angle errors of 13°, 7°, and 5°, respectively, if the molecule is uniformly diffusing within a wedge in the xy plane. The error in rotational constraint decays as wobble decreases. Brighter emitters further reduce errors in rotational constraint. The bias is reduced to 1/e times its maximum, which occurs at γ2D = 0, when γ2D = 0.16, 0.08, and 0.05 for 1000, 2000, and 3000 photons detected, respectively (Fig. 1(a),(b)).
For an isotropic emitter, gi is invariant for different excitation polarizations, and therefore, the precision of the second-moment estimates is expressed as [29]. Therefore, the average apparent rotational constraint is given by
| (6) |
where the bias in the apparent rotational constraint scales linearly with the inverse of the signal-to-noise ratio (SNR, Fig. 1(c)).
We now extend our framework to measurements of 3D orientation, similarly assembling a 3 × 3 second-moment matrix and decomposing it as [29]
| (7) |
where the 3D rotational constraint . If the molecule’s rotational diffusion is symmetric around a certain average orientation, then the smaller eigenvalues λ2 and λ3 are identical due to symmetry. Similarly, the matrix M3D can be viewed as a mixture of a fixed dipole and an isotropic emitter, plus a nuisance term that is orthogonal to ν1 that arises from asymmetric rotation. In contrast to the case of 2D excitation modulation, the eigenvalues of the measured second-moment matrix do not have a closed-form distribution. We therefore perform Monte Carlo simulations on isotropic emitters imaged using the Tri-spot point spread function (PSF) [33] (Fig. S1(c)). The linear relation between the bias in and the inverse of SNR still approximately holds (Fig. 1(c)).
Although both 2D (Eq. (3)) and 3D (Eq. (7)) rotational constraints have identical interpretations for limiting cases, e.g., γ2D = γ3D = 0 represents a rotationally-free emitter, these two quantities may differ for any partially-constrained dipole emitter. That is, identical 3D orientation trajectories can produce different rotational diffusion measurements in 2D versus 3D. Here, we consider a symmetrically-rotating molecule in 3D and assemble M2D using a subset of elements from M3D [29]. The in-plane rotational constraint γ2D is now given by
| (8) |
The 2D and 3D rotational constraints are identical for a molecule exhibiting an average out-of-plane component of (corresponding to a “magic” polar angle ≈ 54.7°, Fig. 2a). Note that γ2D depends on both the 3D rotational constraint γ3D and average out-of-plane orientation ; in-plane orientation measurement methods are only sensitive to γ2D and must incorporate prior knowledge of in order to compute an equivalent 3D rotational constraint γ3D. The average difference in constraint ∆γ = γ2D − γ3D (Fig. 2(c)) is within ±0.1 for , indicating that both γ2D and γ3D quantify the rotational dynamics of a dipole emitter similarly as long as the out-of-plane component is small. However, for a molecule that is almost along the optical axis, e.g. or polar angle = 11°, |∆γ| can be as large as 0.61; a highly-constrained molecule in 3D (γ3D = 0.80 or a cone half-angle of 30°) appears to be almost completely unconstrained using an in-plane measurement method (γ2D = 0.20 or a wedge half-angle of 75°). This interdependence of µz, γ2D, and γ3D has important implications for orientation-measurement techniques. If a technique cannot measure all six second-moments in 3D directly, then one must use a prior assumption on the out-of-plane orientation to calculate the rotational constraint (or vice versa). Any errors in this assumption can dramatically impact measurement accuracy.
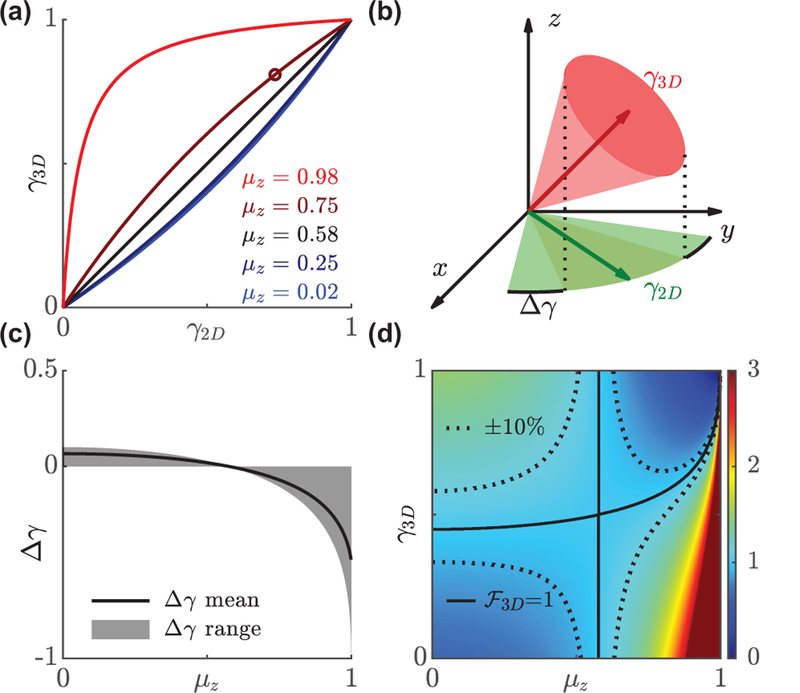
FIG. 2.
Comparison of in-plane γ2D and 3D γ3D rotational constraints. (a) The relation between γ2D and γ3D varies with the average orientation along the z axis, (Eq. 8). Black line corresponds to so that γ2D = γ3D. (b) A dipole emitter with an out-of-plane orientation that has γ3D = 0.81 (a cone half-angle of 30°, open circle in (a)) appears to be more rotationally free in the xy plane (γ2D = 0.73, wedge half-angle of 38°). (c) The mean difference ∆γ across all 3D orientation space ranges from −1 to 0.06. Solid line represents the average across all possible values of γ3D, and the shaded region represents the range of the difference. (d) 3D enhancement factor as a function of γ3D and . Solid line represents the equilibrium point where in-plane and 3D rotational constraints measure changes in rotational dynamics with equal sensitivity. Dashed line represents a ±10% difference in sensitivity.
A natural consequence of using 2D versus 3D orientation measurements is that these techniques have different sensitivities for measuring changes in rotational dynamics. Here, we quantify the enhancement factor as the ratio of partial derivatives of γ3D to γ2D (Fig. 2(d)):
| (9) |
An enhancement factor greater than one implies that a given change in maps to a smaller change in , i.e., for the same measurement uncertainty, it is easier to detect a change in than . The sensitivity of the in-plane measurement to a change in rotational constraint highly depends on the out-of-plane component of molecular orientation. For example, for the aforementioned molecule with , an in-plane technique is especially insensitive to changes in rotational motion for most values of γ3D. However, when the molecule is almost immobile, the in-plane method becomes very sensitive, i.e., a small change in γ3D produces a large, easily-detectable change in .
To provide quantitative metrics for choosing the optimal orientation measurement technique, we compare multiple popular and state-of-the-art methods. We first consider an ideal 3D (6 × 6) basis-image matrix [29]
| (10) |
such that each column of Bideal is orthogonal and has identical energy. The average apparent 3D rotational constraint for an isotropic emitter is given by [29]
| (11) |
where is the expectation of the largest eigenvalue of a Hermitian random matrix H whose elements Hij are i.i.d. standard normal random variables. The imaging system represented by Bideal separates the six second-moments into independent measurements with ideal collection efficiency and, thus, represents a fundamental limit on the measurement accuracy of 3D rotational constraint. That is, for a finite SNR, a freely-rotating molecule would appear to be identical to a partially-fixed emitter using any 3D orientation measurement method, and the apparent constraint is always greater than or equal to that measured by Eq. (11) [29]. To provide physical intuition (Fig. 3(a)), for 1000 signal photons and 30 background photons per pixel detected, the expectation of is 0.12, meaning that an SM diffusing within a cone of half-angle α = 78° would be indistinguishable from a rotationally-free SM (α = 90°).
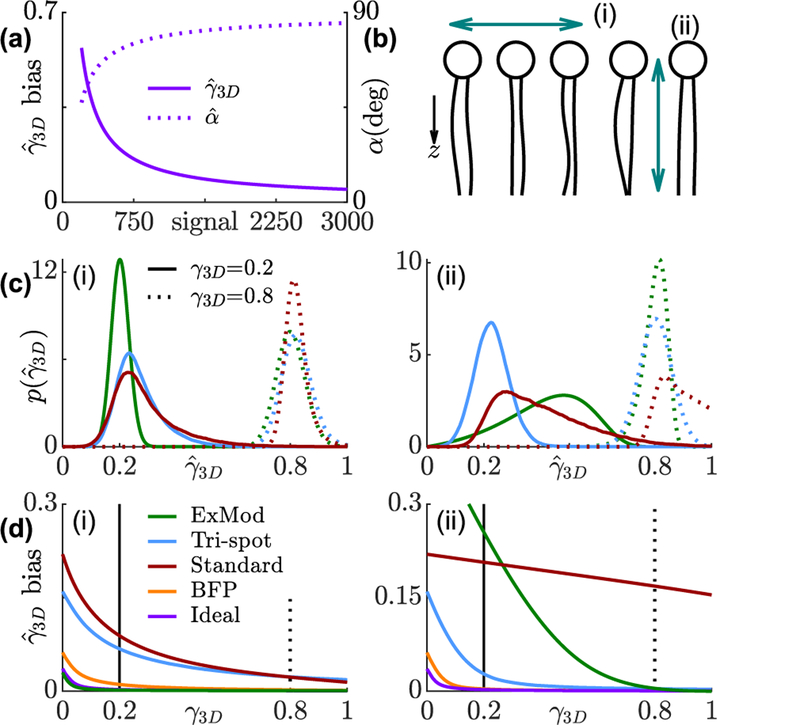
FIG. 3.
Bias and precision of rotational constraint measurements using various techniques. (a) Minimum detectable rotational constraint for various numbers of signal photons and 4860 total background photons. Solid line represents the expectation of measured rotational constraint for isotropic emitters; dashed line represents the corresponding cone half-angle if the molecule is symmetrically diffusing in a cone. (b) Concept of (i) a horizontally- and (ii) a vertically-orientated fluorescent molecule within a lipid membrane. (c) Distribution of 3D rotational constraint estimates . Solid line: true rotational constraint γ3D = 0.2 (cone half-angle α = 72°); dashed line: γ3D = 0.8 (α = 31°). (d) Bias of for each technique. Green: in-plane excitation modulation, blue: Tri-spot PSF, red: standard PSF, orange: back focal plane imaging, purple: ideal basis-image matrix.
Besides the aforementioned ideal, Tri-spot, and in-plane excitation methods, we also analyze the performance of fitting fine features of the standard PSF [34] and direct imaging of the back focal plane (BFP) [25] (Fig. S1(d,e)). We simulated two limiting cases, mimicking two orientations of fluorescent dye molecules embedded within a lipid membrane [35] (Fig. 3(b)), where the average orientation is almost perpendicular (Fig. 3(i), ) and almost parallel (Fig. 3(ii), ) to the optical axis. The simulated SNR for all the methods is 3000 signal photons to 20 total background photons per pixel per unit time [29].
The Tri-spot PSF and BFP imaging exhibit consistent performance for both in-plane and out-of-plane molecules due to their relatively uniform sensitivity for measuring all orientational second-order moments. In-plane excitation, as expected, exhibits high accuracy and precision (Fig. S7) for in-plane molecules. Its bias in is even lower than the ideal 3D technique because of the improved SNR of distributing an SM’s photons over 2× fewer measurements. For out-of-plane molecules however, its bias and precision are much worse compared to 3D methods except when the rotational constraint is sufficiently high. The standard PSF, due to its poor sensitivity to two out-of-plane second moments, also exhibits a large bias and standard deviation for out-of-plane molecules. However, it has better performance for measuring the rotational motion of highly constrained in-plane molecules than the Tri-spot PSF. This analysis implies that a method specifically designed for measuring a subset of, instead of all six (3D), orientational second moments can provide superior performance under certain experimental conditions.
In summary, we analyzed the fundamental bias in measurements of rotational dynamics caused by finite SNR. We derived a lower bound on this bias, that is, no method can detect a rotational constraint smaller than this bound without sufficient prior knowledge. While we defined rotational constraint in terms of the eigenvalues of the second-moment matrix M, any parameterization of rotational diffusion, e.g., fluorescence anisotropy [29, 36], or choice of emitter model, e.g., higher-order multipoles [23, 29], will also suffer bias since any measurement will capture a finite number of photons. Our framework is easily adaptable for characterizing the bias of any orientation-measurement method via calculation of the basis images Bij. We show that there is a complex relationship between in-plane and 3D molecular orientation, such that a molecule’s 2D rotational constraint can appear significantly smaller or larger than its true constraint in 3D. Using our framework, we compared multiple methods for measuring rotational dynamics, revealing how the accuracy and precision of these measurements vary for in-plane and out-of-plane SMs. In particular, our results show that 3D methods are particularly important for quantifying accurately the rotational dynamics of SMs with significant out-of-plane orientations. Our framework should be useful for choosing between existing methods and optimizing new techniques that achieve maximum accuracy and precision in various imaging scenarios.
Supplementary Material
Acknowledgments
This work was supported by the National Science Foundation under grant number ECCS-1653777 and by the National Institute of General Medical Sciences of the National Institutes of Health under grant number R35GM124858.
References
- [1].Ha T, Enderle T, Chemla DS, Selvin PR, and Weiss S, Physical Review Letters 77, 3979 (1996). [DOI] [PubMed] [Google Scholar]
- [2].Ha T, Glass J, Enderle T, Chemla DS, and Weiss S, Physical Review Letters 80, 2093 (1998). [Google Scholar]
- [3].Backer AS, Lee MY, and Moerner WE, Optica 3, 659 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Sosa H, Peterman EJG, Moerner WE, and Goldstein LSB, Nature Structural Biology 8, 540 (2001). [DOI] [PubMed] [Google Scholar]
- [5].Peterman EJ, Sosa H, Goldstein LS, and Moerner W, Biophysical Journal 81, 2851 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Forkey JN, Quinlan ME, Shaw MA, Corrie JET, and Goldman YE, Nature 422, 399 (2003). [DOI] [PubMed] [Google Scholar]
- [7].Beausang JF, Shroder DY, Nelson PC, and Goldman YE, Biophysical Journal 104, 1263 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Lippert LG, Dadosh T, Hadden JA, Karnawat V, Diroll BT, Murray CB, Holzbaur ELF, Schulten K, Reck-Peterson SL, and Goldman YE, Proceedings of the National Academy of Sciences 114, E4564 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Engelhardt J, Keller J, Hoyer P, Reuss M, Staudt T, and Hell SW, Nano Letters 11, 209 (2011). [DOI] [PubMed] [Google Scholar]
- [10].Backlund MP, Lew MD, Backer AS, Sahl SJ, Grover G, Agrawal A, Piestun R, and Moerner WE, Proceedings of the National Academy of Sciences 109, 19087 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Lew MD, Backlund MP, and Moerner WE, Nano Letters 13, 3967 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Lew MD and Moerner WE, Nano Letters 14, 6407 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Backlund MP, Lew MD, Backer AS, Sahl SJ, and Moerner WE, ChemPhysChem 15, 587 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Edmiston PL, Lee JE, Wood LL, and Saavedra SS, The Journal of Physical Chemistry 100, 775 (1996). [Google Scholar]
- [15].Fourkas JT, Optics Letters 26, 211 (2001). [DOI] [PubMed] [Google Scholar]
- [16].Benninger RK, Önfelt B, Neil MA, Davis DM, and French PM, Biophysical Journal 88, 609 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Steinbach G, Pomozi I, Zsiros O, Páy A, Horváth GV, and Garab G, Cytometry Part A 73A, 202 (2008). [DOI] [PubMed] [Google Scholar]
- [18].Berglund AJ, Physical Review E 82, 011917 (2010). [DOI] [PubMed] [Google Scholar]
- [19].Wong Y, Lin Z, and Ober RJ, IEEE Transactions on Signal Processing 59, 895 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Michalet X and Berglund AJ, Physical Review E 85, 061916 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Backlund MP, Joyner R, and Moerner WE, Physical Review E 91, 062716 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Calderon CP, Physical Review E 93, 053303 (2016). [DOI] [PubMed] [Google Scholar]
- [23].Novotny L and Hecht B, Principles of Nano-Optics (Cambridge University Press, Cambridge, England, 2012). [Google Scholar]
- [24].Böhmer M and Enderlein J, Journal of the Optical Society of America B 20, 554 (2003). [Google Scholar]
- [25].Lieb MA, Zavislan JM, and Novotny L, Journal of the Optical Society of America B 21, 1210 (2004). [Google Scholar]
- [26].Axelrod D, Journal of Microscopy 247, 147 (2012). [DOI] [PubMed] [Google Scholar]
- [27].Backer AS and Moerner WE, The Journal of Physical Chemistry B 118, 8313 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Backer AS and Moerner WE, Optics Express 23, 4255 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29]. See supplemental material for additional figures and derivation, which includes Refs. [37–41].
- [30].Valeur B, Molecular Fluorescence: Principles and Applications (Wiley-VCH, Weinheim, Germany, 2002). [Google Scholar]
- [31].Moon TK and Stirling WC, Mathematical Methods and Algorithms for Signal Processing (Prentice Hall, New Jersey, 2000). [Google Scholar]
- [32].Nuttall A, IEEE Transactions on Information Theory 21, 95 (1975). [Google Scholar]
- [33].Zhang O, Lu J, Ding T, and Lew MD, Applied Physics Letters 113, 031103 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Mortensen KI, Churchman LS, Spudich JA, and Flyvbjerg H, Nature Methods 7, 377 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Motegi T, Nabika H, and Murakoshi K, Physical Chemistry Chemical Physics 15, 12895 (2013). [DOI] [PubMed] [Google Scholar]
- [36].Lakowicz JR, Principles of Fluorescence Spectroscopy (Springer Science+Business Media, New York, 2006). [Google Scholar]
- [37].Hell SW and Wichmann J, Optics letters 19, 780 (1994). [DOI] [PubMed] [Google Scholar]
- [38].Rust MJ, Bates M, and Zhuang X, Nature Methods 3, 793 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Betzig E, Patterson GH, Sougrat R, Lindwasser OW, Olenych S, Bonifacino JS, Davidson MW, Lippincott-Schwartz J, and Hess HF, Science 313, 1642 (2006). [DOI] [PubMed] [Google Scholar]
- [40].Hess ST, Girirajan TP, and Mason MD, Biophysical Journal 91, 4258 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Bouhelier A, Microscopy research and technique 69, 563 (2006). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.