Learning common and specific patterns from data of multiple interrelated biological scenarios with matrix factorization

Abstract

High-throughput biological technologies (e.g. ChIP-seq, RNA-seq and single-cell RNA-seq) rapidly accelerate the accumulation of genome-wide omics data in diverse interrelated biological scenarios (e.g. cells, tissues and conditions). Integration and differential analysis are two common paradigms for exploring and analyzing such data. However, current integrative methods usually ignore the differential part, and typical differential analysis methods either fail to identify combinatorial patterns of difference or require matched dimensions of the data. Here, we propose a flexible framework CSMF to combine them into one paradigm to simultaneously reveal Common and Specific patterns via Matrix Factorization from data generated under interrelated biological scenarios. We demonstrate the effectiveness of CSMF with four representative applications including pairwise ChIP-seq data describing the chromatin modification map between K562 and Huvec cell lines; pairwise RNA-seq data representing the expression profiles of two different cancers; RNA-seq data of three breast cancer subtypes; and single-cell RNA-seq data of human embryonic stem cell differentiation at six time points. Extensive analysis yields novel insights into hidden combinatorial patterns in these multi-modal data. Results demonstrate that CSMF is a powerful tool to uncover common and specific patterns with significant biological implications from data of interrelated biological scenarios.

INTRODUCTION

With the rapid development of high-throughput sequencing technologies, numerous omics data have been generated in diverse biological scenarios, which provide unprecedented opportunities to investigate the underlying biological processes among them (1–3). For example, the encyclopedia of DNA elements (ENCODE) project makes a variety of ChIP-seq data of a wide assortment of cell types available; The Cancer Genome Atlas (TCGA) project generates large amounts of omics data for various cancers. Moreover, the throughput of single-cell RNA sequencing (scRNA-seq) (4,5) has been significantly improved, providing a chance for comprehensively viewing the heterogeneity of cells. Integrative and comparative analysis of such data is becoming an urgent need (1). Mathematically, these genomic data can be regarded as data matrices, whose analysis method is based on matrix signal extraction and computing.

Classical matrix signal extraction and pattern discovery tools such as principle component analysis (PCA) (6), independent component analysis (ICA) (7) and non-negative matrix factorization (NMF) (8) are powerful techniques for analyzing high-dimensional data matrices. PCA is an effective tool for dimension reduction and visualization of such data. ICA seeks to separate such data into a set of statistically independent components. However, their decomposition results are restricted to orthogonal or independent vectors in new feature spaces and often lack interpretability. Compared to PCA and ICA, NMF not only performs dimension reduction, but also provides a better way to explain structured data. However, they are only designed for resolving one data matrix at a time. All of this limit their validity in comparative analysis of the accumulated multiple datasets. Early studies have adopted joint non-negative matrix factorization (jNMF) and its network-regularized variants to conduct integrative analysis of multi-dimensional genomics data for extracting combinatorial patterns (9–11). More recently, an integrative NMF study further extended this framework to study heterogeneous confounding effects among different datasets (12). However, these methods mainly focus on uncovering consistent patterns embedded in various types of data from the same biological condition. An unsolved valuable and urgent issue is how to perform integrative and comparative analysis on the same type of data from multiple biological conditions (e.g. transcriptional profiles of various cancer types or subtypes, epigenomic profiles across various cell lines) in the big data era. Thus, the urgent needs for analyzing and comparing omics data generated in multiple conditions prompt us to design new tools to extract hidden structures or patterns for many practical applications.

A few advances have been made toward integrative and/or comparative analysis of omics data from multiple conditions. For example, differential principal component analysis (dPCA) is an efficient tool for analyzing multiple ChIP-seq datasets to discover differential protein–DNA interactions between K562 and Huvec cell lines (13). However, it only extracts differential patterns on two data matrices with matched rows and columns. Tensor higher order singular value decomposition method has also been adopted to perform integrative analysis of DNA microarray data from different studies (14). However, it was only designed for pairwise or multiple datasets (represented by tensors) that have the same row and column dimensions. Therefore, neither of these two methods can be applied to data with only one matched dimension in a unified framework, which limits their applied ranges. What’s more important, omics data under diverse conditions are generally in different sizes of samples. ICA has been recently employed to reveal cancer type-shared and cancer type-specific signals by first applying it to each cancer expression data separately, and then detecting common and specific modules on a relationship network (15). However, this method may overlook the influence between shared and differential features. In more detail, tiny difference compared to shared features may be ignored. Therefore, simultaneous determination of common and specific patterns for the omics data matrices with different row (or column) dimension among multiple biological conditions remains an outstanding challenge.

To this end, we propose an integrative and comparative framework CSMF to simultaneously extract Common and Specific patterns on the omics data of two or multiple biological interrelated conditions via Matrix Factorization (Figure 1). CSMF is suitable for analyzing RNA-seq, ChIP-seq, scRNA-seq and other types of data. Extensive analyses with four biological applications demonstrate that CSMF can help yield novel insights into hidden combinatorial patterns behind interrelated multi-modal data. Specifically, four applications include (i) the histone modification data of K562 and Huvec cell lines profiled using ChIP-seq from ENCODE, (ii) the gene expression data of breast invasive carcinoma (BRCA) and uterine corpus endometrial carcinoma (UCEC) from TCGA, (iii) the gene expression data of three breast cancer subtypes from Breast Cancer International Consortium (METRABRIC) and (iv) single-cell RNA-seq (scRNA-seq) data of six time points about stem cell differentiation. CSMF discovered stable CTCF-binding loci and three differential patterns with consistent marks but differential binding intensities from the epigenomic profiles of K562 and Huvec. By comparing transcriptional profiles of UCEC and BRCA, CSMF identified cancer hallmarks enriched common modules and cancer type-specific biological modules. Furthermore, CSMF detected tiny BRCA subtype-specific biological modules. Meanwhile, CSMF is an effective tool to analyze heterogeneous scRNA-seq data, and it revealed diverse degrees of human embryonic stem cell differentiation. Overall, CSMF is a powerful tool to uncover hidden combinatorial common and specific patterns embedded in the same omics data of interrelated biological scenarios.

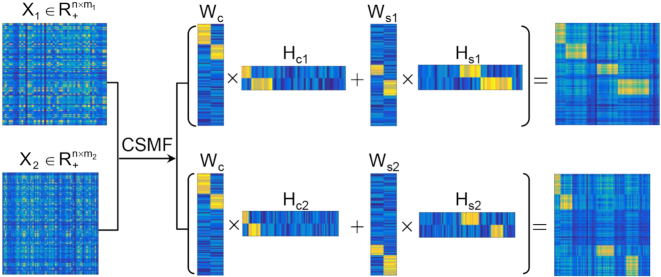
Figure 1.

Illustration of CSMF. X₁ and X₂ are the data matrices as the inputs of CSMF. After applying CSMF on X₁ and X₂, low-rank basis matrices and coefficient matrices are obtained. Then we reorder these low-rank matrices, which are shown in the middle panel. Next, the reordered X₁ (X₂) with obvious patterns (the right panel) is reconstructed by summing the common characteristics W_cH_c1 (W_cH_c2) and specific characteristics W_s1H_s1 (W_s2H_s2).

MATERIALS AND METHODS

Datasets and data preprocessing

We downloaded the normalized ChIP-seq data used in the MYC analysis example from the website of dPCA (http://www.biostat.jhsph.edu/dpca/), which includes 58997 loci, 18 datasets and 70 samples in K562 and Huvec cell lines. Each locus represents an extensional MYC motif site that has significant signal(s) in at least one mark or TF in either cell line. We log-transformed the binding signal with a pseudo-count 1 (i.e. log2(1 + count)), and averaged the values of multiple replicates of each mark for K562 and Huvec cell lines, respectively. Finally, we obtained the data matrix X₁ for K562 and X₂ for Huvec, and both these two matrices consist of 58997 loci and 18 marks.

We downloaded the level 3 gene expression data (illuminahiseq _rnaseqv2 -RSEM_genes_normalized) of UCEC and BRCA on 28 January 2016 from http://gdac.broadinstitute.org/. We log-transformed the expression with a pseudo-count 1 and kept the differentially expressed genes with absolute log2 (fold change) > 2 and Benjamin–Hochberg adjusted P-value < 0.01 between cancer and normal samples by limma (16) for UCEC and BRCA, respectively. Finally, we obtained the two gene expression data matrices with X₁ and X₂ consisting of 6621 genes across 370 UCEC and 1100 BRCA tumors respectively.

The METRABRIC dataset was accessed through Synapse (synapse.sagebase.org), which contained detailed clinical annotations such as PAM50 subtype information (17). We focused on the tumors of luminal A, luminal B, basal and her2 subtypes. We kept genes that were differentially expressed between each of these subtypes and the normal-like subtype using limma with Benijamini–Hochberg adjusted P-value < 0.01 and the absolute value of log2(fold change) > 0.5. We also computed the median absolute deviation (MAD) value of each gene across samples of each subtype and kept the gene with MAD > 0.2 in at least one subtype. Then, we combined these two gene sets. We treated luminal A and luminal B as one subtype, named as lum. Finally, we obtained the expression data matrices X₁, X₂ and X₃ with 2031 genes across 1209 lum, 328 basal and 238 her2 tumors.

We downloaded the scRNA-seq data of human embryonic stem cells and differentiation cells from NCBI’s Gene Expression Omnibus (https://www.ncbi.nlm.nih.gov/geo) with accession number GSE75748. There were 758 cells including 92, 102, 66, 172, 138 and 188 cells at time points 0, 12, 24, 36, 72 and 96 h, respectively. The gene expression values were log-transformed with a pseudo-count 1 and normalized by the media-by-ratio method with SCPattern R package (18). We computed the variation measured by standard deviation for each gene across each time point and selected genes with z-score of the variation > 1. We extracted the differentially expressed genes across six time points by SCPattern (18). In total, 8968 genes were kept in this study (Supplemental Table S1). By this way, we obtained six data matrices (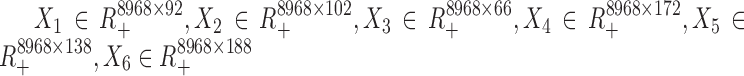) for all time points.

The CSMF model

In this study, we aim to develop a computational method CSMF for simultaneously learning common and specific patterns (or modules) among data from multiple biological conditions (Figure 1). Here, we take the gene expression data X₁ and X₂ of n genes from two conditions with m₁ and m₂ samples, respectively, as an example to illustrate our method. A common pattern in these two gene expression data is defined by satisfying the criterion that ‘the profiles extracted from a set of columns of X₁ and X₂ across a common set of rows have strong association or similar profiles among them’. In contrast, a specific pattern in one gene expression data (e.g. X₁) is defined by satisfying the criterion that ‘the profiles extracted from a set of columns of X₁ across a set of rows have strong association or similar profiles, but are not in any sets of columns of another data (e.g. X₂) across the same set of rows’. As shown in Figure 1, several latent low-rank matrix variables W_c, W_s1, W_s2, H_c1, H_c2, H_s1 and H_s2 are obtained by applying CSMF to data matrices X₁ and X₂. Among them, W_c (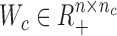, n_c is the common low-rank) is the common basis matrix shared by X₁ and X₂, W_s1 and W_s2 (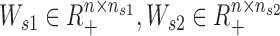, n_s1, n_s2 are the two specific low-ranks) are the specific basis matrices for X₁ and X₂, and H_c1, H_c2, H_s1, H_s2 are the corresponding common and specific coefficient matrices for X₁ and X₂, respectively. Then, we use these variables together to generate the data matrices X₁ and X₂. Specifically, for X₁, the expected expression of g_i in the common pattern k was estimated by 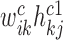, and the expected expression of gene g_i in the specific pattern k₁ was estimated by 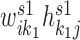. Therefore, the expected expression of g_i in the condition 1 is approximated by summing over common patterns k and specific patterns k₁:

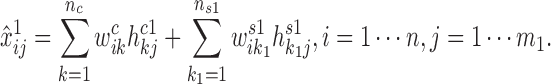(1)

Similarly, we obtain the expected expression of g_i in the condition 2:

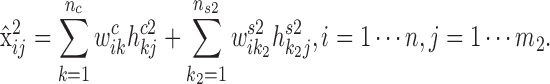(2)

Equations ((1)) and ((2)) can be rewritten in matrix format as follows:

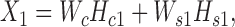(3)

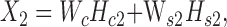(4)

We use the squared loss function to measure the relaxation error as follows:

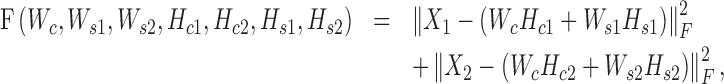(5)

where 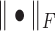is the Frobenius norm of a matrix, and all variables are non-negative matrices. The two terms denote the fitting between the expected and actual expression matrices of each condition. Thus, the latent matrix variables can be learned by solving the following optimization problem:

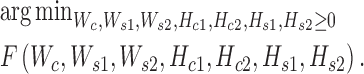Once the latent matrix variables are obtained, we reorder rows of W_c, W_s1, W_s2 and columns of H_c1, H_c2, H_s1, H_s2. Then, the reordered X₁ and X₂ with obvious patterns are obtained and shown in the right panel of Figure 1.

The CSMF algorithm

The objective function 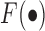is not convex with respect to all variables. Therefore, it is unrealistic to adopt a standard optimization algorithm to find the global minimum. To solve this problem, we develop the following algorithm to find a local minimum solution (or say a stationary point, which means that the relative change of the objective function is less than a small threshold, i.e. 10⁻⁶) by updating each variable alternately. And to obtain a robust solution, we adopt the disturbed solution of a heuristic method iNMF+ as the initial value of CSMF. In more detail, given a best solution (W₀, H₀) of iNMF+, a disturbed solution is obtained by 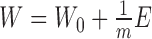, where E is a random noise matrix that follows 0–1 uniform distribution. m is the number of rows of W₀. This procedure based on W₀ is repeated 10 times. Then, these 10 disturbed solutions (W, H₀) are used as initial values of CSMF. Finally, we select the solution with least collinearity (measured by Pearson correlation coefficients between any pairwise columns of W) from these 10 repetitions (Supplementary Data).

From the algorithm, we can see that CSMF optimization problem can be solved by applying the classical NMF algorithm in the inner step. Many approaches have been proposed to solve classical NMF problem (8,19,20). We adopt an effective Nesterov's optimal gradient method to solve the classical NMF problem (NeNMF), which alternatively optimizes one factor matrix with another fixed (20). NeNMF can solve the slow convergence and non-convergence problems of other NMF algorithms (Supplementary Data). The algorithm converges to a local minimum efficiently. It is easy to see that the time complexity of CSMF algorithm is O(T_oT_inr²), where T_o and T_i are the number of outer and inner iterations wherein outer iteration indicates the iteration step t and the inner iteration represents the iteration needed for solving any subproblem in Algorithm for CSMF, respectively, r is the sum of common and specific ranks, and n is the maximum dimension of rows and columns.

General CSMF

In this subsection, we introduce a general framework to learn common and specific patterns among data from multiple biological conditions. Suppose there are K conditions and data X_i represents data matrix under the i-th condition. We need to determine the basis matrices W_c and W_si, and coefficient matrices H_ci and H_si of each condition i for learning the common and specific patterns of each condition i. We can obtain these variables by solving the following problem:

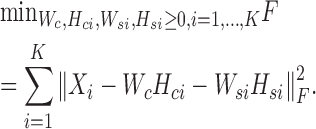(6)

The problem (6) can be solved via a two-step procedure by solving a series of classical NMF subproblems. In the first step, we fix W_si, H_si and let 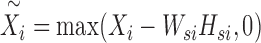. Then, we can obtain W_c and H_ci by solving the following model:

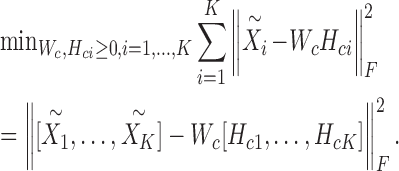(7)

In the second step, we fix W_c and H_ci and let 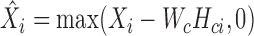. Then, we can obtain W_si, H_si by solving K typical NMF subproblems and the i-th subproblem is formulated as follows:

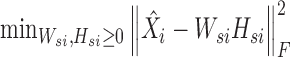(8)

Moreover, we adopt the solution of a naϊve model iNMF+ as the initial one to improve the solution (Supplementary Data; Supplementary Figures S1–S4).

Rank selection for common and specific patterns

Selection of the ranks of the common and specific patterns is an important step in practical applications. How to determine the rank of classical NMF model is still an open problem. In our CSMF model, both the common and specific ranks need to be determined. To address this challenging problem, we propose a heuristic algorithm, which includes the following two steps. (i) We take a stability-based method to infer rank K_i of each dataset by performing NMF. (ii) We decompose the inferred rank K_i into the sum of common rank n_ci and specific rank n_si based on the cross-correlation coefficients between any two basis matrices of different datasets.

Specifically, (i) the rank K_i of the data in the i-th condition is determined based on a metric D that measures the stability distance of the basis matrix relative to the initial starting values (21). Therefore, given a predefined range of ranks, we perform NMF on each data matrix and compute the metric D for each rank in the range. K_i is selected if the magnitude of D begins to increase in a large scale. (ii) K_i (= n_c+n_si) is the sum of ranks of the common pattern and the i-th specific pattern. In the step (i), the basis matrix W_j and coefficient matrix H_j are obtained by NMF. By computing the Pearson correlation coefficient between randomly selected W_j and W_k, we then find the related columns whose correlation coefficients are higher than a threshold T and obtain a new basis matrix W_s by averaging the related columns between them. This procedure is repeated between W_s and a randomly selected basis matrix from the left data matrix until the basis matrices of all the data matrices are considered. Finally, the number of related columns whose correlation coefficients are higher than T is the common rank n_c and n_si = K_i − n_ci is the rank of the i-th specific pattern. In order to avoid any column pair of basis matrices being disorder and high co-linearity, we proposed a heuristic method to fine-tune the ranks as well as the solution of CSMF (Supplementary Figure S5).

Determination of patterns

The obtained W_c, W_si and H_ci, H_si (i = 1, 2, …) are used to assign both rows (features) and columns (samples) to patterns (or say modules). The maximum coefficient can be used in each column of Hs (or each row of Ws) to determine pattern memberships. However, this method restricts the assignment for each sample or feature to one and only one pattern (22). In our application, we expect one sample or feature can be assigned to multiple or none of patterns. Therefore, we employ the column-wise (row-wise) z-score of Ws (Hs) to determine pattern memberships as used before (9). For example, we calculate the z-score for w_ij, which is the element i in the j-th column of W by 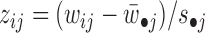, where 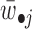is the average value of 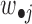and 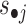is its standard deviation. We assign element j as a member of common pattern i if z_ij is greater than a given threshold T. Smaller T leads to patterns in larger size, which may contain much redundant information, while larger T makes the patterns in smaller size that leaves some patterns out.

RESULTS

Simulation study and comparison

Early studies have adopted jNMF and its various variants to identify common modules across multiple omics data (9–11). Therefore, it can be also applied to the same data type in various conditions to discover common patterns. However, jNMF cannot identify differential patterns. To show the superior performance of simultaneously learning common and specific patterns (or modules) using CSMF, we proposed two naϊve models (i.e. jNMF+ and iNMF+) based on jNMF and NMF as sequential and separated manners, respectively, to identify common and specific patterns (Supplementary Data). We generated five simulated data using the strategy used in a previous study (21) and compared the accuracy of CSMF with these two heuristic methods in identifying common and specific patterns. We adopt the area under receiver operating characteristic curves (AUC) and the area under precision-recall (AUPR) as measures to quantify the accuracy of the embedded patterns. Results showed that iNMF+ performed better than jNMF+ in the identification of both common and specific patterns with varying the ratio of common and specific parts (Supplementary Figure S1), and CSMF exhibited significantly higher accuracy than iNMF+ even for the data with overlap patterns. Therefore, CSMF is an effective method to do integration and differential analysis. Moreover, we found that using the solution of the naive model iNMF+ as the initial input of CSMF can further improve the accuracy of identification (Supplementary Figures S2–S4). These results suggest that CSMF performs better in identifying common and specific patterns, which proves that our simultaneous manner is indeed helpful to discover the hidden patterns compared to the typical separate and sequential manners.

Determine common and specific protein–DNA interaction patterns in enhancer region between K562 and Huvec cell lines

In cellular systems, enhancers can be bound by proteins to influence gene expression by activating or repressing transcription in cells. Differential analysis of modifications of two or multiple cell lines is valuable to decipher their underlying distinct combinatorial and regulatory patterns. Here, we demonstrate that CSMF can reveal not only differential modification patterns but also common ones. We applied CSMF to the pairwise ChIP-seq data with 58 997 loci of 18 histone marks or TFs of K562 and Huvec cell lines with n_c= 1, n_s1= 3, n_s2= 3 (Supplementary Data), and obtained W_c, W_s1, W_s2, H_c1, H_c2, H_s1 and H_s2. Then, we combined them to form W (each row represents a locus) and H (each column represents a mark) by

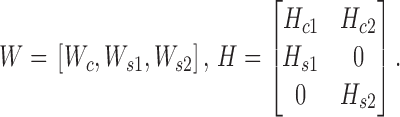Interestingly, we can see that the common pattern (named C) has strong signals with CTCF mark. Coincidently, the loci of C pattern are significantly enriched with the motifs of CTCF (Supplementary Table S5). It is well known that CTCF is a ubiquitously expressed DNA-binding protein. Previous study suggested that CTCF-binding sites are relatively invariant across diverse cell types or cell lines including K562 and Huvec (23). Moreover, DNase mark also shows strong signals in the common pattern C (Figure 2B), which is consistent with that CTCF-binding sites co-localize with DNase I hypersensitive sites. This illustrative example demonstrates that CSMF can reveal common or shared protein–DNA interaction patterns between two cell lines, which was ignored by dPCA (13).

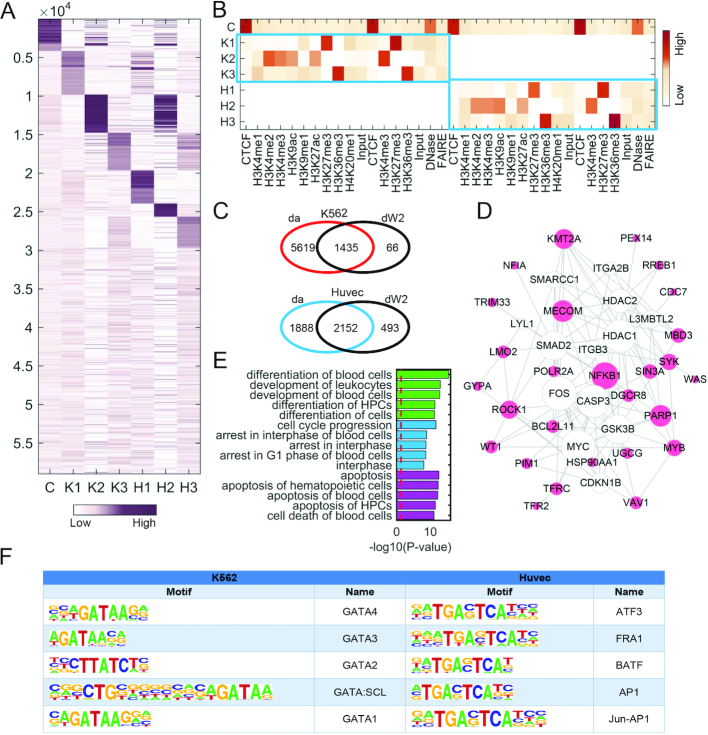
Figure 2.

Pattern discovery from the pairwise ChIP-seq data of K562 and Huvec cell lines with n_c = 1, n_s1 = 3, n_s2 = 3. (A and B) Heat maps of the basis and coefficient matrices W and H, where W is reordered according to the values in each column. Since ChIP-seq data were obtained from two different institutes (i.e. Broad Institute and University of Washington), thus one mark may have two corresponding data. (C) Venn diagram representing the overlap loci of da and dW2 across K562 and Huvec. da represents a locus set in which active marks have strong binding probability in either K562 (compared to Huvec) or Huvec (compared to K562) detected by Wilcoxon tests. dW2 represents the loci with significantly higher binding probability in K2 column of W than that of H2, and vice versa, respectively. (D) The gene network of K2 constructed using IPA and the size of gene node is proportional to its node degree. (E) The top enriched functional terms of the gene network (D) associated with cellular development, cell cycle and cell death, respectively. (F) Top 5 motifs enriched in the loci of K2 and H2 with q-value < 0.0001.

We further note that the three specific patterns (denoted as K1, K2, K3 in K562 and H1, H2, H3 in Huvec) are marked with diverse marks for K562 and Huvec, respectively (Figure 2A and B), and the marks in K1 and K2 patterns are almost the same as marks in dPC1 and dPC2 determined by dPCA. Specifically, K1, K2, K3 are marked by strong signals of a repressive mark (H3K27me3), four active marks (H3K4me2, H3K4me3, H3K9ac and H3K27ac) and a structural mark (H3K36me3), respectively. The entries of a column in W represent the binding potential of marks in the corresponding pattern to the loci. Although the three patterns H1, H2, H3 are marked with the same marks as those in K562 (K1, K2, K3), the corresponding binding loci or binding intensity show distinct difference (Figure 2A), which shapes the specificity of the two cell lines. We extracted the loci with differential binding probability (Supplementary Data) and found that such loci in pattern K2 (dW2) are enriched in the differential loci with strong signals of active marks (da) in K562 compared to signals of active marks in Huvec detected by the Wilcoxon test (Figure 2C). Moreover, the genes closing to the loci of K1, K2 and K3 are significantly enriched in leukemia associated functions (Figure 2E and Supplementary Figure S7), indicating that these patterns indeed show strong specificity relating to K562. We constructed a gene functional network for each specific pattern in K562 and explored their functions by Ingenuity Pathway Analysis (IPA, http://www.ingenuity.com) (Figure 2D and Supplementary Figure S7). In K1, we observe a highly connected gene RUNX1, which is one of the most frequent targets of chromosomal translocations in AML, playing a critical role in leukemia development. Moreover, a previous study (24) suggested that RUNX1 promoter is bound by EZH2 that is negatively regulated by H3K27m3, a key mark in K1. In the gene functional network of K2 (Figure 2D), many genes (e.g. KMT2A, MECOM, ROCK1, VAV1, BCL2L11, SIN3A, PARP1) are related with leukemia, indicating that K2 is indeed a K562-specific pattern. For example, KMT2A (also known as ALL-1 and MLL1) is a key epigenetic regulator in leukemia, which up-regulates mono-, di- and trimethylation of H3K4 (25). Moreover, many genes are connected with MYC in the gene network of K2 (Figure 2D), which is consistent with the fact that these genes locate nearby the MYC motif. These results demonstrate that the specific binding loci of K562-specific patterns revealed by CSMF are significantly associated with leukemia.

Transcription factors (TFs) play a key role in regulating the expression of many cell line-specific genes by binding certain motifs. We note a number of significantly enriched motifs locate in the differential loci using Homer (Figure 2F and Supplementary Table S5). In K2, the top 5 TF motifs are all relate to GATA TFs, which are zinc finger DNA-binding proteins, regulating transcription in cell development and cell differentiation. The functional role of most members of GATA family in leukemia has been reported in literature (26). For example, GATA1 is a relevant biomarker for acute myeloid leukemia and its overexpression is related to the expression of CD34 antigen and lymphoid T markers (27). GATA2 is found in a subset of human chronic myelogenous leukemia (28), and its overexpression determines megakaryocytic differentiation (29). Overall, these results imply that GATA TFs are expected to have a higher level of expression in K562, which is consistent with K2 being a pattern of activate marks. In H2, the top 5 TF motifs are of ATF3, FRA1, BATF, AP1 and Jun-AP1 (Figure 2F and Supplementary Table S5), which play key roles in the development of endothelial cells (30,31). For example, ATF3 is highly expressed in Huvec, which protects Huvec from TNF-α induced cell death (32). FRA1 is up-regulated in endothelial cells (33), which is consistent with that H2 is marked by active marks revealed by CSMF. At last, insulin/IGF pathway, PDGF signaling pathway and VEGF signaling pathway are significantly enriched in the genes locating to the loci in H3, indicating its specificity to endothelial cells.

Determine common and specific gene modules between two types of cancers BRCA and UCEC

We applied CSMF to two gene expression data of BRCA (breast invasive carcinoma) and UCEC (uterine corpus endometrial carcinoma) and obtained five common modules (C1,C2,C3,C4,C5), two UCEC-specific modules (U1,U2) and three BRCA-specific modules (B1,B2,B3) with n_c = 5, n_s1 = 2, n_s2 = 3 (Supplementary Data). Five common modules show diverse enriched biological functions with FDR < 0.05 (Figure 3A). These enriched biological processes relate to several key cancer hallmarks (34,35) including cell cycle, cell division, immune response, cell death and molecule metabolic process, suggesting their underlying common mechanisms between UCEC and BRCA.

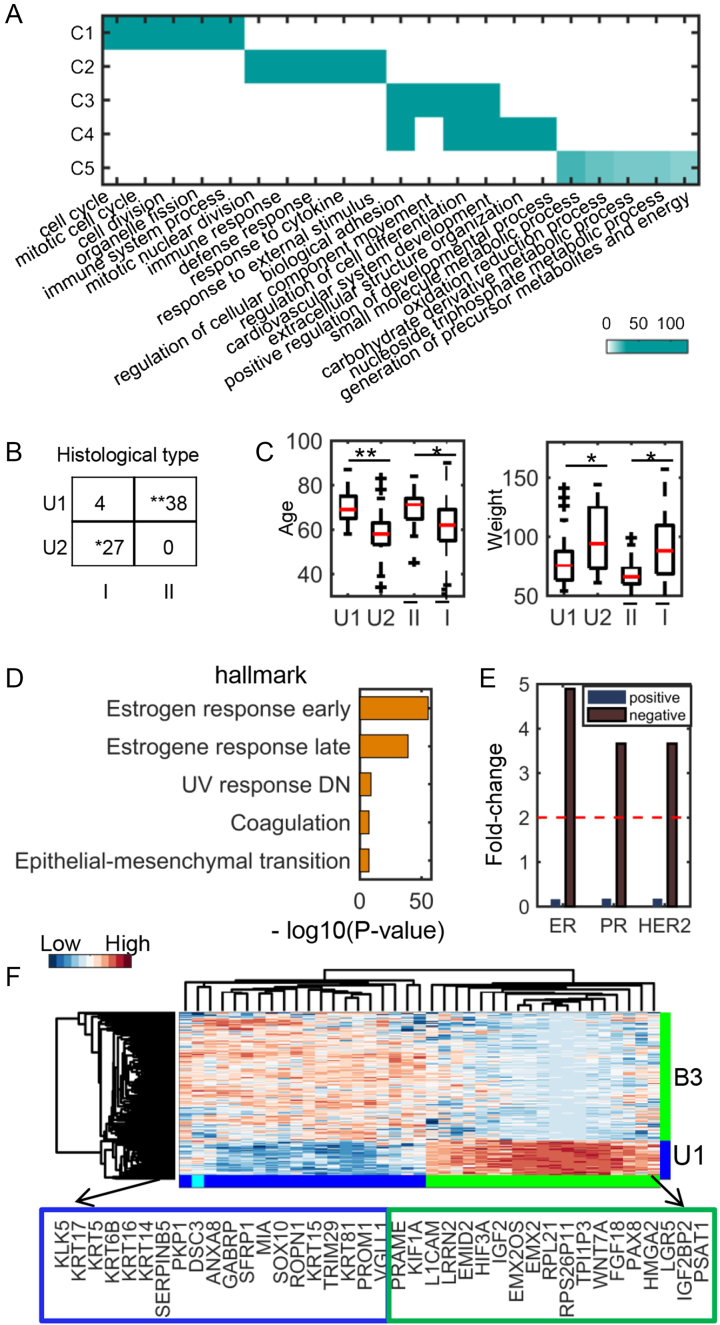
Figure 3.

Functional and clinical analysis of UCEC and BRCA common and specific modules. (A) Functional enrichments of five common modules between UCEC and BRCA. The significance values (-log10(q-value)) of the enriched biological processes are shown. (B) The distribution of histological types of patients in the two UCEC-specific modules (denoted as U1 and U2). Type I and II are endometrioid endometrial adenocarcinoma and uterine serous endometrial adenocarcinoma, respectively. (C) Comparison of age and weight distribution of patients in the two UCEC-specific modules and other patients of type I and II, respectively. and denote the type I and II patients except for those in U1 and U2, respectively. (D) Top 5 enriched hallmark signatures of B1 module. (E) The Immunohistochemistry hormone receptor status enriched in B3 module. (F) The heat map of the combined genes of top 20 highly expressed genes from U1 and B3 modules, respectively. *: 1e⁻⁵< P-value < 0.05, **: P-value < 1e⁻⁵.

We found that the two UCEC-specific modules U1 and U2 are significantly enriched in the two tumor histological types uterine serous carcinoma (type II) and endometrioid tumor (type I) (Figure 3B), revealing their functional specificity as we expected. The biomarkers associated with type II carcinoma (36) such as TROP-2, kallikrein-6 and -10, claudin-3 and -4 are enriched in module U1. Intriguingly, the U1 patients are older and thinner than the U2 patients when they get sick, which is consistent with a previous conclusion about type II and type I tumors (Figure 3C). Moreover, the age difference between patients of U1 and U2 is more significant than that between the remaining ones of type I and type II. At last, the estrogen receptor status of the patients in B1 is almost all positive, and the top two significant hallmark gene sets enriched in this module are all associated with estrogen response (Figure 3D and Supplementary Table S9). In module B3, the estrogen receptor, progesterone receptor and human epidermal growth factor receptor 2 all tend to be in negative status (Figure 3E), implying that the module B3 is enriched with triple-negative breast tumors. Though uterine serous carcinomas share many molecular features with basal breast tumors such as high frequency of TP53 mutation and low frequency of TPEN mutation, they do show some differences including distinct mutation frequency of PIK3CA, PPP2R1A and FBXW7 (37). CSMF reveals differentially expressed genes between triple-negative breast cancer in B3 module and uterine serous carcinomas in U1 module (Figure 3F), in which the overexpressed genes KRT5, KRT6B and KRT14 in B3 are indeed basal markers (38).

Determine common and specific gene patterns among breast cancer subtypes

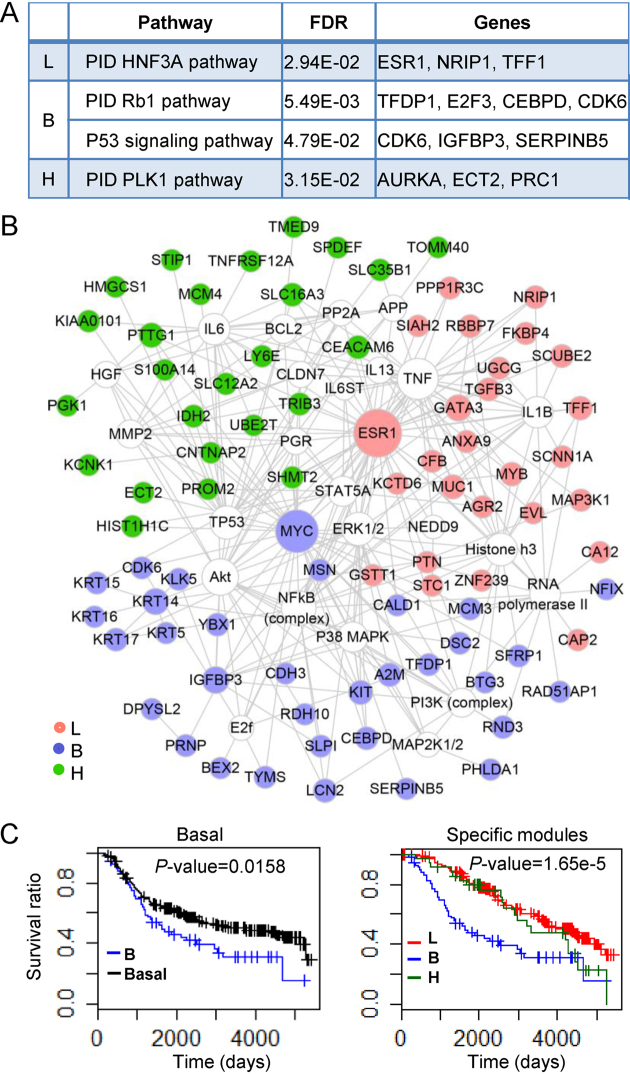
To show the ability in the identification of cancer hallmarks and subtle differences among different cancer subtypes, we applied CSMF to gene expression of three breast cancer subtypes including lum (denoting the combination of luminal A and B tumors), basal and her2 tumors to explore the underlying mechanisms among them with n_c = 4, n_s1 = 1, n_s2 = 1, n_s3 = 1 (Supplementary Data). We determined four common gene patterns (C1, C2, C3, C4) and one specific pattern (L, B, H) for each subtype using CSMF. We can see that these four common gene modules are involved in the typical cancer hallmarks like cell cycle, cell death, immune response and cellular metabolic process (Supplementary Figure S9). More interestingly, each subtype-specific pattern tends to relate to subtype-specific pathways (Figure 4A and Supplementary Table S11). For example, lum-specific pattern is enriched with PID HNF3A pathway, where HNF3A (also known as FOXA1) is a marker of good outcome in breast cancer. Tumors with highly expressed FOXA1 are mostly classified as luminal A ones (39). Thus, this pattern is indeed a subtype-related functional module. Basal-specific pattern B tends to be enriched in PID Rb1 pathway and biological processes like cell cycle, G1 phase and G1/S transition, which is consistent with that the tumor suppressor gene Rb1 plays a key role in regulating the cell cycle process. We note that Rb1 deletion or mutation, INK4a (also known as CDKN2A) deletion, mutation or silencing and CCND1, CDK4 and CDK6 overexpression can cause Rb1 loss or Rb1 hyperphosphorylation that further disorders G1/S checkpoint (40). A previous study uncovered a strict inverse correlation between E2F3 and Rb1 expression in human basal-like breast cancer (41). Surprisingly, E2F3 is highly expressed in B module, which is consistent with that Rb1 loss is more common in triple negative breast cancers than in other subtypes (42). Interestingly, although patients with triple negative breast cancers lacking Rb1 may have good clinical outcome under conventional chemotherapy (40), the clinical performance of patients in the basal-specific pattern B is the worst among all patients in basal subtype. Therefore, the result implies that a simple loss of Rb1 function is not responsible for the increased sensitivity of triple negative tumors to chemotherapy as suggested in a previous study (42). At last, her2-specific pattern H tends to be enriched in PID PLK1 pathway. PLK1 is a key regulator associated with cell cycle, and it is also associated with her2 (43).

Figure 4.

Biological functions and survival analysis of lum-, basal- and her2-specific modules (L, B, H). (A) The selected enriched pathways of each specific module. (B) Networks of genes (filled circles) in the three specific patterns visualized by Cytoscape. (C) The survival curve of patients in the basal-specific module. This curve is compared with that of all patients in the basal subtype (left) and that of all patients in lum- and her2-specific modules (right).

We further constructed a gene functional network considering only the experimentally verified relationships with IPA (Figure 4B) to demonstrate the distinct functional specificity of the three subtype-specific patterns. Literature study suggests that a lot of genes in the network are associated with each breast subtype (Supplementary Table S12). For example, GATA3 has been implicated in the luminal types of breast cancer, which is overexpressed in the lum-specific subnetwork. Moreover, its coding protein is a transcription factor that regulates the differentiation of luminal cells in the mammary glands (30,31). The basal-like tumors associated basal cytokeratins (KRT5, KRT6, KRT14, KRT15, KRT16, KRT17) are highly expressed in basal specific-pattern B, demonstrating its specificity. Particularly, KRT5 serves as an important biomarker distinguishing basal subtype and other subtypes of breast cancer. Moreover, the patients in basal-specific pattern have worse survival performance within the first 5 years relative to the remaining basal tumors and those in other patterns (Figure 4C). PGK1 is a downstream effector of her2 signaling, which contributes to the tumor aggressiveness of breast cancer. It is highly expressed in her2-specific module, confirming the functional specificity of this pattern (44).

Identify common biological process and stage-specific subpopulations along the differentiation of human pluripotent cells

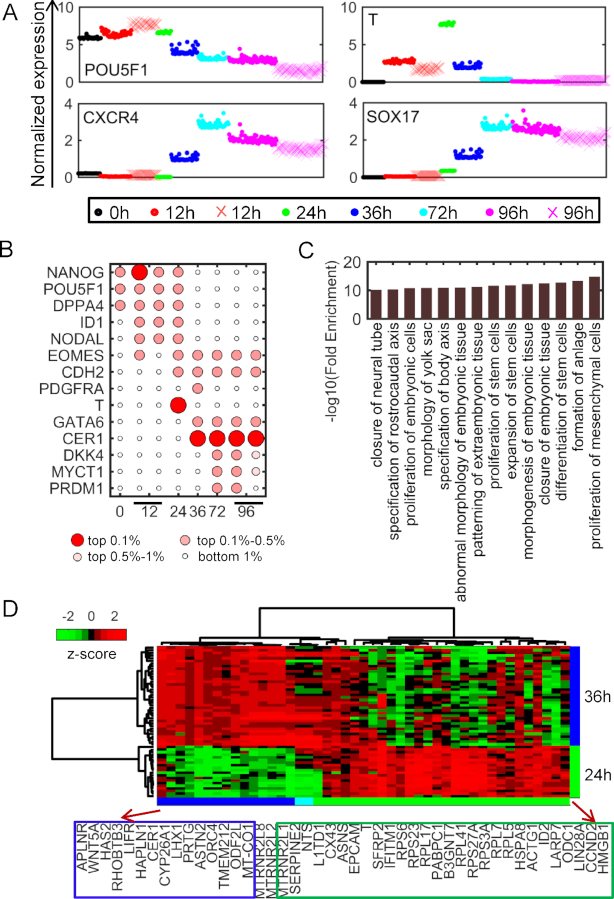
With the development of single cell sequencing technology, it provides us an opportunity to study the underlying cellular heterogeneity at a single cell resolution. We investigated the potential of CSMF to disentangle the heterogeneity during human embryonic differentiation. This time-course scRNA-seq data consists of 8968 genes (rows) and 92, 102, 66, 172, 138, 188 cells (columns) at six time points (0, 12, 24, 36, 72 and 96 h), respectively (18). We identified one common pattern and 1, 2, 1, 1, 1, 2 stage-specific patterns at each time point (Supplementary Data). The highly expressed genes of the common pattern are enriched in the biological processes including cell cycle, biosynthetic process, regulation of catabolic process and RNA processing, suggesting that these biological processes are participant in the embryonic differentiation process (Supplementary Table S14). The expressions of marker genes (POU5F1, T, CXCR4 and SOX17) of embryonic differentiation are highly expressed in their corresponding subpopulations (Figure 5A). Furthermore, we obtained two stage-specific cell subpopulations at 12 and 96 h, respectively. POU5F1 and T show very diverse expressions in the two subpopulations at 96 and 12 h, respectively. It might suggest that one subpopulation differentiates more slowly than another one (Figure 5A).

Figure 5.

Cell subpopulations identified by CSMF from the time-course scRNA-seq data. (A) The expressions of marker genes in each specific pattern. (See online colored version: dots in specific patterns are represented by different colors and dots indicated by × with shallow red and rose red represent cells in 12 h- and 96 h-specific subpopulation II, respectively). (B) Significance of selected markers enriched in each time-specific pattern determined by W. (C) The enriched biological processes of the intersection of genes in Wnt signaling pathway and genes differentially expressed between 24 h- and 36 h-specific patterns. (D) The heat map of genes described in panel (C) in the cells from 24 h- and 36 h-specific patterns.

CSMF can reveal subpopulation-related genes that include known differentiation-associated gene markers (Figure 5B). For example, NANOG and POU5F1 are highly expressed at 0 h during cell differentiation. They indeed play important roles in the maintenance of pluripotency of human embryonic stem cells. However, NODAL, EOMES and ID1 are highly expressed at 12 h and T is highly expressed at 24 h. It is well known that T is the key marker of mesendoderm in embryonic stem cell studies and it is first expressed in the primitive streak (45,46). Moreover, the two definitive endoderm-specific genes CER1 and GATA6 are highly expressed at 36 h. Actually, CER1 is one of the top important genes at 36, 72 and 96 h during differentiation (Figure 5B). These key stage-specific gene markers revealed by CSMF are consistent with a previous study based on a differential expression analysis tool SCPattern (18), which cannot reveal stage-specific cell subpopulations.

The subpopulation-related genes indeed point to key differentiation process such as the birth of definitive endoderm. To our knowledge, the hypoxic treatment experiments suggest that the birth of nascent definitive endoderm cells is a well-timed event (18). We combined the top 30 genes in 24 h- and 36 h-specific patterns together and obtained 45 genes after removing the ERCC family genes. This gene set is enriched in the Wnt signaling pathway, which is crucial for the development of endoderm (47,48). These genes have different expression patterns accompanying differentiation toward definitive endoderm and are involved in differentiation of stem cells and proliferation of mesenchymal cells (Figure 5C and Figure 5D). Previous studies suggested that cells undergo mesenchymal transition when the embryonic stem cells differentiate into definitive endoderm during gastrulation (49). All these observations demonstrate that the patterns uncovered by CSMF reveal novel hidden characteristics among the biological data of interrelated scenarios.

DISCUSSION

With the rapid development of high-throughput technologies (e.g. ChIP-seq, RNA-seq and scRNA-seq), a huge number of genomic data of different biological conditions have been profiled and collected, providing a grand opportunity to decipher the underlying commonality and specialty among diverse biological conditions through large-scale integrative and comparative analysis. However, current integrative methods usually ignore the differential part, and typical differential analysis methods either fail to identify the combinatorial patterns of difference (e.g. differential expression analysis tool limma) or require matched dimensions of the data (e.g. dPCA). To this end, we propose a powerful and flexible mathematical framework CSMF, which only requires one matched dimension and is suitable for analyzing data generated by different techniques such as RNA-seq, ChIP-seq and scRNA-seq. To our knowledge, this is the first report to propose the idea to identify common and specific patterns simultaneously using NMF technique.

We have demonstrated the utility of CSMF as an effective tool to reveal hidden common and specific patterns among complex data across diverse conditions. As we shown in the simulation study, compared to the typical separate and sequential manners based on either differential or integration analysis, our simultaneous manner shows superior performance. Our proposed model is different from differential expression analysis when it is applied on gene expression data between case and control groups, which only identifies a list of genes with statistical significance. On the contrast, CSMF can identify the combinatorial patterns of the differently expressed genes and these combinatorial patterns have strong biological interpretability. To demonstrate its power, we applied CSMF to four applications. Application to the pairwise ChIP-seq data describing the chromatin modification map on protein–DNA interactions between K562 and Huvec cell lines, CSMF discovered stable CTCF binding loci and three differential patterns with consistent marks but with differential binding intensities between K562 and Huvec. By comparing transcriptional profiles of two types of cancers BRCA and UCEC or various subtypes of BRCA, CSMF identified cancer hallmark-enriched common modules and cancer-specific or subtype-specific biological modules. Furthermore, not only differentially expressed marker genes but also the corresponding stage-specific cell subpopulations can be identified when CSMF was applied to the scRNA-seq data with six time points.

Recently, rapid development of single-cell sequencing technology enables fast accumulation of large amounts of scRNA-seq data across different conditions, tissues and platforms. Integrative and comparative analysis of these data is essential for translating it into biological insight (50). For example, Kiselev et al. presented a method for projecting cells from an scRNA-seq data set onto cell types or individual cells from other experiments (51). Butler et al. introduced an strategy for integrating scRNA-seq datasets based on common sources of variation learned from canonical correlation analysis (CCA) (52). CSMF combines dimension reduction and comparative analysis into one paradigm. As a tool for comparative analysis, CSMF is able to identify common and specific gene patterns across different scRNA-seq data sets, providing insights into hidden combinatorial patterns embedded in these interrelated data. As a tool for dimension reduction, the learned low-dimensional representations of the scRNA-seq data, including common and specific sources of variation, are useful for the identification of shared and specific subpopulations across datasets.

Each subproblem of CSMF was converted into the classical NMF problem. Therefore, the runtime of CSMF is currently dominated by the NMF. We improved its computational ability by applying Nesterov’s accelerate method to solve the classical NMF instead of adopting commonly used multiplicate update rule. However, with the increasing number of samples, e.g. tens of thousands of samples, future work is needed to develop more efficient NMF update method and implement in a parallel platform with an accelerated strategy. In addition, selecting a well-reasoned number of common and specific patterns for CSMF is a challenging issue, and we proposed a heuristic method to address it (Supplementary Data). In future studies, we will design more elaborate mathematical penalties onto the factorization to enhance the pattern discovery. Moreover, CSMF should be applicable to many other kinds of data such as copy number variation, DNA methylation and miRNA expression of different conditions, which will help us understand the data heterogeneity and underlying patterns.

DATA AVAILABILITY

A MATLAB package CSMF is available at http://page.amss.ac.cn/shihua.zhang/software.html.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Natural Science Foundation of China [11661141019, 61621003, 61422309, 61379092]; Strategic Priority Research Program of the Chinese Academy of Sciences (CAS) [XDB13040600]; National Ten Thousand Talent Program for Young Top-notch Talents; Key Research Program of the Chinese Academy of Sciences [KFZD-SW-219]; National Key Research and Development Program of China [2017YFC0908405]; CAS Frontier Science Research Key Project for Top Young Scientist [QYZDB-SSW-SYS008]. Funding for open access charge: National Natural Science Foundation of China [11661141019].

Conflict of interest statement. None declared.