SUMMARY
Computational modeling of brain mechanisms of cognition has largely focused on the cortex, but recent experiments have shown that higher-order nuclei of the thalamus participate in major cognitive functions and are implicated in psychiatric disorders. Here, we show that a pulvino-cortical circuit model, composed of the pulvinar and two cortical areas, captures several physiological and behavioral observations related to the macaque pulvinar. Effective connections between the two cortical areas are gated by the pulvinar, allowing the pulvinar to shift the operation regime of these areas during attentional processing and working memory and resolve conflict in decision making. Furthermore, cortico-pulvinar projections that engage the thalamic reticular nucleus enable the pulvinar to estimate decision confidence. Finally, feedforward and feedback pulvino-cortical pathways participate in frequency-dependent inter-areal interactions that modify the relative hierarchical positions of cortical areas. Overall, our model suggests that the pulvinar provides crucial contextual modulation to cortical computations associated with cognition.
In Brief
Very little is known about the function of the thalamus beyond relaying sensory information to the cortex. Jaramillo et al. present a biologically based model of pulvino-cortical interactions and provide a unified account of the pulvinar’s computational role across cognitive tasks.
INTRODUCTION
The thalamus is involved in a myriad of functions essential to an animal’s survival, including linking the sensory world to the cortex and regulating sleep, alertness, and wakefulness (Ward, 2013). Thalamic nuclei are reciprocally connected to the cortex and other subcortical structures (Jones, 2007). Despite links between defective thalamo-cortical circuitry and psychiatric disorders, such as schizophrenia, bipolar disorder, and autism (Anticevic et al., 2014; Nair et al., 2013), thalamic contributions to cognitive processes remain underexplored.
Investigation into the circuit mechanisms of sensory thalamus has already been successful in describing the transfer of sensory information from the periphery into the cortex (Briggs and Usrey, 2009). Much less is known about the computations taking place in higher order thalamic nuclei, i.e., those receiving their driving input from the cortex (Sherman and Guillery, 2013). Far from being a passive relay, the thalamus is now known to play an active role in many of the cognitive functions typically attributed to the cortex alone (McAlonan et al., 2008; Saalmann and Kastner, 2011; Wimmer et al., 2015; Bolkan et al., 2017; Schmitt et al., 2017).
The primate pulvinar is part of the visual thalamus and is a prominent example of a higher order nucleus whose exact function remains unresolved (Saalmann and Kastner, 2011; Halassa and Kastner, 2017). Early studies recognized the pulvinar to play a role in attentional processing, as single neurons in the pulvinar were modulated by attentional cues (Petersen et al., 1985) and lesions to the pulvinar resulted in attentional deficits, including hemispatial neglect toward the contralesional visual field (Wilke et al., 2010, 2013; Karnath et al., 2002) as well as a deficit in filtering of distractors (Desimone et al., 1990). These results have been confirmed in behavioral and fMRI studies (Danziger et al., 2004), although some of the more subtle effects remain disputed (Strumpf et al., 2013). On the other hand, a recent study showed that the firing rate of neurons in the macaque pulvinar correlated with confidence during a decision-making task with an opt-out component (Komura et al., 2013). It is not known how and why the pulvinar contributes to these seemingly disparate cognitive functions.
As part of the visual thalamus, the pulvinar is connected to virtually all of the visual sectors along the cortical hierarchy (Shipp, 2015). Although the lateral and ventral parts of the pulvinar are connected to early visual cortices (Kaas and Lyon, 2007), the medial pulvinar is connected to association cortices, such as the parietal, temporal, and prefrontal cortex (Romanski et al., 1997; Gutierrez et al., 2000). Notably, visual areas and fronto-parietal areas are consistently recruited during tasks that engage or require attention (Buschman and Miller, 2007), working memory (Suzuki and Gottlieb, 2013), and decision making (Siegel et al., 2015). The fact that the neural computations underlying these cognitive functions depend on local, i.e., within-area, as well as on long-range, i.e., across-area, connectivity (Buschman and Kastner, 2015; Christophel et al., 2017; Brody and Hanks, 2016) suggests that the pulvinar could impact cognitive function by modulating cortical computations through pulvino-cortical projections, but a plausible circuit mechanism has not been proposed.
To elucidate the pulvinar’s contributions to cognition, we put forward a framework that connects cortical to thalamic computation. This framework relies on, first, a canonical cognitive-type circuit in the cortex (Wang, 2013; Murray et al., 2017) and, second, on the existence of two well-defined anatomical pathways that connect the pulvinar to the cortex and back: (1) a feedforward or transthalamic pathway that relays cortical information to a second cortical area (Sherman and Guillery, 2013) and (2) a feedback or reciprocal pathway that originates in one cortical area, targets the thalamic reticular nucleus (TRN) and pulvinar, and then projects back to the same cortical area. We built a pulvino-cortical circuit model to map the aforementioned pathways to behaviorally relevant computations for attention, working memory, and decision making and to sharpen the interpretation of recent studies that combined pulvinar electrophysiology with behavior (Komura et al., 2013; Saalmann et al., 2012; Zhou et al., 2016). Overall, our results suggest that the pulvinar, through the feedforward and feedback pulvino-cortical pathways, is uniquely positioned to provide crucial contextual modulation to cortical computations associated with cognition.
RESULTS
We have designed a pulvino-cortical circuit to model cognitive tasks that involve the selection of one of two choices, i.e., two-alternative-forced choice (2AFC) tasks. The three-module circuit we propose consists of two reciprocally connected cortical areas and the pulvinar (see Figure 1 and STAR Methods for details). The two-module cortical circuit in isolation (i.e., without engagement of the pulvinar) can, in principle, support a set of cognitive-type computations, including visual selection, evidence accumulation during decision making, and persistent activity for working memory (Murray et al., 2017).
Figure 1. A Pulvino-cortical Circuit for Two-Alternative Forced Choice Tasks.
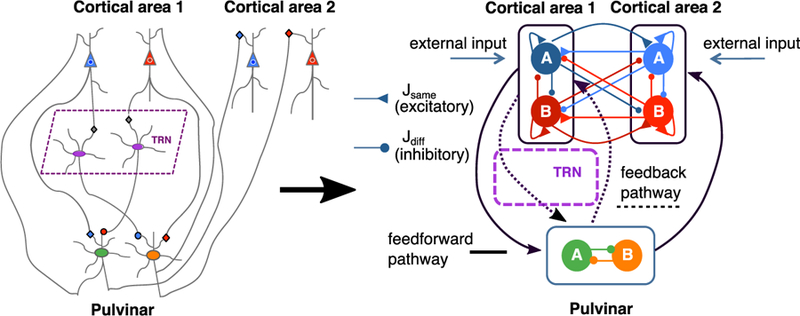
The simplified circuit to the right is composed of three modules: two reciprocally connected cortical modules (1 and 2) and the pulvinar that receives projections from and projects to the cortex through feedforward (solid lines) and feedback (dotted lines) thalamo-cortical pathways. A module here is defined as a set of two excitatory populations (blue and red in cortex; green and orange in pulvinar), where each population is selective to one of two choices, A or B. Inhibition is represented by negative weights, which are meant to represent long-range projections from excitatory neurons onto inhibitory neurons (Wong and Wang, 2006). In general, synaptic weights J can connect two selective populations of either the same (Jsame > 0, excitatory) or opposite (Jdiff < 0, inhibitory) stimulus selectivity and can be either local (within area) or long-range (across areas). The thalamic reticular nucleus (TRN) allows for long-range disynaptic inhibition from the cortex onto the pulvinar as well as mutual inhibition within the pulvinar. The cortico-pulvino-cortical connections follow the general topography of the cortico-cortical connections. Synapses labeled with triangles and circles denote effective excitatory and inhibitory connections, respectively.
To establish the connectivity between the pulvinar and the two cortical areas in our model, we distinguish two pathways (Jones, 2007; Sherman and Guillery, 2013): (1) a transthalamic feedforward pathway that includes a projection from cortical area 1 to a pulvinar relay cell population followed by a projection from the aforementioned relay cells to cortical area 2 and (2) a feedback pathway that originates in either of the cortical areas, targets the TRN and pulvinar, and then projects back to the same cortical area.
For the tasks modeled in Figures 2, 3, 4, 5, and 6, we will model pulvinar activity and study how this activity modulates the cognitive-type computations in the cortex via pulvino-cortical feedforward and feedback pathways. Although we will invoke this general pulvino-cortical circuit architecture throughout the text, we will clarify what region of the pulvinar we are referring to when we introduce experimental or modeling results. We will also consider alternative topologies in Figure S1 and a cortical circuit with laminar structure in Figure 7 when we discuss frequency-dependent inter-areal interactions.
Figure 2. Pulvinar Lesion-Induced Gain Imbalance Produces Asymmetric Attentional Deficits.
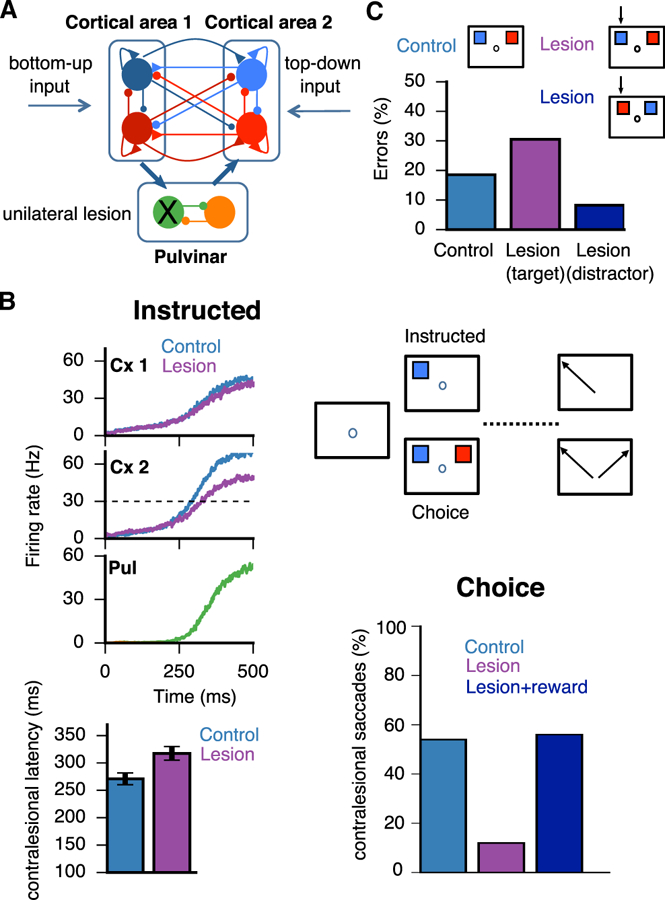
(A) Schematic as in Figure 1, where external inputs are labeled as either bottom-up (sensory) or top-down (internal), with pulvinar excitability λ = 230 Hz/nA. A unilateral lesion to the medial pulvinar is shown that affects the left visual field. Topography thus corresponds to visual and not anatomical space. (B) Visuospatial task based on Wilke et al. (2013), where a subject must make a saccade toward a visual target after a delay period (instructed) or select one of two simultaneously presented visual targets on opposite sides of the visual field (choice). In the instructed task, saccade latencies toward the contralesional field are larger than in controls. In the choice task, the proportion of saccades to the contralesional field is reduced compared to controls but ameliorated with the addition of reward (Wilke et al., 2013). Data are represented as mean ± SD. (C) Visuospatial task modeled after Desimone et al. (1990), where a subject must attend to and select a target (blue) that was flashed at the same position as a cue presented during fixation. A distractor (red) is presented simultaneously in the opposite hemifield. Simulations are performed for control and unilateral lesion of the lateral pulvinar. Black arrows point to the affected visual hemifield, and two conditions can be distinguished: either the target (magenta) or the distractor (dark blue) lies within the affected hemifield. Error rates are shown below.
Figure 3. Gating of Effective Cortico-cortical Connectivity and Persistent Activity through Pulvinar Gain Modulation.
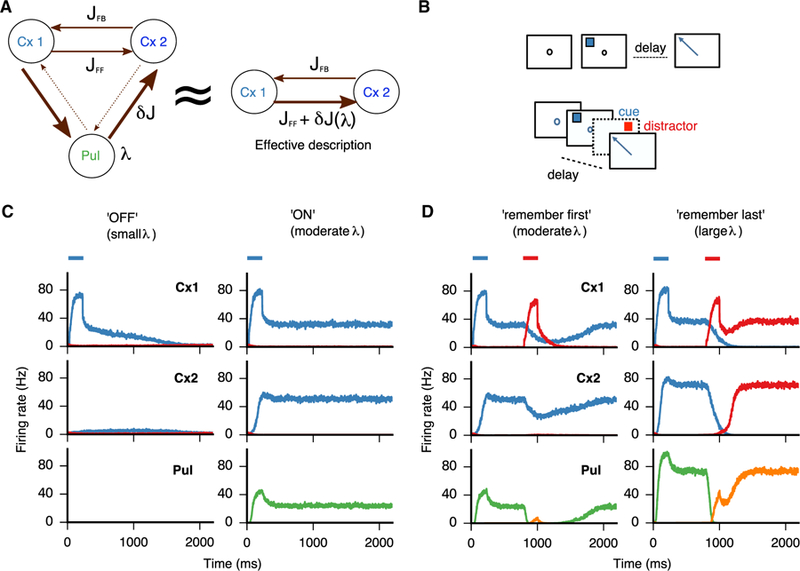
(A) A three-module pulvino-cortical architecture is equivalent to a two-module cortical architecture, where the effective cortico-cortical connectivity is controllable via the pulvinar excitability λ and δJ denotes the λ-dependent extra connectivity provided by the transthalamic route. (B) Schematics of the tasks in (C) (top, simple memory-saccade task) and (D) (bottom, memory saccade with distractor during the delay period). (C) In a simple memory saccade task, persistent activity in the cortico-thalamic system is contingent on the activation of the (medial) pulvinar, which can act as a switch. When the pulvinar is “off” (λ = 120 Hz/nA), the activity decays in the first cortical area and no activity is observed in the rest of the pulvino-cortical system. When the pulvinar is “on” (λ = 220 Hz/nA), reciprocal loops with the cortex are enough to sustain reverberant activity in the cortico-thalamic circuit and a global attractor is reached. (D) In a memory-saccade task with a distractor, the pulvinar can control the response of the system by biasing the circuit into making the system more (“remember first,” λ = 220 Hz/nA) or less (“remember last,” λ = 280 Hz/nA) robust to distractor interference. Blue and red bars denote target and distractor presentation times, respectively.
Figure 4. Pulvinar-Mediated Effective Connectivity between Cortical Areas Resolves Conflict in Decision Making.
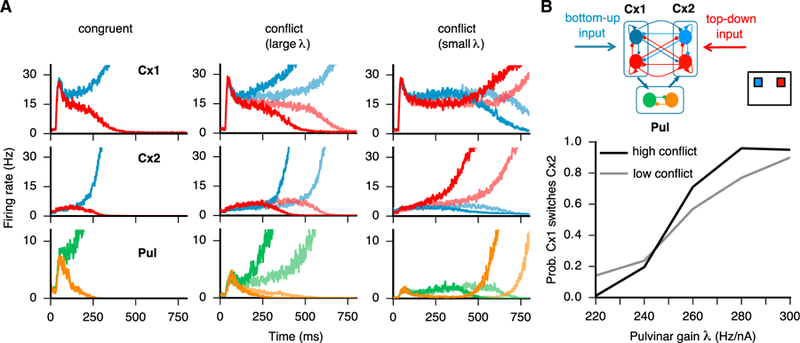
(A) Conflict resolution in the pulvino-cortical model. In the congruent scenario (left), bottom-up and top-down inputs target populations with the same selectivity so that a consistent decision is made. In the conflict scenario (middle and right), bottom-up input favors the blue excitatory population in cortical area 1 and top-down favors the red excitatory population in cortical area 2, resulting in inter-areal competition. For large λ (λ = 290 Hz/nA), the effective feedforward pathway connecting cortical area 1 to 2 is preferentially biased so that the choice reflects bottom-up information (middle). For small λ (λ = 220 Hz/nA), the effective feedforward strength is decreased so that the choice reflects top-down input (right). High (c′ = 20) and low (c′ = 10) conflict trials are shown in thick and thin lines, respectively. (B) Schematic of conflicting stimuli and responses in the pulvino-cortical circuit (top). In the conflict scenario, the probability of cortical area 1—bottom-up recipient—enforcing its encoding to cortical area 2—top-down recipient—depends on the value of the pulvinar excitability λ and on the conflict level c′ (bottom).
Figure 5. Calculation of Absolute Differences by a Circuit that Engages the Cortex, Pulvinar, and TRN.
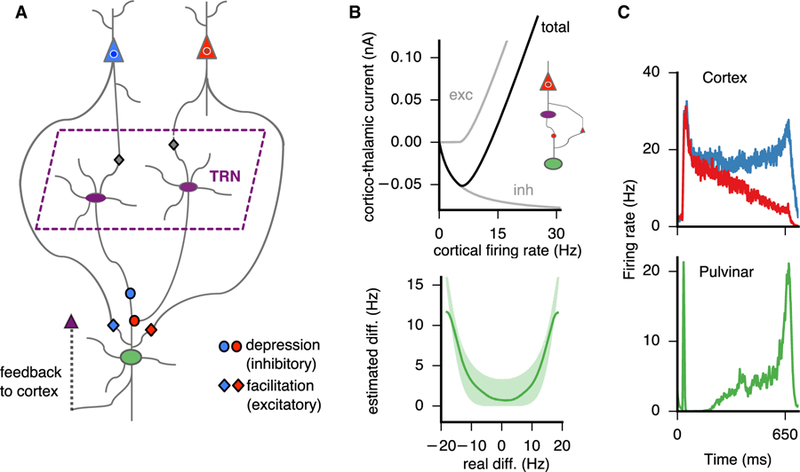
(A) The cortical circuit component consists of two cortical populations (here schematically represented by single neurons) differentially selective to two distinct stimuli, blue and red. The excitatory cortico-pulvinar connection exhibits short-term facilitation, and the inhibitory TRN-pulvinar connection exhibits short-term depression. (B) Top: the short-term synaptic dynamics in the thalamo-cortical circuit result in non-linear function of the cortical firing rate so that the input is effectively inhibitory for low firing rates but excitatory for high firing rates. Inset shows the motif that generates the plot for a single cortical cell. Bottom: the resulting pulvinar activity (λ = 300 Hz/nA) resembles approximately an absolute value function of the difference between the firing rate activities of the two cortical cells. Shaded region (light green) represents individual data points; line (green) represents an average polynomial interpolation. (C) Firing activites of the cortex (top) and pulvinar (bottom), where the pulvinar integrates the cortical activity and approximately calculates the absolute value of the difference between the activities of the competing cortical populations.
Figure 6. A Pulvino-cortical Circuit for Estimating Decision Confidence.
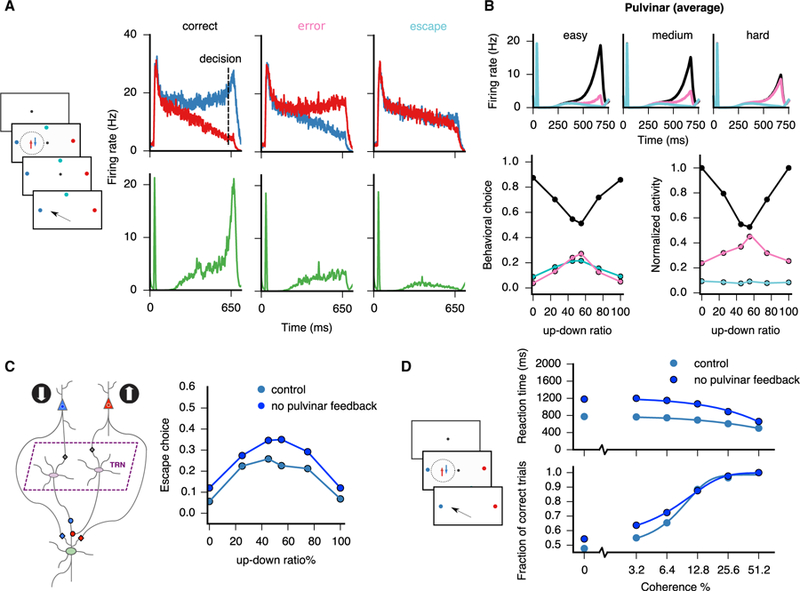
(A) Schematic of the task is shown on the left (see details in main text). Single cells in the pulvinar (green, bottom) represent confidence through their firing rate for correct, error, and escape trials. A necessary condition for a correct trial is that the cortical population representing more evidence, here the blue population (top), has a greater activity than the population representing less evidence, the red population, at the time of decision. Moreover, for both correct and error trials, the difference between the activities at the decision time must be greater than a predefined bound ε = 4 Hz. Otherwise, the subject forgoes the decision and escapes (opts out). (B) Top: average pulvinar firing rates as a function of difficulty (easy, medium, and hard) and trial type (correct, black; error, pink; escape, cyan), color coded as in (A). Bottom: behavioral choice (left) and normalized pulvinar activities (right) as a function of difficulty and trial type are shown. (C) Simulated unilateral lesion to the pulvinar, i.e., no feedback to the cortex, causes an increase in escape frequency with respect to control. (D) In a reaction-time version of the random-dot discrimination task, a lesion to the pulvinar results in slower reaction times with higher accuracy (a form of speed-accuracy tradeoff), more noticeable at low coherence levels.
Figure 7. Thalamic Gating of Gamma and Alpha Oscillations across Cortical Areas.
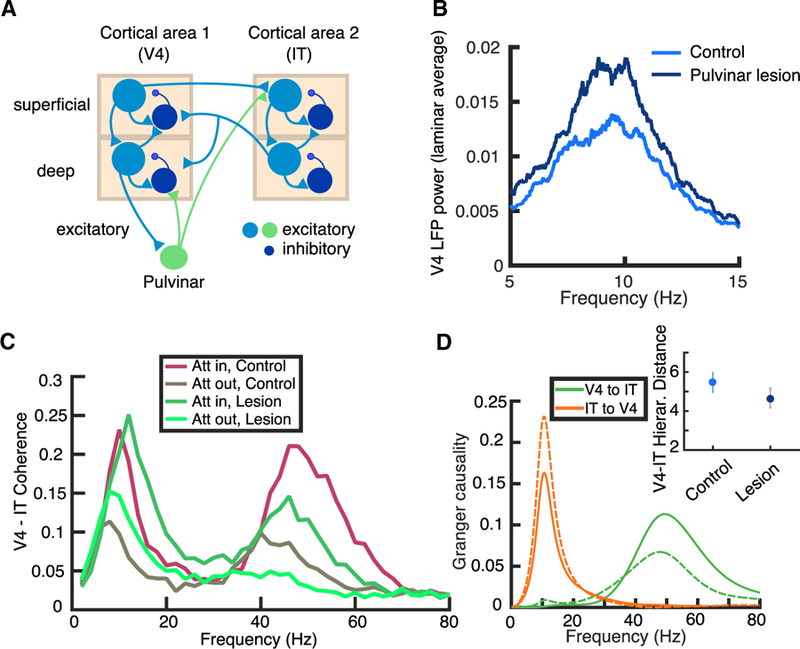
(A) Schematic of a distributed pulvino-cortical circuit with laminar structure. The model is composed of two reciprocally connected cortical modules (here, V4 and IT) and the ventro-lateral pulvinar that both receives projections and projects to the cortical modules. The transthalamic projection targets layer IV in the cortical area 2, which is then relayed to the superficial layers. (B) After a lesion to the pulvinar, the spectral power measured from the V4 population activity exhibits an increase in the low-frequency (alpha) regime. (C) The two cortical areas are coherent at gamma and alpha frequencies. Gamma coherence is decreased after lesioning the pulvinar, and alpha coherence increases. Attention enhances coherence in both alpha and gamma frequencies. (D) The coherence effects observed in (C) extend to Granger causality, which in addition measures directionality. Control and pulvinar lesion scenarios are shown in solid and dashed lines, respectively, in the “attention in” condition. Inset shows that the hierarchical distance between the cortical areas decreases after a pulvinar lesion. See also Zhou et al. (2016) and Saalmann et al. (2012). Data are represented as mean ± SD.
Pulvinar Lesion-Induced Gain Imbalance Produces Asymmetric Attentional Deficits
Lesion studies have provided important insights into the role of the pulvinar in tasks that engage attention (Wilke et al., 2010, 2013; Snow et al., 2009; Desimone et al., 1990). At least two distinct effects have been observed after unilateral lesions of the pulvinar: hemispatial neglect, whereby one area of the visual field is inaccessible either due to lack of perceptual awareness or motivation (Wilke et al., 2010, 2013), and a deficit in distractor filtering, whereby performance in a visual search task decreases when a target is flanked by irrelevant distractors (Desimone et al., 1990; Snow et al., 2009; Strumpf et al., 2013). To better understand and constrain the dynamics of our pulvino-cortical circuit, we first examine the behavioral impact of unilateral lesions to the pulvinar (Figure 2).
The first task was modeled after Wilke et al. (2013). In this task, subjects have to select a target that appears on a screen after a fixation period. In the instructed variant of the task, only one target is presented and subjects have to make a saccade toward the cued target to obtain a reward. In the choice variant, the subjects are presented with two targets that yield equal reward when selected (see Figures 2A and 2B and STAR Methods).
After a unilateral lesion, there is an attentional disruption in the contralesional field of lesioned subjects with respect to control (Figure 2B). On instructed trials, unilateral lesions cause an increase in saccade latency toward the contralesional field. On choice trials, the proportion of saccades toward the contralesional field decreases as compared to control. Interestingly, this effect is ameliorated by the addition of more reward to the target on the contralesional side, as reported by Wilke et al. (2013). In our model, such attentional deficits are observed because the lesion effectively reduces the excitation toward the contralesional, i.e., affected visual hemifield, which in turn induces a gain imbalance in the multi-regional circuit. This pulvinar-induced imbalance is quickly amplified by the recurrent circuitry in the cortex and propagated asymmetrically throughout the pulvino-cortical circuit to produce the impairments described.
Pulvinar lesions are known to affect distractor processing in humans and non-human primates (Desimone et al., 1990; Danziger et al., 2004; Snow et al., 2009). To understand why this is the case, we modeled a second task after Desimone et al. (1990), where a subject must attend to and select a target that was flashed at the same position as a cue presented during fixation (Figure 2C). We found that, only when the target was located in the affected visual hemifield (opposite to the site of the simulated anatomical lesion to the lateral pulvinar), the error rate increased with respect to controls. A slight improvement in performance was observed in the opposite scenario, when the distractor was located in the affected hemifield (Wilke et al., 2010; Desimone et al., 1990). In essence, the non-linear winner-take-all circuit effectively suppresses representations that are not as behaviorally relevant as the target. Along these lines, we suggest that the topography of the pulvino-cortical connections, i.e., excitatory projections between cells having similar selectivity and cross-inhibition between cells with opposite selectivity, is the structural mechanism underlying distractor filtering.
Note that we used the lesion versus control simulations to set the basic parameters for the cortical and thalamic modules that will be used in the rest of the figures (see Table 1).
Table 1.
Parameters for Numerical Simulations
| Parameter | Description | Task/Figure | Value | |
|---|---|---|---|---|
| Cortical Circuit Parameters | ||||
| τ | NMDA synaptic time constant | All figures | 60 ms | |
| τb | AMPA synaptic time constant | All figures | 2 ms | |
| Ib | Base current | All figures | 0.334 nA | |
| a, b, d, γ | (Cortical) FI curve parameters | All figures | 270 Hz/nA, 108 Hz, 0.154, 0.641 | |
| , | Local structure | All figures | 0.34, 0.4 nA | |
| , | Long-range structure | All figures | 0.03, 0.04 nA | |
| , | Local tone | All figures | 0.2588, 0.2588 nA | |
| , | Long-range tone | All figures | 0.0, 0.0 nA | |
| Cortico-thalamic and Thalamo-cortical Projections | ||||
| Area-specific cortico-pulvinar coefficients | Figures 2, 3, and 4 | |||
| Excitatory cortico-pulvinar weight | bp = 0.28 nA | |||
| Inhibitory cortico-pulvinar weight | cinh = −0.81 | |||
| Pulvinar Circuit Parameters | ||||
| τp | Pulvinar synaptic time constant | All figures | 2 ms | |
| Ibp | Pulvinar base current | All figures (except confidence) | 0.334 nA | |
| bλ, dλ | (Thalamic) FI curve parameters | All figures | 112 Hz, 0.2 | |
| Cortical External Input Parameters | ||||
| Ie | External input for attention and conflict | Instructed, choice, target-distractor, conflict/Figures 2 and 4 | 0.011, 0.0156 nA | |
| Itarget/distractor | Target/distractor amplitude | WM switch and regimes/Figure 3 | 0.11 nA | |
| ttarget, tdistractor | Target and distractor onset | WM switch and regimes/Figure 3 | 30, 800 ms | |
| τrise, τdecay, Atarget | Rise/decay time constants and transient amplitude | DM conflict/Figure 4 | 13, 14 ms, 0.115 nA | |
| Pulvinar Confidence Parameters | ||||
| Local structure, base current | Confidence (Figures 5 and 6) | 0.35 nA, 0.3335 nA | ||
| cconf | Differential input/up-down ratio | Confidence (Figures 5 and 6) | [2,5,8] | |
| Ie | Applied current | Confidence (Figures 5 and 6) | 0.007 nA | |
| Ibconf | Pulvinar base current | Confidence (Figures 5 and 6) | 0.35 nA | |
| σconf, dT | Noise amplitude, decision time | Confidence (Figures 5 and 6) | 0.004 nA, 640 ms | |
| Aconf, τptransient | Pulvinar transient amplitude and decay | Confidence (Figures 5 and 6) | 0.38 nA, 30 ms | |
| τF, τD, τthexc, τthinh, aF, p, Jexc, Jinh | Facilitation, depression, excitation, inhibition | Confidence (Figures 5 and 6) | 500, 600, 4, 20 (ms) | |
| Amount of facilitation, release probability, excitatory and inhibitory weights | 0.35, 0.45, 2.85, −2.6 (nA) | |||
Gain Modulation in the Pulvinar Flexibly Controls Effective Cortico-cortical Connectivity
The model of simulated lesions described above hints at a generalized gain function for the pulvinar (Purushothaman et al., 2012). We examined what the hypothesized gain function of the pulvinar implies for cortical processing. In our model, two cortical areas are reciprocally connected via direct anatomical projections but also indirectly connected through interactions with the pulvinar. Therefore, the total connectivity between the two cortical areas—here referred to as “effective” connectivity—has two contributions: a direct cortico-cortical projection and an indirect projection provided by the transthalamic route that engages the pulvinar (Figure 3A). We can show that the amount of extra connectivity from the transthalamic route depends on the pulvinar excitability λ, here defined as the slope of the input output firing rate versus current (FI) curve in the pulvinar (see STAR Methods, Equation 4). In particular, if we assume that the feedforward relay weights in the hierarchy-preserving direction (cortical area 1 → pulvinar → cortical area 2) are larger than in the reverse direction, the overall feedforward strength between the two cortical areas can be controlled via external modulation of the pulvinar excitability λ, with the feedforward strength growing linearly with λ (see Equation 20 and Discussion). Notably, this proposed control mechanism does not depend on any oscillatory processes (Saalmann and Kastner, 2009; Quax et al., 2017), although we will later show that gating of cortical oscillations (Zhou et al., 2016; Saalmann et al., 2012) is readily achievable.
In the following, we examine the computational implications of such pulvinar-mediated control of effective connectivity between two cortical areas in the context of working memory and decision-making tasks.
Pulvinar-Mediated Gating of Persistent Activity in the Pulvino-cortical Circuit
Spatially selective persistent activity is a cognitive computation that is subserved by the cortex, possibly across multiple cortical areas (Suzuki and Gottlieb, 2013; Christophel et al., 2017). Here, we examine how the pulvino-cortical circuit can sustain spatially selective persistent activity in a distributed fashion (Figures 3B–3D). We assume that the (medial) pulvinar is subject to top-down control such that its excitability (here represented by λ) is variable and potentially a function of behavioral state. We examine how the pulvinar-induced modulated connectivity between two cortical areas affects working-memory computations in the pulvino-cortical circuit.
In Figure 3C, we model a simple memory task where a stimulus is presented briefly, and the subject must remember the location of the stimulus as typically done in attentional cuing (Saalmann et al., 2012) and/or memory-saccade tasks (Wilke et al., 2013; Suzuki and Gottlieb, 2013). We consider two scenarios corresponding to two values of the pulvinar excitability λ: a “small” and “moderate” value of λ. If λ is small (pulvinar “off”), the pulvinar is not actively engaged and the distributed circuit cannot reach a global persistent state: the activity of cortical area 1 decays after vigorously responding to the transient stimulus. In this case, there is no propagation to the second cortical area (Theyel et al., 2010) and the excitatory recurrency in cortical area 1 is not sufficient to sustain a persistent-activity (attractor) state. On the other hand, for a larger value of λ (pulvinar “on”), the circuit can reach a state in which both cortical areas and the pulvinar exhibit spatially selective persistent activity. Thus, the pulvinar effectively augments local and long-range projections that help sustain a persistent-activity state in the pulvino-cortical circuit—a global attractor—even if the cortical circuits do not exhibit persistent activity independently (Murray et al., 2017).
Admittedly, a non-linear cortical circuit in isolation can in principle subserve a high and a low stable state that can be interpreted as a memory and spontaneous state, respectively (Wong and Wang, 2006). Gain modulation in the pulvinar could change the amount of effective recurrent excitation in the local cortical circuit, which modifies the dynamical landscape of the circuit as to allow or disallow the existence of these two states. Therefore, the pulvinar gain is effectively a bifurcation parameter of the pulvino-cortical system, i.e., a parameter that can drive the system in and out of a bistable regime.
To conclude, the pulvinar can act as a λ-controlled memory switch. These results are consistent with persistent activity in the pulvinar due to a transient attentional cue (Saalmann et al., 2012; Halassa and Kastner, 2017). Along these lines, we suggest that the documented involvement of various thalamic nuclei in delay tasks (Schmitt et al., 2017; Guo et al., 2017; Bolkan et al., 2017) extends to the medial pulvinar. Furthermore, excitatory pulvino-cortical loops might underlie not only persistent activity, as modeled here, but also the maintenance of stimulus-evoked responses (Purushothaman et al., 2012).
We also analyze the behavior of the distributed pulvino-cortical circuit with respect to temporal processing in a memory-saccade task with distractors (Figure 3D). A distractor is operationally defined as a stimulus presented during the delay period after the target but otherwise identical in amplitude and duration (Suzuki and Gottlieb, 2013). Again, we consider two values of the pulvinar excitability λ, moderate and “large.” Similar to the scenario considered in Figure 3C, the circuit is able to sustain a spatially selective memory state given a sufficiently large value of λ. The behavior of the circuit with respect to distractor processing, however, will depend on how large λ is. If the value of λ is moderate (Figure 3D, left), there is propagation to the second cortical area and the extra feedforward synaptic connectivity is moderately engaged. In this regime, there is enough feedforward drive to engage cortical area 2 to help sustain a more stable attractor and the response to the distractor becomes smaller and transient, especially in cortical area 2 (Murray et al., 2017). On the other hand, if the value of λ is large enough (Figure 3D, right), the extra feedforward synaptic connectivity will be markedly engaged, causing the incoming distractor input to be more effectively propagated to cortical area 2. Thus, in this regime, the strong engagement of the distractor is enough to override the mnemonic encoding of the target.
We suggest that the distributed pulvino-cortical circuit model can operate in two regimes, depending on the value of the pulvinar excitability λ: a “remember first” regime if λ is moderate and a “remember last” regime, if λ is large. The former scenario is consistent with the reported differences in distractor processing between lateral intraparietal (LIP) and prefrontal cortex (cortical areas 1 and 2 in the model, respectively) during a working memory task (Suzuki and Gottlieb, 2013). The latter scenario is consistent with pulvinar involvement during distractor-induced interruption of goal-oriented tasks (Michael et al., 2001; see also Bisley and Goldberg, 2006 for analogous results in LIP). To summarize, our model suggests that the transthalamic feedforward pathway allows the pulvino-cortical cognitive circuit to operate in two distinct working memory regimes, thus augmenting the computational capabilities of an otherwise isolated cortical circuit with fixed long-range connectivity.
Pulvinar-Mediated Effective Connectivity between Cortical Areas Resolves Conflict in Decision Making
Decision making is a cognitive function that potentially involves multiple areas (Komura et al., 2013; Buschman and Kastner, 2015; Brody and Hanks, 2016; Siegel et al., 2015). We explore the relationship between the pulvinar-mediated control of effective connectivity introduced above and decision making. In particular, we consider a conflict scenario, whereby bottom-up and top-down inputs compete for attention and selection to two stimuli located on opposite sides of the visual field (Figure 4). This scenario could result from, for example, a competition between a bottom-up signal, such as luminance biasing one visual hemifield, and a top-down signal, such as reward expectation biasing the opposite hemifield during visual selection (Markowitz et al., 2011). To model such a conflict scenario, we consider external inputs to the circuit that can be segregated into “bottom-up,” targeting cortical area 1 and “top-down,” targeting cortical area 2, following hierarchical processing (Buschman and Miller, 2007). The pulvino-cortical circuit model predicts that, when the pulvinar excitability λ is large, the effective feedforward pathway from cortical area 1 to 2 is strengthened, so that ultimately the choice within cortical area 1 is represented in the pulvino-cortical system (Figure 4A, middle). In contrast, when the pulvinar excitability λ is small, the effective feedforward strength is small (Figure 4A, right) and cortico-cortical feedback enables the choice within cortical area 2 to be represented in the pulvino-cortical system, with dynamics akin to changes of mind (Kiani et al., 2014; Fleming et al., 2018).
The conflict scenario modeled in Figure 4 receives support from an fMRI study from Rotshtein et al. (2011), which showed that the pulvinar resolves the competition between working memory (WM) and visual search: the WM process interfered with the visual search as if the recalled WM item were a distractor. Importantly, the WM-induced distraction in Rotshtein et al. (2011) was accompanied by a decrease in pulvinar activity with respect to control, as hypothesized by our model with small λ (Figure 4A, right). To conclude, our results suggest that the pulvinar mediates the competition between modules or processes across cortical areas that complement the competition between features—here, spatial locations—within a cortical area.
In Figure 4B, we show that the probability of cortical area 1 (bottom-up input recipient) enforcing its choice on cortical area 2 (top-down input recipient) increases as a function of the pulvinar excitability λ. In the case of high conflict between bottom-up and top-down stimuli (high value of c′ ), the transition to switching cortical area 2 is more abrupt as compared to the case of low conflict. Overall, we suggest that gain modulation in the pulvinar can resolve cortical competition and the outcome of such competition depends on the externally controlled pulvinar gain.
In the sections above, we have examined some of the computational capabilities of the transthalamic route that indirectly connects two cortical areas by directly modulating the pulvinar. In Figure S2, we illustrate why it might be computationally advantageous to modulate the pulvinar node in the distributed circuit instead of modulating the cortex directly. We simulated a cortico-cortical system without pulvinar to show that a change in the gain at the level of the cortical modules would modify not only cortico-cortical transmission but also responses at a local level that compromise the generation of winner-take-all competition—for decision making—and well-separated high and low states—for working memory—in the cortical modules (Figure S2A). Furthermore, we show that a fast thalamic module as compared to a putatively slow cortical module is better suited for tracking an input stimulus, as well as rapidly canceling signal propagation from one cortical area to another (Figure S2B). We suggest that pulvinar modulation preserves the dynamical regime of the distributed cortical circuits for cognitive computations (Murray et al., 2017) while maintaining rapid signal transmission between cortical areas.
Now, we analyze the cortico-thalamo-cortical feedback pathway more closely and examine why such pathway might be related to the representation of confidence in the pulvinar in the context of decision making (Komura et al., 2013).
A Cortico-TRN-Pulvinar Circuit Can Account for the Decision Confidence Signals Observed in Pulvinar
In this study, we refer to the confidence concept in the sense of decision confidence: the subjective probability or belief that the chosen option is correct based on the evidence contributing to it (Kepecs et al., 2008; Pouget et al., 2016; Kawaguchi et al., 2018). In a landmark study, Kiani and Shadlen (2009) observed that, during a decision-making task (the Kiani task), both the decision and the confidence associated to that decision were related to activity in area LIP of the macaque. In the Kiani task, decision confidence in particular could be assessed due to the task design that included an opt-out component: the subject had the option to either make a decision based on the stream of evidence and obtain a sizable reward if correct or, conversely, opt out to obtain a smaller reward. For correct trials, the accumulation of sensory evidence eventually led to ramping activity of a population of neurons within their choice receptive field, thus reflecting a decision (Kiani and Shadlen, 2009). For trials where the subject opts out, however, the firing rates of neurons both within and outside their receptive field reached intermediate levels. Thus, the subject was more confident, i.e., would opt out less often, when there was a relative divergence of LIP activity during choice behavior. More precisely, the difference between the firing rate traces within and outside the response field predicted a confidence level (Wei and Wang, 2015).
In a related study, Komura et al. (2013) found single neurons in the medial pulvinar of the macaque whose firing rate predicted whether the animal, in another version of an opt-out task (Komura task), would opt out. In contrast to the LIP neurons in the Kiani study, pulvinar neurons in the Komura study represented confidence explicitly: a single firing-rate trace was informative of the confidence level. The characterization of decision confidence in the Kiani and Komura tasks prompts the following question: why do pulvinar cells represent confidence via their firing rate and how is this representation related to the implicit confidence representation in cortex? Given the known connectivity between parietal cortex and pulvinar (Gutierrez et al., 2000), we explored how a cortico-thalamo-cortical feedback pathway could contribute to the representation of decision confidence in the pulvinar.
The pulvino-cortical circuit we propose is based on that of Figure 1 but now contains explicit TRN-pulvinar connections, as shown in Figure 5A. For simplicity, we focus on one cortical module. The cortical module is composed of two excitatory populations that are selective to two stimuli A; B (e.g., opposite motion directions).
We assume that a model pulvinar neuron integrates input from two excitatory populations from the same cortical area. Such cortico-thalamic input includes, first, a direct monosynaptic connection from cortex to pulvinar and, second, an indirect disynaptic connection through the TRN. In our model, there is a pair of such connections for both cortical populations selective to A and B, respectively (Figure 5A). Crandall et al. (2015) have shown that the direct excitatory cortico-thalamic projection in the somatosensory thalamus exhibits short-term facilitation, and the inhibitory TRN-pulvinar projection exhibits short-term depression (see also Kirchgessner and Callaway for similar results in rodent pulvinar, in vivo; M.A. Kirchgessner and E.M. Callaway, 2017, Soc. Neurosci., abstract). We analyze the implications of these plastic projections in a decision-making task.
During decision making, i.e., the evidence accumulation process, the cortical populations A and B compete for a choice resulting in a “winner” (for example, A) whose firing rate ramps up while the “loser” population (for example, B) ramps down (Figure 5C, top). In this scenario, when the firing rate rA of cortical population A is high, the direct cortico-pulvinar excitatory synapse—from cortical population A to pulvinar—facilitates while the respective inhibitory TRN-pulvinar synapse depresses. This results in a net positive current from population A to the pulvinar (Figure 5B, top). Due to competition between the populations A and B during decision making, the firing rate rB would be low in this scenario and neither the direct cortico-pulvinar excitatory synapse—from cortical population B to pulvinar—facilitates nor the respective inhibitory TRN-pulvinar synapse depresses. Thus, the strong TRN-pulvinar connection results in an effective negative current from population B to the pulvinar (Figure 5B, top). Overall, the positive and negative contributions from the cortical activity result in a cortico-pulvinar current that approximately scales as rA – rB. Because the pulvino-cortical circuit is symmetric, rB – rA will also be represented in case population B wins the competition. We can therefore show that the pulvino-cortical circuit approximately calculates , i.e., the pulvinar represents the absolute value of the difference of the activities between the two afferent cortical populations (see Figure 5B, bottom, and STAR Methods after Equation 24 for details of the calculation). Thus, the stimulus-selective cortical activity in the cortex is effectively transformed to non-selective differential activity in the pulvinar via the plastic cortico-thalamic projections that engage the pulvinar and the TRN (Figure 5C).
Now, we study the implications of the plastic pulvino-cortical circuit model in the context of a decision-making task with an opt-out component. We first consider a fixed-duration version of the task (Figure 6A; see also Komura et al., 2013 and Kiani and Shadlen, 2009), where the subject is presented with a display of random dots and has to decide on the net direction of motion of the display for varying levels of difficulty. Crucially, the subject has the option to forgo the sensory-based decision and opt out—referred to as “escape” by Komura et al. (2013)—for a smaller but sure reward. We modeled such a task by considering motion-direction selective inputs to two cortical populations (Figures 5A and 6A). Due to the trial-to-trial stochastic nature of the cortical response to the stimulus (Equations 5 and 7), the cortico-thalamic circuit model can reproduce correct and error trials, as well as escape trials for which the cortical activities have not diverged (Kiani and Shadlen, 2009; Figure 6A; see figure caption for details of the different trial types). Furthermore, the decision-making readout in the cortex results in a specific psychophysical performance: for correct trials, the proportion of choices exhibits a V shape as a function of task difficulty (inverse to the coherence in Kiani and Shadlen, 2009; see Equation 31), although the opposite is true for error and escape trials (Figure 6B, bottom left). Concurrent with the cortical-based readout of the decision, the pulvinar integrates the activity of the two populations and calculates an approximate absolute value of the cortical firing rate differences, as in Figure 5B. We found that pulvinar responses signaled via their firing-rate amplitude whether a given trial was correct, error, or escape (Figure 6B, top and bottom right). We suggest that, if a cortical area (e.g., parietal cortex) represents decision confidence via the activities of two neural populations (an implicit representation of confidence; Kiani and Shadlen, 2009; Wei and Wang, 2015), the plastic pulvinar-TRN circuitry will transform the implicit representation of confidence in the cortex to an explicit representation in the pulvinar (Komura et al., 2013, their Figure 3).
We tested the role of the return projection from the pulvinar to the cortex (“feedback to cortex” in Figure 5A) by simulating a lesion to the pulvinar. We found that, after the lesion, the number of escape responses increased with respect to control, notably for low-coherence, i.e., difficult, trials (Figure 6C), also consistent with the Komura et al. (2013) study. We also simulated a reaction-time version of the evidence accumulation task without an opt-out component in control and pulvinar-lesion scenarios. We found a speed-accuracy tradeoff: the circuit with the lesioned pulvinar exhibited significantly slower but slightly more accurate responses (Figure 6D). Indeed, a lesion in the pulvinar reduces the overall excitation in the cortex, which makes the decision process slower by giving the system more time to integrate information, which in turn slightly improves performance for difficult trials. We contend that the pulvino-cortical feedback projections enhance the net recurrency in the cortical circuit and that this recurrency modulates the evidence accumulation process in the pulvino-cortical circuit.
Thalamocortical Motifs and Hierarchical Oscillatory Interactions
We have shown how feedforward and feedback pulvino-cortical pathways participate in various cognitive behaviors. In Figure S1B, we investigate plausible interactions between these pulvino-cortical pathways. An intra-pulvinar competition motif, for example, leads to a tradeoff in which one functional circuit is privileged over the other, i.e., a strengthening of a local representation versus propagation of that representation to the next cortical area (Figures S1B and S1C). We now explore a pulvino-cortical interaction motif in the context of oscillatory processing within and across cortical areas.
There is recent evidence from multi-unit activity and local field potentials in the macaque of enhanced cortico-cortical and pulvino-cortical coupling at particular frequencies during tasks that engage attention (Saalmann et al., 2012; Zhou et al., 2016). We focus on the recent study by Zhou et al. (2016), who showed modulation of pulvinar activity during a spatial-attention task and characteristic changes in cortical oscillatory activity after a pulvinar lesion. We reconsidered the multi-regional architecture introduced in Figure 1: two cortical modules (cortical areas 1 and 2) and one thalamic module representing the ventro-lateral pulvinar (Figure 7A).
To address oscillatory processing in the pulvino-cortical circuit, each of the cortical modules has now laminar structure, in that superficial and deep layers are distinguished on the basis of their connectivity within and across areas. Both layers are composed of excitatory and inhibitory populations that interact to produce noisy rhythmic activity in isolation: superficial layers generate gamma oscillations, and deep layers generate alpha (low beta) oscillations (see Figure S3B and Mejias et al., 2016). The excitatory and inhibitory populations in superficial and deep layers have different characteristic time constants in our model—fast and slow for superficial and deep, respectively— that filter the input noise to generate damped oscillations in the gamma and alpha regimes (see Equation 32 and below).
In the laminar circuit model, the pulvinar module sends feedback projections to the cortical module 1 and relays a transthalamic projection to cortical module 2. After lesioning the pulvinar in our model, we observed an increase in low-frequency oscillations in cortical area 1 (Figure 7B). Feedback connections arising from the thalamus target interneurons in deep layers (Cruikshank et al., 2010; Zhou et al., 2018; Audette et al., 2018). Thus, after a lesion to the pulvinar, pyramidal neurons in the deep layers are disinhibited, which subsequently leads to an increase of power in the alpha range due to net excitation in the deep-layer excitatory-inhibitory circuit (Mejias et al., 2016). This result is consistent with the findings by Zhou et al. (2016), who recorded from macaque V4 and observed such increases in alpha-range power after lesioning the ventro-lateral pulvinar with muscimol (their Figure 7). Thus, feedback thalamo-cortical projections in our model regulate the amount of excitation in the cortex (Ferguson and Gao, 2018).
We simulated a spatial-attention task in attention-in and attention-out conditions during visually evoked processing (see Zhou et al., 2016 and STAR Methods for details). We computed the spectral coherence between the two cortical areas, which provides a rough estimate of the degree of mutual oscillatory coupling. The pulvinar, via transthalamic projections, enhances the coherence at gamma frequencies between the two cortical regions (Figures 7C and 7D). After lesioning the pulvinar, the spectral coherence between both cortical areas in the gamma range decreases (Figure 7C), suggesting an important role for the transthalamic connection (see also Figure S3A). Importantly, the effects of the simulated lesion depend on the level of attention. These findings are in line with Zhou et al. (2016), who recorded from V4 and inferior temporal (IT) regions of the visual cortex during a task that required attention and found both attention-dependent enhancements and lesion-dependent reductions in gamma-range coherence (their Figures 7 and 8).
We also found a notable inter-areal coherence in the alpha range for cortico-cortical communication that increases after lesioning the pulvinar (Figure 7C). Note that both attention and pulvinar lesions increment alpha coherence in the circuit but via different mechanisms. More specifically, we suggest that the pulvinar normally inhibits alpha oscillations in the deep layers of the cortex (e.g., V4), and a lesion would disinhibit the deep layers to increase cortical alpha (Zhou et al., 2016). At the same time, attention implemented via top-down excitation onto cortical areas increases coupling at both gamma and alpha frequencies (see Figure 3 from Saalmann et al., 2012). These results extend to Granger causality, which in addition measures directionality: the influence of cortical area 1 to cortical area 2 (2 to 1) is stronger in the gamma (alpha) range and decreases (increases) after a lesion to the pulvinar (Figure 7D). Because these conclusions remain true in the absence of visual stimulation (Figure S4), we predict that pulvinar lesions result in an increase in alpha oscillations not only during stimulus presentation (Zhou et al., 2016) but also during the attention-related delay period (Saalmann et al., 2012).
Overall, we propose that the transthalamic projection enhances the transmission of information through a feedforward gamma channel, as increased excitation onto superficial layers in cortical area 2 enhances gamma activity locally (Mejias et al., 2016). This parsimonious interpretation is consistent with our previously described function of pulvinar-mediated modulation of feedforward connectivity: the increased drive from cortical area 1 to cortical area 2 due to the presence or enhancement of pulvinar activity (Figures 3 and 4) is reflected in an increase in gamma oscillations and coherence (Figure 7). The pulvinar thus acts as a router of oscillatory activity in the cortex. This view is distinct from the proposal from Quax et al. (2017), who suggest that the pulvinar is an alpha generator that, by modulating the alpha-phase difference between the cortical areas, controls cortico-cortical communication through gamma coherence (see also ter Wal and Tiesinga, 2017).
The laminar model of pulvino-cortical interactions shows the presence of an oscillation-based functional hierarchy when the pulvinar is present (Bastos et al., 2015; see STAR Methods for details). After lesioning the pulvinar, we observed a decrease in hierarchical distance between the two cortical areas (Figures 7D, inset, and S3C), which suggested that we can obtain a range of hierarchical distances by manipulating the pulvinar gain. As shown in Figure S5, this is indeed the case: an increase in the pulvinar gain leads to an increase in hierarchical distance between the two cortical modules, consistent with the context-dependent hierarchical jumps observed by Bastos et al. (2015). These results also extend to functional hierarchies defined in terms of the timescale of intrinsic fluctuations during spontaneous activity (Murray et al., 2014), so that the two functional hierarchies we introduced, i.e., oscillation and timescale based, are consistent (Figure S5).
To conclude, the circuit topology presented here instantiates the pulvino-cortical feedforward and feedback pathways concurrently, and we show how the pathways contribute to hierarchical interactions within and across cortical areas.
DISCUSSION
In this study, we propose a multi-regional circuit model that subserves cognitive computations and is composed of two cortical areas and the pulvinar nucleus of the thalamus. We highlight the functional relevance of two pulvino-cortical pathways: a feedforward pathway that connects two cortical areas transthalamically and a feedback pathway that engages the TRN and projects back to the cortex. We summarize how the aforementioned pathways contribute to different cognitive computations, including attention, working memory, and confidence during decision making.
First, lesions to the pulvinar in the model resulted in actionrelated disruptions in the contralesional field, including increased saccade latency and decreased choice performance in a visuospatial task (Desimone et al., 1990; Wilke et al., 2013). These results are consistent with structured cortico-thalamic connections in healthy subjects that allow for distractor-filtering computations during visuo-spatial attention tasks. Second, the circuit model can subserve working memory in the form of spatially selective persistent activity. Crucially, the pulvinar can switch the pulvino-cortical circuit to subserving a global persistent-activity state as well as establish two different dynamical regimes during distractor processing in working memory. Third, modulation of the pulvinar can bias a cortical circuit into a predominantly feedforward mode, in which bottom-up information is preferentially transmitted as opposed to top-down information. Thus, the pulvinar can induce a cortical network reconfiguration that can be used to resolve conflict in decision making (Rotshtein et al., 2011). Fourth, we suggest that decision confidence can be explicitly estimated from activity in the pulvinar as a result of plastic cortico-thalamic projections that engage the TRN. Our model provides a unified account of implicit (Kiani and Shadlen, 2009) and explicit (Komura et al., 2013) representations of decision confidence in the cortex and pulvinar, respectively. Finally, pulvino-cortical feedforward and feedback pathways can regulate hierarchical frequency-dependent interactions within and across cortical areas. We thereby provide a novel and parsimonious interpretation of recent experiments targeting the macaque pulvinar (Saalmann et al., 2012; Zhou et al., 2016).
In light of these modeling results, we suggest that the pulvinar augments the computational capabilities of an otherwise isolated cortical cognitive-type circuit. The cortex “outsources” local and long-range cortical connectivity to pulvino-cortical feedforward and feedback pathways for an additional layer of control. Indeed, instead of being fixed, pulvino-cortical feedforward and feedback pathways can be dynamically engaged through external modulation of the pulvinar. We propose that such cognitive-circuit outsourcing is an organizational principle for flexible distributed computation in the brain.
Pulvinar and Attentional Modulation and Deployment
The pulvinar is part of a complex multi-regional circuitry that is involved in attentional processing in humans (Snow et al., 2009; LaBerge and Buchsbaum, 1990; Danziger et al., 2004; Ward et al., 2002) and non-human primates (Petersen et al., 1985; Desimone et al., 1990; Wilke et al., 2010, 2013; Saalmann et al., 2012; Zhou et al., 2016). Previous models have proposed the existence of a saliency map in the brain that can control the deployment of attention by combining both bottom-up and top-down salience (Itti and Koch, 2001), and the pulvinar may be part of such a map. Interestingly, other thalamic circuits, including the LGN and the TRN, have been involved in attentional enhancement (McAlonan et al., 2008; Wimmer et al., 2015; Halassa and Acsády, 2016). It will be important for future studies to examine and compare contributions from the different thalamic nuclei to computations that generally support selective attention (Buschman and Kastner, 2015; Béhuret et al., 2015).
Attentional processing entails various computations, including spatial shifting and distractor filtering. We suggest that the pulvinar is involved in these computations through reciprocal connections with cortical areas typically recruited in attentional tasks, including the fronto-parietal network (Suzuki and Gottlieb, 2013) and superior colliculus (SC) (White et al., 2017). Because neural circuits controlling attention are thought to enhance neural representations in visual areas via feedback projections (Noudoost et al., 2010; Zhang et al., 2016), we propose that the pulvinar mediates a feedforward attentional circuit that complements top-down control of attention. An important question for future thalamo-cortical studies is to disambiguate between top-down control via cortico-cortical feedback and feedforward transmission via transthalamic pathways by, for example, selectively silencing thalamocortical projections that target disinhibitory circuits (Wall et al., 2016).
We contend that the filtering ability of the distributed attentional network that includes the pulvinar is intimately related to a connectivity profile where same-selectivity populations excite each other and opposite-selectivity populations inhibit each other. Given that the number of inhibitory interneurons in the pulvinar is scarce compared to the cortex, cross-inhibition for the purpose of attentional filtering could arise from interactions of the pulvinar with the TRN (see McAlonan et al., 2008 and Wimmer et al., 2015 for LGN-TRN interactions). We propose that cross-inhibition needs not be explicitly implemented in the pulvinar per se (see Gouws et al., 2014 for evidence of suppression in the human pulvinar), but rather circuits underlying cross-inhibition could be exclusively cortical and amplified via thalamocortical projections. We suggest that compromising interhemispheric competition and inhibition (Szczepanski and Kastner, 2013), possibly mediated by the TRN (Viviano and Schneider, 2015), will lead to distractor-filtering deficits and hemispatial neglect. Moreover, future studies could address the relative contributions of lesions, e.g., the amount of the GABA agonist muscimol (Wilke et al., 2010) and reward expectation (Wilke et al., 2013) on the extent of spatial neglect.
Gain Modulation through External Control of Pulvinar Excitability
In this study, we propose that one key function of the pulvinar is to gate the effective cortico-cortical connectivity via gain modulation (see Cortes and van Vreeswijk, 2012 and Olshausen et al., 1993 for proposals for the pulvinar in propagation and routing of information, respectively). The pulvinar receives inputs from many structures, including the pretectum (Benevento and Standage, 1983), superior colliculus (Baldwin et al., 2013; Zhou et al., 2017), and brainstem (Varela, 2014). Assuming that these areas are external to the pulvino-cortical circuit we considered, they could potentially modulate the pulvinar activity as suggested by our model. Particularly, the medial pulvinar is connected to association cortices, including parietal and frontal cortex, and the ventro-lateral pulvinar is connected to retinotopic visual areas (see Oh et al., 2014 for connectivity between lateral posterior [LP] and parietal and higher visual areas in mouse). The differences between these two pulvinar sectors might also be reflected in the mechanism by which pulvinar excitability is controlled. The medial pulvinar can be directly modulated by prefrontal cortices (Romanski et al., 1997), and both medial and ventro-lateral pulvinar can be subject to midbrain modulation that can change the state of the pulvino-cortical circuit. However, ventro-lateral pulvinar might only receive top-down attentional modulation indirectly through the TRN (Zikopoulos and Barbas, 2006). Whether the effect of such indirect TRN modulation onto the pulvinar is net inhibitory or disinhibitory will depend on the cortical firing rate (Crandall et al., 2015), differences across species in terms of number of local interneurons, and presence of hyperpolarization-dependent bursting in higher order thalamic nuclei.
For simplicity, we have lumped the modulatory effects of the external areas mentioned previously into the control of a single parameter, the pulvinar excitability λ, which in our circuit model represents the slope of the FI curve (Abbott and Chance, 2005). The FI curve and the proposed gain-modulation mechanism in the pulvinar can be further shaped by cortico-thalamic noise (Béhuret et al., 2015) as well as the firing mode of the thalamic relay neurons (Steriade et al., 1990; Saalmann and Kastner, 2011; Sherman and Guillery, 2013). Moreover, other gain-modulation mechanisms may be relevant for selective transmission, including synchronization (Saalmann and Kastner, 2011; Saalmann et al., 2012) and modulation of cortico-cortical gamma coherence via pulvinar-mediated alpha phase differences (Quax et al., 2017). Importantly, the pulvinar “gating policy”—the mechanism that specifies when and under what conditions the pulvinar is controlled—is mostly an open question for future modeling and experimental studies (Wang and Yang, 2018).
Confidence Representation in the Pulvinar and Its Relationship to Attention
In this modeling study, we have examined why and how the pulvinar is involved in confidence in decision making. These modeling results relate to the study by Komura et al. (2013), who found that the firing rate of macaque pulvinar cells correlated with decision confidence during a visuo-spatial categorization task.
Pertinent to our modeling results, there are implicit signatures of decision confidence in the LIP (Kiani and Shadlen, 2009). We suggest that the confidence representation as observed implicitly in the firing rates of LIP neurons is directly related to the explicit representation of confidence in the pulvinar cells (Komura et al., 2013; see also Wei and Wang, 2015). Indeed, pulvinar cells estimate confidence by integrating and transforming cortical signals through an absolute-value-type computation (see Figure 5B, bottom), which involves a plastic corticothalamic circuit that engages the TRN. Along these lines, we predict that, first, the cortex and pulvinar form part of a distributed circuit for decision making so that lesions or disengagement of the pulvinar causally affect the decision-making process (see speed-accuracy tradeoff in Figures 6D and 6E) and, second, a plastic (and intact) TRN-pulvinar circuit is necessary for the pulvinar to estimate confidence. We note, however, that there are differences in the opt-out task design between the Komura et al. (2013) and Kiani and Shadlen (2009) studies, where the opt-out component is always present in the former but randomly interleaved in the latter. Future experiments that consider simultaneous recordings of the cortex and pulvinar as well as optogenetic manipulation (e.g., inhibition) of the TRN-pulvinar circuit in the context of a consistent post-decision wagering task could test these predictions.
Here, we propose that the TRN-pulvinar circuit calculates the absolute difference of firing rate activities of two populations from an upstream cortical area. In the framework of predictive coding, such computation might be useful to represent computational precision (Kanai et al., 2015). Furthermore, we suggest that this TRN-pulvinar computation generalizes across tasks and species. For example, Roth et al. (2016) found that the LP, the rodent analog of the pulvinar, signals the discrepancies, both positive and negative, between self-generated and external visual motion (see in Roth et al., 2016; their Figure 7C). We suggest that this finding, in this case related to locomotion, is another instance of the canonical computation (Carandini and Heeger, 2011) the plastic TRN-pulvinar circuit can perform. Along these lines, the computational significance of the signals observed in a given pulvinar region would depend on the cortical areas projecting to it. Therefore, the pulvinar can represent saliency for visual behavior and that this saliency is interpretable as confidence in the case of visuo-spatial decision making (Komura et al., 2013) or sensory context in the case of locomotion (Roth et al., 2016).
How does the confidence representation in the pulvinar relate to the pulvinar’s involvement in attentional tasks? We found that unilateral lesions to the pulvinar result in an asymmetric gain and connectivity pattern that biases the winner-take-all mechanisms behind visual selection, suggesting that pulvino-cortical input is necessary for normal functioning in this task. On the other hand, in Figure 6, we showed that the pulvinar represents decision confidence through a transformation of the incoming cortical activity, and importantly, the feedback projection arising from the pulvinar was key in regulating the evidence-accumulation mechanism underlying cortical decision making. We propose that, for both attention, i.e., the processes behind distractor filtering, and confidence-related computations, the pulvinar provides contextual modulation to cortical circuits that process visual information. Furthermore, pulvinar signals related to confidence or attentional saliency can be broadcast to multiple cortical areas.
The Functional and Anatomical Organization of the Pulvinar and Other Higher Order Thalamic Nuclei
The pulvinar is endowed with the appropriate circuitry for the computations proposed in this study, namely, control of the effective connectivity between two cortical areas along the visual pathway and explicit saliency representation within one cortical area. The pulvinar is adequate for this computation because its lack of excitatory recurrency results in relatively fast dynamics as compared to the cortex that can aid in the rapid transfer of transthalamic information (Figure S2). To test this argument, future studies could compare the timescale of thalamic fluctuations during spontaneous activity to those of the cortex (Murray et al., 2014). Furthermore, the triangular configuration of cortex and thalamus (Theyel et al., 2010) parsimoniously suggests a direct versus indirect means of communication between two areas. Moreover, the pulvinar receives principal projections as well as neuromodulation from a multitude of cortical and subcortical sources, including TRN, that can influence the pulvinar activity. The pulvinar thus appears to be uniquely positioned to provide contextual modulation to cortical computations associated with cognition as proposed by our model.
The higher order thalamic nuclei have been less well studied than the first-order sensory nuclei, but there has been recent significant progress on this front. For example, Schmitt et al. (2017) showed that mediodorsal (MD) thalamic neurons were crucial to maintain task-relevant information during a delay period, but these neurons did not exhibit the rule tuning of its frontal cortical inputs. Analogously, in Figure 5, we show that differently tuned cortical populations converge onto the pulvinar so that, within the new pulvinar receptive field, the dimensionality of the representation decreases (Komura et al., 2013; Schmitt et al., 2017). This organization is different from that of the plots in Figures 3 and 4 and of other thalamic nuclei, for which receptive fields tightly reflect their cortical input (Guo et al., 2017; Acsády, 2017). Along these lines, we propose that the pulvinar contains at least two receptive field types: a receptive field with similar properties to its cortical driving field (for example, Figure 3) and a receptive field that receives convergent input from differently tuned cortical populations (see Figure 5; Schmitt et al., 2017; Figure 8 from Komura et al., 2013).
An important open question is to which extent signal transmission in the cortex is routed transthalamically (Sherman, 2016). Motivated by the computational capabilities of the thalamocortical circuit we propose and by the fact that the behavioral effects of pulvinar lesions are sometimes subtle, we suggest that the pulvinar predominantly modulates cortical computations. Indeed, our model suggests that gain modulation at the level of the pulvinar results in a change of effective synaptic connectivity between (and within) the two cortical modules. Noting that, first, pulvinar tuning for stimulus features is poor as compared to the cortex (Petersen et al., 1985) and, second, there is a potential downsampling of information from cortex to thalamus due to the fewer number of cell bodies (Jones, 2007), it is possible that transthalamic signaling is used primarily as a boosting mechanism for transmission of low-level information, which complements cortico-cortical feature coding. Future studies that include spatially precise optogenetic manipulation of thalamic circuits could examine the involvement of the pulvinar and other thalamic nuclei in cortical computations.
Model Limitations and Future Directions
Our circuit model can be extended in different ways to address important questions not studied here. To characterize the local cortical circuit and model 2AFC tasks, we used a parsimonious discrete firing-rate model. A ring model with smoothly varying tuning would be more appropriate if we wanted to explore the representation of continuous variables, such as orientation and/or model multi-item decision-making tasks, as well as effects that depend on the distance between distractors and targets for working memory. An extension to multiple neural populations would allow the implementation of more realistic connectivity patterns and differential feature selectivity in the thalamus and cortex. A spiking circuit with explicit ionic currents, such as the low-threshold calcium current, would enable modeling the well-documented dual firing modes of thalamic neurons and their participation in thalamo-cortical rhythms, including the alpha rhythm (Steriade et al., 1990; Bazhenov et al., 2002; Saalmann et al., 2012). Furthermore, an investigation into the dynamics of ionotropic and metabotropic receptors and their respective timescales could refine the hypotheses concerning the function of different thalamo-cortical pathways as introduced here (Sherman and Guillery, 2013; Sherman, 2016).
With respect to oscillatory processing in thalamo-cortical circuits, future instantiations of our pulvino-cortical circuit model could more directly address important differences between the Saalmann et al. (2012) and Zhou et al. (2016) studies, including task design, the cortical regions recorded, and, crucially, the task condition for which the neural data analysis was performed.
To summarize, in this study, we proposed a circuit model to study contributions of the pulvinar to behaviorally relevant computations in the cortex. Our interpretation of feedforward and feedback thalamocortical loops offers a novel perspective on cortico-subcortical processing in general and, moreover, will provide solid ground for the development of large-scale models of the brain (Chaudhuri et al., 2015; Mejias et al., 2016; Wei and Wang, 2016; Joglekar et al., 2018) that incorporate the thalamus in dynamical interplay with the cortex.
STAR★METHODS
CONTACT FOR REAGENT AND RESOURCE SHARING
Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Xiao-Jing Wang (xjwang@nyu.edu).
METHOD DETAILS
Model architecture
We constructed a distributed circuit model that is comprised of two reciprocally interacting cortical modules as well as a thalamic (pulvinar) module (Figure 1). To model 2AFC tasks, each module contains two selective, excitatory populations, labeled A and B. In the mean-field description we consider here, the activity of each population is described by a single dynamical variable (see Cortical and thalamic circuit dynamics for details). Within the cortical modules, the two populations have recurrent excitatory connections and interact through a local inhibitory population (not explicit in the Figure 1 schematic) that allows for cross-inhibition between the two excitatory populations. Each recurrently connected excitatory population receives inhibition from another population representing a common pool of interneurons. Inhibition is linearized so that projections between the two excitatory populations A and B are effectively represented by negative weights (Wong and Wang, 2006).
The local connectivity for each cortical module follows a hierarchical gradient in that the local excitatory recurrence in module (cortical area) 2 is greater than in module (cortical area) 1. The two cortical modules interact through long-range projections that are structured according to the stimulus selectivity of populations within each module, i.e., populations with the same selectivity are connected through excitatory projections whereas populations with different selectivity are connected via net inhibitory projections. This configuration allows the circuit to subserve winner-take-all competition, slow integration for decision making, as well as to maintain stimulus-selective persistent activity (Wong and Wang, 2006; Murray et al., 2017).
The pulvinar module also contains two excitatory populations. However, the excitatory populations do not interact through locally recurrent excitatory projections (Jones, 2007). The thalamic populations can, however, interact via local interneurons (as in the medial pulvinar of the primate; Imura and Rockland, 2006) or through interactions with the inhibitory cells of the thalamic reticular nucleus (TRN). The cortical modules are connected with the thalamic module through cortico-thalamic feedforward and feedback pathways (Sherman and Guillery, 2013). The cortico-thalamic feedforward - or transthalamic - pathway refers to projections from one cortical area to the thalamus, and these projections are relayed to a second cortical area (Sherman, 2016). In our model the transthalamic projections are topographic as in the cortico-cortical connections: same-selectivity populations are connected through excitatory projections while opposite-selectivity are connected through inhibitory projections. The pulvino-cortical feedback pathway refers to connections between one cortical area and the pulvinar that are reciprocated to the same cortical area. These connections include a cortical monosynaptic excitatory as well as a disynaptic inhibitory projection through the TRN. In our model we consider concurrent pathways, i.e., the pulvinar module participates in both pathways as in Figure 1, but in Figure S1 we consider other interaction motifs. In the section Connectivity we formalize these assumptions with specific values for each of the connections.
Cortical and thalamic circuit dynamics
We first consider the dynamics of neural populations in the cortical modules. Each cortical population i =A,B is described by one dynamical variable, its average firing rate. The firing-rate dynamics of the population i in the cortical modules are dominated by the slow dynamics of the average NMDA synaptic gating variable si. Indeed, the dynamics of the NMDA synaptic gating variable is slow compared to the other timescales in the system so that the other dynamic variables, i.e., GABA and AMPA gating variables, are described by their steady-state values (Wong and Wang, 2006; Murray et al., 2017). The dynamical equation for the NMDA gating variable si for the cortical module n = 1,2 is:
| (1) |
where τ = 60 ms is the NMDA time constant, γ = 0.641 controls the rate of saturation of s, and r(Ii) is the firing rate of the population i as a function of the input current Ii. The firing rate as a function of input current is given by the frequency-current (F-I) curve relation (Abbott and Chance, 2005):
| (2) |
with , and c = 0.154 s.
For the two neural populations in the pulvinar module p, we also consider a one-variable dynamical equation for each population. In the circuit model, the non-recurrent dynamics in the thalamo-cortical relay cells are mediated primarily by non-NMDA currents (Bazhenov et al., 2002) so that the dynamical equation for the thalamic gating variable is:
| (3) |
where τp = 2 ms is time constant of fast AMPA thalamo-cortical synapses and is the firing rate of the pulvinar cell population i as a function of the input current Ii. As in the cortical modules, the thalamic firing rate as a function of input current is given by the frequency-current (F-I) curve relation (Abbott and Chance, 2005):
| (4) |
where λ is the pulvinar F-I slope, here referred to as the pulvinar excitability (the value of λ lies between 120 and and is reported in the figure captions), bλ = 112 Hz, and cλ = 0.2 s. The values chosen result in realistic firing rates for pulvinar neurons (Dominguez-Vargas et al., 2017; Komura et al., 2013).
The input current to population i = A,B in both cortical modules is given by:
| (5) |
where the first term of the right-hand side of Equation 5 corresponds to synaptic inputs from cortex and thalamus: is the connection weight from population j in Module m = 1, 2, p to population i in cortical Module n = 1, 2, Ib is the background current, is the noise current to population i in Module n, and is the applied current to population i in Module n from external sources. Below we describe the noise and applied currents in detail. Similarly, the input current to population i =A,B in the pulvinar is given by:
| (6) |
where is the connection weight from population j in the cortical Module m to population i in Module p, is the background current, is the noise current to population i in Module p, and is the applied current to population i in Module n from external sources, typically bottom-up (sensory) or top-down (internal).
For the cortical and thalamic modules, we mimic external non-selective currents through a noise current to each population. The noise current follows Ornstein-Uhlenbeck dynamics with the time constant of AMPA synapses:
| (7) |
where τAMPA = 2 ms, η is Gaussian white noise with zero mean and unit variance, and σnoise sets the strength of noise. Parameter values are reported in Table 1.
We consider the external current Iapp to the cortex for the following scenarios: i) Visual selection (Wilke et al., 2010, 2013; Dominguez-Vargas et al., 2017; Desimone et al., 1990), ii) working memory and distractors (Suzuki and Gottlieb, 2013), iii) decision-making and confidence (Kiani and Shadlen, 2009; Komura et al., 2013). We will specify these external currents after the Connectivity section below.
Connectivity
The connectivity in our model is specified by the sign and magnitude of the connection weights between the selective excitatory populations for each of the three modules: two cortical, one thalamic (pulvinar). We first specify the connectivity for the two-module cortical model (for additional details see Murray et al., 2017). The connections can be local (within a module) and long-range (across modules). To this end, it is useful to express the connection weights with the terms:
| (8) |
| (9) |
where Jsame denotes the positive connection weight between same-selectivity populations, e.g., from population A in Module 1 to population A in (cortical) Module 1 or 2. Jdiff denotes the negative connection weight between different-selectivity populations, e.g., from population A in Module 1 to population B in Module 1 or 2, and k = 11, 12, 21, 22 defines whether the connection is local or long range. We define JS as the structure of the network, since it reflects the magnitude of same-selectivity excitation and different-selectivity cross-inhibition and thus the total recurrent strength. Analogously, we define JT as the tone of the network, which reflects the net input onto a particular population. For both long-range projections between modules, we constrain them to have pathway-specific excitation/inhibition (E/I) balance:
| (10) |
| (11) |
We can easily translate the structure JS and tone JT into individual synaptic weights. For example, denotes the feedforward projection between the population A in the first module onto the population B in the second module and is given by:
We now describe the connectivity between the cortical modules and the pulvinar. Two cortical areas are connected not only via direct, i.e., cortico-cortical, feedforward, and feedback projections, but also indirectly via the thalamus (Theyel et al., 2010). It has been hypothesized that these thalamic-mediated indirect projections arise from cortical layer V. Moreover, cortico-thalamic projections arising from cortical layer VI often engage the thalamic reticular nucleus (TRN), a shell of inhibitory neurons that is an important source of inhibition to the thalamus (Jones, 2007).
Cortico-thalamic projections Jpk that target the pulvinar are represented by matrices of the form
where k = 1, 2 are indices of the cortical modules and A,B denote the stimulus selectivity. Thus, , for example, represents the inhibitory weight between population A in module 1 and population B in the pulvinar. Furthermore, connections are symmetric in that and .
Pulvino-cortical projections Jkp that target cortical Modules 1 and 2 are analogously represented by matrices of the form
where as before, k = 1, 2 are indices of the cortical modules and A,B denote the stimulus selectivity. For both cortico-thalamic and thalamo-cortical excitatory projections we define a generic excitatory projection , where bp is a baseline value and determine the connection weights. For example, denotes the excitatory connection strength between the A population in the pulvinar and the A population in the cortical module 2. For both cortico-thalamic and thalamo-cortical inhibitory projections, we define a generic inhibitory projection as where cinh dictates the degree of excitatory-inhibitory balance for that pathway. cinh = − 1 implies full balance in that Jexc + Jinh = 0. For example, and in the case of full balance, denotes the inhibitory connection strength between the A population in the pulvinar and the B population in the cortical module 2. Thus, the connectivity between the cortical modules and pulvinar in our circuit model is completely specified by assigning values to the cortico-thalamic (and thalamo-cortical) projection parameters w,bp, and cinh. Since the anatomical data to fully specify the values for these projection parameters in this framework is not available (but see Oh et al., 2014), we used the following general constraints: the total cortico-thalamic projection weight is greater than the total thalamo-cortical weight (Jones, 2007), the feedforward relay weights in the hierarchy-preserving direction (cortical area 1 - pulvinar - cortical area 2) are larger than in the reverse direction (cortical area 2 - pulvinar - cortical area 1, see Sherman, 2016). The values for the projection parameters are in Table 1.
Given the input currents to thalamic and cortical cells specified by Equations 5 and 6 and the connectivity specified above, we can now write the general pulvino-cortical model as
| (12) |
where In (n = 1, 2, p) is the total current in each Module n, Jmn are synaptic weight matrices connecting modules n to m, sn are the corresponding synaptic gating vectors, and and are base and applied input currents, respectively.
Visual selection and pulvinar lesions
In Figure 2 we simulated a decision-making task (Wilke et al., 2013) analogous to target selection during visual search. Each module contains two populations that are selective to a target and a distractor, respectively. A distractor was defined as another stimulus simultaneously flashed at an opposite location to the stimulus (Desimone et al., 1990). External stimuli enter as currents into the cortical modules. The external currents are segregated into “bottom-up” corresponding to sensory-type inputs and “top-down” inputs, corresponding to reward expectation, task representations and/or working memory. These applied currents reflect the external stimulus as:
| (13) |
where the first term on the right-hand side represents the transient to the visual stimulus, represents the sensory evidence, Ie scales the overall strength of the input and c′, referred to as the differential input, sets the bias of the input for one population over the other (equivalent to the coherence in Wong and Wang, 2006) and represents the target-distractor similarity in a visual search task, Atarget and ttarget determine the amplitude and the onset of the target, respectively, the time constants τdecay and τrise determine approximately the decay and rise of the target-induced transient response, and C is a normalization factor (see values in Table 1). In our model, the target is associated with a larger value of the differential input c′. A zero-c’ stimulus applies equal input Ie to each population in Module 1. In all of the simulations and when c′ > 0, the target-selective population receives the greater biased input. Due to noise, however, this does not guarantee that the target population will win, especially for low c’ values. Finally, we modeled a lesion by setting the firing-rate of one of the pulvinar populations to zero.
We modeled reward expectation in the task (Wilke et al., 2013) as a current Ireward applied to Module 2, modeled as in Equation 13 but without the visual transient. A saccade to a particular direction was defined as the action obtained after a population selective to a stimulus at that location reaches the firing-rate threshold of 30 Hz. Saccade latency was measured as the time at which the firing rate of a population in Module 2 crossed the 30 Hz threshold. For the Choice experiment in Figure 2, we varied the reward-expectation current onto Module 2 in the scenario lesion+reward so that the new Ireward = 0.012 nA. Proportion of saccades in the Choice task was measured as the fraction of saccades made to either side given the differential input c′ = 0. For the distractor-filtering simulations in Figure 2 C, we simulated lesions in the “target” and “distractor” scenarios, where the lesion was on the pulvinar population selective to the target and distractor, respectively.
Gain modulation and effective cortico-cortical connectivity
The system of equations that describe the dynamics in the pulvino-cortical circuit is given by Equation 12. We will find an approximately equivalent reduced system. To this end, we make the following two approximations. First, we assume that the synaptic dynamics in the pulvinar are much faster than the dynamics in the cortical loop model (τp ≪ τ) and second, we approximate the FI curve in Equation 4 as
We can then write a reduced description of Equation 12 as
| (14) |
where the effective connectivity matrices are
| (15) |
| (16) |
| (17) |
| (18) |
where
and Jpp describes the interactions within the pulvinar and TRN. Moreover, the new effective base currents are
We can write the effective long-range structure (recurrent excitation and cross-inhibition, Murray et al. (2017) in the feedforward direction as
| (19) |
| (20) |
where is the original, i.e., anatomical, feedforward structure from Modules 1 to 2, and δJ(λ) is the pulvinar-excitability-dependent transthalamic weight (see Figure 4A). As mentioned before, we assume that the feedforward cortico-thalamic and thalamo-cortical weights in the hierarchy-preserving direction (cortical area 1 - pulvinar - cortical area 2) are larger than in the reverse direction (cortical area 2 - pulvinar - cortical area 1, see Sherman, 2016). We can then write the ratio of feedforward-to-feedback connectivity as
| (21) |
Simulation of a working memory task with and without distractors
For Figure 3 we simulated two versions of a working memory task. In the first task, the subject must remember the location of the stimulus across a delay period. A flash of 100 ms appears on one of two positions of a screen indicating the target position. In the second version of the task, a distractor is presented during the delay period after 800 ms. The target to be held in WM is the first stimulus presented. We set the target as a current Iapp,A = Itarget of 100-ms duration that is applied to population A in the Module1. Distractors are defined as inputs Iapp,B = Idistractor of equal duration applied to population B arriving after the target and at an opposite location of the visual field. An error (or the “remember-last” regime) is recorded when the population selective to the distractor is at the high memory state at t> 3000 ms. We considered three values of the pulvinar excitability λ: small (corresponding to ‘off’, λ = 120 Hz/nA), moderate (λ = 220 Hz/nA) and large (λ = 290 Hz/nA).
Simulation of a decision-making task with conflicting choices
In Figure 4, we simulated a decision-making task where bottom-up signals or processes were in conflict with top-down signals or processes. More precisely, we simulated a two-alternative forced choice task in two scenarios: a congruent scenario, in which both bottom-up and top-down currents favored the blue target and a conflict scenario, in which the bottom-up signal favored the blue target in cortical area 1, while the top-down signal favored the red target in cortical area 2. We considered two values of the pulvinar excitability λ: small (λ = 220 Hz/nA) and large (λ = 280 Hz/nA).
We calculated the probability of cortical switching during conflict, i.e., the probability that cortical area 1 enforces its preferred selectivity onto cortical area 2 (“Prob Cx1 switches Cx2,” y axis in Figure 4C), as a function of pulvinar gain λ and conflict level. We calculated the fraction of instances (250 trials in total) where the blue population (favored in cortical area 1) won the competition while parametrically varying λ from 220–300 Hz/nA. The high (low) conflict level is given by c′ = 20(10).
Control simulations: cortical versus pulvinar gain modulation
We compared two gating mechanisms for cortico-cortical computations in Figure S2: direct cortical gain modulation and, as in the main text, pulvinar gain modulation. In Figure S2A we simulated working memory and decision-making tasks as previously described, but without the pulvinar module. The excitability parameters λ1 and λ2 now correspond to the cortical excitability, i.e., the slope of the cortical FI curve, for cortical areas 1 and 2, respectively. We considered a range of values for λ1 and λ2 in (270 was “small” and 351 was “large”), none of which could reproduce the two working memory or conflict resolution regimes achievable via pulvinar modulation.
In Figure S2B we simulated a simple signal transmission task with three modules: cortical area 1, an intermediate module which was either putative thalamic or putative cortical, and cortical area 2. This model is a simplification of the pulvino-cortical module introduced earlier in that cortical area 1 was simulated as a current source and the intermediate pulvinar/ cortical modules (green and orange) were simulated as linear systems that only differed in their characteristic time constant: 20 ms for putative pulvinar and 180 ms for putative cortical. Cortical area 2 was modeled as a one-dimensional bistable system with activity R2 given by:
| (22) |
where a = 0.04 and b = 2 are constant parameters, and Iext is the external input current to cortical area 2 given by:
| (23) |
where w12 = 0.03 and wi2 = 0.02 are weights connecting cortical area 1 and intermediate module to cortical area 2, and R1 and Ri are the firing rates of cortical area 1 and intermediate module, respectively, and is a noise current given by Equation 7 with σ = 0.3.
Plastic cortico-thalamic projections and confidence representation
We propose a circuit model composed of a cortical module and the pulvinar to elucidate the mechanisms behind confidence-related computations in cortex and thalamus. We first characterize the cortico-thalamic projections in detail and in particular, include short-term plasticity dynamics (Crandall et al., 2015). The schematic of the circuit is shown in Figure 5. The cortical populations exhibit winner-take-all dynamics and can accumulate sensory evidence. The cortical module sends projections to the pulvinar receives thalamo-cortical feedback in return. Specifically, a cortical population projects directly to the pulvinar forming an excitatory synapse and also indirectly through the TRN, forming an inhibitory synapse. Importantly, both the excitatory and inhibitory connections arise from the same cortico-thalamic projection. The excitatory cortico-thalamic synapse exhibits short-term facilitation so that the dynamics of the respective gating variable sexc are:
| (24) |
where is the time constant of cortico-thalamic excitation, ri (i=A,B) is the cortical firing rate, and F is the facilitation dynamic variable with equation:
| (25) |
where aF determines the amount of facilitation and τF is the facilitation time constant. The TRN is connected to the pulvinar via an inhibitory synapse that exhibits short-term depression:
| (26) |
where is the time constant of reticulo-thalamic inhibition, ri is the cortical firing rate, p is the synaptic release probability, and D is the depression dynamic variable with equation:
where τD is the timescale of depression. Using Equations 24 and 26, we can write the total current Ii→p from a cortical population with firing rate ri (i=A,B) to the pulvinar as a sum of excitatory and inhibitory components:
where is an external noisy base current to the pulvinar. The steady-state value of the pulvinar firing rate as a function of cortical firing rate is shown in Figure 5B, top. The current calculated in Equation 28 is for a given cortical population firing rate. In the context of decision making, two cortical populations integrate sensory evidence and compete in a winner-take-all fashion. The total current is thus a contribution from both cortical populations, i.e.,
Finally, the firing rate of the pulvinar is, as before, a non-linear function of the current:
| (29) |
After obtaining the firing rate as a function of the current, we can calculate the steady-state firing rate of the pulvinar as a function of the difference in firing-rate activities at the level of the cortex, shown in Figure 5B, bottom. The plot resembles a scaled absolute-value function in that the pulvinar activity in the y axis, which we call “estimated difference” is a symmetric and positive function of the difference in cortical activities, which we call “real difference.” The pulvinar thus performs an approximate absolute-value calculation of the difference between cortical activities (see an intuitive description of this calculation in the Results section).
We modeled perceptual decision-making with an opt-out component in Figure 6B: the subject has the option to forgo the decision and opt for a smaller reward (Kiani and Shadlen, 2009; Komura et al., 2013). The subject must integrate evidence to decide between two orthogonal motion directions, A and B, corresponding to up and down, for example (Komura et al., 2013). The strength of sensory evidence is modeled as an external current to the two populations as
| (30) |
where Ie = 0.007 nA scales the overall strength of the input and c′, referred to as the differential input, sets the bias of the input for one population over the other (equivalent to the coherence in Wong and Wang, 2006). For direct comparison with the results from (Komura et al., 2013), we mapped c′ to the related measure ‘up-down ratio’ as
| (31) |
where [45%, 30%, 0%] represents the fraction of dots in the ‘up’ direction (with [55%, 70%, 100%] representing the fraction of dots in the ‘down’ direction). Easy trials thus correspond to or , medium to or , and hard to or .
A decision in the model was recorded at a predefined decision time dT (Kiani and Shadlen, 2009). A correct trial is recorded if the firing-rate activity rA > rB and . (Compare to Wei and Wang, 2015), who used another population selective for the opt-out target). Analogously, an error trial is recorded if the firing-rate activity rB > rA and . Finally an escape trial is registered when at the decision time dT,. For the normalized activities plot in Figure 5B (bottom-right), we calculated the average firing rate in a 250 ms window before the decision time. In the reaction-time (RT) version of the task, we define and calculate the RT as the time at which the firing rate of a population crosses a predefined threshold of 30 Hz. For the RT task, we used a standard set of coherence values to characterize the sensory input (Kiani and Shadlen, 2009): c’ = [0, 3.2, 6.4, 12.8, 25.6].
Pulvino-cortical circuit with laminar structure
Here we describe the cortico-pulvinar model with laminar cortical structure used in Figure 7. This model extends our previous computational multi-scale framework (Mejias et al., 2016) by introducing a pulvinar module and connecting it to and from cortical laminar populations according to anatomical evidence (e.g., Sherman and Guillery, 2013; Jones, 2007). For simplicity, we have considered only one pulvinar module and up to two cortical populations, but generalizations can be made to accommodate larger thalamocortical networks.
Laminar cortical circuit
The circuit of a cortical area consists in two interconnected laminar modules, one corresponding to supragranular (layer 2/3) neurons and another to infragranular (layer 5/6) neurons. Each laminar module contains a recurrently connected excitatory and inhibitory population, with dynamics described by Wilson-Cowan dynamics. The firing rate dynamics of all four populations of a cortical area are given by
where rE2,I2,E5,I5 are the mean firing rates of the excitatory and inhibitory populations in supra- and infragranular layers, respectively. The corresponding time constants, denoted by t, are 6, 15, 30 and 75 ms. are Gaussian white noise terms of strength σ (of values 0.3, 0.3, 0.45, 0.45 respectively), and is the transduction function, or f-I curve, of the neurons. The network input, Inet, is the input arriving to each population from other populations in the network –from the same layer, a different layer, or different areas. The terms Iext are the input from external sources such as sensory stimuli or areas not explicitly included in the model.
Taking into account only local contributions (i.e., assuming an isolated cortical area) the network input is given by
| (32) |
| (33) |
| (34) |
| (35) |
where Jαβ is the mean synaptic strength from population β to population α. Indices E, I refer to the excitatory and inhibitory populations of the same layer, and the inter-laminar projections are denoted as JSI and JIS. Parameter values are JEE = 1.5, JIE = 3.5, JEI = − 3.25, JII = − 2.5, σE,I = 0.3, JIS = 1 and JSI = 0.75. With these parameter values, the circuit displays irregular, noise-driven oscillations in the gamma (supragranular) or alpha (infragranular) rhythms (see Figure S3B).
Pulvinar module To extend our local cortical circuit and include interactions with the pulvinar, we consider a population of excitatory pulvinar neurons of firing rate rp governed by the following dynamics:
| (36) |
with time constant τp = 6 ms, and Gaussian noise ξp of strength σ = 0.75. The pulvinar population receives input from pyramidal layer 5/6 cells, , with JCP = 0.5. Pulvinar also projects back to all cortical populations E2,I2,E5,I5, with projection strengths 0.15, 0.1, 0.05 and 0.65, respectively.
Hierarchical pulvino-cortical model
To consider how cortico-cortical interactions are modulated by pulvinar activity, we introduce a second cortical area, assumed to be higher in the cortical hierarchy than the first one. Following (Mejias et al., 2016), we consider a feedforward cortico-cortical projection from E2 in the first area to E2 in the second area, with projection strength JFF = 1. In addition, we modeled a pulvinar contribution to the feedforward interaction via a pulvino-cortical projection to E2 in cortical area 2, with projection strength 0.5. Finally, cortico-cortical feedback projections stem from E5 in cortical area 2 and reach E2, I2, E5, I5 in cortical area 1 with strengths 0.1, 0.5, 0.9 and 0.5, respectively.
In Figures 7 and S4 we simulated two scenarios corresponding to the spatial-attention task by Zhou et al. (2016): attention in and attention out. The condition ‘Attention in’ was implemented in the model as a constant top-down current Iatt = 5 and ‘Attention out’ with a current Iatt = 0 arriving at all excitatory cortical populations as well as to the pulvinar. The ‘with visual stimulation’ condition (Figures 7 and S4B) was implemented as an external current Istim = 4 arriving to the excitatory superficial population of V4 and for the ‘without visual stimulation condition’ (Figure S4A), Istim = 0. All cortical excitatory and pulvinar populations received in addition a background current Iext = 3 for all conditions.
The simulated LFP R used to estimate the spectral coherence and Granger causality interactions in the model, is estimated as R = (1 — η) rE2 + η rE5 with η = 0.85, so that both layers contribute to the field signal (although in different ways, given that layer 5/6 pyramidal cells are generally larger). We compute the spectral coherence and spectral pairwise conditional Granger causality (GC) between the two cortical areas by using the Multi-Variable Granger Causality Toolbox (Barnett and Seth, 2014) with an optimal AIC model order of up to 120 ms. For Figure 7C, we calculated the spectral coherence between V4 and IT under visual stimulation for the conditions attention in versus out and control versus lesion. Similarly, in Figure S4, we calculated GC between V4 and IT, in the feedforward (V4→ IT) and feedback (IT→ V4) directions, for conditions attention in versus out, control versus lesion, and with versus without visual stimulation.
Spectral Granger causality profiles of cortical interactions can be used to define a functional hierarchy, as defined by Bastos et al. (2015). Briefly, two cortical areas Cx1 and Cx2 are said to show an ascending functional hierarchical relationship if the spectral Granger causality pattern from Cx1 to Cx2 (Cx2 to Cx1) is predominantly strong in the gamma (alpha) range. The level of saliency of such pattern can be quantified by the so-called hierarchical distance, which is a function of the Granger causality profiles. We compute the functional hierarchical distance between cortical areas (Figures 7, S3, and S5) by following the procedure in Bastos et al. (2015) and Mejias et al. (2016). Briefly, we define the directed asymmetry index (DAI) between two cortical areas as the normalized difference between (GC) measurements in both directions, or
| (37) |
We obtain the multi-frequency DAI index (or mDAI) between two areas by averaging their DAI at the gamma and alpha ranges (and flipping the sign of the alpha term), or
| (38) |
We consider the gamma range as [30, 70] Hz, and the alpha/low beta range as [6, 18] Hz. Since in the present study we only consider two cortical areas, the value of mDAI for this pair gives the oscillation-based hierarchical distance between them. To calculate the oscillation-based hierarchical distance as a function of pulvinar gain (Figure S5), we varied the (normalized) pulvinar gain k as
where k = 0,1,2,3,4,5.
Hierarchy can also be defined functionally in terms of the timescale of intrinsic fluctuations during spontaneous activity. Areas high in the cortical hierarchy such as prefrontal areas have larger intrinsic timescales than lower areas such as sensory areas (Murray et al., 2014). We performed an autocorrelation on the firing rate calculated during spontaneous activity (only noise as input) to reveal the intrinsic or fluctuation timescales of spontaneous activity. The firing rate was first filtered with a Gaussian function with window σfilter = 20 ms. To compute the autocorrelation of the firing rate, we substracted the mean from the firing rate and then normalized. We then used Equation 39 to fit the normalized firing-rate autocorrelation and extract the intrinsic timescale τint as
| (39) |
where τint is the intrinsic timescale during spontaneous activity and a1 and a2 are parameters of the fit. The intrinsic timescale difference in Figure S5 was calculated as the intrinsic timescale in cortical area 2 minus the intrinsic timescale in cortical area 1. We calculated timescale differences as a function of pulvinar gain to produce the plot in Figure S5, by varying the (normalized) pulvinar gain k as
where k = 0,1,2,3,4,5.
QUANTIFICATION AND STATISTICAL ANALYSIS
To compute the spectral pairwise conditional Granger causality (GC) between two cortical areas, we use the Multi-Variable Granger Causality Toolbox (Barnett and Seth, 2014) with an optimal AIC model order of up to 120 ms (more information in Method Details above).
Supplementary Material
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Software and Algorithms | ||
| Pulvino-cortical network model simulations | This paper | https://github.com/jojaram/Pulvinar |
| Multivariable Granger Causality Toolbox | Barnett and Seth (2014) | http://www.sussex.ac.uk/sackler/mvgc/ |
Highlights.
Pulvino-cortical pathways modulate attention, working memory, and decision making
The pulvinar controls the effective connectivity within and across cortical areas
A plastic cortico-TRN-pulvinar circuit can estimate decision confidence
The pulvinar can regulate frequency-dependent and hierarchical cortical interactions
ACKNOWLEDGMENTS
Q6 This work was supported by NIH grant R01MH062349 and a Simons Foundation Collaboration on the Global Brain grant (X.-J.W.). The authors would like to thank Robert Yang, Judy Prasad, and Carmen Varela for carefully reading an earlier version of the manuscript and John D. Murray, Yuriria Vazquez, Bijan Pesaran, and especially Murray Sherman for insightful discussions.
Footnotes
DECLARATION OF INTERESTS
The authors declare no competing interests.
SUPPORTING CITATIONS
The following references appear in the Supplemental Information: Helias et al. (2014); Ruff and Cohen (2016).
DATA AND SOFTWARE AVAILABILITY
Software was written in the Python (https://www.python.org/) and MATLAB (https://www.mathworks.com/products/matlab.html) programming languages. Network simulations for the pulvino-cortical network are available at the GitHub repository: https://github.com/jojaram/Pulvinar.
REFERENCES
- Abbott LF, and Chance FS (2005). Drivers and modulators from push-pull and balanced synaptic input. Prog. Brain Res 149, 147–155. [DOI] [PubMed] [Google Scholar]
- Acsády L (2017). The thalamic paradox. Nat. Neurosci 20, 901–902. [DOI] [PubMed] [Google Scholar]
- Anticevic A, Cole MW, Repovs G, Murray JD, Brumbaugh MS, Winkler AM, Savic A, Krystal JH, Pearlson GD, and Glahn DC (2014). Characterizing thalamo-cortical disturbances in schizophrenia and bipolar illness. Cereb. Cortex 24, 3116–3130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Audette NJ, Urban-Ciecko J, Matsushita M, and Barth AL (2018). POm thalamocortical input drives layer-specific microcircuits in somatosensory cortex. Cereb. Cortex 28, 1312–1328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baldwin MK, Balaram P, and Kaas JH (2013). Projections of the superior colliculus to the pulvinar in prosimian galagos (Otolemur garnettii) and VGLUT2 staining of the visual pulvinar. J. Comp. Neurol 521, 1664–1682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barnett L, and Seth AK (2014). The MVGC multivariate Granger causality toolbox: a new approach to Granger-causal inference. J. Neurosci. Methods 223, 50–68. [DOI] [PubMed] [Google Scholar]
- Bastos AM, Vezoli J, Bosman CA, Schoffelen J-M, Oostenveld R, Dowdall JR, De Weerd P, Kennedy H, and Fries P (2015). Visual areas exert feedforward and feedback influences through distinct frequency channels. Neuron 85, 390–401. [DOI] [PubMed] [Google Scholar]
- Bazhenov M, Timofeev I, Steriade M, and Sejnowski TJ (2002). Model of thalamocortical slow-wave sleep oscillations and transitions to activated States. J. Neurosci 22, 8691–8704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Béhuret S, Deleuze C, and Bal T (2015). Corticothalamic synaptic noise as a mechanism for selective Attention in Thalamic Neurons. Front. Neural Circuits 9, 80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benevento LA, and Standage GP (1983). The organization of projections of the retinorecipient and nonretinorecipient nuclei of the pretectal complex and layers of the superior colliculus to the lateral pulvinar and medial pulvinar in the macaque monkey. J. Comp. Neurol 217, 307–336. [DOI] [PubMed] [Google Scholar]
- Bisley JW, and Goldberg ME (2006). Neural correlates of attention and distractibility in the lateral intraparietal area. J. Neurophysiol 95, 1696–1717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bolkan SS, Stujenske JM, Parnaudeau S, Spellman TJ, Rauffenbart C, Abbas AI, Harris AZ, Gordon JA, and Kellendonk C (2017). Thalamic projections sustain prefrontal activity during working memory maintenance. Nat. Neurosci 20, 987–996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Briggs F, and Usrey WM (2009). Parallel processing in the corticogeniculate pathway of the macaque monkey. Neuron 62, 135–146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brody CD, and Hanks TD (2016). Neural underpinnings of the evidence accumulator. Curr. Opin. Neurobiol 37, 149–157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buschman TJ, and Kastner S (2015). From behavior to neural dynamics: an integrated theory of attention. Neuron 88, 127–144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buschman TJ, and Miller EK (2007). Top-down versus bottom-up control of attention in the prefrontal and posterior parietal cortices. Science 315, 1860–1862. [DOI] [PubMed] [Google Scholar]
- Carandini M, and Heeger DJ (2011). Normalization as a canonical neural computation. Nat. Rev. Neurosci 13, 51–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaudhuri R, Knoblauch K, Gariel MA, Kennedy H, and Wang XJ (2015). A large-scale circuit mechanism for hierarchical dynamical processing in the primate cortex. Neuron 88, 419–431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christophel TB, Klink PC, Spitzer B, Roelfsema PR, and Haynes J-D (2017). The distributed nature of working memory. Trends Cogn. Sci 21, 111–124. [DOI] [PubMed] [Google Scholar]
- Cortes N, and van Vreeswijk C (2012). The role of pulvinar in the transmission of information in the visual hierarchy. Front. Comput. Neurosci 6, 29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crandall SR, Cruikshank SJ, and Connors BW (2015). A corticothalamic switch: controlling the thalamus with dynamic synapses. Neuron 86, 768–782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cruikshank SJ, Urabe H, Nurmikko AV, and Connors BW (2010). Pathway-specific feedforward circuits between thalamus and neocortex revealed by selective optical stimulation of axons. Neuron 65, 230–245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danziger S, Ward R, Owen V, and Rafal R (2004). Contributions of the human pulvinar to linking vision and action. Cogn. Affect. Behav. Neurosci 4, 89–99. [DOI] [PubMed] [Google Scholar]
- Desimone R, Wessinger M, Thomas L, and Schneider W (1990). Attentional control of visual perception: cortical and subcortical mechanisms. Cold Spring Harb. Symp. Quant. Biol 55, 963–971. [DOI] [PubMed] [Google Scholar]
- Dominguez-Vargas A-U, Schneider L, Wilke M, and Kagan I (2017). Electrical microstimulation of the pulvinar biases saccade choices and reaction times in a time-dependent manner. J. Neurosci 37, 2234–2257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferguson BR, and Gao WJ (2018). Thalamic control of cognition and social behavior via regulation of gamma-aminobutyric acidergic signaling and excitation/inhibition balance in the medial prefrontal cortex. Biol. Psychiatry 83, 657–669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleming SM, van der Putten EJ, and Daw ND (2018). Neural mediators of changes of mind about perceptual decisions. Nat. Neurosci 21, 617–624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gouws AD, Alvarez I, Watson DM, Uesaki M, Rodgers J, and Morland AB (2014). On the role of suppression in spatial attention: evidence from negative BOLD in human subcortical and cortical structures. J. Neurosci 34, 10347–10360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo ZV, Inagaki HK, Daie K, Druckmann S, Gerfen CR, and Svoboda K (2017). Maintenance of persistent activity in a frontal thalamocortical loop. Nature 545, 181–186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutierrez C, Cola MG, Seltzer B, and Cusick C (2000). Neurochemical and connectional organization of the dorsal pulvinar complex in monkeys. J. Comp. Neurol 419, 61–86. [DOI] [PubMed] [Google Scholar]
- Halassa MM, and Acsády L (2016). Thalamic inhibition: diverse sources, diverse scales. Trends Neurosci 39, 680–693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halassa MM, and Kastner S (2017). Thalamic functions in distributed cognitive control. Nat. Neurosci 20, 1669–1679. [DOI] [PubMed] [Google Scholar]
- Helias M, Tetzlaff T, and Diesmann M (2014). The correlation structure of local neuronal networks intrinsically results from recurrent dynamics. PLoS Comput. Biol 10, e1003428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Imura K, and Rockland KS (2006). Long-range interneurons within the medial pulvinar nucleus of macaque monkeys. J. Comp. Neurol 498, 649–666. [DOI] [PubMed] [Google Scholar]
- Itti L, and Koch C (2001). Computational modelling of visual attention. Nat. Rev. Neurosci 2, 194–203. [DOI] [PubMed] [Google Scholar]
- Joglekar MR, Mejias JF, Yang GR, and Wang X-J (2018). Inter-areal balanced amplification enhances signal propagation in a large-scale circuit model of the primate cortex. Neuron 98, 222–234.e8. [DOI] [PubMed] [Google Scholar]
- Jones EG (2007). The Thalamus, Volume 1889 (Springer Science; ). [Google Scholar]
- Kaas JH, and Lyon DC (2007). Pulvinar contributions to the dorsal and ventral streams of visual processing in primates. Brain Res. Brain Res. Rev 55, 285–296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanai R, Komura Y, Shipp S, and Friston K (2015). Cerebral hierarchies: predictive processing, precision and the pulvinar. Philos. Trans. R. Soc. Lond. B Biol. Sci 370, 20140169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karnath HO, Himmelbach M, and Rorden C (2002). The subcortical anatomy of human spatial neglect: putamen, caudate nucleus and pulvinar. Brain 125, 350–360. [DOI] [PubMed] [Google Scholar]
- Kawaguchi K, Clery S, Pourriahi P, Seillier L, Haefner RM, and Nienborg H (2018). Differentiating between models of perceptual decision making using pupil size inferred confidence. J. Neurosci 38, 8874–8888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kepecs A, Uchida N, Zariwala HA, and Mainen ZF (2008). Neural correlates, computation and behavioural impact of decision confidence. Nature 455, 227–231. [DOI] [PubMed] [Google Scholar]
- Kiani R, and Shadlen MN (2009). Representation of confidence associated with a decision by neurons in the parietal cortex. Science 324, 759–764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiani R, Cueva CJ, Reppas JB, and Newsome WT (2014). Dynamics of neural population responses in prefrontal cortex indicate changes of mind on single trials. Curr. Biol 24, 1542–1547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Komura Y, Nikkuni A, Hirashima N, Uetake T, and Miyamoto A (2013). Responses of pulvinar neurons reflect a subject’s confidence in visual categorization. Nat. Neurosci 16, 749–755. [DOI] [PubMed] [Google Scholar]
- LaBerge D, and Buchsbaum MS (1990). Positron emission tomographic measurements of pulvinar activity during an attention task. J. Neurosci 10, 613–619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markowitz DA, Shewcraft RA, Wong YT, and Pesaran B (2011). Competition for visual selection in the oculomotor system. J. Neurosci 31, 9298–9306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McAlonan K, Cavanaugh J, and Wurtz RH (2008). Guarding the gateway to cortex with attention in visual thalamus. Nature 456, 391–394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mejias JF, Murray JD, Kennedy H, and Wang X-J (2016). Feedforward and feedback frequency-dependent interactions in a large-scale laminar network of the primate cortex. Sci. Adv 2, e1601335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michael GA, Boucart M, Degreef JF, and Godefroy O (2001). The thalamus interrupts top-down attentional control for permitting exploratory shiftings to sensory signals. Neuroreport 12, 2041–2048. [DOI] [PubMed] [Google Scholar]
- Murray JD, Bernacchia A, Freedman DJ, Romo R, Wallis JD, Cai X, Padoa-Schioppa C, Pasternak T, Seo H, Lee D, and Wang XJ (2014). A hierarchy of intrinsic timescales across primate cortex. Nat. Neurosci 17, 1661–1663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray JD, Jaramillo J, and Wang X-J (2017). Working memory and decision-making in a frontoparietal circuit model. J. Neurosci 37, 12167–12186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nair A, Treiber JM, Shukla DK, Shih P, and Müller R-A (2013). Impaired thalamocortical connectivity in autism spectrum disorder: a study of functional and anatomical connectivity. Brain 136, 1942–1955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noudoost B, Chang MH, Steinmetz NA, and Moore T (2010). Top-down control of visual attention. Curr. Opin. Neurobiol 20, 183–190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oh SW, Harris JA, Ng L, Winslow B, Cain N, Mihalas S, Wang Q, Lau C, Kuan L, Henry AM, et al. (2014). A mesoscale connectome of the mouse brain. Nature 508, 207–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olshausen BA, Anderson CH, and Van Essen DC (1993). A neurobiological model of visual attention and invariant pattern recognition based on dynamic routing of information. J. Neurosci 13, 4700–4719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petersen SE, Robinson DL, and Keys W (1985). Pulvinar nuclei of the behaving rhesus monkey: visual responses and their modulation. J. Neurophysiol 54, 867–886. [DOI] [PubMed] [Google Scholar]
- Pouget A, Drugowitsch J, and Kepecs A (2016). Confidence and certainty: distinct probabilistic quantities for different goals. Nat. Neurosci 19, 366–374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purushothaman G, Marion R, Li K, and Casagrande VA (2012). Gating and control of primary visual cortex by pulvinar. Nat. Neurosci 15, 905–912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quax S, Jensen O, and Tiesinga P (2017). Top-down control of cortical gamma-band communication via pulvinar induced phase shifts in the alpha rhythm. PLoS Comput. Biol 13, e1005519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Romanski LM, Giguere M, Bates JF, and Goldman-Rakic PS (1997). Topographic organization of medial pulvinar connections with the prefrontal cortex in the rhesus monkey. J. Comp. Neurol 379, 313–332. [PubMed] [Google Scholar]
- Roth MM, Dahmen JC, Muir DR, Imhof F, Martini FJ, and Hofer SB (2016). Thalamic nuclei convey diverse contextual information to layer 1 of visual cortex. Nat. Neurosci 19, 299–307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rotshtein P, Soto D, Grecucci A, Geng JJ, and Humphreys GW (2011). The role of the pulvinar in resolving competition between memory and visual selection: a functional connectivity study. Neuropsychologia 49, 1544–1552. [DOI] [PubMed] [Google Scholar]
- Ruff DA, and Cohen MR (2016). Stimulus dependence of correlated variability across cortical areas. J. Neurosci 36, 7546–7556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saalmann YB, and Kastner S (2009). Gain control in the visual thalamus during perception and cognition. Curr. Opin. Neurobiol 19, 408–414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saalmann YB, and Kastner S (2011). Cognitive and perceptual functions of the visual thalamus. Neuron 71, 209–223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saalmann YB, Pinsk MA, Wang L, Li X, and Kastner S (2012). The pulvinar regulates information transmission between cortical areas based on attention demands. Science 337, 753–756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmitt LI, Wimmer RD, Nakajima M, Happ M, Mofakham S, and Halassa MM (2017). Thalamic amplification of cortical connectivity sustains attentional control. Nature 545, 219–223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sherman SM (2016). Thalamus plays a central role in ongoing cortical functioning. Nat. Neurosci 19, 533–541. [DOI] [PubMed] [Google Scholar]
- Sherman SM, and Guillery RW (2013). Functional Connections of Cortical Areas: A New View from the Thalamus (MIT Press)
- Shipp S (2015). Pulvinar structure, circuitry and function in primates. In Reference Module in Biomedical Sciences, McQueen CA, Boron WF, Boulpaep EL, Bradshaw RA, Bylund DB, Enna SJ, Hart G, Hughes KT, Kulkarni S, and Maloy S, et al. , eds. (Elsevier; ). [Google Scholar]
- Siegel M, Buschman TJ, and Miller EK (2015). Cortical information flow during flexible sensorimotor decisions. Science 348, 1352–1355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snow JC, Allen HA, Rafal RD, and Humphreys GW (2009). Impaired attentional selection following lesions to human pulvinar: evidence for homology between human and monkey. Proc. Natl. Acad. Sci. USA 106, 4054–4059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steriade M, Jones EG, and Llinas RR (1990). Thalamic Oscillations and Signaling (Wiley)
- Strumpf H, Mangun GR, Boehler CN, Stoppel C, Schoenfeld MA, Heinze H-J, and Hopf J-M (2013). The role of the pulvinar in distractor processing and visual search. Hum. Brain Mapp 34, 1115–1132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suzuki M, and Gottlieb J (2013). Distinct neural mechanisms of distractor suppression in the frontal and parietal lobe. Nat. Neurosci 16, 98–104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szczepanski SM, and Kastner S (2013). Shifting attentional priorities: control of spatial attention through hemispheric competition. J. Neurosci 33, 5411–5421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ter Wal M, and Tiesinga PH (2017). Phase difference between model cortical areas determines level of information transfer. Front. Comput. Neurosci 11, 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Theyel BB, Llano DA, and Sherman SM (2010). The corticothalamocortical circuit drives higher-order cortex in the mouse. Nat. Neurosci 13, 84–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varela C (2014). Thalamic neuromodulation and its implications for executive networks. Front. Neural Circuits 8, 69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Viviano JD, and Schneider KA (2015). Interhemispheric interactions of the human thalamic reticular nucleus. J. Neurosci 35, 2026–2032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wall NR, De La Parra M, Sorokin JM, Taniguchi H, Huang ZJ, and Callaway EM (2016). Brain-wide maps of synaptic input to cortical interneurons. J. Neurosci 36, 4000–4009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X-J (2013). The prefrontal cortex as a quintessential “cognitive-type” neural circuit: working memory and decision making. In Principles of Frontal Lobe Function, Stuss DT and Knight RT, eds. (Oxford University; ), pp. 226–248. [Google Scholar]
- Wang X-J, and Yang GR (2018). A disinhibitory circuit motif and flexible information routing in the brain. Curr. Opin. Neurobiol 49, 75–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ward LM (2013). The thalamus: gateway to the mind. Wiley Interdiscip. Rev. Cogn. Sci 4, 609–622. [DOI] [PubMed] [Google Scholar]
- Ward R, Danziger S, Owen V, and Rafal R (2002). Deficits in spatial coding and feature binding following damage to spatiotopic maps in the human pulvinar. Nat. Neurosci 5, 99–100. [DOI] [PubMed] [Google Scholar]
- Wei Z, and Wang X-J (2015). Confidence estimation as a stochastic process in a neurodynamical system of decision making. J. Neurophysiol 114, 99–113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei W, and Wang XJ (2016). Inhibitory control in the cortico-basal gangliathalamocortical loop: complex regulation and interplay with memory and decision processes. Neuron 92, 1093–1105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White BJ, Kan JY, Levy R, Itti L, and Munoz DP (2017). Superior colliculus encodes visual saliency before the primary visual cortex. Proc. Natl. Acad. Sci. USA 114, 9451–9456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilke M, Turchi J, Smith K, Mishkin M, and Leopold DA (2010). Pulvinar inactivation disrupts selection of movement plans. J. Neurosci 30, 8650–8659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilke M, Kagan I, and Andersen RA (2013). Effects of pulvinar inactivation on spatial decision-making between equal and asymmetric reward options. J. Cogn. Neurosci 25, 1270–1283. [DOI] [PubMed] [Google Scholar]
- Wimmer RD, Schmitt LI, Davidson TJ, Nakajima M, Deisseroth K, and Halassa MM (2015). Thalamic control of sensory selection in divided attention. Nature 526, 705–709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wong K-F, and Wang X-J (2006). A recurrent network mechanism of time integration in perceptual decisions. J. Neurosci 26, 1314–1328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang S, Xu M, Chang WC, Ma C, Hoang Do JP, Jeong D, Lei T, Fan JL, and Dan Y (2016). Organization of long-range inputs and outputs of frontal cortex for top-down control. Nat. Neurosci 19, 1733–1742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou H, Schafer RJ, and Desimone R (2016). Pulvinar-cortex interactions in vision and attention. Neuron 89, 209–220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou NA, Maire PS, Masterson SP, and Bickford ME (2017). The mouse pulvinar nucleus: Organization of the tectorecipient zones. Vis. Neurosci 34, E011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou N, Masterson SP, Damron JK, Guido W, and Bickford ME (2018). The mouse pulvinar nucleus links the lateral extrastriate cortex, striatum, and amygdala. J. Neurosci 38, 347–362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zikopoulos B, and Barbas H (2006). Prefrontal projections to the thalamic reticular nucleus form a unique circuit for attentional mechanisms. J. Neurosci 26, 7348–7361. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


