Abstract
The simplified and modified Bernoulli equations break down in estimating the true pressure gradient across the stenotic aortic valve due to their over simplifying assumptions of steady and inviscid conditions as well as the fundamental nature in which aortic valves are different than idealized orifices. Nevertheless, despite having newer models based on time-dependent momentum balance across an orifice, the simplified and modified Bernoulli continue to be the clinical standard because to date, they remain the only models clinically implementable. The objective of this study is to (1) illustrate the fundamental considerations necessary to accurately model the time-dependent instantaneous pressure gradient across a fixed orifice and (2) propose empirical corrections when applying orifice based models to severely stenotic aortic valves. We introduce a general model to predict the time-dependent instantaneous pressure gradient across an orifice that explicitly model the Reynolds number dependence of both the steady and unsteady terms. The accuracy of this general model is assessed with respect to previous models through pulse duplicator experiments on a round orifice model as well as an explanted stenotic surgical aortic valve both with geometric areas of 0.6cm2 (less than 1cm2 which is the threshold for stenosis determination) over cardiac outputs of 3 and 5 L/min and heart rates of 60, 90 and 120 bpm. The model and the raw experimental data corresponding to the orifice showed good agreement over a wide range of cardiac outputs and heart rates (R2 exceeding 0.91). The derived average and peak transvalvular pressure gradients also demonstrated good agreement with no significant differences between the respective peaks (p>0.09). The new model proposed holds promise with its physical and closed form representation of pressure drop, however accurate modeling of the time-variability of the valve area is necessary for the model to be applied on stenotic valves.
Keywords: Aortic stenosis, pressure gradient, flow unsteadiness, Reynolds number, Bernoulli equation
Introduction
Aortic stenosis is the narrowing and progressive dysfunction of the aortic valve. It is the most common structural heart disease in the elderly, with an estimated increase in prevalence from approximately 38.7 million in 2008 to 88.5 million by 2050[1]. The progressive narrowing of the valve causes temporal changes in the surrounding local fluid dynamics. Generally, blood flow through an aortic heart valve is pulsatile, turbulent and unsteady in nature and is complicated by the time dependent variability of the valve orifice area[2, 3]. Due to such complex fluid dynamics, analytically estimating pressure difference across the valve – clinically referred to as “pressure gradient” (with pressure gradient referring to ΔP as opposed to spatial derivatives of pressure ) - or any other relevant hemodynamic parameter (e.g. energy loss) to assess the severity of aortic stenosis non-invasively, is not a simple task and necessitates semi-empirical approaches.
The need for a more accurate pressure gradient estimation stems from the fact that current evaluation of the severity of aortic stenosis is still not adequate as reviewed in the article by Otto et al[4]. Briefly, accurate severity of stenosis is necessary not only for predicting the optimal timing of valve replacement but also for establishing that the symptoms are indeed due to the stenosis. Currently, the most reproducible parameter that can be clinically measured is the aortic valve jet velocity using echocardiography. Other parameters include the velocity at the left ventricular outflow tract (LVOT) as well as the area at the LVOT. These parameters indirectly yield the valve area through the continuity equation. In order to assess the load on the ventricle, pressure gradient across the valve is estimated using the simplified Bernoulli equation or the modified Bernoulli equation – both being a surrogate of velocity rather than capturing losses. Prospective clinical studies have shown that neither jet velocity, pressure gradient, nor valve area defines symptom onset for any single value[4] which makes clinical decision making more difficult. To elaborate, there appears to be overlaps in velocity, valve area, and gradient with respect to true severity of the disease between asymptomatic and symptomatic patients based on outcomes in these patients. This apparent paradox clearly points to (a) the fact that clinical measures of velocity, valve area, and pressure gradient are too rough and (b) the need for better approaches that take into account the true impact (load) on the left ventricle. The load on the ventricle is the cumulative effect of the ventricle-valve-vasculature interaction. Aortic stenosis ultimately affects the left ventricle and therefore, characterizing the severity of aortic stenosis should not just focus on how fast the jet velocity is or how narrow the orifice has become (each obviously correlating with the disease severity) but rather should capture how much additional load the left ventricle has to overcome. Towards this goal, accurate estimation of pressure gradient becomes critical. To gauge the true impact on the left ventricle, it is important to estimate the true pressure gradient so that it may be further utilized to evaluate ventricular workload. It is well established that the pressure gradient estimated using Bernoulli ignores pressure recovery effects as well as losses[4]. Pressure recovery effects have been shown to be more important when the stenosis is mild/moderate or when the aortic root is small[5]. Another approach to directly gauge severity is to evaluate the ventricular workload through energy loss index (ELI) which has been shown to better correlate with outcome than the more standard parameters[6], While the mathematics behind ELI are rooted in the flow-pressure gradient work, there are assumptions within the formulation of ELI that impact its accuracy. The most notable approximation is the substitution of effective orifice area with continuity based aortic valve area. This approximation ignores the very fundamental ways in which losses occur past a stenotic valve or orifice (e.g. Reynolds number effects, recovery etc.)
As described earlier, the current clinical standard to estimate aortic valve pressure gradients utilizes Doppler Ultrasound Echocardiography where the forward jet velocity at the vena contracta is the independent measurement which then, using simplified (or modified) Bernoulli equation, yields pressure gradient [7, 8]. Several attempts to model pressure gradient across aortic valves were made. A study by Young in 1979 showed a relationship between pressure gradient and the instantaneous variation of flow rate through dimensional analysis[9]. Using this model, Chandran et al attempted to develop expressions for the mean pressure gradient and the peak pressure gradient as part of effective orifice area calculation[10]. Other studies namely Clark et al[11] and Bermejo et al[12] modeled the pressure gradient variability however introduced terms that were highly dependent on the local geometry making their implementation difficult[13]. Garcia et al developed a model that attempted to predict the variation of instantaneous and maximal pressure gradient across the aortic valve based on the application of conservation principles while treating the effective orifice area as an independent variable [13, 14]. However, these models have not become clinical standards because they are dependent on knowing the effective orifice area (EOA), which is not known a priori, in addition to not including Reynolds Number (Re) dependence of the flow re-attachment. In general, models based on fixed EOA of the aortic valve, although analytically elegant, bypass the most important aspect of Reynolds number dependency and flow contraction ratio (ratio of the inlet tube or pipe area to the geometric orifice area) dependency of EOA itself [15-17] that lead to nonphysical representation of the flow physics. Finally, the effects of the flexibility of the calcified leaflets which result in a flow dependent orifice area thereby resulting in an orifice that is no longer of fixed geometric area further complicates the relationship and have never been modeled before. These factors re-iterate the continuing challenge with formulating a closed form model to accurately estimate pressure gradients in stenotic aortic valves that are based on clinically measureable independent variables.
The objective of this study is to reformulate the model by introducing a generalized instantaneous pressure gradient across an orifice that represents aortic valve stenosis throughout systole[18] by considering the turbulent losses as well as the unsteady effects of temporal flow acceleration through the stenotic orifice. The goal is to base the model on parameters measurable clinically along with a physical representation of the dependency on Reynolds number and time rate of change of flow (i.e. acceleration and deceleration). This study constitutes the first step towards attempting to help improve the diagnostic accuracy for assessing the severity of aortic stenosis that account for dissipation, unsteadiness and Reynolds number dependence, all of which are currently ignored.
Methodology
Model setup
High fidelity hemodynamic flow rate and pressure drop measurements across a round orifice as well as across a stenotic calcified aortic valve were obtained corresponding to aortic flow and pressure waveforms in a left heart simulator.
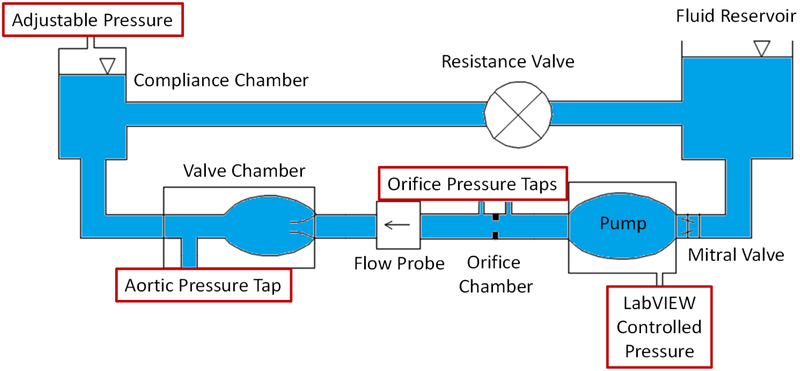
Figure 1 shows a schematic sketch of the experimental setup with the orifice chamber. For the round orifice pressure drop experiments, an orifice chamber with a round orifice area of 0.6 cm2 inside an 2.54 cm diameter tube was placed in series with a non-stenotic 21mm Medtronic Hancock II surgical aortic valve mounted in an idealized aortic root model of a left heart simulator as previously described[19-22]. Figure 2a shows a close-up 3D model of the orifice chamber. The pressure ports used to measure the instantaneous pressure gradient are located at 3cm upstream and 5cm downstream of the orifice respectively.
Figure 1:
Schematic diagram showing the experimental setup.
Figure 2:
(a) Orifice chamber model, (b) 23mm Edwards Perimount calcified aortic valve extracted from a redo surgery patient and (c) Cartoon of the flow through the orifice.
For the stenotic aortic valve experiments, a 23 mm stenotic calcified Edwards Perimount valve (Figure 2b) explanted from a redo surgery patient - as part of an Institutional Review Board–approved study - was placed in the same aortic model in the pulse duplicator without the orifice chamber[20]. The valve area of the stenotic aortic valve was 0.6 cm2 as determined by echocardiography using the continuity equation. The continuity equation valve area was part of the echocardiographic medical report prior to being explanted from the patient and involves the application of the continuity (mass balance) with direct measurements of the left ventricular outflow tract (LVOT) diameter, the velocity at the LVOT and the jet velocity at the valve orifice. Details of this routine clinical implementation of the continuity equation can be found in Baumgartner et al[23].
Hemodynamic assessment
Instantaneous flow rate and pressure gradient were measured under pulsatile flow conditions ensured by a left heart pulse duplicator yielding flow and pressure curves consistent with severe aortic stenosis. Base hemodynamics for all conditions were maintained with a systolic to diastolic pressure of 120/80mmHg, a 60 beat per minute (bpm), 90 bpm and 120 bpm heart rate, a systolic duration of 33% and cardiac outputs of 3L/min and 5L/min for each heart rate (HR). The working fluid in this study was a mixture of water-glycerine producing a density of 1060 kg/m3 and a kinematic viscosity of 3.5 cSt similar to blood properties. Sixty consecutive cardiac cycles of aortic pressure, pressure gradient across the orifice or the stenotic aortic valve, and aortic flow rate were recorded at a sampling rate of 100 Hz. Flow rate was measured using an ultrasonic flow probe (Transonic Inc., Ithaca, NY), and pressures upstream and downstream of the valve were measured using Validyne pressure transducers (Validyne Engineering Corp., Northridge, CA). More details are found in previous publications [19-22].
The mean transvalvular pressure gradient (PG) was defined as the average of positive pressure difference between the ventricular and aortic pressure curves during forward flow. The calcified Edwards Perimount valve was tested at 60 beats per minute at 5 L/min cardiac output.
Pressure gradient as would have been measured clinically was also calculated using simplified Bernoulli given by:
| (1) |
Where:
V is the orifice velocity (m/s) represented by the volume flow rate divided by the orifice area.
Effective orifice area (EOA) calculations were also performed. EOA was computed using the Gorlin’s equation:
| (2) |
Where Q represents the root mean square aortic valve flow over the same averaging interval of the PG.
Particle Image Velocimetry (PIV)
In order to obtain instantaneous velocity through the stenotic aortic valve, particle image velocimetry measurements were performed. The working fluid in the flow loop was seeded with fluorescent PMMA-Rhodamine B particles with an average diameter of 10 μm. PIV involves illuminating the flow across the orifice and the valve using a laser sheet created by pulsed Nd:YLF single cavity diode pumped solid state laser coupled with external spherical and cylindrical lenses; while acquiring high-speed images of the fluorescent particles within the sinus region. Time-resolved raw PIV images were acquired with a resulting spatial and temporal resolutions of 0.159 mm/pixel and 1000 Hz respectively. Velocity vectors were calculated using adaptive cross-correlation algorithms. The commercial PIV software, DaVis (LaVision, Germany) was used for data acquisition and processing. Post processing was executed using adaptive median filtering. Further details of PIV measurements can be found in our previous publications[19-21, 24].
Statistics
All data are presented as mean ± standard deviation. Coefficients of correlation (R2) were computed to assess how strong the relationship is between the experimental data measured and the data derived using our general orifice model (described in the Results section). Analyses were performed over 100 replicates. Student t test was performed and p < 0.05 was considered statistically significant.
Results
Model derivation
Consider the streamline through the orifice shown in Figure 2c. Now, the instantaneous pressure gradient across the orifice can be expressed by considering the unsteady form of Bernoulli equation with losses:
| (3) |
Where the first term represents the flow temporal acceleration or deceleration, 1 the upstream location, 2 the downstream location (indicated on Figure 2c), V the velocity at the specified location, P2 − P1 pressure difference, and HL head loss due to energy losses from the contraction and expansion of the flow through the orifice, typically lumped through a discharge coefficient[25].
Having V1 = V2, the equation becomes:
| (4) |
It is clear that the instantaneous pressure gradient (right hand side) depends on the time dependent term as well as the head loss across the orifice.
With respect to the head loss term, we approximate this by using the classic steady flow orifice pressure drop model[25] given by:
| (5) |
Where K is the orifice resistance coefficient defined below and C1 a constant that we will empirically determine.
| (6) |
Where Cd is the orifice discharge coefficient defined as:
| (7) |
| (8) |
| (9) |
Re is the Reynolds’ number based on the tube diameter D downstream of the valve at the pressure port location and the cross-sectional averaged instantaneous velocity.
| (10) |
With d and D indicated on Figure 2c.
Now, with regards to the time-dependent term in equation 4, this can be further simplified considering that:
| (11) |
Where Q is the flow rate and A is the stream tube area (downstream of the valve) which is dependent on s.
The first term on the left side of equation 4 becomes:
| (12) |
Notice that Q does not change with respect to the s coordinate between 1 and 2 (shown in Figure 2c) but A changes from tube area (1) to EOA back to tube area (2) with the control volume being the streamtube emerging from the flow detachment upstream of the orifice to the re-attachment downstream of the orifice. Normalizing s as s'=s/D and A with Ao (the orifice area), the integral on the right hand side of equation 12 can be expressed as:
| (13) |
With D being the diameter, Ao the orifice area, and K1 a dimensionless factor that is Reynolds number dependent and that represents the factor that accounts for the flow contraction towards the vena contracta and back to re-attachment as shown previously in DeGroff et al[15]. Dimensional analysis highlighting this relationship as well is provided in Appendix A.
The Reynolds number dependence also comes out through an alternative derivation, starting with the time dependent term:
| (14) |
Where is the velocity averaged along the length of the streamtube of length L, and L being the length from the beginning of flow detachment upstream of the orifice to the reattachment downstream of the orifice chamber as denoted in Fig.2c.
The unsteady term can now be expressed as:
| (15) |
Equation (3) then becomes a generalized instantaneous pressure gradient across the orifice model:
| (16) |
The constants K1 and C1 of equation 16 were empirically determined (assuming a power law relationship with Reynolds number) and fine-tuned based on the raw experimental data corresponding to the case where CO = 5L/min and HR = 60 bpm to yield:
| (17) |
| (18) |
Equation 16 will be multiplied by 0.0075 to convert the units of pressure gradient from Pa to mmHg. Reo is the Reynold’s number based on the orifice diameter and Ao the cross sectional area of the orifice.
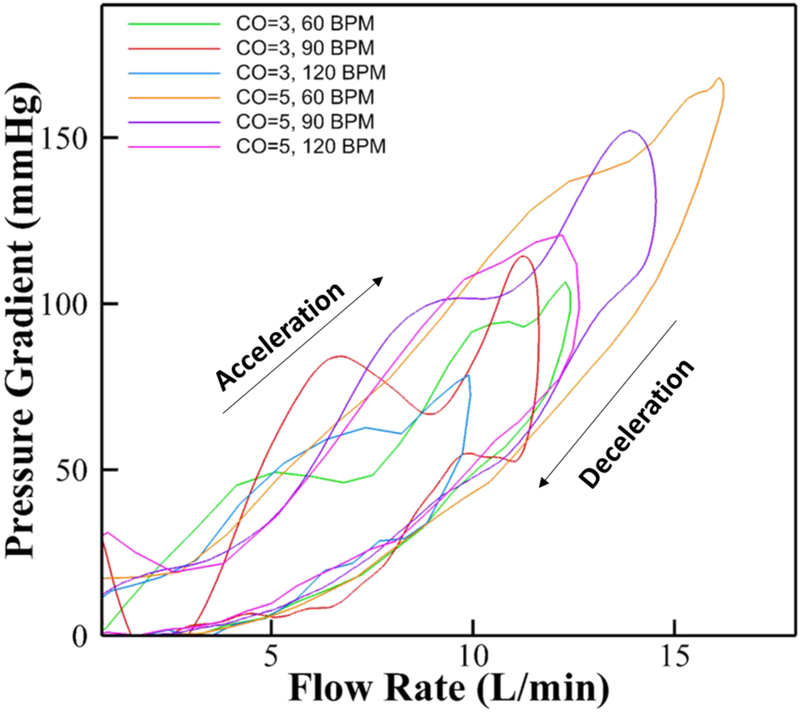
The rationale is that if the model of equation 16 indeed represents a good model, then the constants derived based on one case should be good enough for the model to predict the other cases. Now, because the CO=5 L/min and HR 60bpm case is characterized by the largest range of flow and pressure (as shown in Figure 3), it was chosen as the reference dataset to fine-tune the model parameters.
Figure 3:
Experimental raw instantaneous pressure gradient variations across the orifice versus flow rate for different cardiac outputs and flow rates across the orifice.
Raw experimental data versus derived model
Figure 3 shows the measured raw instantaneous pressure gradient variations as a function of instantaneous flow rate for different cardiac outputs and heart rates across the orifice. The figure shows that the variation in PG is a loop-like function capturing both acceleration and deceleration phases before going back to zero (annotated on the figure). For every instantaneous flow rate, there exist two different instantaneous pressure gradient values depending on whether the phase is acceleration or deceleration of the systolic flow. More pressure gradient occurs during acceleration compared to when the flow rate is same during deceleration.
Comparative plots of the experimental data for every CO and HR condition versus Bernoulli equation (simplified Bernoulli), a derived model from Garcia et al (2005) and the new generalized model (Equation 16) are shown in Figure 4. As can be seen from the figure, the Bernoulli’s equation captures the “middle” part of the instantaneous pressure gradient curves almost bisecting the acceleration and deceleration arms of the experimental pressure gradient loop. Better agreement between the experimental results and the derived model is observed compared with Bernoulli with R2 values exceeding 0.91. The new generalized model captures the acceleration and deceleration arms of the loop of the pressure gradient. This loop like characteristic is obviously absent in the simple parabolic equation representing the Bernoulli equation (equation 1). The new generalized model also captures the pressure variations at higher flow rates (> 5L/min). Comparing our new generalized derived model with that from Garcia et al (2005), it is clear that instantaneous pressure gradient derived in Garcia et al underestimates the peak pressure gradient (raw experimental data) at the higher flow rates and during acceleration, while over-estimating the pressure gradient during deceleration phase particularly for lower cardiac output cases. The new generalized model performs relatively more superior with excellent overall agreement.
Figure 4:
Ensemble averaged measured pressure gradient over 60 cycles, calculated pressure gradient from Bernoulli, pressure gradient from Garcia et al and derived pressure gradient variations versus time for (a) CO = 3L/min, 60 bpm (b) CO = 3L/min, 90 bpm (c) CO = 3L/min, 120 bpm (d) CO = 5L/min, 60 bpm (e) CO = 5L/min, 90 bpm and (f) CO = 5L/min, 120 bpm.
Hemodynamic parameters
Figures 5a and 5b show the average and peak pressure gradients for the different cardiac outputs at different heart rates across the round orifice cases measured experimentally. The range of the pressure gradients is in accordance with Figure 3. At CO = 3 L/min, the average pressure gradients varied inversely with HR starting from 33.73 ± 1.03mmHg at 60bpm, to 28.61±0.97 mmHg at 90bpm to 21.4±0.43mmHg at 120bpm (p<0.01). The peak pressure gradient was lowest at 120bpm reaching 81.02±4.29mmHg compared with 107.56±2.79mmHg and 116.47±4.09mmHg at 60 (p=0.07) and 90bpm respectively (p<0.01). The difference between peak gradients at 60 and 90bpm is not significant (p=0.07). Similarly, at CO=5L/min, The average PGs decrease with increasing HR going from 60.34±0.57 mmHg at 60bpm, to 41.23 ± 0.57 mmHg at 90bpm, to 37.14 ± 0.44mmHg at 120bpm (p<0.01). Peak pressure gradients also follow the same trend varying from 172.66±3.58 at 60bpm, to 154.73±3.83 at 90bpm to 124±6.88 at 120bpm (p<0.01).
Figure 5:
(a) Experimental average pressure gradients variations across the orifice versus different cardiac outputs at different heart rates; (b) peak pressure gradients variations versus different cardiac outputs at different heart rates; (c) Derived model average pressure gradients variations across the orifice versus different cardiac outputs at different heart rates; (d) peak pressure gradients variations versus different cardiac outputs at different heart rates; and (e) Average effective orifice areas EOA variations across the orifice versus different cardiac outputs at different heart rates. Values are reported ± standard deviation.
Figures 5c and 5d show the average and peak pressure gradients for the different cardiac outputs at different heart rates across the round orifice cases our new generalized pressure gradient model (Equation 16). At CO = 3 L/min, the average pressure gradients varied inversely with HR starting from 24.76 ± 0.76mmHg at 60bpm, to 24.18±0.82 mmHg at 90bpm (p = 0.60) to 18.23±0.37mmHg at 120bpm (p<0.01). The peak pressure gradient was lowest at 120bpm reaching 76.47±4.05mmHg (p<0.01) compared with 106.81±2.77mmHg and 108.94±3.83mmHg at 60 and 90bpm respectively (p = 0.92). Similarly, at CO=5L/min, The average PGs decreased with increasing HR going from 47.9±0.45 at 60bpm, to 41.87±0.58 at 90bpm (p = 0.06), to 33.91±0.40 at 120bpm (p<0.01). Peak PGs also follow the same trend varying from 179.3±3.72 at 60bpm, to 164.1±4.06 at 90bpm (p<0.01) to 125.1±6.94 at 120bpm (p<0.01). For some cases, the model provides higher pressure gradient values and for others lower. Thus, there is no uniformity in values trends. While the differences between average PGs obtained experimentally and computed using the derived model are significant, the peak PGs were not (p>0.09).
Average effective orifice areas (EOA) variations across the orifice versus different cardiac outputs at different heart rates are shown in Figure 5e. It is obvious that EOA measurement is highly sensitive to the experimental conditions as in heart rate and cardiac output. The differences were statistically significant (p<0.01) for the same heart rate at different cardiac outputs. Only EOAs at the same cardiac output at 60 and 120 bpm were statistically significant.
Applicability of the model on a stenotic surgical aortic valve
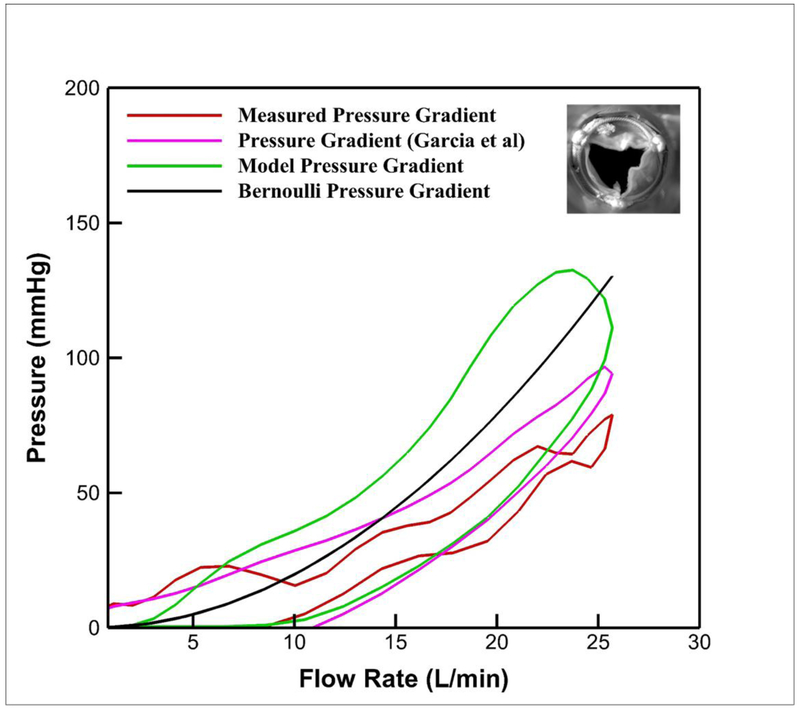
To test the applicability of the new generalized model for the case of a real stenotic aortic valve, the instantaneous pressure gradient measured across the stenotic surgical aortic valve with an aortic valve area of 0.6 cm2 is plotted versus the flow rate (see Figure 6) along with Bernoulli’s model, Garcia et al’s model and our new generalized model. From the PIV measurements, the velocity at the valve exit was obtained and used in equation (16). As noted in Figure 6, the new generalized model captures well the variations of pressure gradient in the deceleration part of the cycle at flow rates up to 10L/min. However, it greatly overestimates the acceleration arm of the loop. The same is observed about the model of Garcia et al’s, only the overestimation in the acceleration portion is lower than the new generalized orifice model derived in this study.
Figure 6:
Ensemble averaged measured pressure gradient across a stenotic aortic valve over 60 cycles, calculated pressure gradient from Bernoulli, pressure gradient from Garcia et al (2005), and derived pressure gradient variations versus time for CO = 5L/min at 60 bpm. The inset of the figure shows the stenotic valve at peak systole.
Discussion
Evaluation of aortic stenosis is one of the most common hemodynamic challenges encountered in cardiology[26]. The simplified Bernoulli formula remains the standard and simplest method to quantify the severity of aortic stenosis and requires accurate determination of velocity across the aortic valve[26]. During clinical examination, the average pressure gradients are indirectly measured using Doppler Echocardiography through measuring the velocity at the vena contracta and using simplified Bernoulli equation or Bernoulli equation[27]. In this study, (1) an empirical generalized model capturing the variations of instantaneous pressure gradients versus instantaneous flow rates during systole across a round orifice was derived, (2) the model was tested on a stenotic aortic valve of area equivalent to that of the orifice in the experiment, and (3) the new generalized model was compared to another model from a study by Garcia et al that requires a priori estimation of the effective orifice area. To our knowledge, this study constitutes the first step towards a more elaborate and comprehensive study where an attempt to model the instantaneous variations of pressure gradient using routinely acquired clinical data as function of Reynolds number is done and is applied on a real stenotic valve.
Assessment of the individual terms that constitute the new generalized orifice model
Here we assess the contributions of each of the constitutive terms (unsteady and steady) of the new generalized model to better understand the importance of these terms as well as the importance of Reynolds number dependence within the constants involved in the respective terms. Figure 7 illustrates the individual contribution of the steady and unsteady terms for each of the orifice experimental condition. From this figure, it is shown that both unsteady and steady terms alone do not reflect the true experimental variations of the pressure gradient as a function of flow rate. The figure highlights the importance of both contributions in reaching a model that best represents the experimental results. The unsteady term is responsible for reproducing the loop shape by adding or subtracting its influence over the monotonic steady term. Compared to the magnitude of the pressure gradient, the steady term is primarily responsible for achieving the overall trend from low to high pressure gradient as a function of flow rate, while the unsteady term’s contributions are of lower magnitudes. In order to investigate how the unsteady and steady terms change with the different flow and frequency (heart rate) variations, the different plots are combined in one comprehensive plot shown in Figure 8. Figure 8 shows that the steady term of all the cases collapses in one curve (as defined by the steady term of equation 16) while the unsteady term overlaps at low flow rates up to 6 L/min in acceleration and up to 9 L/min during deceleration. In addition, notice the asymptotic behavior of the decelerating arm of the unsteady term compared to the accelerating arm.
Figure 7:
Individual contributions of steady and unsteady terms for each one of the orifice cases: (a) CO=3L/min, HR=60bpm; (b) CO=3L/min, HR=90bpm; (c) CO=3L/min, HR=120bpm; (d) CO=5L/min, HR=60bpm; (e) CO=5L/min, HR=90bpm and (f) CO=5L/min, HR=120bpm.
Figure 8:
Individual contributions of steady and unsteady terms for each one of the cases.
Dependence of the terms on the Reynolds number
In this study, the dependence on Reynolds number was highlighted – an addition that was not incorporated in previous models. In order to assess this importance, the variations of K1 term (equation 17) and K term (equation 6) with respect to flow rates with the different cardiac output and heart rate conditions were plotted in Figures 9a and 9b respectively. Both terms are Reynolds number dependent. K1 increases as the flow increases while K reaches a plateau (asymptote) as flow rate increases.
Figure 9:
(a) Variations of (a) K1 and (b) K as a function of flow rate for each of the different orifice flow and heart rate conditions.
To better assess the potential need for Reynolds number dependency on the new generalized model’s terms, Figures 10 and 11 show the variations of the unsteady and steady terms, respectively, with K1 and K either left with Re dependency or approximated to a constant value corresponding to the maximum or minimum value of these constants. Figure 10 clearly demonstrates the importance of retaining the full Reynolds number dependency for the unsteady term. However, for the case of the steady term, approximating K to the asymptotic limit provides a very close profile compared to the one with full Reynolds number dependency. These figures clearly show that Re is important specifically in the unsteady term and cannot be estimated to a constant value, as the overall shape of the curve will not reflect the experimental results.
Figure 10:
Dependence of unsteady term variations with flow rate on Reynold’s number for the different orifice conditions: (a) CO=3L/min, HR=60bpm; (b) CO=3L/min, HR=90bpm; (c) CO=3L/min, HR=120bpm; (d) CO=5L/min, HR=60bpm; (e) CO=5L/min, HR=90bpm and (f) CO=5L/min, HR=120bpm.
Figure 11:
Dependence of steady term variations with flow rate on Reynold’s number for the different orifice conditions: (a) CO=3L/min, HR=60bpm; (b) CO=3L/min, HR=90bpm; (c) CO=3L/min, HR=120bpm; (d) CO=5L/min, HR=60bpm; (e) CO=5L/min, HR=90bpm and (f) CO=5L/min, HR=120bpm.
Raw experimental data versus new generalized model and Applicability of the new model for stenotic aortic valves
The simplified Bernoulli model clearly does not capture the loop like variations in instantaneous pressure gradients seen with pulsatile aortic flows through a simple orifice. This is clear as the simplified Bernoulli model has no dependency with respect to the time rate of change of flow rate or velocity through the orifice. Thus, despite being the clinical standard to estimate pressure gradient in-clinic, the simplified Bernoulli equation is limited due to the assumption of no frictional losses and further ignoring the unsteady effects from the instantaneous acceleration or deceleration of the flow rate.
In contrast to the simplified Bernoulli model, our new generalized orifice model as well as Garcia et al’s model captures the loop like behavior seen in the instantaneous pressure gradient across the orifice as well as the aortic valve. Despite tuning the parameters of our new model (K1 and C1) based on a single case of cardiac output of 5 L/min and a heart rate of 60 bpm, the new model captured the variations of the transvalvular instantaneous pressure gradients with R2 values exceeding 0.91 for all the cardiac output and heart rate conditions. This close agreement can be attributed to the fact that the derived instantaneous pressure gradient model captured the dependency on Reynolds number (particularly arising in the unsteady term).
Comparing our new model with Garcia et al’s model, in principle, both models are mathematically similar in the sense that they both incorporate the unsteady term and the steady loss term, however there are fundamental differences which explain the better and more conservative prediction of the new model. Garcia et al (a) did not implement the dependence on the Reynolds number so the entrance effects as well as the re-attachment location was assumed to be held fixed throughout systole, and (b) they utilized a constant effective orifice area throughout systole. Both of these assumptions can lead to significant drawbacks in accuracy, as it is well known that the entrance and re-attachment locations are strongly dependent on the Reynolds number. Further, it is also known that the vena contracta location and size are also Reynolds number dependent, as well as dependent on the ratio of the geometric orifice area and the tube diameter. The latter is emphasized in Figure 5e which shows significant variations in EOA as a function of cardiac output, heart rate, in addition to being significantly smaller than the geometric orifice area.
Applying both the derived model in this study along with Garcia’s model and comparing them with the experimental pressure gradient obtained from a stenosed aortic valve, it is noted that both models do not quite capture the actual variations of pressure gradient. Both models underestimate pressure gradient at low flows (less than 5 L/min) and overestimate the pressure gradients. Interestingly, the deficiency of the Garcia et al’s model consistently underestimating the pressure gradient for the orifice turned out to its advantage for modeling the stenotic aortic valve. However, we note that both these models physically do not capture the varying area, a very important reason for the breakdown of these models for the case of the stenotic aortic valve. It is well known that unlike the constant orifice area, the stenotic aortic valve area varies continuously with time throughout the cardiac cycle, which imposes large differences on any model derived from a simple constant orifice area. Future models that incorporate an additional flow rate dependency such that it damps the steady flow term is necessary and is the focus of a follow up paper. While this is a test on one stenotic aortic valve, further experimental studies are required to further tune the parameters of the new model when utilizing clinical input parameters based on echocardiographic measurements in addition to relating the temporal variations of the valve orifice area.
Implementation of the derived model and Perspectives
Despite the fact that the derived model in this study does not captures closely the complete variations of pressure gradient throughout the cardiac cycle, in addition to the need of incorporating the time variability of the valve orifice area, the advantages of the new derived model involve the ease of acquiring the necessary variables in the equation. The model necessitates knowledge of echocardiographic parameters – that are routinely obtained in a clinical echocardiogram. These parameters include the left ventricular outflow diameter and area, the flow waveform obtained from the velocity waveform measurement and lastly the aortic valve area through continuity equation. These parameters readily provide the calculation of β necessary for the model.
In summary, in this study, a generalized model to estimate the variations of the instantaneous pressure gradient across an orifice was derived without the need to know the effective orifice area at the vena contracta, with the goal to attempt to estimate instantaneous pressure gradients in a stenotic aortic valve. The model derived includes the effects of flow unsteadiness in addition to friction losses through adopting a discharge coefficient formulation across the orifice. Good agreement was found between the raw orifice experimental data and the model. In addition, applying the model on a stenotic surgical aortic valve also demonstrated a potentially promising first step towards a more comprehensive instantaneous pressure gradient model. Further studies are needed to test the applicability of the model in-vivo and in-vitro with valves of different orifice areas.
Limitations
The derivation of the analytical model expressing the variations of the instantaneous pressure gradients versus the instantaneous flow rates is based on a few assumptions starting from considering (1) steady flow friction losses and discharge coefficients, despite having flow pulsatility; (2) non-varying geometry throughout the cardiac cycle, despite having a valve closing and opening; (3) fully developed flow; (4) no incorporation of dynamic fluctuations that actually occur from starting vortex formation during acceleration phase and valve fluctuation due to adverse pressure gradient at valve closure and (5) application of the model on a stenosed surgical aortic valve of the same aortic valve area as the test orifice. Therefore, further studies are necessary to fine-tune the parameters of the model. Despite a more accurate depiction of instantaneous pressure gradient and because the model has not been tested clinically, it is important to point out that it may be a good predictor for pressure loss, but that does not automatically mean that it will also be a better clinical biomarker for severe aortic stenosis. Clinical applicability and testing are mandatory.
Acknowledgments
Funding: The research done was partly supported by National Institutes of Health (NIH) under Award Number R01HL119824 and the American Heart Association (AHA) under Award Number 19POST34380804.
Abbreviations, symbols and terminology
- PG
Pressure Gradient
- BPS
Beats Per Second
- bpm
Beats Per Minute
- HR
Heart Rate
- CO
Cardiac Output
- EOA
Effective Orifice Area
- Re
Reynolds Number
Appendix A: Non-dimensional analysis
From non-dimensional analysis, we choose to select 6 different variables where v is the kinematic viscosity.
The π groups obtained can be summarized:
| (19) |
| (20) |
| (21) |
Stemming from equation 4, the relationship between the π groups can be written as follows:
| (22) |
| (23) |
| (24) |
| (25) |
Equations 25 and 16 compare.
Footnotes
Publisher's Disclaimer: This Author Accepted Manuscript is a PDF file of an unedited peer-reviewed manuscript that has been accepted for publication but has not been copyedited or corrected. The official version of record that is published in the journal is kept up to date and so may therefore differ from this version.
Conflict of Interest: Dr. Crestanello reports having grants from Medtronic, Boston Scientific and St. Jude in addition to being part of Medtronic advisory board. Dr. Dasi reports having patent applications filed on novel polymeric valves, vortex generators and superhydrophobic/omniphobic surfaces. No other conflicts were reported.
References
- 1.Padala M, Sarin EL, Willis P, Babaliaros V, Block P, Guyton RA, and Thourani VH, An engineering review of transcatheter aortic valve technologies. Cardiovascular Engineering and Technology, 2010. 1(1): p. 77–87. [Google Scholar]
- 2.Sotiropoulos F, Le TB, and Gilmanov A, Fluid mechanics of heart valves and their replacements. Annual Review of Fluid Mechanics, 2016. 48: p. 259–283. [Google Scholar]
- 3.Dasi LP, Simon HA, Sucosky P, and Yoganathan AP, Fluid mechanics of artificial heart valves. Clinical and experimental pharmacology and physiology, 2009. 36(2): p. 225–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Otto CM, Valvular aortic stenosis: disease severity and timing of intervention. Journal of the American College of Cardiology, 2006. 47(11): p. 2141–2151. [DOI] [PubMed] [Google Scholar]
- 5.Baumgartner H, Stefenelli T, Niederberger J, Schima H, and Maurer G, “Overestimation” of catheter gradients by Doppler ultrasound in patients with aortic stenosis: a predictable manifestation of pressure recovery. Journal of the American College of Cardiology, 1999. 33(6): p. 1655–1661. [DOI] [PubMed] [Google Scholar]
- 6.Pibarot P, Garcia D, and Dumesnil JG, Energy loss index in aortic stenosis: from fluid mechanics concept to clinical application. 2013, Am Heart Assoc. [DOI] [PubMed] [Google Scholar]
- 7.Thaden JJ, Nkomo VT, Lee KJ, and Oh JK, Doppler imaging in aortic stenosis: the importance of the nonapical imaging windows to determine severity in a contemporary cohort. Journal of the American Society of Echocardiography, 2015. 28(7): p. 780–785. [DOI] [PubMed] [Google Scholar]
- 8.Berger M, Berdoff RL, Gallerstein PE, and Goldberg E, Evaluation of aortic stenosis by continuous wave Doppler ultrasound. Journal of the American College of Cardiology, 1984. 3(1): p. 150–156. [DOI] [PubMed] [Google Scholar]
- 9.Young DF, FLUID-MECHANICS OF ARTERIAL STENOSES. Journal of Biomechanical Engineering-Transactions of the Asme, 1979. 101(3): p. 157–175. [Google Scholar]
- 10.Chandran KB, Rittgers SE, and Yoganathan AP, Biofluid mechanics: the human circulation. 2012: CRC press. [Google Scholar]
- 11.Clark C, Relation between pressure difference across the aortic valve and left ventricular outflow. Cardiovascular research, 1978. 12(5): p. 276–287. [DOI] [PubMed] [Google Scholar]
- 12.Bermejo J, Antoranz JC, Burwash IG, Alvarez J, Moreno M, García-Fernández MA, and Otto CM, In-vivo analysis of the instantaneous transvalvular pressure difference-flow relationship in aortic valve stenosis: implications of unsteady fluid-dynamics for the clinical assessment of disease severity. The Journal of heart valve disease, 2002. 11(4): p. 557–566. [PubMed] [Google Scholar]
- 13.Garcia D, Pibarot P, and Durand L-G, Analytical modeling of the instantaneous pressure gradient across the aortic valve. Journal of biomechanics, 2005. 38(6): p. 1303–1311. [DOI] [PubMed] [Google Scholar]
- 14.Garcia D, Kadem L, Savery D, Pibarot P, and Durand L-G, Analytical modeling of the instantaneous maximal transvalvular pressure gradient in aortic stenosis. Journal of biomechanics, 2006. 39(16): p. 3036–3044. [DOI] [PubMed] [Google Scholar]
- 15.DeGroff CG, Shandas R, and Valdes-Cruz L, Analysis of the effect of flow rate on the Doppler continuity equation for stenotic orifice area calculations: a numerical study. Circulation, 1998. 97(16): p. 1597–1605. [DOI] [PubMed] [Google Scholar]
- 16.VanAuker MD, Chandra M, Shirani J, and Strom JA, Jet eccentricity: a misleading source of agreement between Doppler/catheter pressure gradients in aortic stenosis. Journal of the American Society of Echocardiography, 2001. 14(9): p. 853–862. [DOI] [PubMed] [Google Scholar]
- 17.LaNieve HL, Entrance effects in non-Newtonian pipe flow. 1963. [Google Scholar]
- 18.Levine RA and Schwammenthal E, Stenosis is in the eye of the observer: impact of pressure recovery on assessing aortic valve area. 2003, Journal of the American College of Cardiology. [DOI] [PubMed] [Google Scholar]
- 19.Hatoum H, Moore BL, and Dasi LP, On the Significance of Systolic Flow Waveform on Aortic Valve Energy Loss. Annals of biomedical engineering, 2018: p. 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hatoum H, Dollery J, Lilly SM, Crestanello JA, and Dasi LP, Implantation Depth and Rotational Orientation Effect on Valve-in-Valve Hemodynamics and Sinus Flow. The Annals of thoracic surgery, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hatoum H, Yousefi A, Lilly S, Maureira P, Crestanello J, and Dasi LP, An In-Vitro Evaluation of Turbulence after Transcatheter Aortic Valve Implantation. The Journal of Thoracic and Cardiovascular Surgery, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hatoum H, Heim F, and Dasi LP, Stented valve dynamic behavior induced by polyester fiber leaflet material in transcatheter aortic valve devices. Journal of the mechanical behavior of biomedical materials, 2018. 86: p. 232–239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Baumgartner H, Hung J, Bermejo J, Chambers JB, Evangelista A, Griffin BP, lung B, Otto CM, Pellikka PA, and Quiñones M, Echocardiographic assessment of valve stenosis: EAE/ASE recommendations for clinical practice. Journal of the American Society of Echocardiography, 2009. 22(1): p. 1–23. [DOI] [PubMed] [Google Scholar]
- 24.Hatoum H, Maureira P, and Dasi LP, A turbulence in vitro assessment of On-X and St Jude Medical prostheses. The Journal of Thoracic and Cardiovascular Surgery, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.White FM, Fluid Mechanics, McGraw-Hill Series in Mechanical Engineering. 1998, McGraw-Hill international editions, Boston. [Google Scholar]
- 26.Fusman B, Faxon D, and Feldman T, Hemodynamic rounds: Transvalvular pressure gradient measurement. Catheterization and cardiovascular interventions, 2001. 53(4): p. 553–561. [DOI] [PubMed] [Google Scholar]
- 27.Carabello BA, Advances in the hemodynamic assessment of stenotic cardiac valves. 1987, Elsevier. [DOI] [PubMed] [Google Scholar]