On the relationship between excited state lifetime and isomerization quantum yield in animal rhodopsins: beyond the one-dimensional Landau-Zener model

Abstract

We show that the speed of the chromophore photoisomerization of animal rhodopsins is not a relevant control knob for their light sensitivity. This result is at odd with the momentum-driven tunnelling rationale (i.e. assuming a one-dimensional Landau-Zener model for the decay) holding that a faster nuclear motion through the conical intersection translates into a higher quantum yield and, thus, light sensitivity. Instead, a model based on the phase-matching of specific excited state vibrational modes should be considered. Using extensive semi-classical hybrid quantum mechanics/molecular mechanics trajectory computations to simulate the photoisomerization of three animal rhodopsin models (visual rhodopsin, squid rhodopsin and human melanopsin), we also demonstrate that phase-matching between three different modes (the reactive carbon and hydrogen twisting coordinates and the bond length alternation mode) is required to achieve high quantum yields. In fact, such “phase-matching” mechanism explains the computational results and provides a tool for the prediction of the photoisomerization outcome in retinal proteins.

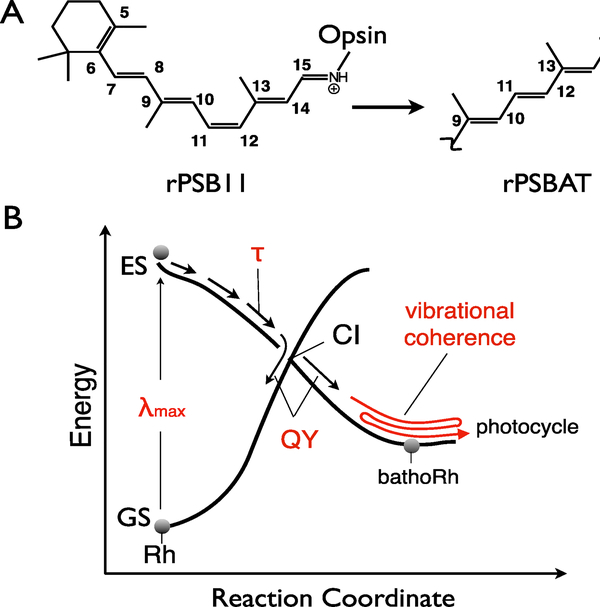
The photoisomerization of the 11-cis retinal protonated Schiff base (rPSB11) chromophore incorporated in animal opsins (Scheme 1A), a landmark example of ultrafast chemical reaction, corresponds to the primary event of vision in both vertebrates and invertebrates^1–4. As a consequence, the mechanism of such an event has been the focus of extensive research aimed at a detailed description of the opsin function^{1, 5–7}. More specifically, different studies have established that properties as the wavelength of the absorption maximum (λ_max), the excited state lifetime (τ), the isomerization quantum yield (QY) and the vibrational coherence observed in the bathorhodopsin (bathoRh) photoproduct (Scheme 1B) are affected by the chromophore environment^8–12. The vibrational coherence observed in bovine rhodopsin (Rh) has been associated to the barrierless ultrafast excited state (ES) isomerization motion of rPSB11 imposed by the Rh cavity⁹. Indeed, in methanol solution^{7, 13} the reaction is slower and occurs without coherent motion at the photoproduct level. Such ultrafast motion would provide “ballistic” access to the ground state (GS) via decay through a peaked conical intersection (CI) resulting in collective torsional oscillations of the all-trans retinal PSB (rPSBAT) chromophore of bathoRh. For this reason, the photoisomerization of Rh is usually regarded as a photochemical process whose efficiency obeys a basic one-dimensional Landau-Zener (1D LZ) model¹⁴ holding that a high speed (i.e. a short τ) along the coordinate described by the C₁₀–C₁₁–C₁₂–C₁₃ dihedral (CCCC) of rPSB11 determines a high isomerization efficiency (QY)¹⁵.

Scheme 1.

Animal rhodopsin isomerization. A. -C₁₁-C₁₂- double-bond isomerization in bovine rhodopsin. B. Schematic representation of the ES and GS energy profiles controlling the ultrafast photoisomerization of bovine rhodopsin. The critical properties relevant to the present work are indicated in red.

In contrast with the 1D LZ hypothesis, experimental^{4, 16–17} and theoretical^{8, 11, 17–20} studies have revealed a complex ES dynamics suggesting a multi-modal reaction coordinate. In fact, it has been reported that both the hydrogen out-of-plane motion described by a combination of CCCC and the H₁₁–C₁₁–C₁₂–H₁₂ dihedral (HCCH) and the bond-length alternation (BLA) motion, also affect the rPSB11 isomerization quantum yield. On such basis, it has been proposed that a “vibronic phase effect”, i.e. the relationship between the direction of motion along specific vibrational modes at the point where the electronic wavefunction changes from ES to GS, modulate QYs. More specifically:

• since HCCH is faster (i.e. higher frequency) than CCCC, the ES population performs few HCCH oscillations before entering the CI region characterized by a highly twisted (ca. 90°) CCCC. It has been, thus, argued that a high isomerization efficiency (i.e. a high QY) would require a “phase matching” (i.e. both geometrical deformations should point towards the product) between HCCH and CCCC at the ES→GS hopping event^21–22. This mechanism is strongly supported by the recent discovery of a vibrational phase isotope effect on quantum yields observed when replacing HCCH with its isotopomers¹⁷.

• since the GS photoproduct formation requires a covalent electronic character, a phase matching between C₁₁C₁₂ (CC) (generally, BLA) and the HCCH and CCCC modes would also be required. In fact, the CC value is related to the chromophore electronic character which may oscillate between covalent and charge transfer (CT) characters in the CI region^22–23.

The points above suggest that modeling the photo-induced dynamics of opsin-embedded rPSB via a 1D LZ model is inadequate. On the other hand, due to its simplicity and intuitive character, such model is still considered for predictions, rationalizations and even applied to the design of artificial pigments^24–28.

Dynamical studies provide the elective tool to address this point. So far, however, only the Rh visual pigment has been explored by three of the authors (by employing statistically meaningful molecular dynamics simulations)^{11, 17}, and most of our “dynamical” insights come either from minimal rPSB models^{21, 29} or from a limited number of trajectories when looking at other animal rhodopsins. In particular, one of the authors has presented a theoretical study of the photoisomerization of three animal rhodopsins: Rh, squid rhodopsin (sqRh) and human melanopsin (hMeOp)¹². In that study QM/MM models of the three pigments were used to investigate the pigment S₁ geometrical and electronic structure dynamics and decay mechanism. In all cases, the reactive event was found to correspond to the ultrafast isomerization of the C₁₁C₁₂ bond of rPSB11 as depicted in Scheme 1. The results also showed that the pigments are characterized by a direct proportionality between the λ_max and τ values, i.e. the higher the λ_max, the higher the isomerization speed. Based on this correlation and following the 1D LZ model mentioned above, it was anticipated that hMeOp should display the highest QY and Rh the lowest¹². However, this result was based on two assumptions: a) the trend in vertical transition energies to the bright state reproduces the trend of the λ_max and b) the vibrational wavepacket motion on S₁ could be represented by a single deterministic semi-classical Franck-Condon (FC) trajectory released with zero initial velocities. Thus, being based on single trajectories, such study could not provide direct access to statistical quantities such as QYs and, for the same reason, the computed τ values have to be considered crude approximations of the real ones.

In the present contribution we employ full sets of semi-classical trajectories and proper room-temperature initial conditions, to test assumptions a-b and confirm the existence of the proportionality between λ_max and τ. We then go well beyond the previous work and use the same trajectories to compute the QY values for the three pigments and assess the validity of the 1D LZ model prediction. More specifically, we report on more realistic simulations of the ES population dynamics and photoproduct formation for Rh, SqRh and hMeOp based on three sets of room-temperature (RT) mixed quantum-classical trajectories (60 per set) using Tully’s fewest switches surface hopping algorithm³⁰. The results show that the calculated QYs are not consistent with the 1D LZ prediction. We show that the origin of such failure lies in the multi-dimensional nature of the chromophore dynamics. We also demonstrate that the QYs computed for the three pigments^{12–13, 31–34} are explained by their HCCH, CCCC and BLA phase relationships as described in the points above.

The employed methodologies are reported in the Supporting Information (SI) material. Here, we only state that the equilibrium structures and trajectories are computed within a hybrid quantum mechanics/molecular mechanics (QM/MM) framework using complete active space self-consistent field (CASSCF) theory. Linear absorption spectra were simulated by means of multiconfigurational second-order perturbation theory (CASPT2). The constructed QM/MM models of Rh, sqRh and hMeOp, which reproduced the results of Rinaldi et al.¹² at equilibrium (see SI for details), were used to sample the vibrational degrees of freedom and to simulate linear absorption spectra. The results show a close agreement between theory and experiment for Rh and SqRh (see SI for details). The simulated spectrum of hMeOp strikes as the outlier in this comparison, showing a clear undersampling in the blue and, hence, reproducing only partially the blue-shift of the absorption band with respect to SqRh. This discrepancy could be attributed firstly to the hMeOp homology model that is based precisely on SqRh, secondly, the strong mixing between S₁ and S₂ states in hMeOp (see SI for details).

Relationship between Vertical Excitation Energy, Steric Strain and Isomerization Speed

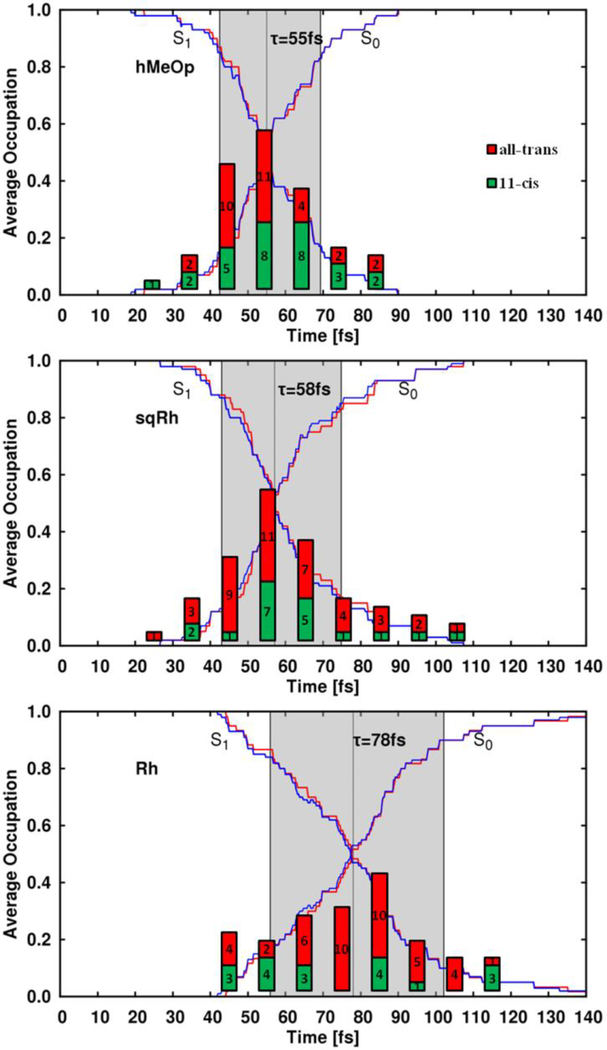
The simulated population dynamics of the three rhodopsins show an ultrafast ES depopulation completed in 150 fs. However, as reported in Figure 1, the three swarms of trajectories exhibit increasing τ values in the order hMeOp (55 fs), sqRh (58 fs) and Rh (78 fs). The larger τ of Rh is associated with a longer decay time-window of ca. 50 fs, whereas in hMeOp and sqRh the decay occurs in ca. 30 fs time-window suggesting the faster population dynamics observed is correlated to a more ballistic motion on S₁. In support of this conclusion, we see a clear Gaussian distribution of hopping events, peaking at the lifetime τ in hMeOp and sqRh (Figure 1, graphs of bars), while in Rh the distribution is more even and spans a broader time range.

Figure 1.

Population transfer dynamics for the three pigments. The average electronic state population of the ensemble and the trajectory occupations (the ratio of trajectories in each state) are shown with blue and red lines, respectively. The decay time-window is highlighted in gray (twice the standard deviation of hopping events times). The height of the bar graphs depicts the distribution of hopping events in terms of the number of all-trans (photoproduct formation, red bar) and 11-cis (reactant back formation, green bar) species formed after hopping.

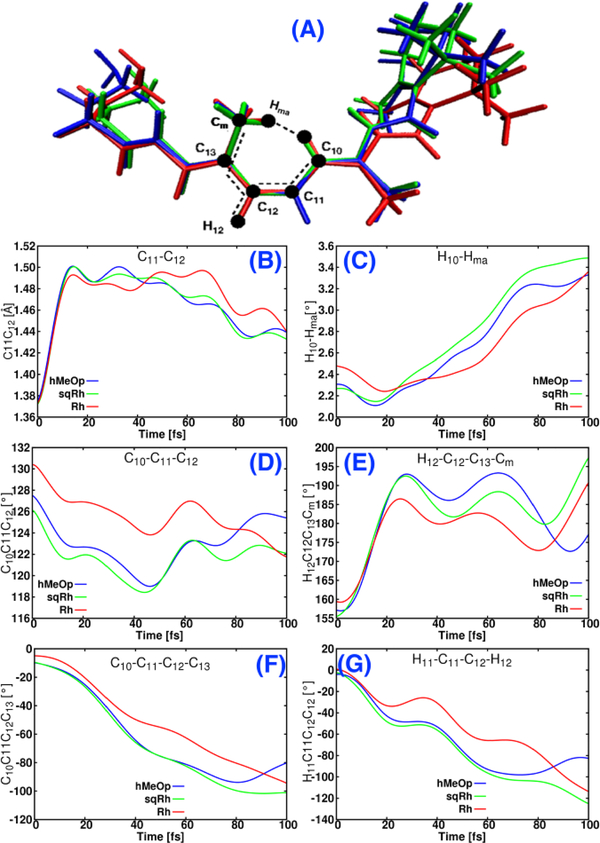
As typical for conjugated π-systems, the driving force of the ES dynamics of rPSB11 is the acquired S₁ antibonding character of the former C₁₁-C₁₂ double bond^{8, 11, 22}. Such character demands a minimization of the π-overlap across the bond and, simultaneously, a maximization of the π-overlap across the neighboring bonds (C₁₂-C₁₃ and C₁₀-C₁₁). Due to the out-of-plane distortion of rPSB11 inside the active site this force translates into complex nuclear motions involving the CC, HCCH and CCCC modes. In fact, an initial rapid BLA decrease associated with increasing CC values occurs immediately after photoexcitation (Figure 2B). Shortly after one observes a HCCH motion in a counter-clockwise (in the sense of increasing negative values) direction leading to a pyramidalization of the C₁₁ and C₁₂ centers which results in a change of orientation of the corresponding p-orbital axis. This, in turn, induces a second effective π-overlap decrease across CC. The somehow slower CCCC change, also in a counter-clockwise direction, leads to a further and obvious π-overlap decrease. Such rapid distortion, after excitation, along the CCCC and HCCH coordinates has been confirmed by Raman intensity analysis of Rh ³⁵.

Figure 2.

Temporal evolution of the relevant geometrical parameters averaged over all trajectories in the three-investigated animal rhodopsins, C_m and H_ma are the carbon and the hydrogen of methyl substituent at C₁₃.

The electrostatic interactions of the rPSB11 chromophore with the rhodopsin cavity residues have been called to account not only for the remarkable shifts of the absorption energy inside the proteins but also for the isomerization speed increase with respect to the solution environment^{1, 7, 13, 36–40}. In support of this view, some of the authors have shown that the application of an external electric field to rPSB11 in gas-phase leads to a correlation between the blue-shift of the excitation energy and the steepness increase of the S₁ potential energy surface (PES)⁴⁰ (see the SI for more details). So far, little attention has been given to steric effects. We now argue that the force provided by the photo-induced antibonding character is modulated and even expanded by the specific architecture of the protein cavity yielding strained rPSB11 chromophores. In fact, the chromophores of sqRh and hMeOp appear more bent at the ß–ionone ring than the Rh one (see Figure 2A). This deformation is accompanied by bent backbones where, relative to Rh, the angles C₁₀–C₁₁–C₁₂ and C₁₁–C₁₂–C₁₃ of sqRh and hMeOp are both ca. 4–5° smaller (see Figure 2D). As a result, in sqRh and hMeOp, the H₁₀ and the methyl substituent at C₁₃ (C_m in Figure 2A) are closer, leading to an augmented strain explaining the increasing CCCC S₀ equilibrium values along the series Rh→sqRh→hMeOp. Moreover, the C_m of sqRh and hMeOp is more out-of-plane twisted than in Rh, implying a more pronounced torsion around the C₁₂–C₁₃ bond. We propose that these steric factors help to gain a higher momentum along the H₁₂ out–of–plane coordinate already in the first 10–15 fs of the trajectories (note, the C_m itself is much heavier than a H atom and it moves slowly on the same time-scale, see the evolution of H₁₂–C₁₂–C₁₃–C_m, Figure 2E). We argue that, due to the momentum gained by H₁₂, the HCCH of sqRh and hMeOp reaches values of ca. 50° already 20 fs after excitation while it reaches only 30° in Rh, Figure 2G. This is in agreement with the reported experimental Raman intensity analysis of Rh in which HCCH reaches a 50° value within 36 fs while CCCC takes 50 fs to achieve the same value³⁵. Thus, the steric effect acts synergistically with the cavity electrostatic field and explains why sqRh and hMeOp reach the CI region faster than Rh.

Rationalization of the Computed Quantum Yields

As shown in Scheme 1B, once a trajectory has reached the CI region, it hops to the S₀ PES and moves either towards the bathoRh equilibrium structure or goes back to the reactant. The computed isomerization QY values are reported in Table 1, together with the values predicted according to the phase rule introduced elsewhere by some of the authors²¹. Both Rh and sqRh display similar high QYs, while hMeOp displays a significantly reduced QY. These results indicate a correlation between speed (i.e. τ) and QY opposite to the one predicted by the 1D LZ model. On the other hand, such data alone do not provide a molecular-level rationalization of such a behavior. For this reason, below we study the surface hoping and electronic character change events occurring along the trajectory sets.

Table 1.

Computed vs. predicted QYs. The computed values are obtained by analyzing the outcome of the individual trajectories for each pigment. The predictions are given on the basis of vibrational phase rules²¹ involving the HCCH direction at the time of hopping to the GS (called “hopping event”) and the time of transition from a CT to a covalent character along the S₀ PES (called “decision event”); defined as the time when the total charge on the N-terminus has reached +0.9 e. This last event corresponds to a change in the S₀ electronic wavefunction (WF) from an antibonding to a bonding character of the reactive double bond.

model	computed QY	predicted QY
		HCCH velocity sign at
		ES→GS hopping (hopping event)	CT→covalent transition (decision event)
Rh	70% [67%]1	78 (+8%)	69 (−1%)
sqRh	68%	64 (−4%)	66 (−2%)
hMeOp	52%	61 (+9%)	54 (+2%)

¹The only known experimental quantity is given in square brackets^41–42. Evidence for similarity between the QYs of Rh and sqRh has been provided⁴³.

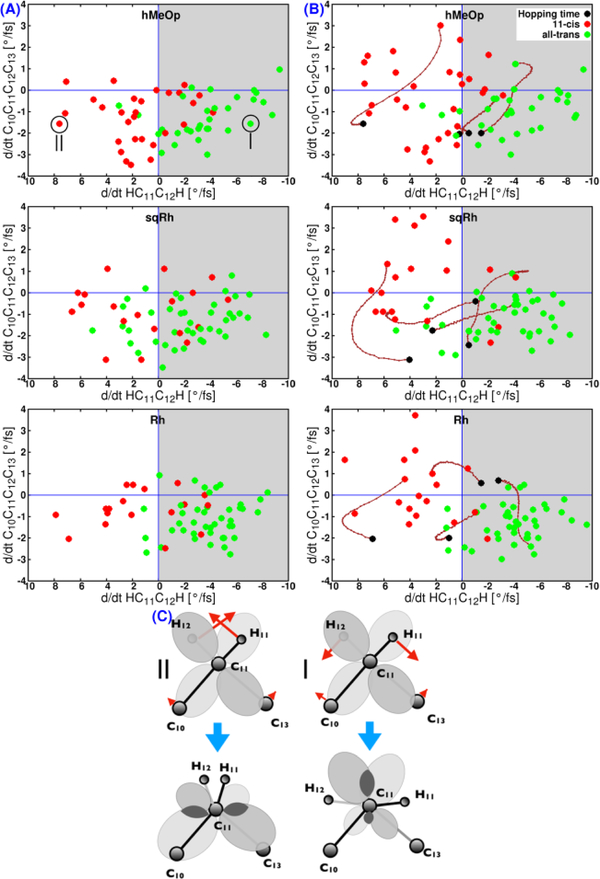
In Figure 3A we show two-dimensional correlation plots reporting the surface hopping events in the three rhodopsins as a function of the CCCC and HCCH velocities (including the directionality) at the time of hopping. The plots demonstrate that the CCCC velocity alone is not controlling the isomerization outcome. In particular, nearly almost all of the hop points show a negative CCCC velocity associated with a counterclockwise motion towards the photoproduct, predicting nearly 100% QY in all three pigments if the CCCC motion would continue in the same direction after the hop. In fact, a considerable number of trajectories reach the reactant basin regardless the magnitude of the CCCC velocity (Table 1 and Figure 3A), which is clearly in contrast with a 1D model.

Figure 3.

Distribution of the hopping (A) and decision (B) events as a function of the magnitude and directionality of the HCCH and CCCC velocities. Green and red circles show trajectories that lead to the photoproduct or reactant formation, respectively. The brown lines show some examples for the change of dihedral angle directionality during the period between the hopping event (black circles) and the decision event. C. Schematic representation of the in-phase (diagram |) and out-of-phase (diagram ||) π-overlap across the C₁₁-C₁₂ bond. Notice that | would lead to a π-overlap (dark grey areas) increase favoring the product formation. Instead, || would favor the reactant back-formation.

In the past, we have reported that it is the phase relationship between the CCCC and HCCH motion, which mainly determines the outcome of single trajectories^{8, 11, 22}. For Rh, the relevance of such phase relationship has been recently confirmed via deuterium substitution of the HCCH hydrogens¹⁷. In fact, the product formation is associated with the counter-clockwise motion of H₁₁ and H₁₂ or, equivalently, with a negative HCCH velocity at the hopping event. When allowing a ca. 10% deviation, this criterion leads to predictions in line with the computed QY (Table 1). Most importantly, unlike the 1D LZ model, it correctly predicts the trend of decreasing QY in the series Rh→SqRh→hMeOp, in spite of the lower τ value and, therefore, faster decay to GS of hMeOp and sqRh. Thus, the HCCH phase at the hop point can be used as an easy–to–apply tool for predicting the outcome of the isomerization, because the velocity along this mode is usually larger than the velocity of the CCCC mode. In other words, by applying such tool, it may not be necessary to propagate the semi-classical trajectories up to the reactant or photoproduct to work out the QY trend.

The first column in Table1 shows that the calculated QYs for sqRh and Rh are nearly identical. On the other hand, the CCCC/HCCH phase rule would predict substantially different QY values (second column of Table 1). Obviously, there must be an additional parameter that influences the decision besides the direction of the HCCH. Based on a limited number of 0K trajectories, Schapiro et al.²² argued that the reactant/product branching decision is not always taken at the hopping event. Indeed, if after the hop the S₀ WF of the reacting chromophore is dominated by the “antibonding” CT character, it would have to acquire a covalent character before the broken CC double bond could be reconstituted. Clearly, the transition between the CT and covalent character is effectively controlled by the BLA coordinate. In order to study the effect of this electronic factor over the QY, the BLA has to be incorporated in our mechanistic picture. This is done in Figure 4 on three examples of three trajectories (for all other trajectories see Figures S13–S15) in which the evolution of the BLA is correlated to the dynamics of the total charge on the N-terminus (C₁₂...N) as a measure of electronic character. Thereby, a covalent WF character is favored by: a) an increase of the BLA, a process leading to the regular single-double bond alternation characteristic for the GS equilibrium; b) an increase of the positive charge on the N-terminus which reflects a bonding character of the reacting double bond. As seen in Figure 4, right after the hop the charge on the N-terminus reaches values close to zero in line with the decrease of the BLA, thus indicating the strong CT antibonding nature of the GS. After half a CC double bond oscillation period (ca. 10 fs), the GS adopts a covalent electronic character associated with rapid increase of the BLA to positive values and the accumulation of positive charge on the N-terminus. Interestingly, the CC bond length does not obey the above rationalization, clearly expanding (and, thus reducing the π-overlap) during the GS wavefunction transition from CT to covalent (see Table S5 in the SI). This indicates that the driving force for this transition is not necessarily the stretching of the CC bond but, rather, the asymmetric stretching phase of the entire conjugated chain. The involvement of the BLA in the investigated mechanism supports the view that the photoisomerization QY of animal rhodopsins involves, effectively, two-electronic states and three geometrical modes.

Figure 4.

Selected examples show the evolution of BLA (bond-length alternation), C₁₁-C₁₂ and charge on C₁₂---N fragment during the simulation in the three rhodopsins, (ΔC₁₁-C₁₂ represents the deviation of C₁₁-C₁₂ form 1.45Å), gray-shaded areas denote the time span in which the WF changes from CT to covalent after a hopping event, vertical dashed and solid arrows show the hopping and decision times, respectively.

Consistently with the above theory, the predicted QY’s based on the same CCCC/HCCH phase matching theory applied to the time step corresponding to the decision event (Figure 3B), rather than to the hopping event (Figure 3A) are in better agreement with the computed QYs (Table 1). More specifically, we find discrepancies for the three pigments below 2%. We note, that about 50% of the trajectories end up in a CT state immediately after the hopping event in case of Rh, such value is ca. 40% for sqRh and hMeOp.

Despite the positive results reported above, one has to reckon that the faster the relaxation the more outliers to the rules proposed above are found. In fact, in Rh there are 5 compared to 9–11 trajectories in sqRh and hMeOp which do not follow the derived phase matching rule. Effectively, the faster the decay through the ES/GS funnel, the more kinetic energy rPSB11 has accumulated and the more often the product formation appears to be decided randomly.

In conclusion, according to QM/MM models capable of reproducing the observed absorption bands and, for Rh, the observed τ and QY (experimental τ and QY are not available for SqRh and hMeOp), the reaction speed along an effective single mode reaction coordinate (see SI Figure S16) is not a relevant control knob of animal rhodopsin QYs and, therefore, photosensitivity. This is at variance with the 1D LZ model. Instead, our computations confirm that phase–matching between the reactive CCCC and HCCH modes is the major control factor (see SI Figure S16 left-panel). Consequently, a mismatch between the CCCC and HCCH phases inevitably reduces the QY. The change in character of the electronic structure during GS relaxation is another important parameter affecting the reactant/product branching. The transition from CT to covalent character is controlled by the BLA coordinate. This transition has an impact on the QY when it occurs within half a CC double bond stretching period after the hopping event (see SI Figure S16 right-panel) and, in our three rhodopisns, modulates non–uniformly the QY within 10% with respect to the HCCH/CCCC phase predictions at the hopping time. Finally, higher momentum accumulated in the leading modes increases the number of random events.

On the basis of the above findings, we can think of two reasons for the reduction (with respect to Rh) of QYs for molecules which decay on a time scale of ca. 60–65 fs: a) HCCH/CCCC phase mismatch; b) an increase of random events in the GS. In the future, it would be useful to investigate the QY of animal rhodopsins or their mutants that isomerize on time-scales longer than that of Rh (i.e. with ES lifetimes beyond 100 fs) but still keeping a vibrational coherent motion. In these cases, one can expect higher QYs due to increased HCCH/CCCC phase matching in such rhodopsins.