Local interactions and their group-level consequences in flocking jackdaws

Abstract

As one of nature's most striking examples of collective behaviour, bird flocks have attracted extensive research. However, we still lack an understanding of the attractive and repulsive forces that govern interactions between individuals within flocks and how these forces influence neighbours' relative positions and ultimately determine the shape of flocks. We address these issues by analysing the three-dimensional movements of wild jackdaws (Corvus monedula) in flocks containing 2–338 individuals. We quantify the social interaction forces in large, airborne flocks and find that these forces are highly anisotropic. The long-range attraction in the direction perpendicular to the movement direction is stronger than that along it, and the short-range repulsion is generated mainly by turning rather than changing speed. We explain this phenomenon by considering wingbeat frequency and the change in kinetic and gravitational potential energy during flight, and find that changing the direction of movement is less energetically costly than adjusting speed for birds. Furthermore, our data show that collision avoidance by turning can alter local neighbour distributions and ultimately change the group shape. Our results illustrate the macroscopic consequences of anisotropic interaction forces in bird flocks, and help to draw links between group structure, local interactions and the biophysics of animal locomotion.

1. Introduction

Highly coordinated collective motion is a cornerstone of many biological systems at all scales, from cell colonies [1,2] to insect swarms [3–6], fish schools [7,8], bird flocks [9–11], ungulate herds [12–14] and even human crowds [15,16]. Moving together in large groups and using social information can provide numerous benefits, including enhanced predator avoidance [17–19], more efficient resource exploitation [20,21], energy savings [22–24] and efficient learning of migration routes [25,26]. Thus, understanding the mechanisms driving the emergence of collectivity in natural systems has significant ecological, evolutionary and cognitive implications [27]. Over the past few decades, theoretical models [28–37] have demonstrated that global-level collective motion can be generated by simple local interactions. However, verification of these interaction rules using data from real moving animals has lagged behind due to measurement challenges. Now that new measurement technologies have made it more feasible to track animal movement, characterizing the local interactions in animal groups in natural environments is critical for advancing our understanding of collective behaviour [38,39].

Bird flocks are one of the most striking and frequently studied examples of collective behaviour. They are often modelled using agent-based frameworks [40–42] where individuals follow simple interaction rules such as long-range attraction, short-range repulsion and intermediate-range alignment. These interactions are treated as social ‘forces’ [43] imposed by the presence of nearby neighbours that thus determine the acceleration of each agent. Although many empirical measurements of bird flocks have been made [44–56], the fundamental interaction rules assumed in the models have still not been fully tested. In particular, the effective attractive and repulsive forces that birds experience while flying in large flocks have not been studied. It thus remains unclear how interaction forces vary depending on the relative positions of neighbouring individuals. Characterizing such interaction forces is, however, critical for understanding the flock mechanics, since the forces acting on individuals will determine their velocities, relative positions in the group and ultimately the shape of the entire group [42,44]. Moreover, from an adaptive perspective, the morphology of animal groups and the distribution of individuals within them influences group members' access to social information and vulnerability to predation [42,57–59].

One way to infer the effective attractive and repulsive forces between group members is by analysing the accelerations of individuals [60,61], since forces are proportional to accelerations. Based on this idea, Katz et al. [60] used optical tracking to measure the acceleration of individuals as a function of the distance to neighbours (known as a ‘force map’) in schools of two or three captive fish, finding evidence for both long-range attraction and short-range repulsion. Similarly, by fitting observational data to a zonal model [43] where individuals' accelerations are explicitly related to the interaction forces, Lukeman et al. [50] found long-range attraction and short-range repulsion in large flocks of sea ducks (surf scoters) congregated on the surface of the sea. In airborne flocks, the only study of forces to date [44] reported force maps for isolated pairs of homing pigeons based on GPS (Global Positioning System) tracking, though the measured forces had large uncertainties, with a position uncertainty of more than two times the bird body size. Thus, well-resolved force maps similar to those measured in fish schools are currently unavailable for bird flocks in flight. More generally, given the reliance of previous research on small groups of (often captive) animals, the interaction forces at play in large, natural collective aggregations such as aerial bird flocks remain unknown. Since birds interact with more than one other individual in large groups [48,55], the forces measured in isolated pairs may not be representative of how birds interact in large flocks.

Current research also tells us little about the mechanisms governing the side-by-side neighbour structure seen in flocks of small birds (e.g. pigeons, starlings or jackdaws) [44,48,49,55], which in turn may determine the overall shape of flocks. One hypothesis, proposed in previous studies [44,62], is that the mechanism of short-range repulsion determines the local neighbour distribution. This hypothesis is illustrated in figure 1: avoiding collisions by changing speed (speeding-based repulsion) is thought to lead to a front-to-back distribution, while avoiding collisions by turning (turning-based repulsion) should result in a side-by-side structure [42]. This hypothesis has been verified in small groups of fish that use speeding-based repulsion [60,62,63], and by pigeons in groups of two that use turning-based repulsion [44]. However, it is not known whether birds in large groups avoid collisions by turning. Therefore, whether this hypothesis explains the side-by-side neighbour structure observed in large bird flocks has yet to be tested.

Figure 1.

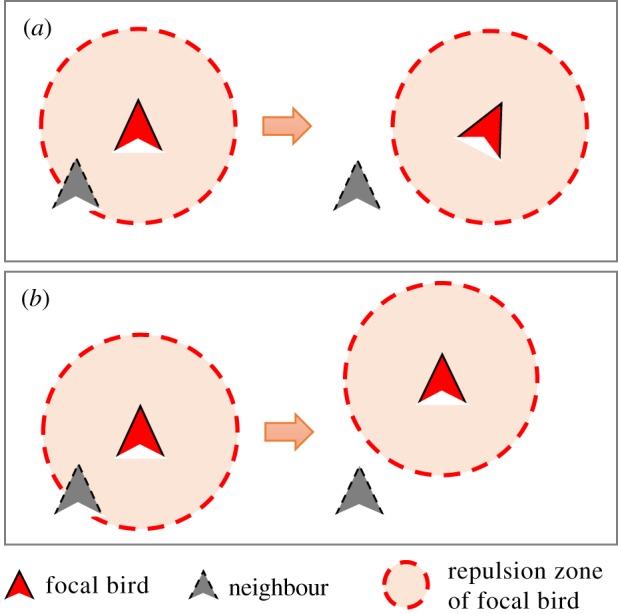
Anisotropic neighbour structure caused by repulsion. (a) Turning-based repulsion creating a side-by-side neighbour structure. (b) Speeding-based repulsion forming a front–back neighbour distribution. (Online version in colour.)

Moreover, the reason why birds flying in small groups prefer to use turning-based repulsion, as reported in a previous study [44], is not fully understood. Previous researchers [38,44] have suggested that the cause is due to the relative ease of turning as opposed to changing speed when flying through a low-density fluid like air and contrasted this with schools of fish moving in denser water, where changes in speed seem to be simpler [60,62–64]. This argument is reasonable, since flight speed is directly related to power consumption for flapping flight [65,66]. However, the energetic cost difference between making turns and changing speed has not been examined for birds flying in flocks. Whether turning is easier than changing speed, and thus the ultimate cause of birds’ use of turning-based repulsion, is unclear.

Finally, it remains unclear how the positions of neighbours determine the overall shape of flocks. In fish schools, there is evidence that the local structure scales up to the school level, leading the entire group to be elongated along the movement direction [62,64]. By contrast, the group-level consequences of the side-by-side local structure typical of many bird flocks have yet to be examined. Consequently, we lack an understanding of the connection between individual interaction forces, local neighbour structures and the overall shape of flocks.

Here, we address these open questions using jackdaws (Corvus monedula), a small corvid species, as a model system. Jackdaws are an excellent system for testing movement interactions since they are highly social on several levels [67]. They form long-term monogamous pair bonds, and bonded pairs frequently fly together, but they also fly in large groups of up to thousands of individuals during the winter roosting season [68]. Flock flight paths are very predictable, allowing us to measure the three-dimensional (3D) trajectories of individuals in these flocks using a ground-based stereo-imaging system [56]. Our uncertainty in the measurement of bird position is about 0.04 m—much smaller than both the body size of a jackdaw (0.3–0.4 m) and substantially lower than in previous studies [44]—allowing very accurate acceleration measurements. Using these measurements, we are able to construct well-resolved force maps, and test for the existence of long-range attraction and short-range repulsion in both isolated pairs and large flocks. We confirm that birds modulate their distance to nearby neighbours primarily by turning rather than changing speed even in large flocks, and therefore explain the side-by-side neighbour distribution. By measuring the wingbeat frequency, we provide evidence that the dominance of turning-based interactions is likely to be due to the biophysics of bird locomotion, as turning is energetically cheaper than changing speed. Finally, we show that the side-by-side local structure does indeed scale up to the flock level, leading to flocks that are elongated transverse to the direction of motion. These results give a more firm foundation for the structure of local interactions in bird flocks, which can be used to develop more accurate theoretical models.

2. Material and methods

(a). Data collection

We used a stereo-imaging system to measure the 3D trajectories of each individual bird within both isolated pairs and large flocks. The system used four synchronized, high-speed USB-3 cameras (Basler ace acA2040–90um, pixel size of 5.5 µm, sensor resolution of 2048 by 2048 pixels) with overlapping fields of view. We placed the imaging system along the typical flight paths of flocks such that the birds flew directly over the camera array. The maximal distance between cameras was between 50 and 60 m, which was on the same order of the distance from the camera to the birds (approx. 50 m). At a height of 50 m, we were able to image an area of 60 by 60 m² and determine bird positions with an uncertainty of 0.04 m—much smaller than the jackdaw body length (0.3–0.4 m). We recorded the birds' movement continuously for 3–20 s at 60 fps. Each flocking event consisted of 180–1200 frames. The imaging locations were in the vicinity of winter roosts near Mabe and Gwennap, Cornwall, UK. More details of the stereo-imaging system can be found in Ling et al. [56]. The camera calibration procedure can be found in the electronic supplementary material.

After recording the image data, we reconstructed the trajectories of individual birds in 3D space (details of the 3D reconstruction and tracking procedures can be found in the electronic supplementary material). Along each bird's trajectory, we measured the position x_i, velocity v_i and acceleration a_i corresponding to the bird bodies in a Cartesian coordinate system, where i ranges from 1 to 3. The direction of gravity was aligned to −x₃. We use x, v and a to denote the vectors of the corresponding quantities, and t to denote time. Moreover, following our previous studies [55,56], we measured the time series of wingbeat frequency along each bird's trajectory, denoted as f_wb (see electronic supplementary material). We also measured the total energy of birds as E = 0.5|v|² + gx₃, where g = 9.8 m s⁻² is the gravitational acceleration. We defined the rate of change of E as E′ = (E(t + dt) − E(t))/dt, where dt is the time step. E′ > 0 indicates an increase in power output, assuming a constant drag force.

(b). Flocking events

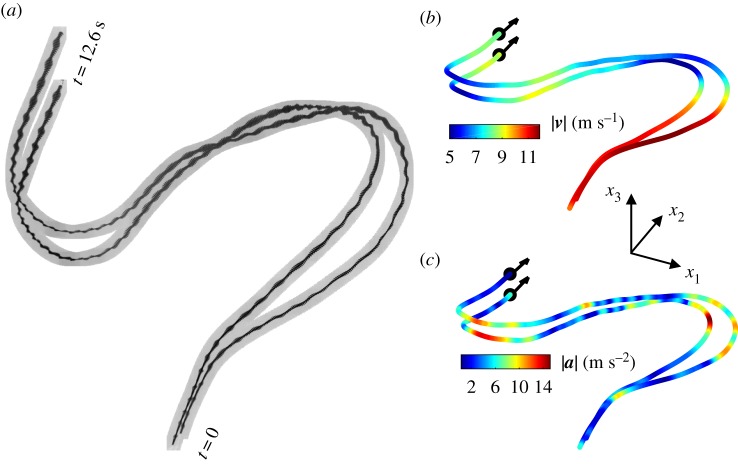
We recorded a number of flocking events from December 2017 to March 2018. The events included groups consisting of as few as two to as many as several hundred individuals. We defined two birds to be an isolated pair if (i) the two birds were not in a large group and (ii) the distance to the closest third bird was larger than 20 m, five times the average distance separating a pair of birds. We obtained 305 isolated pairs of jackdaws with the mean trajectory length of 4.0 s. Recorded bird images and reconstructed 3D trajectories for a sample isolated pair are shown in figure 2. More samples are shown in electronic supplementary material, figure S1.

Figure 2.

(a) Recorded images for isolated pairs. The time step between two consecutive images of the same bird is 1/60 s. (b,c) Reconstructed 3D trajectories for birds shown in (a) coloured by (b) flight speed |v| and (c) acceleration |a|. More samples are provided in electronic supplementary material, figure S1. (Online version in colour.)

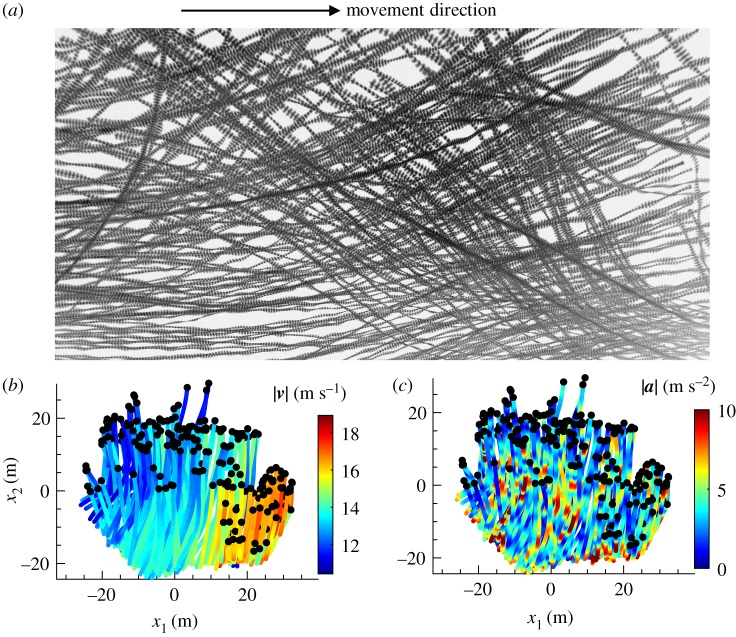
We also recorded six flocks, which we label #1–#6, consisting of 26–338 jackdaws. Criteria for the selection of flocking events are provided in the electronic supplementary material. Recorded bird images and reconstructed 3D trajectories for flock 1 are shown in figure 3. Trajectories for flocks 2–6 are shown in electronic supplementary material, figure S2. Statistics of the distance to nearest neighbours, flight speed and acceleration are listed in table 1. Since the flight speed was primarily in the horizontal plane (v₃ ≪ |v|), we neglect the component in the gravity direction in the following analysis.

Figure 3.

(a) Recorded images of birds in flock 1. The time step between two consecutive images of the same bird is 1/60 s. (b,c) Reconstructed 3D trajectories of flock 1 projected onto the horizontal plane coloured by |v| and |a|. For flocks 2–6, see electronic supplementary material, figure S2. (Online version in colour.)

Table 1.

Statistics of bird flight in isolated pairs and in groups. NND denotes the first nearest neighbour distance, v₃ denotes the velocity in the gravity direction, and a_Wing and a_Move are the accelerations in the wing and movement directions, respectively. The values provided in the table are the means and standard deviations. Positive (negative) values of a_Move mean speeding up (slowing down) and positive (negative) a_Wing implies turning right (left).

event	total no. birds	trajectory length (s)	NND (m)	|v| (m s−1)	v3 (m s−1)	aWing (m s−2)	aMove (m s−2)
isolated pairs	610	4.0±2.0	2.6±1.7	9.4±2.8	−0.3±1.5	−0.3±3.5	−0.1±1.6
flock 1	338	2.4±1.1	1.6±0.9	13.6±1.7	−0.9±0.8	−2.7±3.3	−0.7±1.8
flock 2	112	3.1±1.0	1.7±0.8	13.8±0.5	−0.3±0.6	−0.4±0.8	1.5±1.8
flock 3	106	2.9±1.4	1.7±1.0	12.0±0.7	−0.6±0.7	−0.1±1.1	0.8±1.8
flock 4	81	4.5±1.0	2.9±2.7	10.1±1.0	−0.8±0.8	−0.4±2.1	−0.1±1.4
flock 5	31	2.0±1.2	1.3±0.6	15.2±0.8	−1.4±1.6	−2.1±4.3	−1.2±1.8
flock 6	26	3.4±1.0	2.9±2.7	9.3±0.3	0.6±0.4	−1.0±0.5	−0.6±0.7

(c). Data analysis

As shown in figures 2 and 3, both speed and movement direction varied both in time and between different birds. To understand how birds adjust their velocity, we adopt the force-based approach used by Katz et al. [60]. We approximate the attraction or repulsion force F of a focal bird in response to a neighbouring bird by measuring the relative acceleration between the two, so that F = a^focal − a^neighbour, where the superscripts ‘focal’ and ‘neighbour’ denote quantities measured for the focal and neighbour birds, respectively. We subtracted the neighbour acceleration a^neighbour in order to remove the environmental effects acting similarly on both birds. For example, when both birds are linearly accelerating, a^focal can be very large but does not represent the force due to the neighbour. Only the relative quantity F captures the interaction between two birds.

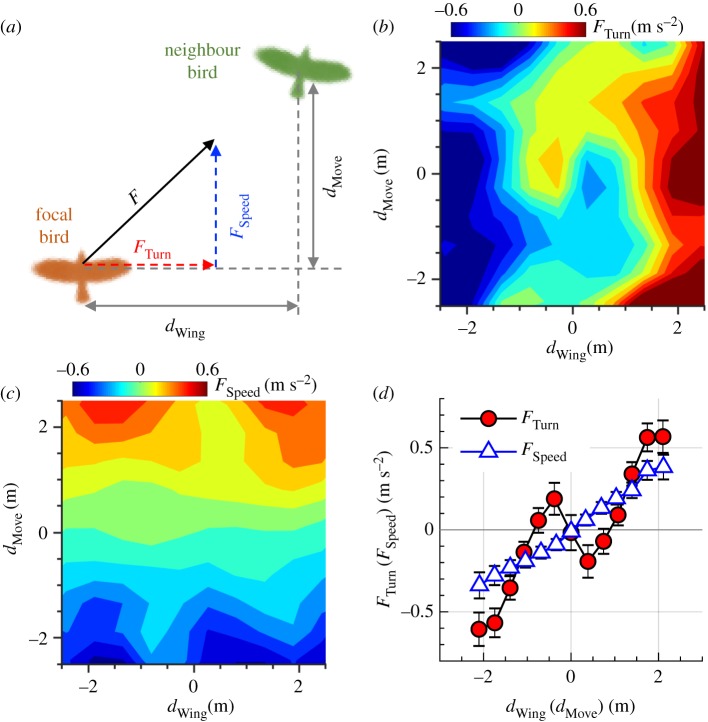
Using the local coordinate system sketched in figure 4a, we decompose F into two components: one projected in the movement direction of focal birds that we denote as a ‘speeding force’ F_Speed, and one projected perpendicular to the flight direction that we denote as a ‘turning force’ F_Turn. Therefore, positive (negative) F_Speed implies speeding up (slowing down), and positive (negative) F_Turn implies turning right (left). For simplicity, we will call the direction perpendicular to the movement direction the wing direction. We label distances in the wing direction as d_Wing and distances in the movement direction as d_Move. Therefore, positive (negative) d_Wing values mean that a neighbouring bird is located on the right (left), and positive (negative) d_Move values mean that a neighbouring bird is located in the front (back). The details of our calculation of 2D force maps and 1D force curves are described in the electronic supplementary material.

Figure 4.

(a) Schematic of the measurement variables. We place the focal bird at the origin and measure the neighbour location denoted as (d_Wing, d_Move) and acceleration of focal bird relative to neighbour denoted as (F_Turn, F_Speed). (b) F_Turn and (c) F_Speed as a function of d_Wing and d_Move. (d) F_Turn as a function of d_Wing (circles), and F_Speed as a function of d_Move (triangles). Data in (b–d) were obtained from 149 230 samples taken from 305 isolated pairs (see electronic supplementary material). For the 149 230 samples, 0.5 m s⁻² is much larger than average values of F_Turn and F_Speed. Error bars are standard errors. (Online version in colour.)

3. Results

(a). Interaction forces

In isolated pairs, the turning force (F_Turn) strongly depends on d_Wing and is relatively insensitive to d_Move (figure 4b). When plotting F_Turn as a function of d_Wing (figure 4d), long-range attraction zones where the focal bird turned right (left) when a neighbour was far on the right (left) and short-range repulsion zones where the focal bird turned left (right) when a neighbour was just on the right (left) are clearly evident. F_Turn switches from repulsive to attractive at |d_Wing| = 0.9 m (approx. 2.5 jackdaw body lengths). Conversely, the speeding force (F_Speed) strongly depends on d_Move and is insensitive to d_Wing (figure 4c). Plotting F_Speed as a function of d_Move (figure 4d) reveals attraction zones where the focal bird slowed down (sped up) when a neighbour was in back (front), but no repulsion zones. The observation that repulsion is only present in the map of the turning force indicates that birds avoid collisions mainly by turning. Moreover, the magnitude of the turning force is about twice as large as the speeding force in the attraction zone. The anisotropy of the force in the wing and movement directions is consistent with the observation that the standard deviation of a in the wing direction was larger than that in the movement direction (table 1). We also find that |F_Speed| increases with the flight speed of focal birds, similar to fish [60], while |F_Turn| does not show a clear relationship with speed (electronic supplementary material, figure S3).

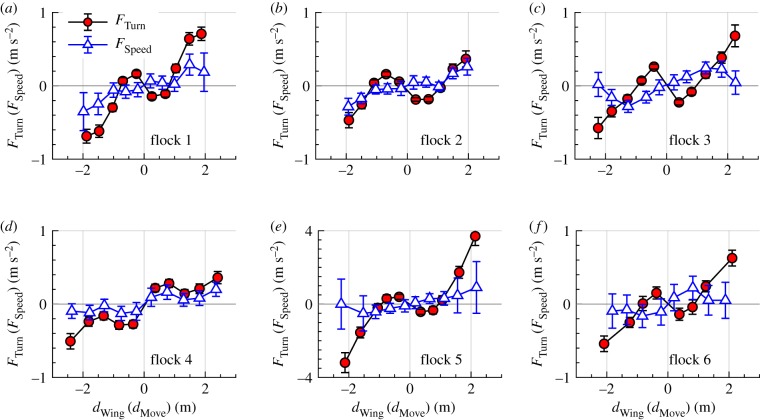
When flying in large flocks (flocks 1–6), the anisotropy of attraction and repulsion in the wing and movement directions persists, with the absolute value of the turning forces larger than that of the speeding forces and with repulsion governed by turning (figure 5). Note that the anisotropy was independent of whether the entire group was making small turns (flock 1, where a in the wing direction was larger than in the movement direction) or changing speed (flocks 2–6, where a in the movement direction was larger than in the wing direction). The results are also consistent for flock sizes ranging from 26 to 338 individuals (figure 5 and table 1).

Figure 5.

(a–f) F_Turn as a function of d_Wing (circles) and F_Speed as a function of d_Move (triangles) for birds flying in large groups. Error bars are standard errors. (Online version in colour.)

(b). Neighbour structure and group shape

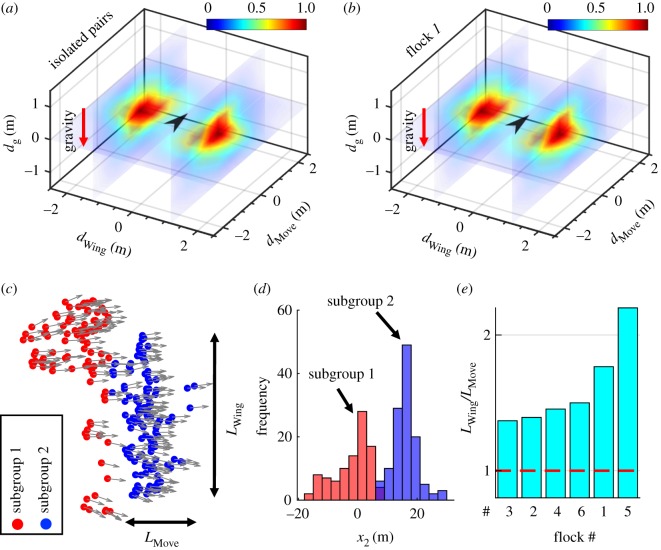
For both isolated pairs (figure 6a) and large flocks (figure 6b; electronic supplementary material, figure S4), we find that birds prefer to fly side by side, in that the most probable location for a neighbouring bird was at d_Wing = 1.0 m (approx. 2.8 jackdaw body lengths) and d_Move = 0. In a previous study [55], we found that these anisotropic spatial distributions of neighbours become isotropic for large topological distance (as in starlings [48]), a feature that we used to estimate the interaction range. We found that birds not part of a bonded pair typically interacted with seven to eight neighbours [55].

Figure 6.

(a,b) Probability density distributions of the location of the first nearest neighbour bird (a) in isolated pairs and (b) in a large flock (flock 1). The focal bird is located at the origin. d_g is the distance in the gravity direction. (c) Distribution of bird locations (dots) projected on the horizontal plane for flock 1, showing two subgroups separated along the flight direction. The vectors are the movement directions of individual birds. (d) Corresponding histogram of bird positions along the flight direction (x₂). Data for flocks 2–6 can be found in electronic supplementary material, figures S4 and S5. (e) Ratio of the subgroup size in the wing direction (L_Wing) to the subgroup size in the movement direction (L_Move). (Online version in colour.)

We then examined whether this local anisotropic structure scales up and causes the overall shape of the flock to be elongated. As shown in figure 6c and electronic supplementary material, figure S5, entire flocks typically appear to consist of several distinguishable subgroups separated along the movement direction. We thus partitioned each flock into N_s subgroups using k-means clustering, where N_s was the number of distinguishable peaks in the distribution of bird positions along the flight direction (figure 6d; electronic supplementary material, figure S5). We considered the largest subgroup in each flock and calculated its extent in the movement and wing directions, which we label as L_Move and L_Wing, respectively. We find that all subgroups are elongated in the wing direction (figure 6e), indicating that the side-by-side local structure does indeed percolate upscale and has group-level consequences. The generation of multiple subgroups along the movement direction is likely due to weaker attractive forces in that direction compared to the wing direction (figure 5). The flocks as a whole are however still elongated in the wing direction (electronic supplementary material, figure S6), though with a smaller L_Wing/L_Move when compared with subgroups.

(c). Wingbeat frequency and flight power output

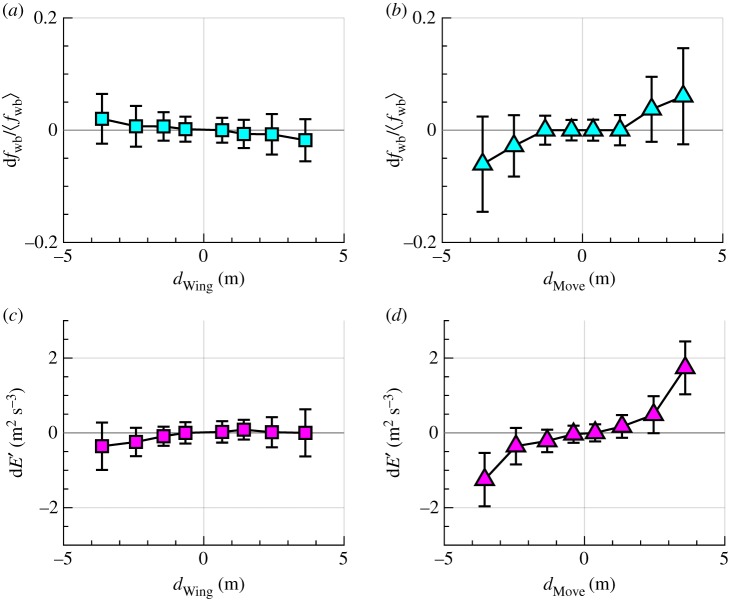
To understand why birds avoid collision mainly by turning instead of changing speed, we examined the dependence of $\mathrm{d}{f}_{\mathrm{wb}}=f_{\mathrm{wb}}^{\mathrm{focal}}\hspace{0.17em}\text{–}\hspace{0.17em}{f}_{\mathrm{wb}}^{\mathrm{neighbour}}$ as a function of d_Wing and d_Move, as shown in figure 7a,b, respectively. We also studied the dependence of dE′ = E′ ^focal – E′ ^neighbour on d_Wing and d_Move, as shown in figure 7c,d, respectively. Both df_wb and dE′ are close to zero for all values of d_Wing, indicating that turning towards a neighbouring bird does not require a change of wingbeat frequency and power output. However, df_wb is up to 10% of the mean wingbeat frequency for large d_Move and dE′ increases linearly with d_Move, indicating that focal birds must increase their wingbeat frequency and power output to achieve a positive speeding force when the neighbouring bird is far to the front. Our results suggest that turning is energetically cheaper than changing speed, and thus provide a possible explanation for the turning-based repulsion used by birds. Additionally, comparing between rear and front birds in isolated pairs shows that rear birds are more likely to change their behaviour (e.g. to generate positive speeding forces, rear birds are more likely to increase their wingbeat frequency and speed up) in response to front birds (see details in electronic supplementary material).

Figure 7.

(a,b) df_wb as a function of d_Wing (a) and d_Move (b). (c,d) dE′ as a function of d_Wing (c) and d_Move (d). Here, df_wb > 0 indicates that focal birds flap their wings faster than their neighbours, and dE′ > 0 indicates that focal birds output more mechanical power than their neighbours. Results were obtained from 149 230 samples taken from 305 isolated pairs. Error bars are standard errors. (Online version in colour.)

4. Discussion

Characterizing the social interactions in large groups of birds is critical for understanding the mechanisms of flocking behaviour. Here, by measuring the acceleration of a focal bird in response to its neighbours, we quantified the social interaction forces in groups with sizes ranging from two to hundreds of individuals. Our measurements of short-range repulsion and long-range attraction in bird flocks agree with agent-based models [29–34,40,41,59] and empirical measurements in insects [61,69,70], fish [8,60,71], birds [44,50] and mammals [72]. Moreover, we find that the effective attraction force (that is, the magnitude of the acceleration) increases linearly with distance in a spring-like fashion, consistent with assumptions made in theoretical models [33,34] and observational results from fish schools [60]. Critically, our analyses reveal that the social forces are highly anisotropic: long-range attractive forces are larger in the wing direction than in the movement direction, and short-range repulsive forces are generated mainly by turning. Although similarly anisotropic forces have been reported previously for pairs of pigeons [44], we show here that this effect extends to large flocks.

Thus, we also provide empirical support for the hypothesis [44,62] that the side-by-side neighbour structures typical of pigeon and passerine bird flocks [44,48,49,55] are a result of the turning-based repulsion mechanism. As shown in previous studies [10,55,56], both jackdaws and pigeons flying in side-by-side configurations in large flocks expend more energy than they do when flying alone. Therefore, the side-by-side neighbour structure is unlikely to arise from aerodynamic interactions, in contrast with V-formation flight of some waterfowl and large migratory birds [22,23,73].

Furthermore, by measuring the wingbeat frequency and the sum of the potential and kinetic energy during flight for birds in isolated pairs, we give an explanation for why birds use turning-based repulsion rather than the speeding-based repulsion seen in fish schools [60,62]. We find that generating large speeding forces requires birds to change their wingbeat frequency and power output, while producing a large turning force does not. Our results suggest that turning is likely to be energetically cheaper than changing speed. This observation can be explained by the physics of bird locomotion: as they travel through the air, birds have to maintain sufficient speed to gain enough lift force and minimize the mechanical power output [65] (since both increasing and reducing speeds may result in an increase in power output). On the other hand, since the drag force in air is relatively small due to its low density, slightly adjusting the flight direction (e.g. by changing body posture [74,75]) will not cause a significant change of speed and thus will require little additional power output. Therefore, it is likely that the physics of bird locomotion make turning easier and energetically cheaper than changing speed, resulting in dominantly turning-based repulsion, in contrast with the changes in speed that control repulsion in fish moving through the higher density medium of water [60,62,63].

Finally, we demonstrate that the local side-by-side structure scales up to the global level, making the entire flock elongated in the direction perpendicular to the movement. This is similar to the way in which fish schools are elongated in the movement direction as a result of the front-to-back local configuration of neighbours [42,62–64]. We note, however, that the elongated group shape was observed here for birds travelling together in a particular direction (in this case, towards evening roosts). Display flocks that make more complex manoeuvres (such as the classic murmurations of starlings) may show different behaviour. For example, when a group of starlings makes a turn, it was found that the group was initially elongated along the direction perpendicular to the movement before the turn but became elongated along the travelling direction after the turn [49].

In conclusion, although many previous models have assumed that interaction forces depend only on the distance between neighbours, we show that due to the physics of bird locomotion (and in particular that turning is easier than changing speed), the social interaction forces in real animal groups are highly anisotropic. Such anisotropic forces have significant consequences both for the local neighbour structure and the macroscopic group shapes, which ultimately impact key functions such as information transfer [64] and predator avoidance [18]. We thus strongly suggest that future models should consider the physics of animal locomotion and the properties of the medium through which animals are travelling when formulating interaction rules.

Ethics

All field protocols were approved by the Biosciences Ethics Panel of the University of Exeter (ref. 2017/2080) and adhered to the Association for the Study of Animal Behaviour Guidelines for the Treatment of Animals in Behavioural Research and Teaching.

Data accessibility

Data and code are available from the Dryad Digital Repository: https://doi.org/10.5061/dryad.kb8js06 [76].

Authors' contributions

H.L., N.T.O., A.T. and R.T.V. conceived the ideas; H.L. and N.T.O. designed the methodology; G.E.M. and A.T. collected the data; H.L., N.T.O. and K.v.d.V. analysed the data; all led the writing of the manuscript. All authors contributed critically to the drafts and gave final approval for publication.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by a Human Frontier Science Program grant to A.T., N.T.O. and R.T.V., award no. RG0049/2017.