Whisker Vibrations and the Activity of Trigeminal Primary Afferents in Response to Airflow

Abstract

Rodents are the most commonly studied model system in neuroscience, but surprisingly few studies investigate the natural sensory stimuli that rodent nervous systems evolved to interpret. Even fewer studies examine neural responses to these natural stimuli. Decades of research have investigated the rat vibrissal (whisker) system in the context of direct touch and tactile stimulation, but recent work has shown that rats also use their whiskers to help detect and localize airflow. The present study investigates the neural basis for this ability as dictated by the mechanical response of whiskers to airflow. Mechanical experiments show that a whisker's vibration magnitude depends on airspeed and the intrinsic shape of the whisker. Surprisingly, the direction of the whisker's vibration changes as a function of airflow speed: vibrations transition from parallel to perpendicular with respect to the airflow as airspeed increases. Recordings from primary sensory trigeminal ganglion neurons show that these neurons exhibit responses consistent with those that would be predicted from direct touch. Trigeminal neuron firing rate increases with airspeed, is modulated by the orientation of the whisker relative to the airflow, and is influenced by the whisker's resonant frequencies. We develop a simple model to describe how a population of neurons could leverage mechanical relationships to decode both airspeed and direction. These results open new avenues for studying vibrissotactile regions of the brain in the context of evolutionarily important airflow-sensing behaviors and olfactory search. Although this study used only female rats, all results are expected to generalize to male rats.

SIGNIFICANCE STATEMENT The rodent vibrissal (whisker) system has been studied for decades in the context of direct tactile sensation, but recent work has indicated that rats also use whiskers to help localize airflow. Neural circuits in somatosensory regions of the rodent brain thus likely evolved in part to process airflow information. This study investigates the whiskers' mechanical response to airflow and the associated neural response. Airspeed affects the magnitude of whisker vibration and the response magnitude of whisker-sensitive primary sensory neurons in the trigeminal ganglion. Surprisingly, the direction of vibration and the associated directionally dependent neural response changes with airspeed. These findings suggest a population code for airflow speed and direction and open new avenues for studying vibrissotactile regions of the brain.

Introduction

Animal nervous systems, and the computations they perform, evolve to process and act on sensory information critical for survival. For rodents, the whiskers (vibrissae) are a particularly important sensory modality, and the brain structures associated with the whiskers are correspondingly expanded (Woolsey and van der Loos, 1970; Welker and Woolsey, 1974). Although the rodent whisker system is a premier model for studying active touch (Knutsen et al., 2006; Kleinfeld and Deschênes, 2011; O'Connor et al., 2013; Maravall and Diamond, 2014; Hobbs et al., 2015; Chakrabarti and Schwarz, 2018), we still lack a full understanding of the stimuli that guided the evolution of vibrissae-related neural structures.

We recently demonstrated that whiskers aid rats in localizing an airflow source, suggesting that somatosensory regions of the rodent brain may have evolved to process signals associated with airflow, in addition to direct touch (Yu et al., 2016b). Such processing is likely to be particularly important in the coordination of whisking and sniffing during olfactory search (Smear et al., 2011; Moore et al., 2013; Ranade et al., 2013; Kleinfeld et al., 2014; Bhattacharyya and Bhalla, 2015). These behavioral findings raise the questions: how do the whiskers mechanically respond to airflow, and how do whisker-sensitive neurons of the trigeminal system represent airflow information?

Previous work has shown that a whisker both bends and vibrates in response to airflow stimulation (Yu et al., 2016a). Vibrissae-responsive neurons would be expected to respond to both of these mechanical components. In the present study, we quantify the magnitude and direction of whisker vibration for a wide range of airflow stimulation parameters. We then record from a small number of vibrissae-responsive primary sensory neurons in the trigeminal ganglion (Vg) while delivering airflow stimuli to the whisker array.

Because the responses of Vg neurons to direct touch are well-characterized, we can confirm expectations for their responses to airflow using only a small set of neurons. We find that Vg firing rates adapt over the course of seconds; firing rates increase with airspeed and are affected by the orientation of the whisker relative to airflow; and spiking periodicity is related to the whiskers' resonant frequencies. We conclude with a synthetic model that hypothesizes how features of both bending and vibration may be coded simultaneously in whisker-responsive afferents, providing the animal cues about both airspeed and direction.

Materials and Methods

All procedures involving animals were approved in advance by Northwestern University's Animal Care and Use Committee.

Mechanical experiments

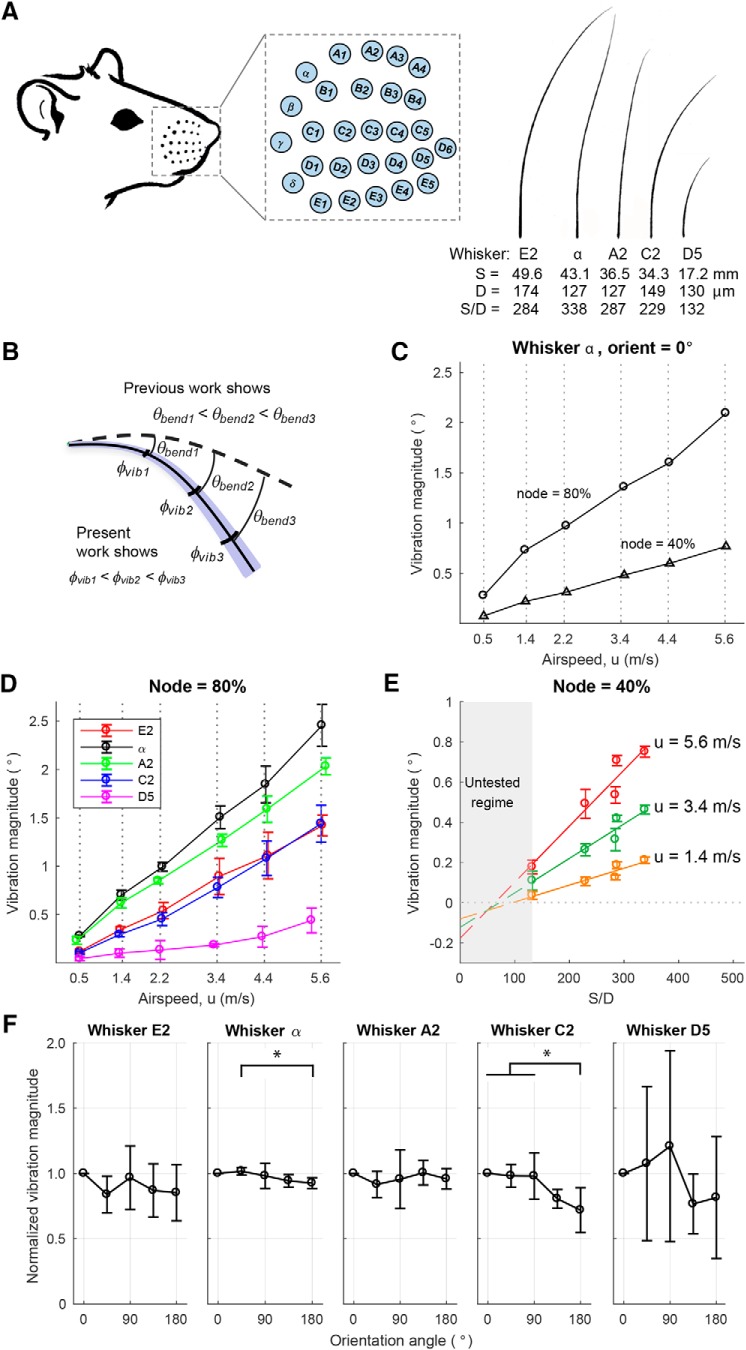
Mechanical experiments were performed on five vibrissae plucked from a single, adult (≥3 months old) female Long Evans rat. Each whisker was identified by its row and column position within the array (van der Loos and Woolsey, 1973): E2, α, A2, C2, and D5. To ensure that the whiskers were representative of typical rat whiskers, we confirmed that their geometric and mechanical parameters (length, base diameter, density) fell well within the range of the dataset described by Belli et al. (2017). This dataset includes parameters for 519 whiskers from both male and female rats, with whiskers obtained in seven different laboratories. We therefore expect all mechanical results to generalize to male rats. The geometry of each whisker was obtained by scanning it on a flatbed scanner (Epson Perfection 4180 Photo) and then manually tracing its shape in Photoshop (Adobe). Detailed descriptions of the experimental setup, 3D video tracking, and vibrissal morphology are provided in previous work (Yu et al., 2016a). Briefly, the base of each whisker was mounted in a clamp, and a hair dryer was used to deliver airflow through a long PVC tube at six different airspeeds (∼0.5, 1.4, 2.2, 3.4, 4.4 and 5.6 m/s). The vibrissae were positioned such that the intrinsic curvature was oriented at five angles relative to the airflow (0°, 45°, 90°, 135°, and 180°).

For each combination of orientation and airspeed, two orthogonally mounted video cameras (Photron, FASTCAM-1024PCI), each fitted with a macro lens, were used to capture the whisker's shape at 1000 frames per second (fps). The two camera views were merged to reconstruct the whisker's 3D shape. To ensure we captured steady-state behavior of the whisker, video recording began at least 10 s after airflow was applied and lasted for 5 s (5000 frames).

The airspeeds were selected based on meteorological studies of land-surface wind speeds, which typically range between 0 and 5 m/s (Monahan et al., 2011). We also used a hot-wire anemometer (Omega, model HHF42, resolution = 0.1 m/s) to measure wind speed in locations where we had observed rats to live (bushes, dumpsters, fields, etc.). These measurements confirmed that the range 0.5–5.6 m/s bracketed the wind speeds that rats would typically encounter.

Reynolds number (Re) calculations were performed for all 519 whiskers in the dataset of Belli et al. (2017). Re was computed as Re = uD/ν, where u is the airflow speed, D is the diameter of the whisker, and ν is the kinematic viscosity of air. For fixed values of u and ν, the maximum value for Re is always found at the whisker base, where the diameter is largest.

Quantifying vibration magnitude

Previous work has shown that, in response to an airflow stimulus, a whisker will bend to a new position and then vibrate around that new deflected position (Yu et al., 2016a). Bending and vibration can thus be thought of as the mean and fluctuations of the whisker's position in airflow. Vibration magnitude was therefore computed as the fluctuations of the whisker about its mean, as follows.

First, each whisker was discretized into nodes, spaced 2 mm apart. Second, we calculated the mean (x, y, z) position of each node in airflow (the temporal average of the position over all 5000 frames). We found the vector connecting the whisker's basepoint to the mean position of that node (Vector 1). Third, for each of the k video frames, we found the vector connecting the whisker's basepoint to the instantaneous (x, y, z) position of that node (Vector 2). For each node and each frame k, the instantaneous vibration magnitude φ_k was then computed as the angle between Vector 1 and Vector 2. Finally, for each node, the vibration magnitude φ_vib was found as the time average of the absolute value of all 5000 instantaneous vibration magnitudes as follows:

where k is the frame number, and T is the video duration (5000 frames).

Quantifying vibration direction

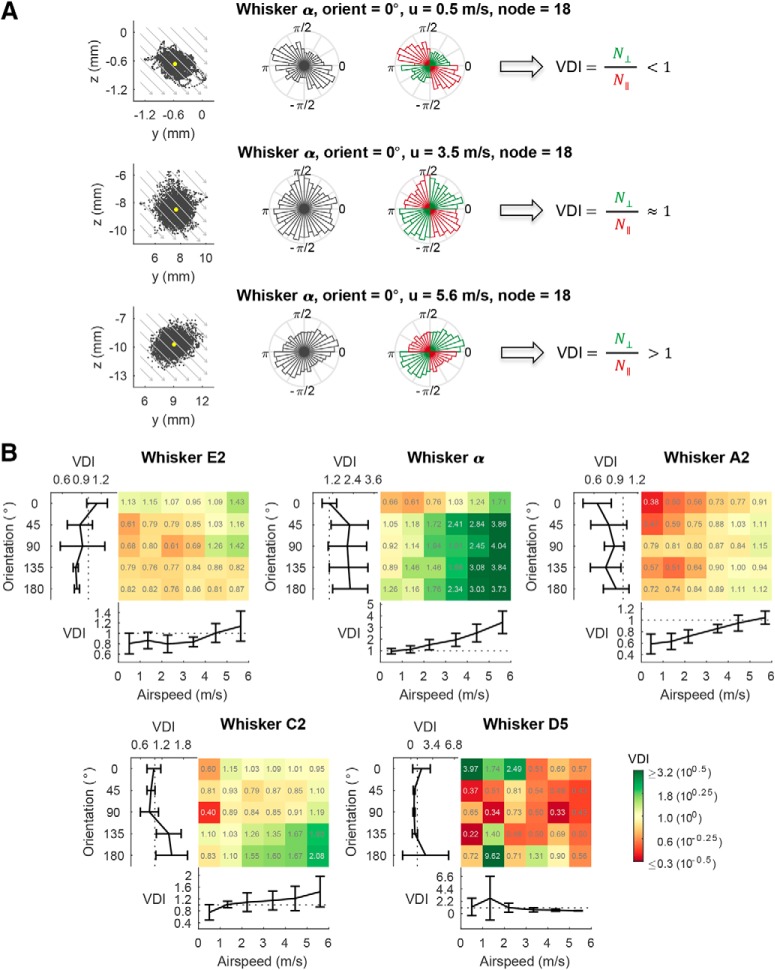
To quantify vibration direction, we used the following method. At each node along the whisker length, we imagined taking a cross-section of the whisker, perpendicular to its long axis. The position of the node in that cross-sectional plane was then plotted for each video frame. This procedure revealed how much the whisker vibrated at each point along its length. We defined the vibration direction index (VDI) to quantify the extent to which this vibration direction is parallel or orthogonal to airflow direction as follows:

where N_⊥ denotes the number of frames in which the whisker nodal position fell in either the first or third quadrants, and N_‖ is the count in either the second or fourth quadrants. Air is always taken to flow from the second quadrant to the fourth quadrant, at an angle −45° relative to the x axis. Therefore, N_⊥ quantifies the number of times that the node was displaced to a position perpendicular to the airflow direction, whereas N_‖ quantifies the number of times that the node was displaced to a position parallel to the airflow direction. The displacements used to compute the VDI contain both perpendicular and parallel (tangential) components. The VDI identifies whether the ratio of the perpendicular to parallel components is greater than or smaller than unity. As seen in Figure 4A, VDI < 1 indicates an ellipse shape with its major axis in the second and the fourth quadrants, VDI > 1 indicates an ellipse shape with its major axis in the first and the third quadrants, and VDI ≈ 1 indicates a circular shape.

Figure 4.

Vibration direction tends to be parallel with the airflow direction at low airspeed and perpendicular to the airflow direction at high airspeed. A, The airflow-evoked vibration of the α whisker at an orientation angle of 0° provides an example of the general finding that increases in airspeed are associated with transitions in vibration direction. The three rows of this figure show vibrations that occur for airspeeds of 0.5 m/s (vibration primarily parallel to airflow direction), 2.3 m/s (vibration equally likely in all directions), and 5.6 m/s (vibration primarily perpendicular to airflow direction). Each row contains three subplots. The first subplot in each row plots a point for the node position at every time point in the trial (5000 samples). Gray arrows indicate airflow direction. Yellow dot indicates the mean of the node position. The second subplot in each row shows the normalized polar histogram of the node positions. The third subplot in each row shows the same normalized polar histogram, but color codes the polar angles of the first and third quadrants in green, and the polar angles of the second and fourth quadrants in red. VDI is <1 in the top row, ∼1 in the middle row, and >1 in the bottom row. N_⊥ indicates the number of perpendicular counts. N_‖ indicates the number of parallel counts. B, The VDI at each orientation angle and each airspeed for each whisker at a node ∼80% out along the whisker length. The color grid plot indicates the VDI at each of the six airspeeds and each of the five orientation angles. The colormap legend is log-scaled, and the value of the VDI for each condition is labeled in each grid. For each whisker, the subplot underneath the color grid plot shows the VDI as a function of airspeed, and the subplot on the left shows VDI as a function of orientation angle. Data are mean ± SEM.

Quantifying whisker resonance

The mass of each whisker was measured using a Mettler-Toledo UMX2 ultra microbalance with a resolution of ±0.1 μg. The whisker's base diameter (D) and tip diameter were measured at 10× magnification (Leica Microsystems, DM750). After measuring the diameter, the whiskers were scanned on a flatbed scanner (Epson Perfection 4180 Photo), and their shapes were traced in MATLAB (The MathWorks). These traces were used to compute the whisker's arc length (S). The whisker was approximated as a truncated cone to compute its volume, and divided by its mass to compute its density (ρ). Equation 3, which describes the resonant modes for a fixed-free tapered cantilever beam, was used to calculate the theoretical resonant frequencies for each whisker (Georgian, 1965) as follows:

All parameters on the right side of this equation, except Young's modulus (E) and the coefficient λ_n, are either measured values or computed directly from measured ones. The coefficient λ_n, associated with resonant mode number (subscript n), was obtained from linear interpolation between tabulated values (Georgian, 1965), as shown in Table 1. Young's modulus was set at either 3 or 11 GPa (Hartmann et al., 2003; Neimark et al., 2003; Birdwell et al., 2007; Quist et al., 2011; Kan et al., 2013) to bracket the possible range of resonance frequencies.

Table 1.

Whisker length, tip diameter, and base diameter, and values of the coefficient (λ_n) used to compute theoretical resonant frequencies^a

Whisker identity	Length (mm)	Tip diameter (μm)	Base diameter (μm)	(At/Ab)1/2	λn for Mode 1	λn for Mode 2	λn for Mode 3
				1.00	3.52	22.03	61.70
				0.50	4.63	19.55	48.50
				0.33	5.29	18.76	43.78
C3	17.7	29	105	0.27	5.70	18.58	42.00
				0.25	5.85	18.51	41.34
γ	40.0	36	150	0.24	5.94	18.52	41.05
C4 (2 speeds)	12.8	16	82	0.19	6.39	18.59	39.65
B3	16.4	10	79	0.12	6.98	18.68	37.80
C2	33.8	13	123	0.10	7.16	18.70	37.23
				0.10	7.20	18.71	37.10
E3	23.8	13	139	0.09	7.31	18.89	37.20
C4 (3 speeds)	12.1	7	84	0.08	7.50	19.19	37.37
D3	17.7	5	98	0.05	7.95	19.92	37.77
				0	8.72	21.15	38.45

^aData indicate the geometric parameters of the whiskers associated with the eight recorded neurons. The variables A_t and A_b indicate the area of the tip and base of the conical cantilever beam, respectively. Rows that leave whisker parameters blank indicate values of λ_n adopted directly from Georgian (1965). The other rows contain values of λ_n computed by finding (A_t/A_b)^1/2 from whisker parameters and then linearly interpolating between the values from Georgian (1965).

Neural recordings during airflow stimulation

Surgical procedures.

Five adult female Long Evans rats (age ∼90 d) were anesthetized with an anesthetic mixture delivered intraperitoneally (60 mg/kg ketamine, 3.0 mg/kg xylazine, and 0.6 mg/kg acepromazine maleate). Due to the limited number of animals, only one sex was used. We expect results to generalize to males, as both follicle structure (Ebara et al., 2002) and primary sensory neuron encoding properties appear consistent across sexes (Gibson and Welker, 1983a,b; Shoykhet et al., 2000; Jones et al., 2004a,b; Stüttgen et al., 2006; Leiser and Moxon, 2007). For the duration of surgery and recording, adequate anesthetic depth was ensured by assessing the toe-pinch reflex every 15 min and by carefully monitoring for any whisker twitches. Boosters were administered as necessary to maintain a deep plane of anesthesia. Body temperature was maintained at ∼37°C using a water-regulated heat therapy pump (HTP-1500, Adroit Medical Systems). With the animal placed in a custom head-fixation apparatus, an incision was made along the midline of the scalp and the skull exposed. Three or four stainless-steel screws were placed in the skull over neocortical areas and covered in dental acrylic. This structure was affixed to the surgical bed to maintain head fixation while nose brace and the ear bars were removed, to allow full access to the left side of the whisker array.

A ∼1-mm-diameter craniotomy was performed ∼2 mm caudal to bregma and ∼2 mm lateral from midline above the Vg. A tungsten electrode (FHC, Metal Electrode; typical impedance 2–5 mΩ) was advanced to a depth of ∼9 mm until multiunit responses to manual whisker deflections were observed. The electrode was then advanced slowly until a single, whisker-responsive neuron was isolated. Neural signals were amplified through an A-M Systems model 1700 amplifier with bandpass filtering between 1 Hz and 10 kHz before digital sampling and acquisition at 40 kHz in DataWave Technologies SciWorks. After isolation of a single vibrissae-responsive unit, airflow stimuli were presented and neural responses were recorded. Recorded voltage signals were digitally bandpass filtered between 300 and 8000 Hz before spike detection and sorting with the open-source software Klusta (Rossant et al., 2016).

Airflow delivery.

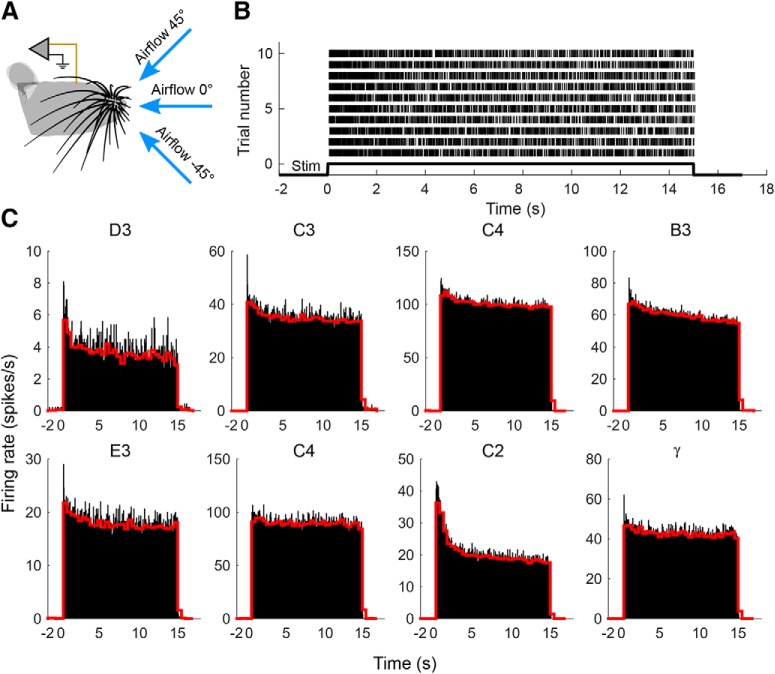
As described above, anesthetized animals were placed in a custom head-fixation apparatus that allowed free access to all whiskers on the left side of the mystacial pad. A regulated compressed air source was connected to a custom airflow delivery apparatus, and airflow was supplied from three directions, −45°, 0°, and 45° relative to the lambda-bregma plane, toward the center of the whisker array. The airflow delivery apparatus was carefully calibrated to direct airflow to the same point at the center of the array from all three directions, and varying the pressure of the compressed air allowed us to control the airspeed at the center of the vibrissal array as measured with the hot-wire anemometer.

Two protocols were used during experiments. In the first protocol, we measured the airspeed at the center of the array before each stimulus condition (speed/direction combination) and adjusted the pressure of the airflow source to obtain the expected airspeed at the center of the whisker array. This protocol used two airspeed conditions: 1 and 3 m/s. The second protocol was optimized to increase the amount of data collected by calibrating the airspeed from a fixed apparatus calibrated once before the collection of data. This protocol used 3 speeds (1, 3, and 5 m/s). Four neurons were recorded using the first protocol, and another four neurons were recorded based on the second protocol.

For each combination of airspeed and direction, we presented the airflow stimuli for 10 trials, with the following exceptions in which 9 trials were performed: whisker D3 at 0 deg, 5 m/s; whisker C3 at 45 deg, 5 m/s; and whisker B3 at −45 deg,1 m/s. A trial consisted of sustained airflow presentation for 15 s. A pause of 4 s between trials was included to allow the whisker to relax to rest.

Airflow stimulus calibration.

All airspeeds were measured using the hot wire anemometer. To calibrate the airspeeds, the airflow apparatus was fixed in position and the anemometer was affixed to a 3 axis motorized manipulator (Sutter Instruments, MP-285). Airspeed measurements were taken from the anemometer at a range of positions for all tested pressures and apparent directions.

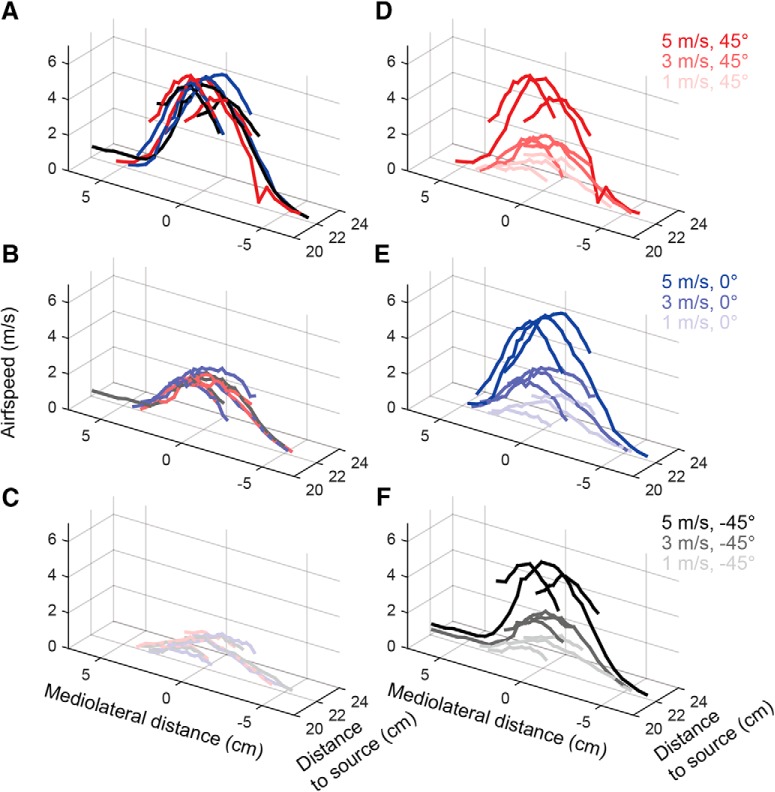
The airflow map for each combination of speed and direction was obtained and is shown in Figure 1. Each panel in the first column (Fig. 1A–C) compares the measured airspeeds for the different directions, keeping supply pressure constant. The overlap at all positions and directions indicates that, for each pressure (intended airspeed) and location, the airspeed is consistent across directions. Each panel in the second column (Fig. 1D–F) shows the measurements for a given direction across airspeeds. The airspeed drops off as the mediolateral distance increases. The airspeed drops off as rostrocaudal distance increases, but not so much so that the apparent speed at the anterior region of the whisker array at one pressure is the same as the apparent speed at the posterior region of the array. The airspeed maps at different speed values are distinct from each other (Fig. 1D–F), allowing us to investigate the effect on the neural response from different airflow directions and airspeeds.

Figure 1.

Airflow stimulus calibration. In all subplots, the origin (0, 0) represents the location of the airflow source, the coordinate (0, 22) is close to the center of the whisker array. All units are in centimeters. Red, blue, and black represent an airflow direction of 45°, 0°, and −45°, respectively. The saturation of the color represents the magnitude of the airspeed. Dark, medium, and light colors represent 5, 3, and 1 m/s, respectively. A–C, Each panel compares the measured airspeeds for the different directions, keeping supply pressure constant. The overlap at all positions and directions indicates that, for each pressure (intended airspeed), there is no bias in airspeed across directions. D–F, Each panel shows the measurements for a given direction across airspeeds. Although airspeed is not constant across all positions in the array, the airspeeds at each position within the array are distinct across pressures. Therefore, comparisons across pressure are equivalent to comparisons across airspeed.

Experimental design and statistical analysis

Five whiskers plucked from an adult female Long Evans rat were used in the mechanical experiment, each with different base diameters and arc lengths. Vibrations of each of the five whiskers were analyzed at six different airspeeds and at five different orientations relative to the airflow. For the neural experiment, responses from eight primary sensory Vg neurons from 5 adult female Long Evans rats were recorded. Airflow was delivered to the whisker array from three directions relative to the rat's head, and at each direction either two or three airflow speeds were used.

Data are presented as either the mean ± SD (see Fig. 2D–F) or as the mean ± SEM (see Figs. 3B, 4B, 6, and 7). Statistical analyses were performed in MATLAB. A repeated-measures one-way ANOVA with Tukey's post hoc test was performed to examine the effect of orientation on the vibration magnitude. A two-way ANOVA test with Tukey's post hoc test was performed to examine the effects of the airspeed and the airflow direction on the firing rate of the Vg neurons.

Figure 2.

Vibration magnitude varies with airspeed and whisker geometry. A, Left, Drawing of a rat and mystacial pad with whisker basepoints highlighted as cyan dots. Drawing adapted from Belli et al. (2018). These whisker basepoints are expanded in the inset to show their identities. Right, Five whiskers with different S/D ratios were used in the experiments. A lower S/D ratio means that the whisker is stiffer compared with a whisker of the same length with a higher S/D ratio. Manual tracings of the scanned whiskers are shown. B, Schematic of bending and vibration magnitudes. Dashed curve indicates the position of the whisker at rest (no airflow). Solid curve indicates the mean position of the whisker in the presence of airflow. Blue transparent region schematizes vibration magnitude around the static bending. θ_bend and φ_vib indicate bending magnitude and vibration magnitude, respectively. For all whiskers in all conditions, we found that φ_vib1 < φ_vib2 < φ_vib3. C, Vibration magnitude is larger at more distal locations along the whisker. The plot represents the vibration magnitude of nodes located at 40% and 80% along the whisker α. In this example, the whisker was oriented concave forward into the airflow, but similar results held for all whiskers at all orientations. D, Vibration magnitude increases linearly with airspeed. Results are shown for nodes 80% out along the whisker length and averaged over all orientation angles (mean ± SD). E, Vibration magnitude increases approximately linearly with the S/D ratio of the whisker. Along the x axis, ordered from small to large S/D ratio, the whisker identities are D5, C2, E2, A2, and α. Results are shown for a node 40% out along each whisker and at airspeeds of 1.4, 3.4, and 5.6 m/s (mean ± SD at five orientations). Linear fits between vibration magnitude and S/D ratio show increasing slopes with airspeed. Because airspeeds were not identical for all five whiskers, values of vibration magnitude have been interpolated between the airspeeds closest to the speed of interest. F, The whisker's orientation relative to airflow did not strongly contribute to vibration magnitude. In each subplot, the vibration magnitude has been normalized by that whisker's vibration magnitude at orientation angle 0° (concave forwards, toward the airflow). Only the α whisker (F_(4,25) = 3.12, p = 0.0329) and the C2 whisker (F_(4,25) = 6.63, p = 0.0009) showed significant changes in vibration magnitude due to orientation (one-way ANOVA with repeated measures). Tukey's post hoc testing indicates that only 4 of 50 pairs of group comparisons show a significant difference: for the α whisker, only the vibration magnitude at 180° is significantly lower than the one at 45° (p = 0.0458); and for the C2 whisker, the vibration magnitude at 180° is significantly lower than the ones at 0° (p = 0.0039), 45° (p = 0.0073), and 90° (p = 0.0079). *p < 0.05. Results show mean ± SD at six airspeeds for a node 40% out along each whisker.

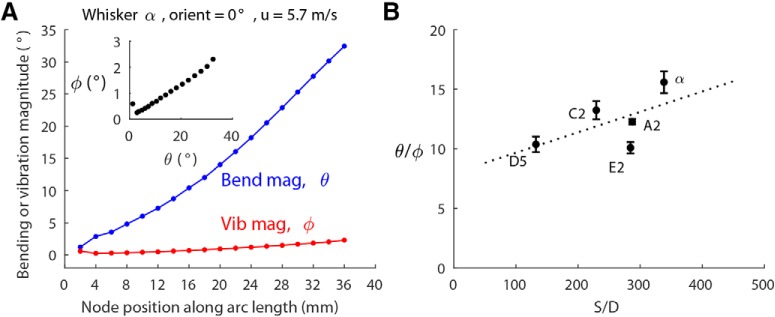
Figure 3.

Vibration magnitude scales with bending magnitude. A, Bending magnitude and vibration magnitude along the arc length of the α whisker with orientation angle 0° and airspeed 5.7 m/s. Inset, Vibration magnitude versus bending magnitude for all the nodes of the α whisker. B, The ratios of bending magnitude to vibration magnitude (θ_bend/φ_vib) of all five whiskers fall within a range of 10–16, and slightly increase with the S/D ratio. Dashed line indicates the line of linear regression over the five means. Data show mean ± SEM over all whisker nodes at all velocities and all orientation angles.

Figure 6.

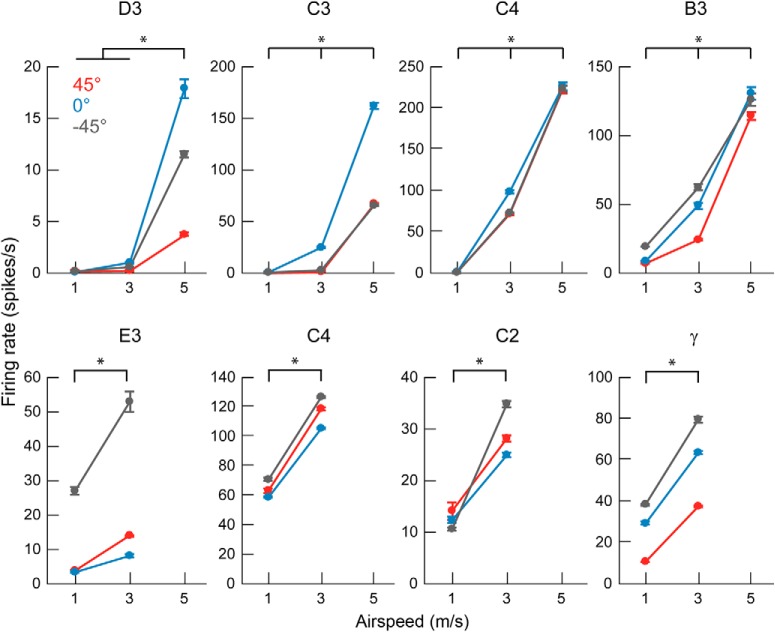
The firing rate of Vg neurons increases with airspeed. All eight neurons show an increase of firing rate with airspeed (two-way ANOVA: main effect of airspeed, p < 0.001 for all neurons). *p < 0.05 (Tukey's post hoc test). Three airspeeds were used for neurons shown in the top row and two airspeeds used for neurons shown in the bottom row. Black, blue, and red represent airflow directions −45°, 0°, and 45°, respectively. Data show mean ± SEM over all tested trials at each condition.

Figure 7.

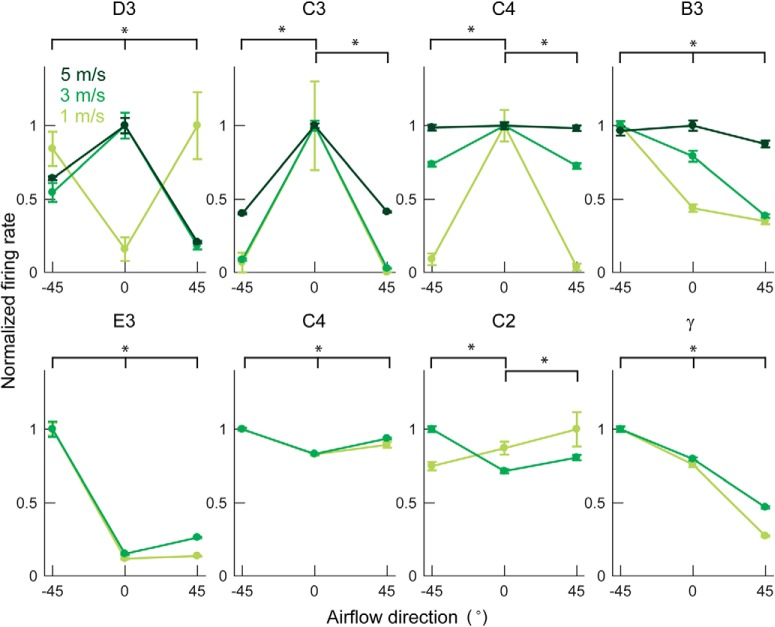
Firing rate changes with airflow direction. All eight neurons show variations in firing rate with airflow direction (two-way ANOVA: main effect of direction, p < 0.001 for all neurons). *p < 0.05 (Tukey's post hoc test). Each neuron is labeled with the row and column identity of the whisker it innervates. Light, medium, and dark green curves indicate slow, medium, and fast airspeed (∼1, 3, and 5 m/s) as indicated by the legend in the first subplot. Three airspeeds were used for neurons shown in the top row and two airspeeds used for neurons shown in the bottom row. Data show mean ± SEM over all trials at each condition. Firing rates are normalized to the maximum mean firing rate for a given airspeed. The absolute firing rates can be seen in Figure 6.

Results

Vibration magnitude increases along the whisker length and depends on airflow speed and the ratio of the whisker's arc length to its base diameter

As described in Materials and Methods, we used high-speed video (1000 fps) to quantify the 3D mechanical behavior of whiskers in response to sustained airflow stimuli. Five whiskers were tested, each identified by their row and column position within the array (van der Loos and Woolsey, 1973): E2, α, A2, C2, and D5. The whiskers' shapes and geometric parameters (arc length S, base diameter D, and S/D ratio) are shown in Figure 2A. Airflow stimuli were delivered at six different speeds (∼0.5, 1.4, 2.2, 3.4, 4.4, and 5.6 m/s) and from five different directions (0°, 45°, 90°, 135°, and 180°). The airflow “direction” was defined as the orientation of the whisker's intrinsic curvature relative to the airflow, with 0° and 180° representing concave forwards and backwards relative to the airflow, respectively, and 90° representing concave upwards relative to the airflow. Discrete 3D positions (“nodes”) along the whisker were tracked at intervals of 2 mm (Yu et al., 2016a). Linear interpolation between these nodes then yielded the complete shape of the whisker.

The whisker, as a nonrigid beam, both bends and vibrates in response to an airflow stimulus. At each point along the whisker, the bending magnitude (θ_bend) can be quantified as the angle between that point on the whisker at rest and the mean position of that point when the whisker is in airflow. As schematized in Figure 2B, previous work has shown that the bending magnitude increases along the whisker length, so that more distal portions of the whisker rotate through larger angles than more proximal regions (Yu et al., 2016a). This earlier work also showed that the bending magnitude at each node depends strongly on airflow speed, the ratio of the whisker's arc length to its base diameter (S/D ratio), and weakly on the whisker's orientation relative to airflow (Yu et al., 2016a).

We anticipated that similar relationships would be found for vibration magnitude, as schematized in Figure 2B. To test this possibility, we quantified vibration magnitude at each node along the whisker by finding the average angular displacement of the node from its mean position (for details, see Materials and Methods). Results showed that, like bending magnitude, vibration magnitude was greatest at distal, rather than proximal, locations along the whisker length. This result is illustrated for two example nodes on the α whisker in Figure 2C. In this example, the whisker was oriented concave forward into the airflow (orientation angle = 0°), and vibration magnitude is plotted as a function of airspeed for nodes at 40% and 80% out along the whisker length. Airspeed strongly drives the magnitude of vibrations at both nodes, but vibration magnitude is always larger at 80% of the whisker length than at 40% of the length. Similar results were found for all orientation angles and for all whiskers.

Vibration magnitude was found to increase with airspeed for all whiskers tested, as shown in Figure 2D. The figure shows that vibration magnitude increases approximately linearly with airspeed, but that the slopes are different for the different whiskers. Again, based on analogy to results for bending magnitude (Yu et al., 2016a), we anticipated that the whisker's S/D ratio could have a strong influence on vibration magnitude. This relationship is plotted in Figure 2E, showing that vibration magnitude scales approximately linearly with the whisker's S/D ratio. For visual clarity, results are shown for only three airflow speeds, but the linear trend applies to all tested airflow speeds. It is unsurprising that a whisker with a low S/D ratio will vibrate less than a whisker with a large S/D ratio as the stiffness of a conical whisker scales as D to the fourth power.

The orientation of the whisker relative to airflow had only a weak effect on vibration magnitude, and the effect was not consistent across whiskers. Figure 2F plots the vibration magnitude obtained at each orientation of the whisker normalized by the vibration magnitude obtained when the whisker was oriented at 0°. Only the α whisker (F_(4,25) = 3.12, p = 0.0329) and C2 whisker (F_(4,25) = 6.63, p = 0.0009) showed significant changes in vibration magnitude due to orientation (one-way ANOVA with repeated measures). This result stands in contrast to results for bending magnitude, which was found to exhibit a weak but significant dependence on whisker orientation relative to airflow for all whiskers tested (Yu et al., 2016a). The effect of the whisker's orientation angle on vibration magnitude is even weaker and less consistent, with only 4 of 50 pairs of group comparisons showing significant differences (Fig. 2F).

Vibration magnitude scales linearly with bending magnitude, except at extreme values of airspeed

As previously shown in Figure 2B, C, both bending magnitude (θ_bend) and vibration magnitude (φ_vib) increase along the whisker length. The bending magnitude defines the static component of whisker deflection in response to airflow. In contrast, the vibration magnitude quantifies the dynamic component. The bending and vibration magnitudes can be conceptualized as the mean and deviation of the deflection, respectively.

Unsurprisingly, we found that bending magnitude is always much larger than vibration magnitude. For a given whisker, however, their ratio remains approximately constant. An example of bending and vibration magnitudes of the α whisker when stimulated at a single airspeed and orientation is shown in Figure 3A. As shown in the inset, vibration magnitude scales linearly with bending magnitude along the whisker length.

Similar results were found for all other whiskers, orientation angles, and airspeeds, with one notable exception to the constant θ_bend/φ_vib ratio: at the highest airspeed, the vibration magnitude of the largest whiskers tended to saturate, whereas the bending magnitude continued to increase. Thus, their ratio decreased slightly (data not shown).

Regardless of whether cases of high airspeed were omitted or included, the ratio of bending magnitude to vibration magnitude was found to increase weakly with the S/D ratio. This effect is shown in Figure 3B for all five whiskers. The θ_bend/φ_vib ratios of these five whiskers fall between 10 and 16, increasing slightly from D5 to α. As found in previous studies (Belli et al., 2017), the S/D ratio varies systematically as a function of both column and row, so we can expect the Greek arc of whiskers to exhibit the largest bending to vibration ratio, and the most rostral whiskers the smallest ratio.

At low airspeed, whiskers vibrate parallel to the airflow direction, transitioning to perpendicular vibration at high airspeed

Previous work has demonstrated that whiskers always tend to bend in the direction of airflow, regardless of airspeed, whisker geometry, or orientation of the whisker relative to the airflow (Yu et al., 2016a). We quantified vibration direction for each whisker by tracking the position of a node located ∼80% out along its length.

Results shown in Figure 4 reveal that the whisker's vibration direction is more complex than its bending direction. The top row of Figure 4A shows the whisker's vibrations during an airflow stimulus of 0.5 m/s. The position of the node, tracked over time, forms an ellipse with its major axis parallel to the airflow direction. This distribution becomes circular as the airspeed increases to 3.5 m/s (Fig. 4A, middle row), and returns to an elliptical shape at a high airspeed of 5.6 m/s, but with the major axis perpendicular to the airflow direction (Fig. 4A, bottom row).

To quantify the degree to which vibrations were parallel or perpendicular to the direction of airflow, we define the VDI as the ratio of the count of time points in which the whisker node fell in the first and third quadrants, to the count in the second and fourth quadrants. A VDI > 1 indicates that a majority of the vibration direction is perpendicular to airflow, and a VDI < 1 indicates vibration direction is parallel with airflow direction.

We calculated the VDI for all orientations and airspeeds for all five whiskers, for a node 80% out along the whisker length, as shown in Figure 4B. With the exception of the shortest whisker (D5) whose vibration displacements were mostly <100 μm, the VDI increases with airspeed, indicating a shift from parallel vibration to perpendicular vibration as airspeed increases. Interestingly, whisker α, which has the largest S/D ratio (Fig. 2A), exhibits a distinct perpendicular vibration at all airspeeds >2.2 m/s. Although the orientation of the whisker relative to the airflow was found to have some influence on vibration direction, no clear trends were found across whiskers.

To investigate the origin of the vibrations, and the potential causes of the shift in direction, we computed the Re for a set of 519 whiskers with different geometries (Belli et al., 2017). Across all 519 whiskers, the maximum Re (always found at the whisker base, where the diameter is largest) ranged between 1.2 and 8.4 for the lowest airspeed of 0.5 m/s, between 8.3 and 57.1 for an airspeed of 3.4 m/s, and between 13.6 and 94.0 for the highest airspeed of 5.6 m/s. Flow mechanics around flexible and thin bodies is not well understood at these low Re values, but we suggest that the observed whisker vibrations may be at least partially aeroelastic in nature (see Discussion).

Recording the activity of Vg neurons in response to sustained airflow stimulation

Decades of research have used the rodent vibrissal system as a model to study tactile coding and somatosensory processing, and numerous experiments have characterized the responses of primary sensory neurons in the Vg to direct touch (Zucker and Welker, 1969; Gibson and Welker, 1983a,b; Lichtenstein et al., 1990; Shoykhet et al., 2000; Szwed et al., 2003; Jones et al., 2004a, b; Arabzadeh et al., 2005, 2006; Stüttgen et al., 2006, 2008; Szwed et al., 2006; Leiser and Moxon, 2007; Kwegyir-Afful et al., 2008; Lottem and Azouz, 2009, 2011; Chagas et al., 2013; Bush et al., 2016; Campagner et al., 2016; Severson et al., 2017). Evaluating the whisker's mechanical responses to airflow in the context of this wealth of neural data allows us to form a set of expectations for how Vg neurons should respond when stimulated by airflow. We collected a set of extracellular recordings from neurons of the Vg to assess the extent to which they responded in a manner consistent with results from previous studies that have used direct tactile stimulation.

The responses of eight Vg neurons were recorded in response to airflow stimulation delivered at different speeds and from different directions. In these experiments, the head of the anesthetized animal was fixed in position, so airflow direction is defined relative to the animal's head rather than with respect to a single whisker (Fig. 5A). Airflow was directed at the whisker array from three different directions (−45°, 0°, and 45°) and at either two or three different speeds (1, 3, and sometimes 5 m/s). Ten trials were performed for each pairing of airspeed and direction, with care taken to align the center of airflow on the center of the whisker array (Fig. 1). On each trial, airflow was directed for 15 s toward the whisker array, and the whiskers were allowed to return to rest during a 4 s intertrial interval.

Figure 5.

Activity of Vg neurons in response to a sustained airflow stimulus. A, Airflow was directed at the center of the whisker array from three different directions. B, Raster plot of action potentials from a neuron innervating the C2 whisker. Data are shown for all 10 trials obtained with an airspeed of 3 m/s and airflow direction of −45°. C, Peristimulus time histograms for all neurons collapsed across all trials and conditions. Airflow stimulus begins at time = 0 s. Neurons are labeled by the row and column identity of the whisker that they innervate. Data for neurons in the top row have been averaged over 90 trials that included three orientations and three airspeeds (1, 3, and 5 m/s), whereas data for neurons in the bottom row have been averaged over 60 trials that included three orientations but only two airspeeds (1 and 3 m/s). Black histograms have a bin size of 50 ms; red histograms have a bin size of 500 ms. Whisker C2 is the same neuron shown in B.

Vg neurons respond continuously to sustained airflow stimulation while exhibiting some adaptation over the duration of the stimulus

All studies of Vg neurons agree that these neurons have no background firing rate, and are excited only during whisker deflections or motion. In view of these previous studies, we would expect Vg neurons to respond sharply at the onset of airflow, and cease firing quickly after airflow ends.

It is more challenging to use studies of direct tactile stimulation to form expectations for how Vg neurons might adapt to sustained airflow stimulation. Numerous studies have used tactile stimulation to show that Vg neurons can be broadly classified into rapidly adapting (RA) and slowly adapting (SA) cell types given a ramp-and-hold (Zucker and Welker, 1969; Gibson and Welker, 1983a,b; Lichtenstein et al., 1990; Jones et al., 2004b; Lottem and Azouz, 2009, 2011).

However, airflow consists of both slow, constant (bending) and fast, changing (vibration) components, so we would expect both RA and SA type neurons to respond throughout the entire duration of the airflow stimulation. The degree of adaptation will depend on complex interactions between the biophysics of the neuron and the variations in both bending and vibration.

An example of the spike train obtained from one neuron is shown in Figure 5B, for a single air speed and direction (3 m/s, −45°). As expected, the neuron begins to respond at the onset of the airflow stimulus and continues until stimulus offset. A high firing rate is associated with stimulus onset. During the intertrial interval, the neuron is silent.

These results were found for all eight neurons on all trials, as shown in the peristimulus time histograms of Figure 5C. For each neuron, two peristimulus time histograms are shown averaging data across all trials and all conditions: the first on a short time scale (black, bin size = 50 ms), and a second on longer time scale (red, bin size = 500 ms). All neurons exhibit a strong response to stimulus onset, fire continuously during airflow stimulation, and are silent in the absence of stimulation. No neuron ceases firing before the end of the stimulus.

Figure 5C further shows that Vg neurons exhibit a variety of adaptation characteristics in response to airflow stimulation. Some neurons adapted on a time scale <50 ms, as shown in the large peaks of the high-resolution histograms for neurons C3, E3, and γ. Other neurons exhibited a slower relaxation with a duration of many seconds, as evident in the low-resolution histograms for C4 (top row), B3, D3, and C2. Notably, some neurons do not reach a clear steady-state response, even after 15 s of sustained stimulation.

All Vg neurons increase firing rate with airspeed

One characteristic feature of Vg responses is that firing rates increase with increased stimulus magnitude. This strong correlation has been found for both ramp-and-hold stimulation in the anesthetized animal as well as during object contact in electrical whisking and awake exploration (Zucker and Welker, 1969; Gibson and Welker, 1983a,b; Shoykhet et al., 2000; Szwed et al., 2003, 2006; Leiser and Moxon, 2007; Kwegyir-Afful et al., 2008; Stüttgen et al., 2008; Lottem and Azouz, 2011; Bush et al., 2016; Campagner et al., 2016; Severson et al., 2017). In addition, numerous studies have demonstrated that Vg neurons respond strongly to vibrational stimuli, both in the anesthetized and awake animal, with both presumptive SA and RA cells increasing their firing rate to increased vibration magnitude (Jones et al., 2004b; Arabzadeh et al., 2005, 2006; Stüttgen et al., 2006; Lottem and Azouz, 2009).

Our studies of the whisker's mechanical response to airflow have indicated that the bending of each whisker increases linearly with airspeed (Yu et al., 2016a). In addition, Figures 2 and 3 of the present work show that vibration amplitude generally increases linearly with airspeed, scaling directly with the bending magnitude. Thus, as airspeed increases, the whiskers will not only bend more, but also vibrate more. Based on studies of direct tactile stimulation, we would therefore expect Vg activity to increase monotonically in response to higher airspeeds.

We computed the average firing rates for each trial at each airflow condition, and results are plotted in Figure 6. In line with expectations, all neurons increase firing rate with airspeed, for all orientations of the whisker (two-way ANOVA: main effect of airspeed, p < 0.001 for all neurons, D3: F_(2,80) = 1126, p = 2.6e-59; C3: F_(2,80) = 8367, p = 1.2e-93; C4: F_(2,81) = 4612, p = 3.6e-84; B3: F_(2,80) = 1530, p = 1.7e-64; E3: F_(1,54) = 184, p = 4.9e-19; C4: F_(1,54) = 4818, p = 1.7e-54; C2: F_(1,54) = 594, p = 7.9e-31; γ: F_(1,54) = 2447, p = 1.2e-46; group comparisons with Tukey's post hoc test p < 0.05 were asterisked in Figure 6). Firing rates are highly variable across neurons (note the y axis scale differences), and the change in firing rate as airspeed increases also varies considerably. Figure 6 also shows that each neuron's firing rate depends on the airflow direction, an effect explored in more detail in the next section.

Vg firing rate depends on airflow direction, and a neuron's preferred airflow direction can change with airspeed

Vg neurons are well known to exhibit strong directional tuning (Zucker and Welker, 1969; Lichtenstein et al., 1990; Jones et al., 2004b; Kwegyir-Afful et al., 2008). During direct tactile stimulation, the direction in which the Vg neuron responds the most strongly is termed that neuron's “preferred direction.” In analogy to direct tactile stimulation, we designated the airflow direction in which the neuron exhibited the highest firing rate that neuron's “preferred airflow direction.”

To observe the effect of airflow direction on the neural response, we account for the effect of firing rate increases associated with higher airspeeds (as was shown in Fig. 6). Therefore, we normalize each neuron's firing rate by its maximum firing rate at each airspeed. Plotting these normalized firing rates as a function of airflow direction (Fig. 7) clearly shows that all neurons change their firing rate with airflow direction. This result was confirmed with a two-way ANOVA (main effect of direction, p < 0.001, D3: F_(2,80) = 183, p = 1.4e-30; C3: F_(2,80) = 1518, p = 2.4e-64; C4: F_(2,81) = 12.2, p = 2.3e-5; B3: F_(2,80) = 51.5, p = 4.2e-15; E3: F_(2,54) = 470, p = 7.0e-35; C4: F_(2,54) = 161, p = 1.8e-23; C2: F_(2,54) = 11.8, p = 5.5e-5; γ: F_(2,54) = 879, p = 6.4e-42; group comparisons with Tukey's post hoc test p < 0.05 were asterisked in Fig. 7; interaction effect of speed × direction, p < 0.001 for all neurons, D3: F_(4,80) = 157 p = 4.6e-37; C3: F_(4,80) = 806, p = 9.2e-64; C4: F_(4,81) = 8.1, p = 1.6e-5; B3: F_(4,80) = 11.9, p = 1.3e-7; E3: F_(2,54) = 40.0, p = 2.4e-11; C4: F_(2,54) = 15.5, p = 4.8e-6; C2: F_(2,54) = 27.8, p = 4.9e-9; γ: F_(2,54) = 36.3, p = 1.0e-10).

More intriguingly, we found that a neuron's preferred airflow direction can change with airflow speed. For example, for airflow stimulation at 1 m/s, the neuron that innervates the D3 whisker prefers airflow directions of ±45°, and responds only weakly to airflow delivered from a direction of 0°. This direction preference reverses for higher airspeeds at 3 and 5 m/s. The neuron that innervates the C2 whisker exhibits a similar shift in preferred airflow direction with increased airspeed. Moreover, the modulation depth (the degree to which a neuron shows differential responses across directions) is often seen to reduce as airspeed increases. In other words, the tuning of the cell's preferred airflow direction weakens as stimulus magnitude increases. This effect is seen clearly for the neurons that innervate whiskers, C3, B3, γ, D3, and C4 (top).

In light of the present study's finding that vibration direction changes with airspeed (Fig. 4), we suggest that these changes in the neuron's preferred direction might be partially explained by shifts in the main axis of the whisker vibration. That is, as airspeed increases, the whisker vibrates in a different direction, altering the mechanical input to the follicle.

The firing periodicities of Vg neurons are close to whiskers' resonances

The whisker's intrinsic dynamics, which includes its resonant properties, are an essential component of any dynamic behavior that it exhibits, including noncontact whisking (Quist et al., 2014; Severson et al., 2017), collisions (Boubenec et al., 2012; Kan et al., 2013; Quist et al., 2014), and texture-induced vibrations (Arabzadeh et al., 2005, 2006; Ritt et al., 2008; Wolfe et al., 2008). Previous studies using direct tactile stimulation have found large increases in Vg firing rates associated with the mechanical amplification of the whisker's vibrations near its resonance modes (Andermann et al., 2004).

Our previous work has indicated that airflow stimulation causes whiskers to vibrate near their resonance modes (Yu et al., 2016a), and Figures 2 and 3 of the present work further indicate that the magnitude of these vibrations depends on airspeed. Interpreting these mechanical results in light of the previous studies of Vg responses to vibrations (Andermann et al., 2004), we might expect Vg neurons to entrain to the whisker's resonant modes. A caveat, however, is that the resonance modes are extremely broad (Yu et al., 2016a), and the vibration direction changes with airspeed, which shifts the Vg neuron's preferred airflow direction (Figs. 4, 7). Therefore, we can form no strong expectations for the magnitude of this postulated entrainment.

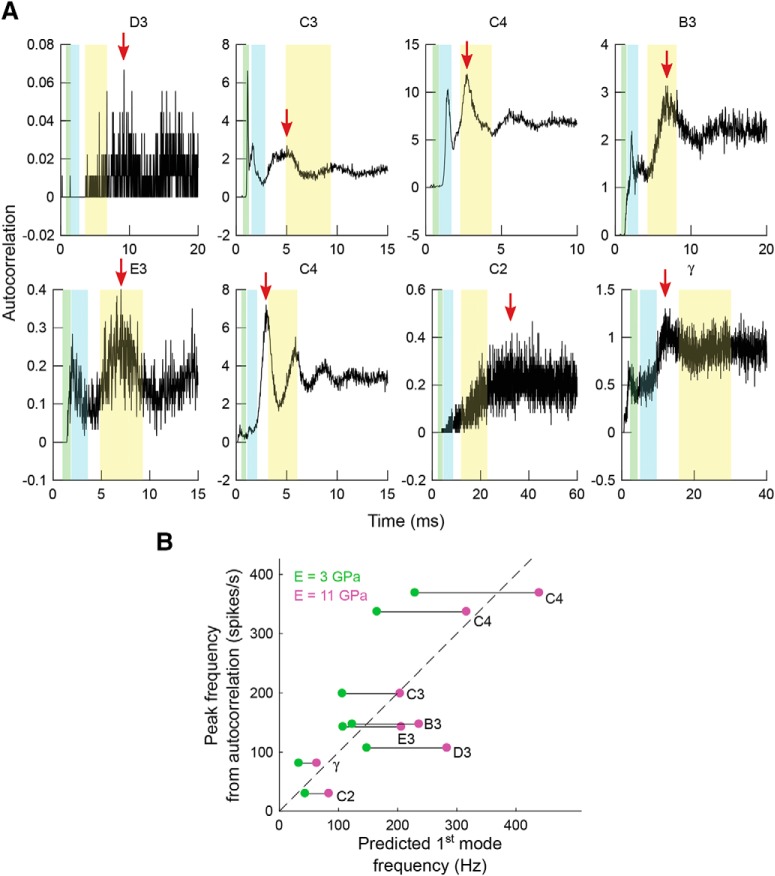
To evaluate the degree to which Vg neurons entrain to the whisker's first resonant mode, we computed the autocorrelation of each spike train for each neuron as a measure of spiking periodicity. Figure 8A shows the autocorrelations of the spike train for each neuron averaged over all conditions and trials. Peaks in the autocorrelation indicate periodicities in the spike pattern. These firing periodicities could result from a neuron's intrinsic cellular dynamics (Hutcheon and Yarom, 2000; Prescott et al., 2008), from the periodicity of the mechanical stimuli (Salinas et al., 2000; Fourcaud-Trocmé et al., 2003), or (most likely) from a complex interaction between neuronal biophysics and the mechanical stimulus.

Figure 8.

The firing periodicities of Vg neurons are related to the whiskers' first-mode resonances. A, Autocorrelation of the spike trains for each neuron across all conditions and trials. Red arrows indicate the peaks of the autocorrelation curves. Shaded regions in yellow, cyan, and green represent ranges for the first, second, and third theoretical resonant modes of the whiskers computed by varying Young's modulus between 3 and 11 GPa. The abscissa has units of time, so the theoretical resonant modes are computed in terms of period, not frequency. B, Relationship between predicted first-mode resonance of the whisker and the observed autocorrelation peak frequency. Dashed line indicates the line of equality. Green and magenta dots indicate the predicted first mode frequency given Young's modulus at 3 and 11 GPa, respectively, and the lines connecting these two dots are the predicted ranges for that neuron.

To determine the extent to which the observed periodicities in the spike trains reflect the vibration of the whisker, we computed the theoretical resonances of the whiskers associated with each neuron (see Materials and Methods). As shown in Figure 8A, the first-, second-, and third-mode resonance ranges are superimposed on the autocorrelation curves, with uncertainty ranges established by varying Young's modulus between 3 and 11 GPa (Hartmann et al., 2003; Neimark et al., 2003; Birdwell et al., 2007; Quist et al., 2011; Kan et al., 2013). The first resonance range (yellow highlight) overlaps with the major peak of the autocorrelation curve for many, but not all, neurons.

We then compared the theoretically predicted first-mode resonant frequency of the whisker (based on the measured whisker shape and mass) with the peaks found from the autocorrelation curves of the neural spike trains. Major peaks in the autocorrelation curves are shown as red arrows for all neurons, except for the neuron that innervated whisker C3. This particular neuron exhibited a unique autocorrelation profile, with the strongest peak close to the third resonance mode with a period of 1 ms (1000 Hz). This large, high-frequency response may indicate that the neuron is firing near its maximal firing rate, with 1 ms representing its refractory period. To appropriately compare this neuron's response with the first-mode whisker resonances predicted from mechanical analysis, we chose the maximum autocorrelation coefficient within the peak closest to the first-mode resonance.

Results of this analysis are shown in Figure 8B. In general, spiking periodicities are close to the theoretical whisker resonances, but responses of some neurons fall outside of the predicted range. These results indicate that the vibrational mechanical stimulus likely contributes to the temporal patterning of Vg neuron spiking but that Vg neurons do not strongly entrain to whisker resonances during airflow stimulation. The weak entrainment likely occurs for three reasons: (1) the resonance modes induced by vibrations are broad (Yu et al., 2016a); (2) the neuron could respond to features of the stimulus other than vibration (e.g., small variations in airflow structure); and (3) the intrinsic properties of the neuron will influence spiking patterns.

Implications for Vg coding of airflow speed and direction

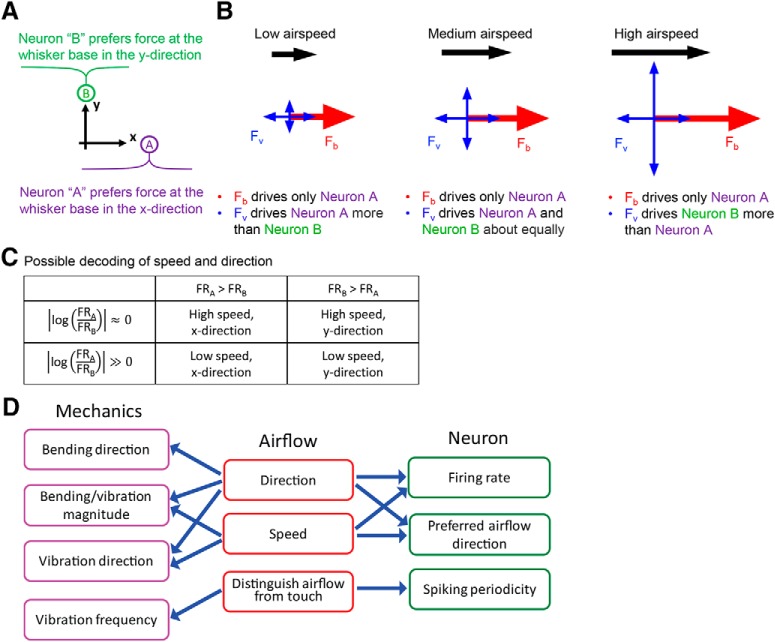
As indicated previously, a whisker will tend to bend in the direction of the wind, regardless of airspeed (Yu et al., 2016a). However, the present study has shown that, in contrast to bending direction, the whisker's vibration direction varies significantly with airspeed (Fig. 4), and that the Vg neuronal response is in part due to this vibration (Figs. 7, 8). Thus, vibration contaminates the airflow direction cue associated with whisker bending.

Figure 9 provides intuition for how airspeed-dependent variations in vibration direction would affect neural responses. The figure schematizes two idealized neurons, A and B, that prefer forces in two orthogonal directions, x and y. The three panels show the forces exerted on the whisker in response to low-, medium-, and high-speed airflow. Assuming that the airflow is in the x direction, the force due to bending (F_b) will drive neuron A because the whisker always bends in the direction of the airflow. Although the magnitude of F_b increases with airspeed, it does not influence neuron B. In contrast, the force due to vibration (F_v) contains components that act in both x and y directions. As airspeed increases, the major axis of vibration direction gradually changes from parallel to the airflow to perpendicular. Thus, at low airspeed, the vibration force primarily affects neuron A; at medium airspeed, both neurons are affected approximately equally; and at high airspeed, the vibration force more strongly drives neuron B. Just as for the bending force, the average magnitude of the vibration force increases with airspeed.

Figure 9.

Idealized forces generated by airflow acting on the whisker. A, Idealized neurons A and B prefer forces in the x and y directions, respectively. B, In all panels, the whisker is imagined to come out of the page. F_b and F_v are the forces exerted by the airflow on the whisker, as they would be measured at the whisker base. These forces represent the combined effect of distributed airflow along the length of the whisker and the way that the whisker's intrinsic mechanical properties filter those forces. F_b indicates force due to bending (a quasistatic force acting solely in the x direction), and F_v indicates force due to vibration (a dynamic term, containing components in both x and y directions). The magnitudes of F_b and F_v both increase with airspeed, but only F_v changes its direction of action. C, A possible two-neuron readout scheme for airspeed and direction. If neurons A (x direction tuned) and B (y direction tuned) exhibit the same response patterns for a given force stimulus, then airflow direction can be determined by comparing which neuron fires more, and speed can be inferred from the ratio of the firing rates. Specifically, with A and B now representing firing rates FR_A and FR_B: if A > B and A/B is small, then airspeed is high in the x direction. If A > B and A/B is large, then airspeed is low in the x direction. If B > A and B/A is small, then airspeed is high in the y direction. If B > A and B/A is large, then airspeed is low in the y direction. If the neurons do not have the same response profile for a given force input, then this scheme still holds, provided the mapping to firing rate is known. The absolute value of the log ensures that the ratio is symmetric with respect to neuron identity (A/B is equivalent to B/A). D, Relationships between the whisker's mechanical response, the physical parameters of airflow, and the responses of primary sensory neurons in the Vg.

If the whisker's vibration in response to airflow were purely random (i.e., without any relationship to airspeed or direction), it would only add noise to the Vg response. However, the whisker's vibration, and thus the neural response, carries significant information about airspeed. Although a single neuron is insufficient to disambiguate direction from airspeed (it cannot be assumed to be able to distinguish the components of F_v from F_b), a population response may suffice. Specifically, as the F_v component perpendicular to airflow increases, the ratio of the forces in the x and y directions, and thus the ratio between the firing rates of neurons A and B decreases. This ratio (Fig. 9C) could be coupled with knowledge of the absolute magnitude of both responses to infer both the speed and direction of the airflow (e.g., if neuron A is firing more than B, then airflow is in the positive x direction, and the speed can be obtained from the ratio of firing rates).

Together with previous descriptions of the whisker's bending and frequency response to airflow (Yu et al., 2016a), the relationships between airflow information, whisker mechanics, and the Vg neural response can be summarized as shown in Figure 9D. Figure 9D (left column) lists the mechanical consequences of airflow. Bending magnitude, vibration magnitude, and vibration direction are related to both airflow direction and speed, whereas bending direction is affected only by airflow direction. Vibration frequency is not strongly affected by these parameters (Yu et al., 2016a).

Figure 9D (right) links airflow information to the Vg neural response. Both the direction and speed of the airflow influence a neuron's average firing rate. Given that the vibration direction changes with airspeed, a neuron might preferentially respond to one airflow direction at low speed and a different airflow direction at high speed. Airflow and touch could be distinguished based on neural response; firing will be sustained and quasiperiodic in response to airflow but would attenuate relatively quickly in response to discrete touch.

We can use the relationships outlined in Figure 9D to link whisker mechanics with the neural response. Larger bending and/or vibration magnitudes in high-speed airflow will tend to generate higher firing rates. Changes of vibration direction with airspeed will alter a neuron's preferred airflow direction, and vibration at a whisker's natural resonance frequency will help drive neural spiking periodicity.

Discussion

Fluid flow sensing in land mammals could aid in several important behaviors, including olfactory search and predator avoidance. We have demonstrated that rats use their whiskers during anemotaxic behaviors (Yu et al., 2016b), and that a whisker's bending response correlates with airflow information (Yu et al., 2016a). The present work is the first characterization of the whiskers' vibrational response and the Vg neural response to airflow.

Mechanical basis driving vibrations

If the whisker did not vibrate in response to airflow, its bending response could be used to uniquely determine airflow speed and direction. Increased airspeed would increase whisker bending, which would increase the firing rate of Vg neurons. The whisker would bend in the direction of airflow, maximally exciting a particular population of Vg neurons best tuned to that direction.

However, whiskers do vibrate in response to airflow; further, the vibration direction changes from parallel to perpendicular as airspeed increases (Fig. 4). Two possible mechanisms could account for these vibrations. Vortex-induced vibrations are expected to occur for Re > ∼40, and will tend to cause the whisker to vibrate perpendicular to the flow direction (Taneda, 1956; Billah and Scanlan, 1991; Williamson and Govardhan, 2004). However, Re calculations indicate that, at airspeeds up to ∼3 m/s, nearly all rat whiskers will be in a regime where Re < 40, suggesting that a second mechanism (i.e., aeroelastic flutter) may be primarily responsible for the parallel vibrations at low airspeeds (Taneda, 1956; Billah and Scanlan, 1991; McKay, 2012). Aeroelastic vibrations are as yet poorly understood but result from positive feedback between the deflection of an object and the forces exerted by fluid flow: the object extracts energy from the airstream through its own motion (Billah and Scanlan, 1991; Abdelkefi, 2016). We therefore suggest that the observed change in vibration direction may represent a transition from a regime dominated by aeroelastic vibrations to one dominated by vortex-induced vibrations. The exact origin of the vibrations and the cause of their directional transition will require further mechanical studies.

Regardless of the physical mechanism, the result is that vibration will cause ambiguity in single-unit Vg coding of speed and direction, which can be resolved when the response of the entire population of Vg neurons is considered (Fig. 9).

Average airflow and the local flow profile

Given that vibrations are a physical consequence of a cantilever exposed to airflow, it seems likely that biology would exploit the information available from vibrations. In contrast to bending, which reflects the low-frequency, time-averaged flow profile, vibrations could provide information about high-frequency changes in local flow structure. This type of spectral division resembles how quasistatic bending information may be used to extract surface contours and shape, with vibrations providing information about texture.

One use for local flow structure is that an animal could potentially determine an object's size or shape based on the “bluff” around the object. Although vortices rapidly dissipate in air, flow past different objects will cause different flow profiles that could be sensed by rodents in a manner analogous to pinniped wake-tracking (Dehnhardt et al., 1998, 2001). Given the close relationship between whisking and sniffing (Moore et al., 2013), local flow structure may also aid in refining olfactory search in rats (Khan et al., 2012; Catania, 2013), as well as in Drosophila (Suver et al., 2019) and lobsters (Park et al., 2014).

Fast vibrations could also help enable rapid escape responses, as do many arthropod flow-sensing hairs (Jacobs, 1995; Catania, 2009; Casas and Dangles, 2010). An important difference, however, is that each arthropod hair tends to rotate at its base as a rigid body (Albert et al., 2001; Magal et al., 2006; Humphrey and Barth, 2007), rather than bend as does a rat whisker. In addition, because arthropod hairs are much shorter than whiskers, they are generally immersed within the boundary layer; the hairs therefore tend to couple mechanically, and a hair's vibration frequency is not dominated by its intrinsic resonance (Humphrey and Barth, 2007). Equally important, arthropods often have distinct hair subtypes: tactile hairs, specialized for touch stimuli, are significantly longer than flow-sensing hairs (Albert et al., 2001; Barth, 2004). In contrast, rat whiskers serve a dual function as touch and flow sensors.

Airflow versus touch stimuli

Given that both airflow and touch cause whiskers to deform in a way that evokes Vg neural firing, an important question is how the animal might distinguish responses due to airflow from those due to touch. The two stimuli differ in several important ways.

During airflow stimulation, all whiskers in the array will bend in the same direction as the airflow. In contrast, a tactile stimulus will cause bending only for those whiskers that are touched, and their bending directions will not necessarily be the same as each other. Whisker curvature, the rat's whisking trajectory, as well as object shape and surface roughness will all jointly cause each whisker to bend and slip in slightly different directions (Solomon and Hartmann, 2008, 2010; Huet et al., 2015; Hobbs et al., 2016; Huet and Hartmann, 2016).

In airflow, a distributed load is exerted along the whisker length, and its magnitude depends on the whisker's diameter and airflow parameters, including Re and airspeed. In touch, however, only a small whisker segment touches an object, and contact is generally intermittent rather than continuous. These two different loading conditions will generate different mechanical signals at the whisker base.

In airflow, all whiskers will simultaneously vibrate near resonance. These vibrations are superimposed on bending and will continue without damping if airflow is sustained. In touch, however, only those touched whiskers will vibrate. A number of parameters, including the whisker's intrinsic dynamics, the contact location along the whisker length, stick-slip, friction, and object surface texture, affect its vibration frequencies (Ritt et al., 2008; Wolfe et al., 2008; Boubenec et al., 2012; Quist et al., 2014; Vaxenburg et al., 2018). Additionally, as the whisker increasingly deflects against an object, these touch-induced vibrations will damp out (Boubenec et al., 2012; Quist et al., 2014; Hobbs et al., 2016). When deflecting past an object edge, whiskers will vibrate near their resonances (just as they do for airflow), but unlike in airflow, these post-touch vibrations will damp and are not superposed on bending. Last, airflow will generate a unique relationship between bending and vibration across the whisker array: longer whiskers will bend and vibrate more than shorter whiskers but will vibrate at lower frequencies. Touch stimuli will not generate this systematic relationship across the array.

Characterization of Vg neuron responses to airflow stimuli compared with touch

Neural encoding of vibration and bending has been well studied at many levels of the trigeminal pathway using direct tactile stimulation; vibrissal deformation induces mechanical signals that are encoded by primary sensory neurons of the Vg. Vg neurons have high temporal bandwidth and respond strongly to both bending and vibration (Gibson and Welker, 1983a,b; Lichtenstein et al., 1990; Shoykhet et al., 2000; Jones et al., 2004a,b; Arabzadeh et al., 2005, 2006; Stüttgen et al., 2006, 2008; Szwed et al., 2006; Leiser and Moxon, 2007; Kwegyir-Afful et al., 2008; Lottem and Azouz, 2009, 2011; Chagas et al., 2013).

Given that rats can and do rely on their whiskers to localize airflow sources, we expected Vg neurons to encode information about airflow stimulus. We further expected responses to be analogous to those obtained during tactile stimulation, as the underlying driver of neural responses (i.e., mechanics at the whisker base) ought to be grossly comparable between touch and airflow stimulation.

This expectation was supported by a small set of Vg neural responses; all neurons responded robustly to airflow but had widely varying maximum firing rates (between 8 and 120 spikes/s) and varying degrees of adaptation (Fig. 5). All neurons increase firing rate with airspeed, consistent with both the increased bending and vibration magnitude associated with higher airspeed. In addition, a neuron's preferred airflow direction can change with airspeed, possibly because the whisker vibrates in a different direction at different airspeeds. Finally, neurons exhibit periodicities in their firing rate related to the predicted resonance frequency for their associated whisker.

This small set of recordings describes the major stimulus–response relationships that lay the groundwork for understanding neural representations of airflow. Comprehensive descriptions of airflow encoding by Vg neurons will require precise (and currently impractical) quantification of 3D whisker motion during neural recording, in addition to a larger sample of neurons. High precision measurements of whisker motion will be required to distinguish small differences in response types across whiskers, and to investigate how the fast whisker dynamics relate to spiking. With the limited stimulus quantification available, we have characterized some primary response characteristics with a small sample; further investigation of this modality is better served when stimulus quantification is improved.