Antagonistic selection and pleiotropy constrain the evolution of plant chemical defenses

Abstract

When pleiotropy is present, genetic correlations may constrain the evolution of ecologically important traits. We used a quantitative genetics approach to investigate constraints on the evolution of secondary metabolites in a wild mustard, Boechera stricta. Much of the genetic variation in chemical composition of glucosinolates in B. stricta is controlled by a single locus, BCMA1/3. In a large-scale common garden experiment under natural conditions, we quantified fitness and glucosinolate profile in two leaf types and in fruits. We estimated genetic variances and covariances (the G-matrix) and selection on chemical profile in each tissue. Chemical composition of defenses was strongly genetically correlated between tissues. We found antagonistic selection between defense composition in leaves and fruits: compounds that were favored in leaves were disadvantageous in fruits. The positive genetic correlations and antagonistic selection led to strong constraints on the evolution of defenses in leaves and fruits. In a hypothetical population with no genetic variation at BCMA1/3, we found no evidence for genetic constraints, indicating that pleiotropy affecting chemical profile in multiple tissues drives constraints on the evolution of secondary metabolites.

Introduction

The accelerating ability to map genetic loci has revealed the prevalence of pleiotropy affecting many traits of interest, including evolutionarily important traits in natural populations, crop disease resistance and yield, and human diseases (Conner 2002; Shi et al. 2009; Sivakumaran et al. 2011; Wisser et al. 2011; Lovell et al. 2013; Pickrell et al. 2016). Genetic correlations caused by pleiotropy can constrain the evolutionary responses of populations to the selective pressures they experience (Lande 1979; Lande and Arnold 1983). Combining traditional quantitative genetics approaches to testing for constraints with an understanding of causal loci has the potential to give new insight (Kelly 2009). Here, we investigate the role of genetic correlations and pleiotropy in constraining the evolution of secondary metabolites in leaves and fruits.

Many species interactions involve multiple traits; this is even more true in the case of diffuse interactions involving a number of species. In antagonistic interactions, such as parasitism, herbivory, or disease, organisms may be under strong selection to evolve resistance; however, effective defenses against all enemies may not be possible. In some cases, such as between herbivores and pathogens, defense responses can be antagonistic (Glazebrook 2005; Thaler et al. 2012). Herbivore species also vary in their reactions to defenses; altering the composition of the insect community can drastically change selection on host defenses (Lankau 2007). Sometimes, chemicals that defend effectively against generalist insect herbivores are the very cues that specialists use to find their hosts (Renwick et al. 1992; Roessingh et al. 1992; Sun et al. 2009). Thus, selective pressures on the chemical composition of defenses may be complex, and vary depending on specific community contexts.

Herbivore and pathogen communities may vary not just between populations, but also among the tissues of a single individual. Some herbivores feed on many parts of the plant, while others specialize on a specific tissue. Both the herbivore community and the presence of certain plant tissues may change seasonally as well (Evans and Murdoch 1968; Janzen 1973; Wolda 1988), so that some combinations may not co-occur. Thus, different tissues on a single plant often interact with partially overlapping communities of herbivores (e.g. Wise and Rausher 2013). As the herbivore community affects the selective regime on chemical defenses, different chemical profiles may be favored in different tissues.

Like many other traits, defenses, both chemical and physical, are not homogeneous within a plant (Nitao and Zangerl 1987; Zangerl and Rutledge 1996; Ohnmeiss and Baldwin 2000). For glucosinolates, the primary defensive compounds found in the Brassicaceae, concentration and composition have been shown to vary among tissue types (Brown et al. 2003; Strauss et al. 2004; Bellostas et al. 2007; Velasco et al. 2008; Keith and Mitchell-Olds 2017). Glucosinolates are not manufactured independently in each tissue; long-distance transport of glucosinolates and precursors has been documented in Arabidopsis thaliana (reviewed in Halkier and Gershenzon 2006; Jørgensen et al. 2015; Burow and Halkier 2017). Thus, glucosinolate concentration and composition is potentially determined by precursor availability in source tissues, selection of compounds for transport, and the later modifications in the sink tissue (Halkier and Gershenzon 2006; Jørgensen et al. 2015). Given this complex interaction of factors, it is likely that glucosinolate profiles in different tissues are not independent, and genetic controls are overlapping among tissues.

When traits share genetic controls, genetic correlations are likely. If genetic covariances are present, selection on one trait may exert indirect selection on another (Lande 1979; Lande and Arnold 1983). Depending on the direction of the genetic covariance and the selection acting on each trait, covariances may speed up (facilitate), slow down (constrain) or have no effect on a population’s approach to the evolutionary optimum (Agrawal and Stinchcombe 2009; Conner 2012). The structure of the genetic variances and covariances is summarized in the G-matrix (Lande 1979; Lande and Arnold 1983). The effects of the G-matrix on the evolution of a population can be studied using the multivariate breeder’s equation, which states that G * β = $\mathbf{\Delta }\overline{z}$; that is, the vector of the responses to selection ($\mathbf{\Delta }\overline{z}$) is equal to the G-matrix multiplied by the vector of selection gradients (β). Thus, in order to understand the effects of the G-matrix on the evolution of a population, we must measure the genetic variances and covariances and the selection gradients acting on the traits (Smith and Rausher 2008; Agrawal and Stinchcombe 2009; Wise and Rausher 2013).

The G-matrix itself evolves in response to selection, and constraints will not prevent a population from reaching the evolutionary optimum unless there is a complete absence of genetic variation in the direction of selection (Conner 2012). Rather, constraints are expected to slow the response to selection, which may be important when evolutionary optima change frequently (Jones et al. 2012). Plant-herbivore interactions may result in just such rapid shifting of selective regime; changes in the composition of the insect community may change selective pressures on defenses (Lankau 2007), sometimes as rapidly as one year to the next (Strauss and Irwin 2004). G has been shown to diverge between populations or closely related species, sometimes within the span of a few generations (Shaw et al. 1995; Beldade et al. 2002; Frankino et al. 2007; Doroszuk et al. 2008; Conner et al. 2011; Delph et al. 2011; Björklund et al. 2013; Paccard et al. 2016; Uesugi et al. 2017), although this is not always the case (Puentes et al. 2016; Delahaie et al. 2017). Contrasting herbivore regimes produced divergence in the G-matrix for secondary metabolites in Solidago after only 12 years (Uesugi et al. 2017). The durability of a constraint under selection is dependent partially on the genetic architecture of the traits. Although linked genes may cause correlations, such linkage disequilibrium (LD) declines with every generation, so these effects will be transient (Falconer 1996). Very tight linkage or pleiotropy are necessary to maintain correlations over longer periods of time (Clark 1987; Falconer 1996), although even in the case of pleiotropy constraints may not persist against selection (Conner et al. 2011).

The number and effect size of pleiotropic genes are also predicted to affect the evolution of correlations (Agrawal et al. 2001; Kelly 2009). Most of the work on genetic correlations and constraints has assumed a model of many loci, each of small effect (Lande 1979; Lande and Arnold 1983). When traits are instead controlled by loci of large effect, behavior of genetic correlations may differ. With large-effect loci, rapid and transient changes in genetic correlations are likely (Carrière and Roff 1995; Agrawal et al. 2001). When pleiotropic genes have large effects, they are also more likely to produce maladaptive trait combinations (Carriere et al. 1994; Agrawal et al. 2001). Theoretical predictions and mounting evidence, however, have demonstrated a number of cases in which quantitative traits are partially controlled by one locus of large or moderate effect, with additional loci of smaller effect contributing further variation (Stinchcombe et al. 2004; Stinchcombe et al. 2009; Lee et al. 2014; Zoledziewska et al. 2015). Given that such genetic architecture seems to be common, it is important to understand how traits influenced by large-effect genes may evolve.

Here, we investigate whether the evolution of defenses in different plant tissues is constrained by genetic covariances in defense profile. We tested this in Boechera stricta, a wild relative of Arabidopsis. Like many species in the Brassicaceae, B. stricta manufactures glucosinolates, which influence plant-herbivore interactions in many species (Hopkins et al. 2009), including B. stricta (Prasad et al. 2012). Both glucosinolate concentration and chemical composition (“glucosinolate profile”) vary genetically among individuals as well as within plants (Prasad et al. 2012; Keith and Mitchell-Olds 2017). B. stricta has four major types of aliphatic glucosinolates. Unlike other relatives of Arabidopsis, Boechera manufactures glucosinolates that are derived from branched-chain amino acids (BC-GS), as well as Met-GS derived from methionine (Windsor et al. 2005). The proportion of BC glucosinolates (BC-ratio) affects herbivore damage and fitness under natural conditions, making it an evolutionarily important trait (Prasad et al. 2012). A single locus on chromosome 7, BCMA1/3, consists of a tandem duplication encoding two P450 enzymes controlling Branch Chain vs. Methionine Allocation (Prasad et al. 2012). Identified in two crosses, this locus causes bimodal variation in leaf BC-ratio; homozygous BC genotypes make variable amounts of BC-GS, while homozygous Met genotypes make predominantly Met-GS (Prasad et al. 2012). Among the BC genotypes, additional heritable variation produces a continuous distribution of BC-ratio. The genetic architecture of BC-ratio follows a pattern also seen in flowering time in Arabidopsis, where one allele at a gene of major effect masks quantitative background variation (Stinchcombe et al. 2004). Two previous crosses have shown that the BCMA1/3 locus controls BC-ratio (Prasad et al. 2012). A Genome Wide Association Study (GWAS) shows that BCMA1/3 controls BC-ratio in both leaves and fruits across the species range in the Western USA (Mojica et al., in prep.). B. stricta displays low levels of LD, decaying to background levels in < 50 kb (Song et al. 2009), so effects of the BCMA1/3 region are likely due to pleiotropy rather than LD with flanking sequence.

We investigated two questions: is the evolution of chemical defenses constrained across multiple plant tissues, and, if so, how does genetic correlation constrain the response to selection? We quantified glucosinolate profile in rosette leaves, cauline leaves, and fruits of 98 genotypes (self-pollinated maternal families) from a single valley, and used a large common-garden experiment to estimate selection on glucosinolate traits in each tissue. We found conflicting patterns of selection on BC-ratio in leaves vs. fruits, resulting in evolutionary constraints and predicted maladaptive change in leaves. These constraints are likely driven by BCMA1/3, suggesting that a pleiotropic gene of large effect can constrain the evolution of defenses throughout the plant.

Methods

Experimental protocol

Study system

Boechera stricta, a relative of Arabidopsis, is a model system for evolutionary genetics (Rushworth et al. 2011; Lee et al. 2017). B. stricta occurs in the western United States, in environments ranging from sagebrush prairie to alpine meadows (Rushworth et al. 2011). B. stricta is predominantly self-pollinating, and endogenous plants are naturally inbred (Rushworth et al. 2011). A short-lived perennial, B. stricta overwinters as a rosette. In a growing season, a plant may enter a reproductive phase, growing a bolting stalk that bears the cauline leaves, flowers, and fruits. A diverse range of herbivores feed on many tissues of the plant (personal observation).

One of the key defenses in B. stricta is glucosinolate compounds. In the population in which this work was completed B. stricta manufactures four types of aliphatic glucosinolates; an individual produces one to four compounds. BCMA1/3 controls much of the variation in allocation between Met-GS and BC-GS (Prasad et al. 2012). Glucosinolates vary among tissues both in total concentration and BC-ratio (Keith and Mitchell-Olds 2017).

Site

Experimental plants were grown in a common garden in central Idaho, USA (44° 10’ 55.28” N, 113° 44’ 20.49” W). This area has been relatively undisturbed for approximately 3,000 years (Brunelle et al. 2005). The garden was located at 2,530 meters elevation, in a sagebrush meadow. The site was used under permit from the Salmon-Challis National Forest Service.

Experimental design

Seeds were collected from naturally inbred endogenous plants growing in the valley near the common garden. The collection area covered approximately 12 square kilometers and sites ranged from 2300 meters to 2880 meters elevation. To avoid collecting clonal replicates, collections were spaced a minimum of 3 meters apart. The habitats of the collections included sagebrush meadows, riparian areas, and alpine forests and meadows. Genotypes were grown for a generation in the greenhouse to minimize maternal effects. 100 accessions were randomly chosen from the collections for inclusion in this experiment.

Plants were germinated and transplanted into the common garden the summer before data collection, as overwintering in the natural environment increases synchronization with endogenous plants. For germination, seeds were placed in petri dishes and kept in the dark for 3 days before being transferred to a growth chamber with 14 hours of light at 20 degrees for 7 days. We transplanted the seedlings into 2.5 cm × 12 cm plastic “conetainers” (Stuewe and Sons, Inc.), and grew them in the Duke University greenhouse for ten weeks. In June of 2014 and 2015 (referred to as the 2015 and 2016 cohorts, respectively), plants were transported to Idaho, USA via overnight shipping. We planted them in the common garden in randomized blocks of 100 plants, divided into sub-blocks of 50 for easier access. Each block had one individual of each genotype. Individuals were planted directly into the surrounding vegetation, 10 cm apart. We watered plants immediately after transplanting and continued watering every 7–10 days through early August, in order to help establishment. After August, plants were dependent on natural moisture. The 2015 cohort was 3,000 plants, and the 2016 cohort was 2,000. We collected data in June-August of the year following transplanting.

Herbivory and fitness censuses

During summer we censused plants during the growing season, scoring height, density of surrounding vegetation, disease severity, herbivore damage, fruit number, and plant stage. Due to mortality, data were analyzed for 98 of the 100 genotypes. Height was measured as distance from the ground to the tallest living part of the plant. Plant stage was defined as dead, rosette, bolting, flowers only, flowers and siliques, or siliques only. Vegetation density (Veg) was scored as percentage of ground cover for a ten-centimeter square around the focal plant. “Top-chewed-off” (TCO) was scored as a binary, 1 if the entire top of the plant had been removed, 0 if it had not. Disease severity was scored using the Schreiner Scale (Schreiner 1959). We scored disease severity on the most heavily infected leaves as light (score = 1), medium (score = 5), or heavy (score = 25). Leaves were categorized as light if they had only a small amount of visible pathogen; medium if they had higher amounts of pathogen present but still appeared functional; and high if the leaves were covered with the pathogen and shriveled. Then we estimated the percentage of leaves that were infected and assigned them to bins, which were <25% (score = 1), 26–50% (score = 2), 51–75% (score = 3), or >75% (score = 4). The two scores were multiplied to produce the final Schreiner score, which ranges from zero (no disease) to one hundred (heavy disease on >75% of the plant).

Herbivore damage was estimated separately for rosette leaves, cauline leaves and fruits. Damage was estimated as the total percentage of each tissue that was removed. We counted the total number of leaves/fruits, the number that were damaged, and the average percentage of tissue removed on the damaged leaves/fruits. The total percent damaged was calculated as (number damaged*percent removed)/total leaf number. Leaf herbivory was censused in late June in 2015 and mid-July in 2016, at approximately peak herbivory. Herbivore damage is visible after it occurs, but the leaves senesce mid-way through the growing season; we timed our census to capture maximum possible damage while most of the leaves were still alive. Fruit damage and fitness were censused in late July, when fruits were mostly mature. Fitness was estimated using fruit number, adjusted for the percentage of fruits removed by herbivores; greenhouse studies in B. stricta indicate that fruit number is a good proxy for seed numer (Anderson et al. 2012). When fruits had been removed partially or entirely by herbivores, the remaining part of the fruit or the stalk made it evident; thus, we estimated the percentage of the fruits removed, multiplied it by the number of fruits, and subtracted the missing amount from the total fruit number observed to account for herbivory. Although B. stricta does experience seed predation by larvae within the fruit, these insects are rare at this experimental site (Keith, unpublished data), suggesting that loss of entire fruit tissue was the main source of seed loss.

HPLC

Samples for glucosinolate analysis were collected from experimental plants in the common garden. We collected rosette leaf, cauline leaf, and fruit samples from three flowering or fruiting individuals of each genotype in each cohort, survival permitting. We collected from plants that were reproducing, and preferentially chose plants that had low levels of disease (Schreiner Score ≤ 15); within those constraints, plants were chosen randomly. Plants with low levels of disease were preferred, as heavily diseased plants often had dry or shriveled leaves, which were not suitable for extracting glucosinolates. If there were not three appropriate plants of a given genotype, we collected from as many as were available. Healthy leaves were collected immediately following herbivory censuses, in late June in 2015 and mid-July of 2016. Fruit samples were collected in late July from immature fruits. In 2015, we collected a total of 275 rosette leaves, 269 cauline leaves, and 256 fruits; in 2016, 247 rosette leaves, 276 cauline leaves, and 233 fruits. In 2015, there were 167 individuals from which we collected all three tissues; in 2016, 159 individuals.

Glucosinolates were quantified using high pressure liquid chromatography, following Prasad et al. (2012). Briefly, glucosinolates were extracted into methanol via leaching for 4 weeks. Glucosinolates were then isolated by washing samples through a DEAE ion exchange column (Sigma-Aldrich, St. Louis, USA), incubation with sulfatase, and elution with water. Purified sinigrin was used as an internal standard. High pressure liquid chromatography was then used to quantify individual glucosinolate compounds in each sample (as in Schranz et al. 2009; Prasad et al. 2012). Samples with irregular peaks were re-run, and excluded if the second run performed poorly (e.g., no peaks, no peak for the standard, or irregular peaks indicating contamination; a total of 45 samples were excluded). Glucosinolate compound concentration was calculated using relative response factors (RRF) (Brown et al. 2003), which were 1.0 for all compounds except 2OH1ME, which has an RRF of 1.32. We calculated the total quantity of each glucosinolate compound using the formula [(0.05 micromole sinigrin) * (area of peak for compound x)]/[(area of sinigrin peak) * (RRF)]. Total concentration in micromole/mg (ConGS) was calculated by dividing the total quantity of glucosinolates by the dry weight of the sample. Glucosinolate traits are reported by tissue; ConGS-R, ConGS-C, and ConGS-F and BC-ratio-R, BC-ratio-C, and BC-ratio-F (concentration and BC-ratio in rosette leaves, cauline leaves and fruits, respectively).

Statistical analyses

Twenty-nine individuals were removed from the dataset due to conflicting stage data indicating an error in censusing. All traits except fitness were standardized to a mean of zero and standard deviation of one. Relative fitness was calculated by dividing fruit number (corrected for damage) by the mean of the population. Standardized traits and relative fitness were used for all subsequent analyses.

Selection

Selection on glucosinolate traits was calculated using a standardized phenotypic-selection analysis (Lande and Arnold 1983). For this analysis we were interested in the fecundity component of fitness in plants that did not suffer major destruction, and so excluded plants that were TCO. Using the lme4 package in R (Bates et al. 2015), we performed multiple linear regression of fruit number on glucosinolate traits and covariates. The complete model was Relative fitness = ConGS-R + BC-ratio-R + ConGS-C + BC-ratio-C + ConGS-F + BC-ratio-F + Cohort + Veg + Stage + Schreiner + Block[Cohort] + Genotype. Block and Genotype were random effects. The regression coefficients from this model provide selection gradients for each trait. The final sample size was 326 individuals, and included 98 families. The variance inflation factors (VIFs) for each effect in the regression were calculated in JMP 13. To investigate potential effects of multicollinearity, we repeated the regression analyses with each glucosinolate trait eliminated in turn.

The difference between the selection gradients of two traits, BC-ratio-C and BC-ratio-F, was of additional interest. Using a custom R script, we performed a permutation test of whether the estimate for BC-ratio-F was significantly different than that for BC-ratio-C. For each of 2,000 permutations, we randomized the BC-ratio values between tissues for each individual. Using the randomized values, we recalculated the selection gradients for each trait, and the difference between them in each permuted dataset. The P-value for this two-tailed test was calculated as the proportion of the permutation results that were less than the observed difference, with two-tailed significance thresholds of P = 0.025.

As glucosinolate samples for leaves and fruits could only be obtained from plants that survived and reproduced, our selection gradients did not account for a potential “invisible fraction” effect, which may mislead fitness estimates (Bennington and McGraw 1995; Nakagawa and Freckleton 2008; Mojica and Kelly 2010). To investigate whether GS traits affected survival, bolting or TCO occurring before sampling, we tested whether the genotype least square means for glucosinolate traits in the sampled plants predicted the percentage of survivors or reproductive plants among the complete cohort. Genotype LS means for each glucosinolate trait were calculated in JMP12 using REML. The model that we used was GS trait = Genotype + Cohort + Block + Schreiner Score + Stage + Height + Veg (N = 317). We used a custom script in R (R Core Team 2016) to calculate the percentage of individuals that survived (N₂₀₁₅ = 2,972, N₂₀₁₆ = 2,000), the percentage of survivors that bolted (N₂₀₁₅ = 2050, N₂₀₁₆ = 1047), and the percentage of those that bolted that had their tops chewed off (TCO) for each genotype in each cohort (N₂₀₁₅ = 779, N₂₀₁₆ = 1047). We then asked whether each glucosinolate trait predicted rates of survival, bolting, or TCO in each cohort. With Bonferroni correction for six independent tests (three traits in two cohorts), our significance threshold was P < 0.00833.

We used early-season stage data from the 2015 cohort to investigate whether phenology affected glucosinolate profile. Stage was first recorded in June, when reproductive plants were bolting (pre-flowering), flowering, or fruiting. Using JMP, we tested whether early-season stage affected each glucosinolate trait at the time of tissue collection. The model was GS trait = Genotype + Block + Schreiner score + Early Stage + Veg, with genotype and block as random effects.

Glucosinolates and interactions

To better understand the selective forces acting on glucosinolates, we tested whether ConGS and BC-ratio in each tissue affected herbivory on these tissues. We did not limit the test to only the glucosinolate profile of the tissue in question, as glucosinolate concentration in one tissue may potentially affect herbivory on another. Thus, every model included ConGS and BC-ratio in each tissue. We calculated genotype least square means for herbivore damage using the same model as above for the glucosinolate means. We then tested whether genotype means for glucosinolate traits predicted mean damage on each tissue (N = 98 families). As we ran three separate models for damage on each tissue, we used Bonferroni correction with significance threshold of P < 0.0167.

We also investigated whether glucosinolate profile affected disease severity. We collected samples only from individuals with low disease severity, and so could not effectively look at the effects of glucosinolates on disease using individual data. Instead, we calculated the genotype LS means for disease severity, using block, cohort, stage and veg as covariates (N = 2148); we did not use height as a covariate since disease may decrease overall growth. We used the genotype LS means for glucosinolates and disease severity to ask whether any of the six glucosinolate traits predicted disease severity (N = 98 families).

Geographical patterns

We tested whether there was spatial structure for glucosinolate profile across the valley where genotypes were originally collected. We quantified the position of the parental plant based on distance in meters north and west from an origin point. We used genotype least square means from BC-ratio-C as the response for a REML model in JMP, with the distance north (equivalent to scaled latitude), the distance west (equivalent to scaled longitude) and elevation as the effects (N = 98 families).

Estimating the G-matrix and the response to selection

We constructed a G-matrix that included ConGS and BC-ratio in rosette leaves, cauline leaves, and fruits. Two G-matrices were compared; one was composed of variance and covariance components, while the other was variances and covariances of line means. Use of covariance components eliminates effects of shared environmental variance, which can inflate estimates of genetic covariances from line means; however, covariance components are much more computationally intensive to calculate.

Genetic variance components were estimated in JMP12 from the variance component for genotype in the model Trait = Cohort + Block + Genotype + Stage + Schreiner Score, with Block and Genotype as random effects and cohort, stage, and Schreiner score as fixed effects. The significance was determined by significance of Genotype in the model. A Bonferroni correction for six tests gave a significance threshold of P < 0.0083. Genetic covariance components were estimated using a SAS script, which calculated the covariance parameters for each pair of glucosinolate traits. Significance of these covariances was calculated by constraining the covariance to zero and using a likelihood ratio test (N = 328).

Genetic variances and covariances were calculated using line means for each glucosinolate trait and the covariates, using a custom R script (N = 98 families). We compared the matrices from each method and found that covariance estimates were highly similar between the two methods (Supplementary Table 1). Given this similarity, we concluded that shared environmental variance had minimal effects on the genetic covariances calculated from line means; as calculating the covariance components was computationally intensive and infeasible for the bootstrapping analyses, further analyses and the results reported here used (co)variances of line means.

The vector of predicted responses to selection, $\mathbf{\Delta }\overline{z}$, was calculated by multiplying the estimated G-matrix with the selection gradients, β (Lande 1979). In order to test for the effects of genetic covariances on the evolution of GS traits, we manually constrained the genetic covariances to 0 to generate G_nc. G_nc was multiplied by β to generate $\mathbf{\Delta }{\overline{\mathit{z}}}_{\text{nc}}$, the predicted response to selection in the absence of genetic covariances. We calculated the Euclidean lengths of vectors $\mathbf{\Delta }\overline{z}$ and $\mathbf{\Delta }{\overline{\mathit{z}}}_{\text{nc}}$ to obtain the magnitude of the responses to selection with or without genetic covariances, R and R_nc, respectively. These represent the amount of change in the next generation; if R < R_nc, this indicates a smaller amount of change when genetic covariances are present, suggesting that the covariances constrain evolution (Smith and Rausher 2008; Agrawal and Stinchcombe 2009; Conner 2012; Wise and Rausher 2013). Conversely, if R > R_nc, this suggests that the genetic covariances are facilitating the response to selection, that the population evolves more rapidly because of them. This measurement does not consider the direction of the response, only the total amount of change.

We used bootstrapping to test whether the difference between $\mathbf{\Delta }\overline{z}$ and $\mathbf{\Delta }{\overline{\mathit{z}}}_{\text{nc}}$ was statistically significant. For each of 2,000 iterations, we re-sampled, with replacement, the families and then the individuals within each sampled family. We then estimated β, G, and G_nc for each bootstrap sample. We then calculated $\mathbf{\Delta }\overline{z}$ and _{$\mathbf{\Delta }{\overline{\mathit{z}}}_{\text{nc}}$} for each bootstrap sample and used them to calculate bootstrap values of R and R_nc.

To determine whether the original values of $\mathbf{\Delta }\overline{z}$ and $\mathbf{\Delta }{\overline{\mathit{z}}}_{\text{nc}}$ were significantly different, we used a discriminant function analysis (DFA) approach in R, using the package MASS (Ripley 2002). The $\mathbf{\Delta }\overline{z}$ and $\mathbf{\Delta }{\overline{\mathit{z}}}_{\text{nc}}$ vectors from each bootstrapped result represent a pair of points in 6-dimensional space. The results of the bootstrapped datasets give a set of 2,000 pairs of points for $\mathbf{\Delta }\overline{z}$ and $\mathbf{\Delta }{\overline{\mathit{z}}}_{\text{nc}}$. To test whether these sets of points differed significantly, we first used DFA to calculate a trait axis from the center of the cloud of points of $\mathbf{\Delta }\overline{z}$ to the center of the cloud of points of $\mathbf{\Delta }{\overline{\mathit{z}}}_{\text{nc}}$. Next, for each pair of points from a bootstrap sample, we used the eigenvector for the first DFA axis and projected the paired points $\mathbf{\Delta }\overline{z}$ and $\mathbf{\Delta }{\overline{\mathit{z}}}_{\text{nc}}$ onto the trait axis, and took the directional difference between these projected values. To infer statistical significance, we then asked whether the 95% confidence interval of the distribution of the differences included zero. If it did not, we concluded that $\mathbf{\Delta }\overline{z}$ and $\mathbf{\Delta }{\overline{\mathit{z}}}_{\text{nc}}$ were significantly different in at least one dimension. Following that multivariate comparison, subsequent univariate analyses were conducted, testing whether the 95% confidence interval of the distribution of the difference $\text{Δ}{\overline{z}}_i$ and $\text{Δ}{\overline{z}}_{i\text{nc}}$ included zero (Scheiner and Gurevitch 2001).

We tested whether covariances affect the magnitude of the response to selection by calculating the absolute difference between R and R_nc for each bootstrap sample; that is, whether covariances affected the total amount of predicted change. In addition to the total length of R and R_nc, we made two comparisons for the responses for each trait individually. First, for each bootstrap sample we calculated the univariate difference between $\text{Δ}{\overline{z}}_i$ and $\text{Δ}{\overline{\mathit{z}}}_{\text{nc}i}$ for the trait to test whether the covariances altered responses to selection. Second, we calculated the absolute difference (i.e., the Euclidian distance) between $\text{Δ}{\overline{z}}_i$ and $\text{Δ}{\overline{\mathit{z}}}_{\text{nc}i}$ vectors, to test whether the total magnitude of change for the trait was affected by the covariances. For significance of both the total magnitude and trait-specific tests, we used a two-tailed test of whether the 95% bootstrap confidence interval of the distribution of differences included zero. If more than 97.5% of the results for |R|-|R_nc| were < 0, we concluded that genetic covariances constrained the response to selection; if more than 97.5% were > 0, we concluded that genetic covariances facilitated evolution. We also performed a similar analysis for each trait individually, asking whether the distribution of $\left|\text{Δ}{\overline{z}}_{\text{i}}\right|-\left|\text{Δ}{\overline{z}}_{nci}\right|$ for a given trait included zero.

Testing between-tissue covariances

The above analysis tested the effects of the complete set of covariances; we also wanted to distinguish the effects of just the covariances between BC-ratio in each tissue. To do this, we repeated the above analyses, except that the only covariances that were constrained to zero while calculating $\mathbf{\Delta }{\overline{\mathit{z}}}_{\text{nc}}$ were those between BC-ratio-R, BC-ratio-C, and BC-ratio-F. Otherwise, the analysis was the same.

BC subpopulation

To consider a hypothetical population of only genotypes that produced BC-GS compounds, we excluded genotypes that had, on average, BC-ratio < 0.15. During the HPLC process small peaks may be erroneously called as minimal amounts of glucosinolates, preventing a complete absence of BC-GS; however, there was a clear discontinuity between BC-ratio ≤ 0.15 and BC-ratio ≥ 0.30. Using this restricted BC population, we repeated the analyses that had been performed on the whole population.

Results

Field

Of the 3,000 individuals in the 2015 cohort, 2,050 survived until data collection; of the 2,000 individuals in the 2016 cohort, 1,047 survived. The primary cause of mortality appeared to be drought, likely in the preceeding fall and winter; some blocks were also affected by burrowing mammals that buried plants. In 2015, 909 plants bolted; in 2016, it was 319. Rosette leaves experience an average of 9.0% herbivore damage; cauline leaves were on average damaged by 13.7%, and fruits by 4.4%. The primary type of herbivore damage that we observed was tissue removal by chewing herbivores. Unexpectedly, both cohorts experienced high frequencies of visible microbial infection, which had not previously been observed in that garden. Similar disease on neighboring endogenous plants was identified as powdery mildew and downy mildew (Posy Busby, personal communication).

BC-ratio in each tissue differed significantly across the valley, although no spatial pattern was apparent for glucosinolate concentration (Supplementary Table 2). Most of the genotypes from near the common garden had low BC-ratio values; genotypes in the rest of the valley tended to have moderate to high BC-ratio, as represented by BC-ratio-C (Figure 1).

Figure 1. Spatial pattern of glucosinolate profile.

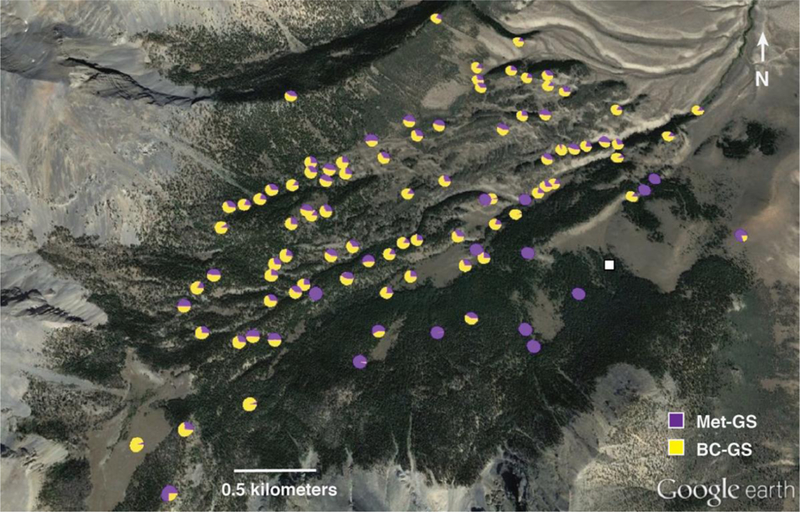
Family mean proportions of methionine-derived glucosinolate compounds (in purple) and branch-chain amino acid-derived compounds (in yellow) in cauline leaves. The white square indicates the location of the common garden. Charts generated by PhyloGeoViz (Tsai 2011). Terrain image copyright by Google Earth.

Selection analyses

Significant selection gradients for the fecundity component of fitness in reproducing individuals were found for 3 traits: ConGS-R, BC-ratio-C, and BC-ratio-F (Table 1), showing strong selection against high ConGS-R. BC-ratio experienced opposing directions of selection in cauline leaves and fruits; a higher BC-ratio was favored in leaves, but was disadvantageous in fruits (Figure 2). VIF values were moderate (Supplementary Table 3). When either BC-ratio-C or BC-ratio-F was eliminated from the regression, the sign of the selection gradient for the other did not change. The permutation test showed a highly significant difference between the selection gradients for BC-ratio-C and BC-ratio-F (P < 0.0001).

Table 1. Selection gradients for glucosinolate traits.

Covariates in the model included Cohort, Block, Veg, Stage, and Schreiner Score. The selection gradient is obtained from the estimate of the trait effect in the model.

	Full Population		BC Subpopulation
	Selection gradient	P-value	Selection gradient	P-value
ConGS-R	−0.10916	0.0002	−0.11839	<0.0001
BC-ratio-R	0.03586	0.4534	−0.03713	0.4787
ConGS-C	−0.01131	0.7261	−0.05047	0.1511
BC-ratio-C	0.16229	0.0070	0.07919	0.2691
ConGS-F	−0.02971	0.3438	−0.03096	0.3093
BC-ratio-F	−0.21807	0.0007	−0.30272	<0.0001

Figure 2. Selection against the direction of the genetic covariance for standardized BC-ratio in cauline leaves and fruits in the observed population and the BC subpopulation.

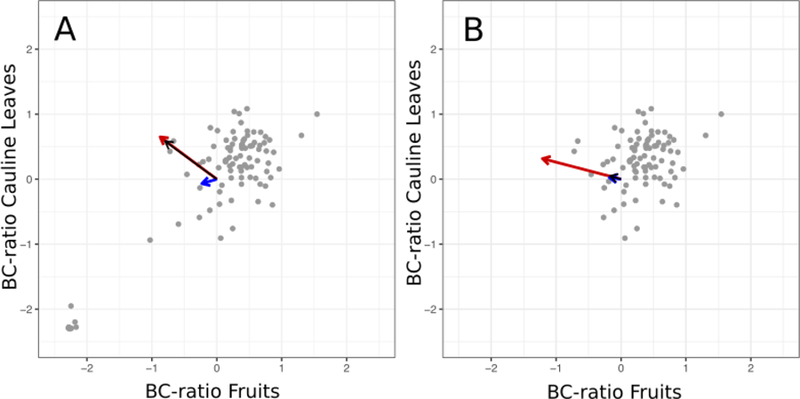
Points represent genotype means, scaled to a mean of zero. Panel A shows the full dataset. The genetic covariance between the two traits was significant (P < 0.0001). Both traits had significant selection gradients (P < 0.05). Panel B shows the hypothetical BC population, the subset of the population that produced BC-GS. In the BC population, the genetic correlation between the two traits was not significant. The selection gradient was significant for BC-ratio in the fruits, but not for the cauline leaves. In both panels, the red arrow indicates β, the vector of selection gradients. The blue arrow indicates $\mathbf{\Delta }{\overline{z}}_i$, the response to selection with the covariances included. The black arrow indicates $\mathbf{\Delta }{\overline{\mathit{z}}}_{\text{nc}i}$, the response to selection when the covariances are computationally set to zero. The length of each of the arrows has been increased by a factor of four for improved visibility.

Selection gradients in the BC subpopulation differed from the full population. Selection on BC-ratio-C was not significant, while selection to decrease BC-ratio-F was significant, and slightly stronger than for the full population.

We found no significant evidence for selection on the “invisible fraction.” None of the glucosinolate traits were significant predictors of survival, bolting, or TCO in either cohort (Supplementary Table 4). Thus, we have no evidence that glucosinolate traits are involved in early selection events that would render our selection gradients inaccurate. The only glucosinolate trait that was affected by early-season stage was ConGS-R, which was higher in later-flowering plants (Supplementary Table 5).

Glucosinolates and interactions

Herbivore damage was not predicted by glucosinolate profile in any tissue (Supplementary Table 6). Similarly, no glucosinolate traits were significant predictors of disease severity (Supplementary Table 7).

Estimating the G-matrix

Significant genetic variance components were found for all traits except ConGS-R and ConGS-F (Table 2; Supplementary Table 8). Six of the fifteen genetic covariance components were significant, using a Bonferroni correction for fifteen tests (Supplementary Table 9). All of the observed covariances were positive. The estimates of genetic covariance components and covariances among line means were very similar (Supplementary Table 1), indicating that shared environmental covariances were minimal in their effects on these traits. Thus, the use of line-mean covariances in the following analyses does not overestimate the genetic covariances.

Table 2. The estimated G-matrix.

Genetic variances are on the diagonal, in italics; off-diagonal elements are the genetic covariances. Significant variances (P < 0.05) and covariances (P < 0.0033) are indicated in bold above the diagonal; see methods for computation of (co)variances and p-values. A) The G-matrix for the full experimental population. B) The G-matrix for the restricted BC population.

A. Full population
	ConGS-R	BC-ratio-R	ConGS-C	BC-ratio-C	ConGS-F	BC-ratio-F
ConGS-R	0.32150	0.14905	0.04231	0.11227	0.02135	0.08760
BC-ratio-R	0.14905	0.84363	0.09965	0.75459	0.09837	0.77397
ConGS-C	0.04231	0.09965	0.55931	0.00483	0.19618	0.15040
BC-ratio-C	0.11227	0.75459	0.00483	0.89930	0.07559	0.80537
ConGS-F	0.02135	0.09837	0.19618	0.07559	0.37218	0.18689
BC-ratio-F	0.08760	0.77397	0.15040	0.80537	0.18689	0.91204
B. BC subpopulation
	ConGS-R	BC-ratio-R	ConGS-C	BC-ratio-C	ConGS-F	BC-ratio-F
ConGS-R	0.3513	−0.0666	0.0322	0.0426	0.0069	0.0128
BC-ratio-R	−0.0666	0.1258	−0.0285	0.0003	−0.0426	0.0096
ConGS-C	0.0322	−0.0285	0.5802	−0.1417	0.1961	0.0214
BC-ratio-C	0.0426	0.0003	−0.1425	0.1526	−0.0631	0.0319
ConGS-F	0.0069	−0.0426	0.1961	−0.0631	0.3954	0.0647
BC-ratio-F	0.0128	0.0096	0.0214	0.0319	0.0647	0.1397

The response to selection and the effects of covariances

The direction of difference between $\mathbf{\Delta }\overline{z}$ and $\mathbf{\Delta }{\overline{\mathit{z}}}_{\text{nc}}$ was consistent in 1,994 of the 2,000 bootstrap iterations, indicating that genetic covariances have a highly significant influence on response to selection (Table 3). Of the six individual traits, $\Delta {\overline{z}}_i$ and $\Delta {\overline{z}}_{\text{nci}}$ differed significantly for ConGS and BC-ratio in both cauline leaves and fruits (Figures 2 and 3; Table 3). For ConGS-C and BC-ratio-C, removal of covariances resulted in a change of sign, from a negative trait change $\Delta {\overline{z}}_{\text{i}}$ to a positive change $\Delta {\overline{\mathit{z}}}_{\text{nc}i}$. Using the observed pattern of antagonistic selection on BC-ratio between cauline leaves and fruits, the total magnitude of $\mathbf{\Delta }\overline{z}$ and $\mathbf{\Delta }{\overline{\mathit{z}}}_{\text{nc}}$ did not differ significantly, indicating that genetic covariances influence the direction but not the magnitude of evolutionary change (Supplementary Table 10).

Table 3. Predicted response to selection with and without covariances.

For each of 2,000 bootstrap samples, we calculated whether the predicted response to selection ($\mathbf{\Delta }\overline{z}$) differed from the predicted response without genetic covariances ($\mathbf{\Delta }{\overline{\mathit{z}}}_{\text{nc}}$) for all six traits collectively, and for each trait individually. For individual traits, the mean $\mathbf{\Delta }{\overline{z}}_i$ and $\mathbf{\Delta }{\overline{\mathit{z}}}_{\text{nc}i}$ results for the bootstrap samples are reported.

	P-value	Mean $\Delta {\overline{z}}_i$	Mean $\Delta {\overline{z}}_{nc\text{i}}$
All traits	0.0010
ConGS-R	0.3200	−0.0528	−0.0476
BC-ratio-R	0.1000	−0.0349	0.0535
ConGS-C	0.0070	−0.0508	0.0014
BC-ratio-C	0.0070	−0.0296	0.1656
ConGS-F	0.0215	−0.0560	−0.0135
BC-ratio-F	0.0225	−0.0891	−0.2642

Figure 3. Selection gradients and predicted responses to selection with and without genetic covariances.

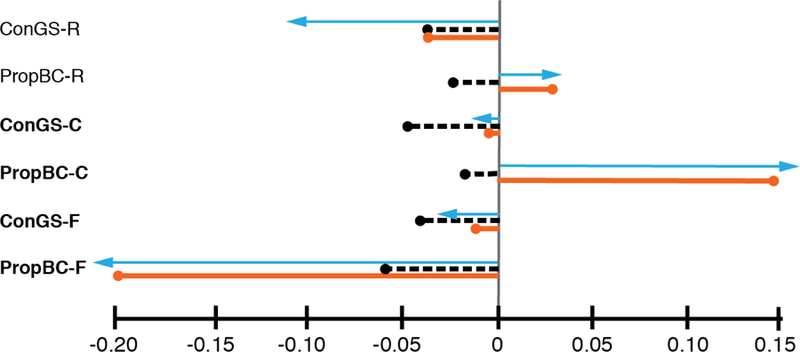
For each trait, we show the selection gradient (blue arrow), $\mathbf{\Delta }{\overline{z}}_i$, the response to selection with covariances (black dotted line), and $\mathbf{\Delta }{\overline{\mathit{z}}}_{\text{nc}i}$, the response to selection when covariances are eliminated (solid orange line). Traits in bold had a significant difference between $\mathbf{\Delta }{\overline{z}}_i$ and $\mathbf{\Delta }{\overline{\mathit{z}}}_{\text{nc}i}$.

Even when only the between-tissue BC-ratio covariances were constrained to zero, they still had a significant effect on the response to selection (Supplementary Table 11). Eliminating those covariances had no effect on the change in ConGS in any tissue, but did show a significant difference between $\Delta {\overline{z}}_i$ and $\Delta {\overline{\mathit{z}}}_{\text{nc}i}$ for BC-ratio-C and BC-ratio-F. The effects on those two traits were similar to that of removing all the covariances; a change in sign for the response in BC-ratio-C, and a significant difference for BC-ratio-F. Unlike the analysis of the full set of covariances, the between-tissue covariances cause an overall effect on the magnitude of the response to selection, as well as altering the amount of change in BC-ratio-F. For these significant responses, the difference was negative, indicating constraint.

Restricted BC subpopulation

The selection gradients, G-matrix, and extent of constraint all differed between the full population and the restricted BC population. The BC population had significant genetic variation for BC-ratio in fruits, but not in other tissues (Supplementary Table 8). Within the BC population, significant selection gradients acted on ConGS-R and BC-ratio-F, in the same direction as in the full population; however, in the BC population we did not observe significant selection on BC-ratio-C. In the BC population, there were no significant covariances in BC-ratio among any of the three tissues. There were positive covariances between ConGS-C and ConGS-F, and ConGS-F and BC-ratio-F, and negative covariances between ConGS-R and BC-ratio-R, and ConGS-C and BC-ratio-C.

These low correlations among traits in the BC population affected the response to selection (Table 4); the response of BC-ratio in any tissue did not change, indicating that within the BC population genetic covariances do not constrain the evolution of BC-ratio.

Table 4. Responses to selection with and without covariances in the restricted BC subpopulation.

We restricted the population to just the genotypes that produce BC-derived glucosinolates. For each of 2,000 bootstrap samples, we calculated whether the predicted response to selection ($\mathbf{\Delta }\overline{z}$) differed from the predicted response without genetic covariances ($\mathbf{\Delta }{\overline{\mathit{z}}}_{\text{nc}}$) for all six traits collectively, and for each trait individually. For individual traits, the mean $\Delta {\overline{z}}_i$ and $\Delta {\overline{\mathit{z}}}_{\text{nc}i}$ results for the bootstrap samples are reported.

	P-value	Mean $\Delta {\overline{z}}_i$	Mean $\Delta {\overline{z}}_{nc\text{i}}$
All traits	0.0180
ConGS-R	0.5040	−0.0595	−0.0630
BC-ratio-R	0.3320	−0.0028	−0.0031
ConGS-C	0.0800	−0.0579	−0.0172
BC-ratio-C	0.2990	0.0163	0.0245
ConGS-F	0.0285	−0.0654	−0.0229
BC-ratio-F	0.5045	−0.0610	−0.0613

Discussion

Genetic constraints

Traits in different tissues may evolve independently if they have independent genetic controls. In the case of pleiotropy or tight linkage, however, selection on one tissue may drive correlated change in another, potentially causing genetic constraints (Lande 1979; Lande and Arnold 1983). We found evidence of such constraints on the evolution of BC-ratio in cauline leaves and fruits. This effect was driven largely by antagonistic selection and positive genetic covariances in BC-ratio between cauline leaves and fruits, consistent with pleiotropy at BCMA1/3. Because natural selection was antagonistic to genetic correlations, predicted evolutionary responses to selection were small (Figure 2). Thus, if there is temporal or spatial variation in selection, evolutionary changes could be very slow, and variation in BC-ratio might persist for many generations.

Selection on ConGS and BC-ratio varied among tissues. Most strikingly, we observed significant antagonistic selection for BC-ratio in cauline leaves vs. fruits; high BC-ratio was favored in leaves, but disadvantageous in fruits. The causes of this antagonistic selection are not apparent from our data, as glucosinolate traits did not predict either herbivory or disease severity. This is unexpected, given previous work that has demonstrated effects of BC-ratio on leaf damage; however, the presence of such effects depends on year and location, and requires large sample sizes to detect (Prasad et al. 2012). We also acknowledge that under field conditions, both infection and herbivory may induce glucosinolate production, despite our attempts to collect tissue before peak damage. The high heritability of BC-ratio in the field indicates that most of the variance is genetic, rather than environmental, suggesting that induction likely had minimal effects on BC-ratio.

Glucosinolates also are involved in plant growth (Tantikanjana et al. 2004), flowering (Mohammadin et al. 2017), drought-related traits (Martínez-Ballesta et al. 2015), and interactions with a large number of species, including pathogens (Halkier and Gershenzon 2006), which may also drive selection. Microbial pathogen(s) were present on a number of plants in our experiment; if glucosinolates in different tissues mediate this biotic interaction, that could also explain the variation in selection. Thus, the potential selective factors acting on glucosinolates are complex, and our field data do not elucidate the functional basis of these selective pressures. Leaves and fruits are present at different times during the growing season, and the herbivore community changes seasonally as well (Keith, personal observation); thus, it seems probable that different communities feed on the two tissues. We observe chewing larvae that move down the stalk of the plant, eating fruits and leaves as they go. These include a Plutellid moth that oviposits in or near the flowers (Mitchell-Olds, personal observation). Defensive compounds attract specialist enemies of plants (Renwick et al. 1992; Roessingh et al. 1992; Sun et al. 2009); one potential explanation of the antagonistic pattern that we observed is that ovipositing insects may be attracted to chemical profiles in the flowers and fruits, increasing the herbivory load on the plant even if other herbivores are deterred.

The combination of antagonistic selection and positive genetic covariances caused evolutionary constraints on BC-ratio in leaves and fruits. The most striking example of constraint was change in the direction of response for BC-ratio-C: although higher BC-ratio-C was favored by selection, the trait was predicted to decrease. This change in sign was driven by antagonistic selection on BC-ratio acting contrary to between-tissue genetic covariances.

The predicted evolutionary trajectories of BC-ratio are consistent with the local geographical distribution of glucosinolate profiles. At the common garden and other sites under similar selective regimes, we would expect primarily Met-GS genotypes; that pattern is what we observed across the valley. This spatial pattern suggests that the selection we observed is representative of the common conditions at the garden, and that our predicted trajectories are accurate. The existing variation across the valley may be explained by spatial variation in selection on glucosinolates, particularly as the north-facing and south-facing slopes vary in light conditions, as well as dominant vegetation and likely herbivore communities.

Previous studies of the importance of evolutionary constraints have been inconsistent. A meta-analysis by Agrawal and Stinchcombe (2009) that focused on the effects of genetic covariances did not find a clear trend towards constraints; in many cases covariances had little effect, and the remainder included both constraint and augmentation. Other studies, however, have identified examples of constraint (Etterson and Shaw 2001; Smith and Rausher 2008), including in the evolution of defenses against herbivores (Wise and Rausher 2013). Wise and Rausher (2013) found strong constraint in the evolution of resistance to multiple herbivores in Solanum. In that case, however, they observed primarily synergistic selection for increased resistance to herbivores. In that study, constraints resulted from negative genetic covariances. In contrast, our analysis of tissue-specific chemical traits also found constraint, but for different reasons: the traits covary positively, but constraints are driven by antagonistic selection.

Genetic constraints and trait polymorphisms

Most of the variation in BC-ratio in rosette leaves is controlled by the BCMA1/3 locus, which produces BC-GS (Prasad et al. 2012). To investigate the role of BCMA1/3 in the evolutionary constraints, we considered a hypothetical population without Met-GS genotypes, focusing on the subpopulation that produces variable quantities of BC-GS. This subpopulation retains the remaining quantitative background variation in BC-ratio.

In this hypothetical BC subpopulation we find no evidence for antagonistic selection. We observed significant selection for lower BC-ratio-F, but no significant selection on BC-ratio-C, suggesting that when BC-GS are present in any quantity, the exact amount is not under selection in cauline leaves. Covariances between BC-ratio in cauline leaves and fruits were driven by pleotropic effects of BCMA1/3 in these adjacent tissues (unpublished GWAS analysis, Mojica et al.). Because antagonistic selection and positive covariances between BC-ratio in leaves and fruits drove evolutionary constraints in the full population, it is not surprising that these constraints were lacking in the BC population, which lacked this genetic covariation. Thus, the evolutionary constraints that we observed were likely driven by pleiotropic effects of BCMA1/3.

This example of constraint differs from the classical quantitative genetics model in which traits are controlled by many loci of small effect (Lande 1980; Agrawal et al. 2001). Theory predicts that the genetic architecture of covarying traits will affect the evolution of G, particularly when variation is due to genes of major effect, rather than polygenic effects (Agrawal et al. 2001). Under these circumstances, change in the allele frequency at a single locus has the potential to rapidly change the genetic variances and covariances of the population, producing rapid changes to G (Agrawal et al. 2001; Kelly 2009). Thus, we expect that allele frequency changes at BCMA1/3 would alter the G-matrix and evolutionary constraints on glucosinolates.

When BCMA1/3 is polymorphic (as in the full experimental population), we observe positive genetic covariances between BC-ratio-C and BC-ratio-F, strong constraints causing maladaptive change in BC-ratio-C, and little overall genetic change. However, in a hypothetical subpopulation without Met-GS genotypes, there are no significant covariances constraining tissue-specific evolution. Furthermore, new mutations that increase MET-GS concentration (such as loss of function of BCMA1/3) would be favored, leading once again to standing polymorphism for BC-ratio. Thus, the existing population may retain BC-ratio polymorphism for generations, while a population without Met-GS would favor loss of function mutations in BCMA1/3 when they arise. Both scenarios are compatible with persistence of BC-ratio polymorphism for many generations.

The constraints we observed in the full population, in which BC-ratio-C was predicted to evolve in a maladapted direction, were more extreme than most observed incidences of evolutionary constraints, in which evolution of traits is merely slowed (Etterson and Shaw 2001; Smith and Rausher 2008; Agrawal and Stinchcombe 2009; Wise and Rausher 2013). This difference is likely explained by the genetic architecture; genes of major effect are predicted to cause such maladaptive changes, as long as the overall fitness of an individual is increased (Carriere et al. 1994; Orr 1998; Agrawal et al. 2001). Here, we add to the empirical examples of this phenomenon, and provide a contrast to other studies of constraints.