Improving estimates of compensatory cis-trans regulatory divergence

Abstract

Interspecific hybrids have played a key role in research on gene expression regulation. A growing number of studies have measured genome-wide allele-specific expression in hybrids and observed that cis-regulatory changes often oppose trans-acting changes affecting the same genes, suggesting stabilizing selection for compensatory changes. However, the most common method for estimating these effects is biased, producing artifactual patterns of compensatory evolution. Here I introduce a simple modification leveraging biological replicates that ameliorates the bias.

First-generation hybrids between divergent lineages have been an invaluable model to study allele-specific expression (ASE), where one allele of a gene is more highly expressed than the other. Hybrid ASE specifically reflects cis-acting differences between alleles, since the two alleles of each gene are exposed to the same trans-acting regulatory environment. Quantifying cis-regulatory divergence can help pinpoint genes and pathways underlying adaptive traits, as well as reveal large-scale patterns of regulatory evolution [1,2].

Using high-throughput RNA-sequencing (RNA-seq), genome-wide ASE has been measured in a diverse menagerie of hybrids [1]. A popular analysis of these data compares hybrid ASE to expression differences between the two parental species; since the parental difference reflects both cis and trans-acting divergence, the trans-effects impacting each gene can be estimated as the parental difference minus the cis-effect (Fig 1a). A surprisingly consistent result of these comparisons has been that compensatory changes, where cis and trans effects on a specific gene differ in sign, are far more common than reinforcing changes [3–11]. Indeed, a recent review highlighted this as a major unsolved puzzle, suggesting mechanisms such as stabilizing selection, feedback, or transvection to explain its ubiquity [1].

Figure 1. Improving estimates of cis-trans divergence.

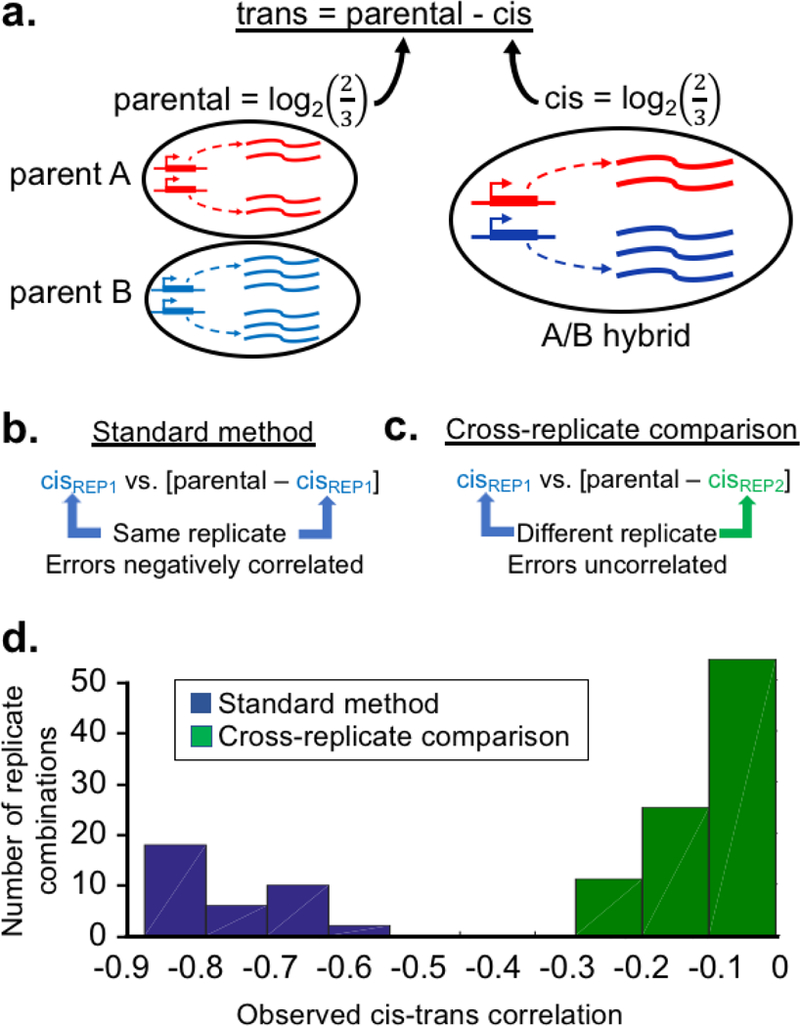
a. Estimating trans-acting divergence from the difference between parental expression and hybrid ASE. Parental divergence is estimated from the ratio of parental expression levels, and is assumed to be the product of cis and trans effects (additive in log-space). Figure adapted from [14]. b. The standard method of cis-trans comparison leads to artifactual negative correlation when cis estimates have any error. Note “REP1” could represent either a single replicate or an average of multiple replicates. c. The proposed method of cross-replicate comparison is not inflated by random measurement error. d. Histogram showing the difference between the two methods applied to the same data set [4]. Each cis-trans correlation is based on one pair of hybrid/parental replicates (36 pairs for the standard method and 90 for cross-replicate comparison, each with over 4,000 informative genes).

My colleagues and I previously noted that this approach is intrinsically biased: any error in estimating cis-effects will introduce an artifactual negative correlation with trans-effects [12] (Fig 1b). In a hybrid between parental species A and B, any error that overestimates the A/B ASE ratio will lead to underestimation of the A/B trans ratio. This leads to the undesirable situation where greater error in ASE estimates will lead to stronger cis-trans correlations. For example, if ASE ratios are estimated with 50% error, then even with no true correlation between cis and trans divergence, the observed (artifactual) cis-trans correlation will be r ≈ −0.5 (see Box 1). Although this concern has been reiterated by others [13], no solution has yet been proposed.

Box 1: Methods.

When no true correlation exists between cis and trans changes, no cis × trans interactions exist, and cis and trans changes have equal variance, the expected cis-trans correlation can be estimated as follows, where cis is the true log₂ ASE ratio, trans is the true log₂ trans ratio, parental is the true log₂ parental ratio, and ε is an error term:

trans = parental – cis
observed cis = cis + ε
observed trans = parental – (cis + ε)
= trans – ε
var(cis + ε) = var(cis) + var(ε)
var(trans – ε) = var(trans) + var(ε)
= var(cis) + var(ε)
cov(cis,trans) = 0
cov(cis + ε, trans – ε) = cov(cis,trans) + cov(ε,-ε)
= 0 – var(ε)
corr(cis + ε, trans – ε) = cov(cis + ε, trans – ε) / sqrt(var(cis + ε) * var(trans – ε))
= -var(ε) / (var(cis) + var(ε))

The numerator of the final equation leads to the artifactual negative correlation; if instead the errors are uncorrelated (as in Fig 1c), the numerator becomes zero. Although it may appear that cross-replicate comparison could increase error, this is not the case (see Supplement).

Applying the equations above, if cis-effects are estimated with 50% error (i.e. r ≈ 0.7 between true ASE and estimated ASE), then var(ε) ≈ var(cis), and the expected Pearson correlation ≈ −0.5. This level of error is not unrealistic; e.g. the average ASE correlation between replicate hybrids is r = 0.32 and r = 0.47 in the mouse and yeast data respectively, suggesting greater than 50% error per replicate. This model is meant only as an approximation to reality; in practice, many other factors (e.g., error in parental estimates) will affect the correlation as well.

Data analysis was performed on raw read counts, requiring at least 5 reads per allele in hybrid samples or per gene in the parental samples to include that gene in the analysis. Results were similar at other cutoffs (e.g. requiring 10 reads in the mouse data, mean r = −0.67 for the standard method and r = −0.071 for cross-replicate comparison). Hybrids from only one direction of the mouse cross were included, to avoid confounding effects of imprinted genes in the reciprocal crosses. I analyzed each replicate separately to maximize the number of comparisons (Fig. 1d), but to achieve a single estimate of cis-trans concordance it is also possible to combine replicates, as long as no replicates are used for both cis and trans-effect estimation.

Although many authors have used discrete cutoffs to classify genes into distinct categories of compensatory or reinforcing changes, I chose to focus on correlation due to its generality. These analyses are not meant to match the details of the previously published analyses, and therefore should not be interpreted as refutation of their specific results; rather my goal was to illustrate a more general issue with the method itself.

I propose a simple solution to this bias: cross-replicate comparison. Instead of using the same ASE measurements for both the trans-estimation and the subsequent cis-trans comparison, performing biological replicate ASE measurements allows one to use one replicate for trans-estimation, and another for cis-trans comparison (Fig 1c). This is not subject to the same bias as the standard method, since any random error (e.g. due to low read counts) from one replicate will generally not be shared by another. Overestimation of the A/B ASE ratio in one replicate will still lead to underestimation of the A/B trans ratio, but this should not be correlated with the ASE ratio of an independent replicate, thus eliminating the bias.

To test this approach, I applied it to an extensively replicated study of two inbred mouse strains, with RNA-seq in six replicates of each parental line and six of each reciprocal hybrid (24 total samples) (Box 1) [4]. Performing a standard cis-trans comparison (Fig 1b), all replicates showed strong negative correlation ranging from Pearson’s r = −0.57 to −0.82 (Fig 1d, blue; mean r = −0.71). However, performing the cross-replicate approach (Fig 1c), these correlations were far weaker (Fig 1d, green; Pearson’s r = −0.21 to −0.004, mean r = −0.079). This suggests that the cross-replicate design eliminates much of the negative bias when comparing cis vs. trans divergence.

The cross-replicate approach can be applied with as few as two replicate hybrid samples and one sample from each parent. For example, this was the number of replicates in a study of two S. cerevisiae yeast strains and their hybrids [13]. With the standard cis-trans approach, the two ASE replicates yielded cis-trans correlations of r = −0.40 and −0.37. However, the cross-replicate design yielded correlations of r = −0.02 and −0.002. Notably, these insignificant estimates are more consistent with results of an earlier study of the same two strains that found a slight excess of reinforcing cis-trans effects, using expression QTL (eQTL) mapping, which is not subject to the negative bias discussed here [12].

In sum, the bias inherent in a widely used method has led to overestimation of the ubiquity of compensatory cis-trans evolution. Although cross-replicate comparison controls for the effects of random error in ASE estimates, any bias that is shared between replicates (e.g., allelic mapping bias) could still lead to an artifactual negative correlation; therefore methods that independently estimate cis and trans-effects, such as eQTL mapping, may still be preferable. Whether previous reports of compensatory evolution can be entirely explained by this bias will be a key question for future work.