Abstract
The zeta potential (ζ) is the effective charge energy of a solvated protein, describing the magnitude of electrostatic interactions in solution. It is commonly used in the assessment of adsorption processes and dispersion stability. Predicting ζ from molecular structure would be useful to the structure-based molecular design of drugs, proteins and other molecules that hold charge dependent function while remaining suspended in solution. One challenge in predicting ζ is identifying the location of the slip plane (XSP), a distance from the protein surface where ζ is theoretically defined. This study tests the hypothesis that the XSP can be estimated by the Stokes-Einstein hydrodynamic radius (Rh), using globular hen egg white lysozyme as a model system. Although the XSP and Rh differ in their theoretical definitions, with the XSP being the position of the ζ during electrokinetic phenomena (e.g. electrophoresis) and the Rh being a radius pertaining to the edge of solvation during diffusion, they both represent the point where water and ions no longer adhere to a molecule. This work identifies the limited range of ionic strengths in which the XSP can be determined using diffusivity measurements and the Stokes-Einstein equation. In addition, a computational protocol is developed for determining the ζ from a protein crystal structure. At low ionic strengths a hyper-diffusivity regime exists, requiring direct measurement of electrophoretic mobility to determine ζ. This work, therefore, supports a basic tenant of EDL theory that the electric double layer during diffusion and electrophoresis are equivalent in the Stokes-Einstein regime.
Keywords: zeta potential, slip plane position, hydrodynamic radius, Stokes-Einstein relation, Gouy-Chapman electric double layer
INTRODUCTION
The zeta, or electrokinetic, potential (ζ) is the effective charge energy of a solvated solute. It can be used to assess how well dispersed colloids remain in solution [1, 2, 3], and to model the electrokinetic behavior in adsorption processes. Protein-based therapeutics may be formulated at high concentrations that are prone to aggregation. Experimentally measured ζ has been applied to optimize therapeutic antibodies and other proteins for formulation conditions that promote long-term dispersion stability [4, 5, 6, 7, 8, 9], and to study interactions between proteins with particles, materials and surfaces [10, 11].
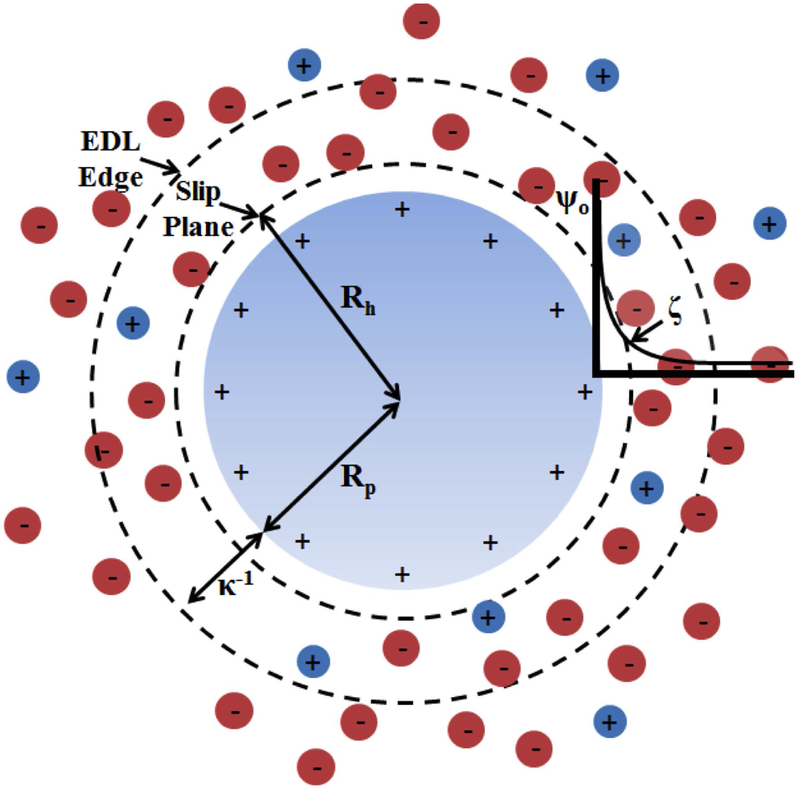
The ability to predict ζ from the molecular structure of proteins would allow modeling of solubility as a parameter in computational protein design. In studies of protein self-assembly, unintuitive charge-dependent behavior may be observed due to a complicated balance between immediate and long-range electrostatic phenomena [5, 12] and between electrostatic and hydrodynamic processes. To model ζ, we treat the protein-solvent interface as an electric double layer (EDL), which is the collection of solvation layers that form around a protein in an attempt to neutralize its charge. Gouy and Chapman [13] developed an EDL model where a molecule with a uniform surface charge is neutralized by a region of diffusing ions that encompass the molecular surface. The propagation of the surface potential and ion concentrations from the surface are defined by the Poisson-Boltzmann equation (PBE). Figure 1 depicts key features of the EDL surrounding an idealized cationic spherical protein, and the electrostatic potential distribution extending into solution from the protein surface. A hydration layer extends from the surface to the slip plane position (XSP), similar to the Stern layer of the Gouy-Chapman-Stern (GCS) EDL. The depicted EDL assumes that the propagation of electrostatic potential and ion concentrations within the hydration layer are defined by the nonlinear PBE, unlike the GCS EDL, which applies a modified PBE to consider ion size constraints [14]. ζ is weaker than the surface potential (ψo) and located at XSP, which is somewhere in the cloud of diffusive ions less than a Debye length (κ−1) away from the surface. The XSP represents the cutoff of an immobile layer of solvent (referred to as “hydration layer” in this work) adhering to the molecule. It is only a few molecular-sized layers thick [15]. Ions adsorbed to the protein in this hydration layer can cause specific-ion effects that can be modeled with the GCS EDL [14, 16].
Figure 1. Idealized EDL around a spherical cation.
Plotted on the right, the surface potential (ψo) propagates outward into the cloud of ions treated as point charges immersed in a solvent with a constant relative dielectric. The zeta potential (ζ) is located at the slip plane, which is proposed to coincide with the hydrodynamic radius (Rh). Rp is the protein radius and κ−1 is the Debye length.
Proteins provide an excellent opportunity for EDL modeling where the molecular structure of their charged surfaces are known [17], and where changes in conformation can be studied experimentally or through simulation [18]. Hen egg white lysozyme, hereto referred to as lysozyme, is one such well-studied protein [19, 20, 21, 22, 23, 24] that can be used to evaluate EDL models.
An obstacle to using atomic structure of proteins to estimate ζ is the lack of general criteria for the location of the XSP [2, 25, 26]. Other studies [7] have used the EDL edge defined by the Debye length, κ−1, as XSP for calculating ζ. However, at the κ−1 motions of the ions are no longer determined by the surface potential, likely resulting in an underestimate of the calculated ζ. We hypothesize that a more accurate placement of XSP is the radius of hydration (Fig. 1).
Theoretically, the Rh was derived as the radius of an uncharged sphere plus its immobile hydration layer undergoing diffusive motion [27]. The XSP and Rh differ in their theoretical definitions, with the XSP being the position of the ζ during electrokinetic phenomena (e.g. electrophoresis) [2] and the Rh being a radius pertaining to the edge of solvation during diffusion [27], defined by the Stokes-Einstein equation (Eq. 1).
| (1) |
where kb is the Boltzmann constant, T is the absolute temperature, η is the pure solvent viscosity and D is the single particle diffusivity.
The idea that the XSP coincides with Rh has been previously considered [19, 25, 26], but to our knowledge, has not been experimentally validated for proteins. The GCS model was shown to be valid for negatively-charged silica nanoparticles, where the XSP was found to be one monolayer of water plus one hydrated counter-ion radius away from the surface [28]. This is consistent with GCS theory that places hydrated cations at the outer Helmholtz plane (OHP), which sits on top of a layer of water directly on the molecular surface [2]. With extensive studies on the hydration [22] and structure of lysozyme [29], we expect it to be a useful model system for the characterization of an EDL around a general globular protein.
In addition to the choice of protein, the role of the counter-ion in determining EDL structure must be considered. Our study involves the positively-charged protein, lysozyme, with weakly hydrated Cl counter-ions [30]. In GCS theory on positively-charged particles, the center of anions make up the inner Helmholtz plane, which is closer to the surface than the OHP, and can allow anions to sit on the molecular surface alongside water molecules [2]. The concentration of counter-ions at the protein surface is physically limited by their size as they pack with water to coat the protein [14]. In considering the finite size of ions, GCS theory is an improvement over GC theory that can model specific adsorption processes, which occur when an ion is attracted to a charged surface by more than just Coulombic forces. Multiple observations support that at pH 7, KCl is an indifferent electrolyte for lysozyme, dominated by Coulombic interactions [31]. For example, key features of an electrostatic-dominated process such as an isoelectric point independent of ion concentration, and concentration dependent counter-ion binding are both observed in this system [23]. Furthermore, small-angle X-ray scattering of lysozyme in KCl has also shown the Cl population in the nearest solvation layer increases with ion concentration [24]. Therefore, chloride-lysozyme interactions can be modeled Coulombically, simplifying our analysis. As will be shown in this work, a modified GC EDL model applied to averaged lysozyme conformations provides an accurate representation of its electrokinetic behavior.
We use the Stokes-Einstein equation to define the hydration layer within the modified GC EDL. Einstein originally derived Eq. 1 from the Navier-Stokes equation for dilute, non-charged spheres. Because lysozyme is charged at physiological pH, we must identify the effect that bearing a charge has on Rh. For example, at low ion concentrations, diffusivity is well known to show marked increases [20, 32, 33, 34] that lead to Rh being smaller than the physical size of the molecule itself – a hyper-diffusive regime. This increase in diffusivity is believed to result from long-range charge repulsion that accelerates diffusion as the κ−1 increases. We will establish the Stokes-Einstein regime - a range of ionic strengths where Eq. 1 is valid for charge-bearing particle.
In order to connect hydrodynamic and electrokinetic phenomena, we define an effective hydrodynamic radius during electrophoresis (i.e. the electrophoretic radius) (Re). Eq. 2a shows the relation between Re, protein radius (Rp) and XSP. Henry derived an equation for electrophoretic mobility (ue) accounting for electrophoretic retardation [2] from the Poisson-Boltzmann and Navier-Stokes equations while assuming the ionic atmosphere surrounding the charged particle to remain in its equilibrium state [35] (Eq. 2b). Henry’s equation has been experimentally tested on nanometer to micron-scale polystyrene, gamboge and silica spheres [36, 37]. Eq. 2c expresses this relationship in terms of the protein net surface charge (Qe) [38], knowing ue, the net valence of the protein (Q), and the pure solvent viscosity (η). Q is determined from controlling the solution pH and knowing the pKa values of the charged surface residues [23, 39, 40, 41]. η can be measured by a rheometer (see Table S1); however, much data already exists on the viscosity of aqueous electrolyte solutions [42] and thus we can use an empirical relationship [43] (see Eq. S3). The Henry correction factor for electrophoretic retardation (f(κRe)) varies between 1 and 1.5 [1], allowing us to calculate it as shown in Eq. 2d.
| (2a) |
| (2b) |
| (2c) |
| (2d) |
where κ is the inverse Debye length and is a shape factor (1.17 for lysozyme [38]).
The central hypothesis is that XSP, Re, Rh coincide, relating the position of the ζ and the edge of solvation. We assess this claim in two ways: first we experimentally determine Re and Rh to assess the similarity of the EDL during electrophoresis and diffusion. Second, in the Stokes-Einstein regime, we use diffusivity alone to specify XSP, and compute the ζ from the molecular structure of lysozyme. This assessment assumes the modified GC EDL model to be accurate for a protein in solution.
MATERIALS AND METHODS
Lysozyme Sample Preparation.
Salt-free hen egg white lysozyme (LYSF, Worthington Biochemical Corporation, Lakewood, NJ) was dissolved in deionized water and filtered through a 20 nm pore-size Anotop syringe filter (GE Whatman, Pittsburgh, PA) to separate monomers from aggregates. pH was measured with a model 14002-850 sympHony pH electrode (VWR, Randnor, PA) following calibration. The measured pH of the deionized water used to dissolve lysozyme was 6.55. Post-filtration lysozyme concentrations were determined with an Aviv Model 14DS spectrophotometer (Lakewood, NJ) by UV absorption at 280 nm using α280=2.64 mL/mg cm [45]. Three protein concentrations were prepared considering the balance between allowing the solutions to remain concentrated enough for accurate light scattering measurements but dilute enough to ensure protein-protein interactions were negligible [46]. Solutions were mixed with 99.995% pure KCl (7447-40-7, VWR, Radnor, PA) to allow a wide range of ion concentrations (10−6 to 1M) at three different protein concentrations.
Electrophoretic Mobility Measurement.
Filtered protein solutions were allowed five minutes of thermal equilibration at 25°C before the addition of the KCl solution, and measured immediately to minimize dimerization. Electrophoretic mobilities were measured at 25°C by phase analysis light scattering (PALS) [47] using a Malvern Zetasizer Nano ZS. Our apparatus used forward scattering of a 4 mW He-Ne laser at λ = 633 nm at an angle of 17° through a 2 mm spaced palladium plated dip cell. A minimum of twenty technical replicates were performed for each KCl concentration (see supplementary methods for details). Samples were checked for monodispersity by dynamic light scattering. Code for determining Re based on previous work [48] is provided as a supplementary file.
Diffusivity Measurement.
Filtered protein solutions were allowed five minutes of thermal equilibration at 25°C before the addition of salt. Then diffusivity measurements were taken immediately after adding salt-containing solutions. Final KCl concentrations were 1.0 μM, 10.0μM, 100.0 μM, 1.0 mM, 5.0 mM, 10.0 mM, 50.0 mM, 100.0 mM, 500.0 mM and 1.0 M. Diffusivities were measured at 25°C by dynamic light scattering (DLS) using a Malvern Zetasizer Nano ZS (Malvern Instruments, Worcestershire, U.K.) with a 4 mW He-Ne laser at λ = 633 nm. Measurements were performed using back-scattering at an angle of 173°. The temperature was maintained to within ±0.1°C by a built-in Peltier element. Six measured autocorrelation functions with acquisition times of about 150 seconds were analyzed by cumulants analysis and averaged to determine the diffusivity of each sample.
Viscosity Measurement.
To ensure the empirical viscosity relationships used in this work (see Eq. S3) were accurate, viscosities were measured with a Malvern Kinexus ultra+ rotational rheometer (Malvern Instruments, Worcestershire, U.K.) and are shown in Table S1. During measurement, 25μL of each solution was held between a 20 mm diameter flat plate upper geometry and 65 mm diameter flat plate lower geometry spaced with a 0.1 mm gap size. A shear rate of 11980 1/s was used as it was found to provide reasonably close values of pure water at 25°C. After allowing 5 minutes between the plates to reach thermal equilibrium, viscosities were measured for 60 seconds. Only the last 55 seconds were averaged to allow a 5 second delay to reach the machine’s steady state.
ζ Calculation from Structure.
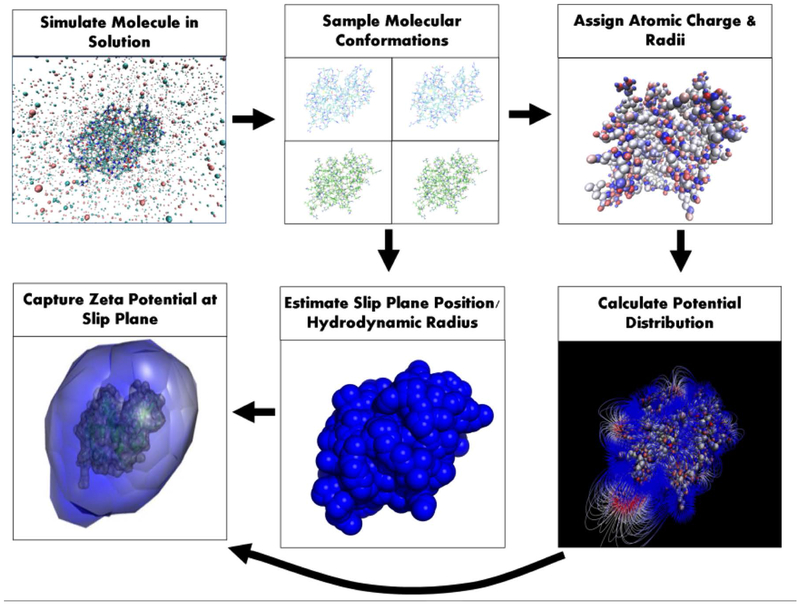
Computation of the ζ of lysozyme from its crystal structure (PDB id: 6LYZ [29]) involves six main steps that account for the structural motions of the solvated protein, its atomic charge distribution, its electric potential distribution into solution, and the distance from the protein, where solvent no longer adheres (Fig. 2). First, molecular dynamics (MD) simulations were performed in AMBER 2015 to produce an ensemble of near-native conformations [18]. Simulations were performed in explicit water extending 20 Å from the molecular surface, using the ff14SB force field [49], and were comprised of three parts: energy minimization, thermal excitation, and simulation in solution. Energy minimization was performed to optimize the initial geometry of the crystal structure in solution for 3000 cycles. Thermal excitation gradually heated the minimized structure from 0 K to 298.15 K over a period of 100 ps with a 2 fs interval to induce thermal motion of the solvent and protein. The heated structure was then allowed to undergo simulation for 100 ns with a 2 fs integration step. Twenty molecular conformations were sampled from the last 20 ns of simulation, one per nanosecond. This ensemble was intended to capture local conformational variation upon simulation equilibration, and not large-scale conformational changes.
Figure 2. Computational ζ prediction from protein structure.
Predicting the ζ of a molecular structure involves six main steps as shown above. Each step provides a necessary piece of information accounting for the structural motions of the solvated molecule, its atomic charge distribution, its electric potential distribution into solution, and the distance from the molecule, where water and ions no longer adhere. The slip plane position in the final step is exaggerated for visual clarity.
The ζ was computed for each of the twenty conformations. PDB2PQR [39, 40] was used to assign atomic charges and radii. The pKa predictor, PROPKA 3.0, was used to identify the protonation state of titratable residues at pH 7.0 [41]. The net +8 valence of lysozyme was in agreement with previous experimental data [23]. Electrostatic potential distributions of the prepared structures were computed by solving the non-linear Poisson-Boltzmann equation over each conformation with the adaptive Poisson-Boltzmann solver (APBS) [50]. A dielectric of 4.0 was used for the protein [51] and the dielectric of water at 25°C, 78.285 [52], was used for the solvent.
Hydrodynamic and protein radii were computed for each conformation. Protein radii (Rp) were calculated as the average distance between the center of mass and a solvent-excluded surface (SES) generated by MSMS [53]. The SES generated used a probe radius of water (1.4 Å). Hydrodynamic radii (Rh) were calculated by Eq. 1 using translational diffusivities computed by HYDROPRO [54]. For lysozyme, HYDROPRO used a bead-per-atom model with an atomic element radius of 2.6 Å. Computed radii were used to estimate the slip plane position by subtracting the protein radius from the hydrodynamic radius of each conformation. In the final step, the coordinates of the edge of the hydrodynamic radius (i.e. slip plane positon) were obtained and used to capture the electrostatic potentials at each point. This involves once again generating a SES on each structure using MSMS [53]. The SES generated is composed of Cartesian coordinates and their normal vectors directed away from the protein surface. Each SES is inflated by translating its initial coordinates to the slip plane position along their respective normal vector. The APBS tool, multivalue, uses the APBS calculated potentials and the inflated coordinates to capture the electric potentials at each point. A zeta potential value for each conformation (ζc) was computed by averaging the captured potentials at the inflated SES as shown below in Eq. 3. Modeled ζ values for lysozyme were computed by averaging the different ζc values of each conformation.
| (3) |
where N is the number of elements in the set S containing the position vectors composing the inflated SES and ϕ(r) is the electrostatic potential at position r.
RESULTS AND DISCUSSION
Assessing the Feasibility of Lysozyme for EDL Analysis.
The lysozyme-KCl solution interface at pH 7 provides an appropriate and well-studied system for assessing the relation between diffusivity, hydration and ζ with varying ionic strength [20, 22, 23, 26]. As a structure, lysozyme is highly spherical holding asphericity [55] and shape parameter [55] values indicative that the molecule can be represented by a sphere. The average asphericity from the 20 conformations produced by molecular dynamics was 0.0514 ± 0.03 and the average value for the shape parameter was 0.0196 ± 0.02 (0 is a perfect sphere for both values [55]). This supports our analysis of the hydration of lysozyme by subtracting the Rp from the Rh. Also, the net valence of the protein remains at +8 and is independent of ion concentration [23] indicating the surface charge distribution provides a comparable EDL foundation for the different ionic strengths.
Although lysozyme can form dimers at pH 7 [23], we ensured monomers were present following filtration as described in the supplement. DLS measurements alone were not sensitive to dimerization (see supplementary methods). Therefore, we determined the oligomerization state using PALS electrophoretic mobility measurements (see Fig. S1). All measurements were performed immediately upon the addition of salt solutions and routinely checked by DLS to ensure monodispersity.
The hydration of lysozyme studied by NMR and X-ray diffraction indicates solvent mostly forms a monolayer over the surface with ordered water structures extending no more than ~4.5 Å [22]. This hydration layer thickness is consistent with our measurements of Rh determined from experimental diffusivities and Re determined from electrophoretic mobilities. The Stokes-Einstein equation (Eq. 1) accurately connects diffusivity and hydration for our system, where it is valid. As the hydration layer thickness is the distance from the surface to where solvent no longer adheres to the protein, it is theoretically similar to the XSP, where the ζ exists. To assess how well the Stokes-Einstein relation provides an estimate of the hydration layer thickness, and thus the XSP, it is first necessary to determine the range of ionic strength in which Eq. 1 is valid. We do this through a combined analysis of the diffusive and electrophoretic behavior.
Electrophoretic Behavior of Lysozyme in KCl.
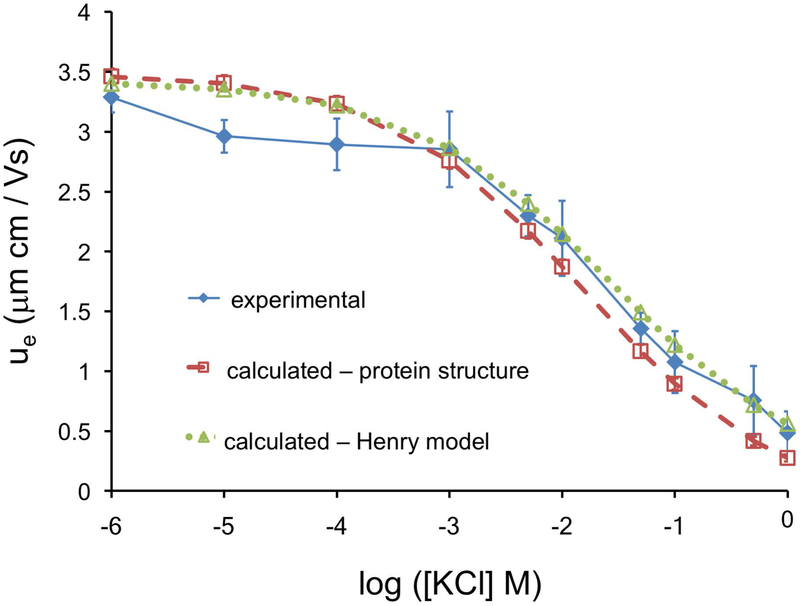
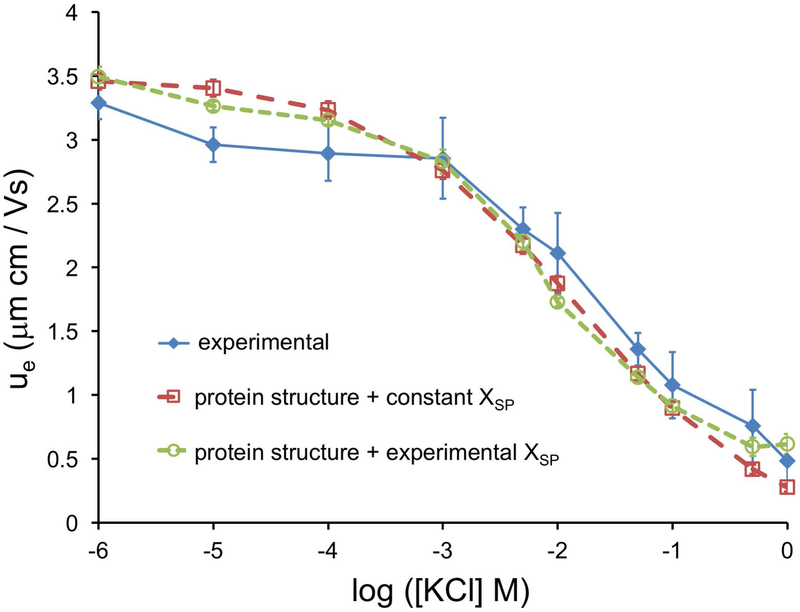
Two approaches for calculating electrophoretic mobility – using the Henry model Eq. 2c, or using explicit protein structure – were compared to experimental values measured for multiple protein concentrations. Lysozyme concentrations were sufficiently low to allow negligible protein-protein interactions. Experimental ue consistently decreased with increasing ion concentration, which is expected of GC EDL behavior [56]. Theoretical mobility values were calculated by rearrangement of the Henry model (Eq. 2c) using pure solvent viscosity values of KCl (Eq. S3) and a constant Re value of lysozyme plus a monolayer of water (1.62+0.284 nm = 1.904 nm) [21, 30]. Structure-derived mobility values using our ζ model were calculated from the average of MD simulations of the lysozyme structure (see methods), and converted into electrophoretic mobilities (Eq. 2b). The Henry equation was the appropriate electrokinetic model under our experimental conditions (i.e. only electrophoretic retardation is considered [2], no EDL polarization [57, 2], and no surface conductivity [57]) [58, 59]. The ζ model used a constant hydrodynamic radius calculated from HYDROPRO (2.02 nm) to estimate the XSP. A comparison of the two calculated and the experimental ue are shown in Fig. 3.
Figure 3. Comparison of experimental and calculated electrophoretic mobilities, ue.
The experimental mobility of lysozyme is well described by both the GC EDL, and by the structure-based modified GC EDL ζ model.
The electrophoretic mobilities of lysozyme are well described by the Henry model indicating the lysozyme-KCl EDL behaves like a GC EDL (Fig. 3). The Henry model [35] treats the protein as a sphere with a uniform surface charge and provides a standard for theoretical comparison with our detailed structure-based ζ model. Considering proteins are not perfectly spherical and hold a hydration layer that dampens their surface charge, measured protein mobilities were expected to be slightly lower than those predicted by the Henry model. Both models adequately represent the electrokinetic behavior of lysozyme in KCl, which indicates the modified GC EDL (structure model) is consistent with GC EDL theory (Henry model). This is significant as we have presented a theoretical validation of the GC EDL on an experimental crystal structure. It is important to note, dimerization can occur rapidly at the higher ionic strengths, and thus mobility values at the higher ion concentrations most likely represents a mixture of monomers and dimers. We sought to minimize these effects as described in our measurement protocol (Fig. S1).
Diffusive Behavior of Lysozyme in KCl.
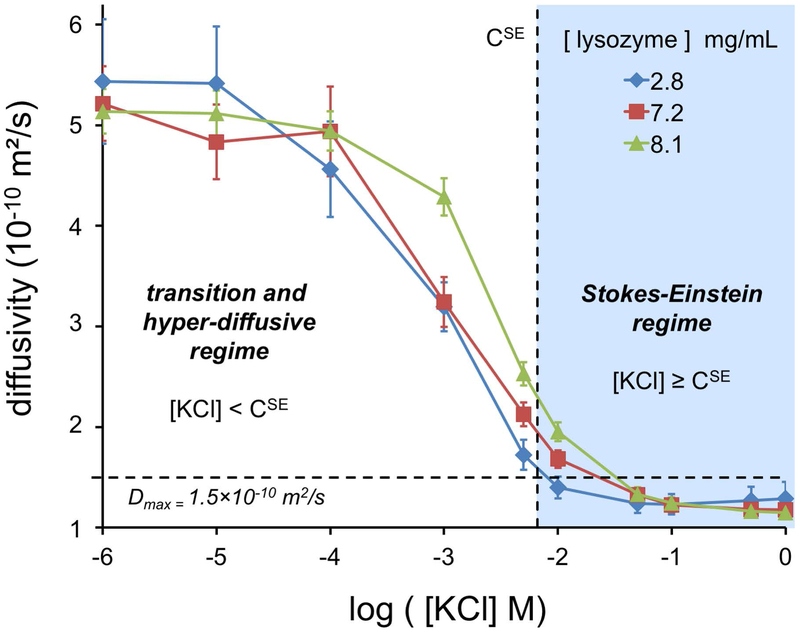
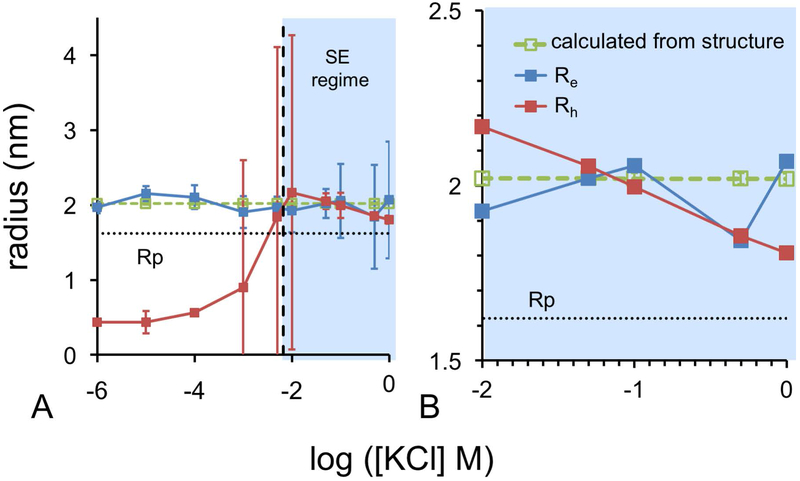
Diffusivities of three concentrations of lysozyme were measured by DLS at a series of ionic strengths from 1.0 μM to 1.0 M KCl (Fig. 4). Diffusivities are in agreement with previous work [20]. Diffusion behavior transitions between two different regimes with increasing ion concentration. The minimum KCl concentration defining the onset of the Stokes-Einstein regime where Eq. 1 is valid, denoted CSE, was determined by comparison of Rh from diffusivity and Re from electrophoretic mobility measurements (Fig. 5). Based on this analysis, the CSE for KCl was interpolated to occur at 6.6 mM.
Figure 4. Measured Diffusivities of Lysozyme at Various KCl and Protein Concentrations.
Low and high salt concentrations induce different regimes of diffusive behavior. The Stokes-Einstein regime was found to occur at KCl concentrations at or above 6.6 mM (marked as CSE) based on an analysis presented in the next figure. Below this concentration, diffusion transitions to a hyper-diffusive regime, where diffusivity exceeds Dmax, which is estimated based on the Rp of lysozyme.
Figure 5. Comparison of Experimental and Computational Radii of Hydration.
(A) Hydration radii for the entire tested range of ionic strengths. (B) Expanded view of the Stokes-Einstein regime.
At low ion concentrations, the hyper-diffusive regime exists in which diffusivity is enhanced by inter-particle electrostatic phenomena. Another possible cause for this enhancement could be a change in structure; however, previous work [60] has shown lysozyme structure is retained at the low KCl concentrations used here. Consequently, the higher diffusivities at lower ion concentrations deviate from Stokes-Einstein theory and despite extensive study still remain difficult to theoretically model [20, 32, 61, 34]. An in-depth discussion of the hyper-diffusivity regime can be found in the work of Muthukumar and colleagues [61]. As counter-ions become incorporated in the EDL, they neutralize the electrostatic enhancement causing a transition. Once enough ions have become incorporated in the EDL to allow each lysozyme molecule to appear neutral to its neighbors (i.e. electroneutrality at the EDL edge), the Stokes-Einstein regime begins. In the Stokes-Einstein regime (i.e. [KCl] > CSE), diffusivity and effective size can be related by the Stokes-Einstein equation (Eq. 1). In addition to the effects of ionic strength on the electrophoretic and diffusive behaviors through long-range electrostatic effects, we expect changes at the local scale in the nearest solvation layer around lysozyme in the Stokes Einstein regime.
EDL Contraction Affects Solvation in the Stokes-Einstein Regime.
EDL contraction refers to the disintegration of the outer solvation layers with increasing ionic strength. This effect can be theoretically quantified with the Debye length, representing the EDL edge from the protein surface [2]. As shown in Fig. 5A, analysis of protein diffusivity is only physically meaningful in the Stokes-Einstein regime. To estimate where the Stokes-Einstein regime becomes valid, we identified the ion concentration, where Rh and Re first coincide. Experimental Rh values were calculated with Eq. 1 using experimentally determined single particle diffusivities (see Fig. S3) and the pure solvent viscosity (Eq. S3). Experimental Re values were calculated with Eq. 2c using experimentally determined electrophoretic mobilities and the pure solvent viscosity. For comparison, we used the HYDROPRO [54] software to model single particle diffusivities based on the ensemble of lysozyme structures sampled by molecular dynamics. The structure of lysozyme during molecular dynamics remains compact with an average radius of 16.27 ± 0.16 Å, calculated from the average center of mass to solvent excluded surface. This value represents the Rp, and is in agreement with past experimental findings [21]. As the EDL contracts with increasing ion concentration in the Stokes-Einstein regime, experimental Rh values decrease (Fig. 5B). Experimental Rh decreases from 2.17 nm to 1.81 nm. The computed hydrodynamic radii from HYDROPRO diffusivities remain constant at 2.02 nm, which is close to Rh for the Stokes-Einstein regime, and Re values across the entire range of ionic strength.
In the Stokes-Einstein regime, calculated radii are all within error indicating agreement in the methods for determining molecular size [27, 48] and thus the hydration layer thickness. This connection indicates the EDL of lysozyme is the same under both electrophoretic and diffusive conditions, supporting our hypothesis that the XSP coincides with Rh. To estimate the slip plane position from experimental, we subtracted the protein radius (Rp) from the measured Rh values in the Stokes-Einstein regime and Re values outside of this regime (Eq. 4).
| (4) |
where XSP is the slip plane position relative to the protein surface, Re is the electrophoretic radius (Eq. 2c), Rp is protein radius, Ci is the ion concentration, CSE is the ion concentration at which the Stokes-Einstein regime begins, and Rh is the hydrodynamic radius (Eq. 1).
Re is approximately equal to the radius of lysozyme plus a water molecule (1.62+0.284 nm), indicating a single layer of water of solvation. However, Rh decreases with increasing ionic strength in the Stokes-Einstein regime, implying a shrinking hydration layer. This begs the question: is the XSP constant or variable with regard to ionic strength? To assess this question, we apply our protein structure derived ζ model using either a constant or a variable slip plane position.
ζ Analysis of the Slip Plane Estimates.
Previously, we demonstrated that an electrophoretic mobility, ue, determined from molecular structure with a calculated XSP using HYDROPRO correlates quite well with experimentally measured ue (Fig. 3). However, this calculated XSP is constant, in contrast to observed changes in hydrodynamic radii based on diffusivity measurements. If we use XSP values derived from experiment (Eq. 4) combined with a structure-based ζ model, we see little improvement in the correlation with directly observed ue values (Fig. 6). This suggests that for the given resolution of our instrument for determining ue, there is no advantage to including a variable XSP. XSP can be represented by the Rh experimentally and, for computational purposes, the XSP can be approximated as constant over a wide range of ionic strengths.
Figure 6. Comparison of measured and computed slip-plane estimates.
CONCLUSIONS
This work demonstrates that the slip plane of the lysozyme-KCl interface is not just a theoretical boundary for estimating the ζ, but also the physical interface between bulk and constrained waters along the protein surface. Future work will test the coincidence of the slip plane and hydrodynamic radius on other proteins. XSP can be estimated experimentally by diffusivity measurements in the Stokes-Einstein regime, thus connecting diffusivity, hydration and ζ. In the absence of diffusivity or mobility measurements, it is possible to accurately predict ζ directly from experimental structures or atomic-resolution models. Our data and ζ model were unable to establish a relationship between XSP and ionic strength. Relative to KCl, stronger kosmotropes or chaotropes along the Hofmeister series (e.g. KH2PO4, KNO3), may alter the hydration layer [62, 63]. Such effects have been systematically studied for lysozyme [45]. It would be valuable to examine how effective the computational protocol developed in this work could recapitulate the effects of ion types on hydration and electrophoretic mobility. The ζ prediction protocol proposed here is an important first step in developing solution conditions for optimizing protein dispersion stability.
Supplementary Material
ACKNOWLEDGEMENTS
The authors wish to thank Avanish Parmar, Troy Shinbrot and Adam Gormley for useful discussions. In addition, the authors wish to give a special thanks to Elliot Campbell for donating some Anotop syringe filters and providing advice in filtering lysozyme solutions. We gratefully acknowledge support from the National Science Foundation (DMR-0907273) and National Institutes of Health (DP2-OD-006478).
ABBREVIATIONS:
- EDL
electric double layer
- GC
Gouy Chapman
- GCS
Gouy-Chapman-Stern
- PBE
Poisson-Boltzmann equation
REFERENCES
- [1].Tuorilla P, “Über Beziehungen zwischen Koagulation, elektrokinetischen Wanderungs-geschwindigkeiten, Ionenhydratation und chemischer Beeinflussung,” Kolloidchemische Beihefte, vol. 27, p. 44, 1928. [Google Scholar]
- [2].Hunter RJ, ZETA POTENTIAL IN COLLOID SCIENCE Principles and Applications, 3rd ed., San Diego, CA: ACADEMIC PRESS, 1988. [Google Scholar]
- [3].Riddick TM, “Control of colloid stability through zeta potential,” Zeta Meter Corp, 1968. [Google Scholar]
- [4].Thiagarajan GA, “A comparison of biophysical characterization techniques in predicting monoclonal antibody stability,” MAbs, vol. 8, pp. 1088–1097, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Parmar AS, James JK, Grisham DR, Pike DH and Nanda V, “Dissecting Electrostatic Contributions to Folding and Self-Assembly Using Design Multicomponent Peptide Systems,” Journal of the American Chemical Society, vol. 138, pp. 4362–4367, 2016. [DOI] [PubMed] [Google Scholar]
- [6].Schermeyer MT, Woll AK, Kokke B, Eppink M and Hubbuch J, “Characterization of highly concentrated antibody solution - A toolbox for the description of protein long-term solution stability,” MAbs, pp. 1–17, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Long WF and Labute P, “Calibrative approaches to protein solubility modeling of a mutant series using physicochemical descriptors,” Journal of Computer Aided Molecular Design, vol. 24, pp. 907–916, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Buck PM, Kumar S, Wang X, Agrawal NJ, Trout BL and Singh SK, “Computational methods to predict therapeutic protein aggregation,” Therapeutic proteins: Methods and protocols, pp. 425–415, 2012. [DOI] [PubMed] [Google Scholar]
- [9].Perchiacca JM, Lee CC and Tessier PM, “Optimal charged mutations in the complementarity-determining regions that prevent domain antibody aggregation are dependent on the antibody scaffold,” Protein Engineering, Design & Selection, vol. 27, pp. 29–39, 2014. [DOI] [PubMed] [Google Scholar]
- [10].Haarmeyer CN, Smith MD, Chundawat SP, Sammond D and Whitehead TA, “Insights into cellulase-lignin non-specific binding revealed by computational redesign of the surface of green fluorescent protein,” Biotechnol Bioeng, vol. 114, pp. 740–750, 2017. [DOI] [PubMed] [Google Scholar]
- [11].Lundqvist M, Stigler J, Elia G, Lynch I, Cedervall T and Dawson KA, “Nanoparticle size and surface properties determin the protein corona with possible implications for biological impacts,” Proc Natl Acad Sci USA, vol. 105, pp. 14265–14270, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Xu F, Li J, Jain V, Tu RS, Huang Q and Nanda V, “Compositional Control of Higher Order Assembly Using Synthetic Collagen Peptides,” Journal of the American Chemical Society, vol. 134, pp. 47–50, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Chapman DL, “LI. A contribution to the theory of electrocapillarity,” The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, vol. 25, no. 148, pp. 475–481, 1913. [Google Scholar]
- [14].Brown MA, Bossa GV and May S, “Emergence of a Stern Layer from the Incorporation of Hydration Interactions into the Gouy-Chapman Model of the Electrical Double Layer,” Langmuir, vol. 31, pp. 11477–11483, 2015. [DOI] [PubMed] [Google Scholar]
- [15].Israelachvili JN and Adams GE, “Measurement of forces between two mica surfaces in aqueous electrolyte solutions in the range 0-100 nm,” Journal of the Chemical Society, Faraday Transactions 1, vol. 74, pp. 975–1001, 1978. [Google Scholar]
- [16].Stern O, “The theory of the electric double layer,” Z. Elektrochem. Angew. Phys. Chem, vol. 30, pp. 508–516, 1924. [Google Scholar]
- [17].Bernstein FC, Koetzle TF, Williams GJ, Meyer EE, Brice MD, Rodgers JR, Kennard O, Shimanouchi T and Tasumi M, “The Protein Data Bank: A Computer-based Archival File For Macromolecular Structures,” Journal of Molecular Biology, vol. 112, p. 535, 1977. [DOI] [PubMed] [Google Scholar]
- [18].Case DA, Berryman JT, Betz RM, Cerutti DS, Cheatham III TE, Darden TA, Duke RE, Giese TJ, Gohlke H, Goetz AW, Homeyer N, Izadi S, Janowski P, Kaus J, Kovalenko A, Lee TS, LeGrand S, Li P, Luchko T, Luo R, Madej B, Merz KM, Monard G, Needham P, Nguyen H, Nguyen HT, Omelyan I, Onufriev A, Roe DR, Roitberg A, Salomon-Ferrer R, Simmerling CL, Smith W, Swails J, Walker RC, Wang J, Wolf RM, Wu X, York DM and Kollman PA, “AMBER 2015,” San Francisco, 2015. [Google Scholar]
- [19].Allison SA and Tran VT, “Modeling the Electrophoresis of Rigid Polyions: Application to Lysozyme,” Biophysical Journal, vol. 68, pp. 2261–2270, 1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Cadman AD, Fleming R and Guy RH, “Diffusion of lysozyme chloride in water and aqueous potassium chloride solutions,” Biophysical Journal, vol. 37, no. 3, pp. 569–574, 1981. [PMC free article] [PubMed] [Google Scholar]
- [21].Sophianopoulos AJ, Rhodes CK, Holcomb DN and van Holde KE, “Physical Studies of Lysozyme,” The Journal of Biological Chemistry, vol. 237, no. 4, pp. 1107–1112, 1962. [PubMed] [Google Scholar]
- [22].Rupley JA and Careri G, “Protein hydration and function,” Advances in Protein Chemistry, vol. 41, pp. 37–172, 1991. [DOI] [PubMed] [Google Scholar]
- [23].Kuehner DE, Engmann J, Fergg F, Wernick M, Blanch HW and Prausnitz JM, “Lysozyme Net Charge and Ion Binding in Concentrated Aqueous Electrolyte Solutions,” The Journal of Physical Chemistry B, vol. 103, no. 8, pp. 1368–1374, 1999. [Google Scholar]
- [24].Schneidman-Duhovny D, Hammel M, Tainer JA and Sali A, “Accurate SAXS Profile Computation and its Assessment by Contrast Variation Experiments,” Biophysical Journal, vol. 105, pp. 962–974, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Delgado AV, Gonzalez-Caballero F, Hunter RJ, Koopal LK and Lyklema J, “Measurement and interpretation of electrokinetic phenomena,” Journal of Colloid and Interface Science, vol. 309, pp. 194–224, 2007. [DOI] [PubMed] [Google Scholar]
- [26].Chae KS and Lenhoff AM, “Computation of the Electrophoretic Mobility of Proteins,” Biophysical Journal, vol. 68, no. 3, pp. 1120–1127, 1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Einstein A, “A New Determination of Molecular Dimensions,” University of Zurich Thesis Dissertation, pp. 1–21, 1905. [Google Scholar]
- [28].Brown MA, Abbas Z, Kleibert A, Green RG, Goel A, May S and Squires TM, “Determination of Surface Potentials and Electrical Double Layer Structure at the Aqueous Electrolyte-Nanoparticle Interface,” American Physical Society Physical Review X, vol. 6, p. 011007, 2016. [Google Scholar]
- [29].Diamond R, “Real-space refinement of the structure of hen egg-white lysozyme,” Journal of Molecular Biology, vol. 82, no. 3, pp. 371–374, 1974. [DOI] [PubMed] [Google Scholar]
- [30].Marcus Y, “Ionic radii in aqueous solutions,” Chemical Reviews, vol. 88, no. 8, pp. 1475–1498, 1988. [Google Scholar]
- [31].Haynes CA, Sliwinsky E and Norde W, “Structural and Electrostatic Properties of Globular Proteins at a Polystyrene-Water Interface,” Journal of Colloid and Interface Science, vol. 164, pp. 394–409, 1994. [Google Scholar]
- [32].Doherty P and Benedek GB, “The effect of electric charge on the diffusion of macromolecules,” The Journal of Chemical Physics, vol. 61, no. 12, pp. 5426–5434, 1974. [Google Scholar]
- [33].Stephen MJ, “Spectrum of light scattered from charged macromolecules in solution,” The Journal of Chemical Physics, vol. 55, no. 8, pp. 3878–3883, 1971. [Google Scholar]
- [34].Schor R and Serrallach EN, “Theoretical studies of the translational diffusion coefficient of charged macromolecules applied to bovine serum albumin,” The Journal of Chemical Physics, vol. 70, pp. 3012–3015, 1979. [Google Scholar]
- [35].Henry DC, “The Cataphoresis of Suspended Particles. Part I. The Equation of Cataphoresis,” Proceedings of the Royal Society A, vol. 133, pp. 106–129, 1931. [Google Scholar]
- [36].Kemp I and Rideal EK, “On the relation between particle size and cataphoretic mobility,” Transactions of the Faraday Society, vol. 31, pp. 1347–1357, 1935. [Google Scholar]
- [37].Ottewill RH and Shaw JN, “Electrophoretic Stuides on Polystyrene Latices,” Journal of Electroanalytical Chemistry and Interfacial Electrochemistry, vol. 37, no. 1, pp. 133–142, 1972. [Google Scholar]
- [38].Basak SK and Ladisch MR, “Correlation of Electrophoretic Mobilities of Proteins and Peptides with Their Physicochemical Properties,” Analytical Biochemistry, vol. 226, pp. 51–58, 1995. [DOI] [PubMed] [Google Scholar]
- [39].Dolinsky TJ, Czodrowski P, Li H, Nielsen JE, Jensen JH, Klebe G and Baker NA, “PDB2PQR: expanding and upgrading automated preparation of biomolecular structures for molecular simulations,” Nucleic Acids Research, vol. 35, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Dolinsky TJ, Nielsen JE, McCammon JA and Baker NA, “PDB2PQR: an automated pipeline for the setup of Poisson-Boltzmann electrostatics calculations,” Nucleic Acids Research, vol. 32, pp. W665–W667, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Olsson MHM, Sondergaard CR, Rostkowski M and Jensen JH, “PROPKA3: Consistent Treatment of Internal and Surface Residues in Empirical pKa Predictions,” Journal of Chemical Theory and Computation, vol. 7, pp. 525–537, 2011. [DOI] [PubMed] [Google Scholar]
- [42].Laliberte M, “Model for Calculating the Viscosity of Aqueous Solutions,” Journal of Chemical and Engineering Data, vol. 52, no. 2, pp. 321–335, 2007. [Google Scholar]
- [43].Goncalves FA and Kestin J, “The viscosity of NaCl and KCl solutions in the range 25 - 50C,” Berichte der Bunsengesellschaft fur physikalische chemie, vol. 81, no. 11, pp. 1156–1161, 1977. [Google Scholar]
- [44].Ohshima H, “A Simple Expression for Henry’s Function for the Retardation Effect in Electrophoresis of Spherical Colloidal Particles,” Journal of Colloid and Interface Science, vol. 168, pp. 269–271, 1994. [Google Scholar]
- [45].Parmar AS and Muschol M, “Hydration and Hydrodynamic Interactions of Lysozyme: Effects of Chaotropic and Kosmotropic Ions,” Biophysical Journal, vol. 97, no. 2, pp. 590–598, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Xu R, Particle Characterization: Light Scattering Methods, New York: Kluwer Academic Publishers, 2002. [Google Scholar]
- [47].Malvern, “Zeta potential quality report for the Zetasizer Nano,” Malvern, [Online]. Available: http://www.malvern.com/en/support/resource-center/technical-notes/TN101104ZetaPotentialQualityReportZetasizerNano.aspx. [Google Scholar]
- [48].Abramson HA, Gorin MH and Moyer LS, “THE POLAR GROUPS OF PROTEIN AND AMINO ACID SURFACES IN LIQUIDS,” Chemical Reviews, vol. 24, no. 2, pp. 345–366, 1939. [Google Scholar]
- [49].Maier JA, Martinez C, Kasavajhala K, Wickstrom L, Hauser KE and Simmerling C, “ff14SB: Improving the accuracy of protein side chain and backbone parameters from ff99SB,” Journal of Chemical Theory and Computation, vol. 11, pp. 3696–3713, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Baker NA, Sept D, Joseph S, Holst MJ and McCammon JA, “Electrostatics of nanosystems applications to microtubules and the ribosome,” Proceedings of the National Academy of Sciences, vol. 98, no. 18, pp. 10037–10041, 2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Neves-Petersen MT and Petersen SB, “Protein electrostatics: A review of the equation and methods used to model electrostatic equations in biomolecules - Applications in biotechnology,” Biotechnology Annual Review, vol. 9, pp. 315–395, 2003. [DOI] [PubMed] [Google Scholar]
- [52].Malmberg CG and Maryott AA, “Dielectric Constant of Water from 0 to 100 C,” Journal of Research of the National Bureau of Standards, vol. 56, no. 1, pp. 1–8, 1956. [Google Scholar]
- [53].Sanner MF, Olson AJ and Spehner J-C, “Reduced Surface: An Efficient Way to Compute Molecular Surfaces,” Biopolymers, vol. 38, no. 3, pp. 305–320, 1996. [DOI] [PubMed] [Google Scholar]
- [54].de la Torre JG, Huertas ML and Carrasco B, “Calculation of hydrodynamic properties of globular proteins from their atomic-level structure,” Biophysical Journal, vol. 78, pp. 719–730, 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Rawat N and Biswas P, “Shape, flexibility and packing of proteins and nucleic acids in complexes,” Phys. Chem. Chem. Phys, vol. 13, pp. 9632–9643, 2011. [DOI] [PubMed] [Google Scholar]
- [56].Hidalgo-Alvarez R, Martin A, Fernandez A, Bastps D, Martinez F and de las Nieves FJ, “Electrokinetic properties, colloidal stability and aggregation kinetics of polymer colloids,” Advances in Colloid and Interface Science, vol. 67, pp. 1–118, 1996. [Google Scholar]
- [57].Shaw DJ, Introduction to Colloid and Surface Chemistry, Burlington, MA: Elsevier Science, 1992. [Google Scholar]
- [58].Wiersema PH, Loeb AL and Overbeek JTG, “Calculation of the Electrophoretic Mobility of a Spherical Colloid Particle,” Journal of Colloid and Interface Science, vol. 22, pp. 78–99, 1966. [Google Scholar]
- [59].Encyclopedia of Colloid and Interface Science, New York, NY: Springer, 2013, pp. 1421–1432. [Google Scholar]
- [60].Sorret LL, DeWinter MA, Schwartz DK and Randolph TW, “Challenges in Predicting Protein-Protein Interactions from Measurements of Molecular Diffusivity,” Biophysical Journal, vol. 111, pp. 1831–1824, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Muthukumar M, “Ordinary-extraordinary transition in dynamics of solutions of charged macromolecules,” Proceedings of the National Academy of Sciences, vol. 113, no. 45, pp. 12627–12632, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Zhang Y and Cremer PS, “Interactions between macromolecules and ions: the Hofmeister series,” Current Opinion in Chemical Biology, vol. 10, pp. 658–663, 2006. [DOI] [PubMed] [Google Scholar]
- [63].Collins KD, “Ions from the Hofmeister series and osmolytes: effects on proteins in solution and in the crystallization process,” Methods, vol. 34, pp. 300–311, 2004. [DOI] [PubMed] [Google Scholar]
- [64].Rubio-Hernandez FJ, Carrique F and Ruiz-Reina E, “The primary electroviscous effect in colloidal suspensions,” Advances in Colloid and Interface Science, vol. 107, pp. 51–60, 2004. [DOI] [PubMed] [Google Scholar]
- [65].Apelblat A, “Effect of temperature on compressibility properties of 0.1, 0.5 and 1.0 molal solutions of alkali metal nitrates. Part 2. Aqueous solutions of lithium nitrate, sodium nitrate and potassium nitrate in the 287.15K to 353.15K temperature range,” Journal of Molecular Liquids, vol. 242, pp. 1236–1247, 2017. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.