Selective hyperpolarization of heteronuclear singlet states via pulsed microtesla SABRE

Abstract

Signal Amplification By Reversible Exchange (SABRE) and its heteronuclear variant SABRE in SHield Enables Alignment Transfer to Heteronuclei create large nuclear magnetization in target ligands, exploiting level crossings in an iridium catalyst that transiently binds both the ligands and parahydrogen. This requires a specific, small magnetic field to match Zeeman splittings to scalar couplings. Here, we explore a different strategy, direct creation of heteronuclear singlet states in the target ligands, which produces enhanced signals at other field strengths, including zero field. We also show that pulsed methods (including pulsed field nulling) coherently and selectively pump such singlets, affording a significant enhancement on the resulting hyperpolarization.

I. INTRODUCTION

Hyperpolarization modalities afford signal enhancements of nuclear magnetic resonance (NMR) techniques that are many orders of magnitude greater than those derived by thermal polarization. Such methods transfer population from a polarization source, typically a spin state prepared with a population on the order of unity, into magnetization on target nuclei. Signal Amplification By Reversible Exchange,^1–6 or SABRE, is a nonhydrogenative variant of Para-Hydrogen Induced Polarization (PHIP)^7,8 that derives hyperpolarization from reversible interactions of substrates with parahydrogen, the readily prepared singlet spin isomer of dihydrogen, via association with an iridium catalyst.^9–12 SABRE has a distinct advantage over other hyperpolarization techniques because the polarization source is prepared as a singlet. This allows one to directly transfer the p-H₂ singlet order onto target spin pairs and store their hyperpolarization in a singlet state at any magnetic field (Table I).

TABLE I.

Acetonitrile-PTC J-coupling network.²⁰

2JHH	−8.0 Hz
2JNH	−25.4 Hz
3JCH	12.4 Hz
1JNC	−31.4 Hz
3JNH	−1.7 Hz
2JCH	−9.9 Hz

While the original implementation of SABRE targets the hyperpolarization of ¹H nuclei, its heteronuclear variant SABRE in SHield Enables Alignment Transfer to Heteronuclei (SABRE-SHEATH) selectively converts the spin-order of the p-H₂ into a chosen magnetized state on the substrate nuclei when held at a μT field.^13–17 For the canonical AA′B and AA′BB′ SABRE systems, the choices for magnetized states on the target nuclei are the Zeeman eigenstates, $\left|\alpha \right.⟩$ or $\left|\beta \right.⟩$, but the targeted state can be, in principle, significantly more complicated with larger spin systems. Recent developments in pulse sequence design have afforded the ability to probe SABRE dynamics at μT fields. Lindale et al. showed the ability to coherently pump heteronuclear Zeeman states via the use of a coherent SABRE-SHEATH pulse sequence.¹⁸

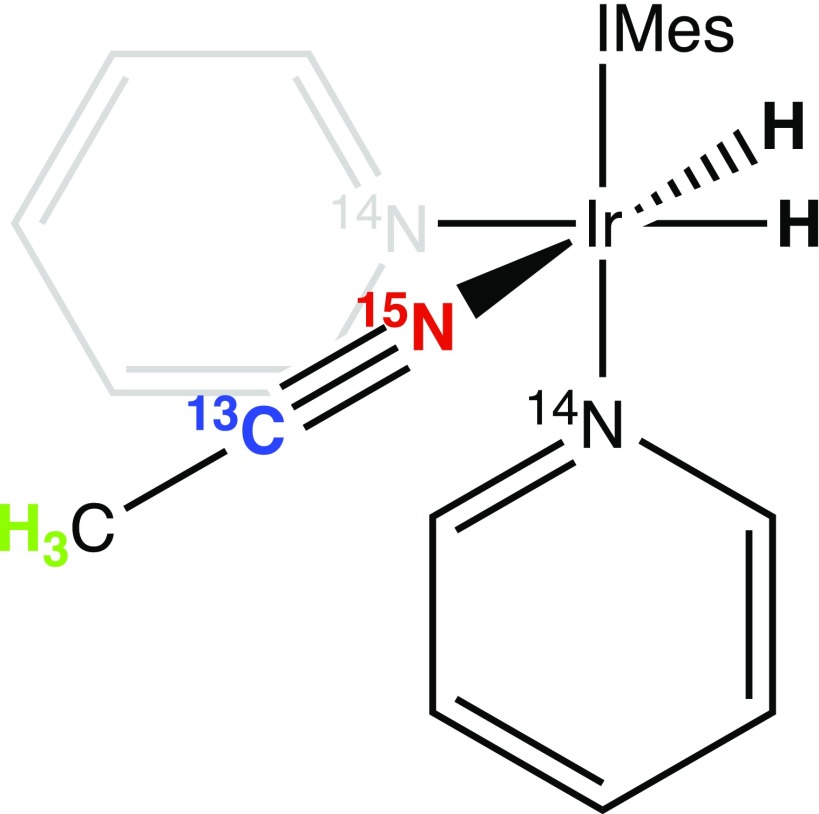
Coherent control of the SABRE-SHEATH dynamics hinges on the ability to truncate the evolution of certain states with the removal of appropriate conditions for polarization transfer. In the most common cases studied to date, the ligands have only one dominant NMR-active nucleus and the dynamics are defined primarily by matching the Zeeman energy difference between hydrogen and the heteronucleus (e.g., ¹⁵N) to other terms, such as the hydride J-coupling. The most notable exception is the family of diazirines,¹⁵ where nitrogen-nitrogen singlets can be directly pumped. Selective creation of singlet states between equivalent spins is interesting since these are protected from certain relaxation mechanisms even at the high field. Here, we explore singlets between nuclei with different γ values (¹³C and ¹⁵N) which at zero to ultralow field conditions remain as stationary eigenstates of the Hamiltonian;¹⁹ a practical and potentially very general example is the doubly labeled nitrile group, which can be inserted into a very wide range of biologically compatible species. Here, we demonstrate that coherent SABRE-SHEATH may be used to coherently and selectively pump the heteronuclear, 7-spin 1-¹³C,¹⁵N-acetonitrile system (Fig. 1) into its hyperpolarized singlet state and that the matching conditions are quite different than normal SABRE-SHEATH (for example, zero magnetic field works sufficiently to transfer order out of the parahydrogen-produced hydride resonances).

FIG. 1.

SABRE complex. The PTC places the 1-¹³C,¹⁵N-acetonitrile, and p-H₂ derived hydrides in magnetic contact, allowing population transfer.

II. FUNDAMENTALS OF COHERENT SABRE-SHEATH

Here, we describe the basis for coherently pumping states via SABRE-SHEATH. In terms of Zeeman product states, the singlet of the parahydrogen-derived hydrides is given by

$$\left|S_H\right.⟩=\frac{1}{\sqrt{2}}\left(\left|\alpha \beta \right.⟩-\left|\beta \alpha \right.⟩\right).$$ (1)

Accessing this polarization source requires breaking the symmetry of the singlet state, which is achieved when the p-H₂ binds to the polarization transfer complex or PTC and the parahydrogen-derived hydrides become inequivalently J-coupled to other spins. This allows population to flow between states when the appropriate level anticrossing (LAC) is established. For heteronuclei such as ¹⁵N, these are usually established at fields on the order of ≈0.5 μT. The Hamiltonian for the SABRE-SHEATH system at this low field is given by the sum of the Zeeman terms and the J-coupling terms in the strong-coupling limit

$$\begin{array}{ccc}\hfill Ĥ& =\hfill & \sum _{i=1}{\omega }_{iI}{Î}_{z,i}+\sum _{k=1}{\omega }_{kS}{Ŝ}_{z,k}+2\pi \sum _{i<j}{\mathcal{J}}_{ij}{Î}_i\cdot {Î}_j\hfill \\ \hfill & \hfill & +2\pi \sum _{k<l}{\mathcal{J}}_{kl}{Ŝ}_k\cdot {Ŝ}_l+2\pi \sum _{i<k}{\mathcal{J}}_{ik}{Î}_i\cdot {Ŝ}_j,\hfill \end{array}$$ (2)

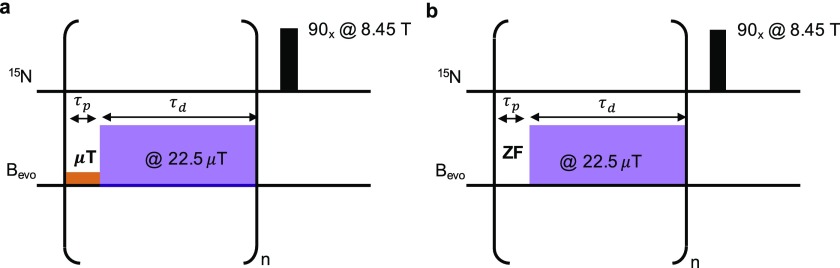
where ω_iI and ω_iS are the Larmor frequencies of the hydrogen atoms and heteronuclei, respectively, while ${\mathcal{J}}_{ij}$ represents the J-coupling between spins i and j. The conventional SABRE-SHEATH experiment simply holds the sample at the field required to satisfy the LAC condition for a time proportional to T₁ of the target nucleus. Coherent control of this process can be achieved by pulsing the μT field, as shown in Fig. 2(a), which allows truncation of the evolution in the following manner: during the pulse, LACs are established allowing coherent population transfer from the hydrides to the target nuclei. Interwoven between pulses are delay times during which the field strength is approximately 50–100 times higher. During these delay times, evolution of the spin dynamics is stopped while the polarized ligand and depleted o-H₂ are allowed to dissociate and the new ligand and p-H₂ rebind. In this way, polarization of the ligands can be built up in a coherent manner.

FIG. 2.

Coherent SABRE-SHEATH pulse sequences: (a) microtesla pulses are applied to coherently pump Zeeman states and (b) pulse sequence for coherently pumping singlet states. ZF refers to zero-field.

Coherent SABRE-SHEATH [Fig. 2(a)] has been shown to effectively hyperpolarize Zeeman states in an AA′B-spin system, such as ¹⁵N acetonitrile in unlabeled pyridine. Calculation of the matrix elements of the Hamiltonian for this system reveals two orthogonal 3 × 3 subspaces, one of which is given by

$$\begin{array}{c}\hfill T_H^{+}{\beta }_N\hfill \\ \hfill T_H^0{\alpha }_N\hfill \\ \hfill S_H{\alpha }_N\hfill \end{array}\left(\begin{array}{ccc}\hfill {\omega }_H-\frac{{\omega }_N}{2}+\frac{\pi }{2}\left(J_{HH}-J_{NH}\right)\hfill & \hfill \frac{\pi J_{NH}}{\sqrt{2}}\hfill & \hfill -\frac{\pi J_{NH}}{\sqrt{2}}\hfill \\ \hfill \frac{\pi J_{NH}}{\sqrt{2}}\hfill & \hfill \frac{{\omega }_N}{2}+\frac{\pi J_{HH}}{2}\hfill & \hfill \frac{\pi J_{NH}}{2}\hfill \\ \hfill -\frac{\pi J_{NH}}{\sqrt{2}}\hfill & \hfill \frac{\pi J_{NH}}{2}\hfill & \hfill \frac{{\omega }_N}{2}-\frac{3\pi J_{HH}}{2}\hfill \end{array}\right).$$ (3)

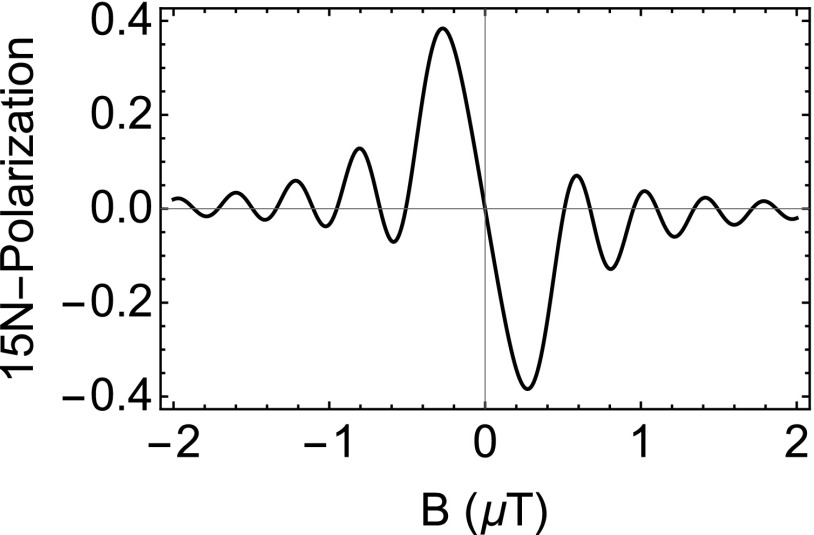
The off-diagonal $-\frac{\pi J_{NH}}{\sqrt{2}}$ coupling connects the S_Hα_N and $T_H^{+}{\beta }_N$ states, allowing for transitions between these two states at the proper magnetic field matching conditions. A simulated field dependence is shown in Fig. 3.

FIG. 3.

Simulation without exchange of magnetic field dependence on ¹⁵N-acetonitrile (ignoring methyl protons) hyperpolarization via SABRE-SHEATH. Polarization after 60 ms of evolution time is plotted.

Maximum polarization is achieved at ≈±0.3 μT. This forms the basis for hyperpolarizing traditional Zeeman states at μT fields via SABRE-SHEATH or coherent SABRE-SHEATH.

The complex shown in Fig. 1 can be treated as a 7-spin system consisting of the two hydrides and the five spins of the 1-¹³C,¹⁵N-acetonitrile. This is because the quadrupolar nuclei do not interact coherently with the system since their lifetimes are so short and so they are ignored. Furthermore, the pyridine protons are ignored here since there is no resonance connecting them to the hydrides at near zero-fields (ZF), which is the focus here. In the strong coupling limit, the SABRE-SHEATH Hamiltonian thus consists of one 6 × 6 and two 4 × 4 orthogonal subspaces, which we present here for demonstrative purposes. The acetonitrile methyl protons are not shown for clarity. The two 4 × 4 blocks are given by

$$\begin{array}{ccc}\hfill \begin{array}{c}\hfill T_H^{\pm }{T}_{NC}^0\hfill \\ \hfill T_H^0{T}_{NC}^{\pm }\hfill \\ \hfill T_H^{\pm }{S}_{NC}\hfill \\ \hfill S_H{T}_{NC}^{\pm }\hfill \end{array}\left(\begin{array}{cccc}\hfill \pm {\omega }_H\hfill & \hfill \pi J_{\mathrm{\Sigma }}\hfill & \hfill \frac{{\omega }_N-{\omega }_C\pm 2\pi J_{\mathrm{\Delta }}}{2}\hfill & \hfill \mp \pi J_{\mathrm{\Sigma }}\hfill \\ \hfill \pi J_{\mathrm{\Sigma }}\hfill & \hfill \pm \frac{\left({\omega }_N+{\omega }_C\right)}{2}\hfill & \hfill \mp \pi J_{\mathrm{\Delta }}\hfill & \hfill \pm \pi J_{\mathrm{\Sigma }}\hfill \\ \hfill \frac{{\omega }_N-{\omega }_C\pm 2\pi J_{\mathrm{\Delta }}}{2}\hfill & \hfill \mp \pi J_{\mathrm{\Delta }}\hfill & \hfill \pm {\omega }_H-2\pi J_{NC}\hfill & \hfill \pi J_{\mathrm{\Delta }}\hfill \\ \hfill \mp \pi J_{\mathrm{\Sigma }}\hfill & \hfill \pm \pi J_{\mathrm{\Sigma }}\hfill & \hfill \pi J_{\mathrm{\Delta }}\hfill & \hfill \frac{\pm \left({\omega }_N+{\omega }_C\right)-4\pi J_{HH}}{2}\hfill \end{array}\right),& \hfill & \hfill \\ \hfill & \hfill & \hfill \end{array}$$ (4)

where $J_{\mathrm{\Sigma }}=\frac{J_{NH}+J_{CH}}{2}$, $J_{\mathrm{\Delta }}=\frac{J_{NH}-J_{CH}}{2}$, and ω_1H = ω_2H = ω_H at μT fields; note that for positive magnetic field, ω_C and ω_H are negative, but ω_N is positive due to the signs of the gyromagnetic ratios. It is clear from Eq. (4) that the magnitude of the evolution field will dictate into which state (singlet or magnetized) the free species is pumped. This field is to be optimized to reduce the amount of magnetization generated while maximizing the singlet population. From Eq. (4), the $S_H{T}_{NC}^{\pm }$ and $T_H^{\pm }{S}_0^{NC}$ states have energies $\frac{\pm \left({\omega }_N+{\omega }_C\right)-4\pi J_{HH}}{2}$ and ±ω_H − 2πJ_NC, respectively. The appropriate resonance conditions for the $S_H{T}_{NC}^{\pm }$ and $T_H^{\pm }{S}_0^{NC}$ transitions are therefore

$$\frac{\pm \left({\omega }_N+{\omega }_C\right)}{2}\mp {\omega }_H\approx \pi J_{\mathrm{\Delta }}+2\pi J_{HH}-2\pi J_{NC}.$$ (5)

We immediately see that at a nonzero field, the resonance condition for the $S_H{T}_{NC}^{+}$ to $T_H^{+}{S}_{NC}$ and $S_H{T}_{NC}^{-}$ to $T_H^{-}{S}_{NC}$ transitions is not equivalent. This will lead to overpopulation of the $T_{NC}^{+}$ or $T_{NC}^{-}$ states and creation of observable magnetization. While some S_NC will be produced at this field, it will quickly evolve into a triplet state due to the difference in carbon and nitrogen Larmor frequencies. However, at the zero field, expression (5) becomes degenerate for the $S_H{T}_{NC}^{\pm }$ to $T_H^{\pm }{S}_{NC}$ transitions. As a result, we achieve a buildup of S_NC without overpopulation of the $T_{NC}^{+}$ or $T_{NC}^{-}$ states. Furthermore, at the zero field, the S_NC singlet will not convert as rapidly into triplet states since there is no longer any difference in Larmor frequencies. Of course, transitions between every state in each orthogonal subspace can occur and the dynamics are not as simple as isolating the $S_H{T}_{NC}^{\pm }$ to $T_H^{\pm }{S}_{NC}$ transitions. Nevertheless, since the energy of the $T_{NC}^{+}$ and $T_{NC}^{-}$ states are degenerate at the zero field, these states will not be preferentially created or depleted due to any other transition elements, ensuring selective creation of a heteronuclear singlet state.

As a result, zero or nearly zero field conditions are required to most effectively pump and protect heteronuclear singlet states. At the zero-field, the Larmor frequency terms disappear and only the J-coupling Hamiltonian remains

$${Ĥ}_{\mathcal{J}}=2\pi \sum _{i<j}{\mathcal{J}}_{ij}{Î}_i\cdot {Î}_j+2\pi \sum _{i<j}{\mathcal{J}}_{ij}{Ŝ}_i\cdot {Ŝ}_j+2\pi \sum _{i<j}{\mathcal{J}}_{ij}{Î}_i\cdot {Ŝ}_j.$$ (6)

In the zero field limit, the subspaces of the Hamiltonian become less highly structured and the two 4 × 4 blocks given above become

$$\begin{array}{c}\hfill T_H^{\pm }{T}_{NC}^0\hfill \\ \hfill T_H^0{T}_{NC}^{\pm }\hfill \\ \hfill T_H^{\pm }{S}_{NC}\hfill \\ \hfill S_H{T}_{NC}^{\pm }\hfill \end{array}\left(\begin{array}{cccc}\hfill 0\hfill & \hfill \pi J_{\mathrm{\Sigma }}\hfill & \hfill \pm \pi J_{\mathrm{\Delta }}\hfill & \hfill \mp \pi J_{\mathrm{\Sigma }}\hfill \\ \hfill \pi J_{\mathrm{\Sigma }}\hfill & \hfill 0\hfill & \hfill \mp \pi J_{\mathrm{\Delta }}\hfill & \hfill \pm \pi J_{\mathrm{\Sigma }}\hfill \\ \hfill \pm \pi J_{\mathrm{\Delta }}\hfill & \hfill \mp \pi J_{\mathrm{\Delta }}\hfill & \hfill -2\pi J_{NC}\hfill & \hfill \pi J_{\mathrm{\Delta }}\hfill \\ \hfill \mp \pi J_{\mathrm{\Sigma }}\hfill & \hfill \pm \pi J_{\mathrm{\Sigma }}\hfill & \hfill \pi J_{\mathrm{\Delta }}\hfill & \hfill -2\pi J_{HH}\hfill \end{array}\right).$$ (7)

Note that at the zero-field both of the magnetized $T_{NC}^{\pm }$ states are pumped equivalently, leading to the selective hyperpolarization of the heteronuclear singlet. However, there are J-coupling allowed transitions between each of the four states. As such, the dynamics of this system is quite complex, especially considering the additional 6 × 6 subspace that also connects other S_H and S_NC states.

Simulating SABRE dynamics, even for 3- or 4-spin systems, is inherently challenging due to the chemical exchange of the ligands and p-H₂ from the PTC, both of which occur on the time scale of the polarization transfer. Additionally, perturbation theory does not apply here as the nondiagonal elements in Eq. (7) are similar in magnitude or even larger than the diagonal elements. As such, the position of the expected level anticrossings may deviate from those predicted by perturbation theory. Therefore, a quantum Monte Carlo (QMC) approach¹⁸ was implemented to fully simulate the evolution of the 7-spin system in Fig. 1 (i.e., the full 128 × 128 Hamiltonian) under the pulse sequence in Fig. 2(b) (see the supplementary material for details). We would like to note that this spin system is outside of the computational limits of the superoperator methods that have been previously used to describe SABRE dynamics.

III. METHODS

Solutions of 1-¹³C,¹⁵N-acetonitrile (100 mM) with pyridine (33 mM; natural abundance) with IrIMes(COD)Cl (5 mM); IMes = 1,3-bis(2,4,6-trimethylphenyl)-imidazol-2-ylidene, COD = 1,5-cyclooctadiene in methanol-d₄ were bubbled with p-H₂ gas (50%) through the solution to create the active [Ir(H)₂(IMes)(Pyr)₂(¹³C,¹⁵N-ACN)₃] species; ACN = acetonitrile. The samples were then hyperpolarized at various evolution fields (B_evo) in a triple μ-metal shield with solenoid compensation coils. After a hyperpolarization time of 45 s, which was determined to be the optimal signal buildup time, the sample was transferred to an 8.45 T Bruker 360DX NMR Spectrometer for detection.

The spin dynamics at the zero field were investigated using the pulse sequence in Fig. 2(b). Zero field conditions were stroboscopically pumped for a variable time, τ_p (0–100 ms). The triple μ-metal shield with solenoid compensation coils was powered by an arbitrary wavefunction generator that controlled the pulse length and duration. Spin dynamics are stopped when a high magnetic field (≈22.5 µT) is turned on for time length τ_d = 350 ms, a previously optimized value,¹⁸ in-between each zero field pulse. The pulse sequence is repeated for 60 s, and the signal is acquired after transfer to the 8.45 T NMR spectrometer.

Due to the difference in Larmor frequencies between carbon and nitrogen, transverse nuclear magnetization may still be detected after applying a $\frac{\pi }{2}$-pulse to a population of heteronuclear singlet. This will give rise to an antiphase signal under the condition of sudden transfer to an arbitrarily higher magnetic field. On the other hand, the triplet state gives a line shape that is symmetric about the center frequency. This requires redefining what spectral response constitutes a singlet or triplet. We define the singlet state population for nucleus “n” as

$$S_n=\frac{I\left[\mathrm{\Omega }>0\right]-I\left[\mathrm{\Omega }<0\right]}{2}$$ (8)

and the magnetized state population as

$$M_n=\frac{I\left[\mathrm{\Omega }>0\right]+I\left[\mathrm{\Omega }<0\right]}{2},$$ (9)

where I[Ω > 0] is the spectral integration over Ω > 0 and Ω is the resonance offset. It is important to note that in experiment, this must be performed on both nuclear channels, which when added would give the expected zero net-magnetization for a singlet state.

IV. RESULTS AND DISCUSSION

The dynamics of the polarization transfer process depend on the J-coupling network of the 7-spin system in Fig. 1. The ²J_NH = −25.4 Hz, ¹J_NC = −31.4 Hz, and ³J_CH = 12.4 Hz J-couplings were determined from line shape analysis of experimental spectra (see the supplementary material). Importantly, the ¹J_NC of the bound species (−31.4 Hz) differs significantly from the ¹J_NC of the free species (≈−17 Hz).

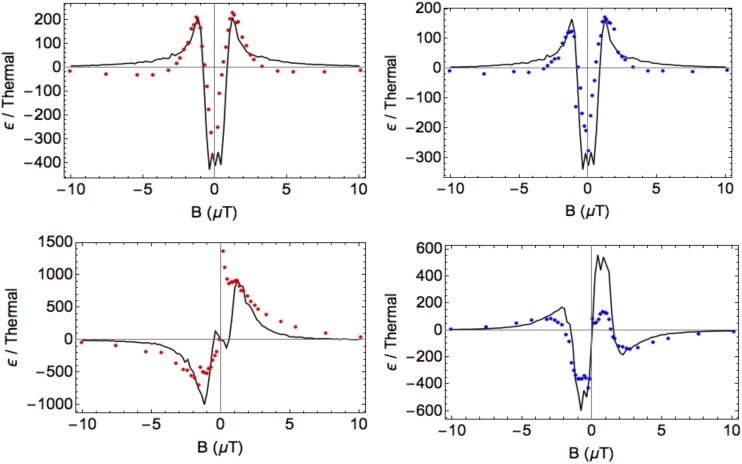
QMC simulations of singlet and magnetization creation as a function of B_evo are shown in Fig. 4 (see the supplementary material for details). Indeed, we do see a maximum singlet creation with no net magnetization at the zero field. The experimental magnetic field profiles confirm these simulations (Fig. 4).

FIG. 4.

Creation of singlet (upper) or magnetized (lower) states on ¹⁵N (red) or ¹³C (blue) as a function of B_evo compared to numerical simulation (black traces). Asymmetry of the experimental data is due to the differential destruction of magnetization as the sample is rapidly removed from the SABRE-SHEATH coil.

We see general agreement between the simulated and experimental singlet B_evo dependence, with some broadening in the simulations with respect to the experimental data. For magnetized states, spin order can transfer directly to the ¹⁵N since it is directly bound to the iridium complex. However, spin order can transfer to the ¹³C either directly through the ³J_CH coupling or indirectly through the ¹J_NC coupling. As a result, magnetization B_evo dependence is not the same for ¹⁵N and ¹³C. In this case as well, there is good qualitative agreement between the simulated magnetization B_evo dependence and experimental data. The discrepancy in the ¹³C magnetization simulation at positive fields arises from the fact that experimentally, ¹³C magnetization is destroyed after exposure to positive B_evo fields as a result of interaction with Earth’s magnetic field after the sample is removed from the magnetic shield. Although significant singlet population is formed at nonzero fields such as 1.68 μT, there is also a significant buildup of magnetized states at these nonzero fields. As a result, the zero field is indeed the optimal matching condition to selectively create a heteronuclear singlet state.

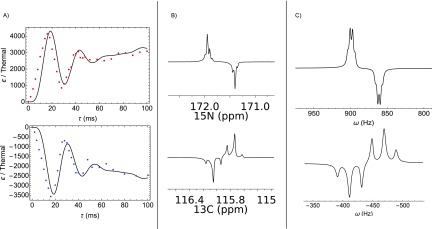
The simulated and experimental dynamics for the formation of heteronuclear ¹³C, ¹⁵N singlet at zero field is shown in Fig. 5(a). The dynamics of the coherent SABRE-SHEATH experiment are extraordinarily complex, as they depend on the evolution field and the J-couplings of the 7-spin system. However, when pulsing the zero field, the Hamiltonian is not as highly structured as all the Zeeman terms drop out [see Eq. (7)]. As a result, they exhibit rather simple oscillations [Fig. 5(a)]. The dynamics are further characterized by a rising baseline dictated by the rate of parahydrogen exchange and damped oscillations arising from the short lifespan (≈25 ms) of acetonitrile on the complex.

FIG. 5.

Simulated and experimental spin dynamics of the creation of heteronuclear singlet states. (a) Experimental dynamics of pumping heteronuclear singlet state at 0 µT on the ¹⁵N channel (red) and ¹³C channel (blue). The black trace is a numerical quantum Monte Carlo simulation including chemical exchange of acetonitrile and p-H₂. (b) Experimental heteronuclear singlet spectra on the ¹⁵N channel (top) and ¹³C channel (bottom) after an 8 ms pulse length. (c) Simulated spectra of singlet states on the ¹⁵N channel (top) and ¹³C channel (bottom).

Simulations of the dynamics (detailed in the supplementary material) are shown in Fig. 5(a) and accurately predict the experimental results. The inclusion of ligand exchange leads to the rather quick damping of the coherent evolution. Additionally, modulating the rate of parahydrogen exchange changes the slope of the baseline, which is ultimately the steady-state SABRE-SHEATH hyperpolarization value. We immediately see from the first peak at 20 ms that larger polarizations than static SABRE-SHEATH are achievable via the coherently pumping zero field. Enhancements in this case are rather low, but when the sample concentration is optimized, enhancements on the order of 4000 times larger than thermal polarization were achieved.

The simulation of heteronuclear singlet dynamics is identical for both the nitrogen and carbon nuclei. However, the sign of the signal is inverted for carbon since the two spins have experimentally opposite gyromagnetic ratio. The characteristic nitrogen spectrum after an 8 ms zero field pulse [Fig. 5(b)] shows an antiphase doublet of quartets split by the carbon and methyl proton spins. The carbon signal is likewise split by the nitrogen spin and the three methyl protons, yet the larger ²J_CH of −9.9 Hz leads to the overlap of the two innermost peaks, resulting in 6 overall peaks [Fig. 5(b)]. Carbon and nitrogen spectra after an 8 ms zero field pulse were simulated. Chemical exchange was ignored since the pulse length was so short in this case. The match between the simulated and experimental spectra is excellent, as the simulations reproduce the characteristic antiphase signal on both channels [Fig. 5(c)].

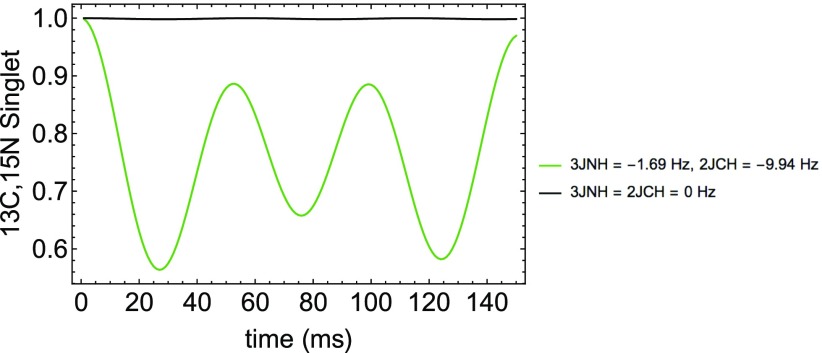
Now that we have shown the ability to pump singlet population into 1-¹³C, ¹⁵N-acetonitrile, we can address the stability of the singlet. Of course at high fields, the singlet will immediately convert into triplet states due to the difference in Larmor frequencies between ¹³C and ¹⁵N. However, near the zero field, the stability of the singlet is dictated by the size of the coupling between the two nuclei.²¹ The near zero field evolution of the ¹³C, ¹⁵N singlet in acetonitrile is shown in Fig. 6. When the coupling to the methyl protons in acetonitrile is ignored, the heteronuclear singlet is very stable, as expected. However, when the ³J_NH and ²J_CH couplings are reinstated, population will flow out of the singlet state. Starting with an initially 100% polarized singlet, about a quarter will flow out into the proton states. Thus, the buildup time is partly limited by the T₁ of the protons, rather than the lifetime of the singlet. SABRE-SHEATH for singlet creation, therefore, works best when the J-coupling between the target ligand and auxiliary protons in the target molecule (here the methyl group) is significantly smaller than the J-coupling between the target ligand and the hydrides. If these J-couplings are comparable, the resonance conditions that promote population transfer to the heteronuclei will also promote further migration of population through the flip-flop terms in the scalar coupling. For magnetization creation (in this and other SABRE-SHEATH targets), where the field is set to make the resonance frequency difference between the hydride protons and the target heteronucleus match the J-coupling between the hydride protons, the critical condition is slightly different: the J-coupling between the target heteronucleus and auxiliary protons should be significantly smaller than the J-coupling between the hydride protons. Otherwise, population will also flow resonantly out of the heteronucleus.

FIG. 6.

Simulated evolution of ¹³C, ¹⁵N singlet in acetonitrile in solution. Starting with 100% singlet, the free species is evolved at 0.05 µT. The black curve is the evolution of a 2-spin system ignoring the methyl protons; the heteronuclear singlet is protected since |¹J_NC| is much greater than the resonance frequency difference between ¹³C and ¹⁵N. The green curve is the evolution of the 5-spin system, including the methyl protons. The singlet state remains mostly protected, but slow population flow into (shorter lived) hydrogen magnetization will reduce the maximum buildup of singlet molecules in solution.

V. CONCLUSION AND OUTLOOK

We have shown, for the first time, the possibility of creating a heteronuclear spin singlet state between ¹⁵N and ¹³C nuclei. Hyperpolarization via SABRE-SHEATH allows for selective creation of singlet states in highly complex systems, resulting in a signal enhancement of up to 4000× thermal polarization. Furthermore, we have shown coherent control of the dynamics of the heteronuclear polarization transfer process via pumping singlet to singlet transitions in a complex regime. This opens the avenue toward selectively pumping singlet and other non-Zeeman states, which have enormous potential in spectroscopic and imaging applications.

SUPPLEMENTARY MATERIAL

The supplementary material includes information on spectral line shapes resulting from singlet or magnetization order on the ¹³C,¹⁵N spin pair. Additionally, it contains spectra of the PTC from which J-couplings are derived, notes on the QMC algorithm, and records of maximum singlet signal enhancements and singlet lifetimes.