Sound-source localization as a multisystem process: The Wallach azimuth illusion

Abstract

Wallach [J. Exp. Psychol. 27, 339–368 (1940)] described a “2-1” rotation scenario in which a sound source rotates on an azimuth circle around a rotating listener at twice the listener's rate of rotation. In this scenario, listeners often perceive an illusionary stationary sound source, even though the actual sound source is rotating. This Wallach Azimuth Illusion (WAI) was studied to explore Wallach's description of sound-source localization as a required interaction of binaural and head-position cues (i.e., sound-source localization is a multisystem process). The WAI requires front-back reversed sound-source localization. To extend and consolidate the current understanding of the WAI, listeners and sound sources were rotated over large distances and long time periods, which had not been done before. The data demonstrate a strong correlation between measures of the predicted WAI locations and front-back reversals (FBRs). When sounds are unlikely to elicit FBRs, sound sources are perceived veridically as rotating, but the results are listener dependent. Listeners' eyes were always open and there was little evidence under these conditions that changes in vestibular function affected the occurrence of the WAI. The results show that the WAI is a robust phenomenon that should be useful for further exploration of sound-source localization as a multisystem process.

I. INTRODUCTION

Wallach published three papers (Wallach, 1938, 1939, 1940) regarding sound-source localization when listeners and sound sources move. Under these conditions, auditory-spatial cues [e.g., interaural time differences (ITDs), interaural level differences (ILDs), and pinna-related spectral cues derived from head-related transfer functions (HRTFs)] change. If the nervous system used only these auditory-spatial cues, determining whether the sound source, listener, or both moved would be impossible. Wallach (1940) suggested that “Two sets of sensory data enter into the perceptual process of localization, (1) the changing binaural cues and (2) the data representing the changing position of the head.” Wallach (1940) demonstrated how applying this principle to scenarios where listeners and sounds rotate accounted for many of his measures of perceived sound-source location. While it may appear obvious that the spatial output of the auditory system must refer to the world around the listener, it is not obvious how the brain does this. Ultimately, obtaining “data representing the changing position of the head” must involve neural systems other than just the auditory system, and these neural estimates of head position must be integrated in some way with neural estimates of the sound-source location, relative to the head, which are derived from auditory-spatial cues. We thoroughly investigated a paradigm developed by Wallach (1940), which appears useful for exploring how the various multisystem cues interact.

In 1938, Wallach derived cone-of-confusion calculations indicating that two sound-source locations on an azimuth plane (azimuth angles, θ, and 180° − θ) would generate the same interaural difference cues (i.e., ITDs and probably ILDs). This ambiguity could therefore lead to front-back reversals (FBRs) in azimuthal sound-source localization. In his 1939 and 1940 papers, Wallach wondered how interaural differences could be used for sound-source localization given the existence of FBRs. He developed a “2-1” rotation scenario as one way to support his contention that the integration of head-position cues with interaural difference cues would allow one to localize sound sources even when FBRs are possible. In the 2-1 scenario, listeners rotate at a particular rate, and the sound rotates from loudspeaker to loudspeaker in the same direction around an azimuth circle at twice this rate. As Wallach (1940) explained in some detail in his paper, he did this because such a scenario would provide the same interaural difference cues (i.e., ITDs and probably ILDs) as a stationary sound source located at the front-back reversed location. Therefore, if listeners did indeed integrate information about the world-centric position of the head with head-related auditory-spatial information (i.e., interaural cues) in order to determine where in the world the sound source was, then listeners would perceive the moving sound source in the 2-1 rotation scenario as stationary at the front-back reversed location. See the Appendix for a more detailed explanation.

While Wallach (1940) was not aware of the HRTF and the role it plays in sound-source localization, he did acknowledge that the pinna probably had some influence on sound-source localization though he thought it was a “secondary factor.” The high-frequency spectral shape cues in the HRTF can disambiguate FBRs (see Blauert, 1997; Middlebrooks and Green, 1991, for reviews), and this brings up a possibility for the 2-1 scenario that Wallach appears not to have considered. Sound stimuli with the high-frequency energy and bandwidth necessary for the use of spectral shape cues would be unlikely to be localized as stationary at the front-back reversed location in the 2-1 rotation scenario. Instead, the sources of such stimuli would be perceived veridically, rotating faster than the listener in the same direction. Calculations demonstrating these relationships are provided in the Appendix.

Wallach (1940) tested five listeners in the 2-1 rotation scenario and, consistent with his argument about the integration of head-position and interaural difference cues, all listeners reported perceiving a stationary source in back when the sound started in front, and a stationary source in front when the sound started in back. Wallach (1940) manually rotated blindfolded listeners in a chair and presented music from Victrola records from different azimuthal loudspeakers. More recently, Macpherson (2011) and Brimijoin and Akeroyd (2012) replicated aspects of these results of Wallach (1940) for normal hearing listeners. Brimijoin and Akeroyd (2012) called the results of the 2-1 rotation scenario the Wallach Azimuth Illusion (WAI), which we will use in this paper. In the more recent studies of the WAI, sound stimuli (filtered noise through HRTF simulations over headphones in Macpherson, 2011; filtered speech over loudspeakers in Brimijoin and Akeroyd, 2012, 2016) were presented as a function of head-tracked listener self-rotation. For normal hearing listeners, Macpherson (2011) and Brimijoin and Akeroyd (2012) showed that stimuli likely to be front-back reversed location elicited the WAI of a perceived stationary sound source, but the illusion was “weaker” with stimuli that were unlikely to generate FBRs. The 2-1 rotation conditions in which sounds were probably not front-back reversed location generated different results among the Macpherson (2011), Brimijoin and Akeroyd (2012, 2016), and Wallach (1940) studies. The results of Macpherson (2011), as well as Brimijoin and Akeroyd (2012, 2016), suggest that evidence for the WAI is weak when FBRs are not likely to occur. Brimijoin and Akeroyd (2016) used their paradigm for testing hearing-impaired listeners with and without hearing aids. Because the present study involves listeners with normal hearing, we will not discuss experiments using hearing-impaired listeners.

The small existing literature related to the WAI (Wallach, 1940; Macpherson, 2011; Brimijoin and Akeroyd, 2012, 2016; and reviews by Mills, 1972; Akeroyd, 2014; van Opstal, 2016) suggests several uncertainties about the conditions that lead to it. The current paper attempts to resolve many, if not most, of these uncertainties in order to establish the 2-1 rotation scenario as a robust means to test the interaction of head-position and auditory-spatial cues:

• (1)While it appears that the illusion may occur only for stimuli prone to FBRs, measures of a direct relationship between data related to the WAI and those related to FBRs have not been well established (but see Macpherson, 2011, who measured FBRs for one listener under virtual/simulation conditions). Knowing how FBRs and the WAI are related might be important, as the literature suggests large differences in the perception of FBRs among individual normal hearing listeners (e.g., see Makous and Middlebrooks, 1990; Wenzel et al., 1993). Thus, measuring the WAI for several listeners is probably necessary to form an estimate of the relationship between FBRs and the WAI.
• (2)All of the existing demonstrations of the WAI involve short-duration rotations over small azimuthal arcs (as would occur for most real-world listener rotations). However, there are several unexplained differences among the outcomes of these various studies. As we will argue in the discussion sections, investigating the illusion over long time periods and large azimuthal arcs helps resolve most of these reported differences.
• (3)The existing literature suggests that the vestibular system provides important head-position information in the 2-1 rotation scenario, yet no study of the WAI has directly manipulated vestibular function. Wallach (1940) points out that “…no direct cues for the position of the head at a given moment are obtained in the vestibular system. Even the angular velocity of the displacement of the head can only indirectly be derived from the stimulation; for only acceleration and not angular velocity as such can stimulate the vestibular apparatus.” The current study directly manipulates vestibular function to shed light on its potential role.
• (4)For any sound prone to FBRs, at any head-related starting position, the WAI should exist, but Wallach (1940) and Brimijoin and Akeroyd (2012) studied only starting positions directly in front and in back of the listener. Macpherson (2011) varied starting loudspeaker location for one listener under virtual/simulation stimulus conditions. The current study involved four different relative starting locations of the sound source in an actual sound field for multiple listeners.
• (5)Most studies (the study by Macpherson, 2011, with one listener is an exception, but little information is provided in the chapter) have asked listeners to judge the relative location of sound sources (e.g., is the source in front?) in the 2-1 scenario and not the actual perceived locations (e.g., which loudspeaker appears to be presenting the sound?). Listeners in the current study were asked to judge perceived sound-source location of 1 of 24 loudspeaker locations around an azimuth circle.
• (6)In most of these studies, listeners were not asked whether the perceived location changes position (e.g., does the sound source appear to rotate or not?) as might happen for stimuli not prone to FBRs. Judgments of stationary and rotating sound-source perceptions were obtained in the current study.

We report two experiments designed to investigate some of these issues concerning the WAI. In experiment I, FBRs for five different filtered noises were measured, where three of the filtered noises were expected to yield a high proportion of FBRs and two were not. The same filtered noises and listeners were used in experiment II, where sound sources and listeners rotated in the 2-1 rotation scenario in an accelerating, constant angular velocity, and decelerating manner. As Wallach (1940) implied, angular listener motion is only sensed via vestibular functioning¹ (i.e., by the semicircular canals) during acceleration and deceleration (see Lackner and DiZio, 2005, for a review). There is no rotational vestibular output change under constant angular velocity listener rotation¹ (Lackner and DiZio, 2005), so varying the manner of listener rotation provides a type of control of rotational vestibular function. Four different relative sound source starting locations were used in experiment II.

II. EXPERIMENT I—MEASURING FBRs

Stationary listeners indicated the perceived sound-source location of filtered noise bursts presented from one of six loudspeakers evenly spaced around the azimuth circle. The main measurements were FBRs.

A. Method

Listeners: Eight listeners (all between the ages of 19 and 46, four females; one listener, L13, is an author, M.T.P.), all of whom reported normal hearing and no problems with motion sickness, participated in experiments I and II. Experiments I and II were approved by the Arizona State University Institutional Board for the Protection of Human Subjects (IRB).

Stimuli: The stimuli were five filtered, 75-ms duration noise bursts, each shaped with 5-ms cosine-squared rise-fall times and presented at 65 dBA. All sounds were filtered by a four-pole Butterworth filter implemented in MATLAB (Mathworks, Natick, MA): a 2-octave wide noise centered at a center frequency (CF) at 500 Hz (LFW), a 2-octave wide noise centered at a 4-kHz CF (HFW), a 1/10-octave wide narrowband noise with a 500-Hz CF (LFN), a 1/10-octave wide narrowband noise with a 4-kHz CF (HFN), and a broader band noise (BB, filtered between 250 and 8 kHz).

Listening room: The listening room was that used in Yost et al. (2015). The room is 12 ft (length) × 15 ft (width) × 10 ft (height) and lined on all six surfaces with 4-in. acoustic foam. The wideband reverberation time (RT₆₀) is 102 ms and the ambient noise level is 32 dBA (all measured at the listener's head). Twenty-four loudspeakers (Boston Acoustics 100× Soundware, Peabody, MA) are on a 5-ft radius circle for an azimuth array with 15° loudspeaker spacing at the height of listener's pinna (see Fig. 8). A number (1–24) is affixed to each loudspeaker, as indicated in Fig. 8, allowing listeners to identify the loudspeaker they perceived as generating a sound by the number of the loudspeaker. Sounds were generated at 44100 samples/s/channel from a 24-channel digital-to-analog converter (two Echo Gina 12 DAs, Santa Barbara, CA). A custom-designed, computer-controlled rotating chair is in the middle of the azimuthal circular loudspeaker array. There is a control room from which listeners are monitored by an intercom and camera. In experiment I listeners were stationary facing the center loudspeaker at all times, and a head-brace kept their heads in the centered position throughout a trial. Listeners were also monitored by an additional experimenter who was always in the listening room.

Procedure: Sounds were randomly presented from one of six equally spaced (60°) loudspeakers around the azimuth circle (three loudspeakers in front: #21, #1, and #5; and three loudspeakers in back: #9, #13, and #17; see Fig. 8) as the stationary listener faced loudspeaker #1. For each of the 5 filtered noises and 6 loudspeakers, the noise bursts were presented 15 times (90 trials per listener and filtered noise, or 450 trials/listener). Sounds were presented from the 6 loudspeakers mentioned above, but listeners were not told this and they could indicate any of the 24 loudspeakers for their response. Listeners' eyes were open, they did not move, and no feedback of any kind was provided. The main dependent variable was FBRs, not measures of sound-source localization accuracy. Listeners were given time at the beginning of the experiment to acquaint themselves with the location of the 24 numbered loudspeakers.

B. Results and discussion

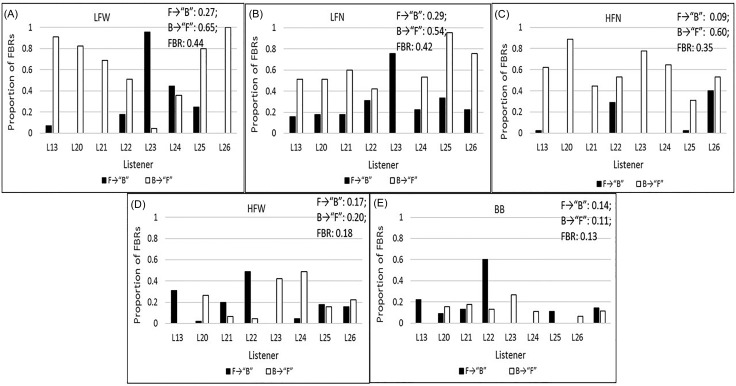
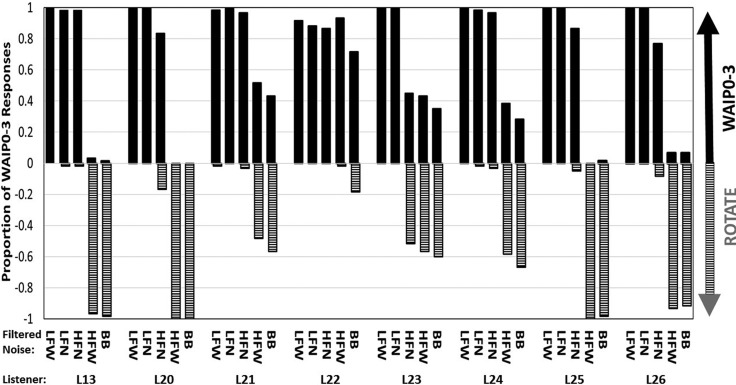
Figures 1(A)–1(E) display the proportion of FBRs for each of the five filtered noises [Fig. 1(A) LFW, Fig. 1(B) LFN, Fig. 1(C) HFN, Fig. 1(D) HFW, and Fig. 1(E) BB; Figs. 1(A)–1(C) are conditions (on top) with a high number of FBRs, while Figs. 1(D) and 1(E) (on the bottom) are conditions with a low number of FBRs] and for each of the eight listeners (L13–L26). The mean proportion (eight listeners) of reversals and overall number of FBRs are tabled in the upper right of each panel. F→“B” (stimulus presented in front and reported in back) indicates the proportion of the sum of the reversals from the 3 loudspeaker locations in front of the listeners/45 trials on which an F→“B” reversal could occur. B→“F” (stimulus presented from behind the listener and reported in front) indicates the proportion of the sum of reversals from the 3 loudspeaker locations in back of the listeners/45 trials on which a B→“F” reversal could occur. “FBR” indicates the total number of FBRs/90 trials. Reversals were determined by using the number of responses that were at the predicted reverse loudspeaker location and within ±1 loudspeaker location of the predicted reverse loudspeaker location. As an example, if a sound was presented from loudspeaker #1, its predicted reverse location is loudspeaker #13; if a listener reported that loudspeaker #12, #13, or #14 presented the sound, the response was considered an F→“B” reversal.

FIG. 1.

Data from experiment I are shown as the proportion of F→“B” (black bars) and B→“F” (white bars) FBRs for each of the eight listeners (L13–L26) and each of the five filtered noises [(A)–(C) in the top row indicate filter conditions with a high number of FBRs: A:LFW, B:LFN, C:HFN, and (D) and (E) in the bottom row those conditions with a low number of FBRs: D:HFW and E:BB]. The mean proportion F→“B” reversals, B→“F” reversals, and overall FBRs are tabled in the upper right of each panel. See text for details.

In experiment I, 92.8% of all responses across all filtered noises (5), all loudspeaker locations presenting sounds (6), repetitions (15) and all listeners (8) yielding 3600 possible responses, were within ±1 loudspeaker location of either the actual loudspeaker presenting the sound source or the reverse sound-source location. Of the 7.2% responses that did not fit this criterion, only 12 responses were not within ±2 loudspeakers of the actual or reverse loudspeaker location. In other words, 96.6% of the time responses indicated loudspeakers that were within ±2 loudspeakers of the actual source or a FBR location. For some conditions, a ±2 loudspeaker spatial window does not allow for separating responses that might indicate the actual sound-source location versus those that might be FBRs. For instance, if the actual sound source is loudspeaker #5, then loudspeaker #9 is the reverse sound-source location. In this case, responses of #4, #5, and #6 would be within ±1 loudspeaker of the actual sound source, #5; and #8, #9, and #10 would be within ±1 loudspeaker of the reverse sound source, #9. A ±2 loudspeaker spatial window would include a response of #7, which could be either in a ±2 loudspeaker spatial widow surrounding the actual sound source or the spatial window surrounding the front-back reversed sound source. Thus, only responses within ±1 loudspeaker of a reverse loudspeaker are considered FBRs.

The data of Fig. 1 are consistent with other data in the literature showing the effect of spectral content on FBRs (see review by Middlebrooks and Green, 1991; additional citations are provided below). That is, sounds with mainly low-frequency energy (e.g., LFW and LFN) generate more FBRs than sounds with high-frequency content (HFW and BB). There is little spectral structure available in low-frequency sounds for the HRTF cue to help disambiguate FBRs (see Middlebrooks and Green, 1991, for a review). When the bandwidth is narrow, as it is in the 1/10-octave conditions (LFN and HFN), there may not be enough bandwidth to judge a pattern of spectral contrast based on the HRTFs to help disambiguate FBRs (e.g., see Middlebrooks, 1992), even at high frequencies (i.e., HFN). The literature also suggests that narrowband, high-frequency stimuli with energy in the 4-kHz region produce many more B→“F” than F→“B” reversals (e.g., see Blauert, 1969, 1997; Middlebrooks et al., 1989). This outcome is borne out in the dominance of B→“F” reversals shown in Fig. 2(C). Also consistent with the literature (e.g., see Makous and Middlebrooks, 1990; Wenzel et al., 1993), there are large individual differences in the number of FBRs and their distribution between F→“B” and B→“F” reversals based on the type of stimulus.

FIG. 2.

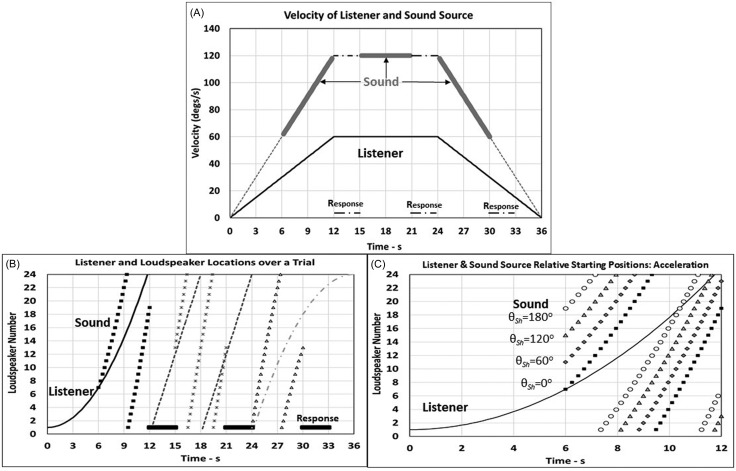
(A) Listener (solid line) and sound (dotted line) angular velocity (^o/s) as a function of time (s) for the accelerating, constant angular velocity, and decelerating stages for a 36-s trial. Six seconds of sound presentations (dark-wide lines on top of the dotted line) started after 6 s of listener acceleration. Three seconds were allotted for listener responses (dashed-dotted line) and sound presentations were turned back on for 6 s during the constant angular velocity stage and then turned off for 3 s for listener responding. During the deceleration stage, sounds were presented for the first 6 s followed by another 3-s response interval. (B) Equation (A3) was used to indicate the azimuthal location (in terms of the 24 loudspeakers; see Fig. 1) of the listener (different dashed lines with different shades of darkness for the three different rotation stages) and which loudspeaker presented sound (symbolically represented by different symbols for different stages of rotation) as a function of time. Only the starting head-centric angle of zero degrees is shown for each stage of rotation. (C) The acceleration stage is shown with loudspeaker position indicated as a function of time [as in (B)] for the sound presentations with the four relative head-centric starting angles (θ_Sh) of 0°, 60°, 120°, and 180° represented by squares [same squares as in (B)], diamonds, triangles, and circles, respectively.

Because the calculations indicate that the WAI depends on the existence of a reverse sound-source angle (see Wallach, 1940, and the Appendix), relatively strong positive correlations are predicted to occur between the proportion of FBRs and the existence of the WAI. Given that FBRs are prone to individual differences, there are likely to be individual differences in the occurrence of the WAI. One goal of experiment II is to estimate these correlations for each listener.

III. EXPERIMENT II—MEASURING THE WAI

In experiment II the 2-1 rotation scenario was used to investigate the WAI.

A. Method

Listeners, stimuli, and listening room: Same as in experiment I.

Procedure: Figure 2(A) indicates the angular velocity of the listener (solid line) and sound source (thick gray dotted line) at times when sound stimuli are presented in experiment II. There were three, 12-s stages of listener rotation: acceleration stage of 5°/s², constant angular velocity stage of 60°/s, and deceleration stage of −5°/s². A 75-ms filtered noise burst was presented once from each loudspeaker in succession in a saltatory rotation around the 24-loudspeaker circular array at twice the rate of listener rotation (accelerating at 10°/s², constant angular velocity at 120°/s, decelerating at −10°/s²).

Listeners always started a trial facing loudspeaker #1 and then rotated clockwise (see Fig. 8). For the acceleration stage, listeners rotated with no sound for 6 s to ensure that the listener was not rotating so slowly that there might not be any perceptible changes in head position. After these first 6 s, the rate of listener rotation was 30°/s and the listener faced loudspeaker #7. For the next 6 s, the 75-ms noise bursts were pulsed on and off from successive loudspeakers, once per loudspeaker. Three seconds of silence were then provided so that the listener could indicate a response, and then the sound was presented during the constant angular velocity stage similar to the way it was during acceleration. Six seconds of stimulus presentation ensued, followed by 3 s of silence for the next listener response, and then the deceleration stage began. The same reasoning explains ending the sound presentations 6 s before the end of the deceleration stage (when listeners' rates of rotation were 30°/s and they faced loudspeaker #19). Yost et al. (2015) also discussed the issue of slow rates of listener rotation.

Figures 2(B) and 2(C) describe listener (solid lines) and sound-source locations (symbols) as a function of time (s) in terms of the 24-loudspeaker locations (see Fig. 8). That is, Eq. (A3) was used to determine the azimuth angle at the time the 75-ms filtered noise burst was presented. This angle was then converted to the relative loudspeaker number (i.e., the location of each symbol represents the approximate time and exact loudspeaker location of each presentation of one 75-ms filtered noise burst, but the width of the symbol is greater than that associated with 75 ms in order for the symbols to be large enough to be seen). In Fig. 2(B), dark black lines and squares are for the acceleration stage, medium dark lines and “x” symbols are for the constant angular velocity stage, and light lines and triangles are for the deceleration stage. The sound presentation starts when the head is facing the same loudspeaker presenting the noise burst (i.e., a sound-source head-centric angle or just head-centric angle of 0°) for each of the three stages of rotation. Thick horizontal black lines indicate the three 3-s response intervals. The listener rotates through 360° during both the acceleration and deceleration stages and 720° during constant angular velocity rotation. The sound rotates at twice the rate of the listener such that there are 36 presentations of the pulsating 75-ms sound over the 6 s of accelerating and decelerating sound rotation, resulting in the sound-source location changing over 540°. During the 6 s of constant angular velocity sound rotation there are 48 75-ms sound presentations changing over 720°. The time between successive saltatory presentations of the 75-ms noise bursts from each of the successive 24 loudspeakers was determined by Eq. (A3) as indicated in Fig. 2(B). During constant angular velocity rotation, the time between the onsets of successive 75-ms noise bursts was 125 ms (50-ms off time). During acceleration/deceleration, the time between the onsets of successive 75-ms noise bursts ranged from 125 to 250\ms (50- to 175-ms off times).

At the beginning of each rotation stage, a starting loudspeaker location for sound presentation was randomly chosen from one of four relative head-centric starting angles θ_Sh: 0°, 60°, 120°, and 180° (see the Appendix). Table I indicates these starting angles and the resulting listener and starting loudspeaker locations for each stage of rotation. Figure 2(C) indicates the location of the loudspeaker during the acceleration stage for each of the four possible head-centric starting angles (different symbols) as compared to the location of the accelerating listener (solid line). Relative head-centric starting angles (θ_Sh, the Appendix) of 0°, 60°, 120°, and 180° are represented by squares, diamonds, triangles, and circles, respectively. Similar changes in loudspeaker locations occurred for the other two stages of rotation (constant angular velocity and deceleration), but are not shown in order to keep the figure uncluttered.

TABLE I.

For each of the four starting head-centric angles and each of the three stages of rotation (acceleration, constant angular velocity, and deceleration), the loudspeaker location (see Fig. 8) the listener faced when sound started (starting listener), the loudspeaker location when the sound started (starting sound), and the location of the exact WAI predicted loudspeaker location (the WAIP0 conditions are shown in a black italic font) are shown.

Acceleration	0°	60°	120°	180°
Head-centric angle
Starting listener	#7	#7	#7	#7
Starting sound	#7	#11	#15	#19
WAIP0	#19	#15	#11	#7
Constant angular velocity	0°	60°	120°	180°
Head-centric angle
Starting listener	#13	#13	#13	#13
Starting sound	#13	#17	#21	#1
WAIP0	#1	#21	#17	#13
Deceleration	0°	60°	120°	180°
Head-centric angle
Starting listener	#1	#1	#1	#1
Starting sound	#1	#5	#9	#13
WAIP0	#13	#9	#5	#1

During each of the three response intervals [see Figs. 2(A) and 2(B)], listeners indicated either the direction of perceived sound-source rotation during the preceding 6 s (i.e., the sound appeared to rotate clockwise, “C,” or counterclockwise, “CC”) or the perceived fixed, stationary sound-source location (i.e., the sound appeared to be stationary at 1 of the 24 loudspeaker locations). Responses of C or CC or #1–#24 were told to the experimenter, who recorded the responses for each stage of rotation on a trial-by-trial basis.

Listeners' eyes were always open (the listening room was fully lit), no feedback of any kind was provided, listeners were monitored and instructed to stay still in the chair and to not move their head, arms, or legs, and a head-rest kept listeners' heads facing steadily forward. For each of the 3 rotation stages, one of the 5 filtered noise bursts was randomly chosen and 1 of the 4 starting loudspeaker locations was also randomly chosen, yielding 20 trials repeated randomly 5 times for 100 trials/rotation stage. Thus, for each listener, there were 300 total presentations (5 filtered noises × 4 starting loudspeaker locations × 3 stages of rotation × 5 repetitions of each condition) and each trial was 36-s long (i.e., three, 12-s stages of listener rotation, each with 6 s of sound presentation).

Recall that the prediction of the location of the sound source in the WAI conditions suggests that for sound sources prone to FBRs, a sound source will be perceived at a stationary loudspeaker location based on the reverse world-centric starting angle (see Wallach, 1940, and the Appendix). For the four head-centric sound source starting angles and each rotation stage, the exact predicted loudspeaker locations leading to the WAI (WAIP0) are also shown in Table I.

To familiarize listeners with their task, they were provided a demonstration at the beginning of experiment II. The demonstration involved the 75-ms BB noise burst rotating once around the loudspeaker array at 120°/s and examples of the 75-ms BB noise at stationary and nearly stationary positions. In this way, the stationary listeners understood what was meant by “stationary” and “rotating” sound sources, and they were reacquainted with the 24 numbered loudspeakers. All listeners participated in a debriefing session following experiment II in which they were asked a series of questions about experiment II and what they perceived.

Controlling listener and sound rotation: Equation (A3) was used to determine the location of the chair and the sound source as a function of time. Rotating control of the chair was custom made in the laboratory² with a 200-step stepper motor, run at 4× microstepping with a 2:1 gear ratio, for a resolution of 0.225°/microstep. MATLAB initiates each trial by sending a signal to an Arduino computer, which has pre-designed instructions for the angular trajectory of the chair. The Arduino controls the stepper motor and reports to MATLAB, in real time, the position of the chair. MATLAB then plays the sound stimuli in real time as a function of the chair's location. Sound playback and chair location were calibrated to within ±1 ms level of synchronization.

B. Results

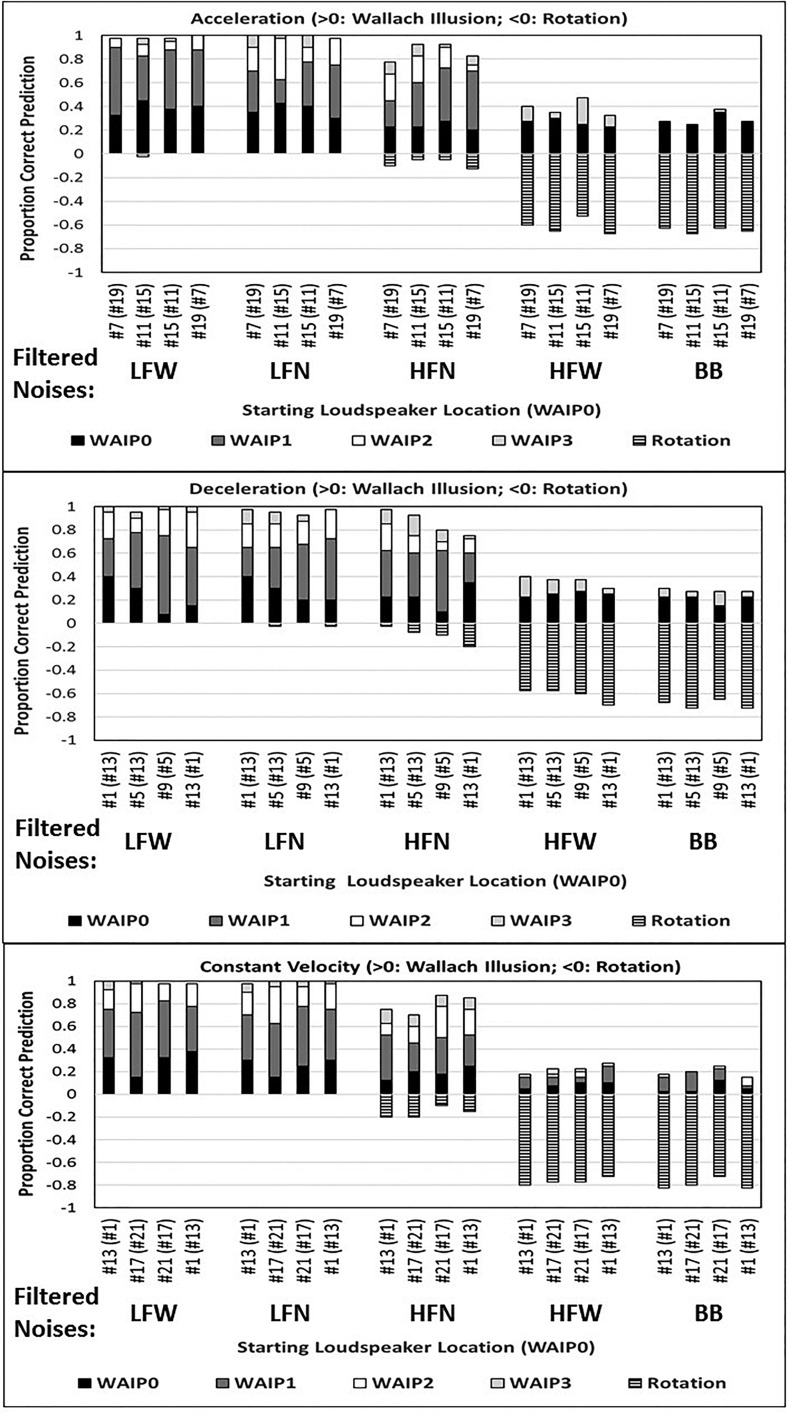
The overall data from experiment II are shown in Fig. 3 with each of the three panels representing the data from one of the three rotation stages [(A) (top) acceleration, (B) (middle) deceleration, (C) (bottom) constant angular velocity). Figure 3 shows the mean (eight listeners) proportion of times the WAI was reported as solid filled bars in the positive direction (0.0–1.0). The mean proportion of times a clockwise rotating sound source was reported is shown as horizontally hashed bars in the negative direction (0.0 to −1.0). For the positive-going bars, the darkest, lower part of the bar represents the proportion of times the average listener reported the exact loudspeaker representing a WAI prediction (WAIP0). The other parts of the positive-going bars indicate the proportion of times the exact WAI predicted loudspeaker ±1 (WAIP1), ±2 (WAIP2), and ±3 (WAIP3) loudspeaker locations were reported. That is, WAIP “n,” n = 0, ±1, ±2, or ±3, specifies the two loudspeakers located ±n loudspeaker locations away from the exact predicted WAI loudspeaker location; see Table I. For example, if the exact WAI predicted loudspeaker location (WAIP0) was #1, WAIP2 would be loudspeakers #3 and #23 (see Fig. 8). The 20 conditions along the x axis represent the four starting loudspeaker locations (with the WAIP0 loudspeaker location in parenthesis; see Table I) for each of the 5 filtered noises. For each filtered noise and stage of rotation, the starting loudspeaker locations are indicated in left-to-right order according to their starting head-centric locations [θ_Sh: 0°, 60°, 120°, and 180°; see Table I, Fig. 2(C), and the Appendix]. In order to represent the sum of the responses within a spatial window surrounding the exact WAI loudspeaker location (WAIP0), WAIP0-n, n = 1, 2, or 3 will be used to indicate all of the loudspeaker locations between WAIP0 and WAIP ± n. For example, if WAIP0 was loudspeaker #13, WAIP0-3 would represent the spatial window of loudspeakers of: #10, #11, #12, #13, #14, #15, and #16 (see Fig. 8).

FIG. 3.

The three panels represent data from the three rotation stages (A) acceleration, (B) deceleration, (C) constant angular velocity. Mean data (eight listeners) indicate proportion of correct predictions as a function of the five types of filtered noise (LFW, LFN, HFN, HFW, BB) and the four starting loudspeaker locations of the noise burst (WAIP0 loudspeaker location is indicated in parenthesis; see Table I). Positive proportions (0–1.0) represent the proportion of WAI responses. The black, bottom portion of each positive histogram bar represents the proportion of responses indicating the exact loudspeaker location predicted by the WAI (WAIP0). The other portions of the positive-going histogram bars represent the proportion of responses for the WAIP1, WAIP2, and WAIP3 loudspeaker locations. The negative going horizontally hashed bars represent the proportion of responses (0 to −1.0) of clockwise rotation. See the text for additional details.

The data in Fig. 3 clearly show that listeners responded with locations within the WAIP0-3 spatial window almost 100% of the time for the two low-frequency filtered noises (LFW and LFN). There was a lower proportion of responses in the WAIP0-3 spatial window for the narrowband high-frequency noise (HFN). Reports of a rotating noise burst occurred most frequently for the two filtered noises containing wideband high-frequency energy (HFW and BB).

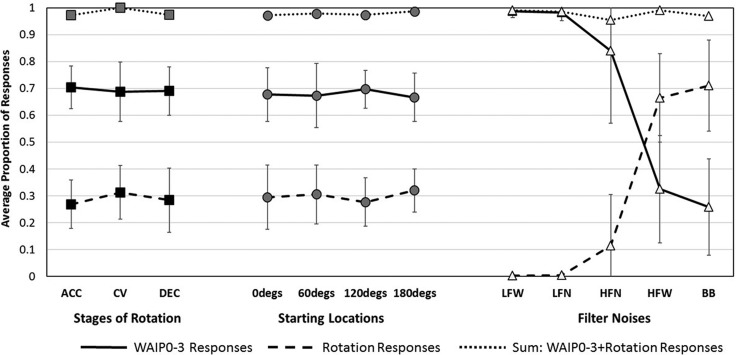
Figure 4 emphasizes the fact that there were almost no changes in the proportion of responses (as seen in Fig. 3) as a function of the three different stages of rotation (acceleration, constant angular velocity, and deceleration) and the four different relative starting sound-source locations (0°, 60°, 120°, and 180°). Figure 4 shows changes in the average proportion of stationary responses for the WAIP0-3 loudspeaker locations (in the middle with solid lines) and rotation responses (on the bottom with dashed lines) as a function of the three stages of rotation (dark squares). The medium dark circles show average responses for the different relative starting sound-source locations (head-centric angle, θ_Sh; see the Appendix). And, the light triangles show average responses when only the type of filtered noises changed. For each of the three variables (stages of rotation, starting locations, and filtered noises), data were averaged over the eight listeners and the other two variables. The standard deviation across listeners is shown as the vertical bars for the responses within the WAIP0-3 spatial window and rotation responses (when the data are near 0.0 and 1.0, the error bars are often less than the height of the symbol). It is clear that there were almost no changes in the average proportion of responses (both for the WAI and the rotation responses) when the stages of rotation and the relative starting sound-source location were different. However, there were very large changes in the average proportion of responses within the WAIP0-3 spatial window as a function of the different filtered noises. To obtain information about the variability in individual listener responses as a function of the five filtered noise conditions, refer to Fig. 6. Thus, for the rest of this paper, data are averaged over starting loudspeaker locations and stages of rotation.

FIG. 4.

The average proportion of responses (eight listeners) are shown for WAIP0-3 responses (middle figures with solid lines), rotation responses (bottom figures with dashed lines), and the sum of the WAIP0-3 and rotation responses (top figures with dotted lines). Data showing average responses over the three stages of rotation (squares), the four starting locations of the noise bursts (circles), and the five filtered noises (triangles) are shown. Error bars are ±1 standard deviation (error bars for data near 0.0 or 1.0 are smaller than the symbols). See the text for details about the averaging.

FIG. 6.

Display is similar to Fig. 3, showing proportion of WAIP0-3 responses averaged over the four starting loudspeaker locations and the three stages of rotation for each of the five filtered noise conditions (LFW, LFN, HFN, HFW, and BB) for each of the eight listeners (L13 and L20–L26). Positive-going. black histogram bars represent WAIP0-3 responses, while horizontally hashed, negative-going bars represent the proportion of clockwise rotating (rotate) responses (see Fig. 4).

At the top of Fig. 4, the sum of the average proportion of responses within the WAIP0-3 spatial window and the rotation responses are shown with dotted lines. Almost 100% of the responses in experiment II were either WAI or rotation responses, consistent with the description of the WAI provided in the Appendix. Only 52 out of the 2400 total responses (2.2%) across all conditions and listeners were not consistent with this description. Of these 52 responses, 16 indicated counterclockwise rotation (mostly for the HFN noise). We have no explanation for these counterclockwise responses. However, during the debriefing session, most listeners indicated that it was most difficult to determine if the sound was stationary or rotating for the HFN conditions. Others of the 52 “errant responses” included 22 WAI responses within a ±4 loudspeaker spatial window of a WAIP0 response, in which 11 responses were either at or within ±1 loudspeaker of the first loudspeaker presenting a sound during the acceleration stage or the last loudspeaker presenting a sound during the deceleration stage (possibly because the rate of listener rotation was slow under these conditions and the illusion started to fail), and there were three unexplainable stationary loudspeaker responses.

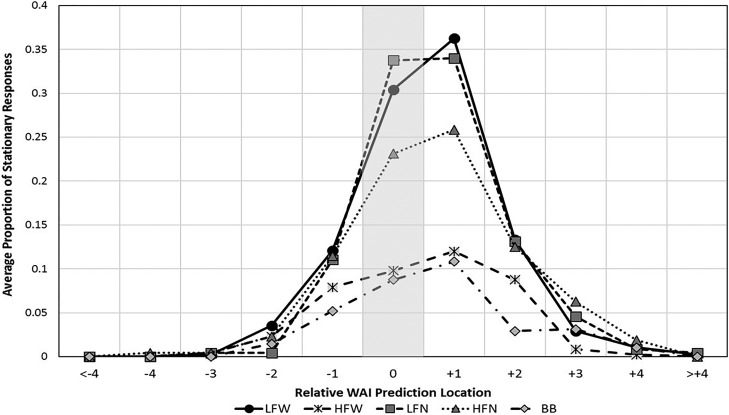
Figure 5 is a replot of the WAI data, averaged over starting loudspeaker locations, stages of rotation, and listeners; it displays the average proportion of stationary responses as a function of the relative WAI predicted location. Positive relative locations indicate loudspeaker locations clockwise relative to WAIP0 locations, and negative relative locations indicate loudspeaker locations counterclockwise to the WAIP0 locations. The relative WAI prediction location of 0 (i.e., WAIP0) is indicated by the light shaded area. The total of all reported relative loudspeaker locations greater than +4 and less than −4 are indicated at the extreme left and right, respectively, of the horizontal axis as “<−4” and “>+4.” The results of these calculations are shown for each of the five filtered noises. For example, for the LFW noise (solid round symbols), the average listener reported that the location of the perceived stationary sound source was at the exact relative WAI prediction location (WAIP0 or “0” in Fig. 5) for 31% of all responses. The average listener reported that the perceived WAI location was one loudspeaker location clockwise (+1) to the exact WAI prediction loudspeaker for 36% of all responses. And the average listener reported that the location was one loudspeaker counterclockwise (−1) to the exact WAI prediction loudspeaker for 12% of all responses. There were no responses at a relative WAI prediction location of less than or equal to −4, only 1.5% at a relative WAI prediction location of +4, and 0.05% for all relative locations greater than +4. The data of Fig. 5 reveal that the width of the spatial window for the WAI is relatively wide for all five filtered noises (23.25° to 35.75° wide at the “half-height” points in Fig. 5). The spatial window is skewed toward positive (clockwise) relative WAI prediction locations, i.e., in the direction of listener and sound rotation.

FIG. 5.

For each of the five filtered noise conditions (LFW, HFW, LFN, HFW, and BB), the average proportion of stationary responses (averaged over eight listeners, four starting locations, and three stages of rotation) are shown as a function of the relative WAI prediction location, where 0 means the exact predicted WAI location (WAIP0), +1 is a location one loudspeaker clockwise to WAIP0, −1 is a location one loudspeaker counterclockwise to WAIP0, etc.; with >+4 and <−4 indicating the sum of all relative loudspeaker locations >+4 or <−4, respectively. The “0” (WAIP0) area is highlighted by the light bar. See the text for additional information about these estimates of spatial windows.

Figure 6 displays mean data for each of the eight listeners (L13 and L20–L26) for each of the five filtered noises in a manner similar to Fig. 3, but the data in Fig. 6 are averaged over the four relative starting loudspeaker locations and the three stages of rotation. The y axis (see Fig. 3) in the positive direction indicates the proportion of responses within the WAIP0-3 spatial window. Proportions in the negative direction indicate the proportion of times listeners indicated a clockwise rotation of the sound source. L22 produced high proportions (>0.75) of responses within the WAIP03 spatial window for the two filtered noises with wideband, high-frequency energy (HFW and BB),³ whereas the other seven listeners responded that these filtered noises mainly appeared to rotate.

Figures 3–6 produce the following summary observations:

• (1)Almost 100% of the responses for the two low-frequency filtered noise bursts (LFW and LFN) were within the WAIP0-3 spatial window with almost no individual listener differences.
• (2)The HFN filter conditions yielded both WAI and rotation responses, but with a higher proportion of responses in the WAIP0-3 spatial window than rotating responses for all listeners but one (L23). A few of the responses for the HFN filter conditions were counterclockwise rotation.
• (3)On average, the HFW and BB filter conditions yielded substantially more rotating sound-source responses than responses within the WAIP0-3 spatial window, but there were individual listener differences.
• (4)When listeners for the HFW and BB filter conditions did not indicate a clockwise rotating sound source, they almost always reported a stationary loudspeaker consistent with the WAI predictions.
• (5)For each filtered noise condition, the pattern of average results was very similar across the four different relative loudspeaker starting locations and three stages of rotation.
• (6)97.8% of all the data were either responses within the WAIP0-3 spatial window or clockwise rotation responses.

IV. OVERALL DISCUSSION

In addition to the observations made above, several aspects of the results of experiment II are worth noting:

• (1)When listeners' eyes are open, the type of listener rotation (acceleration, constant angular velocity, and deceleration) makes little difference to the perception of the WAI. Thus, with the use of vision, the type of vestibular input appears to be irrelevant in the perception of the WAI. Vision appears to dominate in terms of providing head-position cues. We find no interaction between visual input and the type of vestibular input in listener responses.
• (2)We assume that ITDs are the primary auditory-spatial cue for locating low-frequency sound sources. If so, then the fact that the perception of the WAI occurs robustly for stimuli with only low frequencies implicates ITD processing (and the FBRs that can result when ITDs are essentially the sole spatial-auditory cue) as important auditory-spatial cues that are integrated with head-position cues in determining world-centric sound-source location.
• (3)For filtered noises with high frequencies, both ILDs and HRTF-related spectral differences could affect sound-source localization. In these cases, listeners often perceived the sound source as rotating, especially for the HFW and BB filtered noises. This is consistent with the argument that listeners use spectral cues (based on the HRTF) to reduce or eliminate FBRs that might exist based on ILD cues alone.
• (4)When the filtered noise was high frequency, but narrowband (HFN), a condition for which FBRs occur with some regularity (see experiment I), there was evidence for the WAI, but the evidence was weaker than for the low-frequency filtered noises described above. Given that ITDs are probably not useable auditory-spatial cues at high frequencies, and the 1/10-octave bandwidth would make discerning spectral changes difficult, it is probable that ILDs are the major auditory-spatial cue used to localize the sources of the HFN noises. However, explanations of the fact that the WAI is “weaker” for the HFN stimulus than for stimuli with only low frequencies are complicated by individual differences, the dependence of ILD cues on frequency and azimuth (e.g., the “bright spot”; see Macaulay et al., 2010), and the existence of directional bands (see Blauert, 1969, and discussion later in this paper).
• (5)One listener (L22) perceived the stationary WAI far more times than a rotating stimulus for all conditions, implying that this listener may be prone to FBRs for all filtered noises, as was borne out in experiment I for this listener.³
• (6)The 2-1 rotation scenario leading to the WAI provides a robust paradigm for investigating the multisystem interaction of head-position and auditory-spatial cues that are used to determine the world-centric location of a sound source.

A. WAI spatial window

In generating Figs. 3 and 6, it was assumed that responses within ±3 loudspeakers of the exact WAI predicted location, WAIP0-3, should be considered as evidence for the WAI. This is a wider spatial window than was used to determine which responses were FBRs in experiment I (i.e., a WAIP0-1 spatial window). This seems justified, given that almost 100% of the FBRs were within a ±1 loudspeaker spatial window and almost 100% of the WAI predictions were within a ±3 loudspeaker spatial window. This implies that the spatial resolution for determining FBRs is better than that for determining the WAI. If true, this difference in spatial resolution might be due to several causes. First, listeners in experiment I, measuring FBRs, were stationary, while they rotated in experiment II, which measured the WAI. Pilot data suggest that listeners are slightly less accurate (i.e., have slightly higher root-mean-square angular azimuthal errors) in judging sound-source locations when they rotate as compared to when they are stationary (but see Honda et al., 2013). Clearly, a careful evaluation of this claim is required. Second, during the debriefing session of experiment II, several listeners stated that while it was usually clear when a sound source was rotating, sound sources that were obviously not rotating and were therefore more or less stationary sometimes seemed to change location by a small amount, or “drift,” over the 6-s sound presentation. Such small spatial changes could lead to a wider spatial window when perceiving the WAI and identifying a loudspeaker as the location of the putatively stationary sound source. A third possibility is based on the clockwise “skew” in the shape of the spatial window, indicated in Fig. 5 for all five filtered noises. The integration of head-position cues with reverse sound-source location cues must take some time. Also, some change in perceived sound-source position must occur for that change to be compared to a change in head position. Sounds were presented from loudspeakers spaced 15° apart, so this change would take some time to occur. Updating the relative changes in head position with changes in auditory-spatial cues would also take time. Thus, when the sound is initially presented, the head-centric location of the reverse sound source may be registered, but by the time the change in its location is integrated with the change in the head-position cue, the head has moved clockwise a small amount. The integration of the originally estimated head-centric angle and the current angle of the slightly rotated head would produce a world-centric reverse angle slightly clockwise (leading to the skew shown in Fig. 5) to that which would have occurred if the integration had been quicker. A fourth, related possibility is that some stimulus presentations may not have been perceived as a FBR sound until enough noise-burst presentations had occurred. In this case, the spatial estimate of the stationary sound source might be at the location where it was first registered as a FBR sound.

B. Relationship between FBRs and the WAI

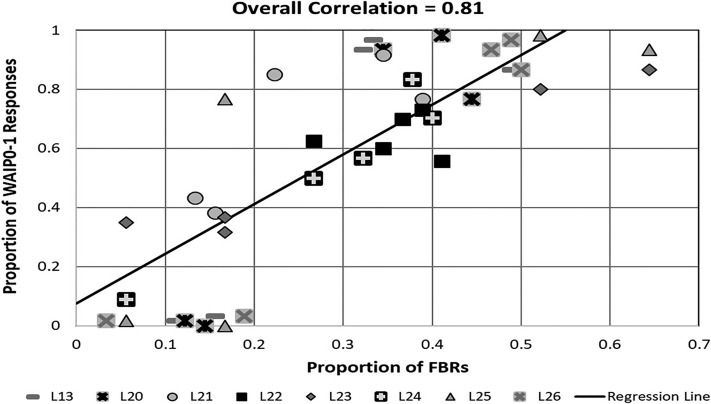
The data of experiments I and II imply a positive relationship between the rate of occurrence of FBRs for stationary sound sources and the existence of the WAI—in other words, listeners for any particular condition who demonstrate high rates of FBRs will be more likely to demonstrate the WAI for that condition. Figure 7 displays a scatter diagram relating the proportion of the WAI occurrence with the proportion of front-back reversed responses with different symbols representing data from the different listeners. So that the same criterion was used for both the WAI and front-back reversed measures, and since the criterion cannot be any larger than ±1 loudspeaker location for FBRs, as explained above for experiment I, a ±1 loudspeaker spatial window was chosen as the criterion for both a WAI location (i.e., WAIP0-1) and FBRs. For example, if loudspeaker #13 was a front-back reversed location, then responses of #12, #13, or #14 counted as a front-back reversed response. If loudspeaker #13 were a WAIP0 location, then the same three responses also counted for a WAIP0-1 response in Fig. 7. The proportion of FBRs in Fig. 7 was based on the total number of FBRs for each filtered noise burst and listener (40 data points). The proportion of responses in the WAIP0-1 spatial window was averaged over the four starting noise burst locations and the three stages of rotation (as has been done for other comparisons in this paper; see Fig. 4) for each filtered noise burst and listener (again 40 data points). In several cases, data points in Fig. 7 overlap. The line in Fig. 7 represents a linear regression fit. The Pearson product moment-correlation is 0.81 (66% of the variance accounted for).

FIG. 7.

Scatter diagram showing the average proportion of WAIP0-1 responses (see Fig. 3) as a function of the average proportion of FBRs (see Fig. 1) for each of the eight listeners (L13 and L20–L26; different symbols). Data include the five filtered noise conditions, but are averaged over starting loudspeaker locations and stages of rotation. See the text for the criterion used to define proportions. Straight line indicates the linear regression fit, and the Pearson product moment-correlation is 0.8.

Table II indicates the Pearson product moment-correlations between proportion of FBRs and proportion of responses in the WAIP0-1 spatial window for each of the eight listeners. The individual listener correlations were based on five points/listener, which is a small number of observations. As can be seen in Fig. 7 for some listeners, most of their responses were either at or near 0 or 1.0 for WAI responses and also at a minimum and a maximum proportion for FBRs. As such, the responses were bimodally distributed. Other listeners' responses were distributed between the “extremes” of proportion of FBRs and WAI responses (i.e., their responses were not bimodal). However, Fig. 7 does indicate a relatively strong relationship across filtered noise conditions and listeners between the proportion of responses in the WAIP0-1 spatial window and FBRs. A larger number of conditions for computing correlations for individual listeners would require a large number of ways to generate different proportions of FBRs. We are not sure how one would do this other than varying listeners along with the spectral content of sound as we did in the current study.

TABLE II.

Overall Pearson product moment-correlation coefficients between the proportion of FBRs and WAI responses within the WAIP0-1 spatial window are shown for each listener (L13–L26).

Listener	Overall correlation
L13	0.88
L20	0.92
L21	0.85
L22	0.14
L23	0.84
L24	0.89
L25	0.92
L26	0.88

The dark square data points in Fig. 7 are for listener L22, the listener with a low correlation coefficient (see Table II). The small variability in FBRs and, especially, WAI responses led to the low correlation result for L22 shown in Table II. However, L22's data clearly lie near the regression line, indicating the overall strong positive correlation between WAI and front-back reversed responses.

Wallach (1940) suggested that the WAI would exist for all stimuli. This is clearly not the case for normal hearing listeners as all recent studies of the WAI have suggested (Macpherson, 2011; Brimijoin and Akeroyd, 2012, 2016; the current study). Only Wallach (1940) measured the WAI for stimuli that may have been broadband. However, Wallach's (1940) use of Victrola records, a 1940s record player, and 1940s loudspeakers (no details of the records, the record player, or the loudspeakers were provided in Wallach's, 1940, paper) might have produced musical sounds that were low-pass filtered, which could therefore lead to FBRs, partially explaining why his listeners may have experienced the stationary WAI prediction and not a rotating sound source.

C. WAI responses versus rotation responses

The 2-1 rotation paradigm used by Brimijoin and Akeroyd (2012, 2016) asked listeners to determine if filtered speech, presented in front of listeners when rotation started (“back illusion” condition), was perceived in “front,” and if the filtered speech signal that was presented in back of listeners when rotation started (“front illusion” condition) was also perceived in front. The proportion of front responses was determined for the back illusion and front illusion conditions as a function of different low-frequency cutoffs for the filtered speech signal as a way of changing the relative incidence of FBRs (although proportion of FBRs was not measured). The proportion of front responses was around 90% for the front illusion condition and 20% for the back illusion condition for the lowest cutoff frequency. Both proportions moved toward 50% front responses as the cutoff frequency increased. Brimijoin and Akeroyd (2012) did not indicate a clear reason why their listeners' responses tended to reach an “asymptote” at approximately 50% front responses. However, their result is consistent with the idea that for low-frequency speech signals there could be substantial FBRs, leading to the WAI. But as the cutoff frequency increases, the prevalence of FBRs decreases, reducing the likelihood of the occurrence of the WAI. Even for the lowest-frequency cutoff, listeners sometimes responded “back” in the front illusion condition, and front in back illusion condition (such inconsistent predicted WAI responses occurred approximately 10%–50% of the time in their study depending on cutoff frequency). In the current study, responses of a front location for a stationary “back illusory” sound source, or a back location for “front illusory” sound source, almost never occurred. The filtered noises in the present study were perceived as located within ±3 loudspeakers of the exact WAI prediction of a stationary sound source (WAIP0-3) or the sound source was perceived as rotating 98.5% of the time (see Fig. 4).

Listener self-rotation in the Brimijoin and Akeroyd (2012, 2016) studies was very brief, over a very small arc (±15°–±30°), and in a back and forth (e.g., clockwise, then counterclockwise) manner. The same was true of the chair rotation in the Wallach (1940) study. This probably made it difficult, if not impossible, for listeners in these studies to perceive a rotating sound source. However, if a sound source was perceivable as rotating, and yet there was not sufficient time or spatial distance (arc) to determine rotation, the brief glimpse listeners had of a sound-source's location might have led them to perceive a sound as occasionally changing from a source in front to one in back or from back to one in front (especially as they rotated back and forth). This could have led, at times, to incorrect front responses as measured by Brimijoin and Akeroyd (2012, 2016). Additional research on the WAI, as a function of the length of time and arc of listener rotation, could be useful. Such research would indicate the time scale of the integration of auditory-spatial and head-position information, as well as the integration time for correlating changes in the two cues. In any case, the procedure described in the present paper appears to robustly demonstrate how the geometry described by Wallach (1940) and in the Appendix applies to sound-source location perceptions in the 2-1 rotation scenario.

Macpherson's (2011) results for one listener, using a virtual/simulated listening condition, did show a higher proportion of reports of rotating sounds for a high-frequency filtered noise than the other two filtered noises used in this study. There was also a correspondence between the prevalence of FBRs and the degree to which evidence for the WAI occurred for this listener, although a measure of a direct relationship was not made. And, Macpherson's (2011) one listener did produce data that indicated the WAI exists when the relative starting sound-source location is not just at back or in front. These results are fairly consistent with the data of the present study and, to some extent, the studies by Brimijoin and Akeroyd (2012, 2016) for normal hearing listeners. However, the degree to which the WAI occurred was somewhat different in Macpherson's (2011) study from results obtained in the current study. Again, additional research is clearly required to fully understand these differences.

D. WAI and the existence of “directional bands”

Blauert (1969, 1997), Morimoto and Aokata (1984), and Middlebrooks et al. (1989) have shown that listeners are likely to perceive a narrowband signal centered at 4 kHz as located in front (e.g., Blauert's directional bands, 1969, 1997). Thus, sounds with these spectral properties presented behind a listener would be perceived as in front, but when the sound was in front of the listener it might continue to be perceived in front. In the latter case, the front-back reversed condition necessary to produce the WAI would not exist, and the WAI might “fail.” Furthermore, if the listener's percept is determined largely in the first few moments after sound rotation starts, then the narrowband, high-frequency stimulus could elicit the WAI when the sound is initially presented from behind the listener (a front-back reversal occurs to facilitate the WAI), but when the sound source eventually rotated, so that it was presented in front of the listener, the “directional band” could inhibit the WAI, since a front-to-back reversal would then be very unlikely. Results from experiment I are somewhat consistent with these observations, i.e., see Fig. 1(C) for the HFN filtered noise and the high proportion of B-“F” reversals, disregarding L22. Recall that this filtered noise condition produced weaker evidence for the WAI than the low-frequency filtered noises, but listeners (with the exception of L22) had a higher proportion of responses in the WAIP0-3 spatial window for the HFN condition than for the HFW and BB conditions. Some of these differences might be due to the directional bands described above. In all cases, the location of the sound source in experiment II was sometimes in front and sometimes in back of the listener as the sound source rotated around the loudspeaker array over the 6-s sound presentation. A front-back change occurred once or twice per rotation stage—to a first approximation, the sound was at a source in front of the listener about as long as it was at a source behind a listener [see Figs. 2(B) and 2(C) to gain an appreciation of how sound-source position changes relative to the listener]. Thus, it is possible that listeners occasionally did not perceive the WAI for the HFN filtered noise because they did not experience FBRs. Assuming that a front-back reversed location is required for the WAI, they might have perceived a rotating sound source, leading to some of the responses shown in Figs. 3 and 6 (see Macpherson, 2011).

E. Temporal and spatial properties of the noise burst presentations

In the present experiment, the 75-ms duration sound stimulus was pulsed on and off at loudspeaker after loudspeaker to create a saltatory “rotation,” with the time between sound presentations depending on the rate of listener rotation. In other studies, the sound was continuous, and often amplitude-panned between loudspeakers (e.g., Brimijoin and Akeroyd, 2012, 2016), and/or there was essentially no time between sounds being presented to different loudspeakers, and/or the duration of the sound presentation to any one loudspeaker was not fixed, but depended on the rate of listener rotation (e.g., Brimijoin and Akeroyd, 2012, 2016; Wallach, 1940). Because all four studies (Wallach, 1940; Macpherson, 2011; Brimijoin and Akeroyd, 2012; the present study) produced strong evidence for the illusion in normal hearing listeners, it is unlikely that these details of how sound is presented over time have much to do with the ability to generate the illusion. However, Macpherson (2011) suggested that short duration listener rotations and, therefore, short sound presentations, might affect the existence of the WAI. It seems reasonable to expect that some minimum time would be necessary for the integration of the outputs of several neural systems indicating head position and then more time to integrate these outputs with information provided by the auditory-spatial cues.

The number of loudspeakers, their spacing, and location (or simulated location) along an azimuth circle differed across the various studies of the WAI. Given the fact that all studies indicated a rather robust occurrence of the WAI, it is not likely that the differences in loudspeaker locations used in these studies would have a noticeable effect on the occurrence of the WAI. However, it is likely that there could be an interaction between the timing of sound presentation and the placement of the sound sources in terms of generating the WAI, especially if there are only a few widely spaced loudspeakers. As suggested above, additional research is required to determine how the details of the time of sound presentations and the spatial arrangement of the sound sources affect the integration of auditory-spatial and head-position cues.

F. Role of head-position cues

A crucial aspect of Wallach's explanation for sound-source localization is information about head position. Wallach (1939, 1940) assumed that three systems could provide head-position information: “proprioceptive stimulation from the muscles engaged in active motion, stimulation of the eyes, and stimulation of the vestibular apparatus.” In the experiments by Macpherson (2011) and Brimijoin and Akeroyd (2012, 2016), listeners rotated themselves (active, self-rotation); however, in Wallach (1939, 1940) and the current experiment, listeners were rotated in a chair (passive rotation). Self-rotation is highly likely to involve proprioceptive, neural-motor control signals that could indicate head position (e.g., via efferent-copy processes; see Freeman et al., 2017; Yost et al., 2015, for explanations). Such control signals would not occur when listeners are passively rotated in a chair, though some degree of muscular “resistance” may occur, which signals listener motion when listeners maintain a particular head position as the chair is rotated. Thus, passive versus active rotation can likely control for proprioceptive/neural-motor control cues indicating head position. Controlling listeners' access to visual cues via blindfolds can control for visual information that indicates head position. It appears as if only Yost et al. (2015) and the present study attempted to control vestibular cues that might indicate head position by passively rotating listeners at accelerating/decelerating versus constant rates. Acceleration and deceleration fully engage the semicircular canals, signaling the presence, direction, and relative rate of change in head position. However, such vestibular output, by itself, does not provide information about actual head position/angle at any moment in time. None of these vestibular signals exist under constant-angular velocity rotation (Lackner and DiZio, 2005). As Yost et al. (2015) argued, varying the type of passive listener rotation can affect vestibular information about head rotation. While the three types of listener rotation were employed in the present study, listeners' eyes were always open, so the role of vestibular function in indicating head position cannot be determined in isolation. As already explained, visual cues appear to have dominated listeners' estimation of head position in the current study. It also seems worth noting that Wallach (1940) induced a perception of listener rotation for stationary listeners when listeners viewed a rotating visual screen (see Trutoiu et al., 2008, for a description of this circular-vection illusion). Under these circular-vection illusion conditions, listeners perceived the WAI for a sound source rotating at twice the rate of the induced listener rotation even while the listener was, in fact, stationary. This implies that stimulation of the semicircular canals may not be enough (or at least not essential) to induce the WAI. Further study under modern laboratory conditions could be helpful in confirming or disputing Wallach's reported outcome for induced circular vection.

However, as Yost et al. (2015) showed, having inexperienced listeners passively rotate at slow rates of constant angular velocity, with their eyes closed, appears to deprive the nervous system of information about head position. Under those conditions, sound-source localization perception appeared to be entirely head-centric, so the WAI should not exist in these conditions, as head-position cues are required for the WAI to occur (Wallach, 1940; the Appendix). On the other hand, rotating in an accelerating or decelerating manner, with eyes closed, might lead to world-centric localization and the occurrence of the WAI for sounds prone to FBRs due to vestibular information. If not, then this would be strong evidence that vestibular function, by itself, does not provide sufficient information about head position to allow for the occurrence of the WAI or world-centric sound-source localization. It is also possible that listeners would perceive a stationary sound source, but not know where it is in the room. That is, listeners may be able to compare the rate of change in head position (under acceleration/deceleration) to the rate of change in sound-source location, but, without any knowledge of the head's position in the room, be unable to determine the location of the sound source in world-centric coordinates even while they judge the sound source to be stationary. Thus, there are several variables that need to be considered in determining the existence of the WAI when different head-position cues are available. Experiments along these lines are currently being performed.

As Yost et al. (2015) cautioned, care must be used in making assumptions about how different head-position manipulations actually influence information about head location provided by any particular system. For instance, Wallach's (1940) listeners were blindfolded, and passively rotated, and his listeners appear to have reliably perceived the WAI. We have already suggested that his “Victrola” record sounds might have been low-frequency, generating FBRs, so his listeners might not have perceived any of the sounds to rotate. And, the short duration and small arc of rotation could have contributed to a lack of sound-rotation perception. Wallach (1940) also concluded that because there were no proprioceptive head-position cues due to passive rotation and no visual cues due to listeners being blindfolded, the occurrence of the WAI was due to vestibular function. This assumes that there were no other cues his listeners could have used to gather head-position information. His experienced listeners were rotated manually in a chair over a short arc (no more than ±30°) over a short period of time (a few seconds), and the same quick back and forth rotation process was repeated, essentially the same way, several times at the same place in the room. It is possible that Wallach's (1940) experienced listeners had a “good sense” of where they were in the room when they were rotated, even though they were blindfolded. If so, that might have been sufficient for them to obtain head-position cues along with the binaural cues to form WAI perceptions. Or, perhaps, vestibular output during acceleration/deceleration may be a useful indicator of head position only when movement is over a short angular distance and a short time period, allowing for memory and estimates of time to establish a spatial map of the local environment (e.g., see Buzsáki and Llinás, 2017). Clearly, additional experimentation on head-position cues and sound-source localization perception is required, and we are currently collecting such data (the current study will provide important baseline conditions/data for determining how various head-position cues affect WAI perceptions).

V. SUMMARY

In summary, the current research reinforces conclusions made by others, such as Wallach (1940), Macpherson (2011), and Brimijoin and Akeroyd (2012, 2016), and Akeroyd (2014), that the 2-1 rotation scenario is a robust paradigm for exploring sound-source localization as an integration of auditory-spatial and head-position cues (sound-source localization as a multisystem process, not just an auditory process; also see Boring, 1942). In this paper, we showed that the perception of the WAI is highly correlated with the degree to which stimuli elicit FBRs. Listeners either report perceiving the illusionary stationary sound source predicted for the WAI, or they perceived the sound source as rotating. The perceived location of the sound source in a WAI condition is that associated with the front-back reversed location corresponding to the starting sound-source position, which can be estimated when rotation begins. When the eyes are open, there was essentially no evidence that changes in vestibular function affected the integration of head-position and auditory-spatial cues. Major questions that remain are related to what the possible head-position cues might be, how they are weighted, how they are integrated with auditory-spatial cues, and what role cognitive variables such as memory, experience, and attention play (e.g., in establishing a spatial map) in determining the world-centric location of sound sources. The paradigm described in this paper, involving passive rotation of listeners over long-time spans and arcs of rotation, and the resulting data, recommends the experimental advantages of this approach for exploring many of these questions in determining aspects of world-centric sound-source localization.

APPENDIX

The following system of notation is used: θ, angle; θ′, an estimate of an angle. The first subscript, in capitals, is the object for which we wish to measure the angle: S, sound source; H, head. The second subscript, in lowercase, is the coordinate system based on the reference for our measurement: w, world-centric; h, head-centric. If there is a third subscript, it is r, front-back reversed location. So, θ′_Swr indicates the estimated angle of the sound source (S) in world-centric coordinates (w), front-back reversed location (r). A subscript (₀) is used to indicate an initial condition (i.e., before a head turn or sound-source location change). For instance, $\theta {\prime }_{H{w}_0}$ indicates the initial world-centric angle of the head before a head rotation occurred after some time t.

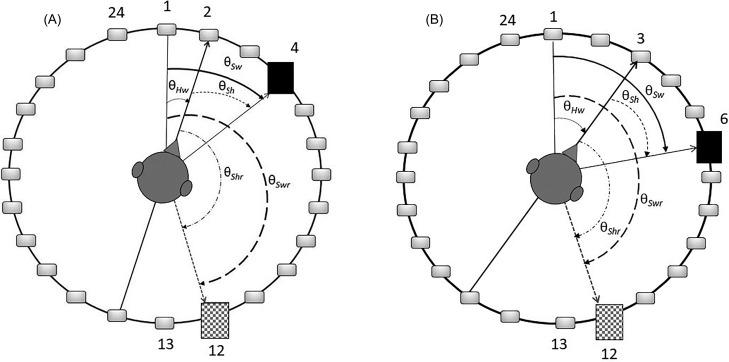
Figure 8(A) shows sound source and listener head locations in an arbitrary 2-1 relationship, with the head facing loudspeaker #2 and the sound source at loudspeaker #4. Then in Fig. 8(B), the head rotates to facing loudspeaker #3, and the sound is presented from loudspeaker #6 consistent with the 2-1 rotation scenario. The five angles used to describe sound-source and head-position angles that are employed in this appendix are also shown: θ_Sw, θ_Hw, θ_Sh, θ_Swr, and θ_Shr. The location of the sound source rotates through an angle (θ_Sw) from loudspeaker #4 to #6 from Fig. 8(A) to Fig. 8(B), but the angle of the reverse sound source (θ_Swr) remains fixed so the sound is at loudspeaker #12. While the angles in Fig. 1 are shown as fixed, each angle is estimated by the nervous system over time (t). The rest of this appendix attempts to show how the location of the reverse world-centric sound source remains stationary over time in the 2-1 rotation scenario used to study the WAI.

FIG. 8.

An example of the WAI conditions with the 24-loudspeaker azimuth array used in experiments I and II. The referent location is loudspeaker #1. (A) An example of a 2-1 rotation of listener and sound source is shown with the head facing loudspeaker #2, sound at loudspeaker #4, and the reversed sound source is loudspeaker #12. Also shown are the initial angles used in the Appendix: θ_Hw = world-centrichead-position angle, θ_Sh = head-centricangle of the sound source, θ_Sw = world-centric sound source angle, θ_Shr = reverse head-centric angle, and θ_Swr = reverse world-centric angle of the sound source. (B) A later moment in time in the 2-1 rotation scenario compared to (A), in which the listener has rotated to face loudspeaker #3, the sound rotated to loudspeaker #6, but the reverse world-centric location of the sound source remains at loudspeaker #12 [as it was in (A)].

We begin by assuming that the world-centric position of a sound source at some time t can be estimated as (see Yost et al., 2015, as well as Mills, 1972, and Braasch et al., 2013)

$${\theta }_{\mathit{Sw}}^{\prime }\left(t\right)={\theta }_{\mathit{Hw}}^{\prime }\left(t\right)+{\theta }_{\mathit{Sh}}^{\prime }\left(t\right).$$ (A1)

In this case, ${\theta }_{\mathit{Hw}}^{\prime }(t)$ could be an estimate from any neural system that senses head motion (e.g., vision) and ${\theta }_{\mathit{Sh}}^{\prime }(t)$ could be an estimate from the neural computation of the auditory-spatial cues. However, there is no direct neural estimate of ${\theta }_{\mathit{Sw}\hspace{0.17em}}(t)$; it must be estimated by integrating estimates of head position, ${\theta }_{\mathit{Hw}}^{\prime }(t)$, and the head-centric angle, ${\theta }_{\mathit{Sh}}^{\prime }(t)$. In the derivations shown here, we are assuming the integration of the estimates of head-position and the head-centric angle can be represented by the sum of the two. We used the word “estimate” literally, not in a statistical sense, to infer perceptual processes. That is, the derivations of this appendix do not represent a model. A model would require connecting auditory-spatial cues to head-centric angle, head-position cues to head angle, and specifying a method of integrating the various cues. Also, the weighting and integration of the various cues would involve estimates of internal noise. This is a task well beyond the scope of this paper, but see Braasch et al. (2013).

With only information about the interaural differences, a front-back reversed location (subscripted r), [${{\theta }^{\prime }}_{\mathit{Shr}}$_r = 180 − ${\theta }_{\mathit{Sh}}^{\prime }$] is also possible for the sound source because both ${\theta }_{\mathit{Sh}}^{\prime }$ and ${{\theta }^{\prime }}_{\mathit{Shr}}$ produce the same ITDs and ILDs. So

$${\theta }_{\mathit{Swr}}^{\prime }\left(t\right)={\theta }_{\mathit{Hw}}^{\prime }\left(t\right)+\left[180-{\theta }_{\mathit{Sh}}^{\prime }\left(t\right)\right].\hspace{0.17em}$$ (A2)

The equation for constant angular acceleration at time t is

$$\theta \left(t\right)={\theta }_{0\hspace{0.17em}}+{\omega }_{0\hspace{0.17em}}t+\frac{\alpha }{2}{t}^2,$$ (A3)

where ${\theta }_{0\hspace{0.17em}}$ is the initial angle, ${\omega }_{0\hspace{0.17em}}$ is an initial angular rotation velocity, and α is angular rotation acceleration.

Note that α and ω can be, for this explanation, positive (clockwise rotation) or negative (counterclockwise rotation). Note also that when α is the same sign as ω there is acceleration, and when they are opposite signs there is deceleration. If α = 0, this term drops out and its sign is unimportant.

At time t, after a head-turn of Δθ_Hw, the angle of the head can be estimated as

$${\theta }_{\mathit{Hw}}^{\prime }\left(t\right)={{\theta }^{\prime }}_{H{w}_0}+\Delta {\theta }_{\mathit{Hw}}^{\prime },\hspace{0.17em}$$ (A4)

where [from equation (A3)[, we can define $\Delta {\theta }_{\mathit{Hw}}\hspace{0.17em}\text{as}$

$$\Delta {\theta }_{\mathit{Hw}}={{\omega }_0}_{\mathit{Hw}}t+\frac{{\alpha }_{\mathit{Hw}}}{2}{t}^2.$$ (A5)

After this head rotation, the head-centric estimate of the sound-source angle will therefore be

$${\theta }_{\mathit{Sh}}^{\prime }\left(t\right)={{\theta }^{\prime }}_{S{h}_{0\hspace{0.17em}}}-\Delta {\theta }_{\mathit{Hw}}^{\prime }.$$ (A6)

In other words, for a stationary sound source, the angular relationship of the sound source to the head changes in the direction opposite to the head turn. Therefore, given a stationary sound source and a head turn, we can substitute Eqs. (A4) and (A6) into Eq. (A1), which gives

$$\begin{array}{c}{\theta }_{\mathit{Sw}}^{\prime }\left(t\right)={{\theta }^{\prime }}_{H{w}_0}+\Delta {\theta }_{\mathit{Hw}}^{\prime }+{{\theta }^{\prime }}_{S{h}_0}-\Delta {\theta }_{\mathit{Hw}}^{\prime }\\ ={{\theta }^{\prime }}_{H{w}_0}+{{\theta }^{\prime }}_{S{h}_0}\\ ={{\theta }^{\prime }}_{S{w}_0}.\end{array}$$ (A7)

Provided the estimate of the stationary sound source is not front-back reversed location, the world-centric estimate of the sound-source angle does not change with head movement. However, the estimated of the reversed world-centric sound-source angle [${\theta }_{\mathit{Swr}}^{\prime }(t)]$ at time t does change from its initial estimate. Substituting Eqs. (A6) and (A4) into Eq. (A2) yields

$$\begin{array}{c}{\theta }_{\mathit{Swr}}^{\prime }\left(t\right)]={{\theta }^{\prime }}_{H{w}_0}+\Delta {\theta }_{\mathit{Hw}}^{\prime }+[180-\left({{\theta }^{\prime }}_{S{h}_0}-\Delta {\theta }_{\mathit{Hw}}^{\prime }\right)]\\ ={{\theta }^{\prime }}_{H{w}_0}+\left(180-{{\theta }^{\prime }}_{S{h}_0}\right)+2\Delta {\theta }_{\mathit{Hw}}^{\prime }.\end{array}$$ (A8)

Noting that Eq. (A2) at the initial time is satisfied within Eq. (A8) yields

$${\theta }_{\mathit{Swr}}^{\prime }\left(t\right)={{\theta }^{\prime }}_{\mathit{Sw}{r}_{0\hspace{0.17em}}}+2\Delta {\theta }_{\mathit{Hw}}^{\prime }.$$ (A9)

Therefore, the reversed world-centric estimate of the sound-source angle has moved by twice the change of the head angle, in the same direction as the head turn.

Wallach (1940) noted that listeners nearly always perceive a stationary sound source as stationary, during and after head movements. But why would the listener choose the stationary estimate of sound-source location, ${\theta }_{\mathit{Sw}}^{\prime }$, over the moving estimate, ${\theta }_{\mathit{Swr}}^{\prime }$? Wallach (1940) developed the selective principle of rest to answer this question: “Of all the directions which realize the given sequence of lateral angles, that one is perceived which is covariant with the general content of the surrounding space.” In other words, if things around the listener are generally not moving, then the listener will choose the estimate that does not change as a result of head movements. This approach gives the listener a strategy for distinguishing his/her own movements from the movement of sound sources. Further note that, Wallach eventually determined that it was not specifically “least displacement” that was used to select a sound source, but “covariance with the general content of surrounding space, however—whether it is perceived at rest or not—can still be regarded as decisive for the selection of the perceived direction.”

Wallach (1940) noticed the symmetry inherent to this process. A stationary sound source gives rise to two estimates, which are both physically possible. The experimenter could therefore “turn the process on its head” by presenting a stimulus that followed the same trajectory as the reversed estimate in the example above, ${\theta }_{\mathit{Swr}}^{\prime }$. Such a stimulus would also give rise to two new estimates, which we will notate with an asterisk. One world-centric sound-source angle estimate, ${{\theta }^{\prime }}_{\mathit{Sw}}^{*}$, would change position during the course of the head turn at twice the angular velocity of that head turn, just as the actual sound source did. The front-back reversed angle estimate, ${{\theta }^{\prime }}_{\mathit{Swr}}^{*}$, would then not change during the head turn. If the listener used the selective principle of rest, and if the sound source were likely to elicit front-back reversals, then the stationary estimate, ${{\theta }^{\prime }}_{\mathit{Swr}}^{*}$, would be selected and perceived. Such a result would provide strong evidence that the listener was comparing information about changes in the world-centric position of the head with changes in binaural cues to localize a sound source.

Adding $2\Delta {\theta }_{\mathit{Hw}}^{\prime }$ to Eqs. (A7) and (A9), i.e., the 2-1 rotation scenario, yields

$${\theta }_{\mathit{Sw}}^{\prime *}\left(t\right)={{\theta }^{\prime }}_{H{w}_{0\hspace{0.17em}}}+{{\theta }^{\prime }}_{S{h}_{0\hspace{0.17em}}}+2\Delta {\theta }_{\mathit{Hw}}^{\prime }={{\theta }^{\prime }}_{S{w}_{0\hspace{0.17em}}}+2\Delta {\theta }_{\mathit{Hw}}^{\prime }.$$ (A10)

And

$${\theta }_{\mathit{Swr}}^{\prime *}\left(t\right)={{\theta }^{\prime }}_{H{w}_{0\hspace{0.17em}}}+\left[180-{{\theta }^{\prime }}_{S{h}_{0\hspace{0.17em}}}\right]={{\theta }^{\prime }}_{\mathit{Sw}{r}_{0\hspace{0.17em}}}.$$ (A11)

The reversed image, ${\theta }_{\mathit{Swr}}^{\prime *}(t)$, is perceived as stationary and the veridical image, ${\theta }_{\mathit{Sw}}^{\prime *}(t)$, is perceived to have rotated by twice the angle of the head turn.