Carbon-nitrogen REDOR to identify ms-timescale mobility in proteins

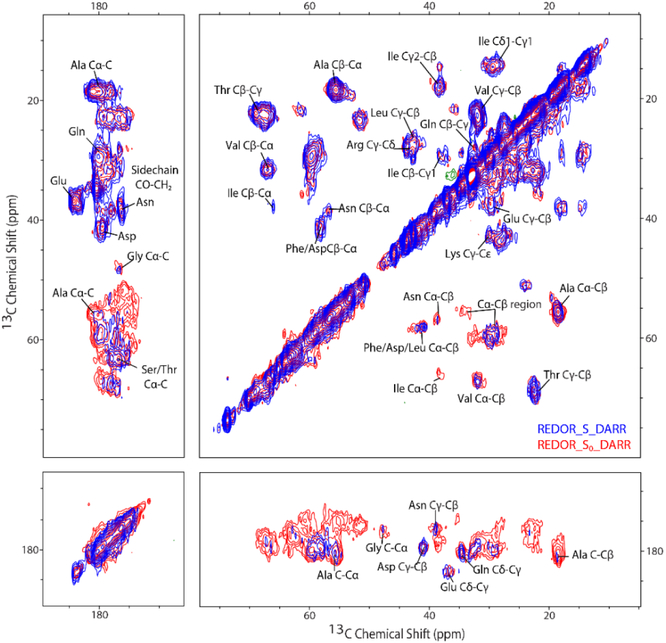
Abstract

Protein dynamics play key mechanistic roles but are difficult to measure in large proteins and protein complexes. INEPT and CP solid-state NMR experiments have often been used to obtain spectra of protein regions that are mobile and rigid, respectively, on the nanosecond timescale. To complement this approach, we have implemented ¹³C{¹⁵N} REDOR to detect protein regions with backbone dynamics on the millisecond time scale that average the ≈ 1 kHz carbon-nitrogen dipolar coupling. REDOR-filtering of carbon correlation spectra removes signals from rigid backbone carbons and retains signals from backbone carbons with ms-timescale dynamics that would be missing in dipolar-driven NCA/NCO spectra. We use these experiments to investigate functionally important dynamics within the E coli Asp receptor cytoplasmic fragment (U-¹³C,¹⁵N-CF) in nativelike complexes with CheA and CheW. The CF backbone carbons exhibit only 60-75% of the expected REDOR dephasing, suggesting that 40-25% of the backbone experiences significant mobility that averages the ¹³C¹⁵N dipolar couplings to zero. Furthermore, the extent of this mobility changes with signaling state.

Graphical Abstract

1. Introduction

Nuclear magnetic resonance provides a variety of powerful tools to measure structure and dynamics in proteins and protein complexes and gain essential insights into their mechanisms. However, making clear connections between dynamics and mechanism remains extremely challenging [1]. Solid-state NMR (SSNMR) experiments provide access to the full frequency range of internal molecular motions within proteins and protein complexes, including challenging systems such as fibrillar and membrane proteins [2]. Many recent SSNMR studies have employed INEPT-based methods to detect regions with ns-timescale mobility [3][4][5][6][7][8][9]. For example, Jaroniec and coworkers measured 2D ¹H-¹³C and ¹H-¹⁵N INEPT spectra of recombinant nucleosome arrays under physiologically relevant conditions comparable to chromatin in cells. These spectra reveal that the histone proteins H3 and H4 have highly flexible, intrinsically disordered N-terminal domains, which may be important for regulation [6]. Siemer and coworkers investigated full length Orb2 in functional amyloids and demonstrated that the part of the protein responsible for the aggregation, which has effects on long-term memory formation, is highly flexible [4]. Because mobility changes are thought to be important to propagate signals in bacterial chemotaxis receptors [10] [11] [12] [13] [14], we recently applied this approach to functional complexes of the E coli aspartate receptor cytoplasmic fragment (CF) assembled into native-like, membrane-bound arrays with its partner proteins, a histidine kinase CheA and a coupling protein CheW. This study revealed that a key part of this receptor has ns-timescale dynamics that change with signaling state, with important implications for signaling mechanisms [9].

The studies described above all detect rigid and flexible segments of the proteins using CP and INEPT experiments, respectively. INEPT (Insensitive Nuclei Enhanced by Polarization Transfer) transfers magnetization from protons to ¹³C or ¹⁵N via J couplings (≈120 & 90 Hz respectively, for the protein backbone), which requires long delays (total of 4*1/(4J) ≈8-11 ms) in the pulse sequence. Magnetization from rigid parts of the protein will decay during these delays, leaving signals in the INEPT spectrum only from regions with ns timescale motion that gives long T₂’ relaxation times (coherence life times) [15]. In contrast, CP-based methods detect regions that are rigid on the ns timescale. CP (cross polarization) transfers magnetization from protons to ¹³C or ¹⁵N via dipolar couplings, and such transfer will not occur if mobility averages the dipolar couplings to zero. In particular, motion must not have a high enough amplitude and rate for significant motional averaging of D_CH (≈23 kHz) and D_NH (≈12 kHz).

Since slow motions on the microsecond-millisecond timescale are biologically important [16], it would be valuable to further edit the CP spectrum based on mobility at such timescales. For instance, a method that selectively detects regions with molecular mobility that averages D_CN (≈ 1 kHz) to zero would detect backbone segments with ms-timescale dynamics, typically important in domain motion and global folding. Such a method would also enable the detection of resonances missing in NC_α and NCO cross polarization-based correlation spectra due to motional averaging of D_CN.

Rotational-Echo Double-Resonance (REDOR) is a robust method to measure the dipolar coupling between heteronuclear spins, and is therefore widely employed for precise distance measurements in structural studies of proteins [17] [18] [19]. REDOR has also been used as a dipolar filter, to remove natural abundance ¹³C contributions and selectively observe spectra of ¹³C-¹⁵N pairs within a protein [20]. Polenova and coworkers have developed REDOR filters for selective detection of residues at protein-protein interfaces in complexes with differential labeling of the binding partners [21] [22] [23]. In one case, ¹⁵N{¹³C} REDOR dephasing completely removes ¹⁵N signals from the U-¹³C,¹⁵N-protein, leaving ¹⁵N magnetization in the ¹⁵N-partner protein, which is then transferred across the protein-protein interface to ¹³C for selective detection of intermolecular ¹⁵N-¹³C contacts[21]. An alternative approach uses double REDOR (dREDOR) to fully dephase proton signals from the U-¹³C,¹⁵N-protein, leaving ¹H magnetization in the unlabeled protein, which is then transferred by cross polarization across the protein-protein interface for selective detection of ¹⁵N or ¹³C nuclei at the interface [22] [23].

Motion on a timescale shorter than the reciprocal of the dipolar interaction averages the dipolar coupling and affects REDOR dephasing curves [24]. For example, in a REDOR study of an inclusion complex of calixarene (host) with p-F-Phe (guest), fitting the REDOR data required consideration of both the internuclear distances and motional averaging of the dipolar couplings [25]. Furthermore, the REDOR-filtered interface detection approaches described above include control experiments that measure signals from mobile residues that are not dephased by the REDOR filters [22] [23].

REDOR experiments can also be designed to probe dynamics rather than structure. For example, Polenova and coworkers employed ¹⁵N{¹³C} REDOR to demonstrate that a specific Tyr residue in the hinge region of an HIV capsid protein is missing from both REDOR ΔS spectra and NC_α spectra, due to dynamics on the millisecond or faster timescale [26]. Because of our interest in the role of dynamics in signal propagation in bacterial chemotaxis receptors, we have designed a REDOR approach to probe ms-timescale dynamics throughout the protein backbone.

Here we report measurements of ¹³C{¹⁵N} REDOR dephasing on a U-¹³C,¹⁵N protein to estimate the fraction of the protein with ms-timescale dynamics. We have applied this method to gain insight into backbone dynamics throughout the aspartate chemotaxis receptor cytoplasmic domain, where we detected a surprisingly large mobile fraction of the receptor backbone (25-40%) in functional, native-like membrane-bound complexes of the chemotaxis receptor cytoplasmic fragment (U-¹³C, ¹⁵N-CF) with its partner proteins CheA and CheW. To selectively observe this mobile fraction, we have implemented a REDOR-filtered C-C correlation experiment. We demonstrate this experiment on the tripeptide MLF, and then discuss its implications regarding CF regions that are rigid vs mobile on the ms timescale within functional complexes.

2. MATERIALS AND METHODS

2.1. Protein purification

Isotopically labeled CF (cytoplasmic fragment of the E. coli aspartate receptor) was expressed in BL21(DE3) E. coli cells from plasmids that encode CF with an N-terminal His tag, as previously described [9]. pHTCF4Q (amp^R) [27] encodes CF with Gln at all 4 methylation sites, for assembly into complexes in the kinase-on state. pCF4Q.A411V (amp^R) [28] encodes the A411V mutant previously shown to lock the receptor in a kinase-off state. These plasmids were co-transformed with pCF430 (tet^R) which encodes lacI^q. Cell growth and protein overexpression was performed as previously described [9], in M9 minimal media containing U-¹³C-glucose and (¹⁵NH₄)₂SO₄ as the carbon and nitrogen sources. U-¹³C,¹⁵N-CF4Q and U-¹³C,¹⁵N-CF4Q.A411V were purified by nickel-affinity chromatography [9]. BCA assay (Thermo Scientific) was used to measure protein concentrations.

Unlabeled CheW, CheA, and CheY were expressed using plasmids pTEV-cheW (kan^R), pTEV-cheA (kan^R), and pTEV-cheY (kan^R) [9], grown in BL21(DE3) cells with 50 μg/mL kanamycin. Each protein was purified by nickel-affinity chromatography, as previously described [9]. These proteins are produced with a TEV-cleavable N-terminal His tag, which must be removed before His-tag mediated assembly of functional CF complexes on vesicles. TEV cleavage of the His tags was performed as previously described [9][28]. The A₂₈₀ was used to measure protein concentrations (using extinction coefficients of 25,000 M⁻¹cm⁻¹ for CheA, 5120 M⁻¹cm⁻¹ for CheW, and 10,700 M⁻¹cm⁻¹ for CheY [29]).

2.2. NMR sample preparation

Microcrystalline U-¹³C,¹⁵N-labeled f-MLF was purchased from Giotto Biotech Laboratories and was center packed in a 1.9 mm rotor with KBr on both sides of the f-MLF. Functional membrane-bound signaling complexes of receptor CF with its two binding partners CheA and CheW were assembled as follows. Vesicles composed of a 1:1.5 ratio of DOGS-NTA-Ni²⁺ (1,2-dioleoyl-sn-glycero-3-[[N(5-amino-1-carboxy-pentyl) and DOPC (1,2-dioleoyl-sn-glycero-3-phosphocholine) lipids (Avanti Polar Lipids) were prepared as previously described [9]. For each NMR sample, 4 ml total volume of complex was assembled by combining (in order) autoclaved water, potassium phosphate kinase buffer (PPKB: 50mM K_xH_xPO₄, 50mM KCl, 5mM MgCl₂, pH 7.5), 1 mM PMSF (from 200 mM stock in ethanol), 12 μM CheA, 24 μM CheW, 30 μM CF (CF4Q or CF4Q.A411V), and 725 μM vesicles. Complexes were incubated at 25°C overnight before measuring ATPase kinase activity and sedimentation as previously described [9][28]. The assembled complex was recovered as the pellet after centrifugation at 55,000 rpm at 25°C for 2 hours in an ultracentrifuge (108,000g in a TLA 120.2 Beckman rotor). Approximately 13 milligrams of the jelly-like pellet were packed into a 1.9 mm rotor by transferring the pellet using a spatula into a flame-sealed gel-loading pipette tip, and then centrifuging the pellet into the rotor.

2.3. NMR Spectroscopy

NMR spectra were acquired in a 14.1 T magnet on a Bruker Avance III spectrometer outfitted with a 1.9 mm HNCF magic angle spinning (MAS) probe; Larmor frequencies are 600 MHz for ¹H, 150 MHz for ¹³C, and 60 MHz for ¹⁵N. ¹³C{¹⁵N} REDOR experiments were performed with π/2 pulse lengths for ¹H, ¹⁵N, and ¹³C of 3.2, 8.1, and 4.5 μs respectively at 11.11 MAS (regulated to within ± 20 Hz by MAS controller) and 1 second recycle delay. ¹H–¹³C cross-polarization was performed with a contact time of 2 ms, ¹³C B₁ of 55 kHz, and ¹H B₁ maximum of 78.1 kHz (30% ramp) with SPINAL-64 decoupling at 71 kHz. Two-dimensional ¹³C-¹³C correlation spectra were collected using crosspolarization followed by t₁, evolution and the dipolar-assisted rotational resonance (DARR) mixing times of 20 ms before ¹³C data acquisition (t₂ evolution). A REDOR-filtered DARR pulse sequence was constructed by inserting REDOR dephasing pulses between the cross-polarization and t1 evolution of a CP-DARR experiment (Figure 1). The S₀ version (no dephasing pulses) of the experiment gives a ¹³C-¹³C DARR spectrum that is uniformly attenuated by T₂’ decay during the REDOR segment. The S version (with an appropriate number of dephasing pulses) will attenuate signals of carbons bound to nitrogen, retaining only the mobile C_α and CO of a protein backbone in t₁, with correlations to nearby carbons in t₂. The 2D DARR and REDOR-filtered DARR experiments on the U-¹³C,¹⁵N -CF4Q sample consist of 600 points in the indirect dimension with 256 scans each (1 s recycle delay) for a spectral width of 44.44 kHz, and a total experiment time of approximately 43 h. The 2D DARR and REDOR-filtered DARR experiments on the f-MLF sample consist of 600 points in the indirect dimension with 16 scans each, for a total experiment time of 170 min. For the CP build-up curves, the π/2 pulse lengths for ¹H and ¹³C were the same as used in the REDOR experiments and the contact times were varied between 0.1-7 ms, with 1 sec recycle delay. To compare intensities in CP spectra for frozen and unfrozen samples, spectra were collected with a 5 sec recycle delay to allow for full relaxation (longer delays did not increase the signals). Intensity comparisons were made for CP times that gave maximum intensities for the carbonyl (170-190 ppm) and Cα (50-75 ppm) regions of the spectra in each sample (see Figure S2). ¹³C chemical shifts were referenced to DSS at 0 ppm, by setting the downfield peak of an external adamantane standard to 40.5 ppm.

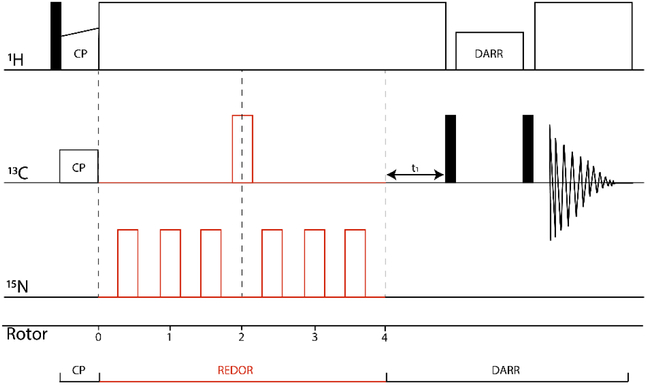
Figure 1.

2D REDOR-filtered DARR pulse sequence. After 1.5 ms REDOR dephasing, only carbons without strong dipolar couplings to nitrogen remain, corresponding to (1) carbons without directly bonded N, and (2) carbons with directly bonded N that experience sufficient ms-timescale dynamics to significantly reduce the effective carbon-nitrogen dipolar coupling. DARR is used to observe ¹³C-¹³C correlations of these remaining carbons. In a protein, correlations with backbone CO and Ca in ω₁ correspond to regions with ms timescale dynamic averaging of the dipolar coupling.

KBr was used to measure frictional heating caused by the mechanical sample rotation about the magic angle, by measuring the spin-lattice relaxation rate [30] at the same gas flow rate as the experiment. TmDOTP added to a DMPC vesicle sample (in the same buffer as the protein sample) was used to measure heating due to rf-irradiation during ¹H decoupling, by measuring the proton chemical shift [31]. At 11.11 kHz MAS, the gas temperature is approximately equal to the sample temperature, and our decoupling conditions heat the sample by approximately 5° C. So, for an unfrozen sample at 11.11 kHz, the gas temperature was set to 283 K to maintain the sample temperature between 283 and 288 K. For frozen samples at the same MAS rate, the gas temperature was set to 248 K, which temperature calibration measurements indicate maintains the sample temperature between 258 and 263 K.

2.4. NMR Data analysis

REDOR data points for U-¹³C,¹⁵N-CF complexes are integrals of the C_α region (50-75 ppm) and CO region (170-190 ppm). ¹³C{¹⁵N} REDOR dipolar dephasing curves are calculated using SIMPSON [32]. These curves are corrected for other contributions to the C_α and CO integrals, as discussed in the text and in Tables 1 and 2. The CheA, CheW, and lipid natural abundance contribution is negligible compared to U-¹³C-CF. With a ratio of CF:A:W in the complexes of 6:1:2, the residue numbers for each protein times the molar ratio times the ¹³C natural abundance percentage give us less than 0.01 contribution for CheA and CheW (CF: 6*310*1=1860, CheA: 654*1*0.01=6.54, CheW: 167*2*0.01=3.34). The lipid:CF = 145:6 and each lipid has two CO, so the lipid also has a negligible contribution (145*2*0.01=2.9). Standard deviations of the S₀ and S peak areas are calculated as the standard deviation of the baseline in the spectra times the square root of the number of points integrated. Standard deviations of ΔS/S₀ are calculated by error propagation; error bars are ± one standard deviation.

Table 1.

Residues (frozen/unfrozen) contributing to C_α resonance for calculation of rigid limit REDOR dephasing curves.¹

	Backbone Cα	Cβ in Cα region2	Cαin other regions3	Total4
S0 spectrum	310/226	+ Thr (21/12)+Ser (31/24)	− Gly (17/14)	345/248
ΔS spectrum	310/226	+ 0/0	− Gly (17/14)	293/212

¹All residues contribute to frozen CP spectra. For unfrozen spectra, previous studies have identified 84 mobile residues which are observable in INEPT rather than in CP spectra. Throughout the table, bold font indicates the CP-detectable residues in the unfrozen sample, after subtraction of the 84 INEPT-detectable residues previously identified.

²C_α region is integrated between 50 ppm and 75 ppm, so Ser C_β and Thr C_β peaks found in this region contribute to the S₀ signal. But with no directly bonded nitrogen, they will not dephase significantly (ΔS=0).

³Gly C_α peak is not in this region, so will not contribute to S₀ or ΔS.

⁴The rigid limit REDOR dephasing curve for C_α (1.46 Å, D_CN=984 Hz) must be corrected for the contribution of non-backbone resonances which do not have directly bonded N (Ser & Thr) and thus will not dephase at this rate. The REDOR curve will plateau at a correction factor equal to the maximum predicted ΔS/S₀ rather than at one: correction factor for frozen REDOR curve = 293/345 = 0.85; correction factor for unfrozen REDOR curve = 212/248 = 0.85.

Table 2.

Residues (frozen/unfrozen) contributing to CO resonance for calculation of rigid limit REDOR dephasing curves.¹

	Backbone CO	CO sidechains2	Total3
S0 spectrum	310/226	+ Gin (25/16)+ Asn (12/9)+ + Glu (21/13) + Asp (16/13)	384/279
ΔS spectrum	310/226	+ Gin (25/16)+Asn (12/9)	347/253

¹All residues contribute to frozen CP spectra. For unfrozen spectra, previous studies have identified 84 mobile residues which are observable in INEPT rather than in CP spectra. Throughout the table, bold font indicates the CP-detectable residues in the unfrozen sample, after subtraction of the 84 INEPT-detectable residues previously identified.

²CO region is integrated between 170 ppm and 190 ppm. CO sidechains in Gln, Glu, Asn and Asp contribute to the S₀ spectrum, but only Gln and Asn sidechain CO are directly bonded to N and contribute to the ΔS spectrum.

³The rigid limit REDOR dephasing curve for CO (1.3 Å, D_CN=1295 Hz) must be corrected for the contribution of non-backbone resonances which do not have directly bonded N (Asp & Glu) and thus will not dephase at this rate. The REDOR curve will plateau at a correction factor equal to the maximum predicted ΔS/S₀ rather than at one: correction factor for frozen REDOR curve = 347/384 = 0.90; correction factor for unfrozen REDOR curve = 253/279 = 0.91.

The 2D DARR and REDOR-filtered DARR spectra were processed in Topspin 3.2. Zero-filling to twice the number of data points was used for both dimensions, followed by linear prediction (16 points) in the indirect dimension. Data were processed with cosine bell multiplication and baseline correction (subtraction of the average intensity for the last quarter of the FID: BC-mod = quad and BCFW = 0.1 ppm in Topspin). Peak volumes and S/S₀ ratios were analyzed with Sparky (UCSF). The lowest contour level was set to 6 times the estimated noise (2000 points) and the peak volumes for all resolved peaks were measured using the Gaussian fitting integration method (default settings plus fit baseline). For unresolved peaks, the sum over the box method was used to find the combined volume of the peaks.

3. Results and Discussion:

3.1. ¹³C{¹⁵N} REDOR reveals extent of ms-timescale backbone dynamics within functional protein complexes

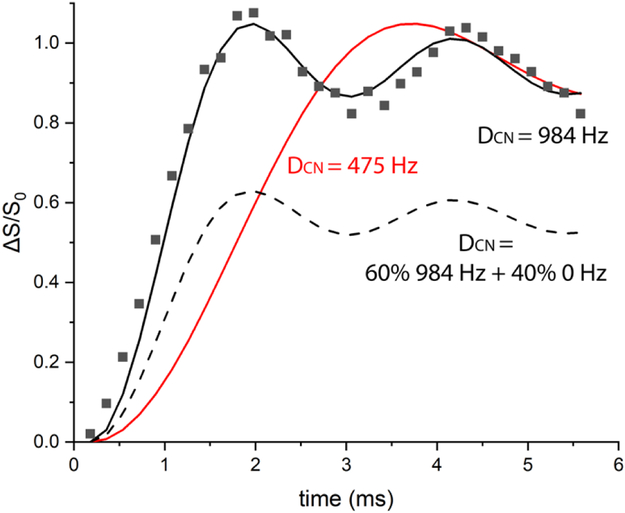
Figure 2 illustrates how ¹³C{¹⁵N} REDOR can be used to detect the presence of ms-timescale mobility in a protein backbone. REDOR data for U-¹³C,¹⁵N-Gly (squares) fits well with the calculated REDOR dephasing curve (solid black line) for the known 1.46 Å C_α to N distance. This is the rigid limit curve, which assumes no motional averaging of the 984 Hz dipolar coupling. Any motion on the ms or faster timescale will average the dipolar coupling. There are two distinct effects of motional averaging on these REDOR curves. (1) Partial averaging of the dipolar coupling will decrease the slope of the curve (eg red curve for a reduced dipolar coupling of 475 Hz) so that it rises more slowly to the complete dephasing value of ΔS/S₀ ≈ 1. Such partial averaging occurs when either the timescale of the motion is too slow or amplitude of the motion is too limited to fully average the dipolar coupling. (2) Complete averaging of the dipolar coupling to zero will eliminate all REDOR dephasing (ΔS/S₀=0 at all dephasing times). If part of the sample experiences extensive motion that averages the dipolar coupling to zero, the REDOR curve will level off at a value less than one. For a sample containing multiple C_αN pairs with a range of dynamics, the REDOR curve will correspond to the average of the behavior across all spin pairs. The dashed black REDOR curve in Figure 2 corresponds to a hypothetical case in which 60% of the C_αN pairs are rigid and 40% have sufficient mobility to average the dipolar coupling to zero. Since all carbons in a protein backbone are directly bonded to nitrogen, measurement of ¹³C{¹⁵N} REDOR dephasing curves for backbone carbons in a U-¹³C,¹⁵N-protein will reveal whether some fraction have significantly reduced dipolar coupling (giving a slower initial rise of the REDOR curve) and/or some fraction have the dipolar coupling fully averaged to zero (giving reduced final values of ΔS/S₀). If such dynamics are detected, then inserting a REDOR filter into an NMR experiment will dephase magnetization from rigid portions of the backbone and allow for selective detection of backbone regions with mobility that significantly reduces the carbon nitrogen dipolar coupling.

Figure 2.

REDOR dephasing as a probe of dynamics. ¹³C{¹⁵N} REDOR data for a rigid sample, U-¹³C,¹⁵N-Gly C_α (squares), show good agreement with the REDOR curve (solid black) predicted for the 1.46 Å C_α to N distance (D_CN= 984 Hz). If motional averaging reduces the carbon-nitrogen dipolar coupling (for instance to 475 Hz), the REDOR curve (red) rises more slowly to ΔS/S₀=1. If motional averaging reduces the dipolar coupling to zero in a fraction of the sample, the REDOR curve rises to less than one. For instance, the dashed black curve is predicted for a protein backbone C_α (same distance) if 60% of the sample is rigid and 40% has ms or faster timescale dynamics that averages the carbon-nitrogen dipolar coupling to zero. REDOR data were recorded at 283K with 11.11 kHz MAS, and 2,4,6,…62 rotor cycles of dephasing.

Since signal propagation through chemotaxis receptors is proposed to involve mobility and mobility changes in the cytoplasmic domain [10] [11] [12] [13] [14], we chose to apply REDOR to detect ms-timescale mobility in U-¹³C,¹⁵N-CF in native-like functional complexes with unlabeled CheA and CheW. Experiments conducted on frozen samples should match REDOR dephasing curves for the rigid limit dipolar coupling, and we can attribute any differences observed on unfrozen samples to backbone mobility in the ms or faster range of correlation times.

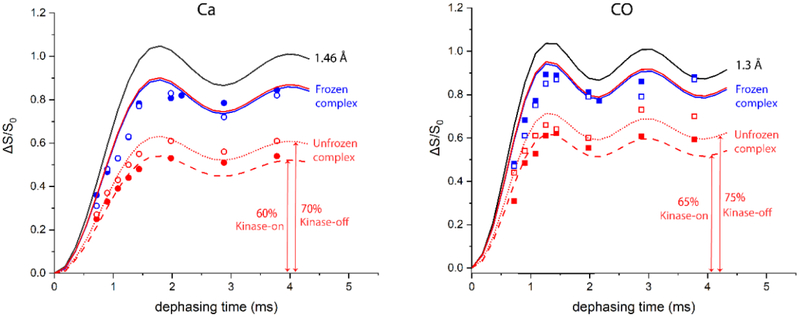
The experiments on frozen samples serve to demonstrate the approach needed to analyze ¹³C{¹⁵N} REDOR of backbone carbons in a U-¹³C,¹⁵N-protein. Figure 3 shows REDOR dephasing curves (black) for the backbone C_α-N (1.46 Å) and CO-N (1.3 Å) distances. The REDOR data for the frozen protein samples (248 K, blue symbols) do not fit these curves, because the carbonyl and alpha carbon regions in the one-dimensional S₀ and S spectra (Figure S1) include overlapping resonances from other carbons. The integrated CO region (170-190 ppm) contains Asp, Asn, Glu, and Gln sidechains, in addition to the backbone CO. The integrated C_α region (50-75 ppm) contains all C_α except Gly, plus Ser C_β and Thr C_β. Tables 1 and 2 illustrate how corrections for these overlapping resonances are made to calculate the rigid limit REDOR curve for the frozen (regular font) and unfrozen (bold font) samples. The strategy is to count the number of carbons contributing to S₀ and ΔS. For the C_α region, S₀ starts with the number of residues, plus the number of Ser C_β and Thr C_β minus the number of Gly. The Ser C_β and Thr C_β do not have directly bonded nitrogens, so they do not significantly contribute to ΔS. For the CO region, S₀ starts with the number of residues, plus the number of Asp, Asn, Glu, and Gln sidechains. The Asp and Glu sidechain carboxyls do not have directly bonded nitrogens, so they do not contribute to ΔS. REDOR curves for pure C_α or CO spin pairs would plateau at ΔS/S =1. Tables 1-2 show the predicted final ΔS/S₀ for the C_α or CO integrated regions. For instance, the C_α dephasing should plateau at 293/345=0.85. The C_α-N (1.46 Å) REDOR curve multiplied by the 0.85 correction factor gives the predicted rigid limit curve for the frozen sample C_α REDOR. The correction factors listed in Tables 1-2 were used to calculate the rigid limit curves for the frozen samples (blue curves in Figure 3). Figure 3 shows good agreement between these curves and the REDOR data for the frozen kinase-on (solid blue symbols) and kinase-off (open blue symbols) samples. The data fit better to scaled curves for slightly longer distances (eg Ca fits 1.50 instead of 1.46 Å, not shown), as observed for previous REDOR measurements of one-bond distances [33],with a slightly larger deviation for CO (fits 1.40 instead of 1.33 Å). This demonstrates that our approach successfully corrects for overlapping resonances in REDOR spectra of a U-¹³C,¹⁵N-protein, to obtain the predicted dephasing for all backbone carbons in a rigid protein.

Figure 3.

REDOR dephasing curves for ¹³C_α (left) and ¹³C0 (right) resonances of U-¹³C,¹⁵N-CF in functional complexes. Black lines are simulated REDOR curves for 1.46 Å and 1.3 Å distances. Solid blue and red lines are the frozen and unfrozen rigid limits calculated based on number of residues contributing to the integrated regions (Figure S1 and Tables 1-2). Red dashed and dotted lines are the unfrozen rigid limit scaled to match the unfrozen data points for kinase-on and kinase-off states, respectively. This scaling suggests that only 60-70% (left) or 65-75% (right) of the backbone is rigid on the ms timescale, and the remaining 30-40% is mobile enough to completely average the ≈ 1 kHz carbon-nitrogen dipolar coupling. ΔS/S₀ data for each dephasing time are calculated from the integrated intensity over the ¹³C_α resonances (circles) and ¹³CO resonances (squares) for frozen (blue) and unfrozen (red) samples of the kinase-on (solid symbols) and kinase-off (open symbols) CF complexes. Error bars are smaller than the data points, so the difference in total dephasing between kinase-on and kinase-off samples is significant. Spectra were recorded at 11.11 kHz MAS, with 10, 12, 14, 16, 18, 24, 34, and 44 rotor cycles of dephasing.

Comparison of REDOR dephasing for backbone resonances between the frozen and unfrozen samples should reveal the presence of dynamics on the ms or faster timescale. However, it is first important to correct for differences in cross polarization between frozen and unfrozen samples due to ns timescale dynamics. Prediction of the rigid limit dephasing curve for the unfrozen sample requires a correction for overlapping resonances that must be calculated for the CP-detectable part of the protein. We have previously identified two segments of the CF that are detected in INEPT spectra [9]. So, to calculate the rigid limit dephasing curves for the unfrozen CF complexes, the 84 residues of the INEPT-detected segments that are not detected in CP spectra are subtracted from total CF residues to yield the CP-detectable residues in the unfrozen CF, listed in Tables 1-2 in bold font This results in a maximum predicted ΔS/S₀ = 212/248 = 0.85 for the C_α dephasing curve and ΔS/S₀ = 253/279 = 0.91 for the CO dephasing curve. These values are similar to the correction factors calculated for the frozen rigid limit curves (0.85 and 0.90, respectively), resulting in essentially the same rigid limit curves for the unfrozen samples (red solid curves in Figure 3).

An additional consideration is that the unfrozen sample exhibits incomplete CP, indicating the presence of dynamics that partially average the CH dipolar couplings. If only the INEPT-detected portion of the protein were missing in the CP spectrum, the numbers in Tables 1-2 indicate that the CP-unfrozen/CP-frozen intensity ratio should be 248/345 = 0.72 for C_α and 279/384 = 0.73 for CO. Our previous report that CP of unfrozen samples efficiently detects all but the INEPT-detectable regions did not use fully optimized CP conditions [9]. Here we report a more detailed study: CP buildup curves were measured to determine the max CP condition for each signal, and the ratios of these intensity maxima were CP-unfrozen/CP-frozen of 0.42 for C_α and 0.39 for CO of kinase-on and kinase-off samples (see Figure S2). This is ~56% of the expected intensity for the 226 residues not observed in the INEPT spectrum. This should not significantly reduce the predicted final ΔS/S₀, because (1) both ΔS and S₀ will be scaled similarly, so the ratio is unchanged, (2) any difference in scaling would reduce ΔS (due to the more rigid portions of the protein) less than S₀, which would increase the predicted final ΔS/S₀, and (3) knowledge of which specific residues have reduced CP is not critical, as the above corrections to remove specific residues observed by INEPT did not significantly change the predicted final ΔS/S₀.

Backbone carbons in unfrozen CF complexes exhibit significantly less ¹³C{¹⁵N} REDOR dephasing than predicted for a rigid protein. The maximum ΔS/S₀ for unfrozen CF complexes (red symbols in Figure 3) is only 60-75% of the expected value, indicating that a significant portion of the protein experiences sufficient backbone mobility to average the carbon-nitrogen dipolar coupling to zero (no dephasing). Such mobility should have a similar effect on REDOR dephasing of C_α and CO. Consistent with this, the final REDOR dephasing level for each sample is similar for C_α and CO, 60-65% for the kinase-on sample (solid red symbols) and 70-75% for the kinase-off sample (open red symbols). This suggests that ~35-40% of the kinase-on CF backbone and ~25-30% of the kinase-off CF backbone has significant ms or faster timescale dynamics that average the carbon-nitrogen dipolar couplings to zero. The similarity of the CP buildup for frozen and unfrozen samples (Figure S2) suggests that the CP-observable parts of CF do not experience significant motional averaging of the ~20 kHz CH dipolar couplings, and thus are rigid on the μs and faster timescales. This suggests that the motional averaging of the ~1 kHz CN dipolar couplings is due to motions on the ms timescale. In the future, more quantitative measurements of dynamics may be used to further establish the timescale of the motions that average the D_CN to zero in the CF, analogous to experiments used to eliminate μs and faster motions in a study by Polenova and coworkers on dynamics of a single residue in HIV-1 capsid protein [26].

The initial slope of the REDOR dephasing reflects the backbone carbon-nitrogen dipolar couplings experienced by the rest of the CP-detectable parts of the CF. The dashed and dotted line REDOR curves in Figure 3, which are scaled to fit the final dephasing levels for the unfrozen CF complexes, also show good correspondence with the data in the initial slope region, which suggests that the backbone carbons that undergo REDOR dephasing have rigid limit dipolar couplings. Therefore, the REDOR data indicate that the CP-detectable parts of the CF backbone experience heterogeneous dynamics on the ms timescale: some parts have sufficient motion to average the CN dipolar coupling to nearly zero, and the rest is rigid on the ms timescale.

Interestingly, for all of the REDOR dephasing times, the kinase-off CF complex exhibits more dephasing than the kinase-on CF complex. This difference is significant, since error bars calculated for each ΔS/S₀ are smaller than the size of the data symbols plotted in Figure 3. Furthermore, a similar difference in maximum dephasing is observed for both the C_α and CO, suggesting the mobile fraction of the kinase-off CF is either smaller or less mobile, as explained below.

It is important to note that the REDOR dephasing provides an estimated range for the mobile fraction. Figure S3 demonstrates for the C_α REDOR data that incomplete dephasing can be fit equally well by a 10% larger mobile fraction that is somewhat less mobile, retaining 50 Hz rather than 0 Hz dipolar coupling. The dephasing curve for 60% rigid/40% mobile with D_CN = 0 Hz (solid red line) is equivalent to the curve for 50% rigid/50% mobile with D_CN= 50 Hz (dashed red line): both fit the kinase-on data (red). This indicates 40-50% of the backbone is mobile in the kinase-on state. Similarly, the dephasing curve for 70% rigid/30% mobile with D_CN = 0 Hz (solid black line) is equivalent to the curve for 60% rigid/40% mobile with D_CN = 50 Hz (dashed black line): both fit the kinase-off data (black). Thus the change from kinase-on to kinase-off could involve either a 10% reduction in the mobile fraction (eg from 40 to 30% with D_CN = 0 Hz, vertical arrow in Figure S3) or a decrease in its mobility (eg from D_CN = 0 Hz to D_CN = 50 or 100 Hz for 40% of the backbone, diagonal arrow in Figure S3).

3.2. REDOR filtering for selective observation of protein regions with ms-timescale dynamics

We implemented a REDOR-filtered DARR pulse sequence, designed to measure ¹³C-¹³C correlations corresponding to regions with ms-timescale dynamics (Figure 1). After ramped cross-polarization from ¹H to ¹³C to create the initial carbon magnetization, a REDOR filter (1.5 ms dephasing time) is inserted to dephase backbone carbon resonances from parts of the sample that are rigid, followed by t1 evolution. The 1.5 ms dephasing time (17 rotor cycles at 11.11 kHz) is chosen based on calculated rigid-limit REDOR dephasing curves. At this dephasing time, C_α and CO lose 90% and 100%, respectively, of their original intensity. The next fastest dephasing occurs for carbons with 2-bond distances to nitrogen (eg C_β), which only dephase by 10% in 1.5 ms. Thus the aω₁ dimension of the REDOR-filtered S spectrum will retain resonances for all ¹³C that are not directly bonded to ¹⁵N, as well as resonances for ¹³C directly bonded to ¹⁵N whose dipolar couplings are reduced to zero through motional averaging. A short carbon-carbon dipolar mixing sequence with a duration of 20 ms using DARR achieves magnetization transfer to neighboring carbons over one- or two-bond distances. The mixing is followed by a t₂ evolution during data acquisition [34], The REDOR-S₀-DARR spectrum, which is equivalent to a DARR spectrum attenuated by T₂’ decay during the dephasing time, has all ¹³C-¹³C correlations from both rigid and mobile regions. The REDOR-S-DARR spectrum exhibits reduced intensity for the backbone carbons, retaining only the mobile C_α and CO in the diagonal peaks, and cross peaks in the ω₂ dimension for nearby carbons in these mobile regions.

The REDOR filter approach is general and can be combined with other experiments to selectively observe mobile regions. Such experiments must employ mixing schemes that are compatible with ms-timescale mobility. Mixing must be mediated by interactions stronger than CN dipolar coupling, so the REDOR filter cannot be incorporated into NC_α or NCO experiments.

3.3. REDOR-filtered DARR on MLF demonstrates effective spectral editing

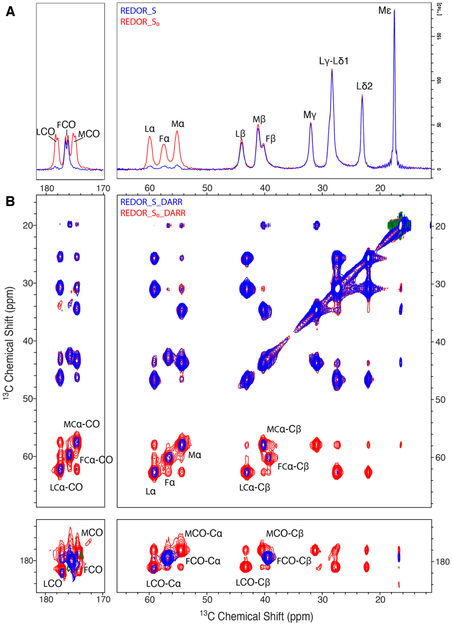
We used the rigid tripeptide f-MLF to demonstrate the REDOR-filtered DARR approach. REDOR spectra of f-MLF are shown in Figure 4A for a 1.5 ms dephasing time. Comparison of the S₀ spectrum (blue) with the S spectrum (red) shows essentially complete dephasing of carbons with directly bonded nitrogen: all three C_α are ≈ 90% dephased, Met and Leu CO are ≈100% dephased, and the terminal Phe carboxyl is not dephased because it lacks directly bonded nitrogen. As predicted, the C_β with the next-closest (2-bond) distance to nitrogen are less than 10% dephased, and there is no detectable dephasing of the C_γ, C_δ and C_ε resonances.

Figure 4.

Overlay of REDOR-S₀ (red) and REDOR-S (blue) and corresponding REDOR-filtered DARR spectra of U-¹³C,¹⁵N-MLF. (A) 1D REDOR spectra compare all ¹³C (REDOR-S₀, red) with ¹³C remaining after dephasing of carbons with directly bonded ¹⁵N (REDOR-S, blue). (B) 2D REDOR-filtered ¹³C–¹³C DARR correlation spectra comparing REDOR-S₀-DARR (red, all ¹³C-¹³C correlations) with REDOR-S-DARR (blue, correlations of carbons remaining after attenuation by dephasing of ¹³C directly bonded to ¹⁵N). Both 1D and 2D spectra show that Phe CO, which is not directly bonded to ¹⁵N, is retained completely, while Met CO and Leu CO are fully dephased. Spectra are at 14.1 T, with an MAS frequency of 11.11 kHz, REDOR dephasing time of 1.5 ms, and DARR mixing period of 20 ms.

The 2-D REDOR-filtered DARR experiment on f-MLF is illustrated in Figure 4B, which is an overlay of the REDOR-S₀-DARR (red) and REDOR-S-DARR (blue) spectra. The REDOR-S₀-DARR spectrum is equivalent to the DARR spectrum (see comparison in Figure S4), with all intensities reduced by T₂’ decay. As expected, based on the lack of significant dephasing in the REDOR spectra (Figure 4A), the REDOR-S₀-DARR and REDOR-S-DARR spectra are equivalent for ω₁ in the 0-45 ppm range. The C_α and CO regions in the ω₁ dimension demonstrate the REDOR filtering. The three small residual C_α peaks give rise to correlations with the closest (directly bonded) carbons (C_β and CO). The terminal Phe CO peak, which has full intensity in ω_1, gives rise to strong correlations with the nearest carbons at one- and two-bond distances, Phe C_α and Phe C_β. A similar behavior would be expected for mobile regions of a protein sample if mobility is sufficient to average the dipolar coupling to zero: the CO and C_α that survive the REDOR filter and appear in ω₁ would transfer magnetization to nearby carbons in those residues during the mixing time, producing CO-C_α, CO-C_β, C_α-CO, and C_α-C_β correlations that would help to identify the mobile residues. Application of this method to a protein with sequence-specific assignments should enable identification of the residues in the mobile fraction.

This experiment can also serve to identify the amino acid composition of the mobile fraction in proteins that lack fully resolved and assigned spectra. Peak volumes in REDOR-filtered DARR spectra of MLF demonstrate a feasible strategy. As shown in Table 3, volumes of correlation peaks in the S₀ spectra are not equivalent for M, L, and F, so these cannot be used to deduce numbers of residues. The ratio S/S₀ corrects for these differences in S₀ and demonstrates equivalent dephasing for the three C_α (only 10% of C_α-C_β and 8% of C_α-C peaks remain in the REDOR-S-DARR spectrum) and for L and M CO (only 5% of C-C_α peaks remain in the REDOR-S-DARR spectrum). The smaller S/S₀ for C-C_α is expected because the REDOR filter dephases more of the CO, due to its stronger dipolar coupling to N (about 10% of the C_α remains after 1.5 ms REDOR dephasing). Note that 95% of Phe C-C_α is retained because Phe CO is not directly bonded to nitrogen. MLF results suggest that for a sample with regions with complete motional averaging of the CN dipolar coupling, the S/S₀ ratio for each resolved residue type would provide an estimate of the mobile fraction of those residues.

Table 3.

S₀ peak volume and S/S₀ for both Cα-C_β and C- C_α of f-MLF sample.

	S0 for Cα -Cβ (normalized to Met)	S0 for C- Cα (normalized to Phe)	S0 for Cα -C (normalized to Met)	S/S0 for Cα- Cβ	S/S0 for Cα- C	S/S0 for C- Cα
Met	1	0.83	1	0.10	0.08	0.05
Leu	0.72	0.88	0.84	0.11	0.08	0.05
Phe	0.76	1	0.68	0.09	0.09	0.95

3.4. REDOR-filtered DARR on U-¹³C,¹⁵N-proteins provides insight into heterogeneous dynamics on the ms timescale

The REDOR-filtered DARR experiment was conducted on U-¹³C,¹⁵N CF in functional complexes with CheA and CheW. Figure 5 shows an overlay of REDOR-S₀-DARR (red) and REDOR-S-DARR (blue). As expected and observed for MLF, a REDOR filter with 1.5 ms dephasing time results in no differences between the blue and red spectra in the upper half of the spectrum (ω₁ ≤ 45 ppm). Differences are observed in the lower half of the spectrum, where resonances of the rigid CO and C_α are removed by the REDOR filter, decreasing the intensities in this region. The remaining peaks in the blue spectrum arise from mobile CO and C_α that are not dephased by the REDOR filter (diagonal) and their correlations. As discussed above, the S/S₀ peak volume ratio in the REDOR-filtered spectra for resolved correlation peaks can provide an estimate of the mobile fraction of the associated residue type. These mobile fractions are tabulated in Table 4, which includes the only resolved C_α-CO correlation for Gly and the strong C_α-C_β correlations (ranging from S₀=1 for Ala to S₀=0.2 for Asn, and excluding the weak Ile correlation with S₀=0.1). The bottom part of the spectrum (ω₁ near 180 ppm) exhibits resolved sidechain correlations (not included in Table 4), with either no significant dephasing for the sidechains lacking nitrogen (Asp C_γ-C_β and Glu C_δ-C_β with S/S₀ of 98 and 102%) or large mobile fractions for the sidechains containing nitrogen (Gln C_δ-C_γ and Asn C_γ-C_β with S/S₀ of 60 and 70%). Asn exhibits a higher mobile fraction for the sidechain (70%) than the backbone (12%), which likely indicates the sidechain has additional mobility. Finally, Table 4 includes S/S₀ for the unresolved ¹³CO-¹³C_α and ¹³C_α-¹³CO regions, corresponding to all CP-detectable residues except Gly.

Figure 5.

Overlay of S₀ (red) and S (blue) versions of REDOR-filtered ¹³C-¹³C DARR spectra of functional complexes of U-¹³C,¹⁵N-CF4Q. REDOR-S₀-DARR spectrum contains ¹³C-¹³C correlations for both rigid and mobile segments, while REDOR-S-DARR retains ¹³C-¹³C correlations with C_α and CO (ω₁) only for residues with millisecond timescale mobility. Dephasing time set to 1.5 ms for complete dephasing of rigid CO peaks and 90% dephasing of C_α peaks (both directly bonded to nitrogen), and only 10% dephasing of C_β (2-bond distance to nitrogen). Spectra collected at 11.11 kHz MAS frequency with DARR mixing period of 20 ms.

Table 4.

Mobile fractions^a of residues observed in CP spectrum.

Correlation	S/S0
Ala Cα-Cβ	39%
Val Cα-Cβ	22%
Phe/Asp/Leu Cα-Cβ	36%
Asn Cα-Cβ	12%
Gly Cα-CO	9%
CO-Cα & Cα-CO	25%
(all except Gly)	27%

^aS/S₀ corresponds to the mobile fraction of the CP signal, N_m/N_T, where N_T = the total number of CP-observable residues, and N_m = the number of mobile residues. Dynamics likely result in non-uniform CP, so S/S₀ cannot be directly related to amino acid distributions in different regions, as they depend on the CP efficiencies.

For a protein that exhibits uniform CP, comparison of the S/S₀ mobile fractions with the fractions of these residues in each CP-detectable region (excluding the INEPT-detected regions) could be used to identify which region(s) have the ms-timescale mobility selected by the REDOR filter. However, uniform CP seems unlikely for a protein that exhibits mobility that averages a significant fraction of backbone carbon-nitrogen dipolar couplings to zero. For example, CP detects about 56% of the expected intensity for the CF (after excluding the INEPT-detected regions). Without knowing the identity and range of CP efficiencies of the CP-detectable regions, the mobile fractions cannot be compared to amino acid distributions to identify mobile regions.

The REDOR and CP efficiency results indicate that CP spectra of CF in functional complexes include regions with different dynamics on the ms timescale. The combination of these experiments can be used to estimate the number of residues that are rigid on the ms timescale, based on rigid-limit carbon-nitrogen dipolar couplings. These likely have 100% CP efficiency and thus correspond to a minimum of 0.56*0.60*226 ≈ 76 residues (the fraction of the CP signal observed times the minimum fraction that is rigid times the number of residues not observed by INEPT). This rigid core of the protein could in principle be identified using NCA and NCO spectra, which we have observed to have very low intensity for these samples (results not shown), consistent with this being only 76/310=25% of the protein.

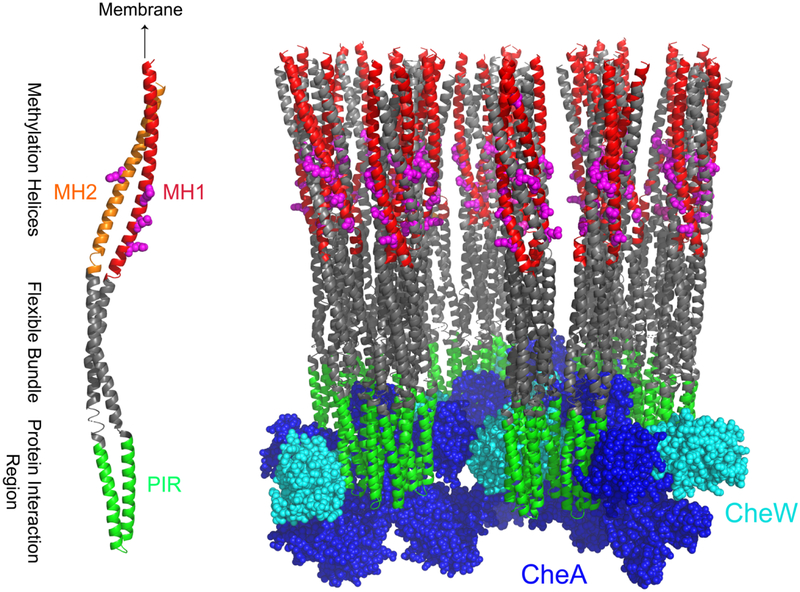
Zhulin and coworkers [35] have used sequence analysis to identify three functionally important regions of the CF, the methylation region, flexible bundle, and protein interaction region that interacts with CheA and CheW. These are represented in color on a CF monomer in Figure 6: methylation helices 1 and 2 (MH1 in red and MH2 in orange), the flexible bundle in gray, and the protein interaction region (PIR) that interacts with CheA and CheW in green. We have recently used HDX-MS to demonstrate that the regions shown in Figure 6 have distinct dynamic properties (Li & Thompson, in preparation) within functional complexes, and that the protein interaction region is significantly more stable than the rest. We hypothesize that the 76 residues that are rigid on the ms timescale correspond primarily to the 57 residues of the protein interaction region.

Figure 6.

Dynamics of the cytoplasmic domain of bacterial chemotaxis receptor in complexes with CheA and CheW. Functional regions of the CF (discussed in the text) are represented by colors on a receptor monomer (left), with methylation sites shown in magenta. One hexagon from the hexagonal array model (right) shows the chemoreceptor cytoplasmic domain (gray) bound to CheA (blue) and CheW (cyan). Structural model for the receptor array (coordinates courtesy of Brian Crane [36]) is based on docking the 3ur1 crystal structure into electron density observed by cryo-electron microscopy. Colors are retained on the model of the complex to convey the dynamics of these regions deduced by NMR and hydrogen exchange: MH1 (red) exhibits ns-timescale dynamics [9] and PIR (green) is proposed to be rigid on the ms timescale. Most of the rest of the CF (gray) is dynamic on the ms timescale within functional complexes, exhibiting either no CP or reduced CP with fully averaged carbon-nitrogen dipolar couplings.

The dynamics of the receptor CF within functional complexes are represented in Figure 6 (right). Methylation sites on the CF are represented in magenta; CheA (blue) and CheW (cyan) are bound at the membrane-distal tip of the receptor. The first methylation helix (MH1, red) is detected in INEPT spectra due to ns-timescale dynamics [9], and also exhibits extremely rapid hydrogen exchange [14]. The protein interaction region (PIR, green) is likely to be the majority of the region that exhibits rigid-limit CN REDOR, and the rest of the CF (gray) is largely dynamic on the ms timescale, exhibiting low CP efficiency and/or motional averaging of CN dipolar couplings, which is consistent with the rapid exchange and instability observed by hydrogen exchange for these regions (Li & Thompson, in preparation).

4. Conclusion

We have demonstrated the use of ¹³C{¹⁵N} REDOR on a U-¹³C,¹⁵N-protein to estimate the fraction of the protein backbone with ms-timescale dynamics. This can be used to gain insight into the overall dynamic properties of a protein, and to detect changes in these dynamics between functionally important states. We have also shown that a REDOR filter can be used to selectively observe backbone carbons with these dynamics, for instance in a REDOR-filtered DARR experiment. For proteins with resolved peaks and sequence-specific assignments, REDOR-filtered DARR would identify the dynamic residues and should selectively detect residues missing in NC^α and NCO spectra due to motional averaging of the carbon-nitrogen dipolar coupling. For complex systems that have only residue-type assignments, the number of residues that are rigid on the ms timescale can be estimated from a combination of the CP efficiency and the extent of rigid-limit ¹³C{¹⁵N} REDOR dephasing. This predicts the number of residues that would be detected in NCA and NCO spectra. Thus INEPT, REDOR-filtered CP, and CP experiments (eg REDOR ΔS) can be used both to estimate the fractions of a protein with dynamics on different timescales, and to edit spectra for selective observation of those fractions.