RELICA: a method for estimating the reliability of independent components

Abstract

Independent Component Analysis (ICA) is a widely applied data-driven method for parsing brain and non-brain EEG source signals, mixed by volume conduction to the scalp electrodes, into a set of maximally temporally and often functionally independent components (ICs). Many ICs may be identified with a precise physiological or non-physiological origin. However, this process is hindered by partial instability in ICA results that can arise from noise in the data. Here we propose RELICA (RELiable ICA), a novel method to characterize IC reliability within subjects. RELICA first computes IC “dipolarity” a measure of physiological plausibility, plus a measure of IC consistency across multiple decompositions of bootstrap versions of the input data. RELICA then uses these two measures to visualize and cluster the separated ICs, providing a within-subject measure of IC reliability that does not involve checking for its occurrence across subjects. We demonstrate the use of RELICA on EEG data recorded from 14 subjects performing a working memory experiment and show that many brain and ocular artifact ICs are correctly classified as “stable” (highly repeatable across decompositions of bootstrapped versions of the input data). Many stable ICs appear to originate in the brain, while other stable ICs account for identifiable non-brain processes such as line noise. RELICA might be used with any linear blind source separation algorithm to reduce the risk of basing conclusions on unstable or physiologically uninterpretable component processes.

I. Introduction

Blind source separation (BSS) techniques and matrix factorization algorithms in general – Independent Component Analysis (ICA), Principal Component Analysis (PCA), Factor Analysis (FA), etc. – have been steadily gaining in popularity in the last years as viable techniques to preprocess multivariate data sets, to disentangle information linearly mixed by volume conduction in the recorded data channels, and to perform or prepare for more general data mining [1]. ICA in particular has been shown to have value for analysis of electroencephalographic (EEG) data. At frequencies of interest (from about 0.1 Hz to a few hundred Hz), each EEG scalp electrode channel records a linear mixture of volume-conducted activities many of which index near-synchronous local field activity across a cortical patch [2]. Instead of solving the undercomplete inverse problem (i.e., determining the time-course and spatial distribution of current in each of a large number of possible cortical source areas from a limited number of scalp data channels), ICA separates the input scalp channel data into a complete set of maximally-independent component processes (as many as channels in the data) by projecting scalp electrode signals into a new spatial basis that may be used to assess individual EEG source dynamics without needing an explicit head model [3, 4]. ICA decomposition takes into account only the recorded signal time courses, and provides each component’s relative projection pattern to the scalp channels as well as the relative, time-varying signed amplitude of its source signal [5].

As with most factorization algorithms, the extracted components need to be interpreted before they can be used in further analyses. Unfortunately, this is often made difficult by several issues including inadequate data sampling (e.g., when recordings are too short and/or have too few channels), inadequate data pre-processing, algorithm deficiencies (lack of convergence, presence of local minima, etc.), and noise (from the electrodes and recording system and/or from a multitude of small, irresolvable signal sources). This has triggered particular interest (within several fields [6]) in finding new ways to assess two main characteristics of the extracted component processes: their reliability (both across and within subjects) and their physiological origins - which ones account for non-brain, and which brain source processes [7]. This latter question is of importance if ICA component signals are to be interpreted in the clinical domain [8].

Reliability across subjects refers to similarities in homologous ICs across subjects sampled from some homogeneous population. Studying across-subject IC clusters is a popular way of assessing the reliability of the results of an EEG study [9], one of the typical goals of ICA investigations being to find classes or clusters of brain-generated IC processes that occur frequently in the population of interest. This can be achieved visually [10], by employing different objective criteria [11], and/or by approaches including deterministic [12] or probabilistic [13] IC source localization.

Reliability within subjects refers to the physiological plausibility and statistical reliability of each IC across the data for each participant. Assessing these qualities is important for preventing unreliable ICs from obfuscating across-subjects IC analysis. Particularly in clinical settings, there may also be a need to know whether a particular component is reliably present and thus accurately represents a source process of interest in the patient. In this work we stress two aspects of IC reliability, its “stability” (e.g., its within-subject reliability [14–17]) and determination of its physiological plausibility and brain or non-brain origin. The few methods so far proposed to assess the stability of individual ICs by taking advantage of data resampling [14–17] each have shortcomings, such as the requirement of a large number of ICA decompositions to avoid unrepresentative resampling, or the use of difficult to interpret metrics (see Discussion for more detail).

Regarding IC origins, many IC scalp maps have been shown to be compatible with generation in local field potential activity that is (fully or partially) coherent across a single cortical patch. The scalp projection of such a source is nearly equal to that of a single current dipole, termed its equivalent dipole, located near the center of the generating patch [18]. Recently, Delorme et al. [19] showed that the stability of an IC across subjects is predicted by the goodness-of-fit of the projection of the IC scalp map to the scalp projection pattern of its best-fitting single equivalent dipole model, and that the relative degree of temporal independence of a set of ICs returned by a blind source separation algorithm is predicted by the number of ICs whose scalp maps are well fit to the projections of their equivalent dipoles.

This is compatible with the assumption that ICs should typically represent the projection of local field activity that is synchronous or near synchronous across a single cortical patch, a set of such sources thus producing the spatially-fixed brain and non-brain EEG source locations and orientations and (maximally) temporally distinct (independently time-varying) source activity time series assumed by ICA to represent source projections.

Delorme et al. defined an index of decomposition “dipolarity,” the number of component scalp maps matching the projection of a single equivalent dipole with less than a given percent residual variance. Here we will also refer to this as the degree of “IC dipolarity.” Delorme et al. also defined Mutual Information Reduction (MIR), a quantitative measure (in bits/sec) of the degree of independence of the extracted component time series relative to the original channel data, and showed that MIR can also be used to measure the relative quality of an ICA decomposition, the two measures proving to be, on average, linearly coupled for the dozen data sets they considered [19].

In this paper we propose RELICA (for “RELiable ICA”), a method that combines the findings of Delorme et al. [19] with a bootstrap data decomposition procedure [20] to assess the reliability of ICs in terms of its within-subject “stability” and its possible brain origin (physiological plausibility). RELICA applies ICA decomposition multiple times to surrogate versions of the input data selected by bootstrap selection, either trial-by-trial (e.g., in Event Related Potential or ERP studies) or time point by time point.

As the ICA algorithm used within RELICA, we here chose to apply Infomax ICA [21, 22], one of the most popular and reliable ICA algorithms [19], whose GPU implementations (e.g., CUDAICA [23], BeamICA [24] ) make feasible its bootstrap repetition, for example here using the ICASSO approach [16] or (modified for the treatment of ERPs) ErpICASSO [20]. By way of comparison, we also performed the analysis using FastICA [25], as it has relatively low execution time in its non-iterative mode even without GPU support.

RELICA proposes use of the distribution of IC dipolarities plus a measure of their replicability across surrogate decompositions as a joint quality index of IC physiological plausibility (via dipolarity) and replicability (stability) respectively. When both IC stability and dipolarity are high, then the IC is a likely candidate for retention and further processing as indexing a physiologically distinct (brain or non-brain) source process. If only the stability of an IC is acceptable, the IC may be a) artifactual (for example, line noise) and not of use for further processing of brain sources, or b) in some cases might represent (typically, small) activity from some mixture of source processes not unmixed by the ICA decomposition, or c) may be part of a subset of ICs that define a dependent subspace that is temporally independent of other single ICs and multidimensional IC subspaces (some posterior alpha activities)[26]. This may also be the case for source processes that appear to travel a long distance across cortex [19] such as slow waves, K-complexes, spindles [27–29], for emotion-related late potentials [30, 31], etc. If the joint quality index is not acceptable, the IC is likely not suitable for retention in further individual and group data processing. In the following sections we briefly review ICA decomposition and then outline the RELICA algorithm in detail. We illustrate its application using several examples of EEG data recorded in a working-memory experiment [11].

II. Materials and methods

The RELICA procedure proposed here was applied to EEG data acquired from fourteen volunteer subjects who performed a visual working-memory experiment approved by an Institutional Review Board of the University of California San Diego. Written consent was obtained from every subject; refer to [11] for further details. These data are publicly available (http://sccn.ucsd.edu/wiki/BSSComparison) and were used by Delorme et al. in their study [19]. Here, we included a 14^th data set that was excluded from [19] because of low data quality. In each trial of the task periods these data record, a central fixation symbol was first presented for 5 s. Then a series of 3–7 letters were presented in sequence, some of which (colored black) were to be memorized while others (colored green) were to be ignored. Each letter was presented for 1.2 s with 200-ms gaps. Following an ensuing 2–4 s memory maintenance period, a probe letter was presented. The participant was asked to press one of two finger buttons with their dominant hand to indicate whether the letter was part of the memorized sequence or not. The participant then received auditory feedback on the correctness of their response (a confirmatory beep or cautionary buzz); this also signaled the end of the trial. On average a series of 100–150 task trials was performed by each of the 14 subjects (7 male, 7 female, ages 20–40 years). Preprocessing of the data, performed using MATLAB scripts using the EEGLAB (12.0.2.2b) environment [9], comprised high-pass FIR filtering (above 0.5 Hz), epoch selection (from 700 ms before to 700 ms after each letter presentation), and whole-data mean channel (“baseline”) value removal, since Groppe et al. [17] showed that removing the whole-data channel means rather than each individual epoch baseline period mean, before ICA decomposition, dramatically improves ICA decomposition reliability and avoids introduction of high-amplitude, highfrequency abnormalities.

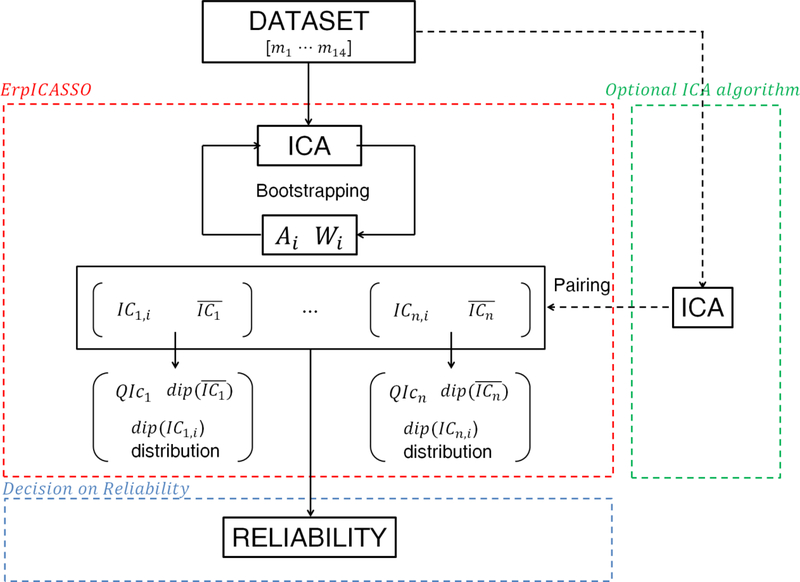
Figure 1 shows a scheme of the entire RELICA procedure following the preprocessing phase. Its concept is 1) to repeatedly decompose the data using Infomax (or another ICA algorithm with acceptable performance) using the ErpICASSO bootstrap approach (red box in Figure 1), 2) to cluster the ICs from every bootstrap decomposition according to their similarity (as a measure of IC reliability), then 3) to calculate for each identified bootstrap IC cluster a cluster quality index QIc, and a measure of physiological plausibility of the cluster IC scalp maps (as the distribution of residual scalp map variance not accounted for by a single equivalent dipole model for ICs within the cluster; Fig. 1, red box). Here, for efficiency, we used the default parameter settings in the GPU-enabled BEAMICA tool [24] to perform the Infomax ICA decompositions. From these stability and dipolarity measures returned by RELICA, a decision may be made about the replicability and possible physiological interpretability of each IC. An optional further step, pairing ICs across decomposition algorithms (Fig. 1, dotted green), will be considered in the Discussion.

Figure 1.

A schematic of the RELICA method to test the reliability of independent component (IC) processes separated from EEG data sets. The data set is first decomposed using an ErpICASSO approach (red box); for each resulting IC cluster a reliability decision is made (blue box). Within ErpICASSO, the ICA decomposition is performed n times, each time yielding a matrix A_i and W_i. ICs are clustered according to their similarities, and one IC $\left(\overline{I{C}_n}\right)$ is extracted from each cluster. Then the IC dipolarity, $dip\left({\overline{IC}}_n\right)$, QIc and dip(IC_n,i) distributions are computed. Based on those values, it is possible to decide on the reliability of a component. For multi-subject experiments, it is possible to add measures of between-subject stability of components as in the ICA data analysis approach now embodied in EEGLAB. (The green box and dotted line represent an optional step that could be added to RELICA, as explained in the Discussion).

The following subsections describe the steps of the RELICA procedure more in detail. These include a) preliminary selection of ICA parameters (optional), b) bootstrap ICA decompositions and IC clustering, c) computation of an IC reliability index for each IC and d) cluster dipolarity for each IC cluster, followed by e) a test to decide on the usability of each IC in further source-resolved EEG analyses.

For purpose of clarity, here we call IC_n the set of ICs belonging to the n^th cluster, while ${\overline{IC}}_n$ is the single IC in the n^th cluster closest to the cluster centroid and therefore, as suggested by Himberg et al. [16], the most representative or exemplar IC for the cluster. QIc is the overall quality index for an IC cluster. The “dipolarity” value for each cluster IC_n is notated as dip(IC_n); similarly the dipolarity of its exemplar ${\overline{IC}}_n$ is notated as $dip\left({\overline{IC}}_n\right)$. It is also possible to define the “dipolarity” of the data set dip_d, after Delorme et al. [19], to be the number of component scalp maps that exhibit a dip(IC_n) larger than a certain threshold.

A. Preliminarily selection of ICA parameters

A wide selection of ICA and related blind source separation algorithms have been provided in the literature. They share the same main goal but focus on different optimization approaches, for instance minimizing instantaneous dependence of the extracted components or reducing redundancy between lagged versions of the data [22]. In general, “slower” methods are reported [7, 32, 33] to be more accurate and less influenced by the choice of parameters than “faster” methods such as SOBI or FastICA. Here Infomax ICA as implemented in BeamICA [24] proved to have better performance using its default parameters with respect to FastICA. Note that BeamICA implements the original Infomax algorithm [21] without its extension by Girolami et al. [34] to take into account the few IC processes with a sub-gaussian probability density function (pdf). BeamICA decompositions were run on a Linux server with 72GB DDR3 RAM hosting an NVIDIA GTX Titan (2688 CUDA cores) GPU board. On average, decompositions were completed in 280 seconds.

To optimize results of FastICA decomposition we tried many combinations of the following parameters: approach (deflatory, symmetric), nonlinearity (tanh – g(u) = tanh (au); pow3 – g(u) = u³; $\text{gauss}-g(u)=u{e}^{-\frac{1}{2}a{u}^2};$ skew – (u) = u²), maximum number of iterations (10², 10³, 10⁴), stopping criterion (ε = 10⁻³, 10⁻⁴, 10⁻⁵, 10⁻⁶, 10⁻⁷), fine-tuning contrast function (tanh, pow3, gauss, skew), step size (1, 0.8), stabilization (on, off). To determine the best combination we used the ICA evaluation measures used also by Delorme et al. [19] (mutual information reduction (MIR) effected by the decomposition and data set dipolarity). The FastICA parameters that seemed to perform best were the symmetric approach, g(u) = tanh (au), with a maximum number of iterations 10⁴, ε = 10⁻⁵, fine tuning and stabilization parameters turned off, and step size = 1. In its symmetric approach, all the FastICA ICs are estimated in parallel (rather than estimating them one by one as in its deflationary approach). It is worth noting that only using this approach is FastICA fast enough to allow performing multiple decompositions on a reasonable time scale with entry-level equipment (e.g., 180 sec per decomposition of 71 channels × 310,000 time points on an entry-level, dual-core, 1.8-GHz AMD laptop). Despite its speed, FastICA also proved less reliable than Infomax; details are provided in the results section III.A.

B. Computing IC reliability indexes using the ErpICASSO approach

B1. ICA rationale

Given an initial multivariate data set x(t), ICA computes a n × p full rank “unmixing matrix” W that linearly projects the data set onto a m-dimensional one, s(t), such that s(t) = W x(t). W is a weight matrix that describes the contributions of the n ICs to each of the p variables. Each column of its pseudoinverse, (A, the “mixing” matrix) can be interpolated and visualized as a scalp map describing the relative weights and polarities of the component projections to each of the original n scalp electrodes. For several ICA algorithms including Infomax, the IC scalp maps for even the same data set may differ slightly across runs, in particular when, as here, the starting point for learning the weight matrix W is selected at random.

B2. Bootstrapping within RELICA

The bootstrapping procedure within RELICA comprises the following steps;

Data resampling

W is computed several times; each time the starting point of the algorithm is randomly selected as well as the distribution of epochs or time points. Using either the epoch-wise bootstrap ErpICASSO approach [20, 30] or point-wise ICASSO approach [16]). To form the surrogate data sets, epochs or of single time points are selected at random from the original data set with replacement always replicating the original data set size.

Clustering

The sets of ICs returned from the M bootstrap decompositions (Figure 1) are clustered according to their mutual similarity, σ, defined as the matrix of absolute values of the correlation coefficients between IC time courses, computed by

$${\sigma }_{ij}=W{R}_{ij}{W}^{{\rm T}}$$

Choice of the number of disjoint clusters may be made using a number of different algorithms e.g., here the R-index algorithm [35]. As Himberg et al. suggest, it is reasonable to start studying the clusters from the number of clusters equal to the data dimension n. Here, 71 clusters of equivalent ICs from the bootstrap decompositions were identified using an agglomerative hierarchical clustering method, giving a dendrogram, with the group average-linkage criterion as the agglomeration strategy. ICA decompositions that gave two or more ICs that were grouped by dendrogram clustering into the same cluster were excluded from further analysis, as we observed that the chance that, in this case, the decomposition had failed to converge is high.

CCA Space Visualization

Curvilinear Component Analysis (CCA) is a multidimensional scaling method used to project multivariate points into a (here) two-dimensional space so as to obtain a similarity map [16]. CCA projection enables a direct 2-D visualization of IC groupings in which visual proximity of points can be interpreted as similarity. Ideally, perfectly replicable ICs should collapse to a single point in this space. For each so-identified cluster, the IC exemplar was identified as the IC nearest in CCA measure space to the centroid of all the cluster ICs.

Quality Index

The quality index QIc measures directly the dispersion of an IC cluster within the 2-D CCA measure space, indirectly indexing the variability of the ICA decomposition. Thanks to the CCA scaling, the quality index QIc (defined as the difference between the average within-cluster similarities and average between-cluster similarities [20]) may be used to measure the compactness and isolation of the cluster from the other IC clusters. If C is the set of indices of all the estimated ICs, C_m the set of IC indices that belong to the m^th cluster, C_−m the set of IC indices that do not belong to the m^th cluster, σ_ij the similarity between ICs i, j is

$$QIc=\frac{1}{{\left|C_m\right|}^2}\sum _{i,j\in C_m}{\sigma }_{ij}-\frac{1}{\left|C_m\right|\left|C_{-m}\right|}\sum _{i,j\in C_m}\sum _{i,j\in C_{-m}}{\sigma }_{ij}$$

B3. Mutual Information

Residual mutual information indicates the mutual information remaining among IC time courses, and can be used, along with decomposition dipolarity, to benchmark the efficiency of an ICA algorithm. Unfortunately, for high-dimensional (many-channel) problems residual mutual information cannot be reliably estimated from a feasible amount of data. However, the Mutual Information Reduction (MIR) produced by any linear decomposition algorithm depends only on the difference between the sums of the marginal entropies of the original data set and its transform, as well as the (log) determinant of W. A detailed explanation of how to calculate MIR can be found in [19] and [36]. A function to compute MIR (getmir.m) is also available within the EEGLAB distribution.

B4. Dipolarity

The dipolarity of a single IC_n, dip(IC_n) is defined as dip(IC_n) = 100(1 – resvar(IC_n))% where resvar(IC_n) is the residual variance (fitting error) between its scalp map projection and that of its single equivalent dipole, here computed using a best-fitting spherical four-shell model head incorporated into the DIPFIT plug-in (version 1.02) of the EEGLAB environment [9]). DIPFT uses a four-shell electrical head model (radius: 71, 72, 79, 85 mm; shell conductances: 0.33, 0.0042, 1, 0.33 μS).

C. Distribution of dip and QIc

For each data set¹, we ran Infomax decomposition on each of 150 trial-by-trial bootstrap data sets with random initial starting points [20]. It is important to note that when performing bootstrapping, as reported in [8], the matrix inversion required to compute A from W (and vice versa) considerably degrades the performance of the decomposition. In the original ICASSO approach, the clustering and CCA projection steps are performed on the replicates of W (rows of W_i in Figure 1) to obtain the final unmixing matrix W. Mixing vectors (columns of A) are then computed as the pseudo-inverse of W. To obtain the final mixing matrix A while avoiding this matrix inversion, it is necessary to perform the clustering and CCA projection steps directly on columns of A_i (see Figure 1). Here we used this approach so as to minimize numerical instabilities.

Each IC cluster then groups the slightly different repetitions of the same IC as produced by each bootstrap ICA decomposition. For each of the n bootstrap IC clusters, we computed $dip\left({\overline{IC}}_n\right)$ and all the others dip(IC_n). We did not perform any dimensionality reduction; here n was equal to the number of EEG channels (71). We also estimated the probability density function (pdf) for dipolarity values of the ICs in each cluster using kernel density estimation [38] with a Gaussian kernel and an optimal width for estimating Gaussian distributions, as this is the width that minimizes the (L2) mean integrated squared error [39].

D. Component reliability criteria

To decide on the reliability of any IC (blue box, Figure 1) it is necessary to select two component retention thresholds based on IC cluster dipolarity (indexing physiological plausibility) and quality index (the compactness of the cluster indexing the stability of the component). However, the optimal retention thresholds are dependent on the type of data and clustering algorithm. A popular choice for acceptable dipolarity is 85% (e.g., [40–42]), although highly quasi-dipolar components may exhibit dipolarities above 95% [19].

Regarding QIc it is possible, as suggested by Himberg et al. [16] to order the clusters according to their quality index and to use as threshold the value at a “knee” (abrupt decrease) in the graph. Here we selected dipolarity and quality index retention thresholds of 85% and 95% respectively, although for the purpose of this work using other thresholds (e.g., both 85%) would not strongly alter the results. In general, if the QIc is above the retention threshold the IC is considered stable, otherwise it may be rejected in further analyses, including inter-subject comparisons.

In sum, there are three main classes into which ICs can be sorted according to their reliability:

1. When quality index and dipolarity are above their retention thresholds, then the IC can be considered stable and physiologically plausible can be therefore called reliable.

2. When the quality index is above the retention threshold and the dipolarity below it, then the IC is either artifactual or might represent two or more processes that are mixed because of the limited number of channels or their participation in a dependent subspace.

3. When the quality index is below its retention threshold, then the IC is not stable. In this case it is possible to analyze $dip\left({\overline{IC}}_n\right)$ and the distribution of dip(IC_n). In fact if $dip\left({\overline{IC}}_n\right)\pm std\left(dip\left(I{C}_n\right)\right)$ is above threshold, the IC may simply have captured inseparable “noise” (degrading the QIc). In that case, it may also be useful to compute the variance explained by the IC. Depending on the perceived quality of such an IC, it is possible to include it in further analyses. In all the other cases, however, it may be advisable to discard it or, if data sets from multiple subjects are available, to further check it for replicability across subjects. For instance, if the $dip\left({\overline{IC}}_n\right)$ is above threshold but inconsistent with the distribution of dip(IC_n), then the IC was likely obtained by chance.

When an IC falls into the first condition (I) then it can be deemed as reliable and usable in further processing. If it falls into the second condition (II), by visual inspection or other testing it can be further tagged either as artifactual (having a non-brain origin) or as mixing multiple processes. ICs falling into the third condition (III), particularly those with marginal dipolarity values, can either be discarded or their repeatability across subjects can be further checked. RELICA users may set their own thresholds depending on the reliability of the ICA decomposition method they choose. For instance in the case of FastICA (which is known to give less consistent results than other methods [19]) the threshold for QIc needs be set lower (e.g., 85%) to take into account the intrinsic instability, relative to Infomax, of the FastICA algorithm.

III. Results

A. Comparison of FastICA and Infomax algorithms

Despite its speed, FastICA proved less reliable than Infomax; approximately 20% of decompositions failed to converge and, replicating the earlier report of Delorme et al. [19], those that succeeded delivered less mutual information reduction (MIR) than the Infomax decompositions. Table 1 shows a comparison of several parameters that define the performance of an ICA algorithm on EEG data: MIR, RV5% (the number of ICs with dipolarity greater than 95% - quasi-dipolar components) and the median QIc (the median quality index provided by RELICA). The highest values for each data set are shaded and the median values across the data sets are shown on the right. It can be seen from Table 1 that, overall, Infomax provides greater MIR for all but one (aberrant) data set (one dropped by Delorme et al., [19] from their analysis), it gives a median of 1.5 more dipolar components, and gives a 10% higher median QIc than FastICA.

Table 1.

Comparison of MIR, RV5% (number of ICs with dipolarity greater than 95%), and QIc yielded by FastICA and Infomax respectively on each of the 14 datasets considered in the present work. The highest values for each dataset are shaded and the median values over all the datasets are displayed in the last column.

MIR (kbit/s)	DS 1	DS 2	DS 3	DS 4	DS 5	DS 6	DS 7	DS 8	DS 9	DS 10	DS 11	DS 12	DS 13	DS 14	MEDIAN
FastICA	44.41	34.35	35.71	38.04	36.85	54.13	29.53	41.53	31.64	28.51	38.69	36.47	43.91	53.91	37.45
Infomax	46.16	35.50	41.89	40.48	40.27	56.04	33.28	45.15	35.89	26.97	40.19	44.28	44.90	55.85	41.18
RV5%
FastICA	28	24	15	18	25	15	19	9	9	2	29	25	21	14	18.5
Infomax	33	28	14	18	28	18	20	1	14	0	25	28	25	20	20.0
median QIc%
FastICA	88.5	79.4	59.7	82.8	90.0	68.4	70.1	39.5	76.7	28.1	92.2	92.2	88.7	83.2	81.1
Infomax	92.5	92.5	84.3	89.7	93.1	84.0	87.8	66.0	85.5	26.0	93.3	94.8	90.7	91.3	90.2

B. ErpICASSO results on a representative data set

Having selected a satisfactorily-performing algorithm (e.g., Infomax) the next steps are to decide on IC reliability by performing ErpICASSO, then for each cluster n to compute IC cluster dipolarity $dip\left({\overline{IC}}_n\right)$, the dipolarity distribution of dip(IC_n) and quality index QIc_n, then finally using these quantities to estimate reliability for this IC cluster.

Figure 2 shows the results of Infomax-based ErpICASSO for one data set: each cluster represents an IC equivalence class; its dimension is closely related to its QIc (see Methods for more details). The Figure also shows scalp maps and power spectral densities (PSDs) for eight IC clusters selected to demonstrate the procedure adopted here. Bootstrap IC clusters 2, 3 and 10 respectively account for activity contributed to the scalp data by blinks, neck muscle activity and line noise (60 Hz); IC clusters 9 and 33 account for posterior alpha and central mu rhythm activities. The QIc for these clusters is over 96%, reflecting the fact that each cluster is tight and well-separated from others. IC clusters 46, 47 show maximal frontal and parietal projections respectively.

Figure 2.

Results of ErpICASSO decomposition applied to a representative data set. Red numbers label the extracted ICs. No dimensionality reduction was performed; n equals the number of EEG channels, here 71. Each dot represents an IC produced by a bootstrap ICA decomposition, projected using CCA on a two-dimensional space with arbitrary units. The (IC) dots are clustered; the centroid is highlighted in orange. The smaller and more definite the cluster, the higher the quality index QIc (e.g., 99 % for cluster IC2). A few select examples are singled out and their centroid scalp maps are shown outside the main box along with their Power Spectral Densities (PSDs), QIc, and dipolarity values. A sample representation of the equivalent dipole model for the cluster IC33 exemplar in template brain 3-D space (IC9) is shown on the right. The labels are colored according to the three classes detailed in the Methods section: Class I, black (high QIc, high dipolarity); Class II, blue (high QIc, low dipolarity); Class III, red (low QIc). The bootstrap IC clusters shown account respectively for line noise (10), blink-related activity (2), neck EMG activity (3), posterior alpha activity (9), central mu rhythm activity (33), frontal activity (47) and parietal activity (46).

C. Quality index and dipolarity

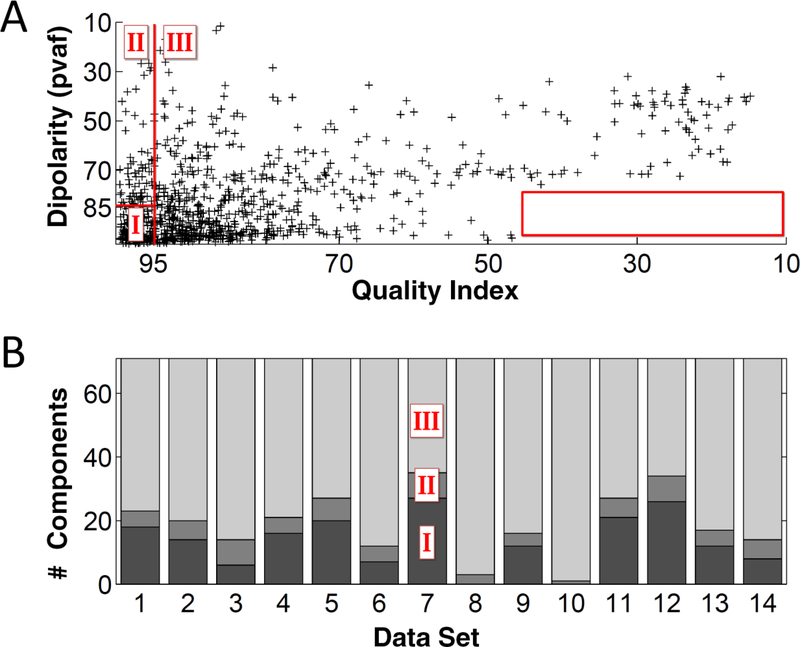
Panel A of Figure 3 shows the IC clusters of all the data sets placed in the bivariate (QIc, dipolarity) space with acceptability thresholds of 95% and 85% respectively (red lines).

Figure 3.

Panel A presents a scatterplot of dipolarity versus quality index values for the IC clusters of all the bootstrap data sets. The red lines (85% and 95% thresholds respectively for dipolarity and quality index) divide the IC dipolarity and quality space into the three Classes identified in the Methods section. The box on the right corner of the panel shows a “forbidden region” (range 0–45% and 75–100% for dipolarity), suggesting that high dipolar components cannot have extremely low QIc. Panel B shows for each data set (1 to 14) the number of ICs in each class.

Although most IC clusters are in Class I (bottom left – zone of acceptance) many appear also in Class II, and Class III. Interestingly, although there is relatively little correlation between the two measures (R² = 0.25) there are no dipolar component clusters with a QIc < 40% (bottom right of panel A). Panel B shows the distribution of IC clusters for each data set across the three classes. As expected, the IC clusters in Class II are not many. A mean of 15 IC clusters per data set are in Class I, deemed very reliable (being both physiologically plausible and stable).

D. Examples

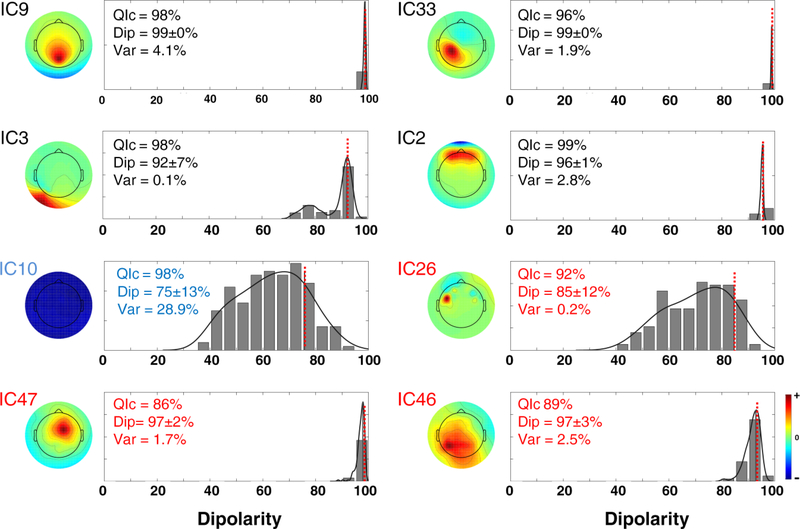
In this section we explore further the problem of the reliability of the ICs identified in Figure 2. Figure 4 shows the scalp maps and the corresponding distribution of dip(IC_n) of ICs belonging to each cluster. The dotted red line highlights $dip\left({\overline{IC}}_n\right)$. When the QIc and dipolarities are high (IC bootstrap clusters 2, 9 and 33), the distribution of dip(IC_n) is very narrow. These IC clusters, according to the criteria explained in the Methods section, are in Class I and should be retained for further analysis, as also confirmed by their high inter-subject repeatability (see [19]). This is true also for cluster IC3 although the standard deviation of its distribution of dipolarity values across bootstrap decompositions is higher (7%). Line noise (IC10) falls into Class II and is very reliably detected by ICA with a high QIc. However for this cluster dipolarity is low and dipolarity distribution wide. IC clusters 46 and 47 have a low quality index, but their dipolarity is above threshold and very narrow, suggesting that they may indeed have a brain origin although slightly corrupted by noise or exhibit activity only intermittently. In this case it may be necessary to perform inter-subject validation to decide on their inclusion in further processing. IC cluster 26, on the other hand, has acceptable dipolarity 85% although its distribution is wide (standard deviation 12%). These aspects and its low explained variance (0.2%) suggest excluding this IC from further analyses.

Figure 4.

Centroid scalp maps and distribution of dip(IC_n) of eight select bootstrap IC clusters extracted from a representative data set. A fit of the distribution of dip(IC_n) was computed using kernel density estimation (black curve), and the value of $dip\left({\overline{IC}}_n\right)$ is marked by a dotted red line. Each panel indicates the quality index QIc (which measures the variability of the ICA decomposition, from 0% – max. variability to 100% – min. variability), the dipolarity and standard deviation, and variance explained of each bootstrap component cluster. The titles are colored according to the IC classes as defined in Figure 2 and in the Methods section.

IV. Discussion

Here we propose a new way to estimate the reliability of (maximally) independent EEG component processes extracted by Independent Component Analysis, an increasingly often-used method for removing contributions of non-brain (artifact) sources from EEG/MEG data [7, 43, 44] as well as for separating individual cortical sources [41, 45, 46]. The RELICA technique proposed here estimates IC reliability in terms both of “stability” (statistical stability to noise and intermittency) and physiological “validity” (the plausibility that the recovered ICs originate in a single brain source). Combining these measures can indicate which ICs to retain in further analyses (e.g., analyses of brain source activities only).

A. ICA Component Stability

One of the main issues concerning blind source separation algorithms is that the input data are projected into a new space which may (also) be difficult to associate with any physiological meaning, particularly considering that the accuracy and validity of the results may depend on the quality of the ICA approach, including both the ICA algorithm and the algorithm parameters used, as well as data amount and quality. In the brain, with a few exceptions, far-field potentials emerging from a restricted spatial source domain should be independent from the far-field signals reaching the scalp electrodes from other domains. Therefore, ICs that exhibit maximally-independent time courses should also be able to be modeled using a single equivalent dipole model with low residual variance [3, 47]. Although in theory (or, using infinite data and processing resolution) ICA algorithms should perform the same, given the same independency maximization goal, as Delorme et al. reported [19] results may depend on the algorithm used.

In particular, Delorme et al. estimated the performance of different ICA algorithms based on their ability to reduce the mutual information present in these same channel data, and to extract a larger number of nearly-dipolar component processes. According to their results, some “slower” ICA algorithms including AMICA [26] and Infomax, have better performance than other methods including the “faster” and popular FastICA algorithm (tested by them using its symmetric mode and default parameters).

We confirmed these findings by applying RELICA to the same data sets: every quality parameter of the ICA decomposition (e.g., Mutual Information Reduction, Average QIc, etc.) was better with Infomax than FastICA. Note that ICA processing speed of “slower” algorithms may be dramatically increased by optimal programming and processing on graphic processing unit GPU hardware [23] which indeed are able to make the speed of Infomax decomposition comparable to that of FastICA.

In any case, when highly parallel or GPU computing power is not available FastICA settings need to be chosen carefully in applications to EEG data; in particular the deflationary approach should be avoided. Further study of FastICA is required to assess with certainty differences in performance between different FastICA approaches.

B. Reliability

Given the blind nature of their extraction, independent components (representing information sources in multichannel EEG data) need to be interpreted in the light of the application at hand [32, 48, 49]. A wrong interpretation, however, may be suggested by artifacts of the ICA extraction algorithm. A seemingly “good” IC may arise by chance if, 1) the algorithm did not converge properly, 2) the data were not preprocessed adequately (e.g., the presence of non-stereotyped artifacts including body and electrode movement artifacts can greatly impair the ICA decomposition [3, 43, 44, 50, 51]), 3) the algorithm was not trained on enough data, or even 4) the algorithm became stuck in a local minimum. Several papers address the problem of IC reliability using a between-subjects approach [11, 33, 46, 52, 53], identifying most frequently-occurring ICs in a population of interest. However, as explained by Groppe et al. [17], between-subject differences (head shape, alertness and cortical folding) may greatly impair results of this method (but see Tsai et al. [54]). “Within-subject” ICA reliability estimation approaches, whenever possible, are to be preferred, as ICA is more accurately performed on single-subject data and by maintaining only reliable ICs it is possible to prevent mistakes in selection for subsequent subject group analysis.

Expert users typically perform a “validity check” to sort out ICs within subjects or to perform between-subject reliability tests. However, a stability check is as important for ICA decomposition because brain sources of interest may often explain relatively little of the variance of the EEG data. In other words, the problem of reliability cannot be dismissed as easily as in the PCA case in which components are ordered according to residual variance and only the first few (largest) are then further explored [6, 34].

Regarding stability, a few methods have been proposed for assessing the stability across the data set of individual ICs. Harmelling et al. [14] used “noise injection,” to identify ICs that were most (and least) altered after adding white Gaussian noise to the data. Meinecke et al. [15], in line with Harmelling et al. [14] and Himberg et al. [16], proposed using bootstrap resampling to estimate IC reliability. Groppe et al. [17], in an effort to overcome the need of performing many bootstrap decompositions using slow ICA algorithms (e.g., single-processor Infomax [21, 22]), assessed IC reliability by applying ICA decomposition separately to split halves of a data set.

Each of these methods has shortcomings. Bootstrap-based methods require multiple decompositions using the same algorithm to ensure adequate resampling of the data [14–16, 55]: while this is acceptable for algorithms such as GPU-optimized Infomax or FastICA, doing so with slower algorithms (which may take many hours to converge) may often be unfeasible. Also, as suggested by Groppe et al. [17], IC reliability metrics are often hard to interpret (in particular, it is not easy to determine which threshold value is best to classify ICs as “reliable” or “unreliable”). His split-half comparison method requires only three ICA decompositions: one on the whole data set and two on split halves of the data. On the downside, as reported by the authors, this approach may underestimate IC reliability: it may be overly conservative as, particularly for small data sets, splitting the data in half could degrade considerably the ICA algorithm performance thus tagging most ICs as unreliable. Also, it considers only the reliability of single ICs, whereas bootstrapping and noise injection enable consideration as well of IC subspaces.

In sum, testing the accuracy of the results of an ICA decomposition is in general not straightforward: it is necessary to know in advance the characteristics of the ICs, for instance using simulated EEG data which, unfortunately, is not easily obtained since it is not clear how a realistic EEG should behave in terms of number and size of sources. Indeed, as all the other methods to determine IC reliability, also with RELICA it is not always clear how to set the acceptability thresholds (e.g., for dipolarity and quality index) to fully classify reliable and unreliable ICs. Although components with high quality and exceeding an 85% dipolarity threshold typically seem to be brain components [19], it is sometimes difficult to discriminate between other components within “gray” zones of these measures. In such cases users should visualize the bootstrap IC cluster reliability distributions and decide whether to trust the value of $dip\left({\overline{IC}}_n\right)$.

While this does not affect the validity of RELICA results, it is worth noting that a general limitation of ICA is the fact that considering different time epochs for the analysis might result in different components extracted (those most expressed during this data segment): ICA may be required to separate components that may be very briefly active, and in so doing missing the component structure in other inactive periods. For this reason, non-stationary algorithms such as AMICA [26] may be useful, at the cost of greater difficulty of analysis and interpretation. For best results, the experimenter should carefully define the time region of interest to apply ICA to, though on the other hand the expected quality of an ICA decomposition depends on data length (e.g., the more data decomposed, the higher the decomposition dipolarity).

On a general note it is also important to note that with Infomax and other instantaneous ICA decomposition methods, a ‘source’ is a single signal projecting simultaneously and with a fixed spatial distribution to the recording channels. In general, distributed cortical activities (e.g., [30] ) should not have this property (exact simultaneity and fixed projection). Distributed phenomena are accounted in ICA models as weak or transient coupling of otherwise and maximally independent sources, each of which (again because of the fixed scalp projection requirement, and the extreme weighting of cortical connectivity towards short connections) typically must represent a signal synchronous across a single cortical patch. Exceptions to this may include an IC capturing simultaneous blinking of both eyes, synchronous alpha activity in two bilaterally symmetric posterior source areas, etc.

C. RELICA results

For each data set RELICA identified on average 15 reliable and physiologically plausible ICs (see Figure 3). The brain ICs selected as examples in Figure 2 (IC clusters 2, 9, 33) have a high quality index and are tightly clustered in the CCA space, and their dipolarity distributions are narrow and well centered on the representative value $dip\left({\overline{IC}}_n\right)$ (Figure 4). While cluster IC3 has high dipolarity, its distribution of dipolarities is higher (7%). Cluster IC10 is also interesting: its quality index is one of the highest shown, but its dipolarity is low and its origin is line noise (as its PSD plot shows). Cluster IC26, without more information, may be discarded from further analysis of brain source processes in these data given its wide distribution, low quality and low variance explained. Clusters IC46 and IC47 give evidence of a situation in which QIc is low although dipolarity is above threshold and dipolarity distribution is narrow (standard deviation 3%). The fact that plausibility and stability are here not equivalent is clearly shown in Figure 3. However, it is interesting to note that no high dipolar component cluster exhibited a low quality index (red box).

Here we used an ErpICASSO approach [20], based on ICASSO [16] modified according to [8] so as to avoid computing the inverse of an ill-conditioned unmixing matrix. As explained in the Methods section, users should remember that, within the ICASSO or ErpICASSO (bootstrap) approaches the columns of A (or rows of W) are extracted by computing the various centroids of the clusters, making the resulting matrices ill-conditioned, so when A⁺ (or W⁺) is computed, results may be unreliable. When dealing with trials, the correct way of implementing bootstrap resampling is to consider as the bootstrap unit the trial itself. Point-to-point bootstrap (as in the ICASSO approach) would here yield better-clustered results, but stability would be overestimated.

D. A possible future step: Pairing ICs across algorithms

A key aspect of RELICA is that it can be used, in theory, in conjunction with virtually any ICA or linear factorization algorithm. Some ICA algorithms involve intensive computations (e.g., AMICA), thus making it prohibitive to use them within the RELICA framework unless specialized hardware (e.g., GPU) and programming are available. It is plausible that reliable components (Class I) are also replicable across algorithms (see Delorme et al. [19]). However, proof of this can be achieved only by applying RELICA using each algorithm. Should this be demonstrated, it would be possible to add to RELICA the step of pairing RELICA ICs to ICs obtained using another ICA algorithm of choice (green dotted box in Figure 1). The procedure would be then to use a preferred ICA algorithm first, then to perform RELICA using it to gain insight into the structure of the IC space stability and dipolarity space, and finally to pair the ICs from the two methods as far as possible. This way, advantages of different methods might be combined: it would be possible to use a preferred ICA algorithm to compute information on IC dipolarity while computing bootstrap IC reliability using RELICA.

V. Conclusions

In this work we introduce RELICA, a novel method to help scientists decide on the reliability of the extracted independent EEG component processes based on their “stability” and physiological “plausibility.” We then demonstrated the application of RELICA to the EEG data of 14 subjects performing a working-memory experiment. We identified on average 15 reliable (i.e. stable and physiologically plausible) independent component processes per subject (of a possible 71) and discussed how to use the information produced by RELICA to decide or further explore uncertain cases. The RELICA framework could be applied to virtually any linear factorization algorithm. Here, thanks to GPU computing and ever-increasing computational power, we were able to test it both using Infomax ICA and using a less robust but also computationally less intensive approach, FastICA.

Highlights.

• RELICA computes ICs reliability as stability and physiological plausibility

• RELICA for the first time combines data bootstrapping and ICs source localization

• RELICA helps scientists make more confident choices on which ICs to discard

• Applied on 14 EEG data sets, RELICA found 15 reliable IC processes per data set

• We selected Infomax but RELICA can be used with other factorization algorithms