Evaluating the Role of Janus Kinase Pathways in Platelet Homeostasis Using a Systems Modeling Approach

Abstract

Maintaining platelet homeostasis is important to avoid spontaneous bleeding and organ damage. Thrombopoietin, the primary regulator of platelet production, is affected by and acts in part via Janus kinase (JAK)‐signal transducer and activator of transcription (STAT)–mediated mechanisms. Interleukin‐6 is also partly responsible for inducing thrombopoietin production via the JAK‐STAT pathway. Although current understanding suggests that JAK2 is a primary mediator of platelet regulation, the emerging data show that a JAK1‐specific inhibitor resulted in the modulation of platelet numbers following dosing. To gain a mechanistic understanding, a model describing platelet regulation based on known physiology and JAK‐STAT pathways was built. The model provides a tool to coalesce biological understanding of platelet physiology and an in silico experimental platform to explore drug effects on platelet homeostasis. In this article, we explain the model construction and demonstrate the use of JAK‐inhibitor programs as informing probes of the physiology, gaining insights on dosing paradigms that avoid platelet‐related safety concerns.

Study Highlights.

• WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

 There are a few models on platelet homeostasis, but a comprehensive model with the effects of cytokines and Janus kinase (JAK) pathway–mediated mechanisms has not been developed yet.

• WHAT QUESTION DID THIS STUDY ADDRESS?

 Why do we see varying platelet effects with compounds that have different in vitro enzymatic and cellular inhibitory effects with respect to various JAK isoforms?

• WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

 A mechanistic model is developed for platelet homeostasis with an emphasis on JAK pathways. This was used to understand the effect of JAK inhibitors on platelet counts. In addition, the relationship between thrombopoietin and platelet counts in different thrombocytopenic or thrombocytotic conditions can be studied to generate the possible hypotheses for disease.

• HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?

 Model‐estimated drug parameters for different JAK inhibitors suggest potential mechanistic insights into their action and influence on the platelet homeostasis process. The model can be used to make decisions about dosing and frequency for the long‐term usage of JAK inhibitors to avoid safety concerns related to platelet counts.

Janus kinases (JAKs) and their associated signal transducers and activators of transcription (STATs) constitute the major intracellular pathway for signaling of cytokines that bind to types I and II cytokine receptors.1 JAK pathways are implicated in the signaling of several proinflammatory cytokines that play an important role in diseases such as psoriasis and rheumatoid arthritis (RA).2 Thus, inhibiting JAK pathways may reduce inflammation and provide a therapeutic benefit in diseases associated with chronic inflammation.3 The first JAK inhibitor approved in the United States for inflammatory diseases, tofacitinib, was approved for RA in 2012, and recently, in 2018, baricitinib was approved for the same indication. The lowering of neutrophil counts in RA, an anti‐inflammatory effect observed with tumor necrosis factor inhibitors, has also been seen with some JAK inhibitors.4 However, the changes in numbers of platelets (PLTs), lymphocytes, and natural killer cells have been observed to be variable across JAK inhibitor compounds.5 In vitro enzymatic or cellular inhibitory concentrations (IC₅₀s) used to describe selectivity for different JAK isoforms for these compounds do not always explain these differences in lab parameters. The differences in methodology using in vitro assays to determine selectivity is a complicating factor. In addition, given the overlap in kinase activity and difficulty in understanding the functions of these kinase‐receptor complexes, it is difficult to translate in vitro IC₅₀ values to cellular changes in patients. Another factor that complicates the comparison between JAK inhibitors is the different dosing regimens used. At higher doses, JAK inhibitors can have off‐target activity and compound selectivity could be diminished. In this article, we focus on PLTs and aim to increase our understanding of the role of JAK‐STAT pathways in PLT homeostasis via a mechanistic model of the PLT life cycle and its relationship with JAK pathways.

Megakaryopoiesis, the process leading to the production of PLTs,6 is one of the three branches of hematopoiesis, the others being erythropoiesis (red blood cell production) and leukopoiesis (white blood cell production). PLTs are important for blood clotting and vascular repairs. Their life span ranges between 7–10 days7 in the vasculature with about 10¹¹ PLTs8 being produced daily. The PLT count in humans ranges from 150–450 cells per nanoliter (nL), with the mean being around 290 cells per nL.

PLT homeostasis is primarily regulated by thrombopoietin (TPO), a glycoprotein hormone. TPO is produced by the liver, bone marrow, and the spleen, with the liver being the major source.9 It induces the maturation of megakaryocyte (MK) progenitors by binding to the myeloproliferative leukemia virus oncogene (mpl) receptor present on them10, 11 through a JAK2 pathway.

In addition to the constitutive mechanism of TPO production in the liver, there are other pathways that could influence this process. Recent literature suggests that aging PLTs contribute to TPO production.12 Aging causes PLTs to lose sialic acid on their surface, which promotes their binding to the Ashwell Morell receptor on hepatocytes. This binding leads to the activation of JAK2, which phosphorylates STAT3. Nucleus translocation of phosphorylated STAT3 in hepatocytes results in TPO production. The cytokine interleukin‐6 (IL‐6) is also believed to influence TPO production via activation of JAK1 in hepatocytes.13

Several modeling efforts to understand thrombopoiesis have a base structure with megakaryocytic progenitors, PLTs, and TPO as the main components.14, 15, 16 Some of these were specifically developed for chemotherapy17 and chronic thrombocytopenia.18, 19 Our work contains similar components to reflect physiology as closely as possible and additionally incorporates the effects of JAK pathway–mediated mechanisms on megakaryocytic progenitors, TPO, and on PLTs themselves.

We use the model together with data from clinical trials with JAK inhibitors—PF‐04965842 (referred to as PF842 in the rest of the text), tofacitinib, and baricitinib—to explore the possible mechanisms for the PLT effects seen with these inhibitors. The process of PLT production and the influence of JAK1‐mediated and JAK2‐mediated mechanisms were modeled as described in the Methods section. The systems model structure was validated under the following three different conditions: (i) TPO observed with mpl/JAK2 deletion only in PLTs and MKs, (ii) relationship between PLT counts and TPO levels under normal and pathological conditions, and (iii) oscillatory PLT counts observed in healthy individuals. The model output was fit to the time course of PLT counts observed with the aforementioned JAK inhibitors, and predictions were made for long‐term dosing.

Methods

Tools used

The model was developed using MATLAB R2016a (MathWorks, Natick, MA) Simbiology version 5.4 and Global Optimization Toolbox Version 3.4. Parameter optimization was performed using simulated annealing with bounds and a nonweighted least squares objective function.

Development of a JAK‐STAT pathway–dependent systems model for PLT homeostasis

The model includes PLT precursors megakaryoblasts (MB) arising from stem cells, MKs, PLTs, IL‐6, TPO, and JAKs (JAK1, JAK2; Figure 1). The following subsections describe each model species and JAK pathway involvement.

Figure 1.

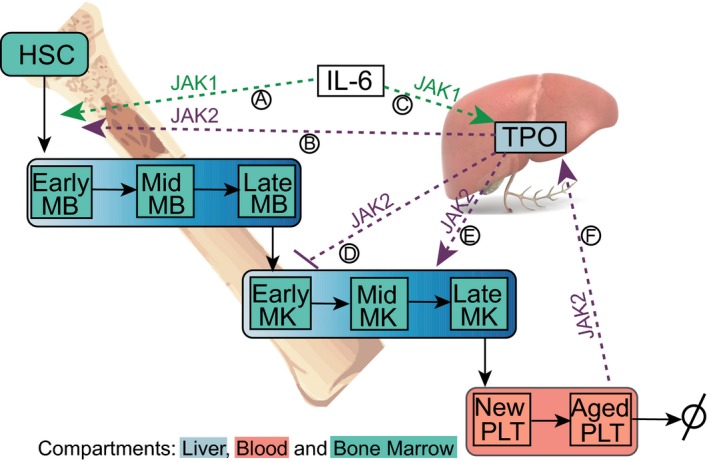
Schematic of base platelet model with three compartments: liver, blood, and bone marrow. Megakaryoblasts (MB) derived from hematopoietic stem cells (HSC) mature in stages to megakaryocytes (MK). MKs develop into platelets (PLTs). Interleukin (IL‐6) is also involved in PLT production (Ⓐ) and thrombopoietin (TPO) production (Ⓒ) via a JAK1 pathway. TPO in involved in platelet production (Ⓑ and Ⓔ) and in limiting MK expansion (Ⓓ) through JAK2 pathways. Aging platelets in blood contribute to production of TPO in the liver through a JAK2 pathway (Ⓕ). JAK, Janus kinase.

Megakaryoblasts

In the model, MBs are assumed to be produced from a constant pool of hematopoietic stem cells at a basal rate. This rate is augmented under the influence of IL‐6 and TPO concentrations. The process of the differentiation of MBs is divided into early, mid, and late stages, and each represented by a compartment, with the late‐stage MBs then differentiating into MKs.

Megakaryocytes

MKs produced from late‐stage MBs undergo polyploidization or endomitosis in about 5 days10 and form PLTs. This process is also divided into early, mid, and late stages, again with each represented by a compartment in the model. The differentiation of MKs into PLTs is stimulated by TPO levels, whereas MK expansion is kept in check.20 These mechanisms are explicitly incorporated into the model.

Platelets

New PLTs formed from MKs are released into the vascular circulation. They age in blood and are either taken up by the immune system, undergo apoptosis, or are internalized by the hepatic Ashwell Morell receptor.

Thrombopoietin

TPO, produced primarily in the liver, is released into the blood and distributed into the bone marrow. In the liver, aged PLTs induce the production of more TPO through the JAK2‐STAT3 pathway. IL‐6 also induces the production of TPO through the JAK1‐STAT3 pathway. TPO in the blood is taken up by PLTs and internalized via the mpl receptor. In the bone marrow, TPO modulates MK and MB cell functions as described in the prior sections, influencing PLT production.

Interleukin‐6

A constant rate of IL‐6 production and a first‐order degradation rate were assumed based on the steady‐state levels reported in the literature in patients with psoriasis.21 The mechanisms affecting IL‐6 dynamics were not considered in the current model.

In summary, the connections in the model as described in Figure 1 are MB cells, produced basally and under the influence of TPO (Ⓑ) and IL‐6 (Ⓐ), differentiate into MK cells. TPO acts on MKs not only to stimulate differentiation into PLTs (Ⓓ) but also to control their expansion (Ⓔ). Aging PLTs (Ⓕ) and IL‐6 (Ⓒ) increase TPO production in the liver, which eventually leads to the formation of new PLTs. PLTs bind and internalize TPO, thereby maintaining blood TPO levels. MB and MK cells also consume TPO, albeit to a lesser extent when compared with PLTs.

Equations and assumptions for the model structure are listed in the Supplementary Information along with a list of parameters. Feedback and feedforward loops in the model are embedded as hyperbolic functions within the differential equations representing inhibition or stimulation.

As an example of how JAK pathway–mediated cytokine effects are incorporated into the model, the rate of MB production and its dependence on cytokines TPO and IL‐6 is shown in Eq. (1).

$$\begin{array}{cc}& \frac{\text{dMB}}{\mathrm{d}\mathrm{t}}=\hfill \\ & {\text{basal}}_{\mathrm{MB}}+g_{J1}\left(\frac{\text{IL}6}{K_{B_{J1}}+\text{IL}6}\right)+g_{J2}\left(\frac{T_{\mathrm{BM}}^{\mathrm{\alpha }}}{K_{B_{J2}}^{\mathrm{\alpha }}+T_{\mathrm{BM}}^{\mathrm{\alpha }}}\right)-k_{\mathrm{MB}}\text{MB}\hfill \end{array}$$ (1)

In this equation, basal_MB represents the MB basal production rate. The next two terms represent the effects of cytokines IL‐6 and TPO (T _BM) on MB production in the bone marrow (BM), respectively—reflecting processes Ⓐ and Ⓑ, respectively, in Figure 1—and the last term represents cell differentiation into MKs. g _J1 is the maximum rate of MB cell production under the influence of cytokine IL‐6; $K_{B_{J1}}$ is the half‐maximal effective concentration of IL‐6; $K_{B_{J2}}$ is the maximal rate of MB production under the influence of TPO; $K_{B_{J2}}$ is the half‐maximal effective concentration of TPO, and α represents the Hill coefficient for this process; k _MB is the rate of differentiation of MBs into MK cells.

Modeling the mechanism of action of selective JAK inhibitors

Six processes in the model involve the JAK‐STAT pathway and are potentially affected by pharmacological inhibition. These include TPO production via two mechanisms—the IL‐6‐JAK1 pathway (Ⓒ) and the Ashwell Morell receptor–PLT–JAK2 pathway (Ⓕ); the effect of TPO on MB production (Ⓑ), MK proliferation (Ⓓ), and MK differentiation (Ⓔ); and the effect of IL‐6 on MB production (Ⓐ). Each of these is modeled as a stimulatory or inhibitory hyperbolic reaction. For example, in the presence of a JAK inhibitor, the effect elicited by a certain TPO concentration (TPO_drug) on MB production is assumed to be attenuated according to a hyperbolic relationship with the JAK inhibitor concentration ([C]_drug) as described in Eq. (2). The effects of IL‐6 (for MB and TPO production reactions) and aged PLT (for TPO production reaction) concentrations in the presence of a JAK inhibitor are calculated similarly.

$${\text{TPO}}_{\mathrm{drug}}=\text{TPO}\left[1-\frac{{\left[C\right]}_{\mathrm{drug}}}{{\text{IC}}_{50,\mathrm{drug}}+{[C]}_{\mathrm{drug}}}\right]$$ (2)

The drug parameter, IC_50,drug, is an effective/apparent IC₅₀ for each process, making the total drug parameters in the model at six.

Integrating pharmacokinetic models for JAK inhibitors

Mean JAK inhibitor concentrations over time were used to drive the drug effects within the model. This was achieved by integrating the systems model with published or internally available population pharmacokinetics models and using estimated typical values of parameters (Table S2 ). For PF842, a one‐compartment model with simultaneous zero and first‐order absorption and first‐order clearance was used. For tofacitinib, parameters from a one‐compartment model with zero‐order absorption (RA patients) were used (US Department of Health and Human Services, US Food and Drug Administration. Clinical Pharmacology and Biopharmaceutics Review(s). Application Number: 203214Orig1s000. 37). For baricitinib, the mean PK data from the literature22 were digitized, and the parameters were estimated from a model fit to that data. A two‐compartment model with first‐order absorption best fit the published baricitinib data. In all cases, the equilibration of compartments was assumed to happen more rapidly than other observed phenomena, and therefore the concentration of drug in the central compartment was used as a driver for drug effects.

Steady‐state optimization

The model was fit to steady‐state mean PLT (PLT₀) and TPO (TPO₀) values from the literature by minimizing a sum of squares objective function as shown in Eq. (3).

$$\text{Error}={({\text{PLT}}_{\mathrm{Model}}-{\text{PLT}}_0)}^2+{({\text{TPO}}_{\mathrm{Model}}-{\text{TPO}}_0)}^2$$ (3)

The parameters were allowed to change within a 10‐fold range from their nominal literature values during the optimization procedure. Varying the initial parameter set did not have a significant effect.

The best set was fixed as the steady‐state parameter set (Table S1 ).

Oscillatory regime parameter exploration

The parameters were explored for the plausibility of observing an oscillating steady state instead of a stable PLT count using this model. The parameters explored included basal MB production rate, maximum MB production rate through JAK pathways, PLT aging and immune clearance rates, TPO decay rates, MB and MK transit rates, maximum TPO consumption rate, TPO levels for half‐maximal consumption by PLTs, and Hill coefficients for MB production through JAK pathways. Period and amplitude parameters of the oscillatory model output were obtained by fitting to a simple Fourier model. Similarly, period and amplitude parameters were calculated for the oscillatory PLT data in the literature. These parameters were then used to minimize an objective function to fit model output with the literature data using Eq. (4).

$$\begin{array}{cc}\hfill \text{Error}=& {({\text{Amp}}_{\mathrm{Model}}-{\text{Amp}}_{\mathrm{data}})}^2+\hfill \\ & {({\text{Period}}_{\mathrm{Model}}-{\text{Period}}_{\mathrm{data}})}^2+{({\text{PLT}}_{b_{\mathrm{Model}}}-{\text{PLT}}_{b_{\mathrm{data}}})}^2\hfill \end{array}$$ (4)

Here, Amp represents oscillation amplitude, and PLT_b represents baseline PLT count.

Model fitting to clinical PLT data

To fit the model to clinical PLT data, cell transit rates and drug‐related parameters were allowed to vary while keeping the other systems parameters fixed. IL‐6 and TPO levels were adjusted to reflect disease states. For example, TPO steady‐state levels in psoriasis patients were twofold higher than in healthy volunteers, although they do not have lower baseline PLT counts.23 Drug parameters and transit rates were estimated by minimizing the sum of squared residuals (as shown in Eq. (5)) for the percentage change from baseline data from three compounds and seven dose groups.

$$\begin{array}{cc}\hfill \text{Error}=& \sum _{\mathrm{dose}}\sum _t{\left(\frac{{\text{PLT}}_{b_{\mathrm{Model}}}-{\text{PLT}}_{b_{\mathrm{data}}}}{{\text{PLT}}_{b_{\mathrm{data}}}}\right)}^2+\hfill \\ & {(\text{PCFB}\_{\text{PLT}}_{t_{\mathrm{Model}}}-\text{PCFB}\_{\text{PLT}}_{t_{\mathrm{data}}})}^2\hfill \end{array}$$ (5)

Here, PCFB_PLT is the percentage change from baseline of PLTs, and the summation for the objective function is over all timepoints (t) and all drugs and dosing regimens (dose) considered. In vitro enzyme assay IC₅₀ values were used as initial conditions for drug parameters during optimization.

Results

Model captures counterintuitive increase in PLT and MK counts in response to mpl receptor mutation in PLTs and MK cells

The mpl‐deficient mice showed markedly decreased PLT and MK levels.24, 25 In humans, too, deficiency in mpl function causes congenital amegakaryocytic thrombocytopenia. In contrast, mice deficient in JAK2 or mpl receptor on PLTs and MKs only (but not in MBs) showed an unexpected thrombocytosis.26, 27 The prevalent theory is that, in the absence of mpl on PLTs and MK cells, more TPO is now available to bind to progenitor cells and hence cause myeloproliferation.

To mimic mpl‐negative mice, all of the TPO‐mediated reactions are silenced in the model by making their rate constants zero. This leads to ~50% decrease in PLT and MK levels (Figure 2 a). TPO levels increase by ninefold. In contrast, on silencing TPO‐mediated reactions in PLTs and MK cells only, there is an approximate fourfold increase in PLTs and MK cells. TPO level does not seem to change much when compared with wild type (Figure 2 b). Although the fold changes from simulations do not match the experimental data in mice quantitatively, they show directionally correct changes, establishing confidence in the structure of the model.

Figure 2.

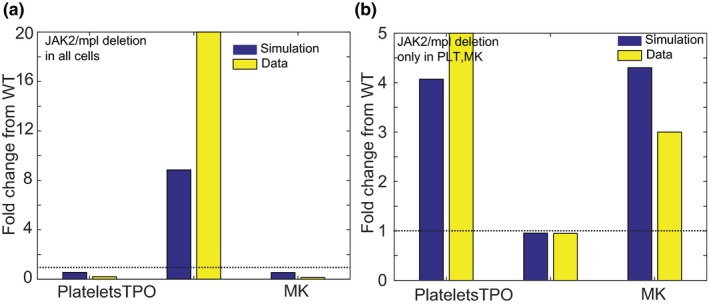
Model shows changes in thrombopoietin (TPO), platelet (PLT) counts, and megakaryocyte (MK) counts qualitatively consistent with literature when the myeloproliferative leukemia virus oncogene (mpl) receptor is modulated in the MK lineage. (a) On deleting the mpl receptor in the entire MK lineage, model (blue) results in a decrease in PLTs and MKs with an increase in TPO levels in blood as seen in the literature (yellow). (b) In contrast, on reducing levels of expression of JAK2 or the mpl receptor in PLTs and MKs only, an increase in PLTs and MKs (blue, model; yellow, data) is observed with no substantial changes in TPO levels. This differential response to TPO with mpl receptor modulation is captured well in the model. As TPO and PLT levels are markedly different in mice and humans, this modeling exercise was to gain confidence in the structure of the model through qualitative comparison. JAK, Janus kinase; WT, wild type.

Relation between PLT and TPO levels at steady state

The model constructed as noted previously provides a platform for exploring the relationship between PLT and TPO levels. Under normal conditions, PLTs in blood bind and remove TPO from circulation, maintaining TPO levels in blood and thereby regulating the production of new PLTs from precursors under the influence of TPO. Based on this physiology, it is expected that increased PLT counts in blood would lead to a decrease in TPO levels and vice versa. This inverse correlation between TPO and PLT levels has been shown to be valid in thrombocytopenic conditions in rabbits and sheep28 and in patients during chemotherapy‐induced thrombocytopenia.29 However, studies of other PLT disorders do not consistently show this inverse relationship, e.g., in chronic and reactive thrombocytosis, PLT counts are elevated, but TPO levels are not very low and are in a detectable range.30 Elevated PLT counts are also seen in essential thrombocythemia, where the TPO levels are low as expected according to the assumed inverse relationship.31 Conversely, low PLT counts with corresponding high TPO levels are seen in aplastic anemia patients still maintaining the inverse correlation.32 In other thrombocytopenic conditions, such as familial thrombocytopenia, myelodysplastic syndromes, and idiopathic thrombocytopenic purpura, this correlation is not maintained as these patients have low or medium TPO levels.31, 32

Modulating system (non‐drug‐specific) parameters in the model, such as PLT production and clearance rates and TPO production and decay rates, allows the model to describe the different relationships between PLT and TPO levels in different disease states. Shown in Figure 3 are model‐generated steady states of seven different conditions ranging from low PLT count and high TPO state to high PLT count and low TPO state. The region in the plot identified by black squares is closest to a normal physiological condition, and fold change in system parameters from the parameters describing this condition for the other six states are shown in detail in the Supplementary File (Figure S1 ).

Figure 3.

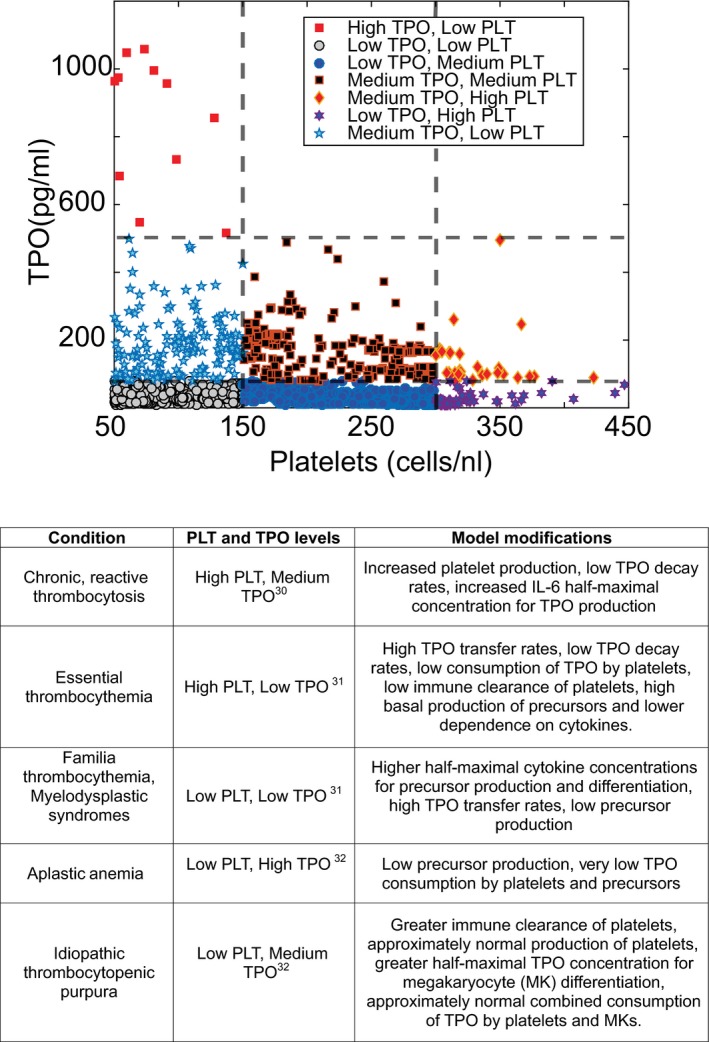
Model parameter exploration shows a range of relationships between platelet (PLT) and thrombopoietin (TPO) levels at steady state. Normal PLT counts fall between 150–450 cells/nL and normal TPO levels between 100–1,000 ng/mL. How the PLT and TPO levels correspond is not clear in the literature. On exploring the model parameter space, the model could show high TPO levels corresponding to low PLT levels, low TPO levels corresponding to high PLT levels, and everything in between. Here we define low, medium, and high for PLT levels as being in between 50–150, 150–300, and 300–450 cells/nL, respectively. Similarly, we define low, medium, and high TPO levels as being in between 1–100, 100–500, and 500–1000 pg/mL, respectively. The corresponding parameter sets for these categories are shown in detail in the supplemental section. The bottom table shows the model‐predicted population characteristics for different scenarios. IL‐6, interleukin‐6.

Model‐predicted population characteristics for PLT count–related pathological conditions are summarized in Figure 3. For example, patients with idiopathic thrombocytopenic purpura who have low PLT count and medium TPO levels are predicted to have greater immune clearance, approximately normal production of PLTs, and normal consumption of TPO by PLTs and MKs. Patients with essential thrombocythemia are predicted to have low TPO decay rates, low consumption of TPO by PLTs, low immune clearance, and high basal production of precursors. Patients with aplastic anemia are predicted to have low precursor production and low TPO consumption by PLTs and precursors. Although the model is not built specifically for a disease, it provides the flexibility to examine these conditions more mechanistically and forms a basis to study disease states.

Model captures oscillations in PLT counts observed in healthy individuals

Literature on PLT numbers in healthy individuals suggests that there are low amplitude fluctuations in PLT counts. These fluctuations have a mean periodicity of 28.3 ± 3.4 days as seen in 7 of 10 individuals studied.15 Morley33 also showed fluctuating PLT counts in 4 of 10 individuals. The model structure described in this article can also reproduce oscillations at steady state by modulating parameters related to progenitor production, TPO, and PLT clearance. The sigmoidicity term associated with TPO effects on MB production (α) was identified as the most sensitive and plausible mechanism by which PLT oscillations may manifest. A high value of α = 6 gave rise to a step‐function effect of TPO stimulation of MBs resulting in downstream oscillations in PLT counts, whereas setting α = 1 resulted in a nonoscillatory steady state. Model fits to the literature data from individuals are shown in Figure 4 a–e. Simulated TPO levels are also shown for each individual, and they show an anticorrelation with PLT numbers.

Figure 4.

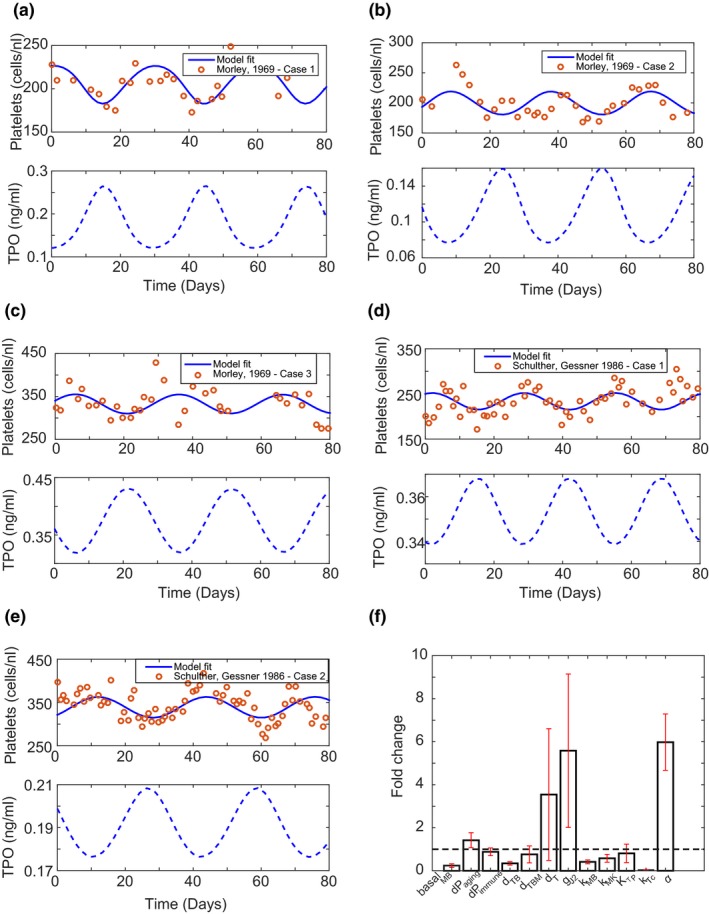
Model structure can produce oscillations in platelet counts as seen in literature in some healthy individuals. (a–e) Model captures oscillations observed in healthy individual platelet counts and predicts corresponding thrombopoietin (TPO) levels. (f) Fold change in parameter values (see parameter definitions in Table S1) between the oscillatory and nonoscillatory state of the model. The sensitivity of megakaryoblast (MB) production to TPO levels (α) seems to be the important parameter for moving the system into an oscillatory state.

The periodicity of oscillations is determined by other parameters such as basal MB production and transit rates for MB and MK maturation in the model. The means of parameters such as basal MB production, TPO decay rate in blood, and MB transit rates are lowered by 0.25‐fold, 0.3‐fold, and 0.5‐fold, respectively, whereas the rate of PLT aging and the maximum rate of MB production via JAK2 pathway are increased by 1.5‐fold and 5.6‐fold, respectively, to match the periodicity of the observed data. Figure 4 f shows the fold change in parameters from a nonoscillatory steady state when fit to the oscillatory PLT data in literature. Mean fold change in the parameters with standard errors are listed in Table S3 . Although these parameters alter the periodicity of oscillations, the key factor driving the oscillatory nature of PLT counts is the sensitivity of MB production to TPO levels. Thus, the current model structure has the capability to show oscillations in PLT levels under normal conditions. As the amount of data supporting the oscillatory steady‐state nature of PLTs is limited, we have used the nonoscillatory steady‐state model for the rest of the analysis.

Comparisons between effects on PLTs by three different JAK inhibitors: What do the IC₅₀s estimated from the model tell us?

PF842, at doses 200 mg twice daily (b.i.d.), 200 mg once daily (q.d.), and 400 mg q.d. showed a decrease in mean PLT counts34 in a phase II trial in psoriasis patients with the nadir occurring around week 3 (refer to Figure  5). Tofacitinib showed no significant changes in PLT counts with dosing at the registered doses of 5 mg b.i.d. and 10 mg b.i.d. At doses substantially above the registered doses—30 mg b.i.d. and 60 mg q.d.—in a phase I psoriasis trial with tofacitinib, an increase in PLT counts of about 10% was observed around week 2. PLT counts return to baseline in the follow‐up period by week 8. Baricitinib, at doses 2 and 4 mg q.d., showed an increase in PLT counts35 around 15% around week 2 in a phase III trial with RA patients. PLT counts return to around 5% above baseline and remain stable at that level beyond week 8.

Figure 5.

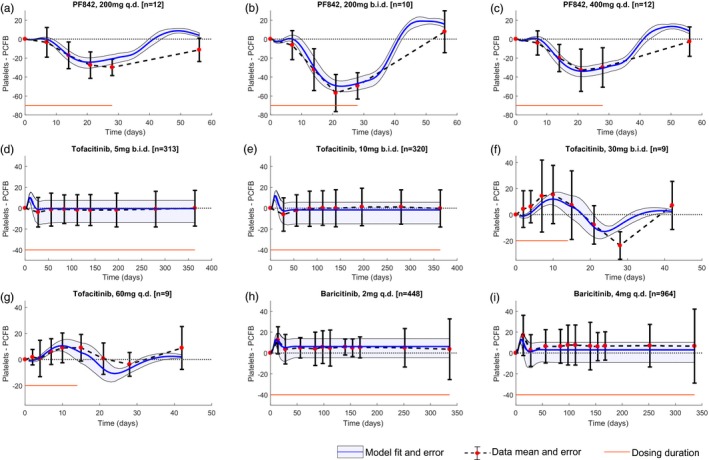
Model fits longitudinal platelet data observed on dosing with different Janus kinase inhibitors reasonably well. (a–c) Model drug parameters are estimated by fitting mean platelet data (shown as red dots with standard deviations in black bars) from clinical trials in psoriasis patients with the PF842 compound at 200 mg once daily (q.d.), 200 mg twice daily (b.i.d.), and 400 mg q.d. doses; (d–g) tofacitinib at 5 mg b.i.d., 10 mg b.i.d., 30 mg b.i.d., and 60 mg q.d. doses; and (h, i) baricitinib in rheumatoid arthritis patients at 2 mg and 4 mg q.d. (d–e) simultaneously. The model fits are shown in blue, and the 90% confidence intervals are shown in gray. The dosing duration is shown in red. PCFB, percentage change from baseline.

Assuming the same model structure and system parameters, drug parameters were fit to the means of clinical PLT data obtained from JAK inhibitor trials in patients (Figure 5). Drug parameter estimates from the model (Table  1) suggest different points of influence in the PLT homeostasis pathway for PF842, tofacitinib, and baricitinib. PF842 seems to affect MB production the most relative to other processes in the model, which causes a drop in PLT count. In comparison, with tofacitinib and baricitinib, there is a stronger drug influence on the antiproliferative effect of TPO on MK proliferation, which causes a slight increase in PLT numbers after dosing and up to around day 10. The levels of TPO, MK, and MB cells in the presence of JAK inhibitors are shown in Figure 6 a. The model suggests an increase in TPO levels in the bone marrow in the presence of PF842 and a slight decrease in the presence of tofacitinib and baricitinib. TPO levels in blood show a similar trend, albeit much milder. Measuring TPO levels in clinical studies might provide more information to assess model results. MB and MK counts decrease on dosing with PF842, whereas with tofacitinib and baricitinib, MBs decrease slightly, but the increase in MK counts through proliferation leads to a slight increase in PLTs during the initial timepoints.

Table 1.

Model‐estimated drug parameters

Process being inhibited by drug	Model‐estimated IC50 (SE) for PF842, ng/mL	Model‐estimated IC50 (SE) for tofacitinib, ng/mL	Model‐estimated IC50 (SE) for baricitinib, ng/mL
MB production through IL‐6 (JAK1)	1.5 (3e‐4)	1,634.6 (1.57)	7 (0.01)
TPO production through IL‐6 (JAK1)	2.9 (0.03)	0.2 (2e‐4)	2.1 (2e‐3)
MB production through TPO (JAK2)	91.4 (0.07)	36.3 (0.04)	8.9 (8e‐3)
TPO production through platelets (JAK2)	14.5 (0.01)	80 (0.08)	11.7 (0.01)
Antiproliferative effect of TPO on MK expansion (JAK2)	7,907.2 (11.6)	20.5 (0.03)	1.9 (2e‐3)
MK differentiation through TPO (JAK2)	992.4 (0.97)	369.4 (0.43)	291 (0.44)

IC₅₀, half‐maximal inhibitory concentration; IL‐6, interleukin‐6; JAK, Janus kinase; MB, megakaryoblast; MK, megakaryocyte; SE, standard error; TPO, thrombopoietin.

Figure 6.

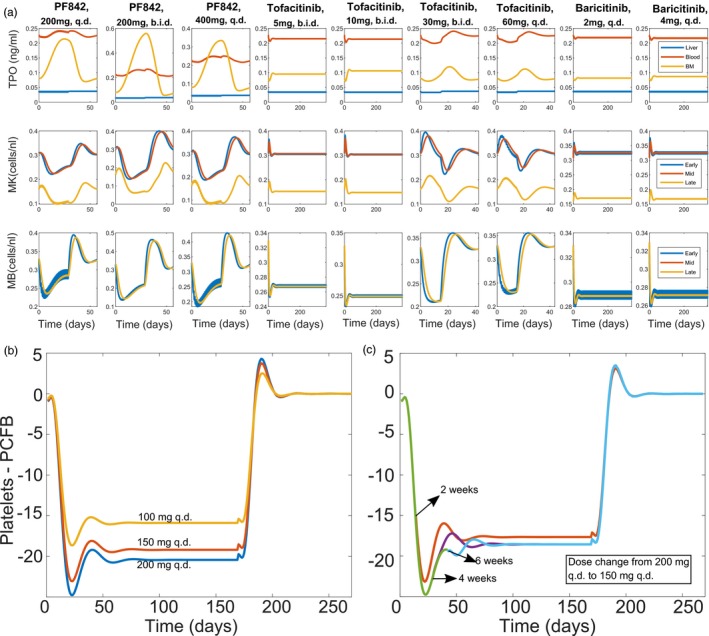
Levels of thrombopoietin (TPO), platelets, megakaryocyte (MK), and megakaryoblast (MB) cells in the presence of different doses of Janus kinase inhibitors and model predictions for long‐term dosing. (a) Species levels predicted by the model when dosed with PF842 compound at 200 mg once daily (q.d.), 200 mg twice daily (b.i.d.), and 400 mg q.d. doses (columns 1–3); tofacitinib at 5 mg b.i.d., 10 mg b.i.d., 30 mg b.i.d., and 60 mg q.d. doses (columns 4–7); and baricitinib at 2 mg q.d. and 4 mg q.d. (columns 8–9). (b–c) Using the model‐estimated drug parameters, simulations were performed to predict long‐term dosing with PF842. (b) Model predicts a maximum decrease in platelets around week 3 for PF842 on dosing for 24 weeks. (c) Model predicts that on lowering the dose from 200 mg q.d. (green) to 150 mg q.d. (orange, after 2 weeks; purple, after 4 weeks; blue, after 6 weeks) beyond the 3‐week mark, there is no impact on platelet counts. BM, bone marrow. PCFB, percentage change from baseline.

Using the drug parameter estimates from the model, simulations were performed to predict the dynamics of change in PLT counts on long‐term dosing (24 weeks) with PF842. The model predicted a nadir at 3 weeks and a return to a new steady state lower than baseline on prolonged dosing as shown in Figure 6 b.

The model was also used to simulate induction‐maintenance dosing to address balance between safety and efficacy for PF842. One such paradigm was an induction dose of 200 mg q.d. with a maintenance dose of 150 mg q.d. This regimen was carefully evaluated using induction times of 2, 4, or 6 weeks before switching to maintenance. The simulations show that initiating the maintenance dose after the earlier predicted nadir timepoint of 3 weeks does not impact the resulting PLT steady state (Figure 6 c).

Discussion

A systems model has been developed that describes PLT homeostasis with an emphasis on JAK‐dependent pathways for JAK‐inhibitor drug development. It provides a basis to explore the relative effects of JAK inhibitors on PLT counts mechanistically. The dual effect of TPO on PLT production, positively influencing MK differentiation while tightly regulating MK numbers by inducing antiproliferative effects, are explicitly present in the model structure. A recently reported positive feedback loop between aging PLTs and production of TPO in the liver is also incorporated into the model. Taken together, the precursors, TPO levels, and PLT counts are mechanistically linked via feedback loops and described by this systems model.

The model recapitulates the increase in PLTs and MKs seen in literature when these cells are depleted of mpl/JAK2. It suggests that the sensitivity of the MB production process to TPO concentrations might be the reason for the oscillatory nature of PLTs observed in some healthy individuals. In addition, the model predicts population characteristics for pathological conditions such as idiopathic thrombocytopenic purpura, aplastic anemia, and essential thrombocythemia, allowing it to be used as a platform to investigate underlying causes for PLT count disorders and JAK‐STAT involvement.

To explore plausible mechanisms for differences in PLT effects with JAK inhibitors, we considered the following three compounds: PF842, tofacitinib, and baricitinib. Fitting the model to clinical trial data from these compounds provides a possible hypothesis for observed contrasting effects. Model‐predicted IC₅₀s suggest that the dominant effect of PF842 is on the precursor production, whereas for tofacitinib and baricitinib, the primary effect is on the inhibition of antiproliferative effect of TPO on MKs relative to the other JAK‐dependent processes considered in the model.

Our simulations offer insights into PLT behavior upon long‐term dosing of JAK inhibitors, e.g., the model predicts that on long‐term dosing with PF842, a maximum reduction in PLTs is seen around 3 weeks, beyond which the PLTs increase and reach a new steady state lower than the baseline. It also predicts that a lower maintenance dose beyond the nadir (~3 weeks) does not affect PLT dynamics. As TPO levels and precursor counts are also predicted by the model, experimental validation of TPO levels in serum and precursor counts through flow cytometry during JAK‐inhibitor studies will help validate and further improve the model.

Finally, although bone marrow is considered to be the site of PLT production in the model, a recent paper suggests that the lung might be a substantial contributor to PLT biogenesis and a reserve for precursors important for PLT release in thrombocytopenic conditions.36 This warrants establishing a composite site for PLT precursor production in the model with parameters describing the combined effects of bone marrow and lungs. This issue is currently beyond the scope of this paper and will be considered in a later iteration of the model. The IC₅₀s predicted by the model are indicative of the effective concentrations needed to inhibit the JAK‐dependent processes and are different in interpretation from the in vitro enzymatic IC₅₀s. Connecting the in vitro and cellular assay IC₅₀s to model‐predicted effective IC₅₀s for JAK‐dependent processes is a challenge and will be a part of future work. The roles of other interleukins such as IL‐11 and oncostatin M receptor in PLT homeostasis will also be explored in a future version of the model. Overall, this model provides a starting platform for exploring the effects of other drug mechanisms and diseases on PLT homeostasis.

Funding

This work was funded by Pfizer.

Conflict of Interest

All of the authors are employees of Pfizer Inc. Clinical trial data from a Pfizer‐sponsored study were included.

Author Contributions

S.K., M.C.P., C.B., and S.P.N. wrote the article. S.K., M.C.P., C.B., and S.P.N. designed the research. S.K. performed the research. S.K. analyzed the data.

Supporting information

Figure S1. Fold change in parameters from normal physiological condition for different thrombocytopenic/thrombocytotic states: (a) Medium TPO, low PLT; (b) low TPO, high PLT; (c) medium TPO, high PLT; (d) low TPO, medium PLT; (e) high TPO, low PLT; (f) low TPO, low PLT. The color coding for parameters on the y axis represent different functions. Parameters in black, green, and gray are related to TPO degradation, transit between compartments, and production, respectively. Magenta represents parameters related to TPO internalization by platelets and precursors. Blue represents parameters related to platelet aging and decay. Red represents parameters related to precursors MB and MKs. Here, the condition with medium TPO and medium PLT in Figure 3 in the main text is considered as the normal physiological condition, and fold change in parameters are calculated with respect to this condition for the other six conditions.

Figure S2. Normalized parameter values for normal physiological condition and different thrombocytopenic/thrombocytotic states. The dots on the plot in Figure 3 in main text, each of which represents one plausible steady‐state condition, are grouped into the seven conditions as listed in the table in Figure 3. For each condition, the parameters are grouped and the normalized mean and standard deviations are shown in Figure S1.

Table S1. List of model parameters and initial conditions.

Table S2. List of PK model parameters.

Table S3. Model‐estimated fold change in steady state parameters to observe oscillations.

Supplementary Materials.