Fuzzy-multidimensional deep learning for efficient prediction of patient response to antiretroviral therapy

Abstract

Drug component interactions are most likely to trigger unexpected pharmacological effects with unknown causal mechanisms, hence, demanding the discovery of patterns to establish suitable and effective regimens. This paper proposes a novel framework that embeds machine learning (ML) and multidimensional scaling (MDS) techniques, for efficient prediction of patient response to antiretroviral therapy (ART). To achieve this, experiment databases were created from two independent sources: a publicly available HIV domain datasets of patients with failed treatment – hosted by the Stanford University, hereinafter referred to as the Stanford HIV database, and locally sourced datasets gathered from 13 prominent healthcare facilities treating HIV patients in Akwa Ibom State of Nigeria, hereinafter referred to as the Akwa-Ibom HIV database: with 5,780 and 3,168 individual treatment change episodes (TCEs) of HIV treatment indicators (baseline CD4 count (BCD4), followup CD4 count (FCD4), baseline viral load (BRNA), followup viral load (FRNA), and drug type combination (DType)), observed from 1,521 and 1,301 unique patient records, respectively. A hybridised (two-stage) classification system consuming the Interval Type-2 Fuzzy Logic (IT2FL) and Deep Neural Network (DNN) was employed to model and optimise patients’ response to ART with appreciable error pruning achieved through MDS. Visualisation of the experiment databases showed remarkable immunological changes in the Akwa-Ibom HIV database, as the FCD4 of TCEs clustered far above the BCD4, compared to the Stanford HIV database, where over 40% of FCD4 clustered below the BCD4. Similar changes were noticed for the RNA, as more FRNA copies clustered below the BRNA for the Akwa-Ibom datasets, compared to the Stamford datasets. DNN classification results for both databases showed best performance metrics for the Levenberg-Marquardt algorithm when compared with the resilient backpropagation algorithm, with improved drug pattern predictions for experiment with MDS. This paper is most likely to evolve an avenue that triggers interesting combination(s) for optimum patient response, while ensuring minimal side effects, as further findings revealed the superiority of the proposed approach over existing approaches.

1. Introduction

Acquired Immunodeficiency Syndrome (AIDS) is a chronic, potentially life-threatening condition caused by the Human Immunodeficiency Virus (HIV)–a persistent pathogen acknowledged as the lentivirus [1, 2]. HIV has no known cure, but the infected patient is treated with highly active antiretroviral therapy (HAART) [3], mainly for the purpose of suppressing the viral load (the amount of HIV in the blood stream) and prolonging the life expectancy of the patient. The viral load and CD4 (cluster for differentiation of Antigen IV) count are regarded as important determinants for measuring one's HIV status (whether positive or negative) and health [4]. By identifying interactive and distinctive drug characteristics, a predictive system can open promising avenues to improved strategies and treatment of HIV/AIDS, since the drug components produce clinical effect as a result of its interface with the virus, ultimately influencing the patients' response. But, the emergence of drug resistance mutation questions the effectiveness of drug therapies such that the selection of most effective drug combinations though a classification sequence of resistant/non-resistant exemplars has become crucial. Selecting the right regimen is a product of several factors that constitutes knowledge of past treatment history including CD4 and viral load (RNA) baselines, combined with expert interpretation and advice [5]. As a result of this activity, interest in modelling drug resistance has increased due to additional pre-exposure prophylaxis to the HIV prevention toolkit [6, 7]. Nevertheless, state-of-the-art models have failed to capture heterogeneities in the risk of drug resistance among individuals, mainly due to model detail diversity, as transmission models of antiretroviral therapy and pre-exposure prophylaxis use simple assumptions to represent short-term risk and long-term effects of drug resistance [8, 9]. Many machine learning (ML) methods have evolved to provide solutions to the model diversity problem. These methods attempt to locate best configurations that yield high performance through the minimisation of an error function defined by the system behaviour produced by trained exemplars.

This paper therefore proposes a hybrid methodology that combines intelligent mechanisms into an effectual and usable application system. The proposed methodology embeds deep learning into a rule-based technique powered by the fuzzy inference system. The novelty in this paper rests on the fusion of two classifiers: the type-2 fuzzy sets (T2FS) and a deep neural network (DNN), where linguistic inputs are translated into representations that generate feature labels for the DNN system. The DNN then drives the fuzzy inference block through adjustable fuzzy rules incorporated by (domain) expert knowledge acquired from the input data–required to explain the behaviour of the fuzzy system. To deal with the highly error-prone nature of real-world datasets, we also incorporate a multidimensional scaling technique for the purpose of enhancing the datasets for precise modelling and prediction of HIV patient response to (varying) treatment change episodes (TCEs).

In the absence of extensive access to personalised laboratory monitoring–an integral part of HIV/AIDS patient management (typical of resource-rich settings), a roll-out of HAART in resource-limited settings (such as those in Sub-Saharan Africa) has adopted a public health approach based on standard HAART protocols and clinical/immunological definitions of therapy failure. Hence, the benefits of this research shall certainly impact the African region, as it represents the commencement of a clinical database gathering to engender further HIV/AIDS research in Sub-Saharan Africa. The research will provide useful spinoffs for deeper interdisciplinary cooperation on personalised therapies and is most likely to produce a robust prediction system that will serve the growing populace in search of quality treatment. Furthermore, it shall aid Physicians on more proactive detection of acute interaction as well as early referrals of patients with failed treatments, for immediate change in treatment episode. The specific objectives of this paper therefore include, to:

• •implement a hybrid framework that combines the strengths of machine learning (ML) and MDS techniques in a supervised learning – for precise patient response prediction and efficient error-pruned datasets;
• •train an optimal sequence of test prototypes – through unified encoding of treatment change episodes (TCEs) of existing patient-specific ART gathered from paediatric records;
• •evaluate the proposed learning model using suitable performance metrics.

The remainder of this paper is structured as follows: Section 2 provides a review of related literature on HIV/AIDS prediction and classification and the extent of research recorded on drug reaction/resistance. Section 3 presents the materials and method employed in the research. Section 4 presents the results obtained from the study. Section 5 discusses the results with reference to existing literature. Section 6 concludes on the paper and points to future research direction.

2. Background

The cost-effectiveness of HIV-1 viral load monitoring at the individual level in such settings has been debated, and questions remain over the long-term and population-level impact of managing HAART without it. Computational models that accurately predict virological response to HAART using baseline data including CD4 count, viral load and genotypic resistance profile, as developed by the Resistance Database Initiative, have significant potential for treatment selection and optimization. However, recently developed models have shown good predictive performance without the need for genotypic data, with viral load emerging as the most important variable. This finding provides further, indirect support for the use of viral load monitoring and long-term optimization of HAART in resource-limited settings.

Several data mining algorithms have been applied to investigate issues relating to HIV/AIDS. In this section, we examine related works carried out by different researchers, including studies on drug resistance cases that have emerged within the last ten years [10, 11, 12, 13]. Most recent studies reviewed in the PubMed database [14] concentrate on problems such as HIV/AIDS prediction of protease cleavage sites and inhibitors, correction usage for viral entry, patient response, resistance and adverse effect of ART. The Agence Nationale de Recherchen sur le SIDA (ANRS) has become a gold standard for interpreting HIV drug resistance using genomes mutations, and in [15], an attempt to improve the ANRS gold standard prediction was made for HIV drug resistance cases using genome sequence and HIV drug resistance measures from the Stanford HIV database (http://hivdb.stanford.edu/). Developing a computational prediction system for drug resistance phenotype can enhance the timely selection of best regimens. In Shen, Yu, Harrison and Weber [16], they applied two machine learning algorithms, the random forest and k-NN, to predict HIV drug resistance from genotype data. In [17], a framework for supporting and managing HIV/AIDS using k-means and random forest algorithms was proposed to mine hidden information from a huge database and to help in decision making for the treatment of HIV related diseases. In [18], the classification and regression tree, was used to predict the survival of AIDS patients receiving antiretroviral therapy in Malaysia, and to discover potential treatment methods and treatment progress of monitoring patients. But the sparseness of data constrained the study and reference to drug resistance cases was missing. Isaakidis, Raguenaud, Te, Tray, Akao, Kumar, Ngin, Nerrienet and Zachariah [19] investigated the high survival and treatment success sustained after two and three years of first-line ART for children in Combodia. The Kaplan-Meier analysis [20] was used to estimate survival, and Cox regression [21] was used to identify the risk associated with treatment failures, where survival, immunological restoration and viral suppression could be sustained after two to three years of ART among children in resource constrained settings. The study was however limited to the use of only CD4 count as predictor variable. In [22], the application of ML to predict future CD4 count changes was investigated. They formulated a mathematical model that can predict the range of change of an individual HIV-1 positive patient's CD4 count, using support vector machine (SVM) classification model that predicts variability level of the CD4 count. Clinical features used as inputs were genome, current viral load and number of weeks from baseline CD4 count. This approach produced acceptable classification accuracy and showed that a change in CD4 count can be accurately predicted using machine learning. The study, however, did not consider drug resistance, which is vital in treatment success appraisal, and had as limitations, low number of datasets and high misclassifications. In [23], neural network was used for a longitudinal assessment of antiretroviral therapy determination, based on Jordan-Elman networks [24] – to longitudinally follow viral surrogate markers and demographics, biochemical and laboratory data that describe drug-virus host interactions in over 4,000 HIV adult patients. They found that neural networks can be applied in real-time context of prospective, longitudinal clinical trials of newer antiretroviral drugs.

Uncertainties abound in many real-world problems and may arise from inputs, outputs, linguistic diversity, change in operational condition, and noisy data. In the case of HIV/AIDS, the disease may present confusable patterns most likely to becloud early diagnoses and treatment. Although the type-1 fuzzy logic [25, 26, 27] has succeeded in solving a wide range of real-world problems, their performance is rendered inappropriate in many complex use cases with highly confusable variables. The type-2 fuzzy logic systems have evolved to complement type-1 fuzzy logic systems because they are more robust to uncertainties in many applications with the block type reduction guided by the inference mechanism playing central role in the systems. They represent input and output results using fewer rules and embed large number of type-1 fuzzy sets to describe variables with detailed description of extra levels of smooth control surface and response. More, outputs that are not feasible in type-1 are possible due to extra dimension provided to the foot print of uncertainty (FOU) [28]. Although the Karnik-Mendel (KM) iterative algorithms are standard algorithms to performing the type-reduction, the high computational cost of type-reduction process may hinder their use in real world applications [29]. Advancements on research in type-2 fuzzy sets and system, have encouraged enhanced type-reduction techniques [30], and the application of learning methods to the type-2 fuzzy logic systems, resulting in hybridised forms that fuses fuzzy type-2 systems with neural, and evolutionary methods or classification algorithms [31, 32].

3. Materials and methods

3.1. Proposed system architecture

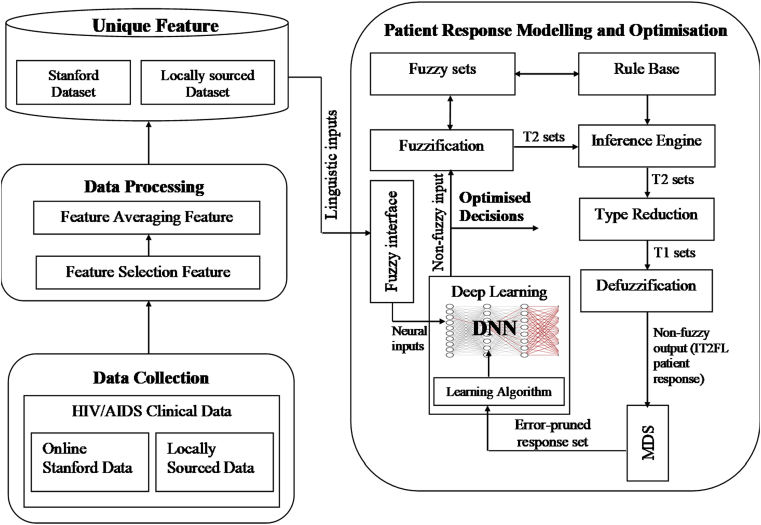
An architecture describing the workflow of our proposed Fuzzy-MDS-DNN system is presented in Fig. 1. The proposed architecture is structured into two major phases namely: (i) data collection and processing, and (ii) patient response modelling and optimisation. The modelling-optimisation phase fusses a two-stage classification system with MDS capability, into a hybridised controller capable of high error-tolerant patient response modelling and optimisation. The controller accepts through a fuzzy interface, linguistic inputs (parameters) from a processed database of unique experimental (Stanford and locally sourced) datasets. Supervised learning is then achieved through the automatic adjustment of the fuzzy model parameters which forms initial inputs to the DNN and initiated by the learning algorithm. An optimised set of non-fuzzy inputs are then fed into the IT2FL section to output precise patient response, which errors are later pruned using an MDS algorithm. The pruned datasets are finally learned to produce optimised predictions of the patient response. Details of each section of the architecture are discussed in the following subsections.

Fig. 1.

Proposed system framework.

3.1.1. Data collection and processing

The Stanford HIV database – a publicly available domain dataset hosted by the University of Stanford was used as a reference dataset in this experiment. This database is archived using the Extensible Markup Language (XML) format (cf. https://hivdb.stanford.edu) and captures details of patients who have failed treatment due to drug resistance. The Stanford database was created in 1999 and hosts a freely available online genotypic resistance interpretation system called HIVdb–to support health workers in understanding HIV-1 genotypic resistance tests [33]. Several studies have followed to confirm the TCEs database as an effective database in the study and monitoring of resistance to HIV drugs therapy. A total of 24 drugs in varying combinations were identified in 1,521 unique patient records with 5,780 individual TCEs – spread across several weeks of treatment. To ensure consistency and attribute unique instances to each patient, a MATLAB script was written to average each patient data (XML sheet) over the various TCEs and extract unique instances for all the patients. Locally sourced data were also collected from case files of paediatric patients receiving treatment at various health centres in Akwa Ibom State of Nigeria, plus, a Community Anti-Retroviral Therapy Programme–periodically carried out to reach rural dwellers. A total of 13 data points (health facilities) were assessed. The Akwa-Ibom database covered patients who registered for treatment at the various facilities from 2015-2018, and contains both resistant and non-resistant exemplars. The investigated facilities accommodate about 10,000 patients in the southeast region currently receiving treatment. However, due to the limited resources in the Nigerian environment, only five drug combinations in three treatment regimens are possible. These regimens are administered to patients (at the various centres) free of charge–through a Family Health International (FHI) HIV/AIDS intervention programme. The Akwa-Ibom HIV database consists of a total of 1,301 unique patients with 3,168 individual TCEs. Features investigated in the study were: baseline CD4 count (BCD4), followup CD4 count (FCD4), baseline viral load (BRNA), followup viral load (FRNA), and Drug Type combination (DType). Ethical issues came to play in this research as the research involved gathering data from human subjects. Although the research did not involve direct contact with patients, access to patients' medical histories and treatment was granted by the responsible authorities after satisfying the ethical consent procedure – for the purpose of sieving the relevant experimental data. Hence, we discuss the ethical issues under two areas: Informed consent: Informed consent through written permission was obtained from the responsible health authority before embarking on the research. Data Protection: Data protection was ensured, as details that could expose the patients’ personal details (e.g., name, address, occupation, etc.), were not extracted.

3.1.2. Patient response inference modelling

Patient's response to treatment depends on several imprecise and confusable factors that direct the outcome of treatment course (including drug side effect and resistance). When these side effects are noticed, contacting one's health provider or pharmacist is needful. Drug resistance on the other hand can be the cause of treatment failure, because as the HIV multiplies in the body, the virus mutates (changes form) and produces fake copies to confuse treatment course, leading to drug-resistant strains of the HIV. In order to eliminate uncertainties in data due to the influence of these confusing factors, an IT2FL (see Fig. 1) was used to provide a knowledge representation of the patient response. The IT2FL modelling section consists of six major components namely, the fuzzifier, fuzzy sets, rule base, inference engine, type-reducer, and defuzzifier. First, the obtained input parameters are fuzzified and then passed to the inference engine–to evaluate the fuzzy set against the rule base. This process produces another type-2 fuzzy set. The fuzzy set is then reduced to a type-1 fuzzy set by the type reduction section. The reduced set is finally defuzzified to give a crisp (non-fuzzy) output.

3.1.2.1. The fuzzy model

3.1.2.1.1. Model description

An Interval Type-2 Fuzzy Set (IT2FS) characterized by $\tilde{A}$ has a FOU bounded by a lower and upper membership functions, ${\underset{¯}{\mu }}_{\tilde{A}}(x,\mu )$ and ${\overline{\mu }}_{\tilde{A}}(x,\mu )\forall x\in X$, respectively, is expressed as:

$$\tilde{A}=\{\left(\left(x,\mu \right),{\underset{¯}{\mu }}_{\tilde{A}}(x,\mu ),{\overline{\mu }}_{\tilde{A}}(x,\mu )\right)|\forall x\in X,\forall \mu \in J_x\subseteq \left[\mathrm{0,1}\right]\}\text{,}$$ (1)

where ${\underset{¯}{\mu }}_{\tilde{A}}(x,\mu )$ and ${\overline{\mu }}_{\tilde{A}}(x,\mu )$ = 1;$x\in X$ and $\mu \in J_x$ [0, 1], are defined on a continuous universe of discourse (UoD); $x$ denotes the primary variable in domain X, $\mu$ denotes the secondary variable in domain $J_x$at each$x\in X$; $J_x$ is called the primary membership of $x$ as defined in (1), which symbolize the interval set; the secondary grades of $\tilde{A}$ is unity, and hence, reduces the IT2FS to,

$$\tilde{A}={\int }_{x\in X}{\int }_{\mu \in J_x}1/(x,\mu )\text{.}$$ (2)

Now, the FOU of $\tilde{A}$ is the union of all primary membership grades and is given by,

$$FOU\left(\tilde{A}\right)=\underset{x\in X}{\cup }{J}_x\text{,}$$ (3)

The UMF: upper membership function (${\overline{\mu }}_{\tilde{A}}\left(x\right)$), and LMF: lower membership function, ${\underset{¯}{\mu }}_{\tilde{A}}\left(x\right)$, are type-1 membership functions (MFs) marking the FOU boundary of an interval type-2 MF. The UMF represents the subset that has the maximum membership grade of the FOU; and the LMF is a subset that has the minimum membership grade of the FOU$\forall x\in X$[34, 35], thus,

$${\overline{\mu }}_{\tilde{A}}\left(x\right)\equiv \overline{FOU\left(\tilde{A}\right)},\forall x\in X\text{,}$$ (4)

$${\underset{¯}{\mu }}_{\tilde{A}}\left(x\right)\equiv \underset{¯}{FOU\left(\tilde{A}\right)},\forall x\in X\text{,}$$ (5)

$$J_x=[{\overline{\mu }}_{\check{A}}\left(x\right),{\underset{¯}{\mu }}_{\tilde{A}}\left(x\right)]\text{.}$$ (6)

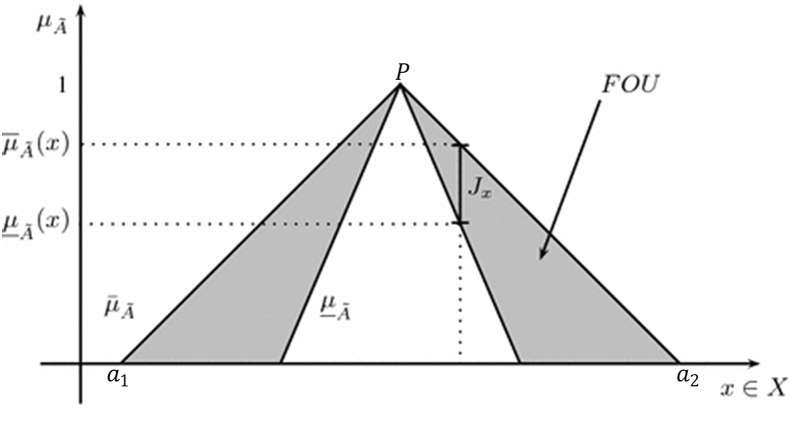
The Triangular Membership Function (TMF) was adopted to evaluate each input and output MFs for the IT2FL system. The description of the TMF using a line or curve is based on three parameters $a_1$, p, and $a_2$, and specifies the mapping of each input or output parameters, to obtain membership values for $n$ membership grades ($M{G}_n;n:1,\dots ,n$), thus:

$$\mu \left(x\right)=\{\begin{array}{l}0;\mathrm{i}\mathrm{f}x<a_{1\left(M{G}_1\right)}\left\{NIR\right\}\\ \frac{x-a_{1\left(M{G}_1\right)}}{a_{2\left(M{G}_1\right)}-a_{1\left(M{G}_1\right)}};\mathrm{i}\mathrm{f}{a}_{1\left(M{G}_1\right)}\le x<a_{2\left(M{G}_1\right)}\\ \frac{a_{2\left(M{G}_2\right)}-x}{a_2\left(M{G}_2\right)-a_{1\left(M{G}_2\right)}};\mathrm{i}\mathrm{f}{a}_{1\left(M{G}_2\right)}\le x<a_{2\left(M{G}_2\right)}\\ \dots \dots \\ \frac{a_{2\left(M{G}_n\right)}-x}{a_{2\left(M{G}_n\right)}-a_{1\left(M{G}_n\right)}};\mathrm{i}\mathrm{f}{a}_{1\left(M{G}_n\right)}\le x<a_{2\left(M{G}_n\right)}\\ 0;\mathrm{i}\mathrm{f}x\ge a_2\left\{NIR\right\}\end{array}\text{.}$$ (7)

where, $a_1$ and $a_2$ are the triangular end points defined by the FOU – region consisting of all the points of primary membership of elements, and NIR signifies values that are not in range. Fig. 2 illustrates a triangular shape IT2FLS with its principal T1FS, showing the end point, and $P$, the triangular peak location.

Fig. 2.

IT2FL FOU.

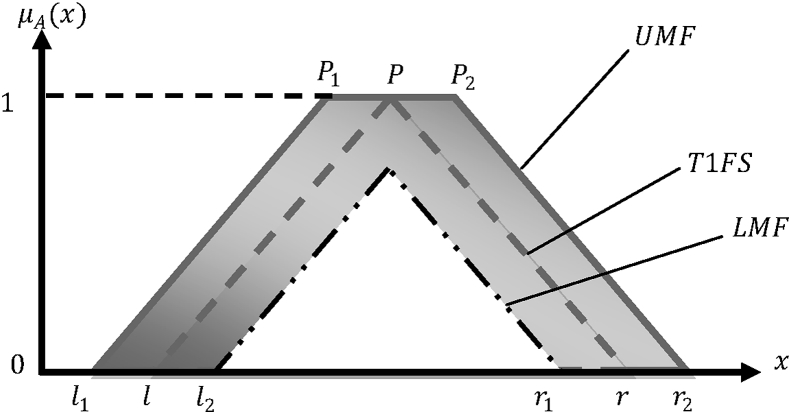
Now, labelling the internal cross section of Fig. 2, the triangular shape of IT2FLS with its principal T1FS bounded by a UMF and a LMF is given in Fig. 3.

Fig. 3.

Internal cross section of IT2FL MF.

where $l$ is the left end point bounded by both UMF ($l_1$) and LMF ($l_2$), and, $r$ is the right end point, also bounded by both UMF ($r_2$) and LMF ($r_1$). The triangular peak location or mean, $P$, of each end point is also bounded by $P_1$ and $P_2$, representing the triangular peak locations of end points $l_1$ and $r_1$, and $l_1$ and $r_2$, respectively.

3.1.2.1.2. Membership function construction

The UoD or universal set denotes the complete range of values assigned to the linguistic variables. We define this measure following (7) for our input and output linguistic variables. The UoD membership ranges were created to align with established ranges from literature and practicing expert physicians in the healthcare facilities studied. Table 1 shows the input and output fuzzy sets derived from these sources.

Table 1.

Input and output fuzzy sets from domain knowledge.

S/N	Membership grade (MG)	BCD4/FCD4 (Input)
		$l_1$	$P_1$	$r_1$	$l_2$	$P_2$	$r_2$
1	Low {L}	0	225	450	50	275	500
2	Medium {M}	300	575	850	350	625	900
3	High {H}	700	1075	1450	750	1125	1500
		BRNA/FRNA (Input)
1	Undetected {U}	0	0.60	1.20	0.30	0.90	1.50
2	Supressed {S}	1.00	2.15	3.30	1.20	2.35	3.50
3	Not Supressed {NS}	2.50	4.00	5.50	3.00	4.50	6.00
		PR (Output)
1	No Interaction {NI}	0	27.50	55	5	32.50	60
2	Very Low Interaction {VLI}	30	47.50	65	35	52.50	70
3	Low Interaction {LI}	62	68.50	75	67	73.50	80
4	High Interaction {HI}	72	78.50	85	77	83.50	90
5	Very High Interaction {VHI}	82	88.50	95	87	93.50	100

Following (7), the UMF and LMF for the CD4, RNA and PR linguistic variables are as realised in (8)–(13), respectively,

$${\underset{¯}{\mu }}_{CD4}\left(x\right)=\{\begin{array}{l}0;\mathrm{i}\mathrm{f}x<0\left\{NIR\right\}\\ \frac{x}{450};\mathrm{i}\mathrm{f}0\le x<450\left\{L\right\}\\ \frac{850-x}{550};\mathrm{i}\mathrm{f}450\le x<850\left\{M\right\}\\ \frac{1450-x}{750};\mathrm{i}\mathrm{f}850<x\le 1450\left\{H\right\}\\ 0;\mathrm{i}\mathrm{f}x\ge 1450\left\{NIR\right\}\end{array},$$ (8)

$${\overline{\mu }}_{CD4}\left(x\right)=\{\begin{array}{l}0;\mathrm{i}\mathrm{f}x<50\left\{NIR\right\}\\ \frac{x-50}{450};\mathrm{i}\mathrm{f}50\le x<500\left\{L\right\}\\ \frac{900-x}{550};\mathrm{i}\mathrm{f}500\le x<900\left\{M\right\}\\ \frac{1500-x}{750};\mathrm{i}\mathrm{f}900\le x<1500\left\{H\right\}\\ 0;\mathrm{i}\mathrm{f}x\ge 1500\left\{NIR\right\}\end{array}\text{.}$$ (9)

$${\underset{¯}{\mu }}_{RNA}\left(x\right)=\{\begin{array}{l}0;\mathrm{i}\mathrm{f}x<0\left\{NIR\right\}\\ \frac{x}{1.2};\mathrm{i}\mathrm{f}0\le x<1.2\left\{U\right\}\\ \frac{3.3-x}{2.3};\mathrm{i}\mathrm{f}1.2\le x<3.3\left\{S\right\}\\ \frac{5.5-x}{3};\mathrm{i}\mathrm{f}3.3\le x<5.5\left\{NS\right\}\\ 0;\mathrm{i}\mathrm{f}x\ge 5.5\left\{NIR\right\}\end{array}\text{,}$$ (10)

$${\overline{\mu }}_{RNA}\left(x\right)=\{\begin{array}{l}0;\mathrm{i}\mathrm{f}x<0.3\left\{NIR\right\}\\ \frac{x-0.3}{1.2};\mathrm{i}\mathrm{f}0.3\le x<1.5\left\{U\right\}\\ \frac{3.5-x}{2.3};\mathrm{i}\mathrm{f}1.5\le x<3.5\left\{S\right\}\\ \frac{6-x}{3};\mathrm{i}\mathrm{f}3.5\le x<6\left\{NS\right\}\\ 0;\mathrm{i}\mathrm{f}x\ge 6\left\{NIR\right\}\end{array}\text{,}$$ (11)

$${\underset{¯}{\mu }}_{PR}\left(x\right)=\{\begin{array}{l}0;\mathrm{i}\mathrm{f}x<0\left\{NIR\right\}\\ \frac{x}{55};\mathrm{i}\mathrm{f}0\le x<55\left\{NI\right\}\\ \frac{65-x}{35};\mathrm{i}\mathrm{f}55\le x<65\left\{VLI\right\}\\ \frac{75-x}{13};\mathrm{i}\mathrm{f}65\le x<75\left\{LI\right\}\\ \frac{85-x}{13};\mathrm{i}\mathrm{f}75\le x<85\left\{HI\right\}\\ \frac{95-x}{13};if85\le x<95\left\{VLI\right\}\\ 0;\mathrm{i}\mathrm{f}x\ge 95\left\{NIR\right\}\end{array}\text{,}$$ (12)

$${\overline{\mu }}_{PR}=\{\begin{array}{l}0;\mathrm{i}\mathrm{f}x<5\left\{NIR\right\}\\ \frac{x-5}{55};\mathrm{i}\mathrm{f}5\le x<60\left\{NI\right\}\\ \frac{70-x}{35};\mathrm{i}\mathrm{f}60\le x<70\left\{VLI\right\}\\ \frac{80-x}{13};\mathrm{i}\mathrm{f}70\le x<80\left\{LI\right\}\\ \frac{90-x}{13};\mathrm{i}\mathrm{f}80\le x<90\left\{HI\right\}\\ \frac{100-x}{13};if90\le x<100\left\{VLI\right\}\\ 0;\mathrm{i}\mathrm{f}x\ge 100\left\{NIR\right\}\end{array}\text{.}$$ (13)

From Fig. 3, the IT2FL LMF and UMF are expressed in (14) and (15), respectively,

$$\underset{¯}{\mu }\left(x\right)=\{\begin{array}{l}0;\mathrm{i}\mathrm{f}x<l_1\\ \frac{x-l_1}{p_1-l_1};\mathrm{i}\mathrm{f}{l}_1\le x<\frac{r_1\left(p_{1-}{l}_1\right)+l_1\left(r_{1-}{p}_1\right)}{\left(p_{1-}{l}_1\right)+\left(r_{1-}{p}_1\right)}\\ \frac{r_1-x}{r_1-p_1};\mathrm{i}\mathrm{f}\frac{r_1\left(p_{1-}{l}_1\right)+l_1\left(r_{1-}{p}_1\right)}{\left(p_{1-}{l}_1\right)+\left(r_{1-}{p}_1\right)}\le x<r_1\\ 0;\mathrm{i}\mathrm{f}x\ge r_1\end{array}\text{,}$$ (14)

$$\overline{\mu }\left(x\right)=\{\begin{array}{l}0;\mathrm{i}\mathrm{f}x<l_2\\ \frac{x-l_2}{p_2-l_2};\mathrm{i}\mathrm{f}{l}_2\le x<p_1\\ 1;\mathrm{i}\mathrm{f}{p}_1\le x<p_2\\ \frac{r_2-x}{r_2-p_2};\mathrm{i}\mathrm{f}{p}_2\le x<r_2\\ 0;\mathrm{i}\mathrm{f}x\ge r_2\end{array}\text{.}$$ (15)

From (14) and (15), the lower and upper membership sets for the CD4 count membership grades are realised in (16)–(21),

$${\underset{¯}{\mu }}_{CD4\left[L\right]}\left(x\right)=\{\begin{array}{l}0;\mathrm{i}\mathrm{f}x<0\\ \frac{x-50}{225};\mathrm{i}\mathrm{f}0\le x<225\\ \frac{450-x}{225};\mathrm{i}\mathrm{f}225\le x<450\\ 0;\mathrm{i}\mathrm{f}x\ge 450\end{array}\text{,}$$ (16)

$${\overline{\mu }}_{CD4\left[L\right]}\left(x\right)=\{\begin{array}{l}0;\mathrm{i}\mathrm{f}x<50\\ \frac{x-50}{225};\mathrm{i}\mathrm{f}50\le x<225\\ 1;\mathrm{i}\mathrm{f}225\le x<275\\ \frac{500-x}{225};\mathrm{i}\mathrm{f}275\le x<500\\ 0;\mathrm{i}\mathrm{f}x\ge 500\end{array}\text{,}$$ (17)

$${\underset{¯}{\mu }}_{CD4\left[M\right]}\left(x\right)=\{\begin{array}{l}0;\text{if}x<300\\ \frac{x-300}{275};\mathrm{i}\mathrm{f}300\le x<575\\ \frac{850-x}{275};\mathrm{i}\mathrm{f}575\le x<850\\ 0;\mathrm{i}\mathrm{f}x\ge 850\end{array}\text{,}$$ (18)

$${\overline{\mu }}_{CD4\left[M\right]}\left(x\right)=\{\begin{array}{l}0;\mathrm{i}\mathrm{f}x<350\\ \frac{x-350}{275};\mathrm{i}\mathrm{f}350\le x<575\\ 1;\mathrm{i}\mathrm{f}575\le x<625\\ \frac{900-x}{900-p_2};\mathrm{i}\mathrm{f}625\le x<900\\ 0;\mathrm{i}\mathrm{f}x\ge 900\end{array}\text{,}$$ (19)

$${\underset{¯}{\mu }}_{CD4\left[H\right]}\left(x\right)=\{\begin{array}{l}0;\mathrm{i}\mathrm{f}x<700\\ \frac{x-700}{375};\mathrm{i}\mathrm{f}700\le x<1075\\ \frac{1450-x}{375};\mathrm{i}\mathrm{f}1075\le x<1450\\ 0;\mathrm{i}\mathrm{f}x\ge 1450\end{array}\text{.}$$ (20)

$${\overline{\mu }}_{CD4\left[H\right]}\left(x\right)=\{\begin{array}{l}0;\mathrm{i}\mathrm{f}x<750\\ \frac{x-750}{375};\mathrm{i}\mathrm{f}750\le x<1075\\ 1\mathrm{i}\mathrm{f}1075\le x<1125\\ \frac{1500-x}{375};\mathrm{i}\mathrm{f}1125\le x<1500\\ 0;\mathrm{i}\mathrm{f}x\ge 1500\end{array}\text{,}$$ (21)

Following similar convention, the lower and upper membership sets for the RNA membership grades can be obtained from (14) and (15), as realised in (22)–(27),

$${\underset{¯}{\mu }}_{RNA\left[U\right]}\left(x\right)=\{\begin{array}{l}0;\mathrm{i}\mathrm{f}x<0\\ \frac{x}{0.6};\mathrm{i}\mathrm{f}0\le x<0.6\\ \frac{1.2-x}{0.6};\mathrm{i}\mathrm{f}0.6\le x<1.2\\ 0;\mathrm{i}\mathrm{f}x\ge 1.2\end{array}\text{,}$$ (22)

$${\overline{\mu }}_{RNA\left[U\right]}\left(x\right)=\{\begin{array}{l}0;\mathrm{i}\mathrm{f}x<0.3\\ \frac{x-0.3}{0.6};\mathrm{i}\mathrm{f}0.3\le x<0.6\\ 1;\mathrm{i}\mathrm{f}0.6\le x<0.9\\ \frac{1.5-x}{0.6};\mathrm{i}\mathrm{f}0.9\le x<1.5\\ 0;\mathrm{i}\mathrm{f}x\ge 1.5\end{array}\text{,}$$ (23)

$${\underset{¯}{\mu }}_{RNA\left[S\right]}\left(x\right)=\{\begin{array}{l}0;\mathrm{i}\mathrm{f}x<1\\ \frac{x-1}{1.15};\mathrm{i}\mathrm{f}1\le x<2.15\\ \frac{3.3-x}{1.15};\mathrm{i}\mathrm{f}2.15\le x<3.3\\ 0;\mathrm{i}\mathrm{f}x\ge 3.3\end{array}\text{,}$$ (24)

$${\overline{\mu }}_{RNA\left[S\right]}\left(x\right)=\{\begin{array}{l}0;\text{if}x<1.2\\ \frac{x-1.2}{1.15};\text{if}1.2\le x<2.15\\ 1;\text{if}2.15\le x<2.35\\ \frac{3.5-x}{1.15};\text{if}2.35\le x<3.5\\ 0;\text{if}x\ge 3.5\end{array}\text{,}$$ (25)

$${\underset{¯}{\mu }}_{RNA\left[NS\right]}\left(x\right)=\{\begin{array}{l}0;\text{if}x<2.5\\ \frac{x-2.5}{1.5};\text{if}2.5\le x<4\\ \frac{\mathrm{5,5}-x}{1.5};\text{if}4\le x<5.5\\ 0;\text{if}x\ge 5.5\end{array}\text{.}$$ (26)

$${\overline{\mu }}_{RNA\left[NS\right]}\left(x\right)=\{\begin{array}{l}0;\text{if}x<3\\ \frac{x-3}{1.5};\text{if}3\le x<4\\ 1;\text{if}4\le x<4.5\\ \frac{6-x}{1.5};\text{if}4.5\le x<6\\ 0;\text{if}x\ge 6\end{array}\text{,}$$ (27)

The lower and upper membership sets for the PR membership grades can also be derived from (14) and (15), and are as realised in (28)–(37),

$${\underset{¯}{\mu }}_{PR\left[NI\right]}\left(x\right)=\{\begin{array}{l}0;\text{if}x<0\\ \frac{x}{27.5};\text{if}0\le x<27.5\\ \frac{55-x}{27.5};\text{if}27.5\le x<55\\ 0;\text{if}x\ge 55\end{array}\text{,}$$ (28)

$${\overline{\mu }}_{PR\left[NI\right]}\left(x\right)=\{\begin{array}{l}0;\text{if}x<5\\ \frac{x-5}{27.5};\text{if}5\le x<27.5\\ 1;\text{if}27.5\le x<47.5\\ \frac{60-x}{27.5};\text{if}47.5\le x<60\\ 0;\text{if}x\ge 60\end{array}\text{,}$$ (29)

$${\underset{¯}{\mu }}_{PR\left[VLI\right]}\left(x\right)=\{\begin{array}{l}0;\text{if}x<30\\ \frac{x-30}{17.5};\text{if}30\le x<47.5\\ \frac{65-x}{17.5};\text{if}47.5\le x<65\\ 0;\text{if}x\ge 65\end{array}\text{,}$$ (30)

$${\overline{\mu }}_{PR\left[VLI\right]}\left(x\right)=\{\begin{array}{l}0;\text{if}x<35\\ \frac{x-35}{17.5};\text{if}35\le x<47.5\\ 1;\text{if}47.5\le x<52.5\\ \frac{70-x}{17.5};\text{if}52.5\le x<70\\ 0;\text{if}x\ge 70\end{array}\text{,}$$ (31)

$${\underset{¯}{\mu }}_{PR\left[LI\right]}\left(x\right)=\{\begin{array}{l}0;\text{if}x<62\\ \frac{x-62}{6.5};\text{if}62\le x<68.5\\ \frac{75-x}{6.5};\text{if}68.5\le x<75\\ 0;\text{if}x\ge 75\end{array}\text{,}$$ (32)

$${\overline{\mu }}_{PR\left[LI\right]}\left(x\right)=\{\begin{array}{l}0;\text{if}x<67\\ \frac{x-67}{6.5};\text{if}67\le x<68.5\\ 1;\text{if}68.5\le x<73.5\\ \frac{80-x}{6.5};\text{if}73.5\le x<80\\ 0;\text{if}x\ge 80\end{array}\text{,}$$ (33)

$${\underset{¯}{\mu }}_{PR\left[HI\right]}\left(x\right)=\{\begin{array}{l}0;\text{if}x<72\\ \frac{x-72}{6.5};\text{if}72\le x<78.5\\ \frac{85-x}{6.5};\text{if}78.5\le x<85\\ 0;\text{if}x\ge 85\end{array}\text{,}$$ (34)

$${\overline{\mu }}_{PR\left[HI\right]}\left(x\right)=\{\begin{array}{l}0;\text{if}x<77\\ \frac{x-77}{6.5};\text{if}77\le x<78.5\\ 1;\text{if}78.5\le x<83.5\\ \frac{90-x}{6.5};\text{if}83.5\le x<90\\ 0;\text{if}x\ge 90\end{array}\text{,}$$ (35)

$${\underset{¯}{\mu }}_{PR\left[VHI\right]}\left(x\right)=\{\begin{array}{l}0;\text{if}x<82\\ \frac{x-82}{6.5};\text{if}82\le x<88.5\\ \frac{95-x}{6.5};\text{if}88.5\le x<95\\ 0;\text{if}x\ge 95\end{array}\text{.}$$ (36)

$${\overline{\mu }}_{PR\left[VHI\right]}\left(x\right)=\{\begin{array}{l}0;\text{if}x<87\\ \frac{x-87}{6.5};\text{if}87\le x<88.5\\ 1;\text{if}88.5\le x<93.5\\ \frac{100-x}{6.5};\text{if}93.5\le x<100\\ 0;\text{if}x\ge 100\end{array}\text{,}$$ (37)

3.1.2.1.3. Rule base design

The dynamic behaviour of our fuzzy logic controller is characterised by its rule base constructed from expert domain knowledge of the consequence heuristics. These rules are necessary to simulate the perceived human reasoning toward a conceptual logic and artificial (fuzzy) reasoning, as well as the implication between the input MF and fuzzy rule inference required to compute the patient response. For designers of expert systems, these aspects of development are the most crucial, as branching constitutes a fundamental property of logic rules, and traversing complex real-world problems may certainly cause unnecessary explosion of traversed routes. Hence, an efficient mechanism is required to ensure that only optimal routes are traversed. In this paper, we introduce experience-based heuristics in addition to the fuzzy rules. The difficulty initiating heuristics and fuzzy rules does not lie in their formulation or in the likelihood of the rule not holding, but in most cases the degree of established confidence limits are not precisely known. The rule base model of our inference system comprises of a set of if-then rules that establishes relationships between the controller input and output linguistic variables. Suppose a Fuzzy Logic System (FLS) permit p inputs, $x_i\in X_1,\dots .,x_p\in X_p$, and one output $y\in Y$, characterized by rules, then, the lth rule is of the form,

$$R^l:\mathbf{i}\mathbf{f}{x}_{i}is{F}_i^l\text{and}\dots \text{and}{x}_{p}is{F}_{p,}^l\mathbf{t}\mathbf{h}\mathbf{e}\mathbf{n}yis{G}^l,l=1,\dots ,M\text{.}$$ (38)

where$R^l$is l^th fuzzy rule, $F_i^l$, $F_p^l$and $G^l$ are the respective linguistic terms, M is the number of rules, $x_{i,\{i=1,\dots p\}}$ is the antecedent, and $y$ is consequent of the lth rule, $l=1,\dots ,p$ of the FLS. Then, the ${\tilde{F}}_i^l$’s are the MFs ${\mu }_{{\tilde{F}}_i^l}\left(x_i\right)$ of the antecedent part assigned to the $ith$ input $x_i$; the ${\text{E}}^{\text{l}}$’s are the MFs ${\mu }_{{\tilde{F}}_i^l}\left(x_i\right)$ of the consequent part assigned to the output y.

To generate the rules, we introduce a Moses-Map (M-Map) rule base matrix that combines the various linguistic terms, $F_i^l,$of the input parameters, $x_i$, to yield a membership grade, $G^l$, a linguistic term of the output linguistic variable, $y$. Our M-Map simplifies the rule base generation process, and ensures that all the possible rule combinations are successfully traversed. The algorithm guiding the construction cascades the input linguistic variables along the row and column tabs (above the cells), similar to a typical speadsheet. Suppose the linguistic variables $L_i(i:1,\dots ,n)$ occupy the column tabs, and the linguistic terms $t_j(j:1,\dots ,m)$ are aligned to the row tabs, then, the length of the column and row tabs is the combined product of the linguistic terms, which anticedent or rule set logic order can be achieved using knowledge of known combinatorics. Hence, the linguistic variables investigated in this paper consist of three linguistic terms each, and the column and row cascades can permit a length of 9. Each rule set is combined such that no rule combination repeats. A total of 81 rules were derived, and is presented in Table 2.

Table 2.

The Mos-Map rule base matrix.

Baseline CD4		L	L	L	M	M	M	H	H	H
Followup CD4		L	M	H	L	M	H	L	M	H
NS	NS	NIr9	VLIr18	VLIr27	VLIr36	VLIr45	LIr54	VLIr63	LIr72	LIr81
NS	S	VLIr8	VLIr17	LIr26	VLIr35	LIr44	LIr53	LIr62	LIr71	HIr80
NS	U	VLIr7	LIr16	LIr25	LIr34	LIr43	HIr52	LIr61	HIr70	HIr79
S	NS	VLIr6	VLIr15	LIr24	VLIr33	LIr42	LIr51	LIr60	LIr69	HIr78
S	S	VLIr5	LIr14	LIr23	LIr32	LIr41	HIr50	LIr59	HIr68	HIr77
S	U	LIr4	LIr13	HIr22	LIr31	HIr40	HIr49	HIr58	HIr67	VHIr76
U	NS	VLIr3	LIr12	LIr21	LIr30	LIr39	HIr48	LIr57	HIr66	HIr75
U	S	LIr2	LIr11	HIr20	LIr29	HIr38	HIr47	HIr56	HIr65	VHIr74
U	U	LIr1	HIr10	HIr19	HIr28	HIr37	VHIr46	HIr55	VHIr64	VHIr73
Baseline RNA	Followup RNA

From Table 2, rules r1, r2 and r3 can be built as follows:

r1.If BCD4 is L-Low and FCD4 is L-Low and BRNA is U-Ubdetected and FRNA is U-Undetected then Interaction is LI-Low Interaction.

r2. If BCD4 is L-Low and FCD4 is L-Low and BRNA is U-Ubdetected and FRNA is S-Suppressed then Interaction is LI-Low Interaction.

r3. If BCD4 is L-Low and FCD4 is L-Low and BRNA is U-Undetected and FRNA is NS-Not Suppressed then Interaction is VLI-Very Low Interaction.

The result of the input and antecedent operations is an interval type-1 set, and is called the firing set [36], thus,

$$F^i\left(x^{\prime }\right)=[\underset{¯}{f^i}\left(x^{\prime }\right),\overline{f^i}\left(x^{\prime }\right)]\equiv [\underset{¯}{f^i},\overline{f^i}]\text{,}$$ (39)

$$\underset{¯}{f^i}\left(x^{\prime }\right)={\underset{¯}{\mu }}_{f_1^i}\left({x^{\prime }}_1\right),\ast \mathrm{...}\ast {\underset{¯}{\mu }}_{f_m^i}\left({x^{\prime }}_1\right)\text{,}$$ (40)

$$\overline{f^i}\left(x^{\prime }\right)={\overline{\mu }}_{f_1^i}\left({x^{\prime }}_1\right)\ast \mathrm{...}\ast {\overline{\mu }}_{f_m^i}\left({x^{\prime }}_1\right)\text{.}$$ (41)

where, $F^i\left(x\right)$is the antecedent of rule $i$, and ${\mu }_{f^i}\left(x\right)$, is the degree of membership of $x$in $F$.${\overline{\mu }}_{f^i}\left(x\right)$ and ${\underset{¯}{\mu }}_{f^i}\left(x\right)$, are upper and lower MFs of ${\mu }_{f^i}$. The $R^i$ fired output consequent set ${\mu }_{\check{\beta }}\left(y\right)$ is the interval type-2 fuzzy set represented as,

$${\mu }_{\stackrel{⌣}{\beta }}l\left(y\right)={\int }_{b^l\in [{\underset{¯}{f}}^1\ast {\underset{¯}{\mu }}_{\tilde{G}}l\left(y\right),\overline{f^i}{\overline{\mu }}_{G}l\left(y\right)]}\frac{1}{b^l},y\in Y\text{.}$$ (42)

where ${\underset{¯}{\mu }}_{\tilde{G}}\left(y\right),\text{and}\overline{f^i}{\overline{\mu }}_G\left(y\right)$ are the lower and upper membership grades ${\mu }_{\tilde{G}}\left(y\right)$. And ${\mu }_{\tilde{\beta }}\left(y\right)$ is obtained as a combination of the fired output consequent set, considering the union of the rule $R^1$ fired output consequent set. The type reduction module maps the reduced set into an interval of uncertainty, producing the output of the IT2FLS. The type reduction can now be expressed as follows using Karnik-Mendel model [37, 38]:

$$y_r=\frac{{{\sum }_{i=1}^{N}f}_r^l{y}_r^l}{{\sum }_{i=1}^N{f}_f^i}\text{,}$$ (43)

and,

$$y_l=\frac{{{\sum }_{i=1}^{N}f}_l^i{y}_l^i}{{\sum }_{i=1}^N{f}_f^i}\text{,}$$ (44)

The defuzzification module is then used to defuzzify the interval set using the average of y_r and y_l, yielding the output of the IT2FLS as,

$$y\left(x\right)=\frac{y_l+y_r}{2}\text{.}$$ (45)

An open-source toolkit: the Juzzyonline Fuzzy toolbox [36] (http://juzzy.wagnerweb.net/), created for the development and sharing of Type-1 and Type-2 fuzzy logic systems, was used to implement the proposed controller, where the input and output variables were shared according to their lower and upper values and used in controlling the models. UMF and LMF were also defined for CD4 count, RNA, and patient response parameters.

3.1.2.2. The MDS model

3.1.2.2.1. Model description

MDS is a data analysis technique that computes relative positions of adjacent objects from high dimension space to low dimension space with high error-tolerance [39]. It is concerned with configuration recovery from distance (dissimilarity) matrices and makes for more understandable data through visualisation. Projecting data into a lower dimensional space can serve two purposes. First, it eliminates irrelevant features, hence, reducing noise that may affect the analysis. Second, an easy visualisation of data using 2- or 3-dimensions – for better interpretation of “hidden” structures can be achieved [40, 41]. We apply MDS in this paper to ensure that the distance between the learning exemplars are best predictors and efficient for classification. Although there are classical, metric, non-metric, and generalised MDS, the non-metric MDS was preferred in this paper. This class of MDS locates a configuration of points in some lower space whose pair-wise Euclidean distances contain approximately the same rank order as the corresponding dissimilarities in higher space [42]. Applying the non-metric MDS within the context of our problem, we reformulate the problem as follows: Let X be an $m\times n$ matrix representing patients unique TCEs in the higher space, ${\mathbb{R}}^n$; Y be an $m\times p$ matrix representing the perturbed data in the lower space, ${\mathbb{R}}^p$; and $\Delta =\left[{\delta }_{ij}\right]$ be the dissimilarity matrix of $X$ for $i;j=\{1,\dots ,m\}.$ The Euclidean distance ($d_{ij}=\sqrt{\sum _{k=1}^m{\left(x_{ik}-x_{jk}\right)}^2}$) is a common measure that is mostly used to describe the dissimilarity $\Delta =\left({\delta }_{ij}\right)$ between the TCE points, $x_i$ and $x_j$. Then, ${\delta }_{ij}=f\left(d_{ij}\right)$, where $f$ is a monotonic function such that $d{}_{ij}<d_{uv}\to {\delta }_{ij}$<${\delta }_{uv}$. Non-metric MDS orders the off-diagonal ${\delta }_{ij}$ such that ${\delta }_{i_{1,}{j}_1}\le ,\dots ,\le {\delta }_{i_m{j}_m}$; where $m=\frac{n(n-1)}{2}$, and seeks a fitted configuration $\hat{X}=\left({\hat{x}}_{i,k}\right)$ in $p$dimensions, such that the fitted distances $\hat{D}=\left({\hat{d}}_{ij}\right)$ (obtained by substituting ${\hat{x}}_{ik}$ and ${\hat{x}}_{jk}$ for $x_{ik}$ and $x_{jk}$, in a matrix of squared proximities, i.e., $P=x_i-{x_j}^2$). This contributes to preserving the ordering, ${\hat{d}}_{i_{1,}{j}_1}\le ,\dots ,\le {\hat{d}}_{i_m{j}_m}$. The squared stress is used to measure how the ordering of the elements between $\Delta$ and $\hat{D}$ differs. Thus,

$$S_p^2\left(\hat{X}\right)=\frac{{{\sum }_{i<j}(d_{i,j}^{\ast }-{\hat{d}}_{i,j})}^2}{{\sum }_{i<j}{\hat{d}}_{i,j}^2}\text{,}$$ (46)

where $p$ denotes the number of dimensions $\hat{X}$, and the denominator of (46) makes $S_p^2\left(\hat{X}\right)$ invariant to uniform scaling. The square root is then taken to give the stress of fit statistic, as,

$$S_p\left(\hat{X}\right)={\left(\frac{{{\sum }_{i<j}(d_{i,j}^{\ast }-{\hat{d}}_{i,j})}^2}{{\sum }_{i<j}{\hat{d}}_{i,j}^2}\right)}^{\frac{1}{2}}\text{.}$$ (47)

The number of dimensions ($\hat{X}$) is iteratively adjusted and the stress $S_p\left(\hat{X}\right)$ recalculated, starting with an initial configuration, ${\hat{X}}^{\left(0\right)}$, in $p$ dimensional space, using the method of steepest descent to minimize $S_p\left(\hat{X}\right)$. When the $S_p\left(\hat{X}\right)$ = 0%, the fitted configuration ($\hat{X}$) is identical to the original configuration. On reaching an acceptable stress of fit statistic, the obtained response set is fed to the DNN for learning and optimisation purposes.

3.1.3. Patient response optimisation

3.1.3.1. DNN model description

In this section, DNN is used to model the current problem by revealing the interactions between the input data samples for optimal patient response prediction. DNN is a hierarchical model where each layer implements a linear transformation followed by a non-linearity to the preceding layer. Let $X\in {\mathbb{R}}^{NxD}$ represent the neural inputs obtained from the fuzzy interface (initiated by the learning algorithm), with each row of $X$being a D-dimensional data point. For the sake of simplicity, we assume that the datasets lie in $\mathbb{R}$; and $N$ is the number of training exemplars. Also, let $W^K\in {\mathbb{R}}^{d_{k-1}.d_k}$ be a linearly transformed matrix applied to the output layer $k-1,X_{K-1}\in {\mathbb{R}}^{N.d_{k-1}}$, to produce a $d_k$-dimensional term $X_{K-1}{W}^K\in {\mathbb{R}}^{N.d_k}$at layer $k$. Suppose, ${\varnothing }_K:\mathbb{R}\to \mathbb{R}$ is a non-linear activation function, e.g., a sigmoid: ${{\varnothing }_K\left(x\right)=(1+e^{-x})}^{-1}$ or hyperbolic tangent: ${\varnothing }_K=\text{tanh}\left(x\right)$, or a rectified linear unit: ${\varnothing }_K\left(x\right)=\text{max}\{0,x\}$, then, the activation function can be applied to each instance of $Y_{K-1}{W}^K$ to generate the $kth$ layer of a neural network, as: $X_K={\varnothing }_K\left(X_{K-1}{W}^K\right)$, and the output $X_K$ of the network becomes:

$$\gamma (X,W^1,W^2,\dots ,W^K)={\varnothing }_K\left({\varnothing }_{K-1}\left(\dots {\varnothing }_2\left({\varnothing }_1\left(X{W}^1\right)W^2\right)\dots W^{K-1}\right)W^K\right)\text{.}$$ (48)

Notice that: $\gamma$ is a $N\times C$ matrix, and $C=d_k$ is the output network dimension, which equates to the number of classes of a classification problem. As such, we can view $\gamma$ as a function map that defines the input data $X$with fixed weights, $W$. In this paper our optimisation system uses the sigmoid activation function.

3.1.3.1.1. Global optimality

Consider the problem of learning the parameters $W={\left\{W^K\right\}}_{k=1}^K$of a DNN from N training exemplars $(X,Y)$. In the configuration setting, suppose a classification problem has $C$ target classes, where each row of $X\in {\mathbb{R}}^{NxD}$ denotes a data point in ${\mathbb{R}}^D$ and each row of ${Y\in \left\{\mathrm{0,1}\right\}}^{N\times C}$ denotes membership of each data point to one out of the $C$ classes; then, $Y_{jc}=1,$ iff the $jth$row of $X$ belongs to class $c\in \left\{\mathrm{1,2},\dots ,C\right\}$; otherwise, $Y_{jc}=0$. The learning problem can be formalised as an optimisation problem, thus:

$$\underset{{\left\{W^K\right\}}_{k=1}^K}{\min }\ell (Y,\gamma (X,W^1,W^2,\dots ,W^k))+\lambda \beta (W^1,W^2,\dots ,W^K)\text{.}$$ (49)

where $\ell (Y,\beta )$ is the loss function that measures the consensus between the true output, $Y$, and the predicted output $\gamma \left(X,W\right);\beta$, is the regularisation or normalisation function which is used to prevent overfitting.

3.1.3.1.2. Universal approximation

Theorem 1

[41]: Let $P\left(\right)$ be a bounded, non-continuous function, and let $I_m$denote a m-dimensional hyperbole, and $C\left(I_m\right)$ denote the space of continuous functions on $I_m$. Given any $f\in C\left(I_m\right)$and $\epsilon >0$, there exists $N>0$ and $v_i,w_i,b_i,i=1\dots N$, such that $F\left(x\right)=\sum _{i\le N}{v}_{i}P(w_i^{T}x+b_i$) satisfies $\underset{x\in I_m}{\sup }\left|f\left(x\right)-F\left(x\right)\right|<\epsilon |.$

Theorem 1 guarantees that even a single hidden layer network can represent any classification problem where the boundary is locally linear (or smooth) but does not give clue to good or bad architectures or how they relate to the optimisation problem.

Theorem 2

The mean integrated square error between the essential network $\hat{F}$ and the target function $f$ is bounded by, $O\left(\frac{C_f^2}{N}\right)+O\left(\frac{N_m}{K}logK\right)$,where $K$ denotes the number of training points, $N$ is the number of neurons, and $m$ measures the global smoothness of $f$.

3.1.3.1.3. Generalisation error

Consider a classification problem with data point, $X\in X_p\in {\mathbb{R}}^D$, corresponding to class label $Y\in Y_c$. The training set of $N$ samples drawn from a distribution $Q$ is given as ${\phi }_N={\{X_i,Y_i\}}_{i=1}^N$ and the loss function is denoted as $\ell (Y,\gamma (X,W))$ – a measure of the discrepancy between the true and estimated labels of $Y$ – provided by the classifier. The empirical loss of the network $\gamma (.,W)$ associated with the training set ${\phi }_N$ is defined as [43]:

$${\ell }_{emp}\left(\gamma \right)=\frac{1}{N}\sum _{X_i\in {\phi }_N}\ell \left(Y_{i,}\gamma \left(X_{i,}W\right)\right)\text{,}$$ (50)

and its expected loss is given as,

$${\ell }_{emp}\left(\gamma \right)={\mathbb{E}}_{(X,Y)\sim Q}\left[\ell \left(Y,\gamma \left(X,W\right)\right)\right]\text{,}$$ (51)

From the above definition, the generalization error becomes,

$$GE\left(\gamma \right)=|{\ell }_{exp}\left(\gamma \right)-{\ell }_{emp}\left(\gamma \right)|\text{.}$$ (52)

And the loss function for deep learning our supervised classification problem is the empirical cross entropy, given as:

$$\overline{\ell }\left(W\right)={\mathbb{E}}_{q\left(X,Y\right)}\left(-log\gamma \left(X,W\right)\right)\text{.}$$ (53)

Eq. (53) is however prone to over-fitting, as the network may trivially the training data instead of learning the underlying distribution measure. This problem can be fixed using normalisation, which may be explicit or implicit in a stochastic gradient descent.

4. Results

4.1. Experiment HIV database analysis

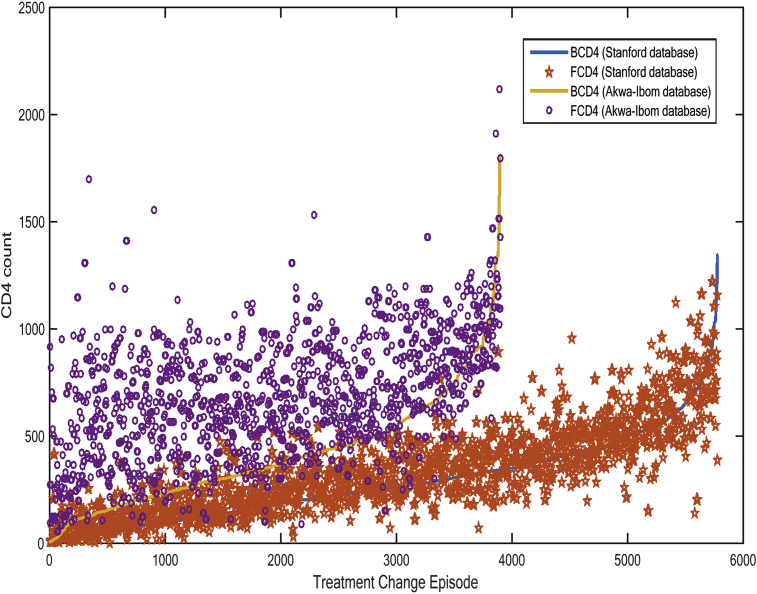
4.1.1. CD4 and RNA visualisation

The CD4 count and RNA give healthcare providers important clues about the following: immune system health, HIV progression, body response to HIV therapy, and virus response to the therapy. In this section, we analyse the empirical datasets of both Stanford HIV and Akwa-Ibom HIV databases, for possible cluster variations and outlier effects. In Fig. 4, a visualisation of the effect of TCE on CD4 count is presented. CD4 count indicates the immune system robustness. Hence, there are enhanced immunological changes defined by higher cluster heights (an indication of low opportunistic infection) in the Akwa-Ibom HIV database, compared to the Stanford database, which changes occurred at a slower rate. Furthermore, more data points in the Akwa-Ibom HIV database clustered far above the baseline CD4, as opposed to the Stanford HIV database, which had about 40% of the data points clustering below the baseline CD4. The Stanford effect may not be unconnected with the fact that the database is made up of patients with resistant exemplars or who had failed treatment due to high level of drug resistance and are being monitored using new drug regimens.

Fig. 4.

Effect of treatment change episode on CD4 count for Akwa-Ibom HIV and Stanford HIV databases.

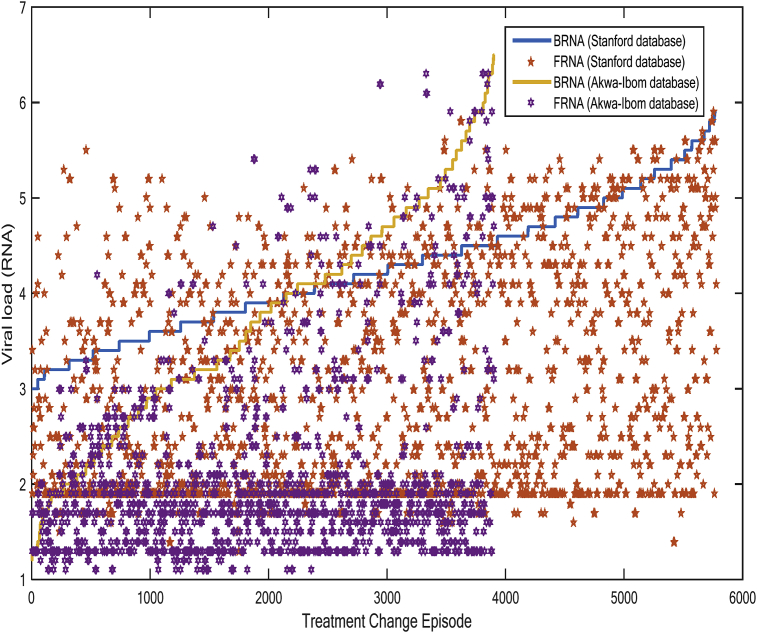
The RNA is an inverse function of the CD4 count. A low RNA indicates relatively few copies of HIV in the blood stream and a pointer to a working HIV therapy. If treatment fails and the RNA levels stage a rebound, then CD4 count will start dropping gradually (within few weeks) in response to the rebound. A visualisation of the consequence of RNA variations is presented in Fig. 5. We observe escalating tendencies of baseline RNA curve in Akwa-Ibom HIV database, compared to the Stanford database, which RNA curve appears to be increasingly steady. The escalating trend of BRNA curve implies that the Akwa-Ibom HIV patients showed more cases of advanced (undiagnosed) HIV, or those who may have ignored early warning signs of the disease. Although FRNA values for both databases showed cases of reduced side effects or adverse reactions in some patients than others with outlier effects, the recovery or improvement rate appears to be more rapid on Akwa-Ibom HIV patients, as over 60% of RNA copies of below 2 $\left({10}^2\right)$ were noticed.

Fig. 5.

Effect of treatment change episode on RNA copies for Akwa-Ibom HIV and Stanford HIV databases.

4.1.2. Patient response inference analysis

A statistic of the fuzzy-MDS patient response inference based on the output membership grades is presented in Table 3. We observe that the Akwa-Ibom database has the least patients with relatively high interaction cases (HI and VHI) of 90 (6.9178%) patients. This confirms the healthcare managers’ claim that only few acute cases of failed treatment were recorded, but further statistical evidence is required to confirm the significance of their claim with respect to the HIV population under study. In contrast, the Stanford (our reference) database has 618 patients (40.6312%) with relatively high interaction and further confirms the purpose of the database (cases of patients with failed treatment). As regards the level of positive response to treatment, the Akwa-Ibom HIV database showed the highest response rate with 841 (64.6426%) patients and 370 (28.4397%) patients having relatively low interaction cases (LI and VLI) and no interaction, respectively. The Stanford database showed relatively low and no response cases of 664 (43.6555%) and 239 (15.7133%), respectively, indicating the accuracy of our fuzzy-MDS-DNN controller at modelling the databases.

Table 3.

Analysis of patient response inference.

Membership grade	Stanford database			Akwa-Ibom database
	TCE	Unique Patient ID	%	TCE	Unique Patient ID	%
VHI	940	248	16.3051	75	25	1.9216
HI	1454	370	24.3261	195	65	4.9962
LI	1546	402	26.4300	883	294	22.5980
VLI	962	262	17.2255	1640	547	42.0446
NI	878	239	15.7133	1110	370	28.4397
Total:	5780	1521	100	3903	1301	100

4.2. DNN optimisation

It is proven that multilayer perceptrons (MLPs) with only one hidden layer are universal function approximators [44]. They are neural networks with multiple parallel node-layer topologies that utilises a supervised learning technique known as backpropagation. Hence, identifying a topology that best drives the problem is important. In this paper, MATLAB 2017a was used to model the classification system as a pattern recognition problem driven by the MLP architecture. A pattern recognition network model called patternnet applying two training algorithms, the Levenberg-Marquardt (trainlm) and Resilient Backpropagation (trainrp) algorithms was adopted for this purpose. The performance of various algorithms can be affected by the accuracy required of the approximation, but applications of the training algorithms in various literatures have shown that the trainlm algorithm is the fastest, although not without the limitation of a larger storage requirement. The experiment databases were distributed in the ratio of 80: 10: 10, for training, validation, and testing, respectively, using a randomised distribution approach that divides up every sample data. Relevant features that served as inputs to the DNN were, baseline CD4 (BCD4), followup CD4 (FCD4), baseline viral load (BRNA), followup viral load (FRNA), drug type combination (DType), and the error-pruned patient response inference set. Five target classes (C1–C5) were created following the output membership grades of the fuzzy-logic system (C1 = VHI, C2 = HI, C3 = LI, C4 = VLI, and C5 = NI) to predict the clustering patterns. Table 4 and Table 5 are sample input and target class data of 20 patients, for the Stanford HIV and Akwa-Ibom HIV databases, respectively.

Table 4.

Input linguistic variables and target classes for Stanford database.

Input linguistic variable							Target class
PID	BCD4	FCD4	BRNA	FRNA	DType	PR	C1	C2	C3	C4	C5
1	330	347	3.7	3.3	3TC + ABC + ATC + AZT + RTV + TDF	32.67	0	0	1	0	0
2	38	53	5.7	5.3	D4T + DDI + NVP	30.00	1	0	0	0	0
3	949	987	3.7	4.4	D4T + DDI + EFV	71.00	0	0	0	1	0
4	281	334	3.6	3.9	D4T + DDI + EFV	30.82	0	0	1	0	0
5	288	426	3.9	3.6	ABC + D4T + EFV	39.27	0	0	0	1	0
6	470	459	4.1	3.2	3TC + D4T + DDI + LPV	48.75	0	0	0	1	0
7	694	717	3.7	4.8	D4T + EFV + NFV	50.34	0	0	0	1	0
8	37	50	5.3	4.9	ABC + EFV + RTV + SQV	30.00	1	0	0	0	0
9	242	358	4.9	3.8	3TC + DDI + RTV + SQV	31.65	0	0	1	0	0
10	213	274	3.7	2	3TC + ABC + AZT + TDF	50.00	0	0	1	0	0
11	88	149	5.3	4.2	ABC + D4T + EFV + NFV	30.00	1	0	0	0	0
12	316	403	4	4	D4T + DDI + RTV + SQV	35.28	0	0	0	1	0
13	50	105	5.1	4.7	APV + D4T + EFV + RTV	30.00	1	0	0	0	0
14	102	159	4.9	3.9	3TC + APV + D4T + DDI + RTV	30.00	0	1	0	0	0
15	103	231	3.7	3.5	3TC + D4T + DDI + FPV + RTV	30.00	0	0	1	0	0
16	72	159	5.1	3.4	AZT + DDI + LPV	31.20	0	1	0	0	0
17	109	258	4.9	1.9	DRV + FTC + RTV + T20 + TDF	50.00	0	1	0	0	0
18	169	213	4.1	4.1	3TC + D4T + RTV + SQV	30.00	1	0	0	0	0
19	212	381	4.5	1.9	3TC + D4T + EFV + NFV	50.00	0	0	1	0	0
20	315	352	4.7	3.1	D4T + DDI + IDV + RTV	38.61	0	0	1	0	0

Table 5.

Input linguistic variables and target classes for Akwa-Ibom database.

Input linguistic variable							Target class
PID	BCD4	FCD4	BRNA	FRNA	DType	PR	C1	C2	C3	C4	C5
1	440	388	4.1	3.7	TDF+3TC + EFV	41.92	0	0	0	1	0
2	429	765	4.1	2.4	TDF+3TC + EFV	57.80	0	0	0	1	0
3	307	354	4.4	1.3	TDF+3TC + EFV	52.74	0	0	1	0	0
4	17	675	4.4	1.3	AZT+3TC + NVP	55.00	0	0	1	0	0
5	291	625	4.4	1.3	TDF+3TC + EFV	53.68	0	0	1	0	0
6	180	380	3.4	1.3	TDF+3TC + EFV	53.56	0	0	0	1	0
7	240	400	3.1	1.3	TDF+3TC + EFV	55.16	0	0	0	1	0
8	315	601	4.1	1.3	TDF+3TC + EFV	53.68	0	0	1	0	0
9	163	875	4.1	1.9	TDF+3TC + EFV	65.57	0	0	1	0	0
10	238	642	4.1	3.7	TDF+3TC + EFV	50.00	0	0	1	0	0
11	362	689	4.2	2.1	AZT+3TC + NVP	51.94	0	0	0	1	0
12	156	512	5.4	2.8	TDF+3TC + EFV	50.00	0	0	1	0	0
13	28	52	6.3	1.6	TDF+3TC + EFV	50.00	0	1	0	0	0
14	217	502	6.1	5	TDF+3TC + EFV	50.00	0	1	0	0	0
15	230	763	5.1	1.8	TDF+3TC + EFV	51.78	0	0	1	0	0
16	415	371	3.4	1.3	AZT+3TC + NVP	56.17	0	0	0	0	1
17	286	842	3.4	1.7	TDF+3TC + EFV	60.10	0	0	0	1	0
18	494	657	3.3	2.1	TDF+3TC + EFV	68.44	0	0	0	0	1
19	266	319	3.2	2	TDF+3TC + EFV	50.82	0	0	1	0	0
20	158	266	4.3	3.1	AZT+3TC + NVP	37.97	0	1	0	0	0

To accelerate training, the network was evaluated using a 5-layer (structure) configuration, each layer representing a target class with the number of neurons (in our case, the maximum number of input variables) distributed in a dropout fashion, resulting in the configuration ([6 5 4 3 2]). The evaluation metrics selected as indicated in Tables 6, 7, 8, 9, include:

Table 6.

Classification results for Stanford database with multidimensional scaling.

No. of layers	Neuron Config.	Train Alg.	R- value	Overall MSE	Val MSE	Test MSE	Gradient	TPR	FPR	Class Acc.
5	[6 5 4 3 2]	Trainlm	0.9545	0.0133	0.0146	0.0108	0.0253	0.9625	0.0108	0.9700
		Trainrp	0.8667	0.0395	0.0461	0.0368	0.0277	0.8635	0.0362	0.8630

Bold signifies performance metric values that meets the defined threshold of this study.

Table 7.

Classification results of Stanford database without multidimensional scaling.

No. of layers	Neuron Config.	Train Alg.	R- value	Overall MSE	Val MSE	Test MSE	Gradient	TPR	FPR	Class Acc.
5	[6 5 4 3 2]	Trainlm	0.9177	0.0257	0.0249	0.0222	0.0308	0.9366	0.0188	0.9323
		Trainrp	0.8120	0.0552	0.0545	0.0508	0.0210	0.8431	0.0419	0.8440

Bold signifies performance metric values that meets the defined threshold of this study.

Table 8.

Classification results of Akwa-Ibom database with multidimensional scaling.

No. of layers	Neuron Config.	Train Alg.	R- value	Overall MSE	Val MSE	Test MSE	Gradient	TPR	FPR	Class Acc.
5	[6 5 4 3 2]	Trainlm	0.9871	0.0038	0.0040	0.0070	0.0364	0.9974	0.0026	0.9887
		Trainrp	0.8323	0.0473	0.0527	0.0612	0.0224	0.9554	0.0446	0.8391

Bold signifies performance metric values that meets the defined threshold of this study.

Table 9.

Classification results of Akwa-Ibom database without multidimensional scaling.

No. of layers	Neuron Config.	Train Alg.	R- value	Overall MSE	Val MSE	Test MSE	Gradient	TPR	FPR	Class Acc.
2	[6 5 4 3 2]	Trainlm	0.9248	0.0236	0.0022	0.0207	0.0357	0.7872	0.0185	0.9244
		Trainrp	0.8009	0.0569	0.0579	0.0604	0.0234	0.8159	0.0501	0.8252

Bold signifies performance metric values that meets the defined threshold of this study.

Regression value (R-value): A coefficient that measures the relationship between the outputs of the network and the targets that provides an idea of how close the output from the model is to the actual target values. A perfect training will yield same network outputs and targets, but this relationship cannot be perfect in practice.

Mean Squared Error (MSE): A loss function averaged over the entire dataset, which measures the distance between the predicted and true outputs. The least MSE has been known to yield the best performance.

Gradient: The direction and magnitude (slope) required in the calculation of weights to be used in the network and is commonly used to train deep neural networks.

True Positive Rate (TPR): Also called Sensitivity, measures in our case, the proportion of patients identified as having failed treatment or adverse drug reaction.

False Positive Rate (FPR): Measures in our case, the proportion of patients identified as not having failed treatment or adverse drug reaction. It is also represented as 1 – (Specificity or True Negative Rate: TNR).

Classification Accuracy (Class Acc.): Measures in our case, the proportion of correctly classified patients’ response.

A performance value of at least 0.9 (90%) was considered as acceptable threshold for the R-value, TPR and classification accuracy metrics; and at most 0.01 (1%) for the FPR and MSE metrics. Significant performances are indicated in bold font type. Overall classification result reveal that the trainlm algorithm gave better optimised predictions compared to the trainrp algorithm, for the Stanford HIV and Akwa-Ibom HIV databases with multidimensional scaling–demonstrating the effectiveness of error pruning before learning. As can be seen in Tables 6 and 8, the introduction of multidimensional scaling produced least MSEs and classification accuracies–indicating good validation and test predictors as well as datasets. Classification performance however degraded when the proposed controller was experimented without multidimensional scaling (see Tables 7 and 9). The implication here is that inference from expert knowledge is invaluable to improved system prediction, and our classification learner was at its best in modelling both HIV databases.

A study of the Receiver Operating Characteristics (ROC) curve (a plot of the TPR vs. FPR for the different possible cut-point of diagnostic tests) shows that the test data of the Akwa-Ibom HIV database for fuzzy-PRI with MDS response inference yielded more accurate results than the Stanford HIV database, as (TPR, FPR) values for both databases were (0.9974, 0.0026) and (0.9626, 0.0108), respectively. However, ROC curve results for the experiment databases for fuzzy-PRI without MDS resulted in less accurate test results for the Akwa-Ibom HIV database, with (TPR, FPR) values of (0.7872, 0.0185), compared to the Stanford HIV database, with (TPR, FPR) values of (0.9366, 0.0188). Despite the poor test result reported for the Akwa-Ibom HIV database, our classification learner still maintained accurate classification accuracy of 92.44%. The results indicate that the Stanford HIV database appears to be more robust to test errors even without MDS. Moreover, varying TCEs exist for individual patients compared to the Akwa-Ibom database, which had only a single regimen of only one drug combination and TCE and no further therapeutic action was recorded even when patients showed failed treatment. Hence, a call for a followup of treatment on patients with low patient response inference (i.e., for high and very high interaction cases), as this parameter is a pointer to failed treatments and establishes drug patterns with multi-drug resistance. This also explains why the Stanford database could perform well without expert response inference, as the experiment data contains treatment failure cases. Our classification learner did not over-fit, as the observed gradients neither vanished nor exploded. Vanishing and exploding gradients are two major obstacles in training DNNs and can result in unstable network structures that at best cannot learn from the training data or at worst results in NaN weights, abruptly terminating updates of the weight values. This difficulty is noticeable when training artificial neural networks with gradient-based learning methods and backpropagation. The current optimal results can be attributed to the error-pruning process achieved during the patient response modelling.

5. Discussion

Recent models have shown robust prediction performance with the viral load emerging as the most important variable [45]. This finding has indirectly initiated support for the use of viral load monitoring for an improved HAART in resource-limited settings such as Sub-Saharan Africa. In [45], over 3000 TCEs data collected from clinics in North America, Europe, Japan and Australia, were trained using a single random forest (RF) system. Results obtained showed virological response predictions of 82%, among 100 independent test cases using baseline variables (including genotype). Further findings showed that new models that excluded genotype information were able to predict virological responses for the same test set with a slightly decreasing accuracy of 78%. Hence, the use of other clinically related data such as treatment history and drug information also need to be tried, as they may partially compensate for the absence of genotype data. Encouraged by this result, [45] set out to develop models that were more relevant to clinical practice in a resource-limited context. By selecting TCEs that involved drugs commonly administered in these countries and trained two RF models with over 8000 TCEs without the use of genotype data. Both models predicted virological response with an accuracy of about 82%. The emergence of new antiretroviral drugs has caused a continual modification of the HIV/AIDS treatment guidelines, hence demanding a treatment-decision capable of self-learning [46]. In [46], a self-learning HIV/AIDS regimen selection system for combined antiretroviral therapy of first round HIV/AIDS treatment was developed considering 32 associated treatment objectives involving four major clinical variables (potency, adherence, adverse effects and future drug options). The prediction accuracy was found between 84.4% and 100% in reduced treatment objectives, but, higher mean prediction accuracies of 94%–97% were obtained when all the treatment objectives were learned. A comparison with our proposed framework shows that improved prediction accuracies of 97% for the Stanford database, and 98.87% for the Akwa-Ibom database were obtained, indicating that improved accuracy can be achieved through efficient error-pruning mechanisms and robust learning algorithms.

6. Conclusions

The performance of machine learning heavily rests on sound knowledge acquisition techniques from available domain experts. This paper employed a fuzzy-multidimensional deep learning framework that combines the strengths of machine learning and multidimensional scaling tools, to facilitate intuitive knowledge elicitation – by transforming domain knowledge into a set of rules that drives the accurate classification of HIV patient response to ART. The proposed controller was able to deal with uncertainty caused by inconsistent input datasets and incomplete domain knowledge, where fuzzy rules were continually fine-tuned for two experiment databases (Stanford and Akwa-Ibom datasets), with patient response re-scaled to reduce the high error-prone datasets typical of real-world data. A deep learning optimisation of trained exemplars using two learning algorithms was then performed to efficiently optimise the datasets. Results obtained showed that inference from expert knowledge (labelled data) as well as the introduction of multidimensional scaling are invaluable for the efficient classification of HIV patient response to ART.

The limitation of this research is the high computational cost of the type-reduction process, typical of the iterative Karnik-Mendel algorithm and the application of a supervised approach to selecting the desired features. Hence, a future direction of this research targets the realisation of an efficient expert system, towards personalised therapy. Furthermore, two major areas of application can be identified: (i) an effective technique for the accurate generation of features, as unsupervised deep learning models (capable of creating features) will expand the horizons of processing new data in limited environments; (ii) exploring enhanced techniques to speed up the type-reduction process or eliminate the high computational cost inherent in existing methods will enhance the system's portability to affordable devices and real-time access to information.

Declarations

Author contribution statement

Moses Ekpenyong: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper.

Philip Etebong: Performed the experiments; Analyzed and interpreted the data; Wrote the paper.

Tenderwealth Jackson: Contributed reagents, materials, analysis tools or data; Wrote the paper.

Funding statement

This research is funded by the Tertiary Education Trust Fund (TETFund) of Nigeria Research grant.

Competing interest statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.