We thank Drs Guo, Gao, Niu, and Zhang for their comments on the article by Fong and others (2018). They pointed out that the more classical methods, MW-MW and SR-MW
and SR-MW , which only make comparisons between
, which only make comparisons between  and
and 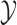 (paired observations) and between
(paired observations) and between 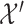 and
and 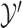 (unpaired observations) were useful alternatives to the proposed tests, MW-MW
(unpaired observations) were useful alternatives to the proposed tests, MW-MW and SR-MW
and SR-MW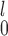 , which made comparisons between all
, which made comparisons between all 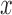 ’s and all
’s and all 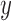 ’s. Dr Guo et al.’s recommendation was “to use MW-MW
’s. Dr Guo et al.’s recommendation was “to use MW-MW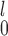 and SR-MW
and SR-MW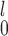 for
for 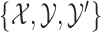 , while use MW-MW
, while use MW-MW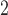 and SR-MW
and SR-MW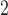 for
for 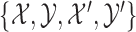 , especially when the correlation between the samples is high.” We agree that MW-MW
, especially when the correlation between the samples is high.” We agree that MW-MW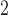 and SR-MW
and SR-MW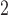 are important to study as alternative approaches, and aim to refine the recommendations in this response so that practitioners may find it easier to choose the appropriate methods.
are important to study as alternative approaches, and aim to refine the recommendations in this response so that practitioners may find it easier to choose the appropriate methods.
Before discussing power comparison, we would like to propose a variant of the MW-MW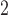 test. Since MW-MW
test. Since MW-MW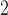 only makes comparisons within the paired subset and the unpaired subset, it is possible to perform permutation tests to obtain p-values to avoid inflated Type 1 error rates under small sample sizes (Tables A.1–A.4 of the supplementary material available at Biostatistics online). We will refer to this test as MW-MW
only makes comparisons within the paired subset and the unpaired subset, it is possible to perform permutation tests to obtain p-values to avoid inflated Type 1 error rates under small sample sizes (Tables A.1–A.4 of the supplementary material available at Biostatistics online). We will refer to this test as MW-MW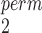 .
.
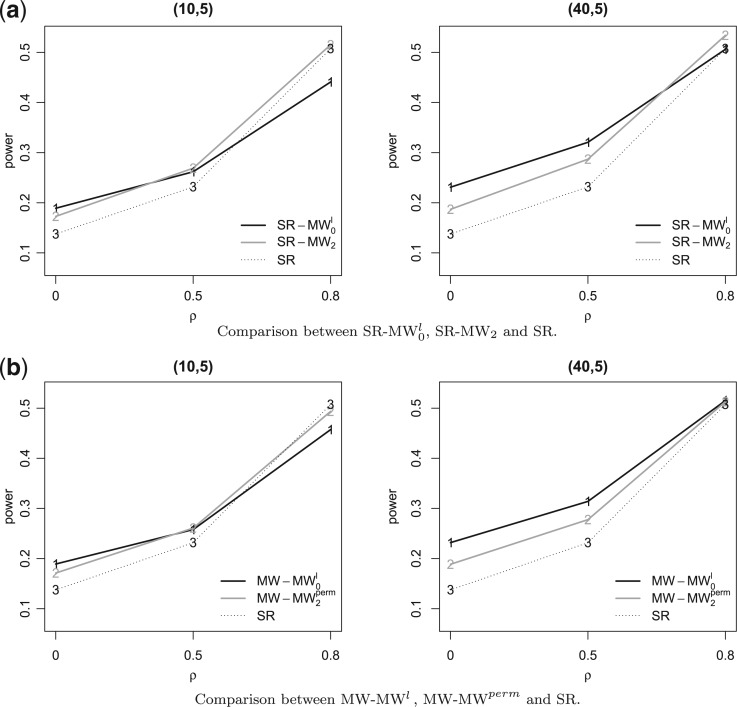
We study power comparison under four different distributional assumptions: normal (Table 1), logistic (Table B.1 of the supplementary material available at Biostatistics online), gamma (Table B.2 of the supplementary material available at Biostatistics online), and lognormal (Table B.3 of the supplementary material available at Biostatistics online). We also plot the results in Figure 1 and Figures B.1, B.2, and B.3 of the supplementary material available at Biostatistics online to help visualize these results. All estimates are based on 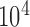 Monte Carlo replicates.
Monte Carlo replicates. 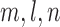 refer to the number of pairs, the number of independent
refer to the number of pairs, the number of independent 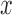 ’s and the number of independent
’s and the number of independent 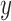 ’s, respectively. Three levels of correlation between the two samples are examined: 0, 0.5, and 0.8.
’s, respectively. Three levels of correlation between the two samples are examined: 0, 0.5, and 0.8.
Table 1.
Estimated power, normal distribution, 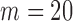
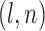
|
MW-MW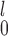
|
MW-MW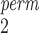
|
SR | SR-MW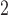
|
SR-MW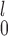
|
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.5 | 0.8 | 0 | 0.5 | 0.8 | 0 | 0.5 | 0.8 | 0 | 0.5 | 0.8 | 0 | 0.5 | 0.8 | |
| (10,5) | 19 | 26 | 46 | 17 | 26 | 49 | 14 | 23 | 51 | 17 | 27 | 52 | 19 | 26 | 44 |
| (10,10) | 20 | 28 | 47 | 18 | 27 | 51 | 14 | 23 | 51 | 19 | 29 | 53 | 20 | 28 | 46 |
| (40,5) | 23 | 31 | 52 | 19 | 28 | 51 | 14 | 23 | 51 | 19 | 29 | 53 | 23 | 32 | 51 |
Fig. 1.
Power comparison when the marginal distribution is normal. Sample sizes: 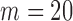 and
and 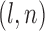 are given in the titles.
are given in the titles.
First, focusing on lines 2 and 3 in the figures, we see that SR-MW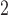 and MW-MW
and MW-MW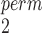 either outperform or closely match the performance of SR at all times. These empirical results are worth noting, because theoretically a test that combines two independent test statistics using weights proportional to the inverse of their variances is not always more powerful than each component test. Based on these results, we can narrow the choice down to be between SR-MW
either outperform or closely match the performance of SR at all times. These empirical results are worth noting, because theoretically a test that combines two independent test statistics using weights proportional to the inverse of their variances is not always more powerful than each component test. Based on these results, we can narrow the choice down to be between SR-MW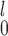 /MW-MW
/MW-MW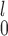 and SR-MW
and SR-MW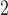 /MW-MW
/MW-MW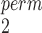 when there are unpaired observations from both samples.
when there are unpaired observations from both samples.
Now, focusing on lines 1 and 2 in the figures, we see that there is a clear trade-off between SR-MW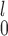 /MW-MW
/MW-MW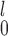 and SR-MW
and SR-MW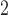 /MW-MW
/MW-MW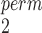 depending on
depending on  and sample sizes. This is true for normal, logistic, and gamma distributions (Figure 1 and Figures B1, B2 of the supplementary material available at Biostatistics online); for lognormal distributions, there is also a trade-off between MW-MW
and sample sizes. This is true for normal, logistic, and gamma distributions (Figure 1 and Figures B1, B2 of the supplementary material available at Biostatistics online); for lognormal distributions, there is also a trade-off between MW-MW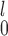 and MW-MW
and MW-MW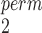 (Figure B3(b) of the supplementary material available at Biostatistics online), but SR-MW
(Figure B3(b) of the supplementary material available at Biostatistics online), but SR-MW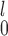 appears mostly preferable over SR-MW
appears mostly preferable over SR-MW (Figure B3(a) of the supplementary material available at Biostatistics online). The cause of the latter result can be attributed to the interesting fact that the SR test is not an efficient test for lognormal data (Table C.1 of the supplementary material available at Biostatistics online). When the SR test does not fully take advantage of the information in the paired data (
(Figure B3(a) of the supplementary material available at Biostatistics online). The cause of the latter result can be attributed to the interesting fact that the SR test is not an efficient test for lognormal data (Table C.1 of the supplementary material available at Biostatistics online). When the SR test does not fully take advantage of the information in the paired data (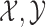 ), comparing
), comparing 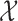 with
with 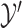 and
and 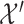 with
with 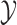 , as SR-MW
, as SR-MW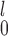 does, improves the efficiency of the overall test. The practical implication of this observation is that we should preprocess the data by applying proper transformation if the distributions appear highly skewed.
does, improves the efficiency of the overall test. The practical implication of this observation is that we should preprocess the data by applying proper transformation if the distributions appear highly skewed.
Our recommendation for the case when there are unpaired observations from both samples has two parts. If a simple rule of thumb is desirable, our recommendation is to choose SR-MW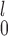 /MW-MW
/MW-MW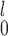 when
when 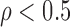 and SR-MW
and SR-MW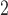 /MW-MW
/MW-MW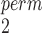 when
when 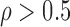 . On the other hand, if an optimal choice is important, we recommend doing a simulation study to find the most powerful approach. To make this a feasible option for practitioners, we provide an easy-to-use function, choose.test, in the R package chngpt. The only information the function needs is the sample sizes and the estimated first and second moments from the data, and it is fast, for example, it takes only 2 s to run on an Intel i7 processor clocked at 2.6GHz when
. On the other hand, if an optimal choice is important, we recommend doing a simulation study to find the most powerful approach. To make this a feasible option for practitioners, we provide an easy-to-use function, choose.test, in the R package chngpt. The only information the function needs is the sample sizes and the estimated first and second moments from the data, and it is fast, for example, it takes only 2 s to run on an Intel i7 processor clocked at 2.6GHz when 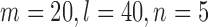 .
.
For the case when there are only unpaired observations from one sample (thus SR-MW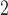 /MW-MW
/MW-MW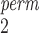 are not applicable), we recommend choosing between SR and SR-MW
are not applicable), we recommend choosing between SR and SR-MW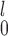 /MW-MW
/MW-MW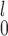 through the choose.test function, since there is a trade-off in power between the two tests depending on
through the choose.test function, since there is a trade-off in power between the two tests depending on 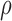 and sample sizes (Tables D.1–D.3 of the supplementary material available at Biostatistics online).
and sample sizes (Tables D.1–D.3 of the supplementary material available at Biostatistics online).
Lastly, given the choice between SR-MW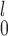 and MW-MW
and MW-MW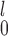 , we recommend SR-MW
, we recommend SR-MW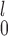 if a monotone transformation can be performed on both samples so that the distributions from both samples are not too skewed. If that is not possible or desirable, for example, when one sample has a highly skewed distribution while the other does not, MW-MW
if a monotone transformation can be performed on both samples so that the distributions from both samples are not too skewed. If that is not possible or desirable, for example, when one sample has a highly skewed distribution while the other does not, MW-MW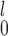 is preferred because it is a more robust test and invariant to monotone transformations applied to both samples. When using MW-MW
is preferred because it is a more robust test and invariant to monotone transformations applied to both samples. When using MW-MW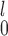 , one should proceed with caution as Type 1 error rates may be inflated when sample sizes are small (Tables D.4–D.6 of the supplementary material available at Biostatistics online). Similar arguments can be applied to the choice between SR-MW
, one should proceed with caution as Type 1 error rates may be inflated when sample sizes are small (Tables D.4–D.6 of the supplementary material available at Biostatistics online). Similar arguments can be applied to the choice between SR-MW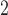 and MW-MW
and MW-MW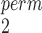 , except that there is no concern of inflated Type 1 error rates here.
, except that there is no concern of inflated Type 1 error rates here.
The chngpt package is available from the Comprehensive R Archive Network, and the Monte Carlo study code can be downloaded at https://github.com/youyifong/response_to_letter_on_rank.
Supplementary Material
Acknowledgments
The authors are grateful to Lindsay N. Carpp for help with editing. Conflict of Interest: None declared.
Funding
This work was supported by R01-AI122991, R01-GM106177, UM1-AI068635, UM1-AI068618, and OPP1099507.
References
- Fong, Y., Huang, Y., Lemos, M. P. and Mcelrath, M. J. (2018). Rank-based two-sample tests for paired data with missing values. Biostatistics, 19, 281–294. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.