ORGAN DOSE ESTIMATION ACCOUNTING FOR UNCERTAINTY FOR PEDIATRIC AND YOUNG ADULT CT SCANS IN THE UNITED KINGDOM

Abstract

Since our previous publication of organ dose for the pediatric CT cohort in the UK, there have been questions about the magnitude of uncertainty in our dose estimates. We therefore quantified shared and unshared uncertainties in empirical CT parameters extracted from 1073 CT films (1978–2008) from 36 hospitals in the study and propagated these uncertainties into organ doses using Monte Carlo random sampling and NCICT organ dose calculator. The average of 500 median brain and marrow doses for the full cohort was 35 (95% confidence interval: 30–40) mGy and 6 (5–7) mGy, respectively. We estimated that shared uncertainty contributed ~99% of coefficient of variation of median brain doses in brain scans compared to unshared uncertainty (1% contribution). We found that the previous brain doses were slightly underestimated for <1990 and overestimated for >1990 compared to the results in the current study due to the revised CTDI models based on CT films.

INTRODUCTION

Computed tomography (CT) is one of the crucial diagnostic tools in modern medicine. However, exposure to ionizing radiation has been a concern especially for pediatric patients due to the higher radio-sensitivity and longer life expectancy in children⁽¹⁾. Several epidemiological studies have reported an increased incidence of different types of cancer in pediatric patients after CT scans^(2–5). The retrospective cohort study of pediatric CT in the UK⁽³⁾, the first epidemiological study of CT risk based on organ dose estimates, reported a positive dose–response relationship for brain tumors and leukemia based on the analysis of ~180 000 children, adolescents and adults younger than 22 years of age after CT scans conducted between 1985 and 2008.

Retrospective organ dose estimation for a large-size patient cohort who underwent CT scans decades ago poses several challenges. Obtaining access to archived CT films or image files may not be practical as films may have been destroyed, and even if available it may be impractical to retrieve them from a resource perspective. Even when films are available, it is challenging to manually extract scan parameters from a large number of CT films for dosimetry. As an alternative, organ dose for retrospective cohorts can be estimated based on national surveys of scanning parameters such as tube current, tube potential, computed tomography dose index (CTDI) and dose–length product (DLP) that are provided from CT scanners^(6–9). Unfortunately, not many countries have performed national-scale surveys with a level of quality sufficient for retrospective organ dose reconstruction. The most comprehensive national CT surveys to date are the ones conducted in the UK in 1989⁽¹⁰⁾, 2003⁽¹¹⁾ and 2011⁽¹²⁾. The surveys for 1989 and 2003 were the basis of organ dose reconstruction⁽⁶⁾ for the study of CT risk in the UK⁽³⁾.

Since the publication of the organ dose database for the UK CT cohort⁽⁶⁾ based on nationwide surveys of hospital protocols, there have been questions about uncertainty in the dose estimates and its impact on risk analysis^{(13, 14)}. In the current study, we identified and quantified the sources of uncertainty in CT parameters based on 1073 CT films or Digital Imaging and Communications in Medicine (DICOM) files extracted from a subset of the hospitals participating in the UK CT cohort study. Temporal trends in tube current and CTDI from this set of CT films were recently published⁽¹⁵⁾. To quantify the magnitude of the uncertainties in our dose estimates we propagated uncertainties in different scan parameters into organ dose estimates by computing multiple realizations of plausible doses using a Monte Carlo sampling technique^(16–18) and an in-house organ dose calculation tool⁽¹⁹⁾. Uncertainties included in some scan parameters are shared to varying degrees by subsets of the cohort, but other uncertainties are specific to each subject (i.e. unshared uncertainty). We categorized the uncertainties as whether they were shared or unshared errors, to facilitate assessment of the potential impact of the uncertainties on the risk coefficients and their confidence intervals. The updated organ doses were then compared with the previous cohort doses⁽⁶⁾ estimated from the two UK surveys.

MATERIALS AND METHODS

In the UK CT cohort study, five parameters are available for each cohort member: age, gender, scan year, hospital and scan type (e.g. head, chest, abdomen). Table 1 summarizes the number of scans for different scan types in the UK CT study. For organ dose calculations in the current study, we adopted an algorithm that we previously published⁽¹⁹⁾. The algorithm requires the following parameters dependent upon the patient and the CT scanner: age and gender, the CT slice locations of scan start and scan end, tube potential (kVp), CTDI_vol and type of CTDI phantom (16 or 32 cm) used for deriving CTDI_vol. We quantified uncertainties in these parameters except age and gender and incorporated them into organ dose in three steps. First, we developed probability distributions and regression models for scan parameters using the CT parameters collected from the UK hospitals. We separated uncertainties in different parameters into shared and unshared uncertainties. Second, 500 realizations of scan parameters for each scan (e.g. three sets of scan parameters were used in case of three repeated scans) in the cohort were generated using a Monte Carlo random sampling approach⁽¹⁶⁾ that allows for the sampling of shared and unshared parameters. Third, organ doses were calculated for each realization of each scan using an in-house CT organ dose calculator⁽¹⁹⁾.

Table 1.

Number of scans for different scan types in the UK CT cohort.

Scan type	Number of scans	Percent (%)
Brain	174 144	54.76
Abdomen	22 529	7.08
Unknown	22 297	7.01
Chest	21 796	6.85
Partial brain	20 933	6.58
Extremity	18 865	5.93
Pelvis	12 573	3.96
Spine	5820	1.83
Facial bones	5363	1.69
Neck	3551	1.12
High resolution CT	2586	0.81
C-spine	1937	0.61
L-spine	1906	0.6
Hip	1647	0.52
Whole body	1310	0.41
Shoulder	471	0.15
T-spine	264	0.08
Total	317 992	100.0

Modeling uncertainty in scan parameters

Extraction of scan parameters from CT data

We retrieved 1073 CT films or DICOM file sets from 36 hospitals out of approximately 100 hospitals that participated the UK CT cohort study. The age of the CT patients ranged from 0 to 19 years old at the time of CT scan, which were conducted between 1978 and 2008. We manually extracted the manufacturer and model of CT scanners, tube current–time product (mAs) (averaged when tube current modulation used) and tube potential (kVp). To extract scan start and end locations from CT images, we obtained whole body CT images of an adult male⁽²⁰⁾ with a slice interval of 1 cm, numbered the slices from the top of the head to the bottom of the feet (e.g. 1–172), and recorded the slice number of axial image visually matching patient images for each scan set. For example, slice #1 to slice #24 were recorded for a head CT scan, meaning scan ranged 0–24 cm from the top of the head. A summary of the CT film data was recently published⁽¹⁵⁾ but detailed evaluation of the scan location was not included in that analysis. It was, however, used in the assessment of the uncertainties (see below) in the current study.

Parameter probability distributions

We developed probability distributions for the following four parameters: tube potential, pitch, scan location (scan start and scan length) and scan type. First, we developed probability distributions by analyzing the association between tube potential values (<120, 120, 120–130, 130–140 kVp) and parameters available from the UK CT cohort (scan year, scan type and patient age) using multinomial logistic regression models. Second, since pitch values were not available from the CT films, either a fixed value of 1.0 was used or parameters for a triangular distribution were derived from the UK CT dose surveys^{(10, 11)} depending on scan type. A fixed pitch value of 1.0 was used for full head, extremity, partial head and spine scans. A triangular distribution spanning from 1.0 to 2.0 with mode of 1.5 was used for abdomen, pelvis, chest and neck scans.

Third, probability distributions for scan start location and scan length for each scan type were developed by combining the scan locations extracted from the UK CT data using the method described in Extraction of scan parameters from CT data and approximate estimates provided by a practicing pediatric radiologist from the UK (K.McH.). The radiologist’s estimates were used as uniform prior distributions in conjunction with the empirical scan location data to estimate distributions of scan location. Scan start location and scan length were assumed to be normally distributed but truncated based on judgment and radiologist’s estimates to prevent simulating highly unlikely or unrealistic values. During simulation a scan start location and scan length were sampled from the truncated normal distribution for the scan type. The scan start location and scan length were added together to derive the scan end location. The scan start and end locations derived for an adult male height (172 cm) were then non-uniformly scaled down to the appropriate age using scan location scaling tables, which were developed based on the growth curve of different body parts (e.g. head/neck, torso and legs) of the reference size computational phantoms⁽²¹⁾.

Finally, we used the distribution of scan types (Table 1) for the cohort members of whom scan type is unknown (~7%, 22 297 scans out of 317 992 scans performed for 180 000 patients). In the previous dosimetry⁽⁶⁾, we averaged organ doses from all scan types for these unknown scans. In the current study, unknown body locations were simulated by a body location sampled from all possible scan types weighted by the relative number of scans (Table 1). A similar approach was used for CT scans defined generically as ‘spine’ scans, without specific locations. These cases were simulated by randomly selecting one of cervical spine, thoracic spine or lumbar spine weighted by the relative number of scans (Table 1).

Regression model of CTDI

A total of 794 scans out of 1073 scans were identified from the UK CT data, where scanner manufacturer and model (represented by scanner-specific normalized CTDI_w), tube potential (kVp) and current–time product were all available. By combining these parameters, we calculated CTDI_w (mGy) using the following equation:

$$\begin{array}{l}\mathrm{C}\mathrm{T}\mathrm{D}{\mathrm{I}}_{\mathrm{w}}\left(\mathrm{m}\mathrm{a}\mathrm{k}\mathrm{e},\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l},\mathrm{k}\mathrm{V}\mathrm{p},\mathrm{C}\mathrm{T}\mathrm{D}\mathrm{I}\mathrm{p}\mathrm{h}\mathrm{a}\mathrm{n}\mathrm{t}\mathrm{o}\mathrm{m}\right)\hfill \\ =\mathrm{n}\mathrm{C}\mathrm{T}\mathrm{D}{\mathrm{I}}_{\mathrm{w}}(\mathrm{m}\mathrm{a}\mathrm{k}\mathrm{e},\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l},\mathrm{k}\mathrm{V}\mathrm{p},\mathrm{C}\mathrm{T}\mathrm{D}\mathrm{I}\mathrm{p}\mathrm{h}\mathrm{a}\mathrm{n}\mathrm{t}\mathrm{o}\mathrm{m})\hfill \\ \times \left(\frac{I\times t}{100}\right)\hfill \end{array}$$ (1)

where $\mathrm{n}\mathrm{C}\mathrm{T}\mathrm{D}{\mathrm{I}}_{\mathrm{w}}(\mathrm{m}\mathrm{a}\mathrm{k}\mathrm{e},\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l},\mathrm{k}\mathrm{V}\mathrm{p},\mathrm{C}\mathrm{T}\mathrm{D}\mathrm{I}\mathrm{p}\mathrm{h}\mathrm{a}\mathrm{n}\mathrm{t}\mathrm{o}\mathrm{m})$ (mGy/100mAs) is the CTDI_w normalized to 100 mAs for a given scanner make and model, tube potential (kVp) and type of CTDI phantom (16 cm or 32 cm in diameter); $I\times t$ (mAs) is the product of the tube current $(I)$ and the single rotation time $(t)$. The values of nCTDI_w, were obtained for each scan from the previously published library⁽²²⁾ based on the scanner make, model, tube potential (kVp) and CTDI phantom type. We then multiplied the nCTDI_w by current-time product (mAs) to obtain CTDI_w.

We then derived a regression model for CTDI_w at 120 kVp and scan parameters available from the UK CT cohort (patient age, scan year, scan type and hospital). To maximize the sample size, we scaled CTDI_w at different tube potentials to 120 kVp based on the fact that weighted CTDI increases with tube potential to the power of 2.5⁽²³⁾. In organ dose calculations later, we scaled CTDI_w at 120 kVp sampled from the regression model back to original tube potentials. Based on the regression analysis reported in the previous paper⁽¹⁵⁾, we assumed that CTDI_w before 1990 would be constant and start decreasing after 1990 exponentially. Variation within hospitals, CT scan studies and residual variations (variation that is otherwise unexplainable by the parameters in our CTDI model) were also incorporated into the CTDI regression model.

Monte Carlo sampling of parameters

We used a Monte Carlo sampling method⁽¹⁶⁾ to generate ‘realizations’ of plausible parameters for each scan. Multiple realizations were generated for each scan while adhering to proper parameter sharing among cohort subgroups defined hierarchically by hospital, scan type and CT study. One ‘study’ was defined as a scan date for one patient in a given hospital possibly being scanned several times, either over the same body region (e.g. chest CT scan before and after contrasting medium injection) or different body regions (e.g. scan of the chest and the abdomen), on a given day. In those situations, scan parameters would be more likely to be similar than when scans occurred on different dates, possibly performed by different radiologists, or for different patients.

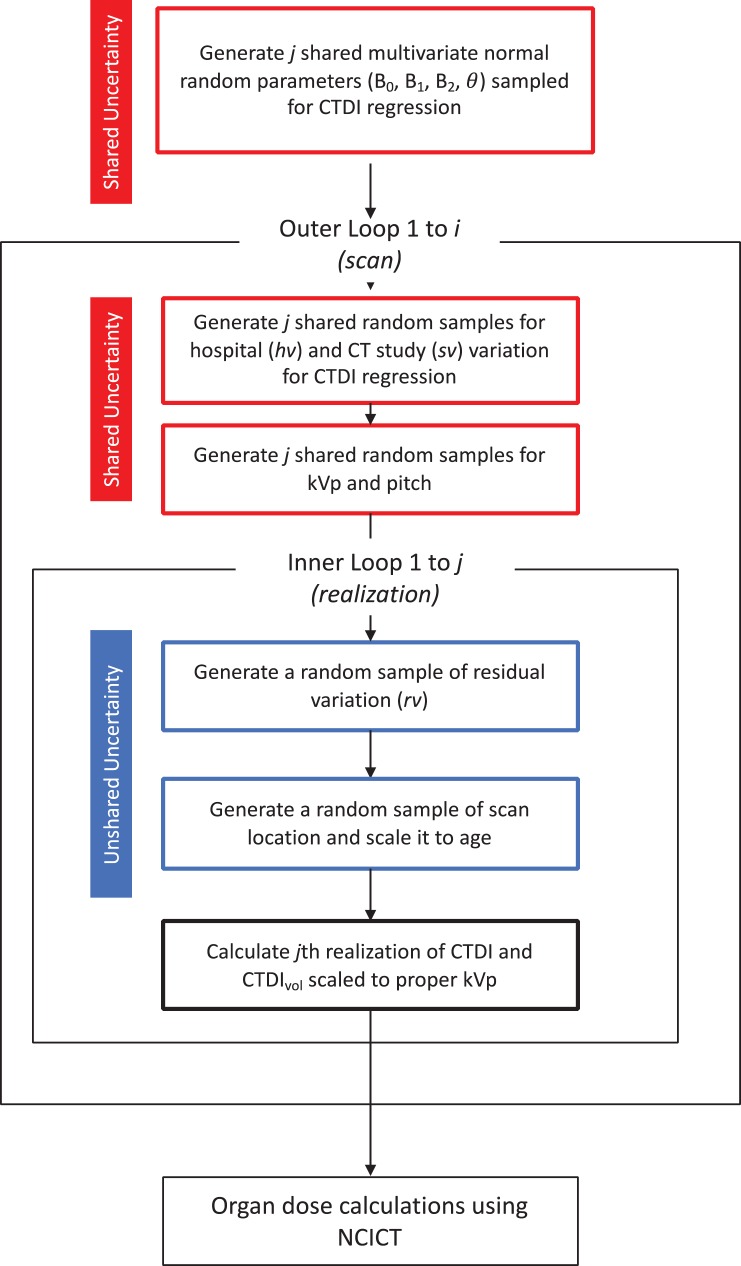
By consulting practicing pediatric radiologists, we separated uncertainties involved in different CT parameters into their respective shared and unshared components. The CTDI regression constant and coefficients were shared across realizations, but scan type coefficient was only shared by those with the same scan types across realizations. Hospital and study variations in the CTDI regression model were shared across realizations, but residual variations in the CTDI model were sampled independently (unshared). Tube potential (kVp) and pitch were shared by hospital and scan type, while scan start location and scan length were sampled independently (unshared). Figure 1 shows the workflow in parameter sampling where shared and unshared uncertainties were propagated into dose in different ways. A total of 500 realizations for 317 992 scans were generated using the sampling scheme by using the NIH Biowulf computer cluster at the National Institutes of Health (http://hpc.nih.gov).

Figure 1.

The workflow of the organ dose calculations by combining the Monte Carlo parameter sampling and NCICT organ dose calculator. Shared and unshared uncertainties in different scan parameters are incorporated in the process.

Organ dose calculation

We imported the 500 realizations of scan parameters into an in-house CT dose calculator, National Cancer Institute dosimetry system for Computed Tomography (NCICT)⁽¹⁹⁾. NCICT is based on a comprehensive library of organ dose conversion coefficients derived from a series of reference computational human phantoms combined with Monte Carlo transport of X-ray from a reference CT scanner. The program selects organ dose conversion coefficients based on patient age, gender, scan locations and X-ray spectrum, and then converts scan-specific CTDI_vol to organ dose. NCICT provides dose to 33 organs and tissues including active marrow. The program can import text files of input parameters and automatically generate output files of organ doses⁽¹⁹⁾. Over 5.2 × 10⁹ (317 992 scans × 500 realizations × 33 organs) organ doses were calculated using this process.

To efficiently analyze the large number of organ doses, we derived probability distribution functions (PDFs) (different from the probability distributions we derived from tube potential described in Parameter probability distributions) and then derived cumulative distribution functions (CDFs) from the full organ doses for major organs and scan types. We then quantified dosimetric uncertainties related to shared and unshared uncertainties in two ways: dose range (min and max) across all dose realizations and coefficient of variation (COV) among median doses of each dose realization. We expected that the higher dose uncertainty, the greater would be the dose range and COV.

To understand the contribution of shared and unshared uncertainty to dose variation, we conducted a sensitivity analysis. We first calculated 500 brain doses for the full cohort by using the 500 parameter realization sets after removing both shared and unshared uncertainties. We then recalculated 500 brain doses after removing shared uncertainties while adding unshared uncertainties. We compared dose range and COV from the two sets of doses with those from the data where both shared and unshared uncertainties were propagated. We also validated that shared uncertainties were actually shared in the final cohort dose as intended through calculating Pearson correlation coefficients for the first 1000 scans out of 317 992 scans with 500 brain dose realizations. We observed how the correlation coefficients changed as we grouped the 1000 scans by two key shared parameters, scan type $(\theta )$ and hospital $(hv)$. We expected that correlation coefficients would increase as we group the scans sharing uncertainties.

RESULTS

Probability distribution and regression models

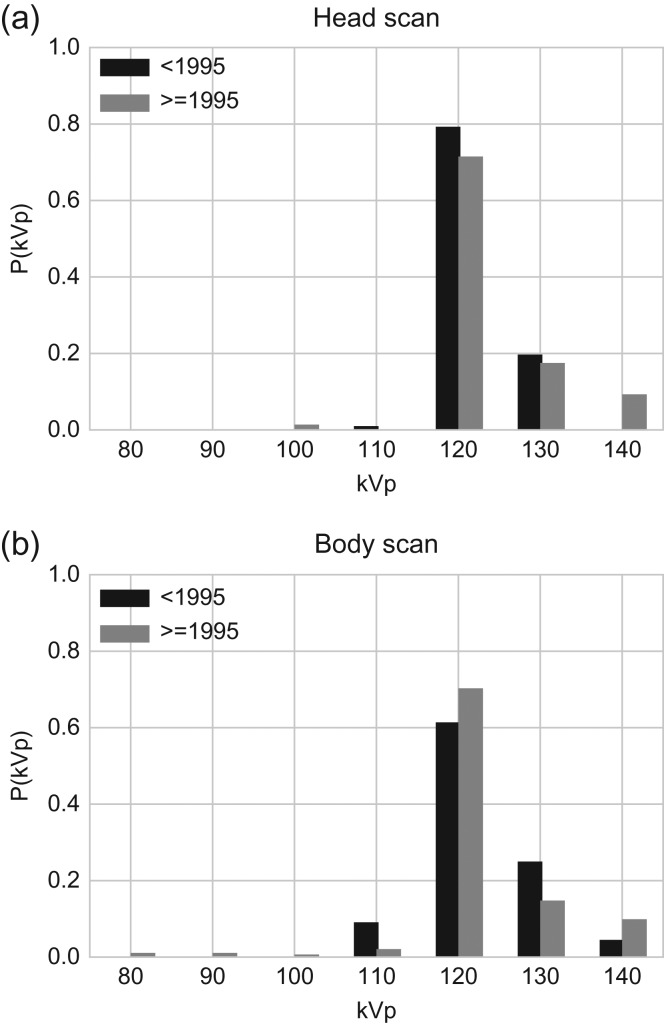
Based on the Akaike Information Criterion (AIC), we found that a model including scan year (<1995, 1995+) and scan type (head and body) had the best goodness of fit for tube potential. Head scans were limited to brain, partial brain and facial bone scans; all other scans were deemed body scans. No further improvement in AIC was obtained when accounting for patient’s age at scan. The probability distributions of tube potential (Figure 2) depict the high frequency of 120 kVp tube potential both before 1995 and 1995+ for head and body scans. The second most frequent tube potential was 130 kVp. A total of 20% (head) and 25% (body) of scans used 130 kVp before 1995. The ratio slightly decreased to 18% (head) and 15% (body) for 1995+. Only 2% (head) and 3% (body) of scans used a tube potential smaller than 120 kVp 1995+.

Figure 2.

Probability distributions for tube potentials for (a) head and (b) body scans by two scan periods (before and after 1995).

From the CTDI_w at 120 kVp derived from CT parameters, we developed the following regression model:

$$\begin{array}{l}\mathrm{C}\mathrm{T}\mathrm{D}{\mathrm{I}}_{\mathrm{w},120}\\ =e^{B_0+B_1\left(age-10\right)+B_2\left(syr-2000\right)+\theta \left(scan\right)+hv+sv+rv}\end{array}$$ (2)

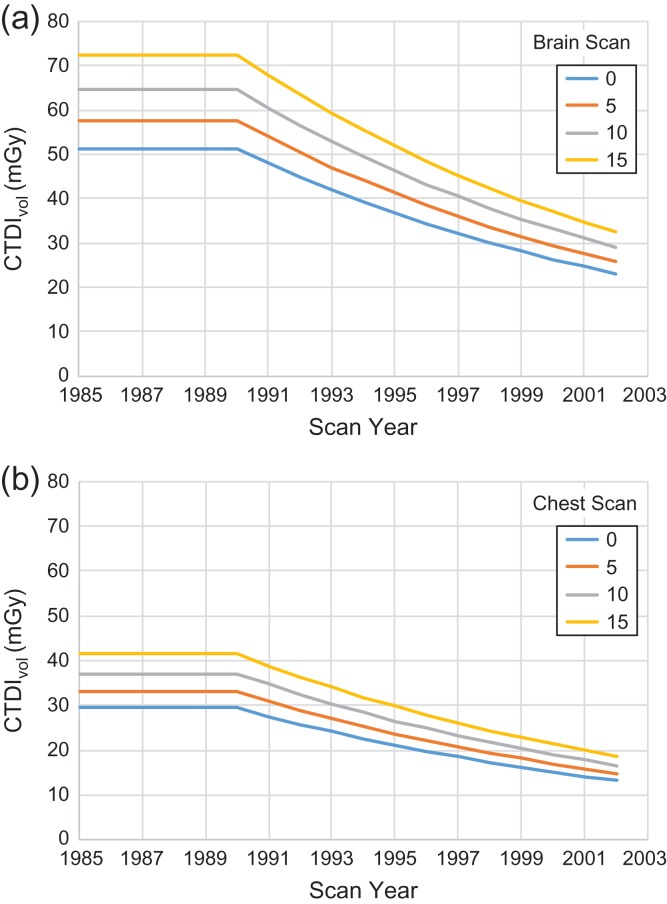
where CTDI_w,120 is the weighted CTDI at 120 kVp, $B_0$ is the intercept for head or body scan, $B_1$ and $B_2$ are coefficients on age and syr (scan year truncated at 1990) variables, respectively, and $\theta$ is scan indicator, a function of scan type. The $B_0$, $B_1$, $B_2$ and $\theta$ are tabulated in Table 2a. The remaining three parameters model shared uncertainty within hospital $(hv)$, CT scan study $(sv)$ and residual random unshared variation $(rv)$, of which distribution type, mean and standard deviation (SD) are shown in Table 2b. The normal deviates used to generate samples for these variables were constrained to the 98% confidence interval to remove unrealistic outliers. The CTDI_vol for (a) brain and (b) chest scan at different age group was calculated from the regression model (Figure 3).

Table 2a.

Parameters for multivariate normal distribution used in the regression model of CTDI_w at 120 kVp. These parameters are shared by all across 500 realizations but $\theta$ was only shared by those with the same scan types.

Parameter	Description	Mean	Standard error
$B_0$ (head)	Intercept	3.500	0.060
$B_0$ (body)	Intercept	3.750	0.060
$B_1$	Coefficient on age variable	0.023	0.004
$B_2$	Coefficient on scan year variable	−0.067	0.005
$\theta$ (head)	Full head scans indicator (reference)	0.000	NA
$\theta$ (abdomen)	Abdomen scans indicator	−0.489	0.077
$\theta$ (pelvis)	pelvis scans indicator	−0.602	0.087
$\theta$ (chest)	Chest scans indicator	−0.807	0.058
$\theta$ (extremity)	Extremity scans indicator	−1.073	0.091
$\theta$ (neck)	Neck scans indicator	−0.744	0.086
$\theta$ (partial head)	Partial head scans indicator	−0.396	0.061
$\theta$ (spine)	Spine scans indicator	−0.242	0.153

Table 2b.

Variations for hospitals, CT scan studies and residual used in the regression model of CTDI_w at 120 kVp. All variations were shared across 500 realizations except residual variations. The normal deviates used to generate samples for these variables were constrained to the 98% confidence interval.

Parameter	Description	Unshared			Shared
		Distribution	Mean	SD	Distribution	Mean	SD
$hv$	Variation within a hospital	—	—	—	Normal	0.000	0.241
$sv$	Variation within a study	—	—	—	Normal	0.000	0.359
$rv$	Residual random variation	Normal	0.000	0.249	—	—	—

Figure 3.

Temporal changes of CTDI_vol for (a) brain and (b) chest scan at different age groups.

Dose realizations for full cohort

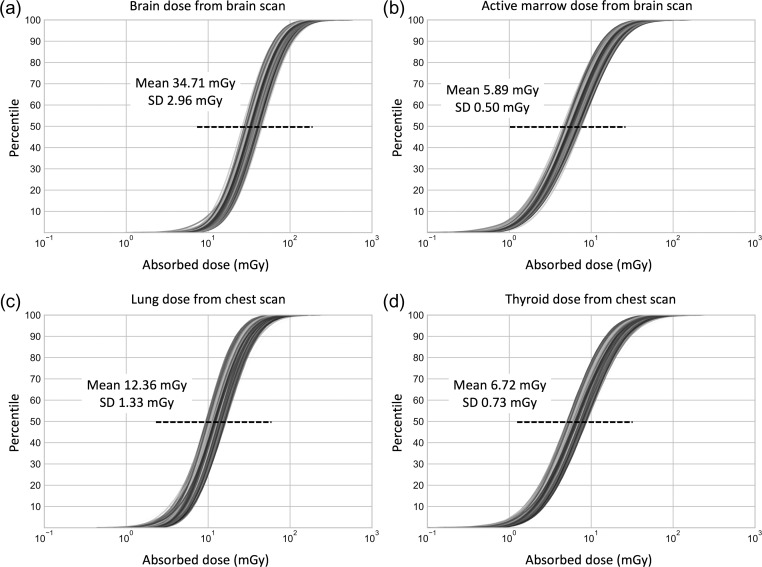
Figure 4 shows the CDFs of the 500 dose realizations for (a) brain and (b) active marrow from brain scans and (c) lung and (d) thyroid from chest scans. The mean of 500 median doses for brain and active marrow from brain scans are 35 (95% confidence interval: 30–40) mGy and 6 (5–7) mGy, respectively. For chest scans, the mean of 500 median doses for the lungs and thyroid are 12 (10–15) mGy and 7 (6–8) mGy, respectively. COV for both brain and active marrow doses in brain scans are 8.5%. For lung and thyroid dose resulting from chest scans, COV are 10.8 and 10.9%, respectively.

Figure 4.

The cumulative distribution functions (CDFs) of the 500 organ dose realizations for (a) brain and (b) active marrow in brain scan and (c) lung and (d) thyroid in chest scan. Mean and standard deviation are included in each plot.

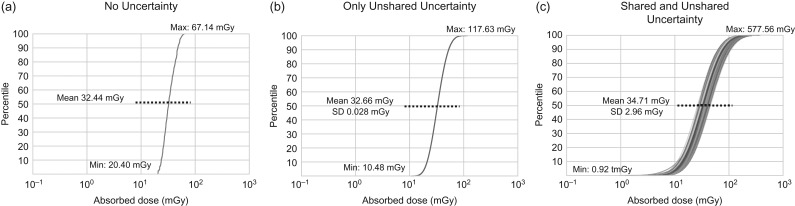
Figure 5 shows the impact of shared and unshared uncertainty on 500 brain doses in brain CT scan. When we removed both shared and unshared uncertainty, the median brain dose was 32 mGy with zero SD (Figure 5a), where 500 brain doses for each scan are identical. The range of full cohort doses was from 47 mGy (min 20 mGy–max 67 mGy) as sampled from this distribution constructed from the 500 scan realizations. When we introduced only unshared uncertainty, the mean of the median brain doses is 33 mGy with SD 0.028 mGy (Figure 5b). The range of full cohort doses increased to 108 mGy (10–118 mGy). With both shared and unshared uncertainties combined (Figure 5c), which is the same case with Figure 4a, the average of median doses is 35 mGy with SD 3 mGy with the dose spread of 577 mGy (1–578 mGy).

Figure 5.

The cumulative distribution functions (CDFs) of the 500 organ dose realizations for brain in brain scans (a) when both shared and unshared uncertainties are removed, (b) when only unshared uncertainties are included and (c) when both shared and unshared uncertainties are included.

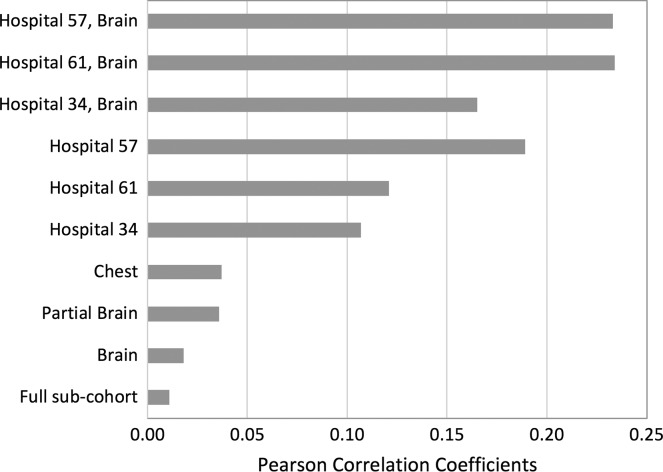
Figure 6 shows changes in Pearson correlation coefficients as we group the scans by shared parameters: scan type and hospital. The correlation coefficient for the full 1000 scans without any grouping was 0.01. By grouping them by scan types (brain, partial brain and chest), we observe correlation coefficients increased to 0.02, 0.04 and 0.04, respectively. By grouping 1000 scans by the three most frequent hospitals (Hospitals 34, 61 and 57), the coefficients increase to 0.11, 0.12 and 0.19, respectively. By grouping scans by brain scan and the three hospitals, the coefficients increase to 0.17, 0.23 and 0.23, respectively. We confirmed that those shared parameters were actually shared in the sub groups as we intended in the sampling process of Figure 1.

Figure 6.

Pearson correlation coefficients among the 500 sub-cohort members by grouping based on different shared parameters: scan type and hospital.

DISCUSSION

In our dose calculations for brain and chest scans shown in Figure 4, we observed ~1.3-fold greater COV in organ doses from chest scans compared to those from brain scans. The key difference in parameter sampling between head and body scans is pitch: we used a fixed value of 1.0 for head scans but sampled from a triangular distribution for chest scans. Uncertainties in scan start and length also have a different impact on dose in head and body scans. The brain and active bone marrow (mainly distributed in cranium and mandible) are completely within the scan range in a head scan. However, for chest scans, the thyroid and bottom of the lungs are close to the scan start and end, respectively, which made those organ doses sensitive to the uncertainty in scan location.

Based on the sensitivity analysis (Figure 5) for brain dose in brain scans, we deducted that the impact of shared uncertainty is much greater than that of unshared uncertainty. The contribution of unshared uncertainty to the total COV is ~1%: 0.086% from unshared uncertainty in Figure 5b out of 8.528% from both shared and unshared uncertainty in Figure 5c. In terms of dose spread, adding unshared uncertainty increases the dose range by 2.3-fold: from 47 mGy in Figure 5a to 108 mGy in Figure 5b. Adding shared uncertainties to Figure 5b increase the dose range by 5.3-fold: from 108 mGy in Figure 5b to 577 mGy in Figure 5c. Therefore, shared uncertainty has about twice greater impact on total dose spread than unshared uncertainty. The results revealed that to increase the accuracy in brain dose in brain CT scans, it will be more efficient to focus on reducing uncertainty in shared parameters such as CTDI_vol, tube potential and pitch rather than unshared parameters. However, we believe the contribution may differ for other scan types.

We compared our revised organ doses with the previous data that were published in 2012⁽⁶⁾. Table 3 shows the median, 2.5th, and 97.5th percentile of all 500 brain and active marrow doses in brain scans for the total scans in the cohort by three time-periods (<1990, 1990–1999 and ≥2000) and age groups. In the scans before 1990 and 1990–1999, age-averaged organ doses are shown but age-dependent organ doses are tabulated for the time period ≥2000. The organ doses we published previously⁽⁶⁾ are tabulated in Table 4, which shows the median, 2.5th, and 97.5th percentile of a single brain and active marrow doses for the total scans. We found that the age-averaged brain median dose <1990 in the previous dosimetry was ~20% smaller than the values given in the current study. This is because our previous CTDI_vol values⁽⁶⁾ based on the UK national surveys were smaller than the values in the current study obtained from CT film data. The brain dose ≥2000 in the previous dosimetry is up to 54% (age 10–14) greater than the dose in the current study because the continuous reduction of CTDI_vol after 1990 (Figure 3) observed from CT films was not accounted for in the previous dosimetry. The active marrow doses in the previous dosimetry are comparable to those in the current study.

Table 3.

Dose to the brain and active marrow for brain scans by three time-periods and age group, which was extracted from the 500 dose realizations simulated in the current study.

Scan year	Age	Brain dose (mGy)			Active Marrow dose (mGy)
		Median	2.5th	97.5th	Median	2.5th	97.5th
<1990	Age-average	52	15	173	11	2	45
1990–1999	Age-average	38	11	132	7	1	31
≥2000	0–4	24	7	80	8	2	26
	5–9	24	7	80	6	2	21
	10–14	26	8	87	4	1	14
	≥15	29	9	98	2	1	8

Table 4.

Dose to the brain and active marrow in brain scans by three time periods, which was extracted from the previous cohort dose⁽⁶⁾ with no uncertainty included.

Scan year	Age	Brain dose (mGy)			Active Marrow dose (mGy)
		Median	2.5th	97.5th	Median	2.5th	97.5th
<1990	Age-average	41	32	56	11	1	17
1990–1999	Age-average	41	32	56	7	1	17
≥2000	0–4	28	23	56	9	8	17
	5–9	34	28	42	8	7	13
	10–14	40	35	42	6	5	7
	≥15	38	32	44	2	1	6

There are a number of limitations in the current study. First, the parameter probability distributions and regression model were derived from a small number of empirical data representing <1% of the total scans in the cohort. However, this is the only set of such scans that we are aware of as it is extremely time consuming to retrieve CT films from hospitals and manually extract scan parameters from the printed films especially for the time period before 2000 when electronic archiving systems were not yet implemented. Some scan parameters such as pitch were not available on CT film or DICOM data, so it was necessary to use UK national surveys. However, we attempted to include uncertainties in all scan parameters including pitch into the revised dose calculations, which we consider a strength of the current study. Another limitation was that we did not account for tube current modulation technique (~5% of scans among the CT film data). Some organ doses in chest (e.g. lung) or abdominal scans might be over-estimated by simplifying tube current variations⁽¹⁹⁾. However, it must be noted that the simplification may have less impact on head CT scans (~60% of the scans in the UK CT cohort) compared with body scans and we are limiting our risk analysis to brain cancer and leukemia in brain scans because of limited number of other cancer cases⁽³⁾. Lastly, we used organ dose conversion coefficients derived from the computational human phantom series with reference body size because body size measurement was not available from the cohort data. However, we plan to incorporate the uncertainty from the variation in body size in the future dosimetry revision by using the body size-dependent computational phantom library⁽²⁴⁾.

CONCLUSION

Using parameter probability distributions and regression models derived from empirical data collected from the subset of participating hospitals in the UK CT cohort study, we have now incorporated uncertainties in CT parameters into our organ dose estimates. This new set of dose estimates revises and augments the previous set of organ dose estimates in which no uncertainties were taken into account. A total of 500 realizations of organ dose were calculated for each scan in the cohort using a Monte Carlo random sampling approach combined with NCICT organ dose calculator. We learned from the sensitivity analysis that in case of brain dose in brain scan shared uncertainties have a major impact on the resulting dose uncertainty compared to unshared uncertainty. We also found that the previous brain doses were slightly underestimated for <1990 and slightly overestimated for >1990 compared to the revised dosimetry results of the present study. A risk analysis using the updated doses is underway to evaluate the impact of dose uncertainties on the risk coefficients and their confidence intervals in the UK pediatric CT cohort. The procedure we developed to quantify uncertainty from dosimetric parameters and propagate them into dose can be applied to other epidemiological studies of medical exposures.

FUNDING

This work was funded by the intramural program of the National Institutes of Health, National Cancer Institute, Division of Cancer Epidemiology and Genetics. This work utilized the computational resources of the NIH HPC Biowulf cluster (http://hpc.nih.gov).