Conversion of Existing Calorimetrically Determined Thermodynamic Properties to the Basis of the International Practical Temperature Scale of 1968

Abstract

Formulas are derived for converting the relative enthalpy, heat capacity, entropy, and Gibbs energy from the basis of one practical temperature scale to the basis of another, when these properties on either scale have been derived from calorimetric measurements of enthalpy as though that scale were the thermodynamic one. These formulas are directly applicable for converting certain other properties as well. The conversion relates the values of the property at the same numerical temperature on both scales. The formulas, given as exact infinite series, are applicable to widely differing scales, one of which may vary linearly with a temperature-measuring quantity such as electrical resistance. However, great simplification is well within most calorimetric accuracy when the conversion is from the International Practical Temperature Scale of 1948 to the corresponding scale of 1968, which has recently replaced it, provided the heat capacity is not changing abnormally rapidly, as in a transition region. For convenient application to conversion between these two scales, relatively simple numerical equations are derived giving the differences between the two scales at temperatures from 90 K to 10,000 K. The problem of avoiding the introduction of discontinuities with temperature in converted tables, arising from the existing discontinuities in the temperature derivative of the differences between the two scales, is discussed.

1. Introduction

The International Practical Temperature Scale of 1968 (“IPTS–68”) was adopted in 1968 [1]¹ as a replacement for the corresponding scale of 1948 (amended edition of 1960) (“IPTS–48”). The IPTS–68 serves the same general purposes as the IPTS–48, but better: its specification is more consistent with current experimental capabilities for reproducing temperature, it more closely approximates the thermodynamic temperature scale, and it extends the temperature range downward (from approximately 90 K in the IPTS–48 to approximately 14 K in the IPTS–68).

The great preponderance of quantitative macroscopic properties of matter vary appreciably with temperature. As a consequence, it will be of interest and concern as to the extent to which numerous existing values of these properties, expressed in reference to temperatures on the IPTS–48 or an earlier scale, would change if referred to temperatures on the IPTS–68. In the case of the most accurate values it will be desirable to make the actual conversion – for the sake of future consistency, for facilitating direct comparison with future values expressed in reference to the IPTS–68, and for better thermodynamic accuracy when this is significant. In what will undoubtedly be the more common case of less accurate values, one will want to know the magnitudes of the errors neglected if such a conversion is not made. Incidentally, tables of thermodynamic properties of ideal gases derived statistical-mechanically from molecular-constant data are based on the thermodynamic temperature scale (as well as on the values of the physical constants used), and are hence independent of any practical temperature scale.

This article is limited to a consideration of the more common thermodynamic properties derived from calorimetric data – enthalpy, heat capacity, entropy, and Gibbs (free) energy – with particular attention to the substitution of the IPTS–68 for the IPTS–48 as a temperature basis. The differences between these two scales (listed numerically in table 4 of this article) are not so large but that very simple procedures which have been previously used,² and which are virtually self-evident, are adequate within the accuracy of most existing calorimetric data. However, it seems worthwhile to outline systematically the rigorous conversion procedures, which may be required not only in regions of sharp transitions but also in those cases where the correction terms are large, as when one is converting from an arbitrary temperature scale such as one related very simply (for convenience) to thermometer resistance, thermocouple electromotive force, or radiative brightness.

Table 4. Approximate difference in the value of temperature, and its temperature derivative, given by the International Practical Temperature Scales of 1968 and 1948.

(The unit of temperature is the kelvin. For both scales, T(K) = t(°C) +273.15.)

T68	T68 – T48	d(T68 – T48)/dT68
90	+0.0076	+0.0022
90.188	.0080	.0021
91	.0095	.0017
92	.0110	.0013
93	.0121	.0008
94	.0127	.0005
95	.0130	.0002
96	.0130	–.0001
97	.0128	–.0004
98	.0123	–.0006
99	.0116	–.0008
100	.0108	–.00089
102	.0088	–.00112
104	.0064	–.00124
106	.0038	–.00130
108	.0012	–.00130
110	–.0013	–.00125
112	–.0038	–.00116
114	–.0060	–.00106
116	–.0080	–.00092
118	–.0097	–.00078
120	–.0111	–.00063
122	–.0122	–.00046
124	–.0129	–.00030
126	–.0134	–.00015
128	–0.0135	0.00000
130	–.0134	+.00015
132	–.0129	.00028
134	–.0122	.00041
136	–.0113	.00052
138	–.0102	.00062
140	–.0088	.00071
142	–.0073	.00079
144	–.0057	.00086
146	–.0039	.00092
148	–.0020	.00096
150	.0000	.00100
155	+.0050	.00103
160	.0102	.00102
165	.0152	.00096
170	.0197	.00087
175	.0238	.00075
180	.0272	.00061
185	.0299	.00047
190	.0318	.00032
195	.0331	.00017
200	.0336	.00005
205	.0335	–.00009
210	.0328	–.00020
215	.0316	–.00029
220	+0.0299	–0.00038
225	.0278	–.00045
230	.0254	–.00051
235	.0227	–.00056
240	.0198	–.00059
245	.0168	–.00061
250	.0137	–.00062
255	.0105	–.00062
260	.0074	–.00061
265	.0044	–.00058
270	.0016	–.00054
273.15	.0000	–.00050
275	–.0009	–.00047
280	–.0031	–.00041
285	–.0050	–.00035
290	–.0066	–.00029
295	–.0079	–.00023
298.15	–.0085	–.00020
300	–.0089	–.00018
305	–.0096	–.00013
310	–.0101	–.00008
315	–.0104	–.00003
320	–.0105	+.00001
325	–.0103	.00006
330	–.0099	.00009
335	–0.0093	+0.00013
340	–.0086	.00016
345	–.0077	.00020
350	–.0066	.00023
355	–.0054	.00026
360	–.0041	.00028
365	–.0026	.00030
370	–.0010	.00033
373.15	.0000	.00034
37S	+.0006	.00035
380	.0024	.00036
385	.0043	.00038
390	.0062	.00039
395	.0082	.00041
400	.0103	.00042
410	.0146	.00044
420	.0190	.00045
430	.0235	.00045
440	.0280	.00045
450	.0325	.00045
460	.0369	.00044
470	.0413	.00043
480	.0454	.00041
490	.0494	.00039
500	.0532	.00037
510	.057	.0003
520	.060	.0003
530	.063	.0003
540	.066	.0003
550	.068	.0002
560	.070	.0002
570	.072	.0002
580	.074	.0001
590	.075	.0001
600	.076	.0001
610	.076	.0001
620	.077	.0000
630	.077	.0000
640	.077	.0000
650	.077	.0000
660	.076	.0000
670	.076	.0000
680	.076	.0000
690	.075	.0000
692.73	.075	.0000
700	+0.075	0.0000
710	.074	.0000
720	.074	.0000
730	.074	.0000
740	.075	+.0001
750	.076	.0001
760	.077	.0001
770	.079	.0002
780	.081	.0003
790	.084	.0003
800	.088	.0004
810	.093	.0005
820	.098	.0006
830	.105	.0007
840	.113	.0009
850	.123	.0010
860	.134	.0012
870	.146	.0013
880	.160	.0015
890	.176	.0017
900	.194	.0019
903.89	.202	a.0020
		b.0027
910	.218	.0027
920	.245	.0027
940	.300	.0027
960	.354	.0027
980	.409	.0027
1000	.464	.0028
1020	.519	.0028
1040	.575	.0028
1060	.631	.0028
1080	.687	.0028
1100	.743	.0028
1120	.800	.0028
1140	.857	.0028
1160	.914	.0029
1180	.971	.0029
1200	1.029	.0029
1220	1.086	.0029
1235.08	1.130	.0029
1240	1.144	.0029
1260	1.202	.0029
1280	1.261	.0029
1300	1.319	.0029
1320	+1.378	+0.0029
1337.58	1.430	b.0030
		c.0016
1350	1.45	.0016
1375	1.49	.0016
1400	1.53	.0016
1425	1.57	.0017
1450	1.61	.0017
1475	1.66	.0017
1500	1.70	.0017
1525	1.74	.0017
1550	1.78	.0017
1575	1.83	.0018
1600	1.87	.0018
1625	1.92	.0018
1650	1.96	.0018
1675	2.01	.0018
1700	2.05	.0019
1725	2.10	.0019
1750	2.15	.0019
1775	2.20	.0019
1800	2.24	.0019
1825	2.29	.0020
1850	2.34	.0020
1875	2.39	.0020
1900	2.44	.0020
1925	2.49	.0020
1950	2.54	.0021
1975	2.60	.0021
2000	2.65	.0021
2050	2.75	.0021
2100	2.86	.0022
2150	2.97	.0022
2200	3.08	.0022
2250	3.19	.0023
2300	3.31	.0023
2350	3.43	.0024
2400	3.55	.0024
2450	3.67	.0024
2500	3.79	.0025
2600	4.0	.003
2700	4.3	.003
2800	4.6	.003
2900	4.8	.003
3000	5.1	.003
3100	+5.4	+0.003
3200	5.7	.003
3300	6.0	.003
3400	6.3	.003
3500	6.6	.003
3600	7.0	:003
3700	7.3	.003
3800	7.6	.004
3900	8.0	.004
4000	8.3	.004
4100	+8.7	+0.004
4200	9.1	.004
4300	9.4	.004
4400	9.8	.004
4500	10.2	.004
4600	10.6	.004
4700	11.0	.004
4800	11.4	.004
4900	11.8	.004
5000	12.3	.004
5500	+14.	+0.005
6000	17.	.005
6500	19.	.005
7000	22.	.005
7500	25.	.006
8000	27.	.006
8500	30.	.006
9000	33.	.006
9500	37.	.006
10,000	40.	.006

See footnotes at end of table p. 470.

^aEq (81).

^bEq (86).

^cEq (89).

In section 2, conversion formulas (exact as infinite series) are derived for converting the thermodynamic properties named above to the basis of a new temperature scale, in terms of the difference between the two scales as a continuous function of temperature. The thermodynamic properties are assumed to be based on experimental measurements of enthalpy increments that span the entire temperature range of interest. Thus the correction to be applied to an enthalpy increment involves merely associating it with different boundary temperatures, but the corrections to the properties derived from the enthalpy (heat capacity, entropy, etc.) involve in addition what is essentially a repetition of the differentiation or integration as if the new temperature scale, not the old, corresponds to true thermodynamic temperatures. The formulas derived convert the properties at a given temperature on the old scale to those at the same numerical value of temperature on the new scale, thus preserving the “round” temperature values of most tables. When, instead, it is desired to make conversion to a fixed-point temperature whose values are different on the two scales, the additional step simply involves the variation of the given property with temperature on one of the scales, and can be readily carried out by standard thermodynamic procedures.

Some non-calorimetric properties may be converted to the basis of the new temperature scale using the same formulas derived in this article. For example, if the linear coefficient of thermal expansion is defined as (1/l) (dl/dt), then this coefficient or ln l can replace C_p or H, respectively.

In section 2.5 it is shown what modifications are needed when extrapolation of calorimetric data to 0 K has been effected by such means as the well-known “T³” law. Simple approximate correction formulas, obtained by dropping all terms of the exact infinite series that are of no practical value when the conversion is from the IPTS–48 to the IPTS–68 and outside sharp-transition regions, are given in section 2.6.

In section 3, a numerical equation giving the difference between the IPTS–68 and the IPTS–48 (T₆₈−T₄₈, or t₆₈−t₄₈) as a function of temperature is derived for each of the four temperature ranges above the oxygen boiling point (approximately 90 K) that are defined separately by the IPTS–68. Values of T₆₈−T₄₈ and its first temperature derivative, calculated from these equations, are tabulated up to 10,000 K in section 3.6, for use in the formulas of section 2; the values of T₆₈−T₄₈(= t₆₈−t₄₈) agree perfectly with a recently published tabulation [1]. Though the IPTS–68 is defined from 13.81 to 90.188 K, the IPTS–48 was not, so the two scales cannot be compared in this temperature range. (Tentative differences in this range between the IPTS—68 and each of four “national” scales are being published, but it is stated that these differences may undergo changes of up to several millikelvins when the national scales are finally compared accurately to the IPTS–68 [3].)

The first temperature derivative of T₆₈−T₄₈ is continuous at the ice point (0 °C), but has sharp discontinuities at the “antimony” and gold points (approximately 631 and 1064 °C) which will introduce corresponding small discontinuities at these temperatures into a heat capacity-temperature function that has previously been smoothed. This problem is discussed in section 3.5. where suggested “smoothing” equations to eliminate these discontinuities are derived.

2. Derivation of General Conversion Formulas

2.1. Enthalpy (H)

The conversion formula derived in this section for enthalpy (and those derived in sections 2.2–2.6 for other properties as well) are for clarity expressed specifically in terms of conversion from the IPTS–48 to the IPTS–68. Because these formulas (in sections 2.1–2.5) are exact, any other pair of continuous temperature scales may be used instead. For example, one of these scales might be defined as some linear function of thermometer resistance or thermocouple electromotive force.

The formulation is given in terms of what is now called the International Practical Kelvin (absolute) temperature (T), which is numerically greater than the International Practical Celsius temperature (t) by 273.15. This constant was adopted for the IPTS–68 [1], and for the IPTS–48 in 1954. (Between 1948 and 1954 this constant was not officially defined, but was usually taken as 273.16.) Thus we shall always use

$$T_{68}=t_{68}+273.15$$ (1)

and

$$T_{48}=t_{48}+273.15,$$ (2)

designating the value of the temperature on either IPTS as Kelvin or Celsius interchangeably as may prove convenient.

We shall often find it convenient to refer specifically to a pair of temperatures ³ (referred to as temperatures 1 and 2 and symbolized by single prime and double prime, respectively), and consider the case of converting the enthalpy (or any other property) from its value on the basis of the IPTS–48 at temperature 1 to its value on the basis of the IPTS–68 at temperature 2. As stated in the introduction (sec. 1), these two temperatures will be related to each other such that numerically

$$T_{68}^{\prime \prime }=T_{48}^{\prime }.$$ (3)

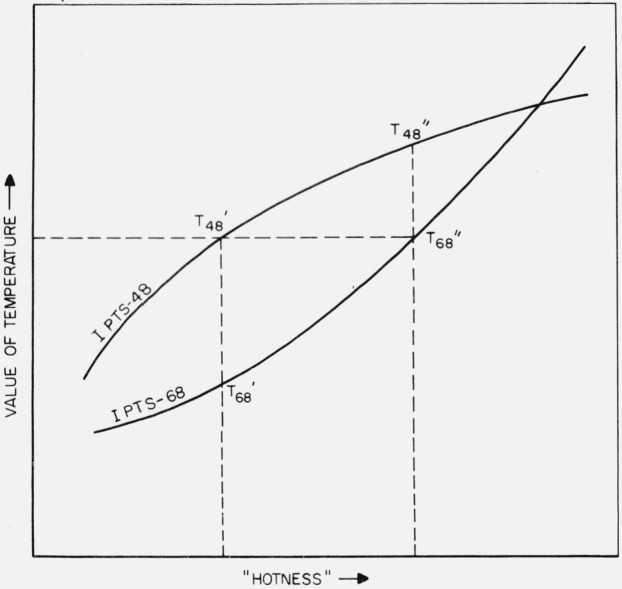
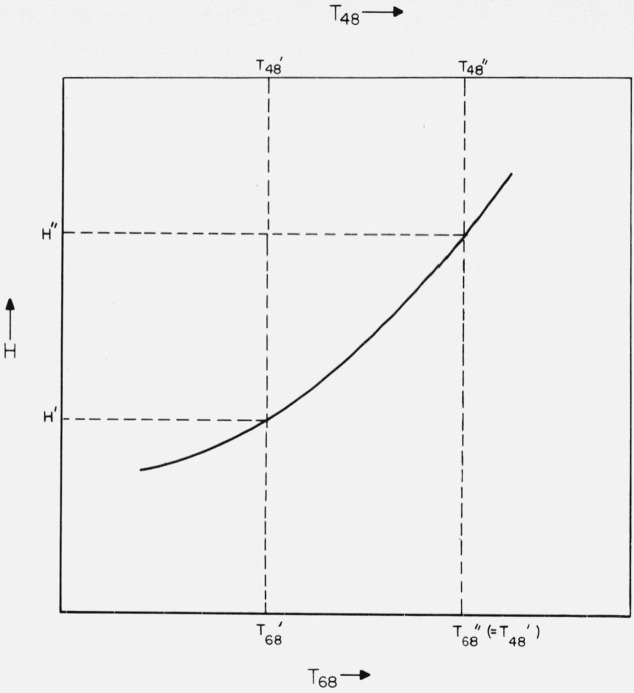
Since such thermodynamic properties as enthalpy cannot be assigned absolute values and therefore are usually expressed numerically as the magnitude in excess of the enthalpy at a reference temperature, it will be convenient to use the symbol H to represent this relative enthalpy. Because it simplifies the treatment, the reference temperature is to be restricted to one having the same value on both temperature scales (e.g., 273.16 K, but not 298.15 K). The situation under discussion may be clarified somewhat by reference to figures 1 and 2, which are schematic and are not to be taken as implying a given sign or magnitude of $\left(T_{68}^{\prime }-T_{48}^{\prime }\right)$ or $\left(T_{68}^{\prime \prime }-T_{48}^{\prime \prime }\right)$.

Figure 1. Schematic example illustrating the relation of T₄₈ and T₆₈ to “hotness.”.

(The thermodynamic or any other temperature scale whose temperature values continually increase with increasing “hotness” may be used as a quantitative measur of “hotness.”)

Figure 2. Schematic example illustrating the conventions used in converting relative enthalpy (H) from the basis of one temperature scale (e.g., T₄₈) to that of another scale (e.g., T₆₈).

H′ (at $T_{48}^{\prime }$) is converted to H″ (at $T_{68}^{\prime \prime }$).

The relative enthalpy will be assumed to be given by heat measurements at constant pressure, but it will be convenient to omit the indication of the constancy of pressure from derivatives of enthalpy. The lack of both a single and a double prime will imply a temperature unspecified in relation to temperatures 1 and 2. For convenience we shall abbreviate according to the further definitions:

$$C_P^{68}\equiv dH/d{T}_{68};$$ (4)

$$C_P^{48}\equiv dH/d{T}_{48};$$ (5)

$$\mu \left[=\mu \left(T_{68}\right)\right]\equiv T_{68}-T_{48}\text{at}\text{a}\text{given}\text{temperature.}$$ (6)

In more specific form for future reference, eq (6) can of course be written

$${\mu }^{\prime }=T_{68}^{\prime }-T_{48}^{\prime }$$ (7)

or

$${\mu }^{″}=T_{68}^{\prime \prime }-T_{48}^{\prime \prime }.$$ (8)

From eq (3) and (8),

$${\mu }^{″}=T_{48}^{\prime }-T_{48}^{\prime \prime }.$$ (9)

From eq (6),

$$\frac{d{T}_{48}}{d{T}_{68}}=1-\frac{d\mu }{d{T}_{68}},$$ (10)

and therefore

$$\frac{d{T}_{68}}{d{T}_{48}}=\frac{1}{1-\frac{d\mu }{d{T}_{68}}}.$$ (11)

The Taylor expansion of H(T₄₈) about H’ is [remembering eq (5)]

$$H=H^{\prime }+\left(T_{48}-T_{48}^{\prime }\right){\left(C_P^{48}\right)}^{\prime }+\frac{1}{2}{\left(T_{48}-T_{48}^{\prime }\right)}^2{\left(\frac{d{C}_P^{48}}{d{T}_{48}}\right)}^{\prime }+\frac{1}{6}{\left(T_{48}-T_{48}^{\prime }\right)}^3{\left(\frac{d^2{C}_P^{48}}{d{T}_{48}^2}\right)}^{\prime }+\dots$$ (12)

Substituting H” for H and $T_{48}^{\prime \prime }$ for T₄₈ in eq (12), then replacing $\left(T_{48}^{\prime \prime }-T_{48}^{\prime }\right)$ from eq (9), gives the desired enthalpy correction δH,

$$\delta H=H^{″}-H^{\prime }=-{\mu }^{″}{\left(C_{{}^P}^{48}\right)}^{\prime }+\frac{1}{2}{\left({\mu }^{″}\right)}^2{\left(\frac{d{C}_{{}^P}^{48}}{d{T}_{48}}\right)}^{\prime }-\frac{1}{6}{\left({\mu }^{″}\right)}^3{\left(\frac{d^2{C}_{{}^P}^{48}}{d{T}_{48}^2}\right)}^{\prime }+\dots$$ (13)

Equation (13) is in a convenient form: H and its derivatives with respect to T₄₈ are presumed known (or evaluable) at the round value of temperature $T_{48}=T_{48}^{\prime }$, whereas μ is assumed to be known as a function of T₆₈ and so can readily be evaluated at the temperature where $T_{68}=T_{68}^{\prime \prime }\left(=T_{48}^{\prime }\right)$, also a round value of temperature.

Equation (13) is exact (as an infinite series). However, of the rhs (right-hand side), only the first term is, usually, not negligible in practice (see sec. 2.6).

Reverting temporarily to the usual definition of the symbol H as representing absolute enthalpy at some one temperature, let us exemplify enthalpy relative to that at a temperature where μ ≠ 0 by H − H_298.15. Obviously δ(H − H_298.15) ≡ δ(H − H_c) − δ(H_298.15 − H_c). Each of the two terms of the right-hand side be evaluated separately from eq (13) with reference to a temperature c (say, 0 K) where μ = 0.

2.2. Heat Capacity (C_p)

The Taylor expansion of heat-capacity as a function of T₄₈ about ${\left(C_P^{48}\right)}^{\prime }$ is [after replacing $C_P^{48}$ by, ${\left(C_P^{48}\right)}^{\prime \prime }$ T₄₈ by $T_{48}^{\prime \prime }$, and then $\left(T_{48}^{\prime \prime }-T_{48}^{\prime }\right)$ from eq (9)]

$${\left(C_{{}^P}^{48}\right)}^{\prime \prime }={\left(C_{{}^P}^{48}\right)}^{\prime }-{\mu }^{″}{\left(\frac{d{C}_{{}^P}^{48}}{d{T}_{48}}\right)}^{\prime }+\frac{1}{2}{\left({\mu }^{″}\right)}^2{\left(\frac{d^2{C}_{{}^P}^{48}}{d{T}_{48}^2}\right)}^{\prime }-\dots$$ (14)

From eq (4), (5), and (11),

$${\left(C_{{}^P}^{48}\right)}^{\prime \prime }={\left(C_{{}^P}^{68}\right)}^{\prime \prime }\left[\frac{1}{1-{\left(\frac{d\mu }{d{T}_{68}}\right)}^{\prime \prime }}\right].$$ (15)

Substituting for ${\left(C_P^{48}\right)}^{\prime \prime }$ from eq (15) into eq (14) and then solving for ${\left(C_P^{68}\right)}^{\prime \prime }-{\left(C_P^{48}\right)}^{\prime }$ gives the desired heat-capacity correction δC_P,

$$\delta C_P={\left(C_{{}^P}^{68}\right)}^{\prime \prime }-{\left(C_{{}^P}^{48}\right)}^{\prime }=-{\left(\frac{d\mu }{d{T}_{68}}\right)}^{\prime \prime }{\left(C_{{}^P}^{48}\right)}^{\prime }+\left[1-{\left(\frac{d\mu }{d{T}_{68}}\right)}^{\prime \prime }\right]\left[-{\mu }^{″}{\left(\frac{d{C}_{{}^P}^{48}}{d{T}_{48}}\right)}^{\prime }+\frac{1}{2}{\left({\mu }^{″}\right)}^2{\left(\frac{d^2{C}_{{}^P}^{48}}{d{T}_{48}^2}\right)}^{\prime }-\dots \right].$$ (16)

Equation (16) is exact (as an infinite series). In practice, $\left|\frac{d\mu }{d{T}_{68}}\right|⪡1$, so that the factor $\left[1-{\left(\frac{d\mu }{d{T}_{68}}\right)}^{\prime \prime }\right]$ may be replaced by 1 (approximate).

2.3. Absolute “Third-Law” Entropy (S)

We wish to find the equivalent of (S⁶⁸)″ − (S⁴⁸)′, each term of which is taken to represent entropy relative to that at 0 K (absolute entropy if the Third Law of Thermodynamics holds) and is evaluated from the enthalpy data at its respective indicated temperature value on the assumption that the respective indicated IPTS represents the thermodynamic temperature.

Since both (S⁶⁸)″ and (S⁴⁸)′ involve integration down to 0 K, it is convenient to formulate them separately, then take the difference. Consider dS⁶⁸ and dS⁴⁸ over a definite infinitesimal temperature range, dH being a fixed experimentally determined quantity. Then

$$d{S}^{68}=\frac{dH}{T_{68}}$$ (17)

and

$$d{S}^{48}=\frac{dH}{T_{48}}.$$ (18)

Replacing dH from eq (5) and T₆₈ from eq (6), eq (17) becomes

$$d{S}^{68}=\left(\frac{C_P^{48}}{T_{48}+\mu }\right)d{T}^{48}.$$ (19)

Integrating eq (19),

$${\left(S^{68}\right)}^{\prime \prime }=\underset{0}{\overset{T_{48}^{\prime }}{\int }}\left(\frac{C_P^{48}}{T_{48}+\mu }\right)d{T}_{48}+{\left(S^{68}\right)}^{\prime \prime }-{\left(S^{68}\right)}^{\prime }$$ (20)

Similarly using eq (5), the integration of eq (18) gives

$${\left(S^{48}\right)}^{\prime }=\underset{0}{\overset{T_{48}^{\prime }}{\int }}\frac{C_P^{48}}{T_{48}}d{T}_{48}.$$ (21)

Subtracting eq (21) from eq (20),

$${\left(S^{68}\right)}^{\prime \prime }-{\left(S^{48}\right)}^{\prime }=-\underset{0}{\overset{T_{48}^{\prime }}{\int }}\frac{\mu C_P^{48}d{T}_{48}}{T_{48}\left(T_{48}+\mu \right)}+{\left(S^{68}\right)}^{\prime \prime }-{\left(S^{68}\right)}^{\prime }$$ (22)

(S⁶⁸)″ − (S⁴⁸)′ is the desired correction (≡ δS), but it remains (a) to formulate μ(T₄₈) from the presumably known μ(T₆₈) for use in eq (22), and (b) to substitute for (S⁶⁸)″ − (S⁶⁸)′ in terms of known quantities, remembering that S⁴⁸ and its derivatives with respect to T₄₈ are known at $T_{48}=T_{48}^{\prime }$, whereas μ and its derivatives with respect to T₆₈ are known at $T_{68}=T_{68}^{\prime \prime }$, numerically the same value of temperature.

Expanding μ(T₄₈) about μ″, then setting μ = μ′,

$${\mu }^{\prime }={\mu }^{″}+\left(T_{48}^{\prime }-T_{48}^{\prime \prime }\right){\left(\frac{d\mu }{d{T}_{48}}\right)}^{\prime \prime }+\frac{1}{2}{\left(T_{48}^{\prime }-T_{48}^{\prime \prime }\right)}^2{\left(\frac{d^2\mu }{d{T}_{48}^2}\right)}^{\prime \prime }+\dots .$$ (23)

Substituting from eq (9), eq (23) gives

$${\mu }^{\prime }={\mu }^{″}\left[1+{\left(\frac{d\mu }{d{T}_{48}}\right)}^{\prime \prime }\right]+\frac{1}{2}{\left({\mu }^{″}\right)}^2{\left(\frac{d^2\mu }{d{T}_{48}^2}\right)}^{\prime \prime }+\dots .$$ (24)

Using eq (11), we can write

$$\frac{d\mu }{d{T}_{48}}\equiv \frac{d\mu }{d{T}_{68}}\frac{d{T}_{68}}{d{T}_{48}}=\frac{\frac{d\mu }{d{T}_{68}}}{1-\frac{d\mu }{d{T}_{68}}}.$$ (25)

Differentiating eq (25) with respect to T₄₈ gives

$$\frac{d^2\mu }{d{T}_{48}^2}=\frac{\frac{d^2\mu }{d{T}_{68}^2}}{{\left(1-\frac{d\mu }{d{T}_{68}}\right)}^3}.$$ (26)

Substituting from eq (25) and (26) for the derivatives in eq (24) gives

$${\mu }^{\prime }=\frac{{\mu }^{″}}{1-{\left(\frac{d\mu }{d{T}_{68}}\right)}^{\prime \prime }}+\frac{\frac{1}{2}{\left(\frac{d^2\mu }{d{T}_{68}^2}\right)}^{\prime \prime }{\left({\mu }^{″}\right)}^2}{{\left[1-{\left(\frac{d\mu }{d{T}_{68}}\right)}^{\prime \prime }\right]}^3}+\dots$$ (27)

We are assuming μ to be available in the form μ(T₆₈). Consider any given value of T₄₈ in the integrand of eq (22); if we temporarily call it $T_{48}^{\prime }$ (not to be confused with the $T_{48}^{\prime }$ which forms the upper limit of integration), then the μ to be associated with it is, of course, μ at $T_{48}=T_{48}^{\prime }$ or μ′. This μ′ can be obtained from eq (27), since, in view of eq (3), the corresponding μ″ is μ at $T_{68}=T_{68}^{\prime \prime }=T_{48}^{\prime }$. Hence the μ to use in the integrand of eq (22) is μ′ of eq (27), where μ″ and its derivatives with respect to T₆₈ are evaluated, with T₆₈ then replaced by T₄₈. Expressed more concisely, where ψ designates a definite function defined by the rhs of eq (27):

$$\begin{array}{l}{\mu }^{\prime }=\psi \left(T_{6\text{8}}^{\prime \prime }\right);\hfill \\ \mu \left(T_{48}\right)=\psi \left(T_{48}\right).\hfill \end{array}\}$$ (28)

Although eq (27) as an infinite series is exact, in practice $\left|\frac{d\mu }{d{T}_{68}}\right|⪡1$, $\mu \left|\frac{d^2\mu }{d{T}_{68}^2}\right|⪡1$, etc., so that

$${\mu }^{\prime }\simeq {\mu }^{″}.$$ (29)

Turning to the formulation of (S⁶⁸)″ − (S⁶⁸)′ [needed in using eq (22)], let us expand S⁶⁸(T₄₈) about (S⁶⁸)′. Then successively replacing S⁶⁸ by (S⁶⁸)″, T₄₈ by $T_{48}^{\prime \prime }$, and $T_{48}^{\prime \prime }-T_{48}^{\prime }$ from eq (9), we get

$${\left(S^{68}\right)}^{\prime \prime }-{\left(S^{68}\right)}^{\prime }=-{\mu }^{″}{\left(\frac{d{S}^{68}}{d{T}_{48}}\right)}^{\prime }+\frac{1}{2}{\left({\mu }^{″}\right)}^2{\left(\frac{d^2{S}^{68}}{d{T}_{48}^2}\right)}^{\prime }-\dots$$ (30)

From eq (19)

$$\frac{d{S}^{68}}{d{T}_{48}}=\frac{C_P^{48}}{T_{48}+\mu },$$ (31)

and differentiating eq (31),

$$\frac{d^2{S}^{68}}{d{T}_{48}^2}=\left(\frac{1}{T_{48}+\mu }\right)\frac{d{C}_P^{48}}{d{T}_{48}}-\frac{C_P^{48}}{{\left(T_{48}+\mu \right)}^2}\left(1+\frac{d\mu }{d{T}_{48}}\right).$$ (32)

From eq (25),

$$1+\frac{d\mu }{d{T}_{48}}=\frac{1}{1-\frac{d\mu }{d{T}_{68}}}.$$ (33)

Equations (31)–(33) convert eq (30) into

$${\left(S^{68}\right)}^{\prime \prime }-{\left(S^{68}\right)}^{\prime }=-\frac{{\mu }^{″}{\left(C_P^{48}\right)}^{\prime }}{T_{48}^{\prime }+{\mu }^{\prime }}\left\{1+\frac{\frac{1}{2}{\mu }^{″}}{\left[T_{48}^{\prime }+{\mu }^{\prime }\right]\left[1-{\left(\frac{d\mu }{d{T}_{68}}\right)}^{\prime }\right]}\right\}+\frac{\frac{1}{2}{\left({\mu }^{″}\right)}^2}{T_{48}^{\prime }+{\mu }^{\prime }}{\left(\frac{d{C}_P^{48}}{d{T}_{48}}\right)}^{\prime }+\dots .$$ (34)

Finally, substituting for (S⁶⁸)″ − (S⁶⁸)′ into eq (22) from eq (34) gives the desired entropy correction δS,

$$\delta S={\left(S^{68}\right)}^{\prime \prime }-{\left(S^{48}\right)}^{\prime }=-\underset{0}{\overset{T_{48}^{\prime }}{\int }}\frac{\mu C_P^{48}d{T}_{48}}{T_{48}\left(T_{48}+\mu \right)}-\frac{{\mu }^{″}{\left(C_P^{48}\right)}^{\prime }}{T_{48}^{\prime }+{\mu }^{\prime }}\left\{1+\frac{\frac{1}{2}{\mu }^{″}}{\left[T_{48}^{\prime }+{\mu }^{\prime }\right]\left[1-{\left(\frac{d\mu }{d{T}_{68}}\right)}^{\prime }\right]}\right\}+\frac{\frac{1}{2}{\left({\mu }^{″}\right)}^2}{T_{48}^{\prime }+{\mu }^{\prime }}{\left(\frac{d{C}_P^{48}}{d{T}_{48}}\right)}^{\prime }+\dots ,$$ (35)

where, if eq (29) is not a sufficiently good approximation, μ(T₄₈) in the integrand can be evaluated as μ′ from eq (27) [in view of eq (28)], and where μ′ and ${\left(\frac{d\mu }{d{T}_{68}}\right)}^{\prime }$ can also be found from eq (27). The contribution of any first-order process (such as a heat of transition, fusion, or vaporization) to $C_P^{48}d{T}_{48}$ in eq (35) is indeterminate, and must be replaced by dH, whose integral is the heat of that process.

Equation (35) as an infinite series is exact, but it does assume calorimetric evaluation of $C_P^{48}\left(T_{48}\right)$ all the way down to 0 K. When this assumption is invalid, see section 2.5.

2.4. Other Thermodynamic Functions

The other thermodynamic functions commonly used in chemical thermodynamics can be readily converted from the basis of one temperature scale to that of another using the corrections found above (secs. 2.1 and 2.3) for the enthalpy, H, and the absolute entropy, S. For example, consider the enthalpy function H/T, more explicitly written (H_T − H₀)/T when H is understood to represent the enthalpy at temperature T relative to the enthalpy at absolute zero. Using eq (3) and our previous notation, the correction δ(H/T) is given by

$$\delta \left(\frac{H}{T}\right)=\frac{H^{″}}{T_{68}^{\prime \prime }}-\frac{H^{\prime }}{T_{48}^{\prime }}=\frac{H^{″}-H^{\prime }}{T_{48}^{\prime }}$$ (36)

or simply the correction to the enthalpy, divided by the value of the Kelvin temperature. The correction δG to the Gibbs energy is given by

$$\delta G={\left(G^{68}\right)}^{\prime \prime }-{\left(G^{48}\right)}^{\prime }=\left[H^{″}-T_{68}^{\prime \prime }{\left(S^{68}\right)}^{\prime \prime }\right]-\left[H^{\prime }-T_{48}^{\prime }{\left(S^{48}\right)}^{\prime }\right]=H^{″}-H^{\prime }-T_{48}^{\prime }\left[{\left(S^{68}\right)}^{\prime \prime }-{\left(S^{48}\right)}^{\prime }\right],$$ (37)

where H and G are both understood to be relative to the enthalpy H at some one temperature which has the same value on both temperature scales. The correction δ(− G/T) to the “free-energy function” − (G_t − H₀)/T, when the latter is abbreviated to − G/T, is analogous to eq (36):

$$\delta \left(-\frac{G}{T}\right)=\left[-\frac{{\left(G^{68}\right)}^{\prime \prime }}{T_{68}^{\prime \prime }}\right]-\left[-\frac{{\left(G^{48}\right)}^{\prime }}{T_{48}^{\prime }}\right]=-\frac{\left[{\left(G^{68}\right)}^{\prime \prime }-{\left(G^{48}\right)}^{\prime }\right]}{T_{48}^{\prime }},$$ (38)

where − [(G⁶⁸)″ − (G⁴⁸)′] is given by eq (37).

2.5. Modifications of Conversion Procedure when Significant Extrapolation to 0 K was Made Using a Theoretical Relation

In evaluating thermodynamic functions based on 0 K, the heat capacity is measured to as low a temperature as practical and then extrapolation to 0 K is carried out on some more or less simple theoretical basis. The following treatment of the conversion to the basis of a new temperature scale will be exemplified by the use of the simple “T³” law. If the extrapolation has been from such a low temperature that the heat capacity at all lower temperatures is very small, the modifications are of little importance. However, a great many heat-capacity investigations have involved experimental measurements only down to the triple point of nitrogen (or oxygen), and it is desirable to know whether the required modifications are significant in preserving a given degree of accuracy.

The “T³” law gives for the fundamental thermodynamic properties

$${\left(C_P\right)}_T=c{T}^3$$ (39)

$$H_T-H_0=\underset{0}{\overset{T}{\int }}{\left(C_P\right)}_{T}dT=\frac{1}{4}c{T}^4=\frac{1}{4}{\left(C_P\right)}_{T}T$$ (40)

$$S_T=\underset{0}{\overset{T}{\int }}\frac{{\left(C_P\right)}_T}{T}dT=\frac{1}{3}c{T}^3=\frac{1}{3}{\left(C_P\right)}_T$$ (41)

where the constant c is dependent on the substance involved. Equation (41) as written assumes the validity of the Third Law of Thermodynamics in the case in question.

According to the Debye theory the constant c is given by

$$c=\frac{12}{5}{\pi }^{4}R/{\theta }_D^3$$ (42)

per gram-atom, where θ_D is the Debye characteristic temperature. However, c is rarely evaluated from eq (42) independently of the heat-capacity data, because the “T³” law expressed by eq (39) and (42) is only approximate: for any given substance the value of θ_D depends on the property from which it is derived. It also varies with temperature when derived from a given property such as heat capacity, and the “T³” law may “fail” well below the highest temperature at which it is desired to apply eq (39).

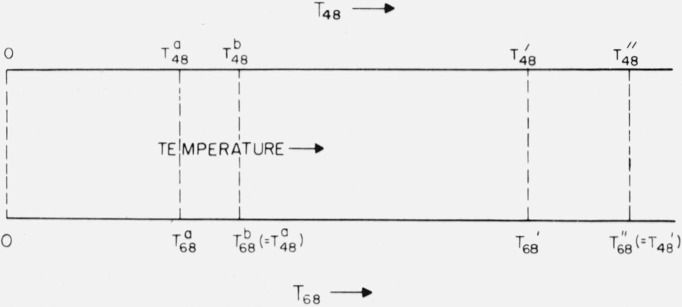
Let us use the T in eq (39)–(41) to represent the temperature on any scale assumed to be the thermodynamic one. In what follows it will be assumed that extrapolation to 0 K using the “T³” law was from a temperature a which is $T_{48}^a$ on the IPTS–48 and $T_{48}^a$ on the IPTS–68, that measurements of enthalpy giving heat capacity are available at the temperatures above temperature a, and that a temperature b (where $T_{48}=T_{48}^b$ and $T_{6\text{8}}=T_{6\text{8}}^b$ is such that $T_{68}^b=T_{48}^a$ [analogous to eq (3)]. As before, it is desired to find the correction converting a thermodynamic property on the basis of IPTS–48 and at $T_{48}=T_{48}^{\prime }$ to the basis of IPTS–68 and at $T_{68}=T_{68}^{\prime \prime }=T_{48}^{\prime }$, where $T_{48}^{\prime }⩾T_{48}^a$ and $T_{\text{68}}^{\prime \prime }⩾T_{6\text{8}}^b$. The temperature ranges of interest are represented by these various symbols in the schematic diagram of figure 3. It will be assumed that c is assigned values such that the heat capacity given by eq (39) agrees with the experimental value of ${\left(C_P^{48}\right)}^a$ if IPTS–48 is the basis, and with that of ${\left(C_P^{48}\right)}^b$ if IPTS–68 is the basis.

Figure 3.

Temperature ranges of interest when extrapolation to 0 K was made using a theoretical relation (schematic).

As before, the desired correction to the enthalpy (this time specified to be relative to that at 0 K) is H″ − H′, which can be found as the sum of the corrections to the enthalpy increment above $T_{6\text{8}}^b$ (or $T_{48}^a$) and the correction to the enthalpy increment below this temperature:

$$\delta H=H^{″}-H^{\prime }\equiv \left[\left(H^{″}-H^{\prime }\right)-\left(H^b-H^a\right)\right]+\left[H^b-H^a\right].$$ (43)

The two parenthesized terms of eq (43) are separately calculable from eq (13), using the heat-capacity data on the IPTS–48 and μ(T₆₈). The second bracketed term in eq (43) is, from eq (40),

$$\begin{gathered} \left[H^b-H^a\right]=\frac{1}{4}{\left(C_p^{68}\right)}^b{T}_{68}^b-\frac{1}{4}{\left(C_P^{48}\right)}^a{T}_{48}^a \\ =\frac{1}{4}\left[{\left(C_P^{68}\right)}^b-{\left(C_P^{48}\right)}^a\right]T_{48}^a, \end{gathered}$$ (44)

since $T_{68}^b=T_{48}^a\cdot \left[{\left(C_P^{68}\right)}^b-{\left(C_P^{48}\right)}^a\right]$ is derivable from eq (16) after replacing temperatures 1 and 2 by a and b respectively.

There is no modification to the heat capacity correction $\left[{\left(C_P^{68}\right)}^{\prime \prime }-{\left(C_P^{48}\right)}^{\prime }\right]$ given by eq (16) ($T_{\text{68}}^{\prime \prime }⩾T_{6\text{8}}^b$ and $T_{48}^{\prime }⩾T_{48}^a$), since the heat capacity in the experimental range is assumed to depend on temperature only in the manner observed experimentally.

As before, the desired correction to the entropy (taken as zero at 0 K because the Third Law of Thermodynamics is assumed) is (S⁶⁸)″ − (S⁴⁸)′, and

$$\delta S={\left(S^{68}\right)}^{\prime \prime }-{\left(S^{48}\right)}^{\prime }\equiv \left[{\left(S^{68}\right)}^{\prime \prime }-{\left(S^{68}\right)}^b\right]-\left[{\left(S^{48}\right)}^{\prime }-{\left(S^{48}\right)}^a\right]+\left[{\left(S^{68}\right)}^b-{\left(S^{48}\right)}^a\right].$$ (45)

From eq (9) (with subscripts changed correspondingly),

$$T_{48}^b=T_{48}^a-{\mu }^b.$$ (46)

If eq (20) is modified by replacing the lower limit of integration by $T_{48}^b$, given by eq (46), it becomes

$${\left(S^{68}\right)}^{\prime \prime }-{\left(S^{68}\right)}^b=-{\int }_{T_{48}^a-{\mu }^b}^{T_{48}^{\prime }}\left(\frac{C_P^{48}}{T_{48}+\mu }\right)d{T}_{48}+{\left(S^{68}\right)}^{\prime \prime }-\left(S^{68}\right)$$ (47)

where (S⁶⁸)″ − (S⁶⁸)′ is given, as before, by eq (34). Similarly, modifying the lower integration limit to $T_{48}^a$, eq (21) becomes

$$-\left[{\left(S^{48}\right)}^{\prime }-{\left(S^{48}\right)}^a\right]=-{\int }_{T_{48}^a}^{T_{48}^{\prime }}\frac{C_P^{48}}{T_{48}}d{T}_{48}.$$ (48)

From eq (41),

$$\left[{\left(S^{68}\right)}^b-{\left(S^{48}\right)}^a\right]=\frac{1}{3}\left[{\left(C_P^{68}\right)}^b-{\left(C_P^{48}\right)}^a\right],$$ (49)

where $\left[{\left(C_P^{68}\right)}^b-{\left(C_P^{48}\right)}^a\right]$ can be found from eq (16) for the two temperatures involved. The substitution from eq (47)–(49) into the last member of eq (45) then gives the desired entropy correction.

2.6. Approximate Conversion Formulas

Instead of using eq (13), (16), and (35) (or those in sec. 2.5) the enthalpy, heat capacity, and entropy may be corrected by the much simpler but approximate formulas below with sufficient accuracy for most purposes – even for the most accurate data except in the case of sharp transitions, and except possibly at very low temperatures. It should be realized, however, that the approximate formulas of this section may not be sufficiently accurate when applied to two temperature scales differing more widely from each other than the IPTS–48 and IPTS–68; in such cases, additional terms of the exact equations of the preceding sections are needed. Incidentally, it is well to point out that when the enthalpy data are sufficiently precise to justify the higher-order correction terms containing temperature derivatives of the heat capacity, it will often be simpler instead to repeat the treatment of the original unsmoothed data after replacing the boundary temperatures of each enthalpy increment in terms of the new temperature scale.

We define

$$\delta X\equiv {\left(X^{68}\right)}_{T_{68}=T_0}-{\left(X^{48}\right)}_{T_{48}=T_0}.$$ (50)

(X ≡ C_P, or H or S relative to that at a temperature where μ = 0. The superscript “68” or “48” indicates the temperature scale with respect to which the given value of X was determined.)

$$\mu \equiv T_{68}-T_{48}=t_{68}-t_{48}.$$ (51)

All properties are those at T₀, the nominal value of T₆₈ where the corrected property is desired, unless otherwise stated. The property values in the rhs of each equation below are as determined on the IFTS–48, and either dT₄₈ or dT₆₈ can be used for dT [dropping the last term of eq (10)].

From eq (13), the only term of importance, usually, is the first, so

$$\delta H=-\mu C_P.$$ (52)

From eq (52),

$$\delta C_P=\delta \left(\frac{dH}{dT}\right)=\frac{d}{dT}\delta H=-C_P\frac{d\mu }{dT}-\mu \frac{d{C}_P}{dT}.$$ (53)

Considering the correction to the absolute entropy, we can first write [using eq (53)]:

$$\frac{d}{dT}(\delta S)=\delta \left(\frac{dS}{dT}\right)=\delta \left(\frac{C_P}{T}\right)=\frac{\delta C_P}{T}=-\frac{\mu }{T}\frac{d{C}_P}{dT}-\frac{C_P}{T}\frac{d\mu }{dT}.$$ (54)

But

$$\frac{d}{dT}\left(-\underset{0}{\overset{T}{\int }}\frac{\mu C_{P}dT}{T^2}-\frac{\mu C_P}{T}\right)\equiv -\frac{\mu }{T}\frac{d{C}_P}{dT}-\frac{C_P}{T}\frac{d\mu }{dT}.$$ (55)

Since the last members of eq (54) and (55) are identical, we can write

$$\delta S=-\underset{0}{\overset{T}{\int }}\frac{\mu C_{P}dT}{T^2}-\frac{\mu C_P}{T},$$ (56)

of which the second member approximates the only important terms in eq (35).

The last member of eq (53) represents the only two terms of eq (16) that are usually of importance; and of these two terms, the first is probably nearly always the much more important (except, of course, when dμ/dT is accidentally very close to zero). According to this term, the relative (fractional) correction to the heat capacity is approximately equal in magnitude to dμ/dT. According to table 4, this does not exceed 0.3 percent below 3000 K. The relative correction to the absolute entropy [eq (56)] tends to be considerably smaller, owing to partial cancellation within the integral and to the magnified weighting by the factor 1/T² of low temperatures where the differences between the IPTS–48 and the IPTS–68 are relatively small.

The corresponding equations that are accurate to the same approximation when the “T³” law is used below absolute temperature τ, with the “T³” and experimental heat capacities required to agree at this temperature, are easily found from section 2.5. Thus, where δH and δS in the rhs are given by eq (52) and (56) respectively:

$$\delta H=\frac{1}{4}\tau {\left(\delta C_P\right)}_{\tau }+(\delta H)-{(\delta H)}_{\tau };$$ (57)

$$\delta C_P\text{ is given by eq }(53);$$ (58)

$$\delta S=\frac{1}{3}{\left(\delta C_P\right)}_{\tau }+(\delta S)-{(\delta S)}_{\tau }.$$ (59)

3. The Numerical Differences Between the International Practical Temperature Scales of 1948 and 1968

The temperature ranges separately defined by the two scales are treated individually in sections 3.1–3.4 (headed by the respective temperature ranges expressed on the IPTS–68), and equations are derived giving numerically the differences μ(≡ T₆₈ − T₄₈ = t₆₈ − t₄₈) between the IPTS–68 and the IPTS–48 in these respective ranges, with sufficient accuracy for most practical purposes.

3.1. 90.188 to 273.15 K (−182.962 to 0 °C)

The realization of both scales is specified to be by the resistance of a suitable platinum thermometer over the entire temperature range from approximately 90 to 904 K (−183 to 631 °C). Since both scales are so defined as to preserve the highest practical continuity over this whole temperature range, their specifications below the ice point depend on those above the ice point. Therefore it will be necessary to consider together the definitions of the two scales in these two regions of temperature.

Using W to represent the ratio of the measured resistance of a particular thermometer at some temperature to its resistance at 0 °C,⁴ the specified functions may be written:

• IPTS–48 (t₄₈, −182.97 to 0 °C) (Callendar-van Dusen equation) [4]:

  $$W=1+\alpha \left(1+0.01{\delta }_{48}\right)t_{48}-{10}^{-4}\alpha {\delta }_{48}{t}_{48}^2-{10}^{-8}\alpha \beta t_{48}^3\left(100-t_{48}\right).$$ (60)
• IPTS–68 (t₆₈, −182.962 to 0 °C) [1]:

  $$W=W_i^{*}+a_4{t}_{\text{68}}+c_4{t}_{68}^3\left(t_{68}-100\right).$$ (61)

  5
• IPTS–48 (t₄₈, 0 to 630.5 °C) (Callendar equation) [4]:

  $$W=1+\alpha \left(1+0.01{\delta }_{48}\right)t_{48}-{10}^{-4}\alpha {\delta }_{48}{t}_{48}^2$$ (62)
• IPTS–68 (t₆₈, 0 to 630.74 °C) [1]:

  $$t^{\prime }=\frac{1}{\alpha }(W-1)+{\delta }_{68}\left(\frac{t^{\prime }}{100}\right)\left(\frac{t^{\prime }}{100}-1\right),$$ (63)

  which when rearranged is

  $$W\left(t^{\prime }\right)=1+\alpha \left(1+0.01{\delta }_{6\text{8}}\right)t^{\prime }-{10}^{-4}\alpha {\delta }_{6\text{8}}{\left(t^{\prime }\right)}^2,$$ (63a)

  where t′ is defined (as a monotonic function) by the equation

  $$t_{68}=t^{\prime }+0.045\left(\frac{t^{\prime }}{100}\right)\left(\frac{t^{\prime }}{100}-1\right)\left(\frac{t^{\prime }}{419.58}-1\right)\left(\frac{t^{\prime }}{630.74}-1\right).$$ (64)

The functions W(t₄₈) and W(t₆₈) differ somewhat from one thermometer to another, and the constants appearing in eq (60)–(63a) are determined for a particular thermometer by measuring W at the fixed points listed in table 1. $W_t^{*}$ which appears in eq (61), is a single-valued reference function given by the equation

$$t_{6\text{8}}=\sum _{i=1}^{20}{A}_i{\left[\ln W_i^{*}\left(T_{\text{68}}\right)\right]}^i,$$ (65)

with the 20 constants A₁ … A₂₀ defined numerically and having 16 significant figures each [1].

Table 1.

Fixed points used for calibration of platinum resistance thermometers using eq (60)–(64)

Fixed point	Temperature value
	IPTS–48 [4, 5]	IPTS–68 [1]
	°C	°C
Normal boiling point of oxygen	–182.970	–182.962
Triple point of water	0.01	0.01
Normal boiling point of water	100	100
Normal boiling point of sulfur	a444.600
Normal freezing point of zinc	a419.505	419.58

^aFor IPTS–48, the “sulfur” point was an official defining fixed point, but the substitution of the “zinc” point and the temperature listed for it were recommended.

Since the correction to the heat capacity is approximately proportional to dμ/dT [eq (53)], we shall be concerned as to whether the latter and its temperature derivative are continuous at 0 °C, above and below which both W(T₄₈) and W(T₆₈) are each defined differently by the above equations. Among W, T₄₈, and T₆₈ there is only one independent variable, so we can write

$$\frac{d\mu }{d{T}_{\text{68}}}=\frac{d\left(T_{68}-T_{48}\right)}{d{T}_{68}}1-\frac{d{T}_{48}}{d{T}_{68}}=1-\frac{dW}{d{T}_{68}}/\frac{dW}{d{T}_{48}}.$$ (66)

It is clear [from eq (60) and (62)] that dW/dT₄₈ and $d^{2}W/d{T}_{\text{48}}^2$ are continuous at 0 °C, but the situation for the corresponding derivatives involving T₆₈ is not obvious. From eq (66), dμ/dT₆₈ and $d^2\mu /d{T}_{68}^2$ are continuous at 0 °C if and only if dW/dT₆₈ and $d^{2}W/d{T}_{\text{68}}^2$ also are.

It turns out that the two derivatives of W involving T₆₈ as defined by eq (61), (63a), and (64) are not identically continuous at 0 °C. The statement has been made, however, that they are continuous at 0 °C for what may be regarded as a typical thermometer having the following constants [1] (using asterisks for this special case):

$$a_4^{*}=c_4^{*}=0;{\alpha }^{*}=3.9259668\left({10}^{-3}\right);{\delta }_{6\text{8}}^{*}=1.496334.$$ (67)

This continuity may be readily demonstrated, as shown below. Incidentally, the corresponding function W*(T₆₈) [$\equiv W_t^{*}$ at and below 0 °C; ≡ W* (t′) at and above 0 °C] may alternatively be regarded as the standard reference function defining t₆₈ from −182.962 to 630.74 °C.

Since $W_t^{*}=1$ at T₆₈ = 273.15, it was found, using eq (65) and the numerical values of the constants A_i, that at 0 °C

$$\frac{d{W}_t^{*}}{d{T}_{\text{68}}}=1/\frac{d{T}_{\text{68}}}{d{W}_t^{*}}=\frac{1}{A_1}=3.98650632\left({10}^{-3}\right)$$ (68)

and

$$\frac{d^2{W}_t^{*}}{d{T}^2{}_{\text{68}}}=-\frac{d^2{T}_{68}}{d{W}_t^{*2}}/{\left(\frac{d{T}_{68}}{d{W}_t^{*}}\right)}^3=\frac{A_1-2A_2}{A_1^3}=-1.2261330\left({10}^{-6}\right).$$ (69)

Similarly, it was found, using eq (63a), (64), and (67), that at 0 °C

$$\frac{d{W}^{*}\left(t^{\prime }\right)}{d{T}_{68}}=\frac{d{W}^{*}\left(t^{\prime }\right)}{d{t}^{\prime }}/\frac{d{t}_6}{d{t}^{\prime }}=3.98650630\left({10}^{-3}\right)$$ (70)

and

$$\frac{d^2{W}^{*}\left(t^{\prime }\right)}{d{t}_{68}^2}=\frac{d^2{W}^{*}\left(t^{\prime }\right)}{d{t}^{\prime 2}}/{\left(\frac{d{t}_{68}}{d{t}^{\prime }}\right)}^2-\frac{d{W}^{*}\left(t^{\prime }\right)}{d{t}^{\prime }}\left(\frac{d^2{t}_{68}}{d{t}^{\prime 2}}\right)/{\left(\frac{d{t}_{68}}{d{t}^{\prime }}\right)}^3=-1.2261327\left({10}^{-6}\right).$$ (71)

The values of eq (68) and (70) differ by a factor of 1 + 5(10⁻⁹), and those of eq (69) and (71) by a factor of 1+2(10⁻⁷). Though the pertinent magnitudes are such that at 0 °C the fractional discontinuity in dμ/dT₆₈ is many times as great as that in dW/dT₆₈, these discrepancies are too small to be of any practical significance and are very likely to be so for all resistance thermometers meeting the standards imposed by the IPTS–68.

For a given resistance thermometer, α has the same value in eq (60), (62), (63), and (63a), because it depends only on the resistances at 0 and 100 °C, which designate the same⁴ (see footnote 4) respective temperatures on the IPTS–48 and the IPTS–68. However, δ₄₈ ≠ δ₆₈, because of the difference in the two values of temperature for the zinc (or sulfur) point (table 1). At the zinc point t₄₈ = 419.505 and t′ = t₆₈ = 419.58. Substituting these values and that of ${\delta }_{68}^{*}$ from eq (67) into eq (62) and (63a) and equating the two expressions for W give

$${\delta }_{48}^{*}=1.49135723.$$ (72)

Since W also is a continuous function of temperature, W and its derivatives may replace H and its derivatives in eq (13) to give an equation from which μ(t₆₈) may be derived,

$$W^{″}-W^{\prime }=-{\mu }^{″}{\left(\frac{dW}{d{t}_{48}}\right)}^{\prime }+\frac{1}{2}{\left({\mu }^{″}\right)}^2{\left(\frac{d^{2}W}{d{t}_{48}^2}\right)}^{\prime }-\dots .$$ (73)

In rhs of eq (73) all terms except the first may with sufficient accuracy be neglected (the ratio of the second term to the first does not exceed 0.00004 between −182.962 and 630.74 °C), giving

$${\mu }^{″}=\left(W^{\prime }-W^{″}\right)/{\left(\frac{dW}{d{t}_{48}}\right)}^{\prime }.$$ (74)

Using for W the standard reference function defined by eq (60)–(65) with the parameter values of eq (67) and (72), we shall derive from eq (74) numerical functions for μ(t₆₈), in this section for the range t₆₈ = −182.962 to 0 °C and in the next section for the range t₆₈ = 0 to 630.74 °C.

Since eq (74) expresses μ at temperature 2, for temperatures at or below 0 °C W′ and (dW/dt₄₈)′ are found from eq (60), (67), and (72), then replacing $T_{48}^{\prime }$ by $T_{68}^{\prime \prime }$ by eq (1)–(3), and W″ from eq (61) and (67). [The value of β is found from eq (60) applied at the oxygen boiling point, where W has the value of $W_t^{*}$ at T₆₈ = 90.188 K and where t₄₈ = −182.970 (table 1).] The final equation is

$$\mu =\frac{250.97\left[1+3.9845170\left({10}^{-3}\right)t_{68}-5.855019\left({10}^{-7}\right)t_{68}^2+4.35717\left({10}^{-12}\right)\left(100-t_{68}\right)t_{68}^3-W_t^{*}\right]}{1-2.9389\left({10}^{-4}\right)t_{68}+4.3741\left({10}^{-9}\right)\left(75-t_{68}\right)t_{68}^2}\left[t_{6\text{8}}=-182.962\text{to}{0}^{°}\text{C}\right].$$ (75)

3.2. 273.15 to 903.89 K (0 to 630.74 °C)

For temperatures at and above 0 °C, eq (74) is applied similarly as was done in section 3.1 for the lower temperature range. W′ and (dW/dt₄₈)′ are found from eq (62), replacing $T_{48}^{\prime }$ by $T_{68}^{\prime \prime }$, and W″ from eq (63a). For replacing t′ in eq (63a) in terms of t₆₈, eq (64) may be written

$$t_{6\text{8}}=t^{\prime }+\phi \left(t^{\prime }\right),$$ (76)

where

$$\phi \left(t^{\prime }\right)\equiv 0.045\left(\frac{t^{\prime }}{100}\right)\left(\frac{t^{\prime }}{100}-1\right)\left(\frac{t^{\prime }}{419.58}-1\right)\left(\frac{t^{\prime }}{630.74}-1\right).$$ (77)

Expanding φ(t′) to two terms about φ(t₆₈) and then replacing φ(t′) from eq (76) gives

$$t^{\prime }=t_{68}-\frac{\phi \left(t_{68}\right)}{1+\frac{d\phi \left(t_{68}\right)}{d{t}_{68}}}.$$ (78)

(The magnitude of dφ(t₆₈)/dt₆₈ never exceeds about 0.001.) Neglecting a term [in φ(t₆₈)] whose magnitude never exceeds approximately 0.00002 °C, the result is

$$\mu =\frac{0.01\left({\delta }_{68}-{\delta }_{48}\right)t_{68}\left(0.01t_{68}-1\right)}{1+0.01{\delta }_{48}-0.0002{\delta }_{48}{t}_{68}}+\phi \left(t_{68}\right).$$ (79)

Substituting the values of δ₆₈ and δ₄₈ for the reference function [eq (67) and (72)] gives the final numerical equation,

$$\mu =\frac{4.904\left({10}^{-7}\right)t_{68}\left(t_{68}-100\right)}{1-2.939\left({10}^{-4}\right)t_{68}}+\phi \left(t_{68}\right),\left[t_{68}=0\text{ to }{630.74}^{°}\text{C}\right]$$ (80)

where φ(t₆₈) is given by eq (77) on replacing t′ by t₆₈. Differentiation of eq (80) gives

$$\frac{d\mu }{d{t}_{68}}=\frac{-4.904\left({10}^{-5}\right)\left[1-0.02t_{68}+2.939\left({10}^{-6}\right)t_{68}^2\right]}{{\left[1-2.939\left({10}^{-4}\right)t_{68}\right]}^2}+\frac{d\phi \left(t_{68}\right)}{d{t}_{68}}.\left[t_{68}=0\text{ to }{630.74}^{°}\text{C}\right]$$ (81)

3.3. 903.89 to 1,337.58 K (630.74 to 1,064.43 °C)

Temperature in this range is measured by a platinum-versus-rhodium-platinum thermocouple of suitable specifications, the temperature being defined on the IPTS–48 [4] by

$$E=a^{\prime }+b^{\prime }{t}_{48}+c^{\prime }{t}_{48}^2,$$ (82)

and on the IPTS–68 [1] by

$$E=a+b{t}_{68}+c{t}_{68}^2.$$ (83)

In these equations E is the electromotive force of the thermocouple, and the six constants a′ … c are evaluated by calibration at the three fixed points listed in table 2. The IPTS–68 specifies that E shall have the respective values listed in the last column of table 2, within specified tolerances. We may regard these nominal values as defining for each of the two scales a “standard” emf-temperature function to which the emf of a given thermocouple may be corrected through its calibration.

Table 2.

Fixed points used for calibration of Pt/Pt – 10% Rh thermocouples using eq (82) and (83)

Fixed point	Defined temperature		Nominal electromotive force (IPTS–68) [1]
	IPTS–48 [4]	IPTS–68 [1]
	°C	°C	μV
Calibrated Pt resistance thermometer	630.5
Calibrated Pt resistance thermometer	(a)	630.74	5534
Normal freezing point of silver	960.8	961.93	9117
Normal freezing point of gold	1063.0	1064.43	10300

^aAccording to eq (80), t₄₈ = 630.538 °C when t₆₈ = 630.74 °C.

The right-hand sides of eq (82) and (83) may be equated, then t₄₈ replaced by (t₆₈ − μ) [eq (1), (2), and (6)]. The result on solving for μ may be written

$$\mu =\frac{\left(a^{\prime }-a\right)+\left(b^{\prime }-b\right)t_{68}+\left(c^{\prime }-c\right)t_{68}^2}{b^{\prime }+2c^{\prime }{t}_{68}-c^{\prime }\mu }.$$ (84)

The term − c′μ in the denominator is virtually negligible, but μ in this term may be replaced by − 1.616 + 0.002864t₆₈, which fits the three values of table 2 within 0.01 °C. After using the values of temperature and electromotive force listed in table 2 to solve eq (82) and (83) for the six constants a′ … c, their substitution into eq (84) gives the numerical equation

$$\mu =\frac{-1.3145+1.5016\left({10}^{-3}\right)t_{6\text{8}}+1.5625\left({10}^{-6}\right)t_{6\text{8}}^2}{1+4.101\left({10}^{-4}\right)t_{6\text{8}}}.\left[t_{68}=630.74\text{ to }{1064.43}^{°}\text{C}\right]$$ (85)

Differentiation of eq (85) gives

$$\frac{d\mu }{d{t}_{68}}=\frac{2.0407\left({10}^{-3}\right)\left[1+1.53135\left({10}^{-3}\right)t_{68}+3.1400\left({10}^{-7}\right)t_{6\text{8}}^2\right]}{{\left[1+4.101\left({10}^{-4}\right)t_{68}\right]}^2}.\left[t_{68}=630.74\text{ to }{1064.43}^{°}\text{C}\right]$$ (86)

3.4. 1,337.58 K (1,064.43 °C) to 10,000 K

Above the freezing point of gold both the IPTS–48 and the IPTS–68 define the temperature by the Planck Radiation Law, according to which, at wavelength λ and in the range dλ, the ratio of the spectral intensity at the absolute thermodynamic temperature T to that at the absolute themo-dynamic temperature of freezing gold, T(Au), is

$$\frac{\exp \left[\frac{c_2}{\lambda T(\text{Au})}\right]-1}{\exp \left[\frac{c_2}{\lambda T}\right]-1},$$ (87)

where c₂ is the so-called second radiation constant. The definition of T₄₈ is obtained by making the replacements T = T₄₈, c₂ = 1.438 cm kelvin, and T(Au) = 1336.15 K in (87) [4], and the definition of T₆₈ by the substitutions T = T₆₈, c₂ = 1.4388 cm kelvin, and T(Au) = 1337.58 K [1|. These functions for the two scales may, of course, be equated; when the equation is solved for T₄₈ and this then subtracted from T₆₈, it gives T₆₈ − T₄₈, or μ(T₆₈), exactly. A simpler numerical equation results by expanding some of the exponentials and dropping negligible terms; when the representative wavelength of optical pyrometers λ = 6.5(10⁻⁵) cm is substituted, the result is

$$\mu =5.56\left({10}^{-4}\right)T_{68}+3.84\left({10}^{-7}\right)\left(1-e^{-22135/T_{68}}\right)T_{6\text{8}}^2\left[T_{68}=1,337.58\text{ to }10,000\right]$$ (88)

Up to 10,000 K eq (88) is insensitive to wavelength, and the error in μ does not exceed about 0.1 kelvin.

Differentiation of eq (88) gives

$$\frac{d\mu }{d{T}_{68}}=5.56\left({10}^{-4}\right)+7.68\left({10}^{-7}\right)T_{68}-\left[8.5\left({10}^{-3}\right)+7.68\left({10}^{-7}\right)T_{68}\right]e^{-22135/T_{68}}\left[T_{68}=1,337.58\text{ to }10,000\right]$$ (89)

3.5. Discontinuities in the Temperature Derivatives of t₆₈ − t₄₈ at 630.74 and 1,064.43 °C

Though both the IPTS–48 and the IPTS–68 treat the “resistance thermometer” temperature range differently below and above 0 °C, the two scales are highly continuous at this temperature and no discontinuity in t₆₈ − t₄₈ (= μ) and its first two temperature derivatives exists, as demonstrated in section 3.1. This is not true where the “thermometer” and “thermocouple” ranges join (630.74 °C), nor where the “thermocouple” and “pyrometer” ranges join (1,064.43 °C). Though μ is continuous at these two temperatures, dμ/dt₆₈ is not, the discontinuity having a magnitude of about 0.001 in both cases.

Though these discontinuities reflect small corresponding discontinuities at these two temperatures in the IPTS–48 or the IPTS–68 or both, it is not the purpose here to discuss this question. The principal additional discontinuity introduced when calorimetric thermodynamic properties are converted from the basis of one temperature scale to that of the other is when the heat capacity-temperature function has been smoothed prior to this conversion: the conversion will introduce an approximately 0.1 percent discontinuity. Such an effect is virtually within the precision of the best present-day calorimetry at temperatures as high as 631 °C, but it may be desirable to avoid it in the systematic conversion of many existing tables.

An obvious simple expedient is to replace the functions μ(t₆₈), over a temperature range extending below and above each temperature of discontinuity, by a function which provides continuity with the pertinent original functions in both μ and dμ/dt₆₈ at the ends of the modified range. That the extent of such a modified range is normally an arbitrary decision is evident from consideration of the idealized simple case (sometimes approximated in reality) in which the heat capacity shows a discontinuity at one temperature but otherwise no change with temperature: How should one join the two disconnected segments smoothly? However, when the effect is as small as in the present case, this question can hardly be important.

The procedure outlined above was followed to derive simple polynomial “smooth” equations for the temperature ranges 570 to 690 °C and 1000 to 1120 °C. These equations are as follows.

$$\mu =0.1162+9.153\left({10}^{-4}\right)\left(t_{68}-570\right)+1.3328\left({10}^{-5}\right){\left(t_{68}-570\right)}^2-3.192\left({10}^{-8}\right){\left(t_{68}-570\right)}^3\left[t_{68}=570\text{ to }{690}^{°}\text{C}\right]$$ (90)

$$\mu =1.241+2.92\left({10}^{-3}\right)\left(t_{6\text{8}}-1000\right)-4.092\left({10}^{-6}\right){\left(t_{68}-1000\right)}^2-7.222\left({10}^{-9}\right){\left(t_{68}-1000\right)}^3\left[t_{68}=1000\text{ to }{1120}^{°}\text{C}\right]$$ (91)

These two equations and their first derivatives are compared in table 3 with the equations which it is proposed they displace in the temperature ranges indicated above when converting values that were previously smoothed with respect to temperature on the IPTS–48. When no such smoothing was done, eq (90) and (91) should not be used.

Table 3.

Comparison of the difference in the value of temperature, and its temperature derivative, given by the IPTS of 1968 and the IPTS of 1948 (a) as the two scales are defined and (b) as smoothed in the regions of discontinuity.

T68 (K)	T68 – T48 (kelvins)		d(T68 – T48)/dT48
	As defined	Smoothed	As defined	Smuothed
840	a+0.113		f+0.0009
850	.123	d+0.123	.0010	d+0.0011
860	.134	.135	.0012	.0013
870	.146	.150	.0013	.0016
880	.150	.166	.0015	.0018
890	.176	.185	.0017	.0020
900	a.194	.205	.0019	.0021
903.89	a, b.202	.214	f.0020	.0022
			g.0027
910	b.218	.227	.0027	.0023
920	.245	.251	.0027	.0024
940	.300	.301	.0027	.0026
960	.354	d.354	.0027	d.0027
980	b.409		g.0027
1260	b 1.202		g.0029
1280	1.261	e 1.261	.0029	e.0029
1300	1.319	1.316	.0029	.0027
1320	b 1.378	1.368	.0029	.0025
1337.58	b, e 1.430	1.410	g .0030	.0023
			h .0016
1350	e 1.45	1.44	.0016	.0022
1375	1.49	e 1.49	.0016	e .0019
1400	e 1.53		h.0016

^aEq (80).

^bEq (85).

^cEq (88).

^dEq (90).

^eEq (91).

^fEq (81).

^gEq (86).

^hEq (89).

3.6. Tabulated Values of (T₆₈ − T₄₈) and d(T₆₈ − T₆₈)/dT₆₈ at Round Temperatures of T₆₈ From 90 to 10,000 K

Values of T₆₈ − T₄₈(≡ μ) and d(T₆₈ − T₄₈)/dT₆₈ (= dμ/dt₆₈), computed from the equations derived in sections 3.1–3.4 [μ from eq (75), (80), (85), and (88); dμ/dt₆₈ from eq (81). (86), and (89)], are tabulated at round temperatures (T₆₈) in table 4. Below 0 °C, d(T₆₈ − T₄₈)/dT₆₈ was taken by averaging successive pairs of differences of values of T₆₈ − T₄₈ tabulated at intervals of 1 kelvin. Double entries are included for those temperatures for which the equations for the adjacent temperature ranges give different values (see discussion in sec. 3.5).

A similar table of T₆₈ − T₄₈ covering the range −180 to 4000 °C has been published [1]. The two tables agree exactly, to the number of significant figures given in each.