How Should Alcohol Problems Be Conceptualized? Causal Indicators Within the Rutgers Alcohol Problem Index

Abstract

Alcohol-related problems have traditionally been conceptualized and measured by an effect indicator model. That is, it is generally assumed that observed indicators of alcohol problems are caused by a latent variable. However, there are reasons to think that this construct is more accurately conceptualized as including at least some causal indicators, in which observed indicators cause the latent variable. The present study examined the measurement model of a well-known alcohol consequences questionnaire, the Rutgers Alcohol Problem Index. Participants were 703 students from a large public university in the Northeast mandated to an alcohol intervention. We conducted a zero tetrad test to examine a measurement model consisting solely of effect indicators and a model with both causal and effect indicators. Overall, the results suggested the hybrid model fit the data better than a model with only effect indicators. These findings have implications regarding the theoretical underpinnings of alcohol-related consequences.

Alcohol-related negative consequences have consistently been identified as a public health concern. More specifically, research has indicated that approximately 40–45% of college students have reported engaging in excessive drinking in the past 2 weeks (i.e., 5+ drinks for men and 4+ drinks for females; Wechsler et al., 2002), which has been found to contribute in the experiencing of negative consequences (Johnston, O’Malley, Bachman, & Schulenberg, 2009). Within the college student population, findings have indicated a variety of problems can occur due to alcohol consumption, such as missing classes, arguing with friends, and engaging in unplanned sexual activity (Wechsler et al., 2002). Hingson, Zha, and Weitzman (2009) found that, in the past year, college students experienced even more severe consequences related to alcohol use, including 646,000 assaults, 97,000 sexual assaults, 600,000 injuries, and 1,800 deaths. Therefore, to better understand the role of problems within college student drinking and help students reduce negative consequences related to alcohol use, the development of valid and reliable assessments that measure theoretically defined constructs has important implications for researchers and clinicians when establishing and implementing harm-reducing interventions.

There are several measures that have been developed and validated to examine alcohol-related problems (e.g., Hurlbut & Sher, 1992; Kahler, Strong, & Read, 2005; White & Labouvie, 1989). However, a unifying theoretical definition of the latent construct “alcohol-related problems” is not clearly stated or detailed in the literature. For example, in the development of the Rutgers Alcohol Problem Index (RAPI), White and Labouvie (1989) assessed types of problems that may occur due to drinking without an explicit definition of alcohol-related problems and highlight alcohol problems within a sample of adolescents using a developmental theoretical framework. Although White and Labouvie (1989) briefly mention two areas of alcohol-related problems (behavioral and physiological), these areas are not integrated into a common definition of the latent construct. Thus, we extend their conceptualization to include several common themes that emerge when examining alcohol-related consequences such as social problems (e.g., fights/arguments with others), physiological issues (e.g., passing out/fainting), and negative psychological states (e.g., guilt/shame). In essence, we propose the latent construct of alcohol-related problems encompasses the negative experiences that can occur simultaneously across biological, psychological, and social domains and are the result of an individual’s quantity and frequency of alcohol use.

RAPI

The RAPI has been a commonly used measure for examining alcohol-related negative consequences among college students. It was developed as a 23-item measure usually scored on a 5-point Likert-type scale ranging from 1 (never) to 5 (more than 10 times), where respondents indicate the frequency in which they experience a particular alcohol-related problem (e.g., “Not able to do homework or study for a test.”) within a specified time frame (e.g., in the past 6 months). Initial validation of the measure was conducted with an adolescent sample and yielded a unidimensional factor structure with good score reliability (α > .90). In an effort to provide support for a dichotomous version of the RAPI, Martens, Neighbors, Dams-O’Connor, Lee, and Larimer (2007) conducted both an exploratory factor analysis and a confirmatory factor analysis (CFA) to examine its factor structure. Results supported a three-factor solution: abuse/dependence, personal consequences, and social consequences. Additionally, the RAPI has been examined using item response theory (IRT), where one study found a reduction in gender bias through the removal of 7 items while retaining the relation between problems and alcohol consumption (Earleywine, LaBrie, & Pedersen, 2008). Another study using IRT suggested an 18-item version was invariant between men and women from senior year in high school to freshman year in college, where items appeared to assess for the more severe range on the latent trait (Neal, Corbin, & Fromme, 2006).

Overall, studies examining the psychometric properties of the RAPI have indicated adequate internal consistency and correlations in expected directions with theoretically relevant constructs (see Devos-Comby & Lange, 2008). Since its inception, researchers have also conducted a substantial number of studies, most notably within the college student population, utilizing the RAPI as an outcome measure in randomized controlled trials (e.g., Larimer et al., 2001; Neighbors, Larimer, & Lewis, 2004) and as a criterion variable in scale validation studies (e.g., Bonar et al., 2011; Collins, Logan, & Neighbors, 2010). However, virtually all researchers have assumed effect indicators comprise the RAPI without taking into consideration possible items actually affecting this latent variable.

Causal and Effect Indicators

In spite of the amount of work devoted to establish the psychometric properties of the RAPI, there is one crucial aspect that has been overlooked in the literature. By relying exclusively on IRT and classical test theory frameworks to examine the psychometric properties of measures assessing alcohol-related problems such as the RAPI, researchers have inadvertently limited their understanding by not conducting preliminary analyses to accurately identify the structure of the measurement model. Analyses based both in classical test theory and IRT have an implicit assumption that any observed variables included in the model are dependent on latent variables (i.e., effect indicators) without considering possible causal indicators.

Within the current literature, there has been an ongoing debate regarding the relevance of identifying causal indicators and even terminology in structural equation modeling (e.g., Bollen, 2011; Diamantopoulos, Riefler, & Roth, 2008; Hardin & Marcoulides, 2011; Howell, Breivik, & Wilcox, 2007; West & Grimm, 2014). We can only present a brief overview here. The perspectives of those arguing against causal indicators involve concerns regarding insufficient theoretical underpinnings, validity issues, misinterpretation of measurement research, and measurement misspecification (see Hardin & Marcoulides, 2011). However, West and Grimm (2014) among others (e.g., Bainter & Bollen, 2014) have asserted that when causal indicator model assumptions are met, the structure of the measurement model is stable and can be trusted to specify models. Indeed, Bainter and Bollen (2014) provided support that coefficients in causal indicator models are invariant. In another review, Diamantopoulos, Riefler, and Roth (2008) encourage the use of causal models by highlighting the importance of theoretical conceptualizations, model specification, and validity. Moreover, Coltman, Devinney, Midgley, and Venaik (2008) have suggested a specific decision-making process when developing a causal model that focus on underlying assumptions, theoretical underpinnings, and importance of empirical evidence. Although the debate continues, there is support in the literature for conducting rigorous, theoretically grounded studies that examine models that incorporate causal measurement indicators.

Because there is conflicting use of terminology when discussing causal indicators, we follow the definitions of Bollen and Bauldry (2011) and refer the reader to their article for more details. We define causal indicators, here, as indicators or measures of a latent variable that affect the latent variable. As measures, the causal indicators should correspond to the theoretical definition of the concept being measured. Furthermore, it is highly unlikely that causal indicators will explain all of the variance in the latent variable; thus, there also will be a disturbance or error term to complete the latent variable.¹

There has been a growing effort to examine the role of causal indicators using analytic techniques, such as a multiple indicators-multiple causes or the vanishing tetrad test (VTT), which could result in either a causal model or a hybrid model consisting of both causal and effect indicators (Bollen, 1990; Bollen & Lennox, 1991; Bollen, Lennox, & Dahly, 2009; Bollen & Ting, 2000). The underlying assumption that all items are effect indicators has consequences associated with model misspecification, biased parameter estimates, inappropriate removal of items, or restricting the understanding of a latent variable’s theoretical underpinnings (Bollen & Bauldry, 2011; Bollen & Lennox, 1991). Failing to consider causal indicators raises the possibility of biased estimates and a flawed understanding of alcoholrelated problems. Therefore, testing effect and causal indicators within the measurement model allows researchers to address these concerns and provide a better conceptualization of the underlying structure for a given instrument.

One underused technique for examining hybrid models consisting of both causal and effect indicators is the VTT used to examine vanishing tetrads implied by a hypothesized model (Bollen & Ting, 1993, 1998, 2000). Tetrads are differences in the products of covariance pairs for four observed variables. Three tetrads can be determined from the four observed variables and six covariances. As described below using notation by Kelley (1928), the population covariance of two variables is represented by σ and τ_ghij refers to σ_gh σ_{ij -} σ_gi σ_hj, where three tetrads are then derived:

$${\tau }_{1234}={\sigma }_{12}{\sigma }_{34}-{\sigma }_{13}{\sigma }_{24},$$

$${\tau }_{1324}={\sigma }_{13}{\sigma }_{24}-{\sigma }_{14}{\sigma }_{23},$$

$${\tau }_{1423}={\sigma }_{14}{\sigma }_{23}-{\sigma }_{12}{\sigma }_{34}.$$

Therefore, a vanishing tetrad is determined when τ_ghij = 0. Depending on the structure of a hypothesized model, some of these tetrads are zero (model-implied vanishing tetrad) while others are not. If nonzero tetrads are discovered within the model implied zero tetrads, the appropriateness of the model is questioned (Bollen & Ting, 1993). Significance testing as described in Bollen and Ting (2000) is one method for selecting model implied vanishing tetrads, where H₀: τ = 0 (all effect indicators) and H₁: τ ≠ 0 (all or some causal indicators). Thus, a significant test statistic supports H₁ and suggests that some of the vanishing tetrads implied by the model are significantly different from zero and indicates poor model fit. This approach can be used for nested and nonnested models to empirically test for effect and causal indicators. In essence, causal and effect indicator models are not necessarily nested in the traditional sense because parameters from the causal indicator model (i.e., unidentified models due to inability to constrain unknown parameters) are inherently different from those of the effect indicator model (i.e., specified models as a function of parameters), as the parameters in one model cannot be the constrained form of the other and cannot be tested using conventional likelihood methods (Bollen & Ting, 2000). However, both models can be nested via vanishing tetrads providing a test for relative model fit, where the null hypothesis is the set of vanishing nonredundant tetrads (i.e., comparisons for intercorrelations between sets of errors that approach zero). Note, this is merely a brief overview of VTT and a more detailed description can be made available by the author or found in Bollen and Ting (1993, 1998, 2000).

Past research regarding the measurement of alcohol-related consequences has focused on models implicitly assuming all variables are effect indicators with no studies examining the possible existence of causal indicators within the measures (e.g., Kahler et al., 2005; White & Labouvie, 1989). To provide an example for applying an important but underused methodological technique, we have examined the RAPI using VTT to extend the theoretical framework of alcohol-related problems. Specifically, the purpose of the present study was to examine the measurement model of the RAPI by specifying a priori a model consisting of both causal and effect indicators compared to models including solely effect indicators or only causal indicators. We hypothesized the model with both causal and effect indicators would fit the data better than a model specifying all effect indicators or a model consisting of causal indicators only.

Method

Participants and Procedures

Participants were 734 students from a Northeastern university who received a judicial sanction for an alcohol-related offense and were participating in a larger study examining the efficacy of three, group-based alcohol interventions (Cimini et al., 2009; see Table 1 for demographic information for Sample 1 and Sample 2). Participants who provided complete data on the RAPI at baseline were included in Sample 1: n = 703, 96% of the total sample. Those who completed the RAPI at 6-month follow-up were included in Sample 2: n = 456, 62.8% of the total sample.

Table 1.

Demographics.

Characteristic	Sample 1, % (n = 703)	Sample 2, % (n = 456)
Gender
Male	62	58
Female	38	42
Ethnicity
White	82.80	82.40
American Indiana	4.40	4.10
Asian	0.30	0.20
Native Hawaiian/Pacific Islander	0.30	0.20
Black	2.50	2.60
Hispanic	6.40	6.70
Multiracial	1.30	1.40
Other ethnicity	2.00	2.40
Age	Mean = 19 (SD = 0.83)	Mean = 19 (SD = 0.82)
Year in school
Freshman	50	48
Sophomore	36	35
Junior	13	15
Senior	1	2
Living situation
On campus	97	98
Off campus	3	2

This study’s procedures will only be summarized here and were reported in detail elsewhere (see Cimini et al., 2009). College students who committed an on-campus judicial infraction involving alcohol and were mandated by the university to attend an alcohol intervention were eligible to participate in the study. They had the option of participating in the research intervention or an alternative intervention provided by the university counseling center, which required a similar time commitment. Those interested in participating completed a series of questionnaires at baseline and attended one of the three 90-min group intervention sessions after completing baseline measures. Participants completed a battery of questionnaires at 6-month follow-up and 12-month follow-up and received a US$25 gift card after completing each portion of the study. Institutional review board approval was obtained for this project. The interventions had no effect on alcohol use or alcohol-related problems (Cimini et al., 2009); thus, for these analyses, participants were collapsed across conditions.

Within the battery of baseline questionnaires, participants were asked to complete demographic items and an alcohol problems measure. Participants completed demographic items that obtained information such as gender, ethnicity, age, and year in school. Additionally, participants were asked to complete the 23-item RAPI (White & Labouvie, 1989) by indicating the frequency they experienced a specific alcohol-related problem within the past 6 months on a 5-point Likert-type scale (1 = never to 5 = more than 10 times).

Models

Before conducting analyses, we examined the 23 RAPI items to determine a priori those items that appeared to reflect and/or affect the latent construct of alcohol-related consequences. When selecting items to be treated as effect indicators, we followed the definition that effect indicators are determined based on both conceptual and empirical grounds, where part of the empirical evidence is garnered through conducting tetrad tests (see Bollen et al., 2009). Since the RAPI was a preexisting measure, we used a similar framework for decision making posited by Coltman and colleagues (2008). In essence, the important conceptual questions Coltman and colleagues (2008) suggested asking include (1) is the latent construct (e.g., alcohol problems) independent of its indicators or a combination of them? (2) what direction is the causality between the latent construct and the items used to measure the construct? and (3) how are the indicators characteristically related such as thematically similar, interchangeable, and if the conceptual domain of the construct changes with the omission or removal of an item? In addition to conceptual questions, we considered empirical questions as suggested in relation to how items intercorrelate and in what ways do the items and latent construct share relationships with related variables used to test convergent/discriminant validity and considerations of measurement error and collinearity (Coltman, Devinney, Midgley, & Venaik, 2008).

There are plausible theoretical reasons to believe that items measuring alcohol-related problems might be better conceptualized as causal indicators. In particular, it is unlikely that a change in the latent variable alcohol-related problems would simultaneously lead to changes in all of its indicators. Instead, it seems more reasonable to think that changes in any of the observed indicators should lead to a change in the latent variable. For example, a single change in the indicator related to negative physiological experiences (e.g., “Passed out or fainted suddenly”) due to the effects of alcohol could lead to a change in the latent variable alcohol-related problems as opposed to the latent variable eliciting changes in all indicators simultaneously that are associated with negative social (e.g., “Had a fight, argument, or bad feelings with a friend?”), physiological, and psychological (e.g., “Caused shame or embarrassment to someone”) experiences. Some items, though, appeared to represent effect indicators (e.g., “Felt that you had a problem with alcohol”). Theoretically, these items would be endorsed after having experience with alcohol problems such as “Passed out or fainted suddenly”; thus, the latent variable would change resulting in change for items that represent an interpretation of the negative experience (e.g., “Felt that you had a problem with alcohol”). Moreover, indicators of alcohol-related problems are not interchangeable, and the omission of some (e.g., items measuring driving under the influence of alcohol) has the potential to bias the coefficients of the causal indicators that affect the latent variable (Bollen & Bauldry, 2011).

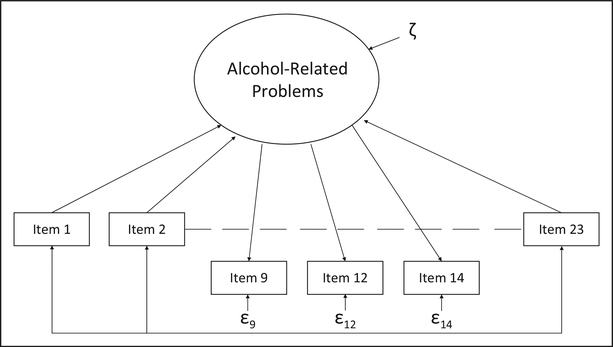
We concluded 3 items could be conceptualized as effect indicators: Item 9, “Tried to control your drinking by trying to drink only at certain times of the day or certain places”; Item 12, “Felt that you had a problem with alcohol”; and Item 14, “Tried to cut down or quit drinking.” Conceptually, these items appeared to assess interpretations individuals had regarding their alcohol-related experiences. The remaining 20 items (e.g., “Passed out or fainted suddenly”) were treated as causal indicators. We determined these items to assess the direct behavior resulting from an individual’s alcohol intake.

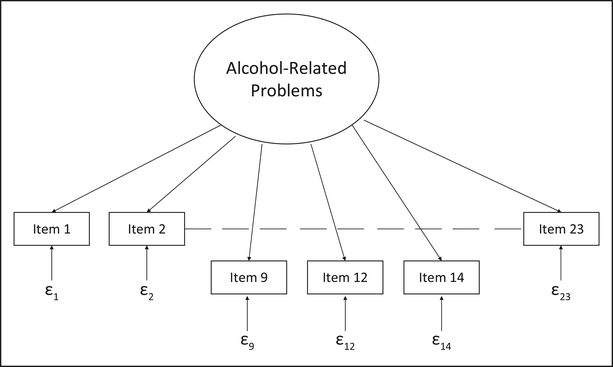
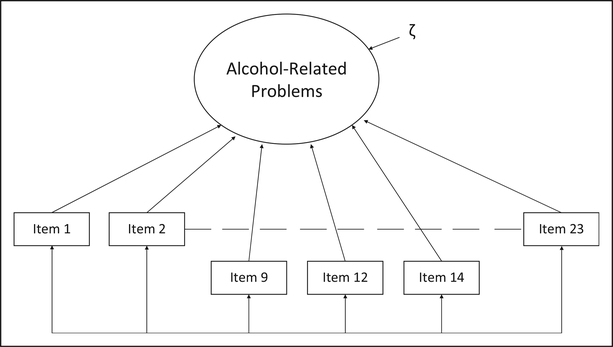
We specified three models to compare and determine which one fit the data better. In Model 1, we included all items as effect indicators (see Figure 1). This was considered the default model, as it is most commonly used when examining the alcohol-related problems latent construct. Although revised versions of the RAPI have been developed, the original unidimensional measure has been the most widely used (see Martens, Arterberry, Cadigan, & Smith, 2012) and will be used here due to its far-reaching importance throughout alcohol research studies. For the RAPI, the effect indicator model implicitly assumes the items to demonstrate experiences of alcohol problems. Model 2 consisted of all causal indicators (see Figure 2). This model was important in considering whether the RAPI would be better modeled using a solely causal indicator framework and constitutes the baseline model for analyses, given that it is a 0 degree of freedom model, against which the other models are initially compared. This comparison provided an important step in examining causal indicators within the RAPI, as prior research had not considered this possibility and it aides in the interpretability of the findings. Finally, we included Model 3 as a hybrid model consisting of both causal and effect indicators and may represent a more comprehensive theoretical understanding of the latent variable (see Figure 3).

Figure 1.

All effect indicators.

Figure 2.

All causal indicators.

Figure 3.

Hybrid model with Items 9, 12, and 14 as effect indicators.

Data Analysis

We used an R (version 3.2.1) package (TetradSEM) to conduct zero tetrads tests. The R package (TetradSEM) utilizes two approaches to conduct zero tetrads tests. The first one requires the identification of nonredundant zero tetrads to construct test statistics. Since the test statistics based on nonredundant zero tetrads follows a χ² distribution, we can conduct a χ² test. The test statistics approximation to a χ² distribution requires an adequate sample size (Bollen & Ting, 1998). Johnson and Bodner (2007) proposed an adjustment to the test statistic that has better finite sample performance than does the original statistic and we use this method for our tests. The VTT has been found to control for Type I error rates adequately, though power does decrease as the number of indicators increase (Bollen & Ting, 1998; Johnson & Bodner, 2007). More technical details on these tests are in Bollen’s (1990), Bollen and Ting’s (1993, 1998, 2000), and Johnson and Bodner’s (2007) studies.

In our study, the second model (all causal indicators) implies no zero tetrads and can therefore be used as a baseline model for comparison. Since our two additional models are nested in terms of their vanishing tetrads, such that the first model (all effect indicators) has more zero tetrads implied than does the third (Items 9, 12, and 14 effect indicators), we can compare these two models by testing whether the additional tetrads for the first model are zero in the population. Since the number of variables in the data was large (23 variables), the identification of nonredundant zero tetrads were computationally extensive. Therefore, we chose to use the bootstrap method for hypothesis testing, where a significant p value indicates poor fit.

Post hoc analyses were also performed. We conducted CFA using Mplus 7.0 (Muthén & Muthén, 2012) to compare and examine model fit indices for the effect indicator model and hybrid model. A CFA was performed for Sample 1 and Sample 2 to examine model fit in two separate samples.

Results

Table 2 shows the correlations among items in the RAPI as well as the means and standard deviations. All items in the RAPI were positively correlated: rs = .14–.62, ps < .01. Although nonzero correlations are expected with an effect indicator model, it does not provide sufficient evidence to dismiss the presence of causal indicators (Bollen & Bauldry, 2011). For this reason, a VTT was conducted to more formally determine the model underlying these data.

Table 2.

RAPI Item Correlations, Means, and Standard Deviations.

Items	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23
1 Not able to do your homework or study for a test?	1
2 Got into fights, acted bad, or did mean things?	.35**	1
3 Missed out on other things because you spent too much money on alcohol?	.42**	.29**	1
4 Went to work or school high or drunk?	.36**	.33**	.35**	1
5 Caused shame or embarrassment to someone?	.32**	.54**	.32**	.31**	1
6 Neglected your responsibilities?	.62**	.37**	.41**	.43**	.42**	1
7 Relative avoided you?	.24**	.16**	.24**	.24**	.30**	.27**	1
8 Felt that you needed more alcohol than you used to use in order to get the same effect?	.37**	.43**	.38**	.37**	.34**	.39**	.22**	1
9 Tried to control your drinking by trying to drink only at certain times of the day or in certain places?	.23**	.21**	.29**	.17**	.23**	.20**	.19**	.33**	1
10 Had withdrawal symptoms, that is, felt sick because you stopped or cut down on drinking?	.30**	.14**	.25**	.22**	.18**	.24**	.43**	.26**	.23**	1
11 Noticed a change in your personality?	.27**	.25**	.21**	.19**	.31**	.30**	.31**	.31**	.27**	.31**	1
12 Felt that you had a problem with alcohol?	.28**	.22**	.24**	.28**	.26**	.33**	.19**	.26**	.30**	.43**	.35**	1
13 Missed a day (or part of a day) of school or work?	.53**	.34**	.39**	.34**	.35**	.55**	.25**	.36**	.20**	.18**	.26**	.19**	1
14 Tried to cut down or quit drinking?	.34**	.30**	.35**	.27**	.34**	.32**	.26**	.32**	.38**	.37**	.38**	.47**	.26**	1
15 Suddenly found yourself in a place that you could not remember getting to?	.34**	.42**	.29**	.40**	.35**	.37**	.21**	.43**	.24**	.28**	.31**	.39**	.33**	.38**	1
16 Passed out or fainted suddenly?	.24**	.25**	.18**	.34**	.26**	.29**	.20**	.25**	.15**	.26**	.20**	.34**	.18**	.25**	.46**	1
17 Had a fight, argument, or bad feelings with a friend?	.37**	.57**	.22**	.28**	.47**	.35**	.16**	.37**	.18**	.19**	.31**	.26**	.34**	.28**	.36**	.26**	1
18 Had a fight, argument, or bad feelings with a family member?	.19**	.30**	.23**	.28**	.38**	.26**	.33**	.25**	.22**	.31**	.31**	.33**	.18**	.30**	.26**	.27**	.40**	1
19 Kept drinking when you promised yourself not to?	.38**	.30**	.30**	.28**	.34**	.36**	.35**	.30**	.34**	.36**	.41**	.44**	.26**	.50**	.37**	.28**	.33**	.32**	1
20 Felt you were going crazy?	.34**	.21**	.24**	.34**	.31**	.36**	.25**	.23**	.16**	.39**	.38**	.46**	.28**	.36**	.36**	.24**	.27**	.30**	.43**	1
21 Had a bad time?	.30**	.31**	.36**	.27**	.33**	.34**	.22**	.37**	.24**	.17**	.32**	.26**	.33**	.31**	.31**	.17**	.36**	.28**	.31**	.25**	1
22 Felt physically or psychologically dependent?	.32**	.32**	.33**	.29**	.35**	.36**	.28**	.33**	.21**	.40**	.34**	.46**	.29**	.36**	.43**	.26**	.28**	.29**	.38**	.45**	.30**	1
23 Was told by a friend or neighbor to stop or cut down drinking?	.28**	.26**	.25**	.25**	.28**	.28**	.30**	.31**	.24**	.46**	.39**	.48**	.24**	.45**	.38**	.32**	.30**	.27**	.46**	.41**	.22**	.42**	1
Mean	.56	.59	.56	.54	.43	.63	.07	.78	.51	.09	.38	.19	.63	.43	.49	.25	.51	.14	.28	.16	.76	.18	.22
SD	0.85	0.84	0.92	1.04	0.72	0.89	0.35	1.13	1.05	0.40	0.8	0.59	0.86	0.81	0.84	0.62	0.74	0.45	0.68	0.56	0.83	0.57	0.61

Note. RAPI = Rutgers Alcohol Problem Index.

^**p < .01.

Results of the zero tetrad test suggested the effect indicator only model was statistically significant (p < .001), which means that some of the vanishing tetrads implied by the model are significantly different from zero, and indicates poor fit (see Table 3). This also supported the hypothesis that causal indicators were part of the measurement model. Because the causal indicator model implies no vanishing tetrads, the zero tetrad test indicated the causal model fit the data better than the effect indicator only model. Additionally, the nested zero tetrad test suggested the hybrid model including both causal and effect indicators fit the data better than the effect indicator only model, as indicated by a nonsignificant test statistic (p = .972). Not only did the hybrid model have a better fit to the data than the effect indicator model but was also a more parsimonious solution than the causal indicator model. Therefore, the hybrid model was not rejected in favor of the causal indicator model.

Table 3.

Zero Tetrad Tests.

Nonnested zero tetrad test
Model		Bootstrapped p Value
Model 1		<.001
Model 3		.972
Nested zero tetrad test
H0	H1	Bootstrapped p Value
Model 1	Model 3	<.001
Model 2	Model 3	.972

Note. χ² values are not available because the bootstrap method was used. Model 1 = all effect indicators; Model 2 = all causal indicators; Model 3 = hybrid model with Items 9, 12, and 14 as effect indicators; H0 = null model; H1 = hypothesized model.

Post Hoc Analyses

Since the hybrid model was identified as the best fitting and most parsimonious model, the variance associated with each effect indicator that was accounted for by the latent variable and model fit indices were also examined. We performed CFAs for the effect indicator model and a hybrid model with both causal and effect indicators. To provide more evidence of model fit after conducting the VTT, we not only performed the CFA on Sample 1 but also supported our findings in Sample 2.

Sample 1

After conducting a CFA for the hybrid and effect indicator model, findings indicated that the hybrid model had better fit, χ² = 155.89, df = 41, p < .001; root mean square of approximation (RMSEA) = 0.06, comparative fit index (CFI) = 0.87, Tucker–Lewis index (TLI) = 0.80, standardized root mean square residual (SRMR) = 0.02, than the effect indicator only model, χ² = 1,425.77, df = 230, p < .001; RMSEA = 0.09, CFI = 0.79, TLI = 0.77, SRMR = 0.06. Furthermore, results indicated R² values for the hybrid model ranged from .16 (Item 9) to .39 (Item 12). The latent variable alcohol-related problems accounted for 16% of the variance in “Tried to control your drinking by trying to drink only at certain times of the day or certain places” (Item 9), 39% of the variance in “Felt that you had a problem with alcohol” (Item 12), and 38% of the variance in “Tried to cut down or quit drinking.” (Item 14).

Sample 2

The CFA using Sample 2 yielded similar results. Findings suggested that the CFA for the hybrid model had better fit, χ² = 111.19, df = 41, p < .001; RMSEA = 0.06, CFI = 0.93, TLI = 0.90, SRMR = 0.02, than the effect indicator model, χ² = 1,347.89, df = 230, p < .001; RMSEA = 0.10, CFI = 0.84, TLI = 0.82, SRMR = 0.06. Additionally, R² values ranged from .32 (Item 9) to .70 (Item 12) for the hybrid model. The alcohol problems latent variable accounted for 32% of the variance in Item 9, 70% of the variance in Item 12, and 45% of the variance in Item 14.

Discussion

The goal of this study was to provide an example for examining causal indicators within a measurement model using a confirmatory test/VTT on the widely used RAPI. Results indicated, as hypothesized, the hybrid model fit better than one consisting exclusively of effect indicators or causal indicators only. These findings were supported in Sample 1 and Sample 2 (baseline and 6-month follow-up). Currently, the status quo for score validation of assessments has focused almost entirely on traditional scale development methods (see Haynes, Smith, & Hunsley, 2011), which implicitly assume models consist only of effect indicators without consideration of possible causal indicators. Modeling both causal and effect indicators, when appropriate, has the potential to provide researchers and clinicians with more accurate assessments and theoretically comprehensive conceptualizations to enhance their understanding of clinically relevant constructs.

Prior research regarding the psychometric properties of the RAPI has relied solely on the notion that each item is an effect indicator (e.g., Martens, Neighbors, Dams-O’Connor, Lee, & Larimer, 2007; Neal et al., 2006; White & Labouvie, 1989). In contrast, our findings suggested that the model containing 20 causal indicators and 3 effect indicators fit the data better than a model with 23 effect indicators. Therefore, items modeled as effect indicators, “Tried to control your drinking by trying to drink only at certain times of the day or certain places,” “Felt that you had a problem with alcohol,” and “Tried to cut down or quit drinking,” were deemed to more accurately reflect behaviors or beliefs that result after experiencing alcohol problems. Not only was the hybrid model a better fit to the effect indicator model but also was replicated using a second sample at 6-month followup. The latent variable also accounted for 16–31%, 39–70%, and 38% of the variance in Items 9, 12, and 14, respectively. Conversely, items modeled as causal indicators such as”Had a bad time,” “Passedout orfaintedsuddenly,” or “Neglected your responsibilities” were considered to represent different forms of alcohol-related problems occurring as a direct result of alcohol use.

In terms of the RAPI, a combined model can potentially maintain adequate internal consistency and dimensionality; however, inconsistencies in score reliability and validation of scores have been detailed throughout the literature, with scale refinement studies eliminating possible items important to measuring the construct (Earlywine et al., 2008; Neal et al., 2006) or identifying multiple dimensions of a traditionally unidimensional measure (Martens et al., 2007). A myriad of reasons could explain these differences, such as error in item selection, sampling differences, and continuous versus categorical response options. Another viable explanation for this inconsistency across studies may be related to our findings that suggested a majority of the items comprising the RAPI are actually causal indicators. Causal indicators perform fundamentally different within the measurement model, in that they can result in positive, negative, or no interitem correlation. The fact that only positive correlations were found among the items (see Table 1) might suggest that potentially relevant items have been removed in the development process of the RAPI because researchers have been looking for “well-behaved” effect indicators. Indeed, White and Labouvie (1989) considered a set of 52 items in the development of the RAPI and retained items based on their loadings. Items that were not retained assessed important dimensions of alcohol-related problems, such as driving under the influence of alcohol, seeking advice or going to treatment for alcohol problems, and not being able to stop drinking. Some of these items would likely be retained if a measure of alcohol-related problems was developed within a causal indicator model conceptualization. Therefore, researchers who expand their view of scale development have an opportunity to move beyond making inherent assumptions about constructs and create more meaningful empirical and theoretical models.

Toward an Improved Conceptualization of Alcohol-Related Problems

These findings regarding the factor structure of the RAPI have important implications for the theoretical underpinnings of alcohol-related problems. Although researchers have developed and examined the psychometric properties of several alcohol-related problems measures such as the RAPI, conceptualizations have been limited by examination of effect indicator only models. These definitions have implications regarding the experience of alcohol-related problems and are important in conceptualizing how it affects an individual. However, researchers have not been able to provide an explicit, comprehensive operationalized definition or theoretical underpinning for this latent construct. Additionally, the RAPI might not be optimal in assessing alcohol-related problems, as causal indicators were not considered during development. This highlights new directions for creating an alcohol problems scale that would incorporate both causal and effect indicators at the development stage, thus representing the latent construct of alcohol-related problems more robustly.²

By determining alcohol-related problems, as assessed by the RAPI, consist of both causal and effect indicators, they can be conceptualized more broadly within a biopsychosocial framework, where causal indicators would be observed behaviors related to physiological and social experiences that affect the latent construct alcohol-related problems such as “Passed out or fainted suddenly” or “Had a fight, argument, or bad feelings with a friend”; and effect indicators would be psychological interpretations (e.g., guilt and shame) and those leading to modification of behavior such as “Tried to cut down or quit drinking” or “Felt you had a problem with alcohol” that would simultaneously reflect change in the latent construct. In essence, alcohol-related problems would consist of both experiencing the direct effects of alcohol use along with an individual’s interpretation of their alcohol use experiences. For example, when using the RAPI as an outcome measure, researchers routinely discuss intervention effects by interpreting RAPI scores as reduction of behaviors that result from alcohol use (e.g., Martens et al., 2004). Several issues arise regarding this type of explanation, such as narrowly conceptualizing alcohol-related problems, inferring a causal model when only an effect model has been examined, thus inaccurately implying an individual’s interpretation of consequences simultaneously has the same repercussions as direct physical/social/emotional consequences that occur based on quantity of alcohol use. By identifying a hybrid model, we have broadened the theoretical underpinnings of alcohol-related consequences that may elucidate the subtleties among at-risk/high-risk/excessive alcohol use and alcohol dependence within a biopsychosocial framework. Therefore, examining the differences between causal and effect indicators has the potential to distinguish alcohol-related problems more accurately based on a more precise theoretical understanding of the latent construct.

Limitations

There were limitations to the study that warrant caution. Although findings suggested the hybrid model fit the data better than an effect only indicator model, model fit indices for the hybrid model were not a good fit in Sample 1 with better fit in Sample 2. These results suggest that other models (e.g., consisting of more/less effect indicators) may exist with a better fit. Additionally, the identification of more effect indicators may be plausible. Thus, future research would benefit from replicating these results through confirmatory testing on other samples and comparing the hybrid model to other a priori models. The indicators in this study may affect the latent construct of alcohol consequences but could also represent another unspecified latent construct as effect indicators. However, this could be related to the naming problem or nominalistic fallacy in latent variable modeling that indicates that the label assigned to a variable is not an indicator for whether it is adequately understood or correctly named (Cliff, 1983). Moreover, there has been an ongoing debate as to limitations in causal models regarding theoretical underpinnings, validity, and model identification when including causal indicators within measurement. Future researchers would benefit from monitoring new developments related to latent variable modeling with causal indicators to ensure they are using the most recent guidelines in incorporating this technique. Finally, the present samples were comprised of a majority of Caucasian, freshmen, and sophomores from one university who had received a judicial sanction for alcohol use and limits the generalizability of the findings. Additionally, Sample 2 had a high attrition rate that could affect direct comparisons of model fit. Future research should determine the extent to which the current findings apply to alcohol-related problems in other populations,³ such as clinical samples in which not only the severity but also the nature of the problems might be different.

In spite of these limitations, our findings have suggested a broader theoretical underpinning of alcohol-related problems, where including causal and effect indicators may provide a more robust understanding of them. Thus, we encourage future research to include the hybrid model suggested here for better understanding and conceptualizing of alcohol-related problems. Additionally, we contend that researchers be more mindful of the analyses used to establish the psychometric properties of scales. The RAPI was used as an example to encourage researchers to use newer psychometric methods instead of relying on traditional methods of psychometric analyses that may be less appropriate. Thus, we urge researchers to take time and consider what the correct methodology would be in order to develop and validate our assessments. Finally, although alcohol use disorders are conceptualized as a harmful dysfunction (Wakefield & Schmitz, 2015) that goes beyond merely experiencing alcohol-related problems, these are clearly related constructs, and future research should determine to what extent this important diagnosis is adequately conceptualized in terms of an effect indicator model, as opposed to a causal indicator or hybrid model.