Abstract
Gene-environment association (GEA) studies are essential to understand the past and ongoing adaptations of organisms to their environment, but those studies are complicated by confounding due to unobserved demographic factors. Although the confounding problem has recently received considerable attention, the proposed approaches do not scale with the high-dimensionality of genomic data. Here, we present a new estimation method for latent factor mixed models (LFMMs) implemented in an upgraded version of the corresponding computer program. We developed a least-squares estimation approach for confounder estimation that provides a unique framework for several categories of genomic data, not restricted to genotypes. The speed of the new algorithm is several order faster than existing GEA approaches and then our previous version of the LFMM program. In addition, the new method outperforms other fast approaches based on principal component or surrogate variable analysis. We illustrate the program use with analyses of the 1000 Genomes Project data set, leading to new findings on adaptation of humans to their environment, and with analyses of DNA methylation profiles providing insights on how tobacco consumption could affect DNA methylation in patients with rheumatoid arthritis.
Software availability: Software is available in the R package lfmm at https://bcm-uga.github.io/lfmm/.
Keywords: gene-environment association, local adaptation, ecological genomics, confounding factors, statistical methods
Introduction
Association studies have been extensively used to identify genes or molecular markers associated with disease states, exposure levels or phenotypic traits. Given a large number of molecular markers, the objective of those studies is to test whether any of the markers exhibits significant correlation with a primary variable of interest. Among those methods, gene-environment association (GEA) studies propose to test for correlation with ecological gradients in order to detect genomic signatures of local adaptation (Savolainen et al. 2013).
Although they bring useful information on the molecular targets of selection, GEA studies suffer from the problem of confounding. This problem arises when there exist unobserved variables that correlate both with the primary variables and genomic data (Wang et al. 2017). Recently, several model-based approaches have been introduced to evaluate GEA while correcting for unobserved demographic processes and population structure. Those methods include the programs BAYENV (Günther and Coop 2013), BAYPASS (Gautier 2015), BAYESCENV (Villemereuil and Gaggiotti 2015), and latent factor mixed model (LFMM) (Frichot et al. 2013; Frichot and François 2015). The use of those methods has become popular in ecological genomics, and several surveys have shown that they are robust to departure from their model assumptions (De Mita et al. 2013; Villemereuil et al. 2014; Lotterhos and Whitlock 2015; Rellstab et al. 2015). One drawback of those approaches, however, is to rely on Markov chain Monte Carlo algorithms or Bayesian bootstrap methods to perform parameter inference and statistical testing. Monte Carlo methods are flexible and allow complex models to be implemented in a computer program, but they can be highly intensive and they run slowly. Although some programs have parallel versions for multiprocessor systems, there is a need to develop fast and accurate methods that scale with the very large dimensions of genomic data sets and save computer energy.
In this study, we present a new version of the LFMM algorithm based on the solution of a regularized least-squares minimization problem. In addition, the new models are extended to handle data other than genotypes, and to perform multivariate regressions with more than one explanatory variable or a more general design matrix. Until now, GEAs have mainly focused on single-nucleotide polymorphisms (SNPs) by examining genetic variants in different individuals. In recent years, other categories of data have emerged and become of specific interest. For example, some epigenome-wide association studies (EWAS) measure DNA methylation levels in different individuals to derive associations between epigenetic variation and exposure levels or phenotypes (Rakyan et al. 2011; Teschendorff and Relton 2018). Here, we extend the definition of the LFMM data matrix to DNA methylation profiles and other molecular markers within a unified framework (Leek and Storey 2007; Carvalho et al. 2008). We present our new LFMM method in the next section. Then we demonstrate that our new method is several orders faster than its previous Bayesian version without loss of power or precision. In a GEA study of individuals from the 1000 Genomes Project, the new program detects genes linked to climate in humans. In an EWAS of patients with rheumatoid arthritis (RA), it identifies a set of genes for which DNA methylation potentially mediates the effect of tobacco consumption on the disease phenotype.
New Approach
GEA methods evaluate associations between the elements of a response matrix, Y, and some variables of interest, called “environmental” or “primary” variables, X, measured for n individuals. The response matrix records data for the n individuals, which often correspond to genotypes measured from p genetic markers. Here we extend the definition of Y to DNA methylation profiles (beta-normalized values) or gene-expression data. Nuisance variables such as observed confounders can be included in the X matrix, which dimension is then , where d represents the total number of primary and nuisance variables.
LFMMs are regression models combining fixed and latent effects as follows
| (1) |
The fixed effect sizes are recorded in the B matrix, which has dimension p × d. The E matrix represents residual errors, and it has the same dimensions as the response matrix. The matrix W is a “latent matrix” of rank K, defined by K latent factors where K can be determined by model choice procedures (Leek and Storey 2007; Frichot et al. 2013). The K latent factors represent unobserved confounders which are modeled through an n × K matrix, U. The matrix U is obtained from a singular value decomposition (SVD) of the matrix W as follows
where V is a p × K matrix of loadings (Eckart and Young 1936). The U and V matrices are unique up to arbitrary signs for the factors and loadings.
L 2-Regularized Least-Squares Problem
In our new version of LFMM, the statistical estimates of latent factors and environmental effects are based on least-squares minimization. More specifically, statistical estimates of the parameter matrices U, V, B are computed after minimizing the following penalized loss function
| (2) |
where is the Frobenius norm, is the L2 norm, and λ is a regularization parameter. A positive value of the regularization parameter is necessary for identifying the parameter matrices and B. For λ = 0, the solutions of the least-squares problem are not defined unequivocally and infinitely many solutions exist. A basic algorithm that computes a low rank approximation of the response matrix using their first K principal components, and then performs a linear regression of the residuals on X is one of the many solutions existing for λ = 0. This algorithm is called principal component analysis (PCA) in the sequel, and it is similar to the correction method of Price et al. (2006) used in association studies.
Ridge Estimates
For , the solution of the regularized least-squares problem is unique, and the corresponding matrices are called the “ridge estimates.” The minimization algorithm starts with an SVD of the explanatory matrix, , where Q is an n× n unitary matrix, R is a d× d unitary matrix and is an n× d matrix containing the singular values of X, denoted by . The ridge estimates are computed as follows
| (3) |
| (4) |
where is the rank K approximation of the matrix A, is the d× d identity matrix, and is the n× n diagonal matrix with coefficients defined as
A mathematical proof of this result is provided in a supplementary text, Supplementary Material online. The above equations describe a fast algorithm for computing the estimates of the parameter matrices U, V, B. The computational cost of this algorithm is mainly determined by the algorithmic complexity of the SVD. According to (Halko et al. 2011), computing the estimates requires operations. This complexity reduces to operations when random projections are used (our implementation). Accounting for the computational cost of , the complexity of the estimation algorithm is of order . For studies in which the number of samples, n, is much smaller than the number of response variables, p, the computing time of the ridge estimates is approximately the same as running the SVD algorithm on the response matrix twice.
Statistical Tests
Our new version of LFMM dissociates the estimation of latent factors from the tests of association with the primary (environmental) variables. To test association between the primary variables and each response variable, Yj, we use the latent score estimates obtained from the LFMM model as covariates in multivariate regression models. Those regression models evaluate the effects of the variables (X) on the molecular markers and test the nullity of effect sizes. Suppose that a single primary variable is tested (d= 1, the extension to d > 1 variables is straightforward). We fit a multivariate linear regression model for each locus ()
| (5) |
where the K factors in are considered fixed and their corresponding effect sizes, , are then (re-)estimated. To test the null hypothesis , we use a Student distribution with degrees of freedom. To improve test calibration and false discovery rate (FDR) estimation, we eventually apply an empirical-null testing approach to the test statistics (Efron 2004).
Separating the estimation of latent factors from the testing phase has the advantage of allowing some flexibility when performing the tests. For example, including the latent factor estimates in tests based on generalized linear models, mixed linear models or robust linear models can be easily implemented in the LFMM framework. In the case of linear mixed models (LMM), the covariance matrix for random effects could be computed from the estimated factors as (Note that the mixed model terminology may sometimes be misleading. LMMs incorporate “fixed and random effects” whereas LFMMs incorporate “fixed and latent effects.” Thus an LMM can use estimates computed by an LFMM.). In practice, we used the simple linear models which revealed themselves computationally efficient and performed well in simulations. Our two-step approach is similar to other methods for confounder adjustment in association studies (Price et al. 2006). It differs from the other approaches through the latent scores estimates, , that, in our case, capture the part of response variation not explained by the primary variable. The methods presented in this study and their extensions are implemented in the R package lfmm.
Results
Simulation Study
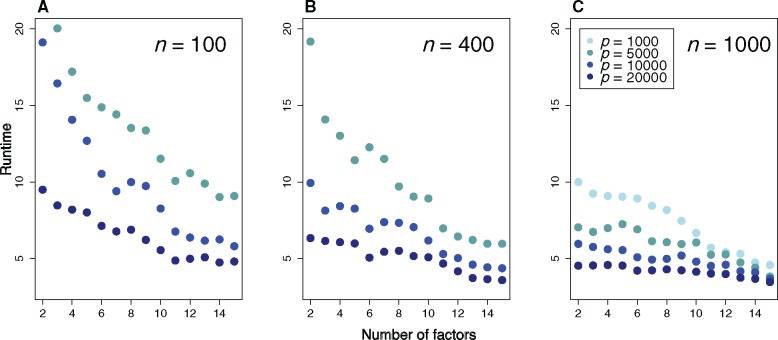
In a first series of computer experiments, we compared the runtimes of the new version of LFMM to the former version used with its default parameter settings (LFMM 1.5, Frichot and François 2015). Several values of the number of individuals (n), markers (p), and number of factors (K) were simulated. The user runtimes for the Markov chain Monte Carlo algorithm implemented in LFMM 1.5 ranged between 8 min (n = 100, p = 1,000, K = 2) and 32.5 h (n = 1,000, p = 20,000, K = 15). Note that the results for LFMM 1.5 were obtained for a single CPU, and that the multi-threated version of the program runs significantly faster. With the same data sets and a single CPU, the user runtimes for LFMM 2.0 ranged between 0.5 s (n = 100, p = 1,000, K = 2) and 12.5 s (n = 1,000, p = 20,000, K = 15). The results represent an improvement of several orders compared with the previous version (fig. 1), meaning that much larger data sets could be analyzed with the new version within much shorter time lags (supplementary fig. S1, Supplementary Material online). For larger value of p, the relative difference between the two versions stabilized, and LFMM 2.0 ran 10,000–100,000 times faster than LFMM 1.5. Because strong effect sizes were simulated at causal markers, both versions had high power to detect those target markers (Supplementary fig. S2, Supplementary Material online). With these simulation parameter settings, the LFMM 2.0 tests had higher power and precision than those of LFMM 1.5.
Fig. 1.
Base 10 logarithm of the ratio of runtimes for LFMM 1.5 and LFMM 2.0. A value of 5 means that LFMM 2.0 runs 105 times faster than LFMM 1.5. (A) n = 100 individuals, (B) n = 400, (C) n = 1,000, p is the total number of markers in the simulation.
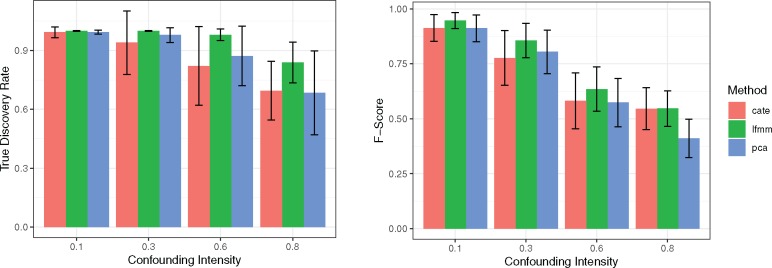
In a second series of computer experiments, three “fast” association methods were applied to the simulated data: PCA (Price et al. 2006), Confounder Adjusted Testing and Estimation (CATE) (Wang et al. 2017) and our new version of LFMM (fig. 2, n = 200, p = 10,000). We compared the relative performances of the methods over 50 replicates by considering low to high intensities of confounding. The intensity of confounding corresponded to the percentage of variance of the variable of interest explained by the confounding factors in the simulated data. The runtimes of CATE and PCA were of the same order as LFMM 2.0. CATE was slower than LFMM 2.0 (for large K), and with our implementation of PCA using an improved SVD algorithm, PCA was faster than LFMM 2.0.
Fig. 2.
True discovery rate and F-score as a function of confounding intensity. Three fast methods are considered: CATE, LFMM 2.0 and PCA. All methods were applied with K = 8 factors as determined by a PCA screeplot. The F-score is the harmonic mean of the true discovery rate (precision) and power.
For lower values of confounding intensity, the three methods had small rates of false discoveries and high power to discover the target markers. For higher values of confounding intensity the performances of LFMM 2.0 were superior to the other methods and showed the best combination of power and FDR as measured by the F-score (fig. 2). Note that the lower performances of PCA were expected because this method does not use the variable of interest when estimating the hidden variables. Thus PCA does not exactly address the problem of estimating confounders, and has lower power than the other methods.
Humans and Climate
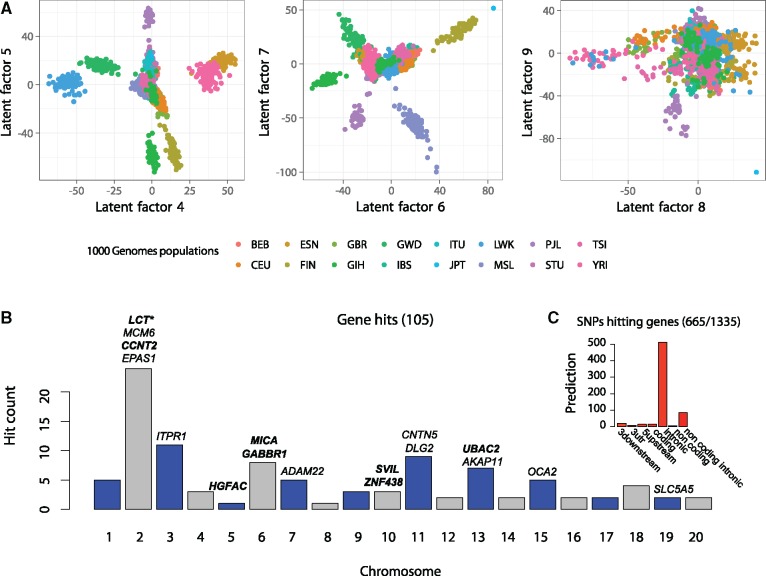
To detect genomic signatures of adaptation to climate in humans, we performed a GEA study using 5,397,214 SNPs for 1,409 individuals from the 1000 Genomes Project (2015), and bioclimatic data from the WorldClim database (Fick and Hijmans 2017). The size of the data sets represents one of the largest GEA study conducted so far. Nine confounders were estimated by a cross-validation approach. This estimated number was confirmed by the visual inspection of factor 9 showing more noise than information (fig. 3A, Supplementary figs. S3 and S4, Supplementary Material online). The factors mainly described correlation between population structure and climate in the sample, and differed from principal components of the genomic data. PCA, CATE, and two variants of LFMM 2.0 led to a list of 1,335 SNPs after pooling the list of candidates from the four methods (expected FDR = 5%, fig. 3B). A variant prediction analysis reported an over-representation of genic regions (665/1,335) with a large number of SNPs in intronic regions (fig. 3C). Top hits represented genomic regions important for adaptation of humans to bioclimatic conditions. The hits included functional variants in the LCT gene, and SNPs in the EPAS1 and OCA2 genes previously reported for their role in adaptation to diet, altitude or in eye color (Fan et al. 2016) (fig. 3B, Supplementary fig. S5, Supplementary Material online, and Supplementary table S1, Supplementary Material online).
Fig. 3.
Human GEA study. Association study based on genomic data from the 1000 Genomes Project database and climatic data from the Worldclim database. (A) Latent factors estimated by LFMM 2.0. (B) Target genes corresponding to top hits of the GEA analysis (expected FDR level of 5%). The highlighted genes correspond to functional variants. (C) Predictions obtained from the VEP program.
RA and Smoking
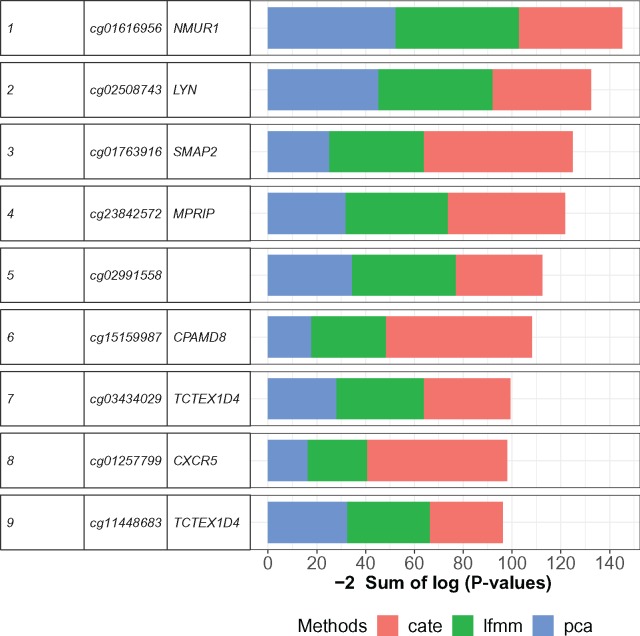
Tobacco smoking is considered an established risk factor for the development of RA, an autoimmune inflammatory disease (Di Giuseppe et al. 2014). We performed an association study using whole blood methylation data from a study of patients with RA considering tobacco consumption as an environmental exposure variable (Liu et al. 2013). The goal of this study was to identify CpG sites exhibiting joint association with smoking and RA. The cell composition of blood in RA patients is a known source of confounding (Jaffe and Irizarry 2014), and we accounted for cell-type heterogeneity by using K = 5 factors in PCA, CATE, and LFMM 2.0. Like in a previous analysis, we combined the significance values of the three methods to increase power. The list of CpG sites showing significant joint association with RA and smoking in at least two approaches was short (nine CpG sites). The top-list included the genes NMUR1 and LYN that play an important role in the regulation of innate and adaptive immune responses (fig. 4). NMUR1 was identified as a hub gene in a protein–protein interaction network of differentially methylated genes in osteosarcoma, and its abnormal DNA methylation may contribute to the progression of the disease (Chen et al. 2018). The gene LYN acts downstream two genes related to RA and synovial sarcoma, EPOR and KIT (Tamborini et al. 2004; Huber et al. 2008; Kosmider et al. 2009), and it mediates the phosphorylation of CBL in relation to RA (Xu et al. 2018). This gene is also linked to IL3 receptors associated to RA and smoking (Takano et al. 2004; Miyake et al. 2014). Regarding the next hits, MPRIP was found to be hypermethylated for patients with RA (Lin and Luo 2017), and association between CXCR5 and RA or upregulation of this gene in the rheumatoid synovium has been reported in the literature (Schmutz et al. 2005; Wengner et al. 2007).
Fig. 4.
EWAS of RA and smoking. Fisher’s scores for CpG sites showing significant association with RA and smoking in at least two of three approaches (PCA, CATE, LFMM 2.0).
Discussion
In this study, we introduced LFMM 2.0, a fast and accurate algorithm for estimating confounding factors and for testing GEAs. The new algorithm is based on the exact solution of a regularized least-squares problem for latent factor regression models. We used LFMM 2.0 for testing associations between a response matrix and a primary variable matrix in a study of natural selection in humans. In addition, we used it to evaluate the importance of DNA methylation in modulating the effect of smoking in patients with an inflammatory disease. Previous inference methods for latent factor regression models were based on slower algorithms or on heuristic approaches, lacking theoretical guarantees for identifiability, numerical convergence, or statistical efficiency (Leek and Storey 2007; Wang et al. 2017). In addition, existing methods do not always address the confounding problem correctly, building their estimates on genetic markers only while ignoring the primary variables. For example, genome-wide association studies adjust for confounding by using the largest PCs of the genotypic data (Price et al. 2006). A drawback of the approach is that the largest PCs may also correlate with the primary variables, and removing their effects results in loss of statistical power. When compared with PCA approaches, LFMMs gained power by removing the part of genetic variation that could not be explained by the primary variables (Frichot et al. 2013). Thus LFMM extends the tests performed by the PCA approaches by improving principal components with factor estimates depending on the primary and response variables simultaneously.
In gene expression and DNA methylation studies where batch effects are source of unwanted variation, alternative approaches to the confounder problem have also been proposed. These methods are based on latent factor regression models called surrogate variable analysis (SVA) (Leek and Storey 2007; Wang et al. 2017). For epigenomic or gene-expression studies, LFMMs extend SVA and their recent developments implemented in CATE. Latent factor regression models employ deconvolution methods in which unobserved batch effects, ancestry or cell-type composition are integrated in the regression model using hidden factors. Those models have been additionally applied to transcriptome analysis (van Iterson et al. 2017). As they do not make specific hypotheses regarding the nature of the data, LFMMs and other latent factor regression models could be applied to any category of association studies regardless of their application field.
Like several factor methods, the computational speed of LFMM methods is mainly influenced by the algorithmic complexity of low rank approximation of large matrices. The algorithmic complexity of the LFMM method was similar to PCA and CATE, of order for LFMM 2.0. These approaches are much faster than the previous version of LFMM or than Bayesian methods currently used in GEAs.
Since the models underlying versions 1.5 and 2.0 of LFMM are alike, their statistical limitations are also similar. More specifically, estimation of latent factors might be complicated by physical linkage, unbalanced study designs or a strong correlation between axes of genetic variation and environmental gradients (McVean 2009; Frichot et al. 2015). Our new implementation of LFMM disconnects the testing steps from the latent factor estimation steps. This disconnection facilitates the implementation of approaches that alleviate the above issues. For example, the human SNP data were pruned for LD by taking the most informative SNPs in genomic windows before estimating latent factors. Although potential improvements such as sparse modeling, random effects, logistic or robust regressions and stepwise conditional tests were not included in our results, those options are available with the lfmm program, and they may provide additional power to detect true associations in GEA studies.
Materials and Methods
Simulation Data
We simulated primary variables, X, latent factors, U, and a response matrix according to a multivariate Gaussian model. In those simulations, we controlled the correlation between the primary variables and the confounders. More specifically, a primary variable, , and three latent variables, U, were simulated by using a multivariate Gaussian distribution to represent individual data
where S was a covariance matrix with diagonal terms , and nondiagonal terms set to zero, except for the covariance between uk and , which was set to the value . We created K = 3 confounders, assuming that their variances, , were equal to the values 15, 3, 0.1, respectively. The ck coefficients were sampled from a uniform distribution taking values in the range , and ρ was inversely proportional to the square root of (which was < 1). The coefficient of proportionality was chosen so that the percentage of variance of explained by the latent factors ranged between 0.1 and 1. The effect size matrix, B, was generated by setting a proportion of effect sizes to zero. Nonzero effect sizes were sampled according to a standard Gaussian distribution, N. The proportion of null effect sizes was set to 99%. We eventually created a response matrix, , by simulating from the generative model of the latent factor model, transforming the values through a probit transform, and generating genotypes according to a binomial distribution bin(2, π), where π resulted from the probit transform. Runtimes of LFMM 2.0 and LFMM 1.5 were measured on a Xeon W-2145 CPU (3.70 GHz). Both programs were used with their default parameters settings including 5 runs of 10,000 cycles for the Markov chain Monte Carlo algorithm in LFMM 1.5. In the programs K was varied in the range 2–15. To evaluate the capabilities of methods to identify true positives, we used the true discovery rate, power and the F-score. The true discovery rate (or precision) is the proportion of true positives in a candidate list of positive tests. Power is the number of true positives divided by the number of true associations. The F-score is the harmonic mean of the true discovery rate and power.
Other Algorithms
In the R programing environment, we considered the following methods and software: 1) We implemented a standard approach that estimates confounders from a PCA of the response matrix Y, and uses linear regression to perform the tests. Principal components were estimated with the svd function of the RSpectra package. Distinct scalings of the response matrix were used in simulations or in EWAS analysis and in the GEA analysis. For the GEA analysis, we used the scaling procedure implemented in the EIGENSTRAT method (Price et al. 2006), whereas in EWAS, we scaled with division by standard deviations. 2) We implemented the CATE method (Wang et al. 2017), which uses a linear transformation of the response matrix such that the first axis of this transformation is colinear to and the other axes are orthogonal to . One property of CATE is to use robust regression models to perform statistical testing. CATE was used without negative controls and with a test recalibration option similar to genomic control (Devlin and Roeder 1999). The CATE method was implemented in the R package cate. 3) We implemented a variant of LFMM 2.0 using an L1 norm regularizer instead of the L2 norm (Lasso estimates). All programs contained several options and many algorithmic variants. Unless specified, we used the default options of programs.
GEA Study
We performed a GEA study using whole genome sequencing data and bioclimatic variables to detect genomic signatures of adaptation to climate in humans. The data are publicly available, and they were downloaded from the 1000 Genomes Project (2015) and from the WorldClim database (Fick and Hijmans 2017). The genomic data included 84.4 millions of genetic variants genotyped for 2,506 individuals from 26 world-wide human populations. Nineteen bioclimatic data were downloaded for each individual geographic location, considering capital cities of their country of origin. The bioclimatic data were summarized by projection on their first principal component axis. The genotype matrix was preprocessed so that SNPs with minor allele frequency <5% and individuals with relatedness >8% were removed from the matrix. Admixed individuals from Afro-American and Afro-Caribbean populations were also removed from the data set. After those filtering steps, the response matrix contained 1,409 individuals and 5,397,214 SNPs. We performed LD pruning to retain SNPs with the highest frequency in windows of one hundred SNPs, and identified a subset of 296,948 informative SNPs. Four GEA methods were applied to the 1000 Genomes Project data set: PCA, CATE, and two LFMM estimation algorithms. For all methods the latent factors were estimated from the pruned genotypes, and association tests were performed for all 5,397,214 loci. Because the results were highly concordant, the significance values were combined by using the Fisher method. The results obtained from clumps with an expected FDR level of 1% were analyzed using the variant effect predictor (VEP) program (McLaren et al. 2016).
RA Data Set
The RA data are publicly available and were downloaded from the GEO database under the accession number GSE42861 (Liu et al. 2013). For this study, beta-normalized methylation levels at 485,577 probed CpG sites were measured for 354 cases and 335 controls (Liu et al. 2013). Following (Zou et al. 2014), probed CpG sites having a methylation level < 0.1 or >0.9 were filtered out. Two primary variables were included in the model, tobacco consumption and the health outcome. Ex-smokers were removed from the analysis, and all filtering steps resulted in 345,067 CpGs and 234 cases and 225 controls. Tobacco consumption was encoded as an ordinal variable with three levels (nonsmokers, occasional smokers, and regular smokers), and the health outcome was encoded as a dichotomous variable. Age and gender were included as nuisance variables. The goal of the study was to identify CpG sites with joint association with tobacco smoking and RA. The data were centered and scaled for a standard deviation of one. Since the cell composition of blood in RA patients typically differs from that in the general population, there is a risk for false discoveries that stem from unaccounted-for cell-type heterogeneity (Jaffe and Irizarry 2014). Since cell-type heterogeneity was not measured, we used latent factors to model it (Zou et al. 2014). Three methods were applied to the RA data set: PCA, CATE, and our new version of LFMM. The number of factors was set to K = 5 according to the screeplot of the PCA eigenvalues. For each method, significance values for the association with smoking and RA were combined using a squared-max transform that guaranteed that the resulting P-values follow a uniform distribution under the null hypothesis. Candidate lists of CpG sites were obtained by using the Fisher method after correction for multiple testing with a 5% type I error.
Supplementary Material
Supplementary data are available at Molecular Biology and Evolution online.
Supplementary Material
Acknowledgments
The authors are grateful to two anonymous reviewers for their constructive comments. They thank M.G.B Blum, all organizers and participants of the SSMPG 2017 workshop held in Aussois for their feedback on the program. They also thank Katie Lotterhos and Matthieu Gautier for fruitful discussions during this workshop. This work was supported by a grant from LabEx PERSYVAL Lab, ANR-11-LABX-0025-01, and by a grant from French National Research Agency (Agence Nationale pour la Recherche) ETAPE, ANR-18-CE36-0005. This article was developed in the framework of the Grenoble Alpes Data Institute, supported by the French National Research Agency under the “Investissements d’avenir” program (ANR-15-IDEX-02).
References
- Carvalho CM, Chang J, Lucas JE, Nevins JR, Wang Q, West M.. 2008. High-dimensional sparse factor modeling: applications in gene expression genomics. J Am Stat Assoc. 103(484):1438–1456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen XG, Ma L, Xu JX.. 2018. Abnormal DNA methylation may contribute to the progression of osteosarcoma. Mol Med Rep. 17(1):193–199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Mita S, Thuillet AC, Gay L, Ahmadi N, Manel S, Ronfort J, Vigouroux Y.. 2013. Detecting selection along environmental gradients: analysis of eight methods and their effectiveness for outbreeding and selfing populations. Mol Ecol. 22(5):1383–1399. [DOI] [PubMed] [Google Scholar]
- Devlin B, Roeder K.. 1999. Genomic control for association studies. Biometrics 55(4):997–1004. [DOI] [PubMed] [Google Scholar]
- Di Giuseppe D, Discacciati A, Orsini N, Wolk A.. 2014. Cigarette smoking and risk of rheumatoid arthritis: a dose-response meta-analysis. Arthritis Res Ther. 16(2):R61.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckart C, Young G.. 1936. The approximation of one matrix by another of lower rank. Psychometrika 1(3):211–218. [Google Scholar]
- Efron B. 2004. Large-scale simultaneous hypothesis testing: the choice of a null hypothesis. J Am Stat Assoc. 99(465):96–104. [Google Scholar]
- Fan S, Hansen ME, Lo Y, Tishkoff SA.. 2016. Going global by adapting local: a review of recent human adaptation. Science 354(6308):54–59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fick SE, Hijmans RJ.. 2017. Worldclim 2: new 1-km spatial resolution climate surfaces for global land areas. Int J Climatol. 37(12):4302–4315. [Google Scholar]
- Frichot E, Schoville SD, Bouchard G, François O.. 2013. Testing for associations between loci and environmental gradients using latent factor mixed models. Mol Biol Evol. 30(7):1687–1699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frichot E, François O.. 2015. LEA: an R package for landscape and ecological association studies. Methods Ecol Evol. 6(8):925–929. [Google Scholar]
- Frichot E, Schoville SD, de Villemereuil P, Gaggiotti OE, François O.. 2015. Detecting adaptive evolution based on association with ecological gradients: orientation matters! Heredity 115(1):22–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gautier M. 2015. Genome-wide scan for adaptive divergence and association with population-specific covariates. Genetics 201(4):1555–1579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Günther T, Coop G.. 2013. Robust identification of local adaptation from allele frequencies. Genetics 195(1):205–220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halko N, Martinsson PG, Tropp JA.. 2011. Finding structure with randomness: probabilistic algorithms for constructing approximate matrix decompositions. SIAM Rev. 53(2): 217–288. [Google Scholar]
- Huber R, Hummert C, Gausmann U, Pohlers D, Koczan D, Guthke R, Kinne RW.. 2008. Identification of intra-group, inter-individual, and gene-specific variances in mRNA expression profiles in the rheumatoid arthritis synovial membrane. Arthritis Res Ther. 10(4):R98.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaffe AE, Irizarry RA.. 2014. Accounting for cellular heterogeneity is critical in epigenome-wide association studies. Genome Biol. 15:R3.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kosmider O, Buet D, Gallais I, Denis N, Moreau-Gachelin F.. 2009. Erythropoietin down-regulates stem cell factor receptor (Kit) expression in the leukemic proerythroblast: role of Lyn kinase. PLoS One 4(5):e5721.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leek JT, Storey JD.. 2007. Capturing heterogeneity in gene expression studies by surrogate variable analysis. PLoS Genet. 3(9):e161.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin Y, Luo Z.. 2017. Aberrant methylation patterns affect the molecular pathogenesis of rheumatoid arthritis. Int Immunopharmacol. 46:141–145. [DOI] [PubMed] [Google Scholar]
- Liu Y, Aryee MJ, Padyukov L, Fallin MD, Hesselberg E, Runarsson A, Reinius L, Acevedo N, Taub M, Ronninger M, et al. 2013. Epigenome-wide association data implicate DNA methylation as an intermediary of genetic risk in rheumatoid arthritis. Nat Biotechnol. 31(2):142–147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lotterhos KE, Whitlock MC.. 2015. The relative power of genome scans to detect local adaptation depends on sampling design and statistical method. Mol Ecol. 24(5):1031–1046. [DOI] [PubMed] [Google Scholar]
- McLaren W, Gil L, Hunt SE, Riat HS, Ritchie GR, Thormann A, Flicek P, Cunningham F.. 2016. The Ensembl variant effect predictor. Genome Biol. 17(1):122.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McVean G. 2009. A genealogical interpretation of principal components analysis. PLoS Genet. 5(10):e1000686.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miyake Y, Tanaka K, Arakawa M.. 2014. IL3 rs40401 polymorphism and interaction with smoking in risk of asthma in Japanese women: the Kyushu Okinawa maternal and child health study. Scand J Immunol. 79(6):410–414. [DOI] [PubMed] [Google Scholar]
- Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, Reich D.. 2006. Principal component analysis corrects for stratification in genome-wide association studies. Nat Genet. 38(8):904–909. [DOI] [PubMed] [Google Scholar]
- Rakyan VK, Down TA, Balding DJ, Beck S.. 2011. Epigenome-wide association studies for common human diseases. Nat Rev Genet. 12(8):529–541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rellstab C, Gugerli F, Eckert AJ, Hancock AM, Holderegger R.. 2015. A practical guide to environmental association analysis in landscape genomics. Mol Ecol. 24(17):4348–4370. [DOI] [PubMed] [Google Scholar]
- Savolainen O, Lascoux M, Merilä J.. 2013. Ecological genomics of local adaptation. Nat Rev Genet. 14(11):807–820. [DOI] [PubMed] [Google Scholar]
- Schmutz C, Hulme A, Burman A, Salmon M, Ashton B, Buckley C, Middleton J.. 2005. Chemokine receptors in the rheumatoid synovium: upregulation of CXCR5. Arthritis Res Ther. 7(2):R217.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takano H, Tomita T, Toyosaki-Maeda T, Maeda-Tanimura M, Tsuboi H, Takeuchi E, Kaneko M, Shi K, Takahi K, Myoui A, et al. 2004. Comparison of the activities of multinucleated bone-resorbing giant cells derived from CD14-positive cells in the synovial fluids of rheumatoid arthritis and osteoarthritis patients. Rheumatology 43(4):435–441. [DOI] [PubMed] [Google Scholar]
- Tamborini E, Bonadiman L, Greco A, Gronchi A, Riva C, Bertulli R, Casali PG, Pierotti MA, Pilotti S.. 2004. Expression of ligand-activated KIT and platelet-derived growth factor receptor β tyrosine kinase receptors in synovial sarcoma. Clin Cancer Res. 10(3):938–943. [DOI] [PubMed] [Google Scholar]
- Teschendorff AE, Relton CL.. 2018. Statistical and integrative system-level analysis of DNA methylation data. Nat Rev Genet. 19(3):129.. [DOI] [PubMed] [Google Scholar]
- The 1000 Genomes Project Consortium. 2015. A global reference for human genetic variation. Nature 526:68–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Iterson M, van Zwet EW, Heijmans BT.. 2017. Controlling bias and inflation in epigenome-and transcriptome-wide association studies using the empirical null distribution. Genome Biol. 18(1):19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Villemereuil P, Frichot E, Bazin E, François O, Gaggiotti OE.. 2014. Genome scan methods against more complex models: when and how much should we trust them? Mol Ecol. 23(8):2006–2019. [DOI] [PubMed] [Google Scholar]
- Villemereuil P, Gaggiotti OE.. 2015. A new -based method to uncover local adaptation using environmental variables. Methods Ecol Evol. 6:1248–1258. [Google Scholar]
- Wang J, Zhao Q, Hastie T, Owen AB.. 2017. Confounder adjustment in multiple hypothesis testing. Ann Statist. 45(5):1863–1894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wengner AM, Höpken UE, Petrow PK, Hartmann S, Schurigt U, Bräuer R, Lipp M.. 2007. CXCR5—and CCR7—dependent lymphoid neogenesis in a murine model of chronic antigen-induced arthritis. Arthritis Rheum. 56(10): 3271–3283. [DOI] [PubMed] [Google Scholar]
- Xu XX, Bi JP, Ping L, Li P, Li F.. 2018. A network pharmacology approach to determine the synergetic mechanisms of herb couple for treating rheumatic arthritis. Drug Des Devel Ther. 12:967.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou J, Lippert C, Heckerman D, Aryee M, Listgarten J.. 2014. Epigenome-wide association studies without the need for cell-type composition. Nat Methods 11(3): 309–311. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.