Beaming of Helical Light from Plasmonic Vortices via Adiabatically Tapered Nanotip

Abstract

We demonstrate the generation of far-field propagating optical beams with a desired orbital angular momentum by using a smooth optical-mode transformation between a plasmonic vortex and free-space Laguerre–Gaussian modes. This is obtained by means of an adiabatically tapered gold tip surrounded by a spiral slit. The proposed physical model, backed up by the numerical study, brings about an optimized structure that is fabricated by using a highly reproducible secondary electron lithography technique. Optical measurements of the structure excellently agree with the theoretically predicted far-field distributions. This architecture provides a unique platform for a localized excitation of plasmonic vortices followed by its beaming.

Structured light beams have been the subject of an intense work in the last years^1,2 due to the numerous potential applications that they may offer in several disparate technological and research fields, ranging from super-resolution imaging³ to optical tweezing⁴ and nanomanipulation⁵ and telecommunications.⁶

The possibility of producing and analyzing singular optical beams at the micro- and the nanoscale led to focus on the interaction of light with metallic nanostructures, resulting in surface plasmon polaritons (SPPs) carrying angular momentum (AM).⁷⁻¹³ We will refer to these waves as plasmonic vortices (PVs). Such modes are generally surface confined helical electromagnetic distributions with a field singularity. The strength of the singularity, termed the topological charge of a vortex, is defined by the phase ramp acquired in one round trip about the singularity center. This charge is proportional to the AM carried by the field.¹⁰

PVs can be generated by coupling AM-carrying beams to the plasmonic modes of metallic films using particular chiral grating couplers, which have been sometimes called plasmonic vortex lenses (PVLs).¹⁰ Several examples of these couplers have been presented so far.⁸⁻¹⁸ A feature common to most of them is the Archimede’s spiral-shaped grooves or slits milled in a noble metal film.

As has been pointed out in several papers, PVLs can be used not only to couple light to plasmonic vortices but also to produce strongly localized sources of light carrying nonzero angular momentum.^{9,15,16,19,20} In this case, incident circularly polarized light interacting with the plasmonic lens excites PV, which is finally scattered into a free space by a proper decoupling structure.

One of the most studied architectures for this aim consists of a PVL with a hole at its center.^9,16,20 The drawback of this scheme is a low efficiency and poor directionality of the far-field beaming due to a small hole size. Moreover, it unavoidably transmits part of the light directly impinging onto the hole, which has not been phase-structured by the PVL. More-complex structures, composed of suspended gold membranes patterned on both sides or multilayer metal–insulator–metal waveguides, were proposed to address those issues.^16,20−22 However, besides an increase in the fabrication complexity, the highly desirable properties of transmitting a well-defined phase-structured beam with high efficiency and good directionality have been not fully achieved at the same time.

Here, we theoretically and experimentally demonstrate a different approach to the efficient PV coupling to the free space, by means of a single-layer PVL structure with a smoothed-cone tip at its center (Figure 1a). We show that, by properly shaping the tip geometry, the PV excited by the spiral structure can be adiabatically coupled to the far-field mode, carrying well-defined AM. A crucial role is played by the strong smoothness of the tip basis. As we shall demonstrate, by simply increasing the curvature radius at the basis of a conical structure, a totally different optical behavior can be achieved, enabling a smooth propagation of the PVs along the tip with a gradual matching to a free-space beam propagating normally to the PVL plane. This mechanism is highly efficient for a large range of AM values carried by the impinging PV, with the only losses attributed to the ohmic dissipation. In addition, our calculations show that by optimization of the geometrical parameters, the circular polarization mixing in the outgoing wave can be kept lower than 15%. As a result, output beams can be theoretically generated at the wavelength scale in an almost-pure electromagnetic eigenstate. Interestingly, we also demonstrate that, by reciprocity, the structure can be exploited in the reverse way as an efficient localized Laguerre–Gaussian beam-to-plasmonic-vortex coupler, with back-reflected power lower than 1%.

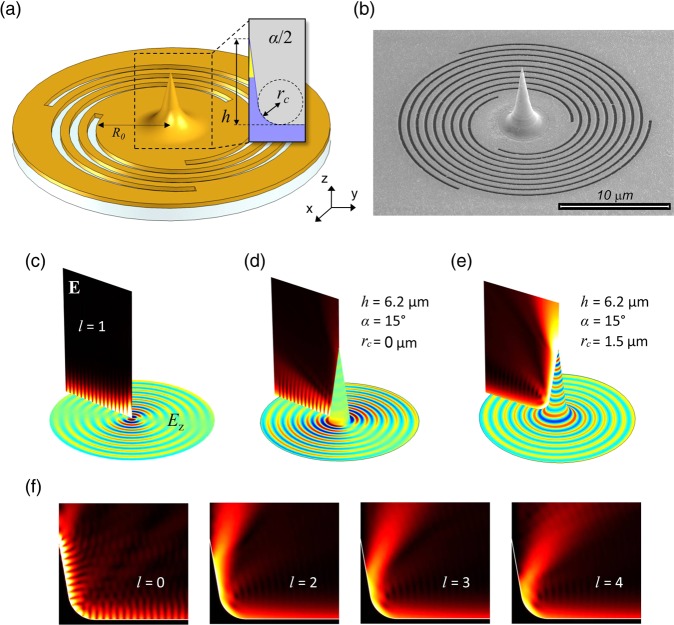
Figure 1.

(a) 3D scheme of the PVL. The geometrical parameters of the spiral slits include a slit width of 200 nm, pitch of 763 nm, gold thickness of 150 nm, and Si₃N₄ thickness of 100 nm. R₀, namely the initial radius of the spirals, is fixed to 4 μm to reduce the effect of direct scattering of light from the grooves. (b) Scanning electron microscope image of an example of fabricated structure. (c–e) |E| maps (vertical cross-section) and E_z maps (metal surface plots) of the central region of the PVLs in the case of a PV impinging with topological charge of l = 1 propagating through a flat PVL center (c), scattered by a conical tip with a zero-basis curvature radius (r_c) (d), and by a conical tip with large r_c (e). (f) |E| maps in the case of a smoothed conical tip (same parameters as in (e)) illuminated by a PV with the indicated l values.

We notice that a number of conical nanotips have already been proposed in combination with PVL architectures²³⁻²⁶ but mainly with the purpose of concentrating the axially symmetric l = 0 PV in very localized volumes (nanofocusing).²⁷ For this purpose, a large curvature radius at the tip basis is not needed or is even detrimental.²⁶ Other vertical or horizontal rod-like solutions have been proposed with the aim to decouple plasmonic vortices to the far-field.²⁸⁻³⁰ Most of the studied conical structures consider an abrupt connection between the antenna basement and the underlying metal surface. In these architectures, the decoupling takes place by means of the excitation of one of the antenna electric resonances,²⁸ whose scattered field pattern is then collected in the far field. The scattering approach to decoupling PV has, however, severe limitations. First, the mechanism can be exploited only to decouple axially symmetric PVs, which have a field maximum in correspondence of the antenna location. PVs with higher topological charge have a field minimum at the PVL center; thus, the antenna resonances cannot be excited. Moreover, PVs can hardly be efficiently decoupled out of the PVL surface, most of the power is being scattered back again in the form of a PV.

The practical exploitation of our plasmonic-vortex-to-free-space mode matcher, presented here for the first time to the best of our knowledge, requires a fine control of the shape of such a nontrivial 3D structure, which is mandatory for obtaining the desired effect. Here, we adopted a powerful technique, sometimes termed as secondary electron lithography.³¹⁻³³ This fabrication procedure proved to enable full control of the shape at the nano- and microscales, even for exotic 3D nanostructures.³² This allowed the fabrication of several PVL and tip structures with excellent matching to the designed profile.

In Figure 1a, we show a 3D scheme of the proposed structure. A multiple-turn spiral slit is milled on a 150 nm gold film deposited onto a 100 nm Si₃N₄ membrane. Its spiral shape is defined by

1

Here, ϕ is the azimuthal angle, ranging from 0 to 2πN, with N being the number of spiral turns, k_SPP is the propagation constant of the SPP mode on a flat gold–air interface, m is an integer denoting the pitch of the spiral, and R₀ is the distance from the center to the nearest point of the groove. To maximize the coupling to the plasmonic vortices, we consider a set of m spirals, each one rotated by 2π/m with respect to the adjacent ones, in such a way that the radial distance between two adjacent grooves is λ_SPP = 2π/k_SPP.

The other geometrical parameters of the spiral (slit width and gold thickness) have been tuned to maximize the coupling efficiency of a circularly polarized plane wave impinging from the Si₃N₄ side to the SPP modes of the upper gold–air interface (details are reported in the figure caption). A conical gold tip, whose profile is reported in the inset of Figure 1a, is located exactly at the center of the spiral. A total of three main parameters define the tip shape: height (h), apex angle (α), and curvature radii at the basis (r_c). The curvature radius at the tip apex is kept fixed to 10 nm throughout the paper. As discussed in the experimental details, the adopted fabrication technique enables us to faithfully reproduce the designed shape (Figure 1b).

We consider a circularly polarized plane wave impinging normally from the Si₃N₄ side. As has been described in several papers,^{8−10,14−16,19} the component of the impinging light electric field locally orthogonal to the slits efficiently couples to the SPP mode of the gold–air interface. The plasmonic field launched by each concentric spiral constructively interferes (thanks to the choice of the spiral period, λ_SPP), producing a PV that radially propagates toward the PVL center. In the absence of a tip, the PV confined by the spiral grooves forms a standing wave, giving rise to the characteristic Bessel interference pattern. We use the finite elements software COMSOL Multiphysics to simulate the electromagnetic distribution in such a flat PVL (see Figure 1c). The z component of the electric field can be expressed analytically, in cylindrical coordinates, as¹⁰

2

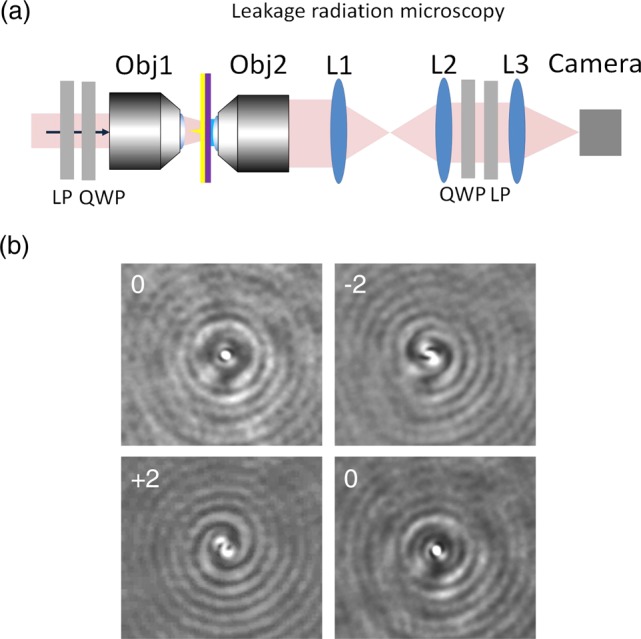
where k_SPP is the wave vector of an SPP propagating on a flat gold–air interface, J_l is the Bessel function of the first kind, and 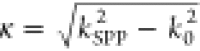, where k₀ = 2π/λ₀ is the vacuum wave vector. It can be shown^8−10,14 that the topological charge of a PV is given by the relation l = m + s_i, where the spin number s_i = 1 corresponds to the right-hand and s_i = −1 to the left-hand circularly polarized light.

When the conical tip is present at the PVL center, the surface confined electromagnetic mode may couple to the guided mode propagating along the tip upward. In Figure 1d,e, we compare the simulations of the same PV, as shown in Figure 1c, converging toward two structures having similar conical tips (height h = 6200 nm and an apex angle α = 15°) but with different curvature radii at the basis. In the case of the negligible curvature radius (r_c → 0), most of the energy is reflected back, which can be clearly deduced from the strong fringe modulation of the intensity (see Figure 1d). This resembles common configurations presented elsewhere.²³⁻²⁶ The fraction of the power scattered to the far-field with respect to the power, incoming at the tip basis (we term this quantity transmittance hereafter) in this configuration is rather low (less than 10%).

This behavior dramatically changes with increasing of the curvature radius at the tip basis. This is shown in Figure 1e, where we consider the tip basis curvature of r_c = 1.57 μm. By looking at the field maps, we now see a smooth intensity pattern close to the metal surface around the tip, which means the absence of back reflected SPP at the tip basis. This is also demonstrated by the E_z field pattern on the metal surface, which shows perfectly spiraling wave fronts propagating along the tip. The smoothed tip in this configuration perfectly matches the PV with the corresponding plasmonic mode of the conical waveguide. Most of the PV power is finally delivered to the free-space as a z-oriented beam.

Figure 1f reports the |E| maps for the PVs with l = 0, 2, 3, and 4. As can be seen, for l > 1, the behavior is similar, and the PV are efficiently decoupled as doughnut-shaped waves propagating in the free space. The case of l = 0 is an interesting exception. This PV propagates to the end of the tip and is almost fully reflected back, which can be deduced by observing the interference pattern along the metal surface.

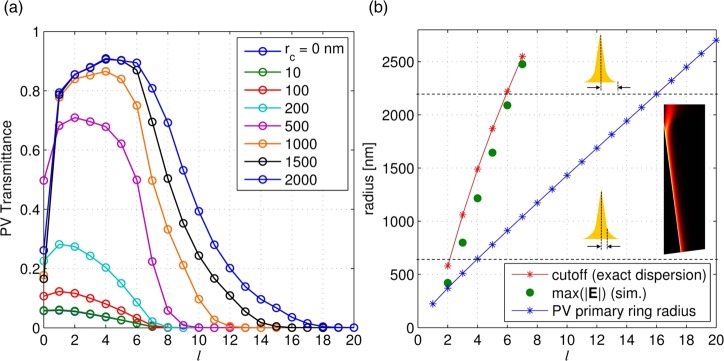
A study of the PV transmittance as a function of l for different values of r_c is summarized in the Figure 2a. It is clearly seen that the increasing of r_c leads to a gradual improvement of the out-coupling efficiencies of the PVs, which can reach values as high as 90%, even for large l values. The only losses can be ascribed to the metal absorption. We notice, however, that the coupling of the PV with l = 0 to the far field is always very poor.

Figure 2.

(a) Fraction of the PV light power transmitted to the air domain as a function of the PV topological charge, l, for increasing values of r_c. (b) Cutoff radii of the plasmonic modes propagating along the tip, calculated by solution of the exact cylindrical mode dispersion equation (red) compared with those extracted from the finite elements simulation (green circles); the blue asterisks denotes the primary ring radii of PVs propagating on a flat gold–air surface; the horizontal dashed lines mark, respectively, the inner tip radius before the smoothing, 650 nm, and the maximum tip radius, 2200 nm; the inset shows an example of an electric field norm map calculated in a model of a semi-infinite gold tip.

To understand the PV propagation along the cone and their final decoupling, we consider the modes of a conducting cylindrical waveguide placed along the z-axis, whose radius, ρ, progressively decreases with z. Their electric field can be expressed as^34,35

3

where the subscript i = 1 or 2 and denotes the region outside and inside the cylinder, respectively; β is the complex propagation constant of the mode; and k_r,i is the transverse wave vector, such that ε_ik₀² = β² + k_r,i, with k₀ = ω/c being the vacuum wave vector and ε₁ = 1, ε₂ = −24.1 + 1.7i being the relative permittivities of vacuum and gold.³⁶ The mode amplitude Ẽ_i (k_r,iρ) as well as β can be obtained from the solution of the Helmholtz equation in cylindrical coordinates in the metal and air domains, respectively, via the imposition of the continuity of the tangential components of the E and H fields at the metal surface. This procedure yields a well-known dispersion equation,³⁵ which we solved numerically. Details of the real and imaginary parts of the modes effective index as a function of the cylinder radius are given in the Supporting Information.

As extensively discussed in the literature,³⁵ the mode with l = 0 has a diverging mode index and experiences zero group velocity close to the ρ = 0. This is the reason why such conical structures have been widely utilized for nanofocusing purposes.^26,27 In the case of adiabatic tapering, corresponding to the small variations of the plasmon wavenumber on the scale of a plasmon wavelength, the mode progressively slows to almost a full stop, leading to a giant concentration of energy at the nanoscale volume.²⁶ In this case, a zero transmittance to the far field would be expected. In our case, the tip aperture is small but non-negligible, so the abrupt termination results in reflections from the tip end, clearly visible in Figure 1f, and in a partial scattering to the far field. The latter is the cause of the low transmittance calculated for l = 0 in Figure 2a.

The l = 1 mode also needs a separate discussion. In this case, the group velocity adiabatically approaches c, and its propagation constant tends to k₀ as ρ → 0.³⁵ This mode is, therefore, guided to the tip end, where it efficiently decouples to the free space. The perfect momentum matching in this case assures no back-reflections, and most of the energy is beamed out. Apparently with this mode, one obtains a Gaussian beam- like source of radiation rather than a localization of the energy at the tip end, which is important in applications where high optical throughput is needed.

All other modes, l >1, exist in a bound form only for ρ larger than some l-dependent cutoff value, at which the modal loss vanishes (Im(β) = 0).³⁷ To verify that such a mode conversion mechanisms takes place along our conical tip, which has a small but non-negligible aperture of α = 15°, we simulate just a portion of a very long metal tip, exciting the lth mode at the basis boundary (Figure 2b inset). This enables us to exclude from the analysis the effects of the finite length of the tip, thus allowing the study of arbitrarily high l values. We empirically estimate the modes detaching points by considering the points at which the electric field norm along the metal surface reaches its maximum. The corresponding radii for l from 1 to 7 are marked in Figure 2b with green dots. As can be seen, the cutoff values obtained from solution of the exact dispersion equation (red asterisks) are in good agreement with the numerical simulation. We notice that the tip we consider (h = 6200 nm, r_c = 1570 nm) has a maximum radius of about 2.2 μm, at the beginning of the smoothed part, while the tip radius at the fillet end is just 650 nm (these radii are marked with horizontal dashed lines in Figure 2b). This latter is the radius at which the tip slope effectively starts to be equal to α/2 = 7.5°. This radius is just larger than the cutoff of l = 2 mode. Nonetheless, a high transmittance is predicted for all modes up to l = 6, as can be seen in Figure 2a (black line). For these modes, the large curvature radius at the basis ensures a smooth transition between the plasmon modes and the free propagating waves in air. For l > 6, transmittance rapidly drops (Figure 2a, yellow line), becoming zero for l > 15. As a matter of fact, we notice that when l > 6, the cutoff radius is larger than the maximum tip radius. For l up to 16, however, we observe that the first maximum of the Bessel interference pattern that would arise in the absence of tip (sometimes called the primary ring;⁹ blue line in Figure 2b) occurs at a radius smaller than the maximum tip radius. This enables an interaction with the tip basis, which determines a partial decoupling of the PV to the free space. For l > 16, instead, the primary ring radius is larger than the maximum tip radius, and therefore, the PV does not interact with the tip at all, resulting in a situation similar to a flat PVL, like in Figure 1c. Accordingly, in this situation, the decoupled power is zero. To increase the maximum lth mode interacting with the tip, a higher tip with the same curvature radius at the basis can be prepared (as can be evinced from Figure 2b).

Once the lth mode detaches from the tip, it propagates in air as a wave with the unique spatial phase-structuring. The radial polarization of the PV at the tip surface collapses in the free space into the scalar components of two opposite circular polarizations, E_± = E − is_oZ₀H,²⁰ carrying OAM of l_o = l – s_o = l ∓ 1, where the OAM of the PV is l = m + s_i = m ± 1; s_i is the incident spin number and s_o is the spin of the outcoupled light. We can summarize the expected OAM content of the output cross-circular polarization components in Table 1.²⁰

Table 1. Topological Charges of the Outcoupled Beam Depending on the Incident and the Emerging Polarization State.

Table 1
	si = +1	si = −1
so = +1	m	m – 2
so = −1	m + 2	m

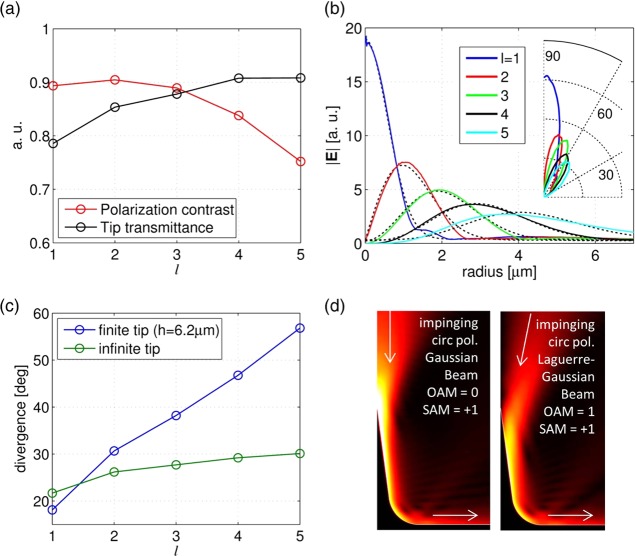
As has been stressed elsewhere,³⁸ the process of the impinging light scattering results in the appearance of some amount of a spin-flip component (that is, the light of opposite handedness with respect to the incident one). This mix of the output polarization states can be large and depends, besides the geometry of the structure, on particular symmetries of Maxwell’s equations.^39,40 In this regard, we notice that our structure behaves as a mode matcher rather than a scatterer. Specifically, the coupling of the incident circularly polarized light to PV followed by its guidance to the tip apex incorporates the 3D transformation of the electromagnetic fields. The surface curvature, combined with an effective index change along the tip, forces the emerging spin to be s₀ = sgn(l).⁴⁰ In other words, for positive topological charges of the PVs, the tip emits the light with an almost-pure spin state of s_o = 1. The tip profile we present has been optimized to simultaneously maximize, for l ranging from 1 to 4, both the tip transmittance and the polarization contrast. The latter is defined as Q = 1 – P₊/P_–, with P₊ and P_– being the light powers decoupled by the tip with right and left circular polarization state, respectively. A plot of transmittance and Q for the first l values is reported in Figure 3a. As can be seen, Q remains higher than 83% for l = 1 to 4. For more details about the tip parameter optimization, we remand attention to the Supporting Information.

Figure 3.

(a) Polarization contrast (red) and tip transmittance (blue) as a function of the PV topological charge, l. (b) Simulated |E| field profiles for various l (colored lines) taken at a horizontal cross-section 1 μm above the tip compared with the corresponding fit curves, obtained by using eq 4. (c) Simulated divergences of the beams in the case of the finite smoothed tip (blue line) compared to the semi-infinite one (green). (d) Examples of simulations of coupling of a focused Laguerre–Gaussian beam to the plasmonic vortex by coaxial illumination of the tip from above. As indicated in the figure, the beams have l_o = 0 and s_o = 1 (Gaussian beam) and l_o = 1 and s_o = 1 (Laguerre–Gaussian beam).

Finally, we characterize the propagating waves decoupled by the tip in terms of divergence and intensity profile. It is important to underline that, unlike other configurations presented in literature,²⁸⁻³⁰ in this case, what is transmitted to the far field is a well-defined beam with a single intensity lobe. Figure 3b reports the electric field norm profiles for l = 1 to 5 calculated on a horizontal cross-section 1 μm above the tip. We notice that profiles are well-fitted by Laguerre–Gaussian beam shapes (dashed black lines), namely

4

with l_o = l – s_o being the OAM of the outgoing wave, w(z) = w₀[1 + (z/z_R)^0.5], z_R = πw₀²/λ₀ being the Rayleigh range and adopting as parameters a and z and the beam waist, w₀. The inset of Figure 3b shows the far-field polar plots for each l. Clearly, the peak intensities are found within a cone of maximum 40° half-aperture. Figure 3c presents the beams divergences (i.e., the angles from the normal at which the intensity drops to 1/e times the peak value) for l = 1 to 5. We compare the cases of finite-height smoothed tips and the infinite tip. As can be seen, the divergences are similar only for l = 1 and 2 because for these l values, in both the realistic and idealized tip models, the PVs propagate along the tapered part of the tip before detaching. Nonetheless, for all l from 2 to 5, the beam divergences are lower than about 60°. Therefore, the output beams are readily measurable by standard microscope objectives, (an angular apertures of 60° corresponds to numerical apertures of 0.866). Interestingly, these results suggest that the smoothed conical structure can be exploited also as a perfect Laguerre–Gaussian beam-to-plasmonic-vortex converter. As an example, in Figure 3d, we simulate the illumination of the tip by normally impinging circularly polarized focused Laguerre–Gaussian beams with l_o = 0, 1 setting the beam parameters to those ones obtained from the fits of the corresponding outgoing waves produced by PV decoupling. As can be seen, the electric field norm distributions show a very smooth coupling to the conical tip modes and, finally, to the PV modes. The calculated back-reflections are lower than 1%, while the power delivered to PVs at the tip base is 76% for l_o = 0 and 84% for l_o = 1.

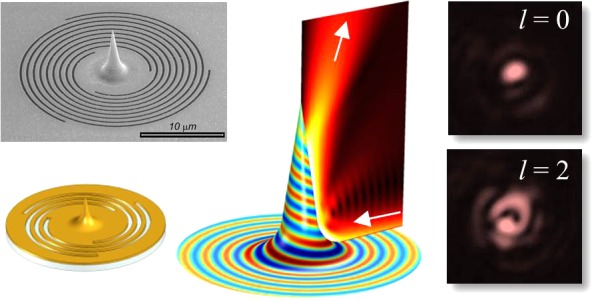
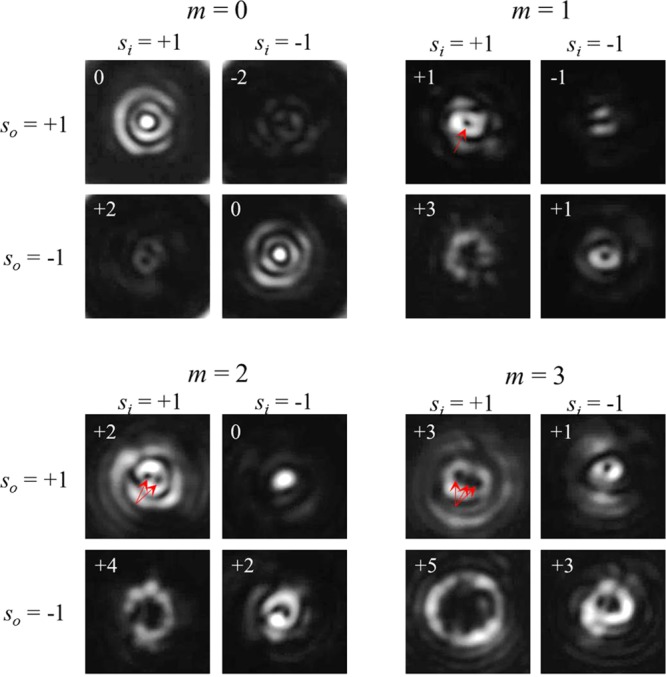
To prove the aforementioned properties of beaming of helical light by means of our adiabatically tapered tip, we provide the experimental demonstrations of the presented analytical and numerical simulations. The sample was illuminated from the bottom with a 20 mW CW single mode pigtailed laser at λ₀ = 780 nm. Its spatially filtered and collimated beam was normally incident from the substrate side on the spiral grooves surrounding the tips, and an additional optical objective (Olympus LMPLANFL 100×, NA 0.8) was used to produce an image the tips at CMOS camera (Hamamatsu Orca R2-cooled CCD). According to our simulations, the NA of the imaging objective is large enough to capture the beaming light distribution of up to l_o = 5. For higher topological charges, a near-field scanning microscopy might be used due to the strong angular deviation of the scattered light. We used a set of a linear polarizer (LP) followed by a quarter-wave plate (QWP) to tune the incident polarization state and an additional set of QWP and an LP to analyze the emerging polarization.

For the sample fabrication, an optimized procedure was developed (fully described in the Supporting Information). The fabrication of such high tips with arbitrary profiles cannot be performed by means of the well-known electron-beam-induced deposition (EBID)⁴¹ because the process is not stable enough. This limitation was solved by using an approach already used in high-aspect-ratio 3D plasmonic structure fabrication.³¹⁻³³ Briefly, the backbone of the 6.2 μm high tip was prepared by means of focused ion beam (FIB) (FEI Novalab 600i) exposure on a thick layer of S1813 resist spun on a thin (100 nm) Si₃N₄ membrane. A 150 nm gold layer was deposited on the membrane, and then the PVL slit patterns with the geometrical vortex topological charges m ranging from 0 to 3 were inscribed on the Au layer using the FIB. An example of the fabricated nanotip with the surrounding PVL is reported in Figure 1b. A scanning electron microscopy (SEM) image of the PVL with the geometric vortex topological charge of m = 3 is illustrated. In the Supporting Information, additional examples of fabricated samples can be seen with details on the 3D profile, providing evidence that the obtained tip shape almost perfectly matches the designed one.

Figure 4 demonstrates the intensity distributions captured by our setup above the structures with m = 0, 1, 2, or 3. We arrange the results for different polarization states in the order prescribed by the Table 1. As expected, our camera captures helical field distributions with topological charges up to l_o = +5. Due to unavoidable imperfections, the singularity of the beam is split into fundamental first-order singularities, providing a convenient way to verify the resultant OAM of the emerging beam, which nicely corresponds to the prediction given in the Table 1. We note that, as expected, the PVLs with m = 0 and m = 2 produce point-like emission expressed as an Airy distribution. In some panels, we added red arrows to guide the eye to the singular points. For m = 3 for (s_i,s_o) = (+1,–1), the beam divergence approaches our imaging limit, and therefore, the singularities are not clearly visible; however, the large primary ring is a clear signature for its high OAM. The helicity conservation effect can be clearly deduced from the PVL structure with m = 0. This structure has a circular symmetry; therefore, the plasmonic vortex topological charge is l = s_i. Accordingly, as stated before, the emerging spin state, s₀ = sgn(l) = s_i. We note that in the experiment, other sources of helicity change, such as scattering from the spiral rings and direct transmission, would limit the polarization contrast to lower values than the ones predicted by our simulations. However, the measured intensity distribution is fully consistent with this selection rule, as one can clearly see the undoubtedly high contrast between the pictures taken with the same polarizer–analyzer state (diagonal) and the ones taken with crossed polarizers (antidiagonal). Due to specific experiment conditions, the results for higher order PVLs presented in Figure 4 do not allow a visual estimation of the polarization contrast, which is one of the topics of our current research.

Figure 4.

Far-field intensity distributions measured using combinations of circular input polarizers and output analyzers. The images are arranged according to the incident and emerging polarization states (s_i and s_o, respectively) as in Table 1. The expected topological charges of the far-field beams, l_o, are reported in each image, and the red arrows are added to guide the eye to the singularity points.

In our last experiment, we utilized the fabricated tips as the plasmonic vortex generator in the near field. To measure this, we slightly modify the fabrication process by preparing a tip on top of a 60 nm thick gold layer without any grating around it. We illuminate the tip by a slightly focused laser beam (20× objective) and image the leakage radiation by using an oil-immersion 100× objective (NA 1.25). This leakage radiation microscopy system (LRM) provides us with a direct image of the plasmonic modes excited at the metal–air interface.⁴²Figure 5 demonstrates the experimental setup along with the measured results. As can be seen from Figure 5b, the stand-alone tip produces plasmonic vortices with l = ±1, which yields in the far field structured waves with l_o = 0 and ± 2, as expected from ideally center symmetric geometry. We verified that the spatial frequency of the measured disturbance, k = 8.45, corresponds to the expected plasmonic wavelength. This confirms that our system indeed captures the near-field surface waves distribution.

Figure 5.

Near-field PV generation by a nanotip. (a) Scheme of the LRM setup used to measure the near field. Polarization components LP and QWP were used to tune and analyze the polarization, a 20× objective (Obj1) was used to prefocus the beam on the tip, an oil immersion 1.25NA objective (Obj2) extracted the leakage radiation, and a set of the lenses (L1–L3) was used to image the SP distribution. (b) Measured LRM in the case of a tip fabricated with a 30 nm gold coating layer.

In summary, we presented a plasmonic vortex lens structure able to couple a circularly polarized light to a plasmonic vortex and to efficiently transmit it to the far-field by means of a smoothed-cone tip placed at its center. The large curvature radius at the cone basis is shown to play a crucial role in enabling an adiabatic coupling of the PV propagating on the flat metal surface to the plasmonic modes of the metal tip, whose tapering, in turn, enables an adiabatic match to the propagating waves in free space. This particular nontrivial geometry has been faithfully experimentally fabricated by the secondary electron lithography technique. The optical characterization revealed that phase-structured beams were successfully transmitted by the tip up to OAM l₀ = 5. Finally, our simulations have shown that this structure can work as an excellent coupler of focused Laguerre–Gaussian beam to PVs. A proof of concept measurement in this illumination condition has been shown by adopting a leakage radiation microscopy setup.

We believe that such architecture can be a key element for the realization of compact focused-beams-to-plasmonic-wave couplers, elements that are highly desirable to fully exploit plasmonic technologies in practical applications, such as sensing, light manipulation in flat guided optics, optical tweezing, etc. On the other side, a scattering-free, highly directional PV read-out element could be also extremely valuable, enabling us to directly visualize any near-field coherent azimuthal interference taking place at the center of a PVL. Thanks to the flexibility of secondary electron lithography (as demonstrated elsewhere),³¹ complete control of the tip shape can be obtained, enabling us to finely tune the coupling–decoupling capability of the tip, thus making it interesting for a large number of applications. For example, smaller tips can be used to decouple PVs produced by simple bull’s eye structures, while a higher tip can enable far-field access to arbitrary high-OAM-carrying PVs.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.6b03359.

• Additional details on the fabrication process of the plasmonic vortex lens with a central tip, mode analysis of gold cylindrical waveguides, and tip optimization studies. Figures showing the SEM image of an isolated tip, a comparison between the designed and fabricated profiles, SEM micrographs of PVLs with topological charge, modal analysis of a cylindrical gold waveguide in vacuum as a function of its radius, and a study of tip transmittance and R parameter as a function of the tip parameters for PV topological charges of l = 1 to 4. (PDF)

Author Contributions

D.G. fabricated the structures; P.Z. ideated, designed, and simulated the structures; Y.G. provided theoretical support and performed the optical characterization; F.T. helped in the optical characterization and optics setup; and F.D.E. supervised the work. D.G., P.Z., and Y.G. contributed equally.

The authors declare no competing financial interest.