Estimating disease prevalence from drug utilization data using the Random Forest algorithm

Abstract

Background

Aggregated claims data on medication are often used as a proxy for the prevalence of diseases, especially chronic diseases. However, linkage between medication and diagnosis tend to be theory based and not very precise. Modelling disease probability at an individual level using individual level data may yield more accurate results.

Methods

Individual probabilities of having a certain chronic disease were estimated using the Random Forest (RF) algorithm. A training set was created from a general practitioners database of 276 723 cases that included diagnosis and claims data on medication. Model performance for 29 chronic diseases was evaluated using Receiver-Operator Curves, by measuring the Area Under the Curve (AUC).

Results

The diseases for which model performance was best were Parkinson’s disease (AUC = .89, 95% CI = .77–1.00), diabetes (AUC = .87, 95% CI = .85–.90), osteoporosis (AUC = .87, 95% CI = .81–.92) and heart failure (AUC = .81, 95% CI = .74–.88). Five other diseases had an AUC >.75: asthma, chronic enteritis, COPD, epilepsy and HIV/AIDS. For 16 of 17 diseases tested, the medication categories used in theory-based algorithms were also identified by our method, however the RF models included a broader range of medications as important predictors.

Conclusion

Data on medication use can be a useful predictor when estimating the prevalence of several chronic diseases. To improve the estimates, for a broader range of chronic diseases, research should use better training data, include more details concerning dosages and duration of prescriptions, and add related predictors like hospitalizations.

Introduction

Information on disease prevalence is important for assessing the health needs of populations.¹ Several sources can deliver population disease prevalence estimates, such as surveys,^2–4 dedicated epidemiologic studies using diagnostics^5–7 or administrative data sources.^8–12 Drug use data, especially on prescription drugs, has also frequently been used to estimate disease prevalence.^13,14 In many countries insurers or providers maintain extensive prescription databases, allowing easy access to national drug use data.

Drug use has several advantages over other sources. Surveys are costly to execute on a large scale. Hospital discharge registers are large, but involve hospital-related events only. In addition, in the Netherlands, the GP-serves as a gatekeeper, implying that patients—except in emergencies—can only visit a medical specialist with a referral of the GP. This means that the GP sees both patients that see only the GP and those he refers to specialist care. Hospital data is therefore more likely that GP data to underestimates the prevalence.^15,16 GP-registers containing diagnosis codes are not readily available in all countries. Furthermore, GPs may have different coding habits, hindering comparisons between GPs.¹⁷

While drug use data is often recorded without a diagnosis, some studies base disease prevalence estimates on direct links of specific drug use to the presence of certain diseases.^{9,13,14,18,19} The links are based on literature or medical guidelines. For two reasons, this procedure is problematic. First, many drugs are used for the treatment of multiple diseases; assuming that all patients who take a specific drug do have a specific disease will then lead to overestimation. Second, some patients with a disease are not prescribed the specific drug, and this will lead to underestimation of prevalence.

To overcome these two problems, it is better to estimate the probability of having a specific disease given all different medications a person uses. Avoiding any a priori assumption on the relationship between the drugs and diagnoses, machine learning algorithms can be used to estimate this relation from data. In this paper more specifically the Random Forest (RF) algorithm will be applied, as this method yielded the best results in comparison with others.^20,21

This algorithm requires a test set with both diagnosis data and drug use. This diagnosis data could also be used directly to estimate disease prevalence. This is the case particularly when it is possible to assume that the set containing diagnosis data is representative for the population of interest. However, using the diagnosis data in combination with drug use as proposed alters the assumption. Rather than that the diagnosis data should be representative for the population of interest, the relationship between diagnosis and drug use should be similar as in the population of interest. This might be a more reasonable assumption in many cases, as medical professionals are influenced by standardized prescription guidelines. Countries which do have a prescription registration, but lack population surveys on disease prevalence, as is often the case, can use the relation derived in comparable countries to obtain prevalence estimates.

Existing applications of RF analysis to the problem of disease prevalence estimates have some limitations. Chaudhry²⁰ used RF to predict the population prevalence of diabetes and dementia from administrative data in GP and hospital records. However, his choice of predictors was informed by a priori knowledge. Khalilia et al.²¹ predicted the presence of eight diseases with RF from hospital in-patient data, but did not make any population prevalence estimates.

In contrast, we apply the RF approach to a broad range of 29 diseases. The RF algorithm allows us to select important predictors from the full range of possible drug use predictors. Afterwards, we have a list of predictors for comparison with existing theory based lists of predictors, e.g. the Dutch Pharmacotherapeutic compass.²²

The objective of this paper hence is to examine for which diseases the prevalence can be estimated using the RF algorithm, and if so, to see which drug groups should be used.

Methods

Random Forest

Estimating the probability that an individual has a certain disease could be considered a mathematical classification problem. RF is a non-parametric method to address classification problems.²³ For implementation the R-package ‘Random Forest’²⁴ was used.

Data

Drug use data of the entire Dutch population is available from the National Health Care Institute (ZiN).²⁵ The ZiN claims database covers all outpatient prescriptions reimbursed under the Dutch mandatory Health Insurance scheme. Drugs were classified in 204 pharmaceutical groups according to the four position ATC-code. To these groups, age and gender were added as predictors. The dataset contained 47 million individual prescription records in 2010, covering a population of 16.7 million, of which 70% had at least one prescription.

A training set with disease information was obtained from the primary care database of the Netherlands Institute for Health Services Research (NIVEL).²⁶ As every citizen is required to have a GP—with the exception of those living institutionalized—this means the dataset is likely to cover the whole Dutch population, with the exception of the 80+ population of which in 2010 a significant part lived institutionalized.²⁷ All patient contacts were labelled with a diagnostic code, ICPC.²⁸ A person was defined to have a disease when he/she had at least one contact with a GP for this disease over a period of 3 years. All GP-patients with full data available over 2008–2010 were selected. This resulted in a training set of 276 723 individuals. The selection of 29 diseases was based on a list provided by O’Halloran et al.²⁹ See Supplementary file S1 for details. We combined the available data (drug utilization, age and gender, and ICPC codes) at Statistics Netherlands within the System of Social Statistical Datasets (SSD). The SSD allows data from different administrative registers to be combined using an anonymous patient identifier for research purposes.^30,31

Implementation of RF

Usually, all observations in a training set and all predictors are combined in one RF-analysis. However, within the SSD system, computing power is limited, and analysis with our dataset (276 723 records with 206 variables) proved to be difficult. We therefore used a two-step approach. First, for each chronic disease, persons with the disease were randomly selected, up to a maximum of 5000 patients. To this set, an equal number of persons without the disease was randomly selected and added. For each of these smaller sets, the RF algorithm was applied. The variable importance measure,²⁴ defined as the average decrease in accuracy when a predictor is left out of the analysis, was evaluated. For each disease, the 10 drug groups with the highest variable importance were selected. By selecting 10 drug groups, the most important predictors were included for all diseases, while limiting the computing times. Second, a new dataset was created for each disease based on the full training set, but only age, gender and the drug groups selected in the first step were added as predictors (276 723 records with 12 variables for each disease), and we applied RF a second time. For each disease this second RF-model was then applied to obtain the probability of having this disease for each individual in the prescriptions database, hence for the 11.6 million Dutch inhabitants that were reimbursed a prescription drug in 2010. The model was also applied to the remaining 5. million Dutch individuals without any prescription. They received for each of the 29 diseases a probability equivalent to the age and gender specific probability in the training set for those diagnosed with the disease, but not receiving any prescription.

Outcome measures

For each disease, the most important drugs according to the variable importance were compared with theoretical drug classifications included in relevant guidelines. For 13 of the 29 chronic diseases pharmaceutical groups used in the Dutch insurance system were available.³² In addition, for four other diseases the drugs found were compared with Dutch treatment guidelines: tuberculosis,³³ MS,³⁴ chronic back or neck disorder^35,36 and gastric or duodenal ulcer.³⁷

To measure the performance of the final RF-models, the area under the Receiver-Operator Curve (AUC) was measured for the training set for each disease separately. An AUC-value above .7 is generally considered useful.³⁸ To prevent overfitting, 10-fold cross validation was applied.

The AUC and a 95% confidence interval around the AUC-value were obtained using the R-package ‘cvAUC’.³⁹ If the lower boundary of this interval was above .5, we considered the model to perform better than a random prediction.

The predicted population prevalence by age and gender for the Netherlands was graphically compared with a prevalence estimate based on direct extrapolation of the training set prevalence. Correlations were computed as well for the six diseases with lower confidence bound (95%) of the AUC >.70. The age range considered was 30–80 years, since the prevalence below 30 is very low for most chronic diseases and the 80+ population was not well covered in our training set.

For a binary classification of each individual, a cut-off needs to be chosen. This was done by setting an age and disease-specific cut-off value. All persons with a probability higher than the cut-off were classified as ‘ill’. The cut-off was chosen to minimize the deviation between the observed and the predicted prevalence in the training set for each age, gender and disorder.

Results

Table 1 gives descriptives for the training set. The average annual number of different pharmaceutical drugs taken by patients in the training set was 2.9, which is very comparable with the utilization in the total Dutch population in the same year (2.8). Table 1 also shows that the number of ATC groups utilized by an individual patient rises proportionally with the number of chronic diseases present.

Table 1.

Pharmaceutical utilization in dataset

	Persons with at least one recorded episode for each chronic disease in 2008–2010	Total number of pharmaceutical groups utilized in 2010	Average number of pharmaceutical groups utilized per person
Persons without disease	184 826	328 385	1.8
Persons with 1 chronic disease	60 065	235 032	3.9
Persons with 2 chronic diseases	20 090	125 335	6.2
Persons with 3 chronic diseases	7609	63 064	8.2
Persons with 4 chronic diseases	2697	27 190	9.9
Persons with 5 or more chronic diseases	1436	17 219	11.6
Total	276 723	796 225	2.9
Percentage with at least one chronic disease:	33.2%
Percentage study population with multiple diseases:	11.5%

Legend: Training set population has been divided into six strata, based on the number of chronic diseases present. First column presents stratum. Second column gives population size. Third column gives total number of pharmaceutical groups utilized. Pharmaceutical groups have been defined in terms of an ATC 4 position code: A01A, A02A, etc. Last column gives average utilization in stratum.

Table 2 lists the AUC values produced by our analysis, sorted by average AUC. For 17 diseases the lower boundary of the 95% AUC confidence interval was >.5. For 10 diseases the average AUC was .7 or higher, but for only six the lower boundary of the AUC 95% confidence interval was >=.7: Parkinson’s disease, diabetes mellitus, osteoporosis, heart failure, asthma and chronic obstructive pulmonary disease (COPD).

Table 2.

Model outcome AUC with confidence interval, ordered by mean AUC

Disease	AUC (95% conf. interval)	Prevalence in training set per 10 000 persons
Parkinson’s disease	.89 (.77–1.00)	15
Diabetes mellitus	.87 (.85–.90)	421
Osteoporosis	.87 (.81–.92)	103
Heart failure	.81 (.74–.88)	82
Chronic obstructive pulmonary disease	.79 (.75–.83)	209
Chronic enteritis/colitis ulcerosa	.79 (.68–.90)	31
HIV/AIDS	.78 (.39–1.00)	4
Asthma	.77 (.74–.80)	424
Epilepsy	.77 (.66–.87)	41
Coronary heart disease	.70 (.66–.74)	255
Visual disorder	.69 (.64–.73)	191
Schizophrenia	.69 (.48–.89)	10
Rheumatoid arthritis	.68 (.60–.76)	66
Dementia	.67 (.54–.80)	28
Congenital neurological anomaly	.67 (.01–1.00)	3
Multiple sclerosis	.66 (.42–.90)	9
Cancer	.60 (.56–.64)	264
Chronic alcohol abuse	.59 (.49–.69)	45
Depressive disorder	.58 (.54–.63)	253
Stroke (including TIA)	.57 (.52–.63)	137
Congenital cardiovascular anomaly	.57 (.37–.77)	7
Chronic back or neck disorder	.56 (.53–.60)	432
Osteoarthritis	.56 (.52–.60)	282
Anxiety disorder, neurosis, PTSS	.56 (.50–.61)	154
Mental retardation	.55 (.36–.74)	13
Hearing disorder	.52 (.44–.61)	62
Anorexia	.52 (.33–.71)	8
Gastric or duodenal ulcer	.50 (.39–.62)	25
Tuberculosis	.50 (.06–.94)	2

Legend: First column gives name of chronic disease. Second column gives model outcome of RF-analysis as AUC with 95% confidence interval, in order of decreasing AUC. Third column states prevalence of chronic disease or condition in the training set. (n = 276 723).

There is some association between the frequency of the disease and the prediction of the AUC. For almost all 12 diseases with a prevalence in the training set higher than 100 per 10 000 persons, the prediction is better than a random assignment. The only exception is anxiety disorder (154 cases per 10 000 persons), with a very poor performance and AUC of .56 (95% cf. = .50–.61). For 11 out of 17 diseases with a frequency below 100 per 10 000 persons, performance is poor, i.e. the lower boundary of the AUC 95% confidence interval was below .5. A notable exception was Parkinson’s disease which despite a low frequency (15 per 10 000 persons) seems to be very predictable from drugs utilization.

In table 3 predictors of all model output from the RF-analysis are ranked by importance. The shaded areas denote drugs that are also mentioned as indicator drugs for these diseases in the theoretical drug classifications we compared with. Only for cancer we found no similarities. For all other diseases, the ATC codes mentioned by insurers and guidelines are also strong predictors for the corresponding diseases in our RF-models. However, our models show a number of additional predictors for most disorders. Supplementary file S2 gives more information.

Table 3.

Predictors of chronic diseases in Random Forest analysis

Disease	ATC4 groups with strongest relation with disease in RF-analysis
	[1]= strongest relation, [10]= weakest relation
	[1]	[2]	[3]	[4]	[5]	[6]	[7]	[8]	[9]	[10]
Parkinson's diseasea	N04B	N04A	Birthyear	L04A	A07E	C10A	C09B	N05A	C03C	N06D
Diabetes mellitusa	A10A	A10B	C10A	B01A	H04A	C09A	C09B	C08C	C03C	C07A
Osteoporosis	M05B	A12A	A11C	L04A	C10A	B01A	C09D	D01A	C09C	D06A
Heart failure	C03C	C03D	A12B	C01A	C08D	C08C	C01D	C03A	C10A	C07B
Chronic obstructive pulmonary diseasea	R03A	R03B	R06A	A01A	R01A	N06B	J01F	R05D	A06A	J01C
Chronic enteritis/colitis ulcerosa	A07E	L04A	L01B	B03B	A06A	J01M	A11C	A07D	N02A	M01A
HIV/AIDSa	J05A	J01E	J04A	J01F	N01B	J07B	D06B	A02B	J01C	J01A
Asthmaa	R03A	R03B	R03C	Birthyear	H02A	A07A	S01G	R01A	R06A	R05D
Epilepsya	N03A	N05B	Birthyear	A03F	N05A	B01A	N06A	D04A	D11A	N05C
Coronary heart diseasea	C01D	C08D	C03C	C01B	C03A	C09A	D06A	C01E	C09C	B03A
Visual disorder	S01E	S01B	Birthyear	S01C	A10B	S01F	D02A	S01A	A10A	S01X
Schizophreniaa	N05A	N05B	N05C	N04A	N06A	N06B	Birthyear	N03A	A06A	N07C
Rheumatoid arthritisa	L04A	P01B	A07E	B03B	N02A	L01B	H02A	D02B	M05B	D06A
Dementiaa	N06D	Birthyear	N05A	A12A	C03C	N03A	M05B	Y	D03D	C09D
Congenital neurological anomaly	M03B	G04B	N03A	J01X	D07X	N05A	J01E	A12A	D01A	N05B
Multiple sclerosisb	L03A	M03B	G04B	N03A	N06A	N04B	B03B	S01A	J01X	C03C
Cancera	Birthyear	L02B	H03A	Y	D06A	A04A	Gender	L02A	G03C	A12A
Chronic alcohol abusea	N07B	N05A	Birthyear	N05B	G04C	A02B	N06A	M04A	A10B	N05C
Depressive disordera	N06A	N05A	N05B	N06B	N05C	N07B	N03A	A03F	A11C	G04B
Stroke (including TIA)	B01A	V03A	C01D	C01B	C07A	Birthyear	C08C	C01A	S01C	S01E
Congenital cardiovascular anomaly	B01A	C07A	J01C	N03A	C09A	D06A	R03B	Y	D02A	S02C
Chronic back or neck disorderb	N02A	M01A	A02B	A06A	N02B	C05A	S02C	N03A	H02A	R05D
Osteoarthritis	Birthyear	B01A	Gender	M04A	C10A	N02B	C10B	C03A	S01E	N02A
Anxiety disorder, neurosis, PTSS	N06A	N05B	N05A	C07A	N01B	N05C	A03F	A06A	N03A	D05A
Mental retardation	N05A	N03A	D02A	D06A	A06A	N05B	Y	D10A	S01F	N01B
Hearing disorder	Birthyear	L02A	B02A	S01X	D05A	G04C	H02A	A10B	C08D	C07B
Anorexia	Gender	G03A	A06A	A01A	Y	J01X	G03H	R05D	G01A	A12B
Gastric or duodenal ulcerb	A02B	D05A	G04B	A07A	A03A	A03F	M01A	A11C	D06B	A06A
Tuberculosisb	J04A	D02A	D07X	C01B	J01A	C08C	C03C	S01C	S02C	C03E

Legend: First column gives name of chronic disease. The next 10 columns list the predictors used in the final RF-model, in order of decreasing importance. To facilitate comparison, diseases are presented in the same order as in table 2.

^aFor these diseases, comparison is possible with pharmaceutical groups listed in risk adjustment compulsory insurance. The shaded groups are also used for the detection of these diseases by Dutch insurers.³²

^bThese diseases have been compared with ATC-groups mentioned in the relevant Dutch treatment guidelines. The shaded groups are included in these guidelines.^33–37

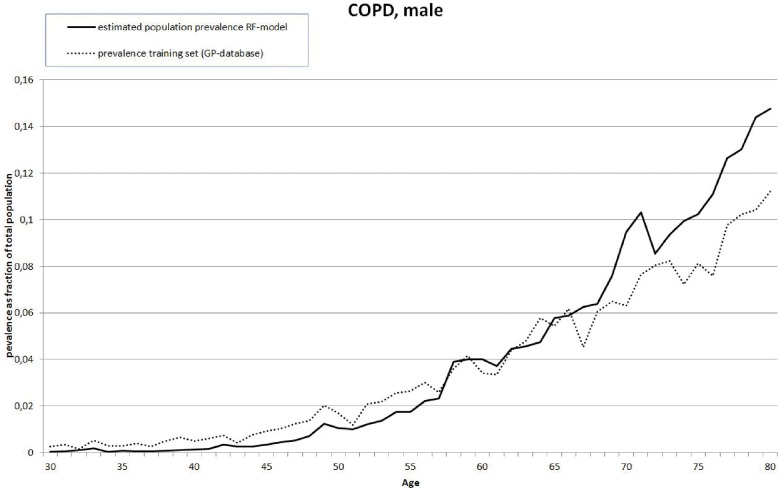
The actual prevalence in the training set and the calculated prevalence based on applying the final RF-models have been compared for the six diseases with a lower bound of the AUC 95% confidence interval >.7. Except Asthma, correlations are above .9. Asthma shows correlations of .43 for males and .66 for females, indicating poor performance. Looking at the graphs for osteoporosis, a large discrepancy exists between predicted and observed prevalence around the age of 70. Figure 1 gives an example (COPD, male). A full set of figures is found in Supplementary file S3.

Figure 1.

Example of comparison between Dutch population prevalence for ages 30–80 estimated from model applied to drug utilization data and estimation based on training set for COPD, male

Discussion

For a broad range of 29 diseases, RF was used to predict disease prevalence based on medication use. Predictive performance was acceptable for 6 out of 29 diseases and would result in reliable estimates of population prevalence. Furthermore, we find that theory-based indicator drugs were included in the range of diseases identified by the RF model. This seems to be independent from the performance of the models, which indicates that the RF algorithm can also be used to identify suitable predictors, even in those cases were the predictive performance is low. Especially for diabetes, heart failure and COPD we observe a high correlation between estimated and observed population.

Our outcomes can be compared with a few other studies. Chaudhry²⁰ predicted the presence of diabetes with an AUC of .95 and dementia with an AUC of .875, higher than the .87 and .67 we found. However, for dementia he used dementia-coded doctor visits as predictors, while we use this as our definition of disease. Khalilia et al.²¹ used data on hospital stays as predictors, on a very large set (8 million records). A training set was generated by bootstrapping. The average AUC he reports (.88) is much higher than those we found. For the two diseases which could be directly compared (diabetes and osteoporosis) he finds almost the same AUC (.879 and .870 respectively) as we found, .87 for both. Compared with these two previous studies, we included a relatively broad range of diseases and added the comparison with theory-based models.

While the method seems useful for some diseases, the predictive performance is still low for most diseases. This could have multiple causes. First, for some diseases, there is no standard pattern of drugs included in all treatment options. In addition, drugs might be prescribed for multiple diseases. For instance, the two strongest predictors for asthma and COPD are the same (R03A and R03B, table 3). As a result, misclassification of asthma and COPD patients is likely to occur, which has not been further investigated in this study. Furthermore, patients and GPs may deal with diseases in different ways. Based on patient characteristics a GP will sometimes advise lifestyle changes instead of drugs, but will treat similar cases in other instances immediately with drugs. In addition, the patient may have treatment preferences. The relationship between diagnosis and drugs can also change over time. Innovation or policy changes can strongly influence prescription behaviour, making regular calibration of the algorithms necessary.

Second, the predictive power is likely limited due to weaknesses of the current data. In the current training set, only 3 years of diagnoses are used. While many patients with a chronic disease are visiting a GP more than once every 3 years, some patients who visit less frequently will not occur as diseased in the training set. Furthermore, some diseases might not be treated primarily by a GP, but directly in the hospital, also resulting in missing diagnoses in the training set. As the training set serves as a ‘golden standard’, any diagnosis errors in the training set will translate into the final predictions. Investing in a smaller set of persons for which disease diagnosis is even more reliable, e.g. through the use of cohort studies may provide a training set with better performance. The disadvantage of such a cohort, and the advantage of our current approach is that for rare diseases, relationships between disease and drugs would have to be derived from only a very limited number of disease cases.

Next to errors in disease diagnosis, drugs use measures could also be improved. Drug use often varies between years. Grouping multiple years of drug use could improve results. Also, more complete drug utilization data could be obtained by including inpatient drugs. For some diseases, utilizing more detailed pharmaceutical predictors, such as ATC4 or ATC5 groups, would improve results.

Even though improvements might be needed to obtain reliable prevalence estimates for most diseases, for 16 out of 17 diseases for which theory-based predictors were found within existing guidelines, important similarities were found. This means that even though the predictive power of the algorithm on the current data is insufficient, it is still possible to identify relevant drug groups. Compared with purely theory-based models, the RF algorithms have the important advantage of coming with confidence intervals and information about model performance. From this similarity we also infer that Dutch general practioners broadly follow existing pharmaceutical guidelines. Cancer was the only disease for which the drugs found using the RF algorithm differ from theory. This could be the result of grouping all cancers together, and many drugs used in cancer treatment were not covered by the dataset as they were prescribed in a hospital setting.

We do not want to suggest that prediction models can entirely replace current GP registers or population surveys. On the contrary, since without these registries the models cannot be built or validated. However, even in countries like the Netherlands which are covered by both population surveys and GP networks the method is of practical value, as it allows for analysis on subgroups, such as regions or stratifications by socio-economic status. The primary care database used as training set has been enlarged in recent years, but still covers at this moment only 10% of the population and the Dutch GPs. Using drug use will allow for better prevalence estimates for the 90% not covered.

Because the full population is covered in the prescription data we use, and the model provides estimates of the probability of having a disease at the individual level, other useful applications would be pre-selecting subjects for medical trials, or making case-mix corrections, e.g. for comparing hospital performance.

To conclude, combining diagnosis data and drug use by the RF algorithm provides can be a useful tool to predict population prevalence. Applications include situations where the diagnosis data is not necessarily representative for the population of interest, but the relation found between diagnosis and drug use is representative. Furthermore, it can be used to select relevant drug use groups in almost all cases.