REDAN: Relative Entropy-Based Dynamical Allosteric Network Model

Abstract

Protein allostery is ubiquitous phenomena that are important for cellular signaling processes. Despite extensive methodology development, a quantitative model is still needed to accurately measure protein allosteric response upon external perturbation. Here, we introduced the relative entropy concept from information theory as a quantitative metric to develop a method for measurement of the population shift with regard to protein structure during allosteric transition. This method is referred to as relative entropy-based dynamical allosteric network (REDAN) model. Using this method, protein allostery could be evaluated at three mutually dependent structural levels: allosteric residues, allosteric pathways, and allosteric communities. All three levels are carried out using rigorous searching algorithms based on relative entropy. Application of the REDAN model on the second PDZ domain (PDZ2) in the human PTP1E protein provided metric-based insight into its allostery upon peptide binding.

Introduction

Molecular dynamics (MD) simulations have been widely applied to investigate protein structures and functions.[1] Function regulations of many proteins involve external or internal perturbations including light stimulation[2], ligand or peptide binding[3], stress activation [4], pH activation[5] etc., which are essential for protein regulations. In general, the regulations of protein function due to external perturbations are referred to as allostery [6], which are ubiquitous molecular processes in biological systems. Recently, a population shift model was proposed that different function related protein conformations could coexist [7,8]. Upon external perturbation, the free energy landscape of a target system could change significantly whereas the populations of different states are shifted. These changes of free energy landscape are essential for so-called dynamics-driven allostery.[6,9–13]

Dimensionality reduction methods could be applied to investigate the distribution changes using only limited number (usually up to three) of collective variables.[14] Due to unavoidable structural information loss, it is difficult to investigate how the dynamics lead to the distribution changes, and how the perturbation information propagates inside protein. To address this difficulty, an improved method is needed to accurately compare the distribution between the simulations of two allosteric states to offset the structural information loss due to dimensionality reduction analysis.

One metric to quantitatively measure the difference between two probability distributions is relative entropy[15]. Relative entropy, also known as Kullback–Leibler divergence, is a concept in statistics to measure how one probability distribution diverges from the expected distribution with broad application in many fields[16–20]. By adapting this metric into MD simulation analyses, one would be able to quantitatively describe how one simulation diverges from other simulations. This measurement could be applied on many distributions. The distribution differences measured by relative entropy are equivalent to the free energy changes upon external perturbations, and can be considered as one of the allostery effects.

To analyze protein structure-function relations and quantify the communication among residues inside protein, a group of approaches referred to as protein structure network methods were developed to identify network of residues to model residue communication based on protein structural dynamics. In protein structure network analysis, each amino acid residue is considered as a node, and edges are built to connect nodes to obtain different network representation of a protein. Specifically, protein contact network (PCN) and residue interaction network (RIN) models were developed and applied to reveal the residues crucial for protein stability, and identify domains, hubs, and clusters of residues correlated with protein functions[21–23]. Elastic network models (ENM) were developed to investigate the interactions among residues through approximating inter-residue interactions by harmonic elastic restraints [24,25]. The network analysis has also been adapted broadly to analyze MD simulations. Dynamics network analysis (DNA) method models the residue interaction in the network using the correlation matrix based on MD simulations [26]. These network analyses have been widely applied to investigate the communication among residues in proteins [27]. However, no method has been developed to utilize simulation distribution information, which closely correlates with the functions, and is readily available from the MD simulations of macromolecules. In addition, few methods could quantitatively characterize the allosteric effects of proteins upon external perturbations. Here, we developed a novel quantitative network analysis method utilizing distribution information from MD simulations specifically targeting protein allostery. This method is referred to as relative entropy-based dynamical allosteric network (REDAN) model, and could be applied to compare distribution differences of two allosteric states upon perturbation and build quantitative network model.

In REDAN model, each amino acid residue is considered as a node, and connection between any node pair is considered as an edge. The change of distance distribution between any node pair can be calculated using relative entropy method and used as the weight for the corresponding edge. These weights quantitatively measure the response of protein dynamics upon perturbation, and could be used to characterize allostery induced by the same perturbation. Therefore, this network model could quantitatively describe protein allosteric effects from the perspective of structural biology and population shifting. Higher relative entropy indicates significant allosteric effect or larger distribution shift due to perturbations. Using this allosteric network model, we can quantitatively compare allosteric effects upon perturbation with minimum structural information loss.

Similar with other network models[21,26], the pathway and community analyses could also be conducted in this allosteric network model. A typical allosteric pathway consists a series of edges connecting two distal residues to exhibit the potential communication between residues leading to the allosteric effects. An allosteric community represents a group of residues with minimum allosteric effects upon perturbation. The second PDZ domain (PDZ2) in the human PTP1E protein[28] is an allosteric protein which could propagate signals to other part of molecular complex upon peptide binding[28,29], and is subjected to the allosteric pathway and community analysis using REDAN method to reveal potential allosteric mechanism and identify allostery-related residues.

Materials and Methods

Molecular Dynamics Simulation

For PDZ2 system, the initial structures were obtained from the Protein Data Bank (PDB)[30] with the ID as 3LNX (peptide unbound state) and 3LNY (peptide bound state), respectively. After adding hydrogen atoms, PDZ2 is solvated using explicit water model (TIP3P)[31] and neutralized with sodium cations and chloride anions to maintain 0.1M ionic strength. The simulation system was then subjected to the adopted basis Newton-Raphson (ABNR) energy minimization, which yielded a total gradient of less than 0.001 kcal/(mol•Å). After the minimization, 10 nanoseconds (ns) of isothermal-isobaric ensemble (NPT) MD simulations followed by 100 ns of canonical ensemble (NVT) Langevin MD simulation at 300K were conducted for both PDZ2 domain unbound and bound states. For all simulations, SHAKE constraint was applied to constrain all bonds associated with hydrogen atoms. Step size of 2 femtosecond (fs) was used and simulation trajectories were saved every 100 picosecond (ps). Cubic simulation box and periodic boundary condition were applied for all MD simulations. Electrostatic interactions were calculated using particle mesh Ewald (PME) method[32]. All simulations were carried out using CHARMM[33] simulation package version 41b1 with the support of GPU calculations based on OpenMM[34].

Relative Entropy

Relative entropy method was applied to calculate the difference between the distributions of the distance between the alpha carbon (Cα) of two residues upon perturbation. The probability distributions of the Cα distance before and after allosteric perturbation are represented as P and Q, respectively, with p(x) and q(x) as the distribution density at distance x. The relative entropy D_KL between P and Q is calculated as the following

$$D_{KL}(P||Q\text{)}=ʃp(x)\text{ln}\frac{p(x)}{q(x)}dx$$ (Eq. 1)

Because the above equation is not symmetrical measurement for P and Q, we symmetrize the relative entropy between P and Q by taking the average of D_KL(P∣∣Q) and D_KL(Q∣∣P). This averaged relative entropy is referred to as the perturbation relative entropy (PRE) between two distributions of the same distance in different allosteric states upon perturbation (Eq. 2).

$$PRE(P||Q\text{)}=\frac{D_{KL}(P||Q\text{)}+D_{KL}(Q||P\text{)}}{2}=\frac{1}{2}ʃ(p(x)-q(x))\text{ln}\frac{p(x)}{q(x)}dx$$ (Eq. 2)

In any distribution, e.g. P, the free energy at distance x (A_Px) can be estimated from the distribution probability at x as the following

$$A_{Px}=-k_{B}T\text{ln}p(x)$$ (Eq. 3)

where k_B is the Boltzmann constant, and T is the temperature. Combining Eq. 2 and Eq.3, the PRE between distributions P and Q is a direct measurement of the free energy difference for the given order parameter between two states:

$$PRE(P||Q\text{)}=\frac{1}{2}ʃ\left(p(x)-q(x)\right)\text{ln}\frac{p(x)}{q(x)}dx=-\frac{1}{2 k_{B}T}ʃ\left(p(x)-q(x)\right)\left(A_{Px}-A_{Qx}\right)dx$$ (Eq. 4)

Allosteric Pathways

The allosteric networks can be built based on PRE matrix. PRE value measures the magnitude of the distribution shifting upon perturbations, and can be considered to indicate the significance of the allosteric effects. To identify potential allosteric pathways between two distal residues with large PRE, a cutoff value to control the edge length is necessary to facilitate the analysis. An edge between any residue pairs will be chosen if the most probable distance between the Cα of these two residues is smaller than the given cutoff value. For each chosen edge, a weight is defined as 1/PRE. Therefore, the pathway with the smallest overall weight implies the propagation channel with the largest allosteric effect. The shortest pathway was identified by the Dijkstra’s algorithm [35], which is the most common pathway-searching algorithm. Using Dijkstra’s algorithm, the search starts with the starting node, and iteratively loops all the available nodes until reaching the destination node to identify the shortest path connection two nodes. More details could be obtained by referring to the literature [35].

Allosteric Communities

The main objective for community analysis is dividing the residues into different communities, so that the total PRE associated with residue pairs within each community is a minimum, and the total PRE associated with residue pairs across different communities is a maximum. Therefore, the overall allosteric effects upon perturbation could be projected onto the correlation among communities. Both Girvan-Newman[36] and Kernighan-Lin[37] algorithms are implemented in this study to construct communities.

Girvan-Newman (GN) algorithm

The GN algorithm is a top-down community detection approach, which removes the “most valuable edge” in each iteration, and recalculates the betweenness of all remaining edges until no edge remains. This algorithm depends on the graph construction and cutoff values. The optimal communities are determined by modularity value[36], which is the measurement of the strength of the community separation. Better community structure is indicated by larger modularity value. Final communities are selected with the highest modularity during iteration.

Kernighan–Lin (KL) algorithm

The KL algorithm[37] is a heuristic algorithm for finding the partition of graphs. The algorithm is independent to the graph construction and cutoff value, and only depends on the relative entropy matrix. Multiple random initializations are carried out in KL algorithm to search for the lowest possible relative entropy value within each community. The KL algorithm is outlined as the following.

Assuming n communities labeled as C₁ through C_n, the total PRE inside communities are defined as

$$T=\mathrm{ }{\sum }_l{\sum }_{i,j\subseteq C_l}{PRE}_{ij},$$ (Eq. 5)

where i, j are the residues in Community C_l, and PRE_ij is the perturbation relative entropy between distance distribution of residues i and j upon perturbation.

Assuming that node i belongs to Community C_m, the internal PRE of node i in community C_m is defined as Eq. 6, and the external PRE of node i with reference to community C_q is defined as Eq. 7:

$${In}_i=\mathrm{ }{\sum }_{j\subseteq C_m}{PRE}_{ij},$$ (Eq. 6)

$${Ex}_{i,C_q}=\mathrm{ }{\sum }_{j\subseteq C_q}PR{E}_{ij}.$$ (Eq. 7)

The allosteric communities can be optimized by inserting node i from C_m into C_k or swapping node i from C_m with node j from C_k. The benefits of the total PRE inside communities are calculated as Eq. 8 and Eq. 9 for inserting and swapping operations, respectively:

$$\mathrm{B}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{t}=\mathrm{ }{T}_{new}-T_{old}=\mathrm{ }{Ex}_{i,C_k}-{In}_i.$$ (Eq. 8)

$$\mathrm{B}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{t}=T_{new}-T_{old}=\left({Ex}_{i,C_k}+{Ex}_{j,C_m}\right)-\left({In}_i+{In}_j\right)-{2\mathrm{*}PRE}_{ij}$$ (Eq. 9)

Therefore, the optimal KL communities can be computed by selecting maximum benefit operation during each iteration until converging to a minimum total PRE value inside communities. However, the KL algorithm can only achieve a solution as a local minimum. In the current study, we repeat the KL algorithm until the lowest PRE value in communities remains unchanged for more than 1,000 times, then the current partition is selected as the final community configuration. In addition, the KL algorithm could be applied on the GN searching results to further optimize the communities until convergence. This combination of GN and KL methods is referred to as a hybrid GN-KL algorithm.

Results

Although PDZ2 exhibits signal propagation upon ligand binding, the structures of the PDZ2 unbound state (3LNX[38]) and bound state (3LNY[38]) are very similar. It was shown that the distributions between the unbound and bound simulations are significantly different[39]. REDAN model is built based on those differences. Considering each residue as a node, the significance of allosteric effects for any node pair is measured as the relative entropy divergences between its distributions in two states, and treated as the weight of the edge connecting these two nodes. These weights could reflect the allosteric response of the corresponding edges upon peptide binding, and are referred to as PRE. It is worth to mention that because the free energy can be computed based on probability distribution P as A = −k_BTlnP, the PRE measures the change of free energy upon peptide binding. Therefore, the edges along with their weights can be used to model the direction of free energy propagation upon perturbation.

The PRE values of all edges in PDZ2 are calculated and illustrated in Figure S1. For most residue pairs, the PRE values upon peptide binding are close to zero, and are significant for only part of the residue pairs, making it a sparse matrix. The sparsity of the PRE matrix makes it suitable for a sparse protein network as illustrated in Figure S2. Comparing with other network methods including protein contact network, residue interaction network, and dynamical networks analysis[21,26], the REDAN method could identify key allosteric edges between the residues far from each other rather than adjacent residues.

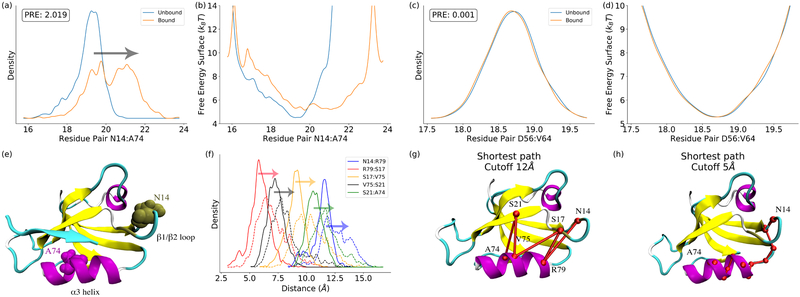
The distributions of edges with the highest and lowest PRE values are illustrated in Figure 1, respectively. Clearly, the peptide binding does not equally influence the distance distributions of different residue pairs. For the residues pair N14:A74 with the highest PRE, the unbound state has the distance around 19Å with the peak density. Upon peptide binding, the distribution is broadened with a new peak appearing around 21Å (Figure 1a), leading to the PRE of this edge upon peptide binding as 2.019. As a comparison, for the residue pair D56:V64, the peptide binding does not lead to observable distribution changes, which results in the PRE of this distribution close to zero (Figure 1c). The probability distribution was closely related to the free energy. The free energy profiles with reference to the edge distance between residue pairs N14:A74 and D56:V64 are plotted in Figure 1b and 1d, respectively. With the large PRE value, the change of the free energy profile upon perturbation is more significant for the N14:A74 pair than the D56:V64 pair. Therefore, the PRE can be used as an adequate metric to measure the free energy changes upon external perturbations. These calculated PRE values are used in REDAN model to identify allostery related residues, residue pairs, allosteric pathways, and allosteric communities.

Figure 1:

The significance of distribution changes and free energy surface changes quantified by perturbation relative entropy (PRE). (a) Residue pair (N14:A74) with the highest PRE in the protein; (b) The free energy surface of the N14:A74 distance distribution; (c) The residue pair (D56:V64) with the lowest PRE; (d) The free energy surface of the D56:V64 distance distribution; (c) Residues N14 and A74 illustrated in PDZ2; (d) Pathway decomposition: the distributions for decomposed residue pairs; (e) Pathway decomposition analysis of N14:A74 pair with cutoff value as 12Å; (f) Pathway decomposition analysis of N14:A74 pair with cutoff value as 5Å. These results demonstrate that the PRE is an effective measurement to quantify allosteric effect as residue pair level.

Identification of Allosteric Effects and Allostery Related Residues

The REDAN model provides a tool to easily detect the residues and residue pairs that are more responsive to allosteric perturbations. For PDZ2, residue pair N14:A74 has the highest PRE upon peptide binding. The top five residue pairs with the highest PRE value are listed in Table S1. The residue pairs with the highest PRE are all correlated with β1/β2 loop with α3 helix (Figure 1e). Interestingly, the peptide-binding site is formed between β2 strands and α3 helix.

For each residue, the PRE associated with all edges which include that specific residue could be summed together as residue specific total PRE. This total PRE may reflect the significance of allosteric effects between each individual residue and the rest of protein upon perturbations. All residues in PDZ2 are sorted using their total PRE with the top 15 residues listed in Table 1 and the complete list provided in Table S2. Because the edge can be considered as the direction of free energy propagation, the total PRE could reflect the magnitude of free energy passing through that residue as a node upon perturbation. The top 15 residues cover exactly the residues from G68 to V75 and V26 to H32 (Figure S3). Comparing with a previous network analysis and an NMR study related to PDZ2 bound with the same peptide[29,40,41], 12 out of these 15 residues have been identified as allosterically or functionally related residues (Table 1). The residues V26 to H32 form β2/α1 loop and the residues G68 to V75 form β5/α3 loop and part of α3 helix. Those regions are highlighted as allostery related structures in many studies [28,29,40,41].

Table 1:

Top 15 residues with the highest residue specific PRE

Rank	Residue	Total PRE	Rank	Residue	Total PRE	Rank	Residue	Total PRE
1	T70b	54.99	6	Q73b	46.70	11	V75b	37.07
2	V26a,b	54.86	7	A69a,b	46.67	12	K72	35.88
3	N27a,b	52.62	8	R31a	45.32	13	H32	34.75
4	H71a,b	50.49	9	T28a,b	43.28	14	V30a,b	32.03
5	A74b	46.76	10	S29b	38.14	15	G68	30.76

^[a]Residues identified through an NMR study[40]

^[b]Residues identified through two network analyses[29,41]

Allosteric Pathways

The residue pairs identified above with significant allosteric effects usually are not adjacent with each other. For example, the distance between N14:A74 residue pair is around 20Å. The significant allosteric effect between these two residues could not be fully accounted for by non-bonded interactions between them, because the non-bonded interactions are too small at this distance to exert any significant impact. Alternatively, significant distribution changes correlated with large allosteric effect could stem from the accumulation of shorter-range allosteric effects. In REDAN model, the decomposition analysis of the long-range allosteric effect into sequential short-range and smaller allosteric effects is carried out using the shortest pathway searching algorithm. For example, in the PDZ2 protein, the large allostery effect displayed by N14:A74 residue pair (Figure 1a) is decomposed into a series of sequential residue pairs with short-range allosteric effect using a cutoff value as 12 Å: N14:R79, R79:S17, S17:V75, V75:S21 and S21:A74 (Figure 1g). Comparing distributions in Figure 1f and 1a, it is clear that the decomposed residue pairs have smaller shift of distribution upon peptide binding but all in the same direction to the larger allosteric effect displayed by N14:A74 residue pair. This series of short-range edges with significant PRE values may contribute to the large allosteric effect between N14:A74 as one important pathway consisting of N14, S17, S21, V75 and R79. It should be noted that the potential allosteric communication between residues N14 and A74 does not necessarily propagate only though this identified pathway. However, all five residue-pairs as part of this pathway have increasing distance distribution upon peptide binding, which is consistent with the target N14:A74 edge, making it likely that this pathway correlates with the overall allosteric effect.

The PRE values of the short-range residue pairs listed above are 1.385 (N14:R79), 0.660 (R79:S17), 1.337 (S17:V75), 0.815 (V75:S21), and 1.045 (S21:A74) as shown in Figure 1f and individually in Figure S4. Residues N14 and S17 belong to β1/β2 loop (covering residues 13 through 19), and residue S21 belongs to β2 strand. Residues A74, V75, and R79 belongs to α3 helix. N14:R79 pair has the highest PRE along this pathway. Comparing with the β1/β2 loop region, the α3 helix as a stable secondary structure could be more stable. Therefore, this pathway decomposition may reveal that the large PRE between N14:A74 may stem from the fluctuation of β1/β2 loop. Among A74, V75, and R79 residues, R79 is the closest residue in α3 helix structure with regard to the β1/β2 loop. Therefore, to further evaluate allosteric response from the β1/β2 loop, the distribution of residue pair distances and corresponding PRE values between R79 and all β1/β2 loop residues (10 through 21) are plotted in Figure S5. Among these residue pairs, the PRE values increase from the lowest one between E10:R79 with 0.020 to the highest one between N14:R79 with 1.385, and sequentially decrease to 0.182 as the one between S21:R79. Central three residues N14, D15, and N16 have PRE values higher than 1, suggesting that this loop region significantly changes the conformation upon peptide binding.

It has been suggested that allostery was a complex biological function, and multiple pathways could co-exist and lead to the allosteric effects, ranging from long-range global pathways to short-range local pathways[42]. Although some pathways may be more dominant than other pathways for propagation purpose, the allosteric effect should be considered as the result of cooperation among multiple pathways[42]. To identify potential multiple pathways, a cutoff value was applied to differentiate allosteric pathways with different interaction ranges. This cutoff value is used as the upper bound to search for the shortest allosteric pathway connecting the target residue pair. This gives flexibility of this model to survey important allosteric pathways at any distance range. To evaluate the impact of different cutoff values on allosteric pathways, sixteen different cutoff values ranging from 5 Å to 20 Å are used for allosteric pathway identification (Table 2). Cutoff values shorter than 5 Å do not lead to any allosteric pathways. Different cutoff values do lead to different allosteric pathways. But for each specific cutoff value, unique allosteric pathway could be determined. For the cutoff value of 5Å, the adjacent residues as N14-K13-A12 and residues from 83 through 74 are identified as the shortest allosteric pathway (Figure 1h), highlighting the importance of the local interaction for the allosteric effect. The allosteric pathway identified using the cutoff value as 12Å is illustrated in Figure 1g, because this value was used in another allosteric pathway analysis [26] and also used as the cutoff value for non-bonded interaction in the MD simulations. Overall, different cutoff values leading to different allosteric pathways provide the flexibility to identify pathways targeting the interactions within different ranges, and could provide insights into allosteric effects from different aspects.

Table 2:

Different pathways with different cutoff values

Cutoff value (Å)	Shortest allosteric pathway	Cutoff value (Å)	Shortest allosteric pathway
5	N14, K13, A12, Q83, G82, T81, N80, R79, L78, T77, E76, V75, A74	13	N14, R79, N16, V75, S21, A74
6	N14, N16, K13, Q83, G82, T81, N80, T77, A74	14	N14, R79, S17, A74
7	N14, A45, K13, Q83, N16, R79, T81, L78, A74	15	N14, R79, S17, A74
8	N14, A45, K13, G44, S17, R79, T81, T77, Q73, T70, G25, A74	16	N14, L78, K13, A74
9	N14, G44, I20, V22, H71, G25, A74	17	N14, L78, K13, A74
10	N14, G44, S17, V75, G25, A74	18	N14, L78, K13, A74
11	N14, G44, S21, H71, V22, A74	19	N14, L78, K13, A74
12	N14, R79, S17, V75, S21, A74	20	N14, A74

Allosteric Communities

The allostery could be referred to as the distribution changes related to protein conformation upon perturbations. The influence of perturbation is not equally exerted on each residue. Some residue pairs could be affected more than others upon perturbations as demonstrated in Figure 1. Using the PRE values of the different residue pairs, the residues can be divided into different groups, with which the total PRE value within each group is minimized, and the total PRE values across different groups are maximized. These groups are named as “allosteric communities” as domains that are less affected by the perturbations.

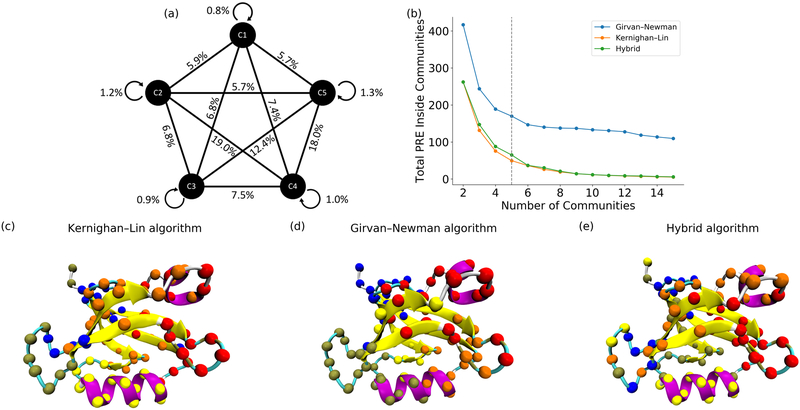
To construct communities through the minimization of total PRE value within each community, both GN and KL algorithms as well as the hybrid GN-KL algorithm are implemented in this study. GN algorithm[36,43] has been widely applied in biological and social network community analyses. As described in the methodology section, GN algorithm iteratively removes the most valuable edge in the network to identify the community without minimizing the PRE inside the community. As comparison, the KL algorithm[37] is a minimization algorithm which iteratively reaches local minimum. The total PRE values inside communities using these algorithms are plotted in Figure 2b. Apparently, the KL algorithm is much better than the GN algorithm to identify communities with the minimum PRE values. However, the computational cost of KL algorithm is much higher than the GN algorithm. Overall, the hybrid GN-KL algorithm could produce comparable results to the KL algorithm with much lower computational cost.

Figure 2:

Comparison of different community detection algorithms. (a) Total PRE within and between communities using Kernighan-Lin (KL) algorithm; (b) Minimization of total PRE within allosteric communities using different algorithms; (c) Communities constructed using KL algorithm (residues in different community are colored differently, same as for d and e.); (d) Communities constructed using Girvan-Newman (GN) algorithm; (e) Communities constructed using the hybrid GN-KL algorithm. The GN algorithm is effective to determine the suitable number of communities, but could be trapped in local minimum. The KL algorithm could optimize the communities significantly with high computational cost. The hybrid GN-KL algorithm is both computationally efficient and rigorous with the results similar to the KL algorithm.

As one of its advantages, the GN algorithm is parameter-free, and could be used to determine the optimal number of allosteric communities with maximum modularity of the network[36]. Applying GN algorithm, it was determined that five communities are the most suitable for PDZ2. Community analysis using GN, KL, and the hybrid GN-KL algorithms are illustrated in Figure 2c, 2d and 2e, respectively. Usually, the allosteric effects induced by external perturbations alter the protein conformation without changing the secondary structure. Therefore, stable secondary structures including α-helices and β-strands likely belong to same community. Overall, most α-helix and β-strand secondary structures are conserved in the community analyses.

For five communities in PDZ2 domain using KL algorithm (Figure 2a), the percentage of total PRE values of all residues pairs within each community are only 0.8%, 1.2%, 0.9%, 1.0% and 1.3% of the overall total PRE values of PDZ2 upon peptide binding as allosteric perturbation, respectively. Therefore, the PRE values among these communities account for 94.8% of total PRE values related to protein allostery. The total PRE value between communities 2 and 4 accounting for 19.0% and the one between communities 4 and 5 accounting for 18.0%. Actual total PRE value for each community pair is listed in Table S3, and the residues in each community are listed in Table S4. The community 4 (residues 66–80) is potentially the most important, and contains β5/α3 loop (66–70) and entire α3 helix (71–79).

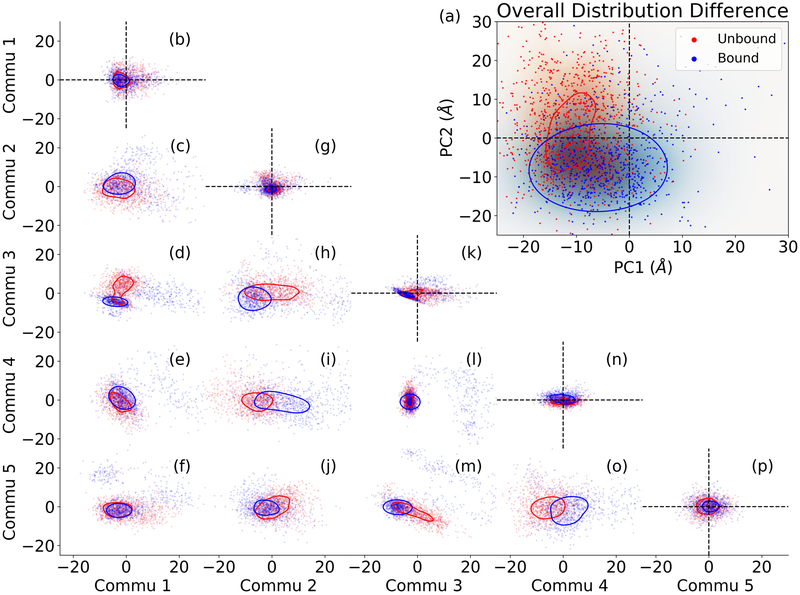
The community analysis is further evaluated through comparison with the principal component analysis (PCA). First, the simulations of the PDZ2 unbound and bound states are projected onto the two main components (PC1 and PC2) from PCA (Figure 3a). Clustering analysis reveals that two states of PDZ2 are significantly different in the PC1/PC2 space. Consequently, all community pairs (including self pair) from different states are also projected onto the principal component space (Figure 3b-3p). It should be noted that for each community pair including self-pairs, PCA was carried out separately to construct PC1/PC2 surface for projection specifically for that community pair. All community self-pairs do not show significant distribution changes between two states (Figures 3b, 3g, 3k, 3n and 3p). Other community pairs generally show significant differences between two states with the most significant changes coming from pairs including 1:3, 2:3, 2:4, 3:5, and 4:5.

Figure 3:

Projection of PDZ2 unbound and bound states and communities using principal component analysis (PCA). (a) Projection of unbound and bond states onto PC1 and PC2 surface; (b-q) Projections of different community pairs onto pair-specific PC1/PC2 surfaces. The unbound and bound states are well separated on PC1/PC2 surface. None of community self-pairs is well separated using PCA. Most different community pairs are well separated using PCA, indicating that the community analysis projects the major part of allosteric effect among different communities.

Through this community analysis, the distribution shifting upon peptide binding as PDZ2 allostery can be quantified as the correlation among the allosteric communities. This community analysis provides a quantitative tool with statistical significance to quantify the distribution changes induced by allosteric perturbation from different regions in the protein.

Discussion

The REDAN model approaches protein allostery based on the population shift concept through relative entropy measurement, and can quantitatively measure difference between two probability distributions[15]. Based on MD simulations, a distribution could be obtained for many collective variables to represent their free energy profile. Relative entropy could be calculated to measure the response of any collective variables with regard to allosteric perturbations. Higher relative entropy indicates larger change of distributions upon perturbations, and could be closely related to allostery. Therefore, the relative entropy could be considered as the amplitude of allosteric effect.

The REDAN method could be used to identify the most affected residues and residue pairs upon allosteric perturbations. In PDZ2 domain, the Cα pair distance with the highest PRE reveals that the distance distribution between β1/β2 loop and α3 helix is significantly affected by the peptide binding. The significance of β1/β2 loop has been identified in many studies related to PDZ2 allostery [28,41]. In a dynamical interaction correlation analysis conducted by Karplus and coworker [28], the loop β1/β2 is referred to as a key part in the allosteric pathway. Another study also emphasized the importance of β1/β2 loop through structural network and elastic network analysis [41]. For each individual residue, the summation of all PRE values between this particular residue and all other residues can be considered as a metric to measure the total amount of information passing through this residue upon perturbation. The residues with the highest total PRE values also have significant agreement with those network or experimental studies [28,29,40,41].

Comparing with individual residues, potential allosteric pathways are more informative to demonstrate the allosteric mechanisms. The shortest pathway algorithms were applied to identify the pathways between two distal residues with significant PRE. Through pathway decomposition analysis, the large allosteric effect between two distal residues could be decomposed into several short-range residue pairs with smaller PRE values. These short-range residue pairs may provide structural information important for allostery. This is also supported by other studies, which indicate that multiple pathways may coexist and be responsible for the allostery effect between two distal residues [42]. Using cutoff value for pathway searching, the REDAN model provides flexibility to explore the allosteric pathways at different scales.

The distribution shift upon allosteric perturbation can be represented as the allosteric communities in the REDAN model. The allosteric communities are constructed through the minimization of total PRE values within each community. As shown in Figure 3, the distribution changes within each community are insignificant, and the majority of distribution differences come from across communities. Therefore, the amount of distribution changes upon allosteric perturbation is quantified as the interactions among different communities.

The construction of allosteric communities is not a trivial task since searching communities with minimum total relative entropy is known as an NP-Hard problem. In this study, widely applied GN and KL algorithms are shown to be suitable for the purpose of allosteric community analysis. The GN algorithm[36] can determine the optimal number of communities based on the modularity of remaining network after decomposition, without explicitly minimizing the total PRE in each community. As comparison, the KL algorithm is an explicit minimization algorithm, which can obtain a local minimum value of the total relative entropy within each community. But the computational cost of the KL algorithm is significantly higher than the one of the GN algorithm, and the number of communities needs to be pre-determined. The hybrid GN-KL algorithm was developed to take advantage of both algorithms by applying GN algorithm to select communities as an initial guess, and KL algorithm to optimize the partitions. The detailed comparison of these three algorithms is provided in Table S5. Among five allosteric communities identified for PDZ2, the community 4 has a total PRE correlated to the rest of protein as more than 50%, indicating that the peptide binding can significantly alter the interaction of the residues in community 4 (L66 to N80) with the rest of protein. Community 4 also includes all the residues in β5/α3 loop and α3 helix, which consists of the binding pocket of peptide. This highlights the importance of the peptide binding pocket in the allosteric processes. In general, allosteric community analysis could be utilized to divide the protein residues into different allosteric communities to investigate the allosteric mechanism from a global point of view.

Conclusion

The current study introduced a new method named related entropy-based dynamical allosteric network (REDAN) model to quantitatively characterize protein allosteric effects upon external perturbations. Relative entropy was applied to quantify the allosteric effects for pair-wised residues based on the distribution differences. Because the population distribution is directly linked to the free energy, any changes of population distributions essentially reflect the changes of free energy surface due to external perturbations. Adapting the shortest pathway searching algorithms, multiple potential allosteric pathways connecting two distal allosteric residues could be identified. The flexibility of using different cutoff values and identifying multiple allosteric pathways could provide deep insight into protein allostery. The allosteric community analysis could further identify the communities, which hold significant contribution to overall relative entropy among them but have minimum relative entropy within each community. Both GN and KL algorithms, and the hybrid GN-KL algorithm were implemented for community identification. The application of the REDAN model on allosteric PDZ2 protein demonstrates its effectiveness and efficiency for protein allostery analysis. Overall, this method could be applied on any two different protein states upon perturbations, and quantify the impacts from the perturbation on the internal dynamics and function related residues.