Abstract
Recent advances in high-throughput biotechnologies have provided an unprecedented opportunity for biomarker discovery, which, from a statistical point of view, can be cast as a variable selection problem. This problem is challenging due to the high-dimensional and non-linear nature of omics data and, in general, it suffers three difficulties: (i) an unknown functional form of the nonlinear system, (ii) variable selection consistency, and (iii) high-demanding computation. To circumvent the first difficulty, we employ a feed-forward neural network to approximate the unknown nonlinear function motivated by its universal approximation ability. To circumvent the second difficulty, we conduct structure selection for the neural network, which induces variable selection, by choosing appropriate prior distributions that lead to the consistency of variable selection. To circumvent the third difficulty, we implement the population stochastic approximation Monte Carlo algorithm, a parallel adaptive Markov Chain Monte Carlo (MCMC) algorithm, on the OpenMP platform which provides a linear speedup for the simulation with the number of cores of the computer. The numerical results indicate that the proposed method can work very well for identification of relevant variables for high-dimensional nonlinear systems. The proposed method is successfully applied to identification of the genes that are associated with anticancerdrug sensitivities based on the data collected in the cancer cell line encyclopedia (CCLE) study.
Keywords: Cancer Cell Line Encyclopedia, Parallel Markov Chain Monte Carlo, Omics Data, OpenMP, Nonlinear Variable Selection
1. Introduction
Recent advances in high-throughput biotechnologies, such as microarray, sequencing technologies and mass spectrometry, have provided an unprecedented opportunity for biomarker discovery. Molecular biomarkers can not only facilitate disease diagnosis, but also reveal underlying, biologically distinct, patient subgroups with different sensitivities to a specific therapy. The latter is known as disease heterogeneity, which is often observed in complex diseases such as cancer. For example, molecularly targeted cancer drugs are only effective for patients with tumors expressing targets (Gru¨nwald and Hidalgo, 2003; Buzdar, 2009). The disease heterogeneity has directly motivated the development of precision medicine, which aims to improve patient care by tailoring optimal therapies to an individual patient according to his/her molecular profile and other clinical characteristics.
From a statistical point of view, the discovery of biomarkers is best cast as variable selection, where the variable refers to the molecular attributes under investigation, e.g., genes, genetic variation, or metabolites. Variable selection in omics data is challenging. First, the omics data is high-dimensional, while the sample size is typically much smaller than the number of variables (a.k.a. small-n-large-P). Second, certain processes of the cell are interconnected in complex patterns due to cellular regulations or some environmental factors influencing the cell. This results in an unknown, complex, nonlinear relationship among variables. For example, either a high or low expression level of gene ORMDL3 is associated with a high risk of progression for breast cancer (Curtis et al., 2012; Prat et al., 2010; Anders et al., 2011; Jonsson et al., 2010); one can imagine how complex the interactions between ORMDL3 and other genes are. However, most of the current variable selection methods are developed for linear systems, rendering imprecise discovery of useful biomarkers. This may partially explain the reason why the number of biomarkers approved for clinical use by the FDA each year is still in single digits, despite intense effort and significant investments in labor and funding. The methodology development for variable selection from high-dimensional nonlinear systems is still in its infancy, see Section 2 for an overview. How to select relevant variables for general high-dimensional nonlinear systems has posed a great challenge on the existing statistical methods.
In this paper, we propose a Bayesian neural network (BNN) method to tackle this problem, and applied the proposed BNN method to selection of drug-sensitive genes. The proposed method is motivated by the universal approximation ability of the feed-forward neural networks (FNNs)(Cybenko, 1989; Funahashi, 1989; Hornik et al., 1989), i.e., an FNN is capable of approximating any continuous functions on compact subsets to any desired degree of accuracy. The effectiveness of the proposed method is partially evidenced by Zhang et al. (2007), where they use an feed-forward neural network to build a discrimination model for detecting Stage I epithelial ovarian cancer with multiple known serum tumor markers as input variables, and the neural network model significantly outperforms its linear competitors. The consistency of the proposed method is established under the framework of posterior consistency developed in Jiang (2007) and Liang et al. (2013). The posterior consistency refers to that the true density of the nonlinear system can be consistently estimated by the density of the models sampled from the posterior distribution of feed-forward neural networks. To resolve the computational issue involved in Bayesian inference for such a complex model, we implement the population stochastic approximation Monte Carlo (pop-SAMC) algorithm (Song et al., 2014), a parallel adaptive MCMC algorithm, on the OpenMP platform, which provides a linear speedup for the simulation with the number of cores of the computer. We have made extensive comparisons for the performance of BNN with other approaches, such as the generalized additive models (Chouldechova and Hastie, 2015), random forest (Breiman, 2001), and Bayesian additive regression trees (Chipman et al., 2010; Bleich et al., 2014). Numerical results show that the proposed method can work much better than other methods in identifying true predictors for general high dimensional nonlinear systems.
Toward the ultimate goal of precision medicine, i.e., selecting right drugs for individual patients, a recent large-scale pharmacogenomics study, namely, cancer cell line encyclopedia (CCLE), has screened multiple anticancer drugs over hundreds of cell lines in order to elucidate the response mechanism of anticancer drugs. The dataset consisted of the dose-response data for 24 chemical compounds across over 400 cell lines. For each cell line, it consisted of the expression data of 18,926 genes. Our goal is to identify the genes that are sensitive to the chemical compounds, which is fundamental to elucidate the response mechanism for anticancer drugs.
The remainder of this article is organized as follows. Section 2 provides a brief overview for the methods of variable selection for high-dimensional nonlinear systems. Section 3 describes the feed-forward neural networks and establishes the consistency of variable selection under the Bayesian framework. Section 4 provides a short description for the pop-SAMC algorithm and its OpenMP implementation. Section 5 illustrates the performance of the BNN method using simulated examples. Section 6 applies the proposed BNN method to selection of drug-sensitive genes. Section 7 concludes the paper with a brief discussion.
2. Variable Selection for High-Dimensional Nonlinear Systems
During the past decade, substantial progress has been achieved for variable selection from linear systems for which the regression function can be described by a linear or generalized linear model. Methods have been developed from both the frequentist and Bayesian perspectives. The frequentist methods are usually regularization-based, which enforce the model sparsity through imposing a penalty on the likelihood function. For example, Lasso (Tibshirani, 1996) employs a l1-penalty, elastic net (Zou and Hastie, 2005) employs a combination of l1 and l2 penalties, Fan and Li (2001) employs a smoothly clipped absolute deviation penalty, and Song and Liang (2015a) employs a reciprocal l1 penalty. The Bayesian methods enforce the sparsity of posterior models through choosing appropriate prior distributions. For example, Liang et al. (2013) and Song and Liang (2015b) suggest choosing priors that lead to the posterior consistency, and Johnson and Rossel (2012) suggests some non-local priors. Though these methods can generally work well for linear systems, most of the real systems are truly nonlinear. Despite this fact, there are only scattered efforts for nonlinear systems.
For nonlinear systems, a straightforward approach is to consider a dictionary of nonlinear features and then use a regularization method to select relevant elements of the dictionary by assuming that the true regression function of the nonlinear system can be approximated by a linear combination of nonlinear features included in the dictionary. For example, Ravikumar et al. (2009) considered a generalized additive model (GAM), where each nonlinear feature in the dictionary is expressed as a basis function of a single variable. Recently, this approach has been further generalized by Chouldechova and Hastie (2015) and Lou et al. (2014) to include both the linear and nonlinear features in the dictionary. A shortcoming of this approach is that it fails to model the interactions between variables. Lin and Zhang (2006) worked with a dictionary which encodes more complex interactions among the variables, e.g., the features defined by a second-degree polynomial kernel. However, the size of the dictionary in their approach can grow more than exponentially when high-order interactions are considered.
Toward simultaneous modeling of nonlinearity and interactions effects, the tree-based approaches, such as random forest (Breiman, 2001), dynamic trees (Taddy et al., 2011; Gramacy et al., 2013), Bayesian additive regression trees (BART) (Chipman et al., 2010; Bleich et al., 2014), seem promising. The tree-based approaches make use of internals of the decision tree structure in variable selection. In these approaches, all observations begin in single root node and are split into two groups based on whether Xk ≥ c or Xk < c, where Xk is a chosen splitting variable and c is a chosen splitting point. The two groups form the left daughter node and the right daughter node, respectively. Then additional binary splits can be chosen for each of the two daughter nodes. Variable selection can be made based on the splitting variables. For example, the random forest measures the importance of a variable by looking at how much prediction error increases when the out-of-bag data (i.e., those not included in the bootstrap samples) for that variable is permuted while all others are left unchanged. The dynamic tree (Gramacy et al., 2013) selects the variables according to the average reduction in posterior predictive uncertainty within all nodes that use the variable as the splitting variable. The BART makes use of the frequency how often the variable appears as a splitting variable in the regression tree.
In this paper, we propose a Bayesian neural network (BNN) method to tackle this problem, motivated by the universal approximation ability of the feed-forward neural networks. The BNN method samples a large number of neural networks with different structures from its posterior distribution using a parallel MCMC algorithm (Song et al., 2014), and then selects variables based on the frequency how often the variable appears in the sampled neural networks. In BNN, the nonlinearity of the system and the interaction effects between different variables are modeled by including a hidden layer. Our numerical results indicate that BNN is indeed very good in modeling nonlinearity and variable interaction effects for the underlying system. Feed-forward neural networks have been traditionally viewed as a blackbox approximator to an objective function. However, the proposed research indicates that this view is not completely correct for BNN: The structures of the networks sampled from the posterior distribution indicate the relevance of the selected covariates to output variables.
3. Bayesian Feed-forward Neural Networks
3.1. Feed-forward Neural Networks
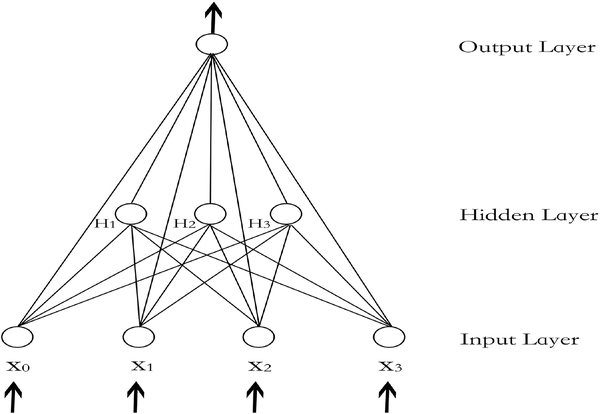
Consider a feedforward neural network, illustrated by Figure 1, which is also known as multiple-layer perceptron (MLP) in machine learning. Let x0,x1,...,xP denote input values, which are fed to the bias unit and P input units, respectively. In this paper, we set x0 ≡ 1. Let ψh(·) denote the activation function of the hidden unit, and let aj denote the output of the hidden unit j; that is,
| (1) |
where is the indicator for whether the connection from input unit i to hidden unit j is included in the network; and, if included, wij denotes the weight on the connection. In this paper, we set ψh(z) to be the hyperbolic tangent function, i.e., ψh(z) = tanh(z). An alternative choice of ψh(z) is the sigmoid function ψh(z) = 1/(1 + e−z). The theoretical results established in this paper for the tangent function can be established to the case of sigmoid function with a slight modification of the conditions. We note that in the society of neural computation, it is widely acknowledged that the neural networks with the tanh activation function tend to converge faster than those built with the sigmoid activation function.
Figure 1:
A fully connected one hidden layer MLP network with three input units (x1, x2, x3), one bias unit (x0), three hidden units (H1, H2, H3), and one output unit (O). The arrows show the direction of data feeding.
Let ao denote the output of the network, and let ψo(·) denote the activation function of the output unit; that is,
| (2) |
where H denotes the number of hidden units, wio denotes the weight on the connection from input unit i to the output unit, wjo denotes the weight on the connection from hidden unit j to the output unit, and is the indicator for the effectiveness of the corresponding connection. We set ψo(z) to be the identity function (i.e., ψo(z) = z) for normal regression problems, and set ψo(z) to be the sigmoid function for binary classification problems. For normal regression, we generally assume the response variable Y ∼ N(μ∗(x),σ2), where x = (x0,x1,...,xP ), μ∗(x) is an unknown nonlinear function, and σ2 denotes the variance of y. For binary classification, we generally assume that the response variable Y is a Bernoulli random variable with the success probability ψ0(μ∗(x)). In this case, ao works as an approximator of the success probability.
The connections from input units to the output unit, i.e., wio’s, are called shortcut connections. With the shortcut connections, the neural network model includes conventional normal linear regression and logistic regression as special cases. As a by-product, we can conduct a Bayesian test for the nonlinearity of the system by testing the null hypothesis for j = 1,2,...,H. To be more precise, we can test the nonlinearity of the system using the Bayes factor
| (3) |
where denotes the set of BNN models with only short-cut connections (i.e., for j = 1,2,...,H), denote the complementary set of ; Dn denotes a dataset with n observations; and and denote the prior and posterior probabilities of the set , respectively. In practice, both the ratios and can be estimated via Monte Carlo simulations.
Let denote the collection of all connection weights and their indicators, which consists of Kn = (P +1)(H +1)+H elements. A neural network with all indicator variables equal to 1 is called a full neural network, and Kn is the total number of connections of the full neural network. In what follows, with a slight abuse of notation, we also write with βi defined as the product of the corresponding connection weight and indicator. Furthermore, we define
| (4) |
define , which specifies the structure of the BNN; and define , which specifies the connection weights associated with the BNN.
With the above notation, we can unify the two cases, normal regression and logistic regression, by writing the density function of the neural network model in a similar way to generalized linear models as
| (5) |
where A(μ) = μ/σ2, B(μ) = −μ2/2σ2, and for normal regression, and A(μ) = μ, B(μ) = −log(1 + eμ), and C(y) = 1 for logistic regression. For simplicity, we assume here that σ2 is known. Extending our results to the case that σ2 is unknown is simple, following the same arguments as given in Jiang (2007). In this case, an inverse gamma prior can be assumed for σ2 as suggested in Jiang (2007).
Given the universal approximation ability of feed-forward neural networks, the problem of variable selection for nonlinear systems is reduced to selecting appropriate variables for μ(β,x) such that it can provide an adequate approximation to μ∗(x). Here, stemming from the universal approximation property, we have implicitly assumed that μ∗(x) can be well approximated by a parsimonious neural network model with relevant variables, and this parsimonious model is called the true model in the context of the paper. In the next subsection, we describe how to consistently identify relevant variables for the model (5) under the Bayesian framework.
3.2. Posterior Consistency
As implied by the theory developed in Liang et al. (2013) and Song and Liang (2015b), posterior consistency provides a general guideline in prior setting for high-dimensional variable selection problems. Otherwise, under the small-n-large-P situation, the prior information may dominate the data information, rendering a biased inference for the true model. Furthermore, under mild conditions for the identifiability of the true model, the posterior consistency can lead to the consistency of Bayesian variable selection (Liang et al., 2013; Song and Liang, 2015b).
To ensure the posterior consistency to be satisfied by BNN, we give in the supplementary material the general conditions for the prior setting similar to the conditions (N) and (O) of Jiang (2007). To be specific, we let (γ,βγ) be subject to the following priors. Conditioned on γ, βγ follows N(0,V γ), where V γ is a |γ| × |γ| covariance matrix, and |γ| is the number of nonzero elements of γ. An explicit specification for the prior probability π(γ) is difficult, as some configurations of γ cannot form a valid neural network, e.g., those without connections to the output unit. For this reason, we simply assume that for any valid neural network,
| (6) |
where is the maximum network size allowed in the simulation, λn can be read as an approximate prior probability for each connection to be included in the network, and is the set of valid neural networks. In general, we set the hyperparameter λn → 0 as Kn → ∞, which provides an automatic control for the multiplicity involved in variable selection (Scott and Berger, 2010).
Let rn denote the prior expectation of the model size |γ| before applying size restriction and network structure validity restriction; that is, rn = Knλn. Here we assume, for convenience, that rn is some integer smaller than . Let chi(Σ) denote the ith largest eigenvalue of the matrix Σ. Under the normality assumption for the connection weights, we define , , , and . For two densities f1(x,y) and f2(x,y), we measure their distance using the Hellinger distance defined by
To establish the posterior consistency, we assume that the true model is sparse and satisfies the condition
where denotes the connection weight vector of the true model. Further, we assume that all the input variables are bounded and standardized such that |xj| ≤ 1 for all j = 0,...,P. Theorem 1 follows from Jiang (2007) with modified conditions. The proof can be found in the supplementary material.
Theorem 1. Let the connection weights be subject to a normal prior distribution, and let the network structure be subject to a truncated Bernoulli prior distribution. Assume that |xj| ≤ 1 for all j, , where Kn is a nondecreasing sequence in n.
Let ϵn be a sequence such that ϵn ∈ (0,1] for each n and and assume that the following conditions also hold:
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
Let , and let π[A|Dn] denotes the posterior probability of the event A. Then we have the following results:
For some c1 > 0, and for all sufficiently large n,
For some c1 > 0, and for all sufficiently large n,
Remarks:
The validity of this theorem depends on the choice of the prior covariance matrix V γ or, more precisely, the smallest and largest eigenvalues of Vγ. For most choices of Vγ, and hold for some positive constants B and v. For example, if V γ = cI|γ| for some constant c > 0, where Ik is an identity matrix of order k, then both B(rn) and are constants.
The key to the proof of this theorem is to bound the Hellinger distance d(p,p∗) by a function of γ and βγ. Thanks to the mathematical tractability of the activation function tanh(·), which is bounded and has a bounded derivative function, the distance function has a simple analytic bound. Then the prior distribution can be elicited to have an asymptotic focus on a neighborhood of the true model, which, as a consequence, leads to the posterior consistency. Since the sigmoid function has the same property as tanh(·), i.e., being bounded and having a bounded derivative, Theorem 1 also holds for the networks with the sigmoid hidden unit activation function.
Corollary 1 concerns the convergence rate ϵn, which can be proven by checking the conditions of Theorem 1.
Corollary 1. Suppose that Kn < exp(Cnα) for some constant C and α ∈ (0,1), and the prior specified at the beginning of subsection is used such that for some positive constants B and v. Take
for some k > 0 or
for some 0 < q < min(1 − α,1/v). Then the convergence rate in Theorem 1 can be taken as
or
Parallel to linear models, as an alternative to the normal prior used in the paper, one might consider a Laplace prior for BNNs. The Laplace prior, also known as Bayesian Lasso prior (Park and Casella, 2008), is given by
where λ is a scale parameter depending on n and Kn. Although the theoretical property of Lasso for linear models has been thoroughly studied in the literature, there are few work on the asymptotics of Bayesian Lasso under the high-dimensional setting. For normal means models, Castillo et al. (2015) and Bhattacharya et al. (2015) showed that Bayesian Lasso is suboptimal, although the posterior consistency can still be obtained. It is unclear if this result holds for BNNs. To us, the major weakness of the Bayesian Lasso prior is due to its exponential tails. If a hyper-prior is imposed on λ, which changes the tail shape of the prior of β, then the posterior consistency can possibly hold. Other shrinkage priors, such as the horseshoe prior (Carvalho et al., 2010), are also of interest for BNNs in both theory and practice.
3.3. Consistency of Variable Selection
To serve the purpose of variable selection, we consider the marginal inclusion probability approach (Liang et al., 2013). For each variable xi, we define its marginal inclusion probability as
where is the marginal probability mass function of the model γ, and is the indicator for whether xi contributes to the output in the model γ. Similarly, we define ei|γ∗ as the indicator whether variable xi is included in the true BNN model, where γ∗ denote the true model. The proposed approach is to choose the variables for which the marginal inclusion probability is greater than a threshold value ; that is, setting as an estimator of the set {xi : ei|γ∗ = 1,i = 1,...,Pn}.
To establish the consistency of the proposed approach, the following identifiability condition for the true BNN model γ∗ is needed. Let , where d(·,·) denotes the Hellinger distance between and f. For convenience, we rewrite the model γ as , where denote the indicator variable for connection k in the model γ. Define
which measures the distance between the true model and sample models in the ϵn-neighborhood . Then the identifiability condition can be stated as follows:
| (15) |
that is, when n is sufficiently large, if a model has the same density function as the true model then the model must coincide with the true model.
Viewing (1−ei,ei) and (1−qi,qi) as two distributions defined on the space {0,1}, we define d(qi,ei) as the Hellinger distance between the two distributions. Lemma 1 concerns the upper bound of d(qi,ei), whose proof can be found in the supplementary material.
Lemma 1. Assume the conditions of Theorem 1 and the condition (15) hold. Then, for any δn > 0 and sufficiently large n,
| (16) |
for all i = 1,...,Pn.
Lemma 2 concerns the sure screening property and consistency of the variable selection rule , which corresponds to Theorem 3.1 of Liang et al. (2013). The proof follows the same arguments as for Theorem 3.1 of Liang et al. (2013) except for some notational changes.
Lemma 2. Assume that the conditions of Theorem 1 and the identifiability condition hold.
- For any δ > 0 and sufficiently large n,
- (Sure screening) For all sufficiently large n,
for some constant c > 0 and some ∈ (0,1), preferably one not close to 0 or 1. - (Consistency) For all sufficiently large n,
Following from the condition stated in Theorem 1, as n → ∞. To determine the threshold value for a finite sample size problem, a multiple hypothesis testing method, e.g., the one developed in Liang and Zhang (2008), can be used. It is to first transform qi to a z-score through the probit transformation zi = Φ−1(qi), and then apply the multiple testing method to identify the variables for which the marginal inclusion probability is significantly higher than others under a prespecified false discovery rate (FDR), which is usually measured using Storey’s q-value (Storey, 2002). Compared to other multiple hypothesis testing methods, the method by Liang and Zhang (2008) allows general dependence between test statistics. For simplicity, we set in this paper and this leads to the so-called median probability model (MPM) criterion.
Other than input variables, the marginal inclusion probability approach can also be used to select network structures. Moreover, if the true function μ∗(x) is a neural network function, under the identifiability condition (15), we can follow Liang et al. (2013) to show that the marginal inclusion probability approach will lead to the global convergence, i.e., it will select the same network as the posterior mode-based approach. However, if the true function μ∗(x) is not an exact neural network function, e.g., it can only be expressed as a mixture of a few neural networks (with the number of hidden units upper bounded), then the marginal selection may have some advantages over the posterior mode-based approach.
3.4. Determination of Free Parameters
The proposed BNN model mainly contains two free parameters, namely, the number of hidden units H as defined in (2) and the prior hyperparameter λn as defined in (6). Note that H just provides an upper bound for the actual number of hidden units used in the BNN, and it represents the approximation capability of the BNN. The actual number of hidden units used in the BNN is determined through variable selection. For this reason, we suggest to set a large enough value for H. It is interesting to point out that for many high dimensional problems, we found that H = 5 or even 3 has been large enough given the sparsity of the underlying true model. Also, we found that for a given value of λn, the performance of BNN is quite robust to the value of H. This issue will be explored later via a simulation study.
For a given value of H, the choice of λn affects largely on the network size, connection weights, and thus fitting and prediction errors. To determine the value of λn, we propose the following procedure:
Specify a sequence of different values:
- For each value of , l ∈ {1,. . . . ,L} run BNN for a short number of iterations and for each of the BNN samples generated in the run calculate the statistic
where denotes the likelihood function of Y with respect to the parameters (βγ,γ), N denotes the total number of network samples generated in the run, (,γi) denotes the i-th sample, |γi| denotes the number of connections contained in the network γi, and ξ is a userspecified parameter taking a value of 0 or 1. If the likelihood function contain other nuisance parameters, such as σ2 in the case of normal regression, one may choose to integrate them out analytically or numerically. - Choose the value of λn at which the average of attains its minimum, i.e., set
The statistic measures the quality of a BNN sample. When there are no nuisance parameters, it is reduced to BIC/2 if ξ = 0 and EBIC/2 if ξ is chosen properly (Chen and Chen, 2008). In this paper, we set ξ = 1 for all examples, which corresponds to an EBIC/2 approximation. Although the proposed procedure is very simple, it works very well in this paper for both simulated and real data examples. We have also tried the BIC-like procedure for the examples of this paper, it works very well. Similarly, AIC can also be adopted here.
It is interesting to point out that when H is fixed, i.e., the parameter space of (βγ,γ) is fixed, minimizing the average of with respect to λn is equivalent to minimizing the Kullback-Leibler divergence between the posterior and the distribution g(βγ,γ,ξ) ∝ exp{−EBIC(βγ,γ,ξ)/2}. Here we use the subscript λn to indicate the dependence of the posterior distribution on the value of λn. The distribution g(βγ,γ,ξ) or its AIC counterpart has been used to weight different models, see e.g., Akaike (1979) and Kapetanios et al. (2006).
Other than determination of prior hyperparameters, we expect that the proposed procedure can be used for other purposes in a different context, such as Bayesian model determination as a competitor of DIC (Spiegelhalter et al., 2002). This will be studied elsewhere. In what follows, we will call the proposed procedure an average EBIC-like procedure.
Alternative to the proposed procedure, we can impose a hyper-prior distribution on λ, such as a Beta distribution. In this case, the parameters of the hyper-prior distribution can be determined using the empirical Bayes method, see e.g., Carlin and Louis (1996), and the effect of the parameters can be assessed using the sensitivity analysis method.
4. The Pop-SAMC algorithm and Its OpenMP Implementation
4.1. Pop-SAMC Algorithm
Markov chain Monte Carlo (MCMC) has proven to be a powerful tool for analyzing data of complex structures. However, its computer-intensive nature, which typically requires a large number of iterations and a complete scan of the full dataset for each iteration, precludes its use for big data analysis. To accelerate the computation of MCMC, one feasible way is to conduct parallel MCMC simulations. People have debated for a long time to make a long run or many short runs. For conventional MCMC algorithms, such as the Metropolis-Hastings algorithm(Metropolis et al., 1953; Hastings, 1970) and the Gibbs sampler (Geman and Geman, 1984), parallel runs may not provide any theoretical advantages over one long run. In general, if you cannot get a good answer with one long run, then you cannot get a good answer with many short runs either. However, this situation differs for the population stochastic approximation Monte Carlo (pop-SAMC) algorithm. In Song et al. (2014), it is shown that running pop-SAMC with κ chains for T iterations is asymptotically more efficient than running a single SAMC chain for κT iterations when the gain factor sequence decreases slower than O(1/t), where t indexes iterations and κ denotes the number of SAMC chains running in parallel. This is due to that the chains in pop-SAMC interact with each other intrinsically.
Like the SAMC algorithm, the pop-SAMC algorithm possesses the self-adjusting mechanism, which operates through adjusting a working parameter θ based on past samples. Through adjusting the working parameter, the algorithm penalizes the over-visited subregions and rewards the under-visited subregions and thus enables the system to escape from local traps very quickly. This is very important for BNNs, for which the energy landscape is known to be rugged. Refer to the supplementary material for a detailed description of the algorithm for Bayesian neural networks.
4.2. OpenMP Implementation
OpenMP is an application programming interface (API) for parallel programming on multiprocessors, which are now available in regular desktops/laptops. OpenMP works in a shared memory mode with the fork/join parallelism. When the program begins execution, only a single thread, called the master thread, is active, which executes the sequential portion of the algorithm. At the points where parallel operations are required, the master thread forks additional threads. The master thread and the forked threads work concurrently through the parallel section. At the end of the parallel code the forked threads die, and the flow of control returns to the master thread. This is called the join. Compared to the message passing interface (MPI), a parallelism running on a distributed memory system, OpenMP can often achieve better performance due to its shared-memory mode.
OpenMP is particularly suitable for a parallel implementation of the pop-SAMC algorithm. The fork step, which works on population sampling, costs the major portion of the CPU and the parallel execution provides a linear speedup for the simulation with the number of cores of the computer. The join step works on θ-adjusting, where distributing the adjusted θt to different threads is avoided due to its shared memory mode.
5. Simulation Studies
We illustrate the performance of the proposed BNN method using three simulated examples. It is known that the BNN model is non-identifiable due to the reasons: (i) the output is invariant to relabeling of hidden units; and (ii) since the activation function tanh(·) is used for the hidden units, the output is invariant to a simultaneous sign change of the weights on the connections from the input units to the hidden units and the weights on the connections from the hidden units to the output unit. To make the BNN model identifiable, we impose the following constraint:
that is, all the weights on the effective connections from the hidden units to the output unit are restricted to be non-negative and non-increasing (arranged from the first hidden unit to the last one). The identifiability of the constrained BNN model facilities our inference for the sampled networks. For example, the marginal inclusion probability of each connection can be simply calculated by averaging over sampled BNN models. Note that the identifiability considered here is slightly different from that considered in Section 3.3. Here the identifiability concerns the uniqueness of the neural network with exactly the same output value, whereas the one in Section 3.3 concerns the uniqueness of the true BNN model.
5.1. An Illustrative Example
In this example, we generated 10 datasets from a neural network model with the corresponding nonlinear regression given by
| (17) |
where σ = 0.5, ϵ ∼ N(0,1), P = 500, w0o = 1, w1o = 2, w11 = 1, w21 = 2, w3o = 2, and wio = 0 for i = 4,...,P. For the variables, we set x0 ≡ 1, and generated the remaining variables via the equation
| (18) |
where e and zi are independently generated from N(0,1). That is, the variables x1,...,xP are mutually correlated with a correlation coefficient of 0.5. Each dataset consists of 500 observations. We used 200 observations for training and the remaining 300 observations for testing. Therefore, this example forms a small-n-large-P nonlinear system, and our goal is to show that the proposed method is able to identify the true structure of the neural network model even when the variables are highly correlated.
For each dataset, we fit the nonlinear regression with a neural network of P = 500 input units and H = 3 hidden units, for which the full model consists of 2007 connections. Note that the true neural network consists of only one hidden unit. Here we set H = 3 to show that the proposed BNN method is able to automatically select the number of hidden units. We applied the pop-SAMC algorithm to simulate from its posterior distribution with and V γ = 5I|γ|. That is, we assumed that each connection weight is a priori independently distributed according to a normal distribution with a variance of 5. Here, such a small variance for the prior distribution is chosen to improve the generalization ability of the BNN models. As discussed in Liang (2005), utilizing a prior distribution of small variances is helpful to constrain the connection weights of BNN models to a small range around zero, and such models are less sensitive to small changes of input values than those with extreme connection weights. For the variance σ2 in (17), we let it be subject to an inverse-gamma prior distribution IG(0.01,0.01). The value of λn is determined using the average EBIC-like procedure, for which we tried four different values 0.01, 0.05, 0.1 and 0.2. For each value of λn, pop-SAMC was run for 1.2 × 106 iterations with κ = 20 SAMC chains. The first 2×105 iterations were discarded for the burn-in process and the samples were collected from the remaining iterations with a thinning factor of 100. Each run cost 23.2 minutes (real time) on a 24-core Dell Precision T7610 workstation, and the total CPU time is 374.4 minutes. The OpenMP implementation has reduced the real computational time of the pop-SAMC algorithm substantially.
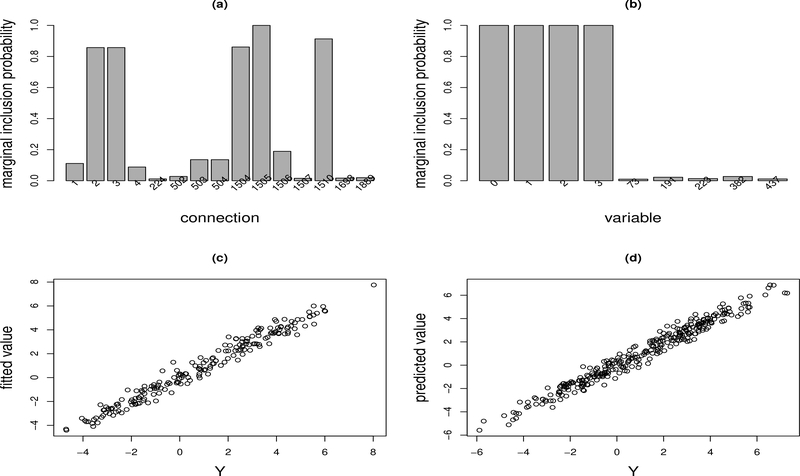
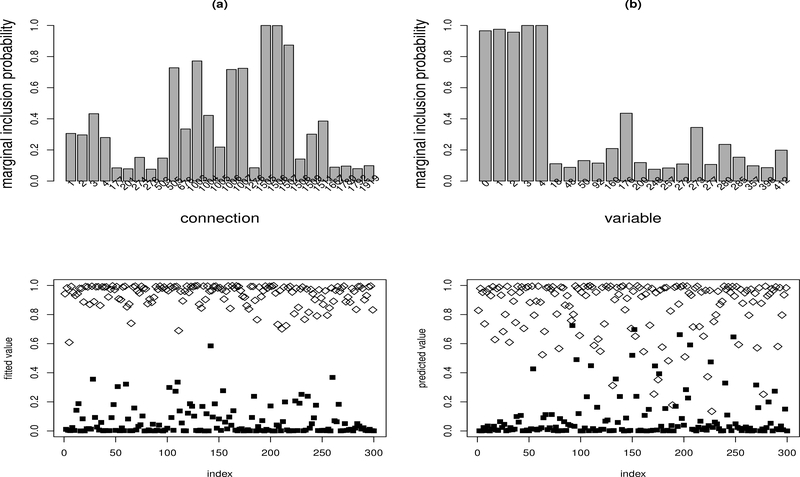
Figure 2 summarizes the results for one dataset. The results for other datasets are very similar. For this dataset, λn = 0.01 was selected by the average EBIC-like procedure. Figure 2(a) shows the marginal inclusion probabilities of the connections with the marginal inclusion probability greater than 0.01. It shows that there are five connections, labeled by 2, 3, 1504, 1505 and 1510, with the marginal inclusion probabilities greater than 0.5. In terms of Barbieri and Berger (2004), we call the network formed by the five connections the median probability neural network. For this example, the median probability neural network is exactly the same as the true neural network according to our coding scheme for network connections. Our coding scheme is the same as the one used in the R package nnet. For this example, connections 1–501, 502–1002, and 1003–1503 are for the connections from the input variables x0,x1,...,xP to the first, second and third hidden unit, respectively; connections 1504, 1505, 1506 and 1507 are for the connections from x0, H1, H2 and H3 to the output unit, respectively; and connections 1508–2007 are for the short-cut connections from the input variables x1,...,xP to the output unit. Therefore, the bars labeled by 2 and 3 are for the connections from x1 and x2 to H1, respectively, i.e., w11 and w21 in (17); the bar 1504 is for the connection from X0 to the output unit, i.e., the bias term w0o; the bar 1505 is for the connection from H1 to the output unit, i.e., w1o in (17); and the bar 1510 is for the shortcut connection from X3 to the output unit, i.e., w3o in (17). This example indicates that the proposed BNN method is able to identify the true structure of the neural network model even when the number of hidden units is misspecified and the input variables are highly correlated.
Figure 2:
Illustrative Example: (a) Marginal inclusion probabilities of the connections with the marginal inclusion probability greater than 0.01; (b) marginal inclusion probabilities of the covariates with the marginal inclusion probability greater than 0.01; (c) scatter plot of the response Y and the fitted value Ŷ for the training data; and (d) scatter plot of the response Y and the predicted value Ŷ for the test data.
Figure 2(b) shows the marginal inclusion probabilities of the variables with the marginal inclusion probability greater than 0.01. Each of the four true variables, x0, x1, x2 and x3, has a marginal inclusion probability of nearly 1, while all other variables have a very low marginal inclusion probability. This is consistent with the theoretical results established in Lemma 2: As the sample size becomes large, the marginal inclusion probability tends to be dichotomized, 1 for the true variables and 0 for the others. The results from other datasets are very similar: For all datasets, each of the true variables x0, x1, x2 and x3 can be identified with a marginal inclusion probability of close to 1.
Figure 2(c) shows the scatter plot of the response Y and its fitted value for the training data, and Figure 2(c) shows the scatter plot of the response Y and its predicted value for the test data. They indicate that the effectiveness of BNN in nonlinear modeling of the system (17).
In summary, this example indicates that the proposed method is able to identify the true BNN structure as well as relevant covariates for high-dimensional nonlinear systems. In the next two examples, we will show that even when the true BNN structure does not exist, the relevant covariates can still be correctly identified using the proposed method.
5.2. A Nonlinear Regression Example
In this example, we generated 10 datasets from the nonlinear system
| (19) |
where ϵ ∼ N(0,1). The variables x1,...,x5 together with additional 495 variables were generated as in (18); that is, all P = 500 explanatory variables are mutually correlated with a correlation coefficient of 0.5. Each dataset consists of 500 observations, where 200 observations were used for training, and the remaining 300 observations were used for testing. As aforementioned, the goal of this example is to show that the proposed method is able to identify relevant covariates for such a high dimensional nonlinear system even without existence of the true BNN structure. The high correlation and nontrivial interaction between the predictor variables have posed a great challenge on the existing nonlinear variable selection methods. As shown below, the existing methods all failed for this example.
The BNN method was first applied to this example with λn chosen from the set {0.05,0.1,0.2} using the average EBIC-like procedure. Each run consisted of 20 SAMC chains and 1.2 × 106 iterations, and cost about 18.9 minutes real time and 332 minutes CPU time on a workstation of CPU@2.6GHz by running with 20 threads. The CPU time may vary slightly with the value of λn. Figure 3 and Figure 4 summarizes the numerical results for one dataset, and Table 1 summarizes the results of variable selection and prediction for all ten datasets. We have also tried the average BIC-like criterion, the results are almost the same.
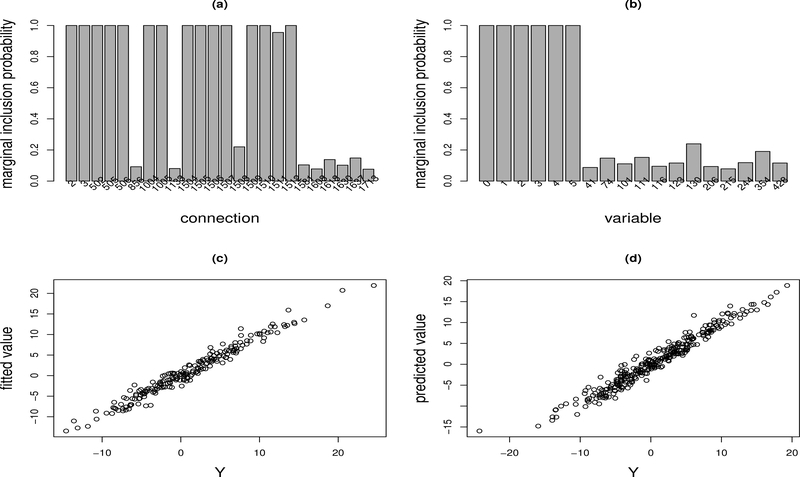
Figure 3:
Nonlinear Regression Example: (a) marginal inclusion probabilities of the connections with the marginal inclusion probability greater than 0.075; (b) marginal inclusion probabilities of the covariates with the marginal inclusion probability greater than 0.075; (c) scatter plot of the response Y and the fitted value Ŷ for the training data; and (d) scatter plot of the response Y and the predicted value Ŷ for the test data.
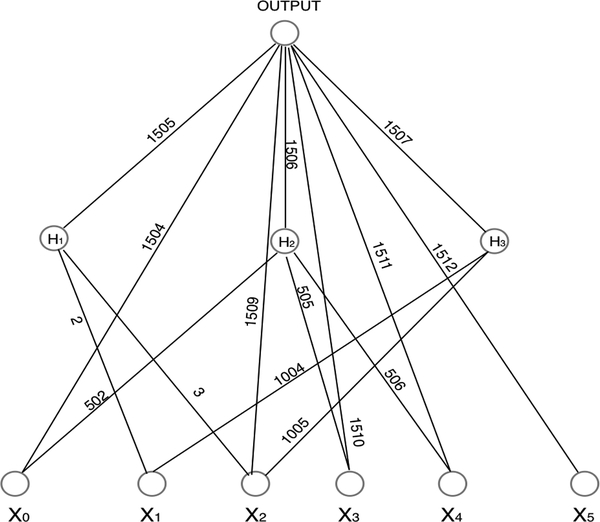
Figure 4:
Median probability network produced by BNN for the simulated nonlinear regression example: the corresponding marginal inclusion probabilities are shown in Figure 3(a).
Table 1:
Comparison of BNN, GAM, random forest, and BART in variable selection and nonlinear prediction for the simulated nonlinear regression example: “MPM” denotes the median probability model, i.e., selecting only the variables with the marginal inclusion probability greater than 0.5; “MSFE” denotes the mean squared fitting error; “MSPE” denotes the mean squared prediction error for the mean response; denotes the average number of variables selected for the 10 datasets; the numbers in parentheses denote the standard deviations of the corresponding values;
| Methods | Setting | fsr | nsr | MSFE | MSPE | |
|---|---|---|---|---|---|---|
| BNN | MPM | 5.2 (0.13) | 0.038 | 0 | 1.53(0.09) | 2.03(0.20) |
| BRNN | 195.9+ (0.09) | 0.667 | 0.60 | 0.013(9.9×10−4) | 19.51(0.82) | |
| GAM | 41.3 (6.77) | 0.898 | 0.16 | 3.78 (0.37) | 6.09 (0.29) | |
| RF | 7.1 (0.43) | 0.76 | 0.66 | 1.83 (0.05) | 9.71 (0.34) | |
| 20 trees | 5.9 (2.87) | 0.64 | 0.58 | 2.79 (0.17) | 8.45 (0.34) | |
| BART | 35 trees | 8.0 (4.34) | 0.75 | 0.60 | 1.54 (0.09) | 8.57 (0.42) |
| 50 trees | 4.3 (2.53) | 0.56 | 0.62 | 0.82 (0.07) | 8.34 (0.38) | |
| SIS-SCAD | 12.4 (5.37) | 0.83 | 0.58 | 5.79 (0.81) | 9.32 (0.91) | |
BRNN reports the effective number of parameters instead of the number of selected variables.
Figure 3(a) shows the marginal inclusion probabilities of the connections with the marginal inclusion probability greater than 0.075. It indicates that there are 15 connections with the marginal inclusion probabilities greater than 0.5. Figure 4 shows the corresponding median probability neural network. From this plot, we can say that neural network is not a completely black box: It can be used to identify potential interactions between variables. To be precise, the connections from variables x1 and x2 to the hidden units H1 and H3 indicate interactions between x1 and x2; and the connections from variables x3 and x4 to the hidden unit H2 indicate the interactions between x3 and x4. The shortcut connection from x5 to the output unit indicates the linear term of x5. All these observations are consistent with the true system (19).
Figure 3(b) shows the marginal inclusion probabilities of the variables with the marginal inclusion probability greater than 0.075. It indicates that all the true variables x1, x2, ..., x5 have been correctly identified. Since the true neural network does not exist for this example, the bias term x0 is usually selected. Figure 3(c) shows the scatter plot of the response Y and its fitted value for the training data, and Figure 3(d) shows the scatter plot of the response Y and its predicted value for the test data. They indicate the effectiveness of BNN in modeling general nonlinear systems.
To systematically measure the performance of the BNN method in variable selection, we calculated the false selection and negative selection rates. Let s denote the set of true relevant variables, and let denote the set of selected variables for data set i. Define
where | · | denotes the cardinality of a set. The smaller the values of fsr and nsr are, the better the performance of the method is. To measure the predictive performance of the BNN method, we calculated the mean squared prediction error for the mean of Y , which is known for the simulated data. Compared to the mean squared prediction error for Y , it provides a direct measure for the approximation to the underlying true system. The results are summarized in Table 1.
For comparison, we have also applied the generalized additive model (GAM), random forest (RF), Bayesian adaptive regression trees (BART), and Bayesian regularized neural network (BRNN) to this example. GAM provides a penalized likelihood approach for fitting sparse generalized additive models in high dimension. For GAM, we adopt the R package gamsel recently developed by Chouldechova and Hastie (2015). Both RF and BART are regression tree-based methods, which can yield a flexible model capturing nonlinearities and interaction effects in the unknown regression function. For RF, we adopt the R package h2o, which produces an importance measure for each predictor variable. The variable importance is determined by calculating the relative influence of each variable: whether that variable was selected during splitting in the tree building process and how much the squared error (over all trees) improved as a result. RF has been widely used as a variable selection approach for high dimensional nonlinear systems. In this paper, we selected the variables with the importance percentage greater than 1%. For BART, we adopt the R package bartMachine, where the importance of each variable is measured by the frequency that it is used as a splitting variable in the regression trees. Bleich et al. (2014) suggest three threshold-based procedures for variable selection, including local, global Max and Global SE. Refer to Bleich et al. (2014) for the details of these procedures. For each dataset, the procedure that returned the lowest cross-validation mean squared errors was used and coined as the “best” procedure. For both GAM and RF, we run the package under the default parameter settings. For BART, we tried different number of trees, 20, 35 and 50.
The BRNN used in Okut et al. (2011); Gianola et al. (2011) is very different from the proposed BNN. BRNN aims at data fitting and prediction, where the Gaussian prior distribution, equivalent to an l2-penalty, is used as a regularization term to penalize large connection weights. The l2-penalty, unlike the l1-penalty, cannot shrink many connection weights to zero exactly. Consequently, BRNN is dense, which can contain a large number of effective parameters and tends to be overfitted. From this perspective, BRNN still belongs to the class of traditional neural networks, working as a “black box” for function approximation. For BRNN, Okut et al. (2011) suggested to select relevant variables according to the magnitudes of connection weights, but the consistency of this approach is unclear. In the current R package (Rodriguez and Gianola, 2016), BRNN is only implemented for normal regression. For this example, we set the number of hidden units to 2 and calculate fsr and nsr based on top 6 relevant variables ranked by BRNN. The numerical results are summarized in Table 1.
The comparison indicates that BNN is superior to other methods in both variable selection and prediction. As implied by the the values of fsr and nsr, BNN can accurately identify the true variables for almost all datasets. Other methods perform far less than satisfactory. GAM selected too many variables for each dataset, while still missed some important variables, such as variables x1, x3 and/or x4, for some datasets. RF, typically, selected the variable x2 only or the variables x2 and x5, which have strong linear effects, and missed the variables x1, x3 and x4. In particular, it never selected variable x1 for all 10 datasets. With default 50 trees, BART overfit the data, with the fitting error less than σ2 = 1.0. With 35 trees, it produced about the same MSFE as BNN, but its prediction error is much worse than that of BNN. With 20, 35 and 50 trees, BART has very similar performance in variable selection. It typically selected only variables x2 and x5 and missed all other variables, but for some datasets it could select over 20 variables. For this reason, has a large standard error as shown in Table 1. For this example, BRNN is terribly overfitting and, consequently, it has a very large mean squared prediction error. Its high fsr and nsr values indicate that it did not produce a good rank for the relevance of the predictors to the response variable.
To show inappropriateness of applying a linear model to nonlinear systems, we have applied SISSCAD to this example under its default setting given in the R package SIS. SIS-SCAD is to first conduct variable screening based on the theory of Fan and Lv (2008a) and then conduct penalized linear regression for variable selection with the SCAD penalty (Fan and Li, 2001). The numerical results, summarized in Table 1, indicate that SIS-SCAD failed for this example.
Later, to examine the effect of the number of hidden units on the performance of BNN, BNN was re-run with H = 5 and H = 7. To accommodate the enlarged parameter space, we increased the total number of iterations to 2.0 × 106 iterations for both values of H, where the first 5 × 105 iterations were discarded for the burn-in process. The results are summarized in Table 2. For comparison, the results with H = 3 are also included in the table. The comparison shows that the performance of BNN is pretty robust to the choice of H. In general, as H increases, the full network size increases and thus the number of selected variables tends to increase and the fitting error tends to decrease, provided that the value of λn does not decrease accordingly. For real data problems, we suggest to set H to a little large value such that the network has enough capability to approximate the underlying nonlinear system but at a higher computational cost.
Table 2:
Effects of the number of hidden units on the performance of BNN. Refer to Table 1 for notations of the table.
| Methods | Setting | fsr | nsr | MSFE | MSPE | |
|---|---|---|---|---|---|---|
| BNN(H=3) | MPM | 5.2 (0.13) | 0.038 | 0 | 1.534(0.089) | 2.028(0.197) |
| BNN(H=5) | MPM | 5.6 (0.31) | 0.107 | 0 | 1.319 (0.086) | 1.559(0.253) |
| BNN(H=7) | MPM | 5.4 (0.22) | 0.074 | 0 | 1.416 (0.087) | 1.908(0.242) |
5.3. A Nonlinear Classification Example
In this example, we generated 10 datasets from the nonlinear system
| (20) |
where the variables x1,...,x4 together with additional 496 variables were generated in (18); that is, all P = 500 explanatory variables are mutually correlated with a correlation coefficient of 0.5. Each dataset consists of 600 observations, where 300 observations have a response value of 1 and the others have a response value of 0. We used 300 observations as the training data, and the remaining for testing. In both the training and testing datasets, the numbers of 1- and 0-response values are chosen to be the same. The goal of this example is to show that the proposed BNN method is able to identify relevant covariates for such a nonlinear classification system even without existence of the true BNN structure.
The proposed algorithm was run for this example with the value of λn determined using the average EBIC-like procedure, where λn ∈ {0.025,0.05,0.1,0.2}. For each value of λn, pop-SAMC was run for 1.2 × 106 iterations with κ = 20 SAMC chains, where the first 2 × 105 iterations were discarded for the burn-in process the samples were collected from the remaining part of the run at every 100th iterations. Each run cost about 22.9 minutes real time and 349.7 minutes CPU time on a workstation of CPU@2.6GHz by running with 20 threads. The numerical results are summarized in Figure 5 and Table 3. With the average BIC-like procedure, the algorithm produced slightly better results in prediction. Figure 5(a) shows the marginal inclusion probabilities of the connections with the marginal inclusion probability greater than 0.075. It indicates that all the variables x1, x2, x3 and x4 interact with each other, as the connections 1004, 1005, 1006 and 1007 (which correspond to variables x1,x2, x3 and x4, respectively) all go to the same hidden unit. This matches with the underlying system (20), where all the variables work dependently to produce the binary response value. Also, the high bars 1006 and 1007 indicate that x3 and x4 have more interactions than with others. Figure 3(b) shows the marginal inclusion probabilities of the variables with the marginal inclusion probability greater than 0.075. It indicates that all the true variables x1, x2, x3 and x4 can be correctly identified. Figure 3(c) shows the fitted values of Y for the training data, Figure 3(d) shows the predicted values of Y for the test data. They indicate that the effectiveness of BNN in modeling nonlinear classification systems. For comparison, we have applied the GAM, RF, BART and SIS-SCAD to this example. For RF, we tried three different numbers of trees, 5, 10 and 25. With 25 trees, RF obtained a perfect training error. For BART, we tried four different numbers of trees, 20, 35, 50, and 75, where 50 is the default value. The numerical results indicate that the performance of BART is quite robust to the number of trees. SISSCAD was run under its default setting with the regularization parameter tuned by cross-validation. The comparison indicates that BNN outperforms the other methods in both variable selection and prediction. Among the five methods, BNN achieved the lowest prediction error and negative selection rate, while keeping the false selection rate at a low level. To compare the prediction errors produced by BNN with those by other methods, paired-t tests were conducted with the resulting p-values given in Table 3. The results indicate again that BNN outperforms other methods.
Figure 5:
Nonlinear classification example: (a) marginal inclusion probabilities of the connections with the marginal inclusion probability greater than 0.075; (b) marginal inclusion probabilities of the covariates with the marginal inclusion probability greater than 0.075; (c) fitted value of Y (open diamond for true Y = 1, filled square for true Y = 0); and (d) predicted value of Y (open diamond for true Y = 1, filled square for true Y = 0).
Table 3:
Comparison of BNN, GAM, random forest, and BART in variable selection and class prediction for the simulated classification example: “MPM” denotes the median probability model, i.e., selecting the variables with the marginal inclusion probability greater than 0.5; “Fitting” denotes the error rate of fitted class for the training data; “Prediction” denotes the error rate of predicted class for the test data; denotes the average number of variables selected for the 10 datasets; the numbers in parentheses denote the standard deviations of the corresponding values; and p-value is calculated using a paired-t test for BNN versus every other method.
| Methods | Setting | fsr | nsr | Fitting(%) | Prediction(%) | p-value | |
|---|---|---|---|---|---|---|---|
| BNN | MPM | 4.3 (0.26) | 0.093 | 0.025 | 3.57 (0.47) | 9.70 (0.99) | — |
| GAM | 13.5 (3.68) | 0.73 | 0.10 | 12.13 (1.34) | 15.57 (1.97) | 2.75 × 10−3 | |
| 5 trees | 17.3 (2.23) | 0.79 | 0.075 | 2.19 (0.41) | 18.6 (2.18) | 7.45 × 10−4 | |
| RF | 10 trees | 8.2 (0.76) | 0.56 | 0.10 | 0.67 (0.15) | 17.2 (1.80) | 2.98 × 10−3 |
| 25 trees | 5.2 (0.39) | 0.31 | 0.10 | 0.0 (0.0) | 14.3 (1.04) | 1.27 × 10−3 | |
| 20 trees | 2.8 (0.33) | 0.0 | 0.30 | 9.90 (1.04) | 17.72 (1.83) | 2.01 × 10−4 | |
| BART | 35 trees | 3.0 (0.26) | 0.0 | 0.25 | 6.83 (0.89) | 17.00 (1.34) | 3.35 × 10−6 |
| 50 trees | 3.0 (0.30) | 0.0 | 0.25 | 5.33 (0.75) | 15.57 (1.42) | 7.46 × 10−4 | |
| 75 trees | 3.3 (0.33) | 0.03 | 0.20 | 4.47 (0.55) | 16.90 (1.58) | 2.22 × 10−4 | |
| SIS-SCAD | 5.0 (1.45) | 0.46 | 0.325 | 18.70 (2.91) | 21.43 (2.48) | 6.87 × 10–4 | |
6. Selection of Drug Sensitive Genes
The CCLE dataset consisted of 8-point dose-response curves for 24 chemical compounds across over 400 cell lines. For different chemical compounds, the numbers of cell lines are slightly different. For each cell line, it consisted of the expression data of 18,926 genes. The dataset is publicly available at www.broadinstitute.org/ccle. Our goal is to use the BNN model to identify the genes that are associated with the drug sensitivity. Our study addresses the problem why some some cell lines are more responsive to the chemical compounds in terms of their gene expression, which is fundamental to elucidate the response mechanism of anticancer drugs and critical to precision medicine. We used the area under the dose-response curve, which is termed as activity area in Barretina et al. (2012), to measure the sensitivity of a drug for each cell line. Compared to other measurements, such as IC50 and EC50, the activity area could capture the efficacy and potency of a drug simultaneously. An exploratory analysis indicates that the distribution of the activity area tends to be right-skewed. To shorten the tail, we made a square-root transformation for the activity area. The transformed variable tends to be bell-shaped and was used as the response variable of the BNN model. The underlying scientific motivation for this study is that the drug sensitivity should be a nonlinear function of gene expression, which might also contain some complex interactions between different genes. We note that the drug-sensitive genes, that are identified by the BNN model based on the CCLE data, may differ from those genes that respond to the drug. To truly identify the genes whose expression changes with drug treatments or dose levels, statistically we have to take the drug level as covariates and the gene expression as the response variable.
For each drug, we used the first 80% available cell lines (in the order published at the CCLE website) as training samples and the remaining 20% available cell lines as test samples. The performance of the proposed and competing methods is measured based on the number of selected genes and the prediction error on test samples. Since the true drug-sensitive genes are unknown and the underlying drug sensitivity model is assumed to be sparse, a smaller number of selected genes and a smaller prediction error are generally preferred.
Since each cell line consists of a large number of genes, to accelerate computation, we applied a hybrid approach to analyze the data. That is, we first applied a marginal feature screening approach to reduce the number of genes to a reasonable number, and then applied the BNN method to select right genes from the reduced candidate set of genes.
6.1. Marginal Feature Screening
As a dimension reduction tool, marginal feature screening has received much attention in recent literature. Motivated by the success of marginal feature screening for linear models (Fan and Lv, 2008b; Fan et al., 2009; Wang, 2009; Li et al., 2012), quite a few model-free feature screening procedures, such as Zhu et al. (2011), He et al. (2013), Cui et al. (2015) and Authors (2017), have been proposed. These model-free procedures are suitable for nonlinear models. To accelerate the computation of BNN, the procedure developed in Authors (2017) was adopted in this paper. The basic idea of this procedure is as follows. Let Fy(·) denote the CDF of the response variable Y , and let Fxi(·) denote the CDF of the variable Xi. Consider the probit transformations
| (21) |
where Φ(·) denotes the CDF of the standard Gaussian distribution. It is easy to see that Y is independent of Xi if and only if (, ) forms a bivariate random vector following the distribution N2(0,I2), where I2 denotes the 2 × 2 identity matrix. The latter can be tested using a multivariate normality test, e.g., Henze-Zirkler’s test (Henze and Zirkler, 1990), with the known covariance structure. If (, ) does not follow the distribution N2(0,I2), then the Henze-Zirkler’s test statistic tends to take a large value. In practice, since Fy and ’s are unknown, we can estimate them using a nonparametric method, and the resulting transformation (21) is called nonparanormal transformation in Liu et al. (2009). The nonparanormal transformation has been implemented in the R package huge. Like other screening procedures, e.g., those proposed in Zhu et al. (2011), He et al. (2013) and Cui et al. (2015), this procedure also possesses the sure screening property as shown in Authors (2017). Following the general guideline of sure screening procedures, we reduced the number of genes to p′ = O(n/log(n)), where n is the number of training samples. For simplicity, we set p′ = 80 for each drug, which is slightly larger than n/log(n). Note that the value of n varies a little from drug to drug. In summary, the procedure consists of the following steps.
Apply the nonparanormal transformation (Liu et al., 2009) to get transformed variables and
- For each k = 1,P,calculate the Henze-Zirkler test statistic
where is the smoothing parameter, , and and denote the kth elements of and , respectively. Select genes with the largest value of ω(·,·) for further analysis.
For each drug, other than the p′ genes with the largest ω values, we also included the target gene into the candidate set if it did not pass the screening procedure. Compared to other model-free sure screening procedures, such as those proposed in Zhu et al. (2011), He et al. (2013) and Cui et al. (2015), the above procedure is more robust to the outliers of the data due to the transformation (21), where a robust nonparametric estimator of the CDF is involved. Since the CCLE data are of high quality, other nonlinear screening procedures should also work well here.
6.2. Gene Selection
we first applied the BNN method to each drug with the reduced gene sets. For this example, although the number of genes included in the reduced set is smaller than the training sample size n, the BNN model should still be considered as high-dimensional. This is because the total number of possible connections, Kn, which should be considered as the dimensionality of the BNN model, can still be close to or larger than n. For example, for the drug Irinotecan, the reduced gene set consisted of 81 genes and the maximum number of hidden units was set to 3, so Kn = 331, which is greater than the training sample size n = 245.
For each drug, BNN was run with λn chosen from the set {0.0025,0.05,0.1,0.2} according to the average EBIC-like procedure, and each run consisted of 20 SAMC chains and 1.7×106 iterations, where the first 2 × 105 iterations were discarded for the burn-in process. Each run cost about 15.3 minutes real time and about 278 minutes CPU time on a workstation (of CPU@2.6GHz) by running with 20 threads. The CPU time for each run may vary slightly with the value of λn. In general, a larger value of λ will cost longer computational time, as the involved neural networks tend to have more connections. For all drugs, λn = 0.025 was selected according to the average EBIC-like procedure. The results are summarized in Table 4.
Table 4:
Comparison of BNN with SIS-SCAD, GAM, RF, BART, and BRNN in gene selection for 24 drugs: “Training error” denotes the average mean squared fitting error, “Prediction error” denotes the average mean squared prediction error, and #gene denotes the average number of selected genes, where the averages are over 24 drugs; the numbers in parentheses denote the standard deviations of the corresponding averages;
| Method | Training error | Prediction error | #gene |
|---|---|---|---|
| SIS-SCAD | 0.0248(0.0020) | 0.1757(0.0132) | 62.92(0.97) |
| BRNN | 0.0587(0.0059) | 0.1420(0.0151) | 84.06*(7.64) |
| GAM | 0.0719(0.0063) | 0.1253(0.0091) | 41.75(2.76) |
| RF | 0.0137(0.0010) | 0.1176(0.0087) | 30.54(1.75) |
| BART | 0.0366(0.0031) | 0.1249(0.0092) | 7.92(0.47) |
| BNN | 0.0855(0.0061) | 0.1201(0.0089) | 2.38(0.40) |
BRNN reports the effective number of parameters of the neural network instead of the number of selected genes.
For comparison, we first applied the SIS-SCAD method to this problem with the results summarized in Table 4. For SIS-SCAD, since it itself includes a sure independence screening procedure, it was directly applied to the original datasets. Under its default setting, SIS-SCAD produced a small training error, but a large prediction error. A paired t-test shows that the prediction error produced by SIS-SCAD is significantly larger than that produced by BNN, with a p-value of 1.5 × 10−7. On average, SIS-SCAD selected over 62 genes, which is much larger than that selected by BNN. Just as expected, the linear model does not work well for nonlinear systems.
For a thorough comparison, we also applied BRNN, GAM, RF, and BART to the datasets, which are all designed for nonlinear systems. These methods were run under their default settings with the results summarized in Table 4. Compared to BNN, BRNN overfit the data, and its prediction error was slightly worse than that of BNN. In addition, it cannot be used for variable selection. GAM selected too many genes and its prediction error was also slightly worse than that of BNN. RF produced a very small training error and a comparable prediction error with BNN, but it selected much more genes than BNN. BART worked reasonably well for this example: For each dataset, it selected a reasonably small number of genes and produced a reasonably low prediction error. Overall, BNN outperforms all other methods: it tends to select a sparse model, while producing a small prediction error.
Later, to assess the stability of gene selection, we performed a five-fold cross-validation for each drug; that is, for each drug, the dataset was partitioned into five subsets with each consisting of 20% of samples, and each run took four of the five subsets as the training data. Meanwhile, for each drug, we calculated the Bayes factor (3) for testing nonlinearity of the drug sensitivity as a function of gene expression. For this purpose, we fix λn = 0.025 for each run, at which prior probabilities and are of about the same order with the ratio ranging from 0.5 to 20 depending on the number of genes. For each drug, Table 5 reported all genes selected with the median probability criterion (i.e., the marginal inclusion probability exceeds 0.5 in any of the five cross-validation runs), and the mean and standard deviation of the Bayes factors calculated from the five cross-validation runs.
Table 5:
Drug-sensitive genes identified by BNN, where the number in the parentheses is the number of times that the gene was selected in five-fold cross-validation runs, the mean and standard deviation of the Bayes factors were calculated based on five cross-validation runs.
| Drug | Target | Bayes Factor | Genes |
|---|---|---|---|
| 17-AAG | HSP90 | 0.001(0.001) | NQO1(5), ATP6V0E1(5), MAP7D2(4), CASP3(3), OGDHL(2), MMP24(2), RPUSD4(1), CDH6(1), ZNF610(1), CBFB(1), INO80(1), SEC23IP(1) |
| AEW541 | IGF1R | 0.465(0.294) | IGF1R(3), IQGAP2(2), MT2A(2), C11orf2(1), LOC100506319(1), ACVR2B(1), MID2(1) |
| AZD0530 | ABL | 0.141(0.052) | CAPN1(1), ENPP1(1), GLRX2(1), APOO(1), ST13(1) |
| AZD6244 | MEK | 0.021(0.015) | LYZ(5), RNF125(5), ETV4(3), DUSP6(2), PHLDA1(1), HIVEP1(1), ZC3H12C(1) |
| Erlotinib | EGFR | 0.071(0.030) | EGFR(5), SYTL1(3), PTPN6(1), MGC4294(1), BCR(1) |
| Irinotecan | TOP2 | 0.098(0.023) | SLFN11(5), ARHGAP19(5) |
| L-685458 | GS | 2.669(0.958) | GSS(3), RGS18(2), RHOC(1), CTSL1(1), ARHGAP4(1), CHERP(1), E2F2(1), SPCS2(1), GSK3B(1) |
| Lapatinib | EGFR | 0.567(0.107) | GRB7(3), SYTL1(2), EPHA1(1), MIR100HG(1) |
| LBW242 | XIAP | 16.865(7.138) | KRTAP4–6(1*) |
| Nilotinib | ABL | 0.160(0.068) | ABL1(4), FAM117A(3), ARID1B(1), ZNF793(1) |
| Nutlin-3 | MDM2 | 1.156(0.372) | MDM2(2), PVR(1) |
| Paclitaxel | TUBB1 | 0.002(0.001) | BCL2L1(4), ZNRD1(4), SSRP1(3), LOC100288637(2), SPATA5L1(2), MAP3K4(1), CNTRL(1), DUT(1), CSNK1G2(1) |
| Panobinostat | HDAC | 0.270(0.108) | MYOF(5), LARP6(3), TGFB2(1), CLCF1(1),ARID3A(1) |
| PD-0325901 | MEK | 0.000(0.000) | RNF125(5), SPRY2(5), LYZ(4), ETV4(3), KLF3(3), ENAH(2), PLEKHG4B(2), C9orf167(1), OSBPL3(1),DBN1(1), TMC6(1), TESK1(1), TM7SF3(1), EML1(1) |
| PD-0332991 | CDK4 | 0.887(0.420) | COX18(2), TSEN34(2), FAM129B(1) |
| PF2341066 | c-MET | 0.104(0.051) | HGF(5), ENAH(5), LRMP(2), ELF2(1), RPA2(1),CBFA2T3(1), METTL21C(1) |
| PHA-665752 | c-MET | 0.688(0.231) | INHBB(3), TNFRSF1B(2), TSEN34(1), SPCS2(1) |
| PLX4720 | RAF | 0.083(0.026) | CD200(4), RBP1(1), CRABP2(1), TRPV2(1),IL20RA(1), ZADH2(1) |
| RAF265 | RAF | 0.139(0.051) | SEPT11(4), CMTM3(2), KALRN(1), LOC100505986(1) |
| Sorafenib | RTF | 1.410(0.281) | LAIR1(5), RPL22(3) |
| TAE684 | ALK | 9.611(4.527) | ARID3A(5) |
| TKI258 | FGFR | 1.019(0.361) | DDR1(1), C4orf46(1), MET(1) |
| Topotecan | TOP2 | 0.016(0.008) | SLFN11(5), CD63(5), HMGB2(1), ELAVL1() RFXAP(1), KBTBD8(1), DSP(1), ORC1(1), LCN2(1),SF3A2(1), ZCCHC3(1), NSMCE4A(1) |
| ZD-6474 | EGFR | 0.037(0.009) | KLF2(5), APOO(5), NMI(4) |
For LBW242, KRTAP4-6 has only a marginal inclusion probability of 0.487 in one cross-validation run.
Table 5 indicates that the BNN-based gene selection is quite stable and successful: For many drugs, the selected genes are highly consistent with our existing knowledge and they repeatedly appeared in different cross-validation runs. For example, for both drugs Topotecan and Irinotecan, BNN repeatedly selected SLFN11 as the top drug-sensitive gene in all five cross-validation runs. In the literature, both Barretina et al. (2012) and Zoppoli et al. (2012) reported that SLFN11 is predictive of treatment response for Topotecan and Irinotecan. For the drug 17-AAG, BNN repeatedly selected NQO1 as the top drug-sensitive gene in all five cross-validation runs, and Hadley and Hendricks (2014) and Barretina et al. (2012) reported NQO1 as the top predictive biomarker for 17-AAG. For the drug Paclitaxel, BNN selected BCL2L1 as the top drug-sensitive gene in four of five cross-validation runs. In the literature, many publications, such as Lee et al. (2016) and Dorman et al. (2016), reported that the gene BCL2L1 is predictive of treatment response for Paclitaxel. For the drug PF2341066, Lawrence and Salgia (2010) reported that HGF, which was selected by BNN as the top drug-sensitive gene in all five cross-validation runs, is potentially responsible for the effect of PF2341066. It is interesting to point out that for the drugs AZD6244 and PD-0325901, which share the same target gene MEK, BNN selected similar drugsensitive genes for them. In addition, for the drugs AEW541, Erlotinib, and Nilotinib, BNN selected their target genes as the top drug-sensitive genes. Consistent literature can also be found for the gene selection results for some other drugs, such as Lapatinib (Nencioni et al., 2010), AZD6244 (Holt et al., 2012) and TAE684 (Liu et al., 2010). Nencioni et al. (2010) reported that the removal of GRB7 by RNA-interference reduces breast cancer cell viability and increases the activity of Lapatinib, and they concluded that GRB7 upregulation is a potentially adverse consequence of HER2 signaling inhibition, and preventing GRB7 accumulation and/or its interaction with receptor tyrosine kinases may increase the benefit of HER2-targeting drugs. Holt et al. (2012) reported that DUSP6 is one of the key genes under MEK function control, while MEK is the target gene of AZD6244. Liu et al. (2010) reported that ARID3A plays important roles in embryonic patterning, cell lineage gene regulation, and cell cycle control, chromatin remodeling and transcriptional regulations, and has potential values in future drug discovery and design.
Although many of the gene selection results can be validated by existing knowledge, some cannot now. The failure of validation can be due to a few reasons. For example, it may be due to the feature screening procedure, which fails to include the drug-sensitive genes into the candidate set. It may be due to the data transformation (on activity areas), which can twist the relationship between the drug sensitivity and gene expression. It may also be due to the genetic heterogeneity; that is, the cell lines may contain a few groups and each group have different drug-sensitive genes. The genetic heterogeneity may also partially explain unrepeatedness of gene selection in some cross-validation runs. We note that the unrepeatedness problem can be alleviated by increasing the value of λn; when λn becomes large, more common genes can be found in different cross-validation runs. In general, the genetic heterogeneity adversely affects on the performance of BNN. How to deal with the genetic heterogeneity with BNNs will be pursued in the future.
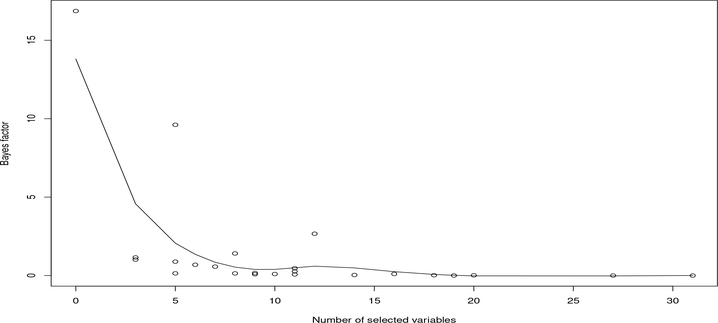
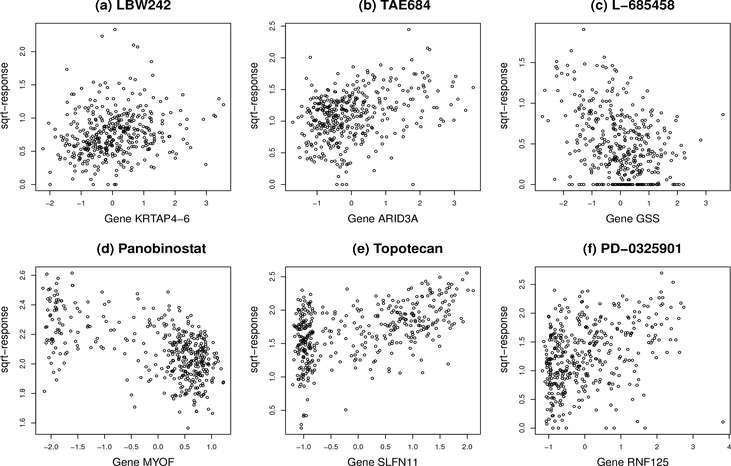
As a summary of the results on Bayes factors, we showed in Figure 6 a pattern for Bayes factors that a linear model (with a higher Bayes factor value) is generally preferred when the number of selected genes is small. This is consistent with our intuition. For example, for the drug LBW242, none of the genes was selected according to the median probability criterion, where the gene KRTAP4–6 has only a marginal inclusion probability of 0.487 in one cross-validation run. As a result, the BNN model has a high Bayes factor value, which provides a strong evidence against the assumption that the sqrt-transformed activity area is a nonlinear function of gene expression. See Kass and Raftery (1995) for interpretation of Bayes factors. Similarly, for the drug TAE684, which selected only a single gene in all five cross-validation runs, the Bayes factor provides a substantial evidence against the nonlinearity assumption for the sqrttransformed activity area. Further, we showed in Figure 7 the scatter plots of the sqrt-transformed activity area versus the expression data of the major drug-sensitive gene selected by BNN for a few drugs, including LBW242, TAE684, L-685458, Panobinostat, Topotecan and PD-0325901, which cover the cases with small, medium and large Bayes factors. The scatter plots show patterns consistent with the reported Bayes factors: A large Bayes factor supports a linear or null pattern (the plot for LBW242 shows a null pattern).
Figure 6:
Scatter plot of averaged Bayes factors versus averaged numbers of selected genes for 24 drugs, where the averages were calculated based on five-fold cross-validation runs, and the curve was fitted using a smoothing spline method.
Figure 7:
Scatter plots of sqrt-transformed activity areas versus the expression data of the major drug-sensitive genes identified by BNN for the drugs LBW242, TAE684, L-685458, Panobinostat, Topotecan and PD-0325901. The Bayes factors of the six drugs are 16.865, 9.611, 2.669, 0.27, 0.016 and 0, respectively.
7. Discussion
The main contribution of this paper is to propose to use BNN models to conduct variable selection for high-dimensional nonlinear systems and extend the theory of posterior consistency from generalized linear models Jiang (2007) to nonlinear models. From the perspective of applications, this paper has successfully applied the proposed BNN methods to identify the genes that associated with drug sensitivity for 24 anticancer drugs. From the perspective of statistical theory, the results of this paper imply the existence of consistent estimates for high-dimensional BNNs when the number of hidden units is allowed to grow with the sample size n. The growth condition has been embedded in the condition of Kn in Theorem 1. We note that for the case that the number of hidden units is fixed (to a large enough number), the existence of consistent estimates can also be implied by the theory established by Yang and Tokdar (2015). Let ds denote the number of effective connections to the hidden unit Hs, and let d0 denote the number of effective shortcut connections from the input units to the output unit.
According to the theory of Yang and Tokdar (2015), if ds remains bounded as H increases with n, and , i.e., the total number of important predictors is o(n), then a consistent estimator of the neural network model exist. However, how to find such a consistent estimator is not studied in Yang and Tokdar (2015). For the low-dimensional case, the approximation and estimation bounds of the neural network model have been established in Barron (1994).
The computational issue involved in the proposed BNN method is resolved by implementing a parallel adaptive MCMC algorithm on the OpenMP platform. Although the pop-SAMC algorithm possesses the self-adjusting mechanism and is essentially immune to local traps, it may still take a large number of iterations to converge when the proposal distribution is ineffective. The proposal distributions currently used include birth (adding edges), death (delete edges) and block updating (for weights) (Liang, 2005; Green, 1995). To accelerate convergence, the crossover operators prescribed in Liang (2005) can be implemented, which will accelerate the convergence of the simulation significantly. In addition to OpenMP, the pop-SAMC algorithm can also be implemented on the message passing interface (MPI) platform to facilitate the use of supercomputers which are usually provided at the college or university level.
In practice, we have often encountered the problems with multi-responses, such as multivariate normal regression or multinomial regression used in disease subtype analysis or other scenarios. The proposed method can be simply extended to these problems by considering a network with multiple output units. We do not anticipate any essential difficulties in extending the theory developed in Section 3.2 to the case of multi-responses.
In this big data era, we have often the same type of datasets available from multiple sources, e.g., the same type of genomic data across multiple studies. Integrating the data information from multiple sources into variable selection can be done using a meta-analysis approach. Let denote the marginal inclusion probabilities of the P covariates obtained by BNN from dataset i for i = 1,...,m, where m denotes the total number of data sources. We can first transform the marginal inclusion probabilities into z-scores via the probit transformation , and then combine the z-scores using Stouffer’s meta-analysis method (Stouffer et al., 1949; Mosteller and Bush, 1954). Then a multiple hypothesis test can be done on the combined z-scores to identify the variables relevant to the outcome.
Recently, deep neural networks have been successfully used in a wide range of pattern recognition problems. In theory, extension of the proposed one-hidden layer BNN to deep BNNs is straightforward, as long as a bounded activation function such as the sigmoid or hyperbolic tangent function is used. However, when more hidden layers are included into the model, the number of possible connections will increase dramatically and the computation can be very cumbersome. In this case, the computation may need to be accelerated using Graphics Processing Units (GPUs), see e.g., Lee et al. (2010) and White and Porter (2014). The effect of the depth of deep neural networks has been studied in the literature, see e.g., Sun et al. (2016) and Raghu et al. (2017). Sun et al. (2016) pointed out that as the depth increases, the prediction error may first decrease and then increase. We expect that a deep BNN with an appropriate depth will further improve the prediction performance of the proposed one-hidden-layer BNN.
Finally, we would like to note that the proposed BNN is essentially a mixture of weak models, for which a large number of one-hidden layer neural network models are used for data fitting and prediction via Bayesian model averaging. Although each model can be relatively weak compared to deep neural network models, the whole mixture model can still perform well in data fitting and prediction. For this reason, we suspect that the deep structure might not be crucial for BNNs. As an alternative to deep BNNs, we will also try boosting BNNs based on the idea of the Boosting algorithm (Schapire, 1990). We believe that the representation power of the shallow BNNs can be improved by boosting; that is, we will be able to iteratively learn weak BNNs and add them to form a strong learner.
Supplementary Material
Acknowledgments
Liang’s research was support in part by the NSF grants DMS-1612924 and DMS/NIGMS R01GM117597. The authors thank G. Miao and V. Sundaresan for their help on data pre-processing, and thank the Editor, Associate Editor and two referees for their constructive comments which have led to significant improvements of this paper.
Footnotes
Package
The proposed BNN method has been implemented into a R package, which will be made publicly available at CRAN upon acceptance of the paper.
Contributor Information
Faming Liang, Department of Statistics, Purdue University, West Lafayette, IN 47906, fmliang@purdue.edu.
Qizhai Li, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100864, China.
Lei Zhou, Department of Molecular Genetics & Microbiology, University of Florida, Gainesville, FL 32611.
References
- Akaike H (1979), “A Bayesian extension of the minimum AIC procedure of autoregressive model fitting,” Biometrika, 66, 237–242. [Google Scholar]
- Anders C, Fan C, Parker J, Carey L, Blackwell K, Klauber-DeMore N, and Perou C (2011), “Breast carcinomas arising at a young age: unique biology or a surrogate for aggressive intrinsic subtypes?” Journal of clinical oncology, 29, e18–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Authors (2017), “Robust model-free feature screening for ultrahigh dimensional data,” Journal of Computational and Graphical Statistics, in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbieri M and Berger J (2004), “Optimal predictive model selection,” Annals of Statistics, 32, 870–897. [Google Scholar]
- Barretina J, Caponigro G, Stransky N, Venkatesan K, Margolin A, Kim S, Wilson C, Lehar J, Kryukov G, Sonkin D, Reddy A, Liu M, Murray L, Berger M, Monahan J, Morais P, Meltzer J, Korejwa A, Jane-Valbuena J andMapa F, Thibault J, Bric-Furlong E, Raman P, Shipway A, Engels I, and et al. (2012), “The Cancer cell line encyclopedia enables predictive modeling of anticancer drug sensitivity,” Nature, 483, 603–607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barron A (1994), “Approximation and Estimation Bounds for Artificial Neural Networks,” Machine Learning, 14, 115–133. [Google Scholar]
- Bhattacharya A, Pati D, Pillai NS, and Dunson DB (2015), “Dirichlet-Laplace priors for optimal shrinkage,” Journal of the American Statistical Association, 110, 1479–1490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bleich J, Kapelner A, George E, and Jensen S (2014), “Variable selection for BART: An application to gene regulation,” The Annals of Applied Statistics, 8, 1750–1781. [Google Scholar]
- Breiman L (2001), “Random Forest,” Machine Learning, 45, 5–32. [Google Scholar]
- Buzdar A (2009), “Role of biologic therapy and chemotherapy in hormone receptor and HER2-positive breast cancer,” The Annals of Oncology, 20, 993–999. [DOI] [PubMed] [Google Scholar]
- Carlin B and Louis T (1996), Bayes and Empirical Bayes Methods for Data Analysis, New York: Chapman & Hall. [Google Scholar]
- Carvalho C, Polson N, and Scott J (2010), “The horseshoe estimator for sparse signals,” Biometrika, 97, 465–480. [Google Scholar]
- Castillo I, Schmidt-Hieber J, and van der Vaart A (2015), “Bayesian linear regression with sparse priors,” Annals of Statistics, 43, 1986–2018. [Google Scholar]
- Chen J and Chen Z (2008), “Extended Bayesian information criteria for model selection with large model spaces,” Biometrika, 95, 759–771. [Google Scholar]
- Chipman H, George E, and McCulloch R (2010), “BART: Bayesian additive regression trees,” The Annals of Applied Statistics, 4, 266–298. [Google Scholar]
- Chouldechova A and Hastie T (2015), “Generalized additive model selection,” arXiv:1506.03850.
- Cui H, Li R, and Zhong W (2015), “Model-free feature screening for ultrahigh dimensional discriminant analysis,” Journal of the American Statistical Association, 110, 630–641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Curtis C, Shah S, Chin S, and et al. (2012), “The genomic and transcriptomic architecture of 2,000 breast tumours reveals novel subgroups,” Nature, 486, 346–352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cybenko G (1989), “Approximation by superpositions of a sigmoidal function,” Mathematics of Controls, Signals, and Systems, 2, 303–314. [Google Scholar]
- Dorman S, Baranova K, Knoll J, Urquhart B, Mariani G, Carcangiu M, and Rogan P (2016), “Moleular Oncology,” Genomic signatures for paclitaxel and gemcitabine resistance in breast cancer drived by machine learning, 10, 85–100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan J and Li R (2001), “Variable selection via nonconcave penalized likelihood and its oracle properties,” Journal of the American Statistical Association, 96, 1348–1360. [Google Scholar]
- Fan J and Lv J (2008a), “Sure Independence Screening for Ultrahigh Dimensional Feature Space,” Journal of the Royal Statistical Society, Series B, 70, 849–911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan J and Lv J (2008b), “Sure independence screening for ultrahigh dimensional feature space (with discussion),” Journal of the Royal Statistical Society, Series B, 70, 849–911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan J, Samworth R, and Wu Y (2009), “Ultrahigh dimensional feature selection: Beyond the linear model,” Journal of Machine Learning Research, 10, 1829–1853. [PMC free article] [PubMed] [Google Scholar]
- Funahashi K (1989), “On the approximate realization of continuous mappings by neural networks,” Neural Networks, 2, 183–192. [Google Scholar]
- Geman S and Geman D (1984), “Stochastic relaxation, Gibbs distributions and the Bayesian restoration of images,” IEEE Transactions on Pattern Analysis and Machine Intelligence, 6, 721–741. [DOI] [PubMed] [Google Scholar]
- Gianola D, Okut H, Weigel K, and Rosa G (2011), “Predicting complex quantitative traits with Bayesian neural networks: a case study with Jersey cows and wheat,” BMC Genetics, 12, 87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gramacy R, Taddy M, and Wild S (2013), “Variable selection and sensitivity analysis using dynamic trees, with an application to computer code performance tuning,” Ann. Appl. Stat, 7, 51–80. [Google Scholar]
- Green P (1995), “Reversible jump Markov chain Monte Carlo computation and Bayesian model determination,” Biometrika, 82, 711–732. [Google Scholar]
- Gru¨nwald V and Hidalgo M (2003), “Developing inhibitors of the epidermal growth factor receptor for cancer treatment,” Journal of the National Cancer Institute, 95, 851–867. [DOI] [PubMed] [Google Scholar]
- Hadley K and Hendricks D (2014), “Use of NQO1 status as a selective biomarker for oesophageal squamous cell carcinomas with greater sensitivity to 17-AAG,” BMC Cancer, 14, 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hastings W (1970), “Monte Carlo sampling methods using Markov chain and their applications,” Biometrika, 57, 97–109. [Google Scholar]
- He X, Wang L, and Hong H (2013), “Quantile-adaptive model-free variable screening for highdimensional heterogeneous data,” Annals of Statistics, 41, 342–369. [Google Scholar]
- Henze N and Zirkler B (1990), “A class of invariant consistent tests for multivariate normality,” Communications in statistics - Theory and Methods, 10, 3595–3617. [Google Scholar]
- Holt S, Logie A, Davies B, Alferez D, Runswick S, Fenton S, Chresta C, Gu Y, Zhang J, Wu Y, Wilkinson R, Guichard S, and Smith P (2012), “Enhanced apoptosis and tumor growth suppression elicited by combination of MEK (selumetinib) and mTOR kinase inhibitors (AZD8055),” Cancer Research, 72, 1804–1813. [DOI] [PubMed] [Google Scholar]
- Hornik K, Stinchcombe M, and White H (1989), “Multilayer feedforward networks are universal approximators,” Neural Networks, 2, 359–366. [Google Scholar]
- Jiang W (2007), “Bayesian Variable Selection for High Dimensional Generalized Linear Models: Convergence Rate of the Fitted Densities,” Annals of Statistics, 35, 1487–1511. [Google Scholar]
- Johnson V and Rossel D (2012), “Bayesian Model Selection in High-dimensional Settings,” Journal of the American Statistical Association, 107, 649–660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jonsson G, Staaf J, Vallon-Christersson J, and et al. (2010), “Genomic subtypes of breast cancer identified by array-comparative genomic hybridization display distinct molecular and clinical characteristics,” Breast cancer research, 12, R42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kapetanios G, Labhard V, and Price S (2006), “Forecasting using predictive likelihood model averaging,” Economics Letters, 91, 373–379. [Google Scholar]
- Kass R and Raftery A (1995), “Bayes factors,” Journal of the American Statistical Association, 90, 773–795. [Google Scholar]
- Lawrence R and Salgia R (2010), “MET molecular mechanisms and therapiesin lung cancer,” Cell Adhesion & Migration, 4, 146–152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee A, Yau C, Giles M, Doucet A, and Holmes C (2010), “On the utility of graphics cards to perform massively parallel simulation of advanced Monte Carlo methods,” Journal of Computational and Graphical Statistics, 19, 769–789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee H, Hanibuchi M, Lim S-J, Yu H, Kim M, He J, Langley R, Lehembre F, Regenass U, and Fidler I (2016), “Treatment of experimental human breast cancer and lung cancer brain metastases in mice by macitentan, a dual antagonist of endothelin receptors, combined with paclitaxel,” NeuroOncology, 18, 486–496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li R, Zhong W, and Zhu L-P (2012), “Feature screening via distance correlation learning,” Journal of the American Statistical Association, 107, 1129–1139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang F (2005), “Bayesian neural networks for non-linear time series forecasting,” Statistics and Computing, 15, 13–29. [Google Scholar]
- Liang F, Song Q, and Yu K (2013), “Bayesian Subset Modeling for High Dimensional Generalized Linear Models,” Journal of the American Statistical Association, 108, 589–606. [Google Scholar]
- Liang F and Zhang J (2008), “Estimating FDR under general dependence using stochastic approximation,” Biometrika, 95, 961–977. [Google Scholar]
- Lin Y and Zhang H (2006), “Component selection and smoothing in multivariate nonparametric regression,” Annals of Statistics, 34, 2272–2297. [Google Scholar]
- Liu G, Huang YJ, Xiao R, Wang D, Acton TB, and Montelione1, G. T. (2010), “Solution NMR Structure of the ARID Domain of Human AT-rich Interactive Domain-Containing Protein 3A: A Human Cancer Protein Interaction Network Target,” Protein, 78, 2170–2175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu H, Lafferty J, and Wasserman L (2009), “The nonparanormal: Semiparametric estimation of high dimensional undirected graphs,” J. Mach. Learn. Res, 10, 2295–2328. [PMC free article] [PubMed] [Google Scholar]
- Lou Y, Bien J, Caruana R, and Gehrke J (2014), “Sparse partially linear additive models,” arXiv:1407.4729. [Google Scholar]
- Metropolis N, Rosenbluth A, Rosenbluth M, Teller A, and Teller E (1953), “Equation of state calculations by fast computing machines,” Journal of Chemical Physics, 21, 1087–1091. [Google Scholar]
- Mosteller F and Bush R (1954), “Selected quantitative techniques,” in Handbook of Social Psychology (eds. Lindzey G ), Addison Wesley, Cambridge, vol. 1, pp. 289–334. [Google Scholar]
- Nencioni A, Cea M, Garuti A, Passalacqua M, Raffaghello L, Soncini D, Moran E, Zoppoli G, Pistoia V, Patrone F, and Ballestrero A (2010), “Grb7 Upregulation Is a Molecular Adaptation to HER2 Signaling Inhibition Due to Removal of Akt-Mediated Gene Repression,” PLoS One, 5, e9024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okut H, Gianola D, Rosa G, and Weigel K (2011), “Prediction of body mass index in mice using dense molecular markers and a regularized neural netwok,” Genet. Res. Camb, 93, 189–201. [DOI] [PubMed] [Google Scholar]
- Park T and Casella G (2008), “The Bayesian Lasso,” Journal of the American Statistical Association, 103, 681–686. [Google Scholar]
- Prat A, Parker J, Karginova O, Fan C, Livasy C, Herschkowitz J, He X, and Perou C (2010), “Phenotypic and molecular characterization of the claudin-low intrinsic subtype of breast cancer,” Breast cancer research, 12, R68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raghu M, Poole B, Kleinberg J, Ganguli S, and Dickstein J (2017), “On the expressive power of deep neural networks,” , arXiv:1606.05336v6.
- Ravikumar P, Lafferty J, Liu H, and Wasserman L (2009), “Sparse additive models,” Journal of the Royal Statistical Society, Series B, 71, 1009–1030. [Google Scholar]
- Rodriguez P and Gianola D (2016), “Package ‘brnn’: Bayesian Regularization for feed-forward neural networks,”.
- Schapire R (1990), “The Strength of Weak Learnability,” Machine Learning, 5, 197–227. [Google Scholar]
- Scott J and Berger J (2010), “Bayes and empirical-Bayes multiplicity adjustment in the variable selection problem,” Annals of Statistics, 38, 2587–2691. [Google Scholar]
- Song Q and Liang F (2015a), “High-Dimensional Variable Selection with Reciprocal L1Regularization,” Journal of the American Statistical Association, DOI: 10.1080/01621459.2014.984812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song Q and Liang F (2015b), “A Split-and-Merge Bayesian Variable Selection Approach for Ultra-high dimensional Regression,” Journal of the Royal Statistical Society, Series B, DOI: 10.1111/rssb.12095. [DOI] [Google Scholar]
- Song Q, Wu M, and Liang F (2014), “Weak Convergence Rates of Population versus Single-Chain Stochastic Approximation MCMC Algorithms,” Advances in Applied Probability, 46, 1059–1083. [Google Scholar]
- Spiegelhalter D, Best N, Carlin B, and van der Linde A (2002), “Bayesian measures of model complexity and fit (with discussion),” Journal of the Royal Statistical Society, Series B, 64, 583–639. [Google Scholar]
- Storey J (2002), “A Direct Approach to False Discovery Rates,” Journal of the Royal Statistical Society, Series B, 64, 479–498. [Google Scholar]
- Stouffer S, Suchman E, DeVinney L, Star S, and Jr Williams R (1949), The American Soldier, Vol.1: Adjustment during Army Life, Princeton University Press, Princeton. [Google Scholar]
- Sun S, Chen W, Wang L, Liu X, and Liu T-Y (2016), “On the depth of deep neural networks: A theoretical review,” Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, 2066–2072. [Google Scholar]
- Taddy M, Gramacy R, and Polson N (2011), “Dynamic trees for learning and design,” J. Amer. Statist. Assoc, 106, 109–123. [Google Scholar]
- Tibshirani R (1996), “Regression shrinkage and selection via the LASSO,” Journal of the Royal Statistical Society, Series B, 58, 267–288. [Google Scholar]
- Wang H (2009), “Forward regression for ultrhigh dimensional variable screening,” Journal of the American Statistical Association, 104, 1512–1524. [Google Scholar]
- White G and Porter M (2014), “GPU accelerated MCMC for modeling terrorist activity,” Computational Statistics & Data Analysis, 71, 643–651. [Google Scholar]
- Yang Y and Tokdar S (2015), “Minimax-optimal nonparametric regression in high dimensions,” Annals of Statistics, 43, 652–674. [Google Scholar]
- Zhang Z, Yu Y, Xu F, Berchuck A, van Haaften-Day C, Harvrilesky L, de Bruijn H, van der Zee A, Woolas R, Jacobs I, Skates S, Chan D, and Bast RJ (2007), “Combining multiple serum tumor markers improves detection of stage I epithelial ovarian cancer,” Gynecol. Oncol, 107, 526–531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu L-P, Li L, Li R, and Zhu L-X (2011), “Model-free feature screening for ultrahigh-dimensional data,” Journal of the American Statistical Association, 106, 1464–1475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zoppoli G, Regairaz M, Leo E, Reinhold W, Varma S, Ballestrero A, Doroshow J, and Pommier Y (2012), “Putative DNA/RNA helicase schlafenl1 (SLFN11) sensitizes cancer cells to DNAdamaging agents,” Proceedings of the National Academy of Sciences USA, 109, 15030–15035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou H and Hastie T (2005), “Regularization and variable selection via the elastic net,” Journal of the Royal Statistical Society, Series B, 67, 301–320. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.