SANTIS: Sampling-Augmented Neural neTwork with Incoherent Structure for MR image reconstruction

Abstract

Purpose:

To develop and evaluate a novel deep learning-based reconstruction framework called SANTIS (Sampling-Augmented Neural neTwork with Incoherent Structure) for efficient MR image reconstruction with improved robustness against sampling pattern discrepancy.

Methods:

With a combination of data cycle-consistent adversarial network, end-to-end convolutional neural network mapping, and data fidelity enforcement for reconstructing undersampled MR data, SANTIS additionally employs a sampling-augmented training strategy by extensively varying undersampling patterns during training, so that the network is capable of learning various aliasing structures and thereby removing undersampling artifacts more effectively and robustly. The performance of SANTIS was demonstrated for accelerated knee imaging and liver imaging using a Cartesian trajectory and a golden-angle radial trajectory, respectively. Quantitative metrics were used to assess its performance against different references. The feasibility of SANTIS in reconstructing dynamic contrast-enhanced images was also demonstrated using transfer learning.

Results:

Compared to conventional reconstruction that exploits image sparsity, SANTIS achieved consistently improved reconstruction performance (lower errors and greater image sharpness). Compared to standard learning-based methods without sampling augmentation (e.g., training with a fixed undersampling pattern), SANTIS provides comparable reconstruction performance but significantly improved robustness against sampling pattern discrepancy. SANTIS also achieved encouraging results for reconstructing liver images acquired at different contrast phases.

Conclusion:

By extensively varying undersampling patterns, the sampling-augmented training strategy in SANTIS can remove undersampling artifacts more robustly. The novel concept behind SANTIS can particularly be useful for improving the robustness of deep learning-based image reconstruction against discrepancy between training and inference, an important but currently less explored topic.

INTRODUCTION

There has been much recent interest in applying deep learning to a wide range of medical imaging applications, including disease classification (1,2), tissue segmentation (3–8), and lesion detection and recognition (9–12). Deep learning also holds great promise for reconstructing undersampled MRI data, providing new opportunities to further improve the performance of rapid MRI. Preliminary studies performed over the past few years (13–22) have demonstrated the ability of deep learning-based reconstruction methods to provide improved image quality with reduced reconstruction time. Compared to conventional rapid imaging techniques, such as parallel imaging (23–25) and compressed sensing (26–28), deep learning-based reconstruction uses a data-driven approach to characterize image features and removes undersampling artifacts by inferencing features from a large image database. For example, a straightforward end-to-end mapping using convolutional neural networks (CNNs) has been shown to efficiently remove artifacts from undersampled images (16–18), translate k-space information into images (19), estimate missing k-space data (20,21), and reconstruct MR parameter maps(22). More importantly, upon completion of the CNN training for a particular application, a deep learning system can reconstruct newly-acquired undersampled images efficiently, generally in order of seconds (13–22).

In existing deep learning-based reconstruction methods, supervised training is performed using high-quality reference images and their corresponding undersampled pairs (13–22). The undersampled images are typically generated by a fixed undersampling pattern for network training, and the trained network is then applied to reconstruct new images acquired with the same undersampling pattern. While such a training strategy can achieve a favorable reconstruction performance for a pre-selected undersampling pattern, the robustness of the trained network against any discrepancy of undersampling schemes is typically poor. For example, a recent study has shown that a deviation of undersampling patterns between the training and inference can degrade image quality (29). This observation emphasizes the need for better network training strategies that can more robustly remove image artifacts from a wide variety of undersampling patterns.

The main contribution of this work is to propose a new training strategy for improving the robustness of a trained network against discrepancies of undersampling schemes that may occur between training and inference. The hypothesis was that deep learning-based reconstruction could benefit from extensively varying undersampling patterns during the training process, leading to better generalization and performance of the trained network for removing undersampling artifacts. Such a training strategy enforces sampling or k-space trajectory augmentation, providing an optimal method for highly efficient and robust image reconstruction. The technique may also be better suited for applications that employ non-repeating continuous k-space undersampling. This new framework, termed as Sampling-Augmented Neural neTwork with Incoherent Structure (SANTIS), was implemented using a novel data cycle-consistent adversarial network(30) and was evaluated in retrospectively undersampled knee and liver MR image datasets using variable-density Cartesian sampling and golden-angle radial sampling, respectively.

THEORY

CNN-Regularized Image Reconstruction

In MR image reconstruction, an image is estimated from a discrete set of k-space measurements that can be expressed as:

$$d=Ex+\epsilon$$ (1)

Here, d is a vector of length N for measured k-space data and N = N_x×N_y is the total number of k-space samples. x is the image to be reconstructed, and ε represents complex noise in the measurements. In a general case, the encoding matrix E can be expanded as:

$$E=U\Im C$$ (2)

where $\Im$ is the Fourier transform operator and C represents coil sensitivities. In the case of undersampling, U is an undersampling mask to select desired k-space data points. An SNR-optimized reconstruction can be accomplished in the least squares sense as:

$$\widehat{x}=\text{arg}\underset{x}{\text{min}}\frac{1}{2}\Vert Ex-d{\Vert }_2^2$$ (3)

where ∥.∥₂ is the l₂ norm. Eq.[3] can be poorly-conditioned with a high undersampling factor, and thus, a regularization term can be additionally incorporated as:

$$\widehat{x}=\text{arg}\underset{x}{\text{min}}\left(\frac{1}{2}\Vert Ex-d{\Vert }_2^2+\lambda \Re (x)\right)$$ (4)

The design of the penalty function $\Re$ is governed by prior knowledge about the image x, with a regularization parameter λ controlling the trade-off between the data fidelity (the left term) and prior information assumptions (the right term). In conventional MR reconstruction, $\Re$ is often chosen as

$$\Re (x)=\Vert \mathrm{T}x{\Vert }_P$$ (5)

where ∥.∥_P represents a p-norm and T is a specific transform operator, which, for example, is often selected as the wavelet transform or finite differences in the context of compressed sensing (26).

In contrast to conventional regularizations, the penalty function can be implemented by learning an end-to-end deep CNN mapping from an undersampled image to its corresponding fully sampled pair, similar to many recent proposals (13–15,17). In other words, CNN can serve as a spatial or spatial-temporal regularizer in constrained image reconstruction, and Eq.[4] can be rewritten as:

$$\widehat{x}=\text{arg}\underset{x}{\text{min}}\left(\frac{1}{2}\Vert Ex-d{\Vert }_2^2+\lambda \Vert F(x_u)-x{\Vert }_P\right)$$ (6)

Here, $F:f_{gen}(x_u\mid \theta )\to \widehat{x}$ is a generator function using a deep CNN conditioned on network parameters θ, and the x_u is an undersampled image to be reconstructed.

In a practical implementation from recent CNN reconstruction studies (14,31), a data fidelity loss can be incorporated to enforce data fidelity in combination with the CNN-regularization as shown in Figure 1. The image reconstruction, expressed in Eq.[6] can then be approximated as:

$$\widehat{F}=\text{arg}\underset{F}{\text{min}}\left({\lambda }_{loss2}{\mathbb{E}}_{x_u\sim P(x_u)}\left[{\Vert {\Phi }_{u}F(x_u)-x_u\Vert }_P\right]+{\lambda }_{loss1}{\mathbb{E}}_{x_u\sim P(x_u)}\left[{\Vert F(x_u)-x\Vert }_P\right]\right)$$ (7)

where two loss functions were generated including a CNN generator term for CNN-regularization (pixel-wise loss 1: the right term) and a data fidelity loss term for data consistency (pixel-wise loss 2: the left term). ${\Phi }_u=C^H{\Im }^{H}U\Im C$ is the undersampling encoding operator and ${\Phi }_u\widehat{x}=C^H{\Im }^{H}U\Im C\widehat{x}\to {\widehat{x}}_u$ generates undersampled images using the undersampling mask and coil sensitivities. ${\mathbf{E}}_{x_u\sim P(x_u)}[\cdot ]$ is the expectation of a probability function given x_u belongs to the data distribution of the undersampled image domain P(x_u). λ_loss1 and λ_loss2 are corresponding weighting parameters controlling the balance between the two loss terms. More specifically, the first loss term (pixel-wise loss 1) removes aliasing artifacts such that the reconstructed images look like their reference, while the second loss term (pixel-wise loss 2) ensures that the reconstructed images from the CNN generator produce undersampled images matching the acquired k-space measurements.

Figure 1.

Illustration of the SANTIS reconstruction using a data cycle-consistent adversarial network, which features three loss components. The first loss term (pixel-wise loss 1) removes aliasing artifacts such that the reconstructed image $\widehat{x}$ looks like their reference (x). The second loss term (pixel-wise loss 2) ensures that the reconstructed images from CNN generator (e.g., Residual U-Net) produce undersampled images ${\widehat{x}}_u$ matching the acquired k-space measurements (x_u). The adversarial loss term enforces a high perceptional quality for the reconstructed image to maintain image details and texture using a CNN discriminator (e.g., PatchGAN). The notation in this figure follows the main text description.

Adversarial Loss

A l₁ norm or a l₂ norm is often chosen for the pixel-wise loss terms (loss 1 and 2) of Eq.[7] in most studies. While either of these two norms can ensure good reconstruction performance by suppressing noise and artifacts, such a reconstruction scheme has been demonstrated to be suboptimal for restoring undersampled images with a ‘natural’ appearance as in corresponding fully sampled images (14,15). Several studies have shown that using CNN mapping only with pixel-wise losses can result in image blurring, detail loss, and degraded perceptional quality (14,15). Therefore, Generative Adversarial Network (GAN) has been recently proposed to overcome the drawbacks of l₁ or l₂ norm, where an adversarial loss is used to promote image texture preservation in image restoration (32). In the context of image reconstruction as shown in Eq.[7], an adversarial loss can be incorporated into the CNN generator as an additional loss term to promote texture preservation as shown in Figure 1. In other words, in addition to the CNN generator function F, another multiple layer CNN discriminator D:f_dis(x∣δ) → 1 conditioned on network parameters δ is designed to distinguish reconstructed images versus corresponding reference images in the fully sampled image domain P(x). Mathematically, this discriminator D(x) outputs a scalar representing the probability that x comes from the fully sampled image domain rather than the CNN generator output F(x_u). The adversarial loss is formatted as:

$$L_{\mathit{gan}}(F,D)={\mathbf{E}}_{x\sim P(x)}\left[\log D(x)\right]+{\mathbf{E}}_{x_u\sim P(x_u)}\left[\log (1-D(F(x_u)))\right]$$ (8)

Data Cycle-Consistent Adversarial Network

Following all loss terms mentioned above, a Data Cycle-Consistent Adversarial Network (30) can be formulated for reconstructing undersampled MR images using a multi-loss joint training model as shown in Figure 1. This model consists of a CNN generator that generates a pixel-wise loss term (loss 1) and an adversarial loss term as CNN regularization. An additional data fidelity loss path creates another pixel-wise loss term (loss 2) for enforcing data fidelity. Therefore, a full objective function can be written as:

$$\begin{gathered} L_{\mathit{full}}=L_{\mathit{cyc}}+L_{\mathit{gan}}={\lambda }_{loss2}{\mathbf{E}}_{x_u\sim P(x_u)}\left[{\Vert {\Phi }_{u}F(x_u)-x_u\Vert }_P\right]+{\lambda }_{loss1}{\mathbf{E}}_{x_u\sim P(x_u)}\left[{\Vert F(x_u)-x\Vert }_P\right] \\ +{\lambda }_{\mathit{gan}}\left({\mathbf{E}}_{x\sim P(x)}\left[\log D(x)\right]+{\mathbf{E}}_{x_u\sim P(x_u)}\left[\log (1-D(F(x_u)))\right]\right) \end{gathered}$$ (9)

Here, λ_gan is a weighting factor to control the contribution of the GAN regularization to the reconstruction. The overall aim of the training is to solve the full objective function in a two-player minimax fashion (32) as:

$$\widehat{F},\widehat{D}=\text{arg}\underset{F}{\text{min}}\underset{D}{\max }{L}_{\mathit{full}}(F,D)$$ (10)

Namely, F aims to minimize this objective function against the adversary D that seeks to maximize it. In other words, F tries to reconstruct undersampled images to look similar to corresponding fully sampled images, while D aims to distinguish reconstructed images from real fully sampled images. As demonstrated in the studies for natural image-to-image translation (32–34), successful training using such a competing scheme can result in an optimal CNN generator capable of generating artificial images indistinguishable from the original images. It should be noted that optimizing Eq.[10] aims to search for optimal network parameters $\widehat{\theta }$ for $F:f_{gen}(x_u\mid \theta )\to \widehat{x}$during the training phase, so that once the training is completed and satisfied, $\widehat{\theta }$ can be fixed for the CNN generator and directly applied to reconstruct a new undersampled image by using the CNN mapping F to the undersampled image as:

$$x_{cnn}=f_{gen}(x_u\mid \widehat{\theta }),x_u\in P(x_u)$$ (11)

Sampling-Augmented Data Cycle-Consistent Adversarial Network

To strengthen the robustness of the trained network towards sampling pattern discrepancy, the training of Eq.[10] can be further augmented in a manner where x_u is generated to have different artifact patterns at each training iteration. Once the training is successful, the trained network is capable of learning a variety of aliasing artifact patterns and can then be generalized towards removing a broad range of artifacts. This can be achieved by varying the undersampling mask for generating each training data pair throughout the entire training iterations. Eq.[9] is then updated as:

$$\begin{gathered} L_{\mathit{full}}=L_{\mathit{cyc}}+L_{\mathit{gan}}={\lambda }_{loss1}{\mathbf{E}}_{x_{u,ij}\sim P(x_u)}\left[{\Vert {\Phi }_{u,ij}F(x_{u,ij})-x_{u,ij}\Vert }_P\right]+{\lambda }_{loss2}{\mathbf{E}}_{x_{u,ij}\sim P(x_u)}\left[{\Vert F(x_{u.ij})-x\Vert }_P\right] \\ +{\lambda }_{\mathit{gan}}\left({\mathbf{E}}_{x\sim P(x)}\left[\log D(x)\right]+{\mathbf{E}}_{x_{u,ij}\sim P(x_u)}\left[\log (1-D(F(x_{u,ij})))\right]\right) \end{gathered}$$ (12)

where i denotes the i^th image in the training dataset and j denotes the j^th training iteration. In other words, x_u has a different aliasing artifact pattern in each image of the dataset (x_u,i), and the artifact is also changing for different iterations (x_u,ij). Accordingly, the undersampling operator Φ_u,ij is rewritten as:

$$\begin{gathered} {\Phi }_{u.ij}=C^H{\Im }^H{U}_{ij}\Im C \\ {\Phi }_{u.ij}\widehat{x}=C^H{\Im }^H{U}_{ij}\Im C\widehat{x}\to {\widehat{x}}_{u.ij} \end{gathered}$$ (13)

to reflect the variation of undersampling patterns U_ij during training.

METHODS

In-Vivo Image Datasets

The study was performed in compliance with the Health Insurance Portability and Accountability Act (HIPPA) regulations and was approved by the local Institutional Review Boards (IRB). Knee datasets were acquired on 30 patients undergoing a clinical knee MRI examination, with a waiver of written informed consent. The datasets were acquired on a 3.0T scanner (Signa Premier, GE Healthcare, USA) equipped with an 18-element knee coil array using a clinical two-dimensional (2D) coronal proton density-weighted fast spin-echo (Cor-PD-FSE) sequence. Relevant imaging parameters included: matrix size = 420×448, FOV = 15×15 cm², TR/TE = 2500/20ms, flip angle = 111°, echo train length = 5, slice thickness = 3mm, number of slices = 30-38, and scan time of 210 seconds

Liver datasets were acquired on 63 patients undergoing a clinical liver MRI examination, with written informed consent. The datasets were acquired approximately 20 minutes after the injection of Gd-EOB-DTPA contrast (Eovist) on a 3.0T scanner (TimTrio, Siemens Medical Systems, Germany) equipped with a 12-element body matrix coil using a prototype fat-saturated stack-of-stars golden-angle radial sequence (35,36). Relevant imaging parameters included: matrix size = 256×256, FOV = 33×33cm², TR/TE = 3.40/1.68ms, flip angle = 10°, slice thickness = 5mm, number of slices = 44, 80% partial Fourier along the slice dimension, 1000 spokes acquired in each partition, and scan time of 178 seconds.

In addition, a dynamic contrast-enhanced liver image dataset was also acquired on one healthy volunteer, with written informed consent. This dataset was acquired during contrast injection using the same golden angle radial sequence with a similar protocol as previously described except 1222 spokes for each partition and longer scan time of 190 seconds to ensure capture of contrast dynamics from a pre-contrast phase to a delayed phase.

Implementation of Neural Network

A U-Net architecture (Supporting Information Figure S1) with residual learning was adapted from previous image-to-image translation studies (5,34) (https://github.com/phillipi/pix2pix) for the CNN generator (F) to map undersampled image domain into corresponding fully sample image domain. This U-Net structure is composed of an encoder network and a decoder network with multiple shortcut connections between them (37). The encoder is used to achieve efficient data compression while probing robust and spatial invariant image features of input images. A decoder network with a mirrored structure of the encoder is applied for restoring image features and increasing image resolution using the output of the encoder network. Multiple shortcut connections are incorporated to concatenate entire feature maps from encoder to decoder to enhance mapping performance. Residual learning is implemented to further boost learning robustness and accuracy (38,39). Such a network structure and its variants have shown promising results for image-to-image translation in many recent deep learning studies (5,37–39). For the adversarial configuration, a network architecture developed in PatchGAN (34) was used for the discriminator network (D), which aims to differentiate real from artificial images in the adversarial process using image patch-based assessment on input images. An illustration of the applied PatchGAN is shown in Supporting Information Figure S1. Such a patch-level discriminator architecture provides efficient network training with fewer network parameters and has demonstrated favorable results at differentiating real from artificial images in many recent GAN studies (5,34,40,41).

Network Training

In our framework, the complex MR image $x\in {\mathbb{C}}^M$ is converted into a new representation $x\in {\mathbb{R}}^{2M}$ so that the real and imaginary components are treated as two individual image channels for the network input (14,17). Twenty-two of the 30 knee datasets were randomly selected and used for training the deep learning network, while the remaining eight datasets were used for evaluation. Similarly, 55 of the 63 liver datasets were randomly selected and used for training, while the remaining eight datasets were used for evaluation.

The network weights for the training were initialized using the initialization scheme as described in (42) and were updated using Adam algorithm (43) with a fixed learning rate of 0.0002. The training was performed in a mini-batch manner with three image slices in a single mini-batch (5). The l₁ norm was applied for the pixel-wise loss terms in Eq. [12] to promote image sharpness following recent GAN studies (15). Total iteration steps corresponding to 200 epochs were carried out to ensure convergence of the training (see Supporting Information Figure S2). During each iteration, a two-step training strategy was applied where the CNN generator (F) and adversarial discriminator (D) were updated alternatively (5). After qualitative evaluation with a broad range of combinations, the parameters for the weight factors in the full objective function of Eq. [12] were empirically selected as λ_loss1 = 10, λ_loss2 = 10 and λ_gan =0.1 for our study.

All the proposed algorithms were implemented in Python (v2.7, Python Software Foundation, Wilmington, DE). The CNNs were designed using the Keras package (44) running Tensorflow computing backend (45) on a 64-bit Ubuntu Linux system. All the training and evaluation were performed on a computer server with an Intel Xeon W3520 quad-core CPU, 32GB RAM, and an Nvidia GeForce GTX 1080Ti graphic card with a total of 3584 CUDA cores and 11GB GDDR5 RAM.

Fixed Training vs. Sampling-Augmented Training

Two training strategies were investigated in the study for both knee and liver imaging, including 1) the fixed training strategy (referred to as CNN-Fix hereafter) and 2) the sampling-augmented training strategy (SANTIS).

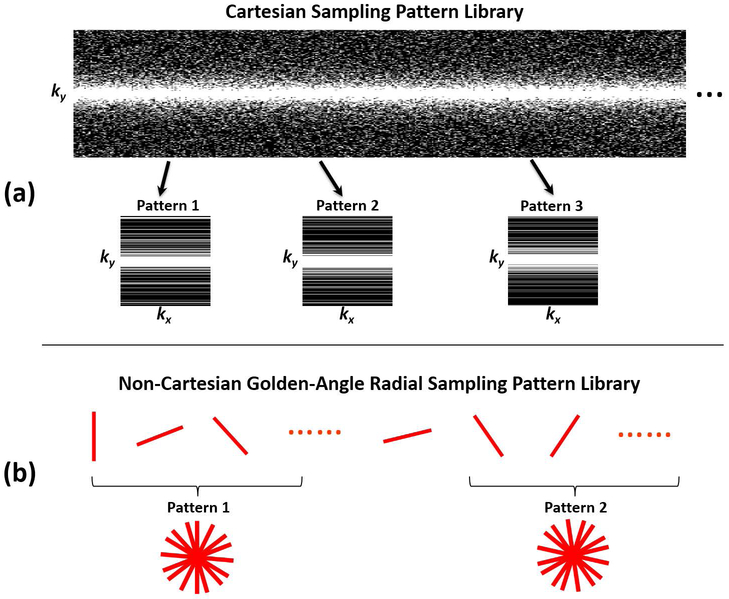
A library of one-dimensional (1D) variable-density Cartesian random undersampling patterns (26), consisting of 3000 different undersampling masks, were generated for the knee datasets as shown in Figure 2a. Each random sampling pattern was generated using Monte-Carlo simulation with a fixed probability density function, and corresponding sampling pattern lines were selected randomly according to this density. For each undersampling mask, the k-space center (5% of the total measurements) was consistently fully sampled. For the training of CNN-Fix, only the first undersampling mask was used throughout the entire training process as outlined in Eq. [9]. For the training of SANTIS, in contrast, an undersampling mask was randomly selected from this library for each image in each training iteration, as shown in Eq. [12]. This operation ensures that different artifacts can be created for each image at each training iteration so that the network can learn a wide range of undersampling artifact structures during training. As a pre-processing step, all the knee datasets were compressed into eight virtual coils to fit into GPU memory, and corresponding coil sensitivity maps were estimated using the adaptive combination approach (46). To test the acceleration performance, two acceleration rates (R=3 and R=5) were investigated for knee imaging. In addition, experiments for the uniform Cartesian undersampling patterns were also performed and described in the Supporting Information.

Figure 2.

Schematic demonstration of the undersampling patterns used in the study. (a) Examples of the 1D variable-density Cartesian random undersampling patterns used for knee imaging. (b) Example of the gold-angle radial undersampling masks used for liver imaging. The undersampling mask was varying for each iteration during the network training to augment the training data for SANTIS framework.

The training for the liver datasets was performed using the following steps. First, all the datasets were compressed into four virtual coils, and a multi-coil three-dimensional (3D) liver image (e.g., without coil combination) was reconstructed using a standard gridding algorithm for each dataset. Corresponding coil sensitivity maps were estimated using the adaptive combination approach (46). Second, a library of radial trajectories consisting of 3000 consecutive golden-angle rotations was calculated, from which different undersampled golden-angle patterns could then be generated by combining a subset of consecutive radial trajectories (89 consecutive spokes in this study). Third, using these radial undersampling patterns, corresponding undersampled radial spokes and radial images could then be generated using non-uniform fast Fourier transform (NUFFT) and inverse NUFFT, respective. Fourth, similar to knee imaging, the training of CNN-Fix was performed with only the first undersampling pattern (e.g., the 1^st to the 89^th spokes), while the training of SANTIS was performed by random selection of a radial undersampling pattern from the trajectory library. Due to the GPU memory limit, the 3D liver datasets were treated as multi-slice 2D images, so that both the training and reconstruction were performed slice-by-slice. As a pre-processing step, self-calibrating GRAPPA Operator Gridding (GROG) (47,48) was applied to all the generated reference-undersampled radial data pairs, so that the subsequent training could be performed entirely on a Cartesian grid.

Evaluation of Reconstruction Methods

In the first experiment, the robustness of the different training strategies was compared. Specifically, the trained networks from CNN-Fix and SANTIS were applied to reconstruct (the inference step) undersampled images generated with two undersampling masks/patterns, including the one used for CNN-Fix training (denoted as MaskC1 for knee imaging and MaskR1 for liver imaging hereafter) and a newly-generated one not used for training (denoted as MaskC2 for knee imaging and MaskR2 for liver imaging hereafter). It was ensured that both undersampling patterns were not included in the training of SANTIS to fully assess its robustness.

In the second experiment, both CNN-Fix and SANTIS were compared with conventional reconstruction methods, including a combination of compressed sensing and parallel imaging (CS-PI) (49) and a recently proposed Variational Network (VN) (13,29) that represents the current state-of-the-art deep learning-based reconstruction approach. For the CS-PI method, reconstruction was performed slice by slice, and coil sensitivity maps were generated as previously described. A Daubechies-4 wavelet transform was selected as the sparsifying transform. The VN method was implemented using the source code provided by the original developers (https://github.com/VLOGroup/mri-variationalnetwork) using reconstruction parameters previously configurated for accelerated knee imaging (13,29). The VN approach was used as a reference for knee imaging as it has been previously described for this application. The undersampling patterns MaskC1 and MaskR1 were used for the comparison for knee and liver imaging, respectively.

Reconstruction performance was evaluated using quantitative metrics focusing on different aspects of the reconstruction quality. The normalized Root Mean Squared Error (nRMSE) was used to assess the overall reconstructed image errors. The Structural Similarity Index (SSIM) was used to estimate the overall image similarity with respect to the reference. The image sharpness was evaluated by calculating the relative reduction of Tenengrad measure (50) between the reconstructed and reference images, where local characteristics of pronounced image edges were explored. Differences were evaluated using a paired non-parametric Wilcoxon signed-rank test with statistical significance defined as p-value less than 0.05.

In the third experiment, the trained network was evaluated on the dynamic contrast-enhanced liver dataset with retrospective undersampling to test the robustness of SANTIS for reconstructing images with different image contrasts. Specifically, the liver dataset was reconstructed using RACER-GRASP (51) with a temporal resolution of 15 seconds, resulting in a pre-contrast phase, three arterial phases, two venous phases, and several delayed phases. Undersampled radial images were then generated from these reconstructed contrast phases using different newly-generated golden-angle radial sampling patterns with 89 consecutive spokes each.

RESULTS

Figure 3 shows a comparison of different reconstruction methods for a representative knee dataset at R=3 with MaskC1. Compared to the CS-PI, learning-based reconstruction methods (VN, CNN-Fix-MaskC1, and SANTIS) provided better removal of aliasing artifacts in the bone and cartilage, as illustrated in the zoomed images. SANTIS showed the best reconstruction performance, creating a high-quality reconstructed image. A sharp texture, as indicated by the green arrows, was better preserved in SANTIS compared to the other methods. Similar result for uniform undersampling patterns is shown in Supporting Information Figure S4.

Figure 3.

Representative examples of knee images obtained using the different reconstruction methods at R=3. SANTIS showed the highest image quality with favorable preservation of tissue sharpness (green arrows) and texture comparable to the reference.

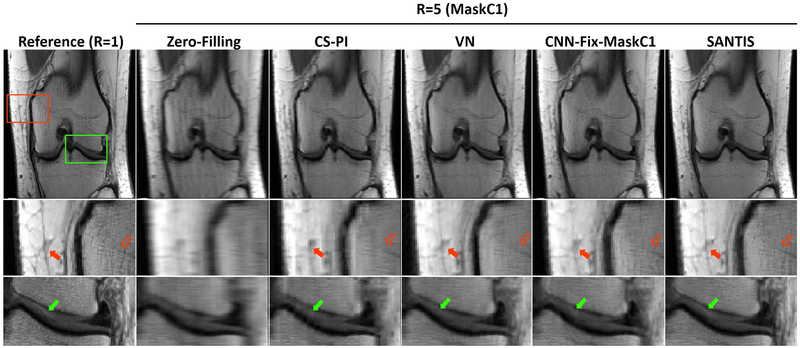
Figure 4 shows a comparison of different reconstruction methods for another knee dataset at R=5. Similar improvement in image quality was observed for SANTIS, with better representation of the layered structure of the femoral and tibial cartilage (green arrows). At this acceleration, CS-PI failed to effectively reconstruct the undersampled image, and both VN and CNN-Fix suffered from notable residual blurring and loss of image details, as shown by the red arrows in the zoomed bone and subcutaneous fat regions.

Figure 4.

Representative examples of knee images obtained using the different reconstruction methods at R=5. SANTIS showed the highest image quality with a better representation of the layered structure of the femoral and tibial cartilage (green arrows) with favorable preservation of tissue sharpness and texture (red arrows) comparable to the reference.

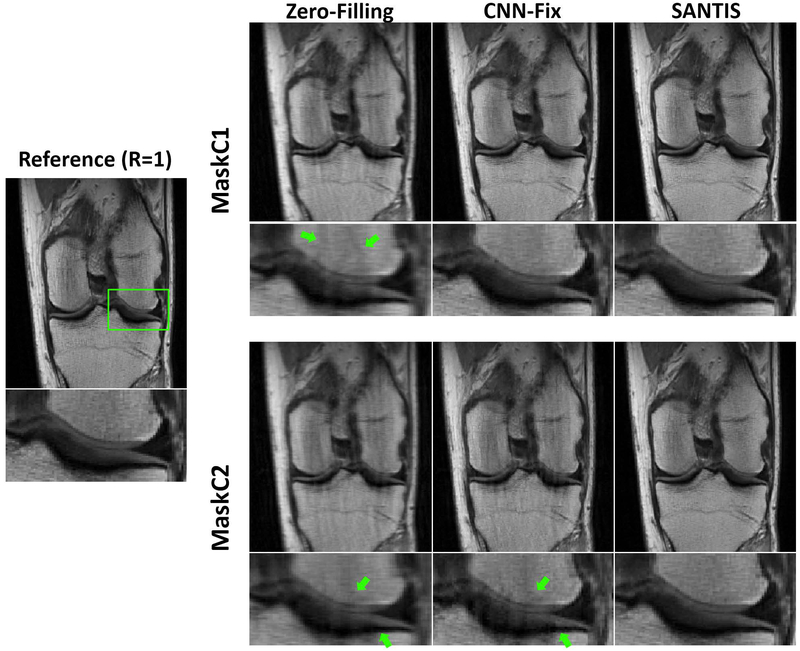
Figure 5 shows knee images comparing CNN-Fix with SANTIS using both MaskC1 (top row) and MaskC2 (bottom row) at R=3. As described in the Methods, MaskC1 was only used for the training of CNN-Fix training, while neither MaskC1 or MaskC2 were used for the SANTIS training. As expected, MaskC1 and MaskC2 created different aliasing artifacts, as highlighted by the green arrows in the zero-filling images. While CNN-Fix-MaskC1 showed decent image quality, CNN-Fix-MaskC2 failed to effectively reconstruct the undersampled image generated with MaskC2, with noticeable residual aliasing artifacts in the zoomed image, as indicated by the green arrows. In contrast, SANTIS demonstrated consistent reconstruction performance for both MaskC1 and MaskC2. Similar result for uniform undersampling patterns is shown in Supporting Information Figure S5.

Figure 5.

Evaluation of reconstruction robustness at different undersampling masks for MaskC1 and MaskC2. The fixed training CNN-Fix failed to reconstruct MaskC2 with noticeable residual artifacts, as indicated by the green arrows. SANTIS provided a consistent high-quality reconstruction for both masks.

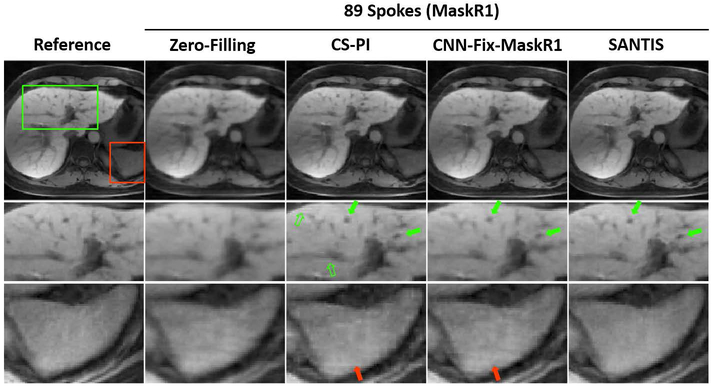
Figure 6 shows a comparison of different reconstruction methods for radial liver imaging with MaskR1. Similar to knee imaging, SANTIS achieved the best image quality with better removal of streaking artifacts and preservation of tissue texture. CS-PI generated pseudo residual structures (hollow green arrows), which were potentially caused by the use of wavelet constraint. Meanwhile, CNN-Fix-MaskR1 suffered from noticeable residual blurring as indicated by the green arrows. For both CS-PI and CNN-Fix-MaskR1, residual streaking artifacts were present, as illustrated by the red arrows in the zoomed region.

Figure 6.

A representative comparison of different reconstruction methods in radial liver imaging with MaskR1. SANTIS showed the highest image quality with successful removal of streaking artifacts and with favorable preservation of tissue sharpness and texture. CS-PI showed pseudo residual structures (hollow green arrows). Meanwhile, CNN-Fix-MaskR1 suffered from noticeable residual blurring, as indicated by the green arrows. For both CS-PI and CNN-Fix-MaskR1, residual streaking artifacts could be noted, as highlighted by the red arrows in the zoomed region.

Figure 7 shows zoomed liver images with a tumor (green box in the reference image) comparing CNN-Fix and SANTIS using both MaskR1 and MaskR2. CNN-Fix-MaskR1 and CNN-Fix-MaskR2 suffered from residual streaking artifacts. SANTIS provided improved image quality for both sampling patterns, with a reduced level of residual streaking artifacts and a better delineation of the tumor. Corresponding full FOV images of this comparison are shown in Supporting Information Figure S3.

Figure 7.

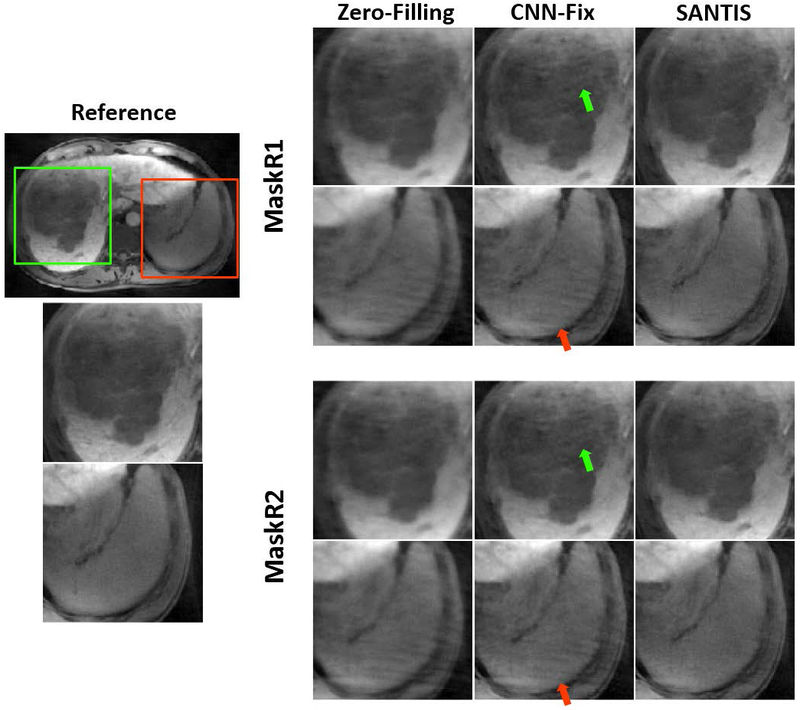
Example of zoomed liver images with a tumor comparing CNN-Fix and SANTIS using both MaskR1 and MaskR2 for inference. Both CNN-Fix-MaskR1 and CNN-Fix-MaskR2 suffered from residual artifacts (red arrows), while SANTIS consistently showed improved image quality for both MaskR1 and MaskR2, with a reduced level of residual streaking artifacts and a delineation of the tumor that is closer to the reference.

The group-wise quantitative analyses further confirmed the qualitative observations in the exemplary figures. The comparisons of reconstruction methods using different metrics, including the nRMSE, SSIM and Tenengrad, are summarized in Table 1 and Table 2 for all the testing knee and liver datasets. For knee imaging at both R=3 and R=5 (Table 1), all the deep learning-based reconstruction methods (VN, CNN-Fix-MaskC1, and SANTIS) achieved significantly better image quality (p<0.05) than CS-PI. Among different deep learning-based methods, SANTIS achieved significantly better image quality than CNN-Fix-MaskC1 for nRMSE (p=0.003) and Tenegrad (p=0.001) at R=3 and significantly better image quality (p<0.003) than CNN-Fix-MaskC1 at R=5. Image quality was significantly degraded (p<0.003) from CNN-Fix-MaskC1 to CNN-Fix-MaskC2 when an unmatched undersampling mask (MaskC2) was used for inference, while SANTIS achieved more consistent performance for both MaskC1 and MaskC2 (p>0.05).

Table 1.

Quantitative metrics comparing the reference fully sampled images and the reconstructed images from different reconstruction methods for Cartesian knee imaging. Results were averaged over the eight test datasets and represent mean value ± standard deviation. SANTIS achieved the highest and most robust reconstruction performance at both R=3 and 5.

Method		R=3				R=5
		nRMSE [%]	SSIM [%]	Tenengrad [%]	Average Recon Time [s]	nRMSE [%]	SSIM [%]	Tenengrad [%]	Average Recon Time [s]
ZF		9.87 ± 1.16	82.25 ± 3.77	43.75 ± 2.69	0.001	13.58 ± 1.75	75.38 ± 4.92	55.19 ± 3.52	0.001
CS-PI		6.74 ± 0.63	87.64 ± 2.22	15.66 ± 1.99	2.12	10.91 ± 1.13	83.78 ± 3.80	33.01 ± 2.99	2.21
VN		6.01 ± 1.12	90.21 ± 2.54	10.11 ± 2.06	0.11	10.61 ± 1.67	85.11 ± 3.96	20.13 ± 3.10	0.12
CNN-Fix	MaskC1 (match training)	5.67 ± 0.94	90.78 ± 2.89	10.30 ± 2.34	0.06	10.48 ± 1.41	85.06 ± 4.79	19.63 ± 4.10	0.06
	MaskC2 (unmatch training)	6.92 ± 1.09	86.33 ± 2.91	10.67 ± 2.86	0.06	11.56 ± 1.94	82.98 ± 4.84	20.59 ± 4.95	0.06
SANTIS	MaskC1	5.15 ± 1.07	91.41 ± 2.82	8.67 ± 2.45	0.06	9.60 ± 1.81	89.06 ± 4.97	17.29 ± 3.79	0.06
	MaskC2	5.10 ± 1.02	91.96 ± 2.90	8.51 ± 2.38	0.06	9.66 ± 1.40	88.66 ± 4.62	17.11 ± 3.84	0.06

Table 2.

Quantitative metrics comparing the reference fully sampled images and the reconstructed images from different reconstruction methods for golden-angle radial liver imaging. Results were averaged over the eight test datasets and represent mean value ± standard deviation. SANTIS achieved the highest and most robust reconstruction performance.

Method		89 spokes
		nRMSE [%]	SSIM [%]	Tenengrad [%]	Average Recon time [s]
ZF		11.69 ± 1.39	85.80 ± 2.38	37.98 ± 2.92	0.001
CS-PI		9.50 ± 1.56	87.42 ± 3.14	3.55 ± 2.75	2.32
CNN-Fix	MaskR1 (match training)	9.00 ± 1.32	91.07 ± 2.27	6.16 ± 2.33	0.06
	MaskR2 (unmatch training)	9.29 ± 1.32	89.80 ± 2.24	6.76 ± 2.43	0.06
SANTIS	MaskR1	8.82 ± 1.31	92.66 ± 2.00	2.00 ± 2.72	0.06
	MaskR2	8.78 ± 1.29	92.17 ± 2.00	1.77 ± 3.19	0.06

For liver imaging (Table 2), CNN-Fix-MaskR1 and SANTIS also achieved significantly better image quality (p<0.001) than CS-PI for nRMSE and SSIM. However, different from Cartesian imaging, the results of CNN-Fix-MaskR2 was only marginally (p= 0.01 for nRMSE and SSIM; p=0.03 for Tenengrad) degraded compared to CNN-Fix-MaskR1, which was likely due to the more incoherent undersampling behavior of radial sampling. Nevertheless, SANTIS produced significantly better image quality than CNN-Fix-MaskR1 for SSIM (p=0.01) and Tenengrad (p=0.001).

For both knee and liver imaging, although SANTIS was better than CNN-Fix in general, there was no significant difference between SANTIS and CNN-Fix-MaskC1 for SSIM (p=0.1) in knee datasets at R=3 and there was no significant difference between SANTIS and CNN-Fix-MaskR1 for nRMSE (p=0.07) in liver imaging. These observations indicated that CNN-Fix can provide reconstruction quality that is statistically comparable to SANTIS at certain aspects. Regarding reconstruction time, deep learning-based methods provided faster reconstruction speed compared to CS-PI. Both SANTIS and CNN-Fix reconstruction could be completed in approximately 60ms per image slice.

Figure 8 demonstrates the performance of SANTIS for reconstructing accelerated dynamic contrast-enhanced liver images at different contrast phases. Although the SANTIS training was performed using images acquired in a delayed contrast phase, the method was able to effectively reconstruct images in a different contrast phases (e.g., pre-contrast phase, arterial phase, or venous phase) without affecting image contrast. The recovery of image quality from the zero-filling results could be clearly noted.

Figure 8.

Examples demonstrating the performance of SANTIS in reconstructing accelerated dynamic contrast-enhanced liver images at different contrast phases. SANTIS effectively reconstructed images at a different contrast phase (e.g., pre-contrast phase, arterial phase, or venous phase) without affecting image contrast, and the recovery of image quality from the zero-filling results could be clearly noted.

DISCUSSION

The main contribution of this work is a new training strategy for improving the robustness of a trained network against discrepancies of undersampling schemes that may occur between training and inference. The performance of SANTIS was demonstrated for accelerating Cartesian-based knee imaging and radial-based liver imaging by comparing with fully sampled references images and different reference reconstruction approaches. Utilizing a network architecture combining end-to-end CNN mapping, data fidelity enforcement, and adversarial training using GAN, the SANTIS approach additionally performs an extensive variation of undersampling patterns during training, referred to as sampling or k-space trajectory augmentation. Such a training strategy allows the network to explore a variety of aliasing artifact structures during the training process, thus providing more effective and robust removal of undersampling artifacts during reconstruction compared to network trained with a fixed undersampling pattern, as demonstrated for the accelerated knee and liver imaging in this work. Moreover, the SANTIS framework might be particularly useful in imaging applications where a non-repeating sampling scheme is performed. An example of this application scenario is the combination of continuous golden-angle radial sampling scheme(35,52) with SANTIS, in which a trained network can be employed to reconstruct undersampled images acquired with varying patterns in different time points, as demonstrated for the accelerated liver imaging in this study. Meanwhile, the SANTIS framework may also be useful to better handle trajectory variations caused by system imperfections (e.g. eddy current and field inhomogeneity) that are often different from scanner to scanner.

Despite the recent interest in deep learning-based reconstruction, most existing work has focused on improving reconstruction accuracy, applicability, and efficiency (13–21). The robustness of the reconstruction methods, despite its importance, has been less studied but remains an essential component in the emerging era of deep learning-based reconstruction. Here, a general open question is whether a trained network that performs well on one image dataset can be effectively used for reconstructing different image datasets with varying image contrasts, noise levels, imaging hardware, or acquisition protocols. A pilot study by Knoll et al. has investigated this question using a variational network (29). Although their findings were insightful, a practical solution was not provided. The SANTIS framework represents a first attempt to solve this challenging question in deep learning-based reconstruction. Although our current study focused on the robustness of acquisition trajectories, the framework could be potentially extended to handle different types of image contrasts and even different noise levels.

The performance of CNN-Fix and SANTIS was compared for accelerated knee imaging using Cartesian trajectories and accelerated liver imaging using radial trajectories. While SANTIS achieved relatively consistent performance, our results found that the differences between CNN-Fix-MaskC1 and CNN-Fix-MaskC2 were more pronounced than the differences between CNN-Fix-MaskR1 and CNN-Fix-MaskR2. This can be attributed to the fact that radial sampling is more incoherent, resulting in more benign undersampling artifacts. As a result, the change of undersampling mask has less of an influence on radial sampling than Cartesian sampling. Our results also showed that the performance of SANTIS was better than CNN-Fix for both Cartesian and radial sampling in general. The superior performance of SANTIS may be due to two factors. On the one hand, when the number of training datasets is relatively small, successful training does not ensure good reconstruction performance in the testing datasets. Although datasets were acquired on the same organ, corresponding images likely show substantial variations between patients. Thus, when image features are limited, the network may be over-adapted to the training datasets and may not be well-generalized to the testing datasets. The variation of undersampling patterns in SANTIS creates abundant image features, which allow the trained network to better characterize undersampling artifacts for improved image reconstruction. On the other hand, the variation of the undersampling pattern can introduce additional incoherence, thereby facilitating better recognition of undersampled artifacts from underlying image structure. This is similar to the effect of time-varying incoherent sampling in temporal compressed sensing methods (26) and randomized acquisitions in MR fingerprinting (53). However, it should be noted that CNN-Fix also yielded comparable results to SANTIS at certain aspects, indicating that the sampling augmentation might have preferably more contribution to certain image features than others. It is also anticipated that the effectiveness of the data augmentation in image reconstruction is dependent on the deep learning model complexity, the training accuracy and the data size. Further investigations to better understand the comprehensive relationship of the reconstruction improvement via sampling augmentation and penitential affecting factors are needed in future work.

This study also investigated whether the SANTIS framework could be used for reconstructing liver images acquired in different contrast phases during dynamic contrast-enhanced imaging. Our proof-of-concept investigation on a single patient showed encouraging results for reconstructing a rapid contrast wash-in phase (e.g., arterial phase) image using image features learned from a delayed phase image. This suggests the potential to reconstruct accelerated dynamic contrast-enhanced images using transfer learning. Our example showed that SANTIS is capable of learning essential image features that are uniquely dependent on the undersampling pattern with the reconstruction less affected by the change in image contrast caused by contrast injection. In addition to the sampling-augmented training, such performance is also partly due to the use of a combination of residual learning and data fidelity loss. The data fidelity consistency ensures that the reconstructed image matches the acquired undersampled measurement. The residual learning strategy aims to directly subtract image artifacts from undersampled input images, which is advantageous in identifying artifacts without affecting image contrast and anatomy (38,39). However, additional studies on larger image datasets are needed to more thoroughly investigate the applicability and utility of this intriguing feature of SANTIS.

The application of adversarial training has proven to be quite successful in preserving perceptional image structure and texture in reconstructed images, as shown in (14,15). In contrast to the reconstruction methods using solely pixel-wise losses that may alter underlying image texture and noise spectrum, the reconstructed images using adversarial loss is more advantageous for maintaining a visually plausible image appearance. The adversarial learning ensures that the restored images fall into the same data distribution as the fully sampled reference images in a transformed high dimensional image manifold (32,54). The data cycle consistency enforces data fidelity and further prevents degradation of the adversarial process from generating hallucinated image features (33). The combination of these two components in SANTIS imposes both high-quality image feature learning and information consistency to provide efficient and accurate CNN end-to-end mapping. Although the data cycle-consistent network implemented in the current study is similar to that in our previous report (30), the intriguing contribution of this work is the idea of SANTIS, which is expected to be a generalizable framework that can be combined with other network structures. Moreover, our experiments were performed on multi-coil k-space data in both Cartesian and golden-angle radial trajectories in the context of parallel imaging, which is also different from prior works that have used adversarial training on simulated single-coil k-space datasets. Further investigation will also focus on incorporating dedicated network structures (such as deep cascade network(17), KIKI-net(20) and RAKI(21)) into the data cycle-consistent network to maximize the benefits of both the database feature learning and case-specific feature estimation with multi-coil data.

Our study has several limitations. First, although the SANTIS training was performed using a library of different undersampling patterns, they were generated to have the same variable-density distribution in Cartesian imaging. The robustness of the trained network for reconstructing a completely different sampling scheme remains to be explored. However, it is straightforward to extend the SANTIS training to incorporate different undersampling schemes with varying distributions of sampling and different acceleration rates, so that the generalization of the network can be further extended. However, such a training scheme may require an increased number of iterations to achieve convergence. Second, our study did not analyze the speed of training convergence between CNN-Fix and SANTIS. For both networks, the training was performed with a sufficient number of epochs to ensure training convergence. Thus, further studies are needed to evaluate the influence of sampling-augmented training and training parameters on convergence speed. Third, the reconstruction parameters, as shown in Eq. [12], were empirically determined in our study. The weight of the GAN regularization, in particular, is vital to ensure good reconstruction performance (14,15). However, the selection of reconstruction parameters is not only a challenge for our work but remains an open question in constrained image reconstruction in general. Finally, due to the need for large training datasets, the SANTIS approach was evaluated on a relatively small number of knee and liver image testing datasets and only a single dynamic contrast-enhanced liver testing dataset. Additional studies with larger testing datasets are needed to further evaluate SANTIS before the approach can be used in clinical practice to accelerate knee and liver imaging.

CONCLUSIONS

SANTIS represents a novel concept for deep learning-based image reconstruction. With sampling or k-space trajectory-augmented training by extensively varying undersampling pattern, SANTIS can recognize more aliasing artifact structures and thereby provide more robust and effective removal of image artifacts. The SANTIS framework can be particularly useful for improving the robustness of deep learning-based image reconstruction against discrepancies of undersampling schemes that may occur between training and inference.

Supplementary Material

Supp figS1-5

Supporting Information Figure S1: Illustration of the residual U-Net and PatchGAN implemented in SANTIS for end-to-end CNN mapping and adversarial training. The U-Net structure consists of an encoder network and a decoder network with multiple shortcut connection (e.g., concatenation) between them to enhance mapping performance. The abbreviations for the CNN layers include BN for Batch Normalization, ReLU for Rectified Linear Unit activation, Conv for 2D convolution, and Deconv for 2D deconvolution. The parameters for the convolution layers are labeled in the figure as image size @ the number of 2D filters.

Supporting Information Figure S2: Evolution of different loss components, including the discriminator loss (First part of L_gan term in Eq. [9]), the generator loss (Second part of L_gan term in Eq. [9]) and the pixel-wise image loss (L_cyc term in Eq. [9]) at R=3 and with mini-batch size of 3 for a knee dataset. The generator loss is trying to compete with the discriminator loss, which checks how well the generator network can fool the discriminator network during adversarial training. It is apparent that the pixel-wise image loss monotonically decreases, and it reaches an equilibrium status after ~160 epochs, indicating training convergence. The reconstructed images from a validation dataset also show improvement of image quality (with a decrease of nRMSE) at different training epochs. There is a gradual decrease in nRMSE from 0 to 160. After 160 epochs, there is no noticeable improvement based on qualitative observation and nRMSE, showing training convergence.

Supporting Information Figure S3: The corresponding full FOV images of Figure 7 comparing CNN-Fix and SANTIS using both MaskR1 and MaskR2 for inference. Red arrows indicate residual streaking artifacts in CS-PI and CNN-Fix-MaskR1

Supporting Information Figure S4: Representative examples of knee images reconstructed from CNN-Fix and SANTIS at R=3 with uniform undersampling. A uniform undersampling pattern leads to aliasing artifacts and blurring in the zero-filling reconstruction. Both CNN-Fix and SANTIS were able to remove the aliasing artifacts. SANTIS achieved slightly better performance with better-preserved sharpness (green arrows) and texture comparable to CNN-Fix.

Supporting Information Figure S5: Evaluation of the reconstruction robustness of CNN-Fix and SANTIS with uniform undersampling at R=3. Although CNN-Fix trained using MaskC1 can reconstruct an undersampled image with MaskC1, it failed to reconstruct the undersampled image with MaskC2, resulting in noticeable residual artifacts as shown by green arrows. SANTIS, on the other hand, was able to reconstruct the undersampled image with both MaskC1 and MaskC2. It should be noted that MaskC1 and MaskC2 created different aliasing artifacts, as highlighted by the green arrows in the zero-filling images.