Homeorhesis and ecological succession quantified in synthetic microbial ecosystems

Significance

Many ecological processes, such as births, deaths, invasions, or predation, are largely stochastic in nature. Nevertheless, the dynamics occurring in ecosystems following a major change, such as regrowth of a forest after a fire, often follow regular temporal patterns, a phenomenon called ecological succession. We observed similar succession in simple microbial communities consisting of algae and ciliates colonizing a new environment and studied it by measuring dozens of replicates over a period of several days. Abundances, which were initially highly variable across replicates, rapidly converged to similar trajectories, a phenomenon called homeorhesis. These experiments show that fundamental phenomena in ecology, such as succession and homeorhesis, can be observed and quantitatively studied in the laboratory with simple synthetic ecosystems.

Abstract

The dynamics of ecological change following a major perturbation, known as succession, are influenced by random processes. Direct quantitation of the degree of contingency in succession requires chronological study of replicate ecosystems. We previously found that population dynamics in carefully controlled, replicated synthetic microbial ecosystems were strongly deterministic over several months. Here, we present simplified, two-species microbial ecosystems consisting of algae and ciliates, imaged in toto at single-cell resolution with fluorescence microscopy over a period of 1 to 2 weeks. To directly study succession in these ecosystems, we deliberately varied the initial cell abundances over replicates and quantified the ensuing dynamics. The distribution of abundance trajectories rapidly converged to a nearly deterministic path, with small fluctuations, despite variations in initial conditions, environmental perturbations, and intrinsic noise, indicative of homeorhesis. Homeorhesis was also observed for certain phenotypic variables, such as partitioning of the ciliates into distinct size classes and clumping of the algae. Although the mechanism of homeorhesis observed in these synthetic ecosystems remains to be elucidated, it is clear that it must emerge from the ways each species controls its own internal states, with respect to a diverse set of environmental conditions and ecological interactions.

Homeorhesis is a term coined by C. H. Waddington to describe a property of a dynamical system to return to a particular trajectory after an external perturbation or despite the continuous presence of random noise (1) (Box 1). It is thus a generalization of the concept of homeostasis to nonstationary systems. By definition, experimental studies of homeorhesis involve gathering large amounts of temporal statistics, which makes them more difficult, and thus less common, than those of the well-known property of homeostasis.

Homeorhesis has been studied experimentally and theoretically, mainly in developmental biology, where it is also called developmental robustness, or “canalization” (2–5). The main reason for the existence of homeorhesis in organismal development, such as fruit fly embryogenesis, as suggested by Waddington and his scientific descendants, is the evolutionary adaptation of the adult organism to its natural environment. In order for the organism’s body plan to be robustly developed, and well-fitted to its environment, many dynamical processes taking place in the embryo must be insensitive to internal molecular and cellular fluctuations, as well as to external noise. Since the molecular processes controlling an organism’s development are genetically encoded and thus heritable, it is easy to imagine how the property of developmental homeorhesis has been evolved through successive rounds of natural selection. Evolutionary origins can also be invoked for other phenomena of homeorhesis, such as the robustness of temporal dynamics of circadian clocks or mitosis (6, 7).

The notion of homeorhesis is also prevalent in ecology, particularly in studies of succession, which try to determine how the structure of an ecological community changes over time—in particular, during an initial colonization or after a significant perturbation (8). For example, plots of land cleared of vegetation by fire or abandoned following agricultural use often undergo a series of colonizations by particular species in a stereotypical order, converging to a community structure which is highly similar across separate plots (9). The degree to which ecological succession is deterministic—i.e., whether it exhibits homeorhesis—is a central focus of such studies. In contrast to the developmental program of an individual organism, it is more difficult to imagine how homeorhesis could evolve for communities of free-living organisms. In addition, since it is impractical to replicate independent time series of ecological dynamics, one cannot directly study the extent of homeorhesis in natural ecosystems. However, it is possible to perform laboratory studies of succession in microbial communities—i.e., “microsuccession” (10)—opening the possibility to precisely quantify population dynamics and phenotypic changes over many independent replicates.

Laboratory studies of microsuccession have been conducted in two distinct ways—a “top-down” approach, using samples from natural microbial communities to inoculate well-defined and well-controlled ecosystems (10–12), and a “bottom-up” approach, creating synthetic ecosystems by combining individual strains (13, 14). The primary focus of both types of experiments has been the study of community assembly—i.e., succession at the level of species or taxonomic units—and their survival or extinction over time. Here, we take an alternative approach to the bottom-up study of microsuccession, using simple synthetic microbial ecosystems (SMEs) to quantitatively study population dynamics at high spatial and temporal resolution over many replicates.

Our group previously used SMEs to study the degree of contingency and determinism in ecological dynamics (15, 16). These SMEs consisted of communities of interacting microbes, maintained in well-defined and controlled physical environments. The communities were composed of three model species—the photosynthetic alga Chlamydomonas reinhardtii, the bacterium Escherichia coli, and the ciliate Tetrahymena thermophila—and such SMEs were prepared in tens of replicates, contained in milliliter-scale glass containers, sealed to material exchange, and maintained at constant light intensity and temperature for several months. Rich stochastic phenomena were observed in replicate SMEs, including phenotypic switches such as the appearance of large ciliates capable of ingesting algae, events of predation, replication and death, and spatial heterogeneities involving phenotypes apparently adapted for niches at interfaces. The degree and timing of such events differed from replicate to replicate. The sources of stochastic events were both intrinsic—i.e., originating in molecular, cellular, or demographic fluctuations—and extrinsic—i.e., originating in variations of temperature or illumination.

In the presence of both intrinsic noise and external perturbations, population abundances were found to vary across replicates around a reproducible mean, with a stable covariance structure, dubbed “ecomodes” (15). By controlling the environmental conditions more carefully, sources of external perturbations were effectively eliminated, and in such conditions, the population dynamics in replicate SMEs were strongly deterministic (16). The spatial abundances were similarly deterministic across replicates. However, the observation of strongly deterministic dynamics does not imply that the population abundances were insensitive to external conditions. Indeed, when the external conditions were purposefully varied, the resulting abundance variations across all replicates were significant, characterized by long time scales, and dominated by one ecomode, representing strong positive correlations among all three species. These properties were quantitatively similar to those for abundance variations observed in the presence of external perturbations, leading us to conclude that ecomode structure is determined by effective internal interactions, but excited by external conditions. The strongly deterministic dynamics observed in the presence of intrinsic noise suggested that abundance dynamics in microbial ecosystems may be homeorhetic.

Motivated by these results, we describe here experiments in which we sought to directly investigate homeorhesis in microbial ecosystems by deliberately varying the initial abundances and measuring the subsequent dynamics. In contrast to previous experiments, we were able to investigate homeorhesis at the scale of the entire ecosystem, by simultaneously imaging the full volume of each replicate. This was possible since the microbial community was simplified; the nontrivial dynamics we observed previously for single-species communities (17) motivated us to simplify the composition to two species—algae and ciliates. By omitting bacteria, it was possible to observe all individuals at relatively low magnification. Previous experiments performed with well-controlled environmental conditions were strongly deterministic on all time scales (16, 17). For the present experiments, conducted with an extensive degree of environmental control (SI Appendix, Table S1), we chose to shorten the duration of each experiment, and thus many replicates could be measured serially with a single device.

The main questions addressed in the present experiments were thus:

• 1)Can homeorhesis be observed if one deliberately varies initial abundances? Will all replicates of the ecosystem converge toward a single canalized trajectory with buffered variations around it?
• 2)By using comprehensive imaging of entire ecosystems, if one observes the appearance of different behaviors, or different morphological phenotypes of two microbial species, can a phenomenon similar to ecological succession be observed? In more precise terms: Can one “align” the temporal dynamics of different ecosystem replicates, so that they present similar sequences of abundances of different species and behavioral and morphological phenotypes?

In what follows, we shall see that the response to both questions is in effect positive.

Results

Choice of the Microbial System and the Experimental Setup.

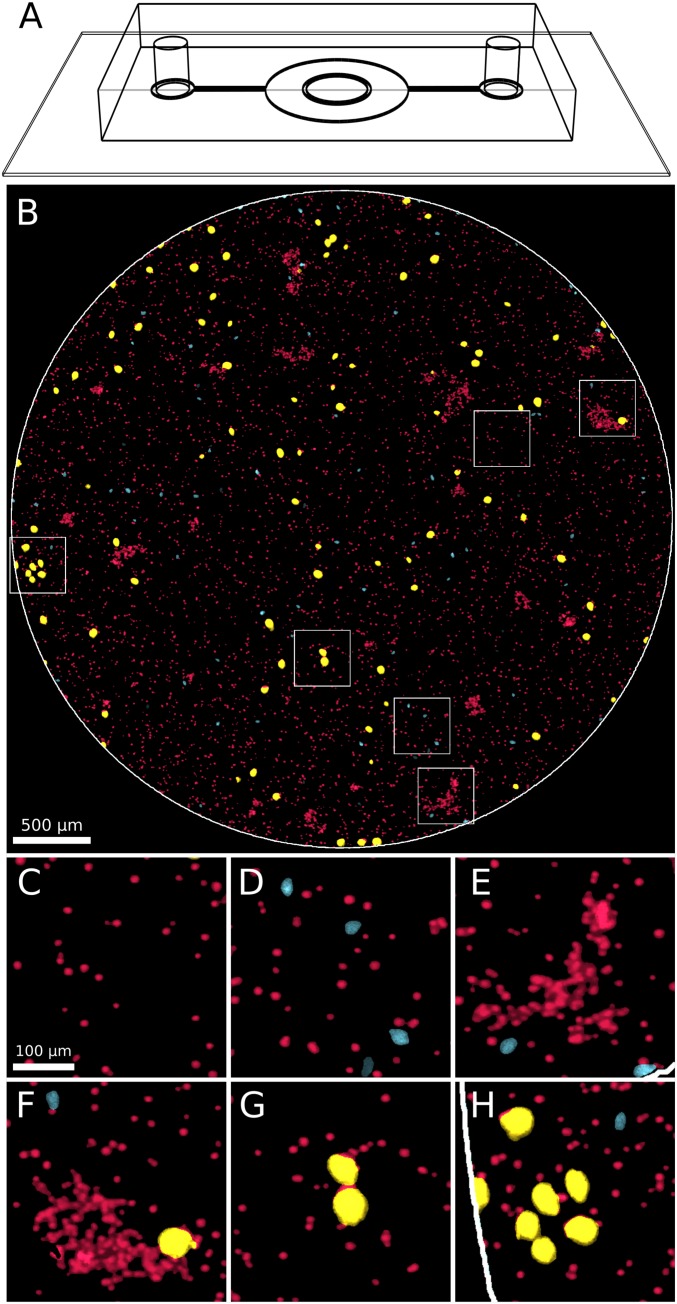
We designed experiments to allow for the automatic, noninvasive imaging of entire SMEs with single-cell resolution. This was accomplished by the following: (i) decreasing the ecosystem size to fit into a short cylindrical microfluidic chamber (Fig. 1A) and (ii) imaging the entire volume of the chamber using a custom-made, inexpensive fluorescence microscope based on a digital SLR camera (SI Appendix, Fig. S1), which allowed for time-lapse color imaging of both interacting microbial species. To achieve the latter goal, we chose the depth (110 $\mathrm{\mu }$m) and diameter (4.3 mm) of the cylindrical microfluidic chamber to match the depth of focus and field of view of our optical setup. However, at this relatively wide field of view, requiring low magnification ($5.6\times$), small cells such as the bacteria E. coli would not be resolved. Therefore, (iii) we simplified the previously studied microbial community (15, 16) by including only the two larger species: the photosynthetic alga C. reinhardtii (denoted here by “Cr”) and the ciliate T. thermophila (denoted here by “Tt”).

Fig. 1.

Week-long imaging of all cells of a ciliate/algae ecosystem in a microfluidic chamber. (A) Schematic drawing of the PDMS microfluidic chamber bonded to a glass coverslip. C. reinhardtii (Cr) and T. thermophila (Tt) cells trapped in the central circular chamber (4.3 mm in diameter and 110 $\mathrm{\mu }$m in depth) are time-lapse imaged in the custom-made fluorescent microscope (SI Appendix, Fig. S1). (B) Sample image showing the entire 4.3-mm chamber (white circle boundary) containing Cr and Tt cells. Cells are pseudocolored by class (Cr in red, s-Tt in cyan, and l-Tt in yellow) to improve contrast and facilitate distinguishability. (C–H) Six small $4\times$-magnified subregions (corresponding to the white squares in B), showing Cr singlet cells, Cr clumps (E and F), s-Tt cells (smaller cyan cells in D, E, F, and H), and l-Tt cells (larger yellow cells in F–H).

The two species were mixed in medium that supported the photoautotrophic growth of Cr, but did not support the growth of Tt on its own. The mixture was then loaded into the microfluidic chamber, which was placed into the microscope. The time between mixing the two species and the beginning of data acquisition was between ∼30 min and 1 h. In the following, we will mean by “initial conditions” the state of the system corresponding to the first acquired images ($t=0$).

Fluorescence Imaging—Cell Morphology and Aggregation.

Color images of the whole chamber showed Cr cells predominantly in the red channel due to chlorophyll fluorescence, while Tt cells appeared predominantly in the green channel. The strain of T. thermophila did not express any fluorescent protein marker, but exhibited autofluorescence when excited with light at 470 nm, having a broad emission peak between 520 and 550 nm. Time-lapse images of the whole chamber were acquired from 25 replicate ecosystems, every 5 min, for durations between 5 and 14 d.

As seen in Figs. 1 B–H and 2 and Movie S1, morphologies of Cr and Tt varied significantly. The Cr cells initially existed as spatially separate single cells and later formed dense clumps, which reached sizes of several hundred cells in some replicates (SI Appendix, Figs. S2 and S3). Initially, most Tt cells were small (<700 μm² in imaged area); however, with time, a population of larger Tt cells arose in each replicate, with cells of at least twice the area of the smaller phenotype, a rounder shape, and the capability to ingest Cr cells (Fig. 2). Tt cells were occasionally observed swimming in groups, or “swarms,” of several cells (SI Appendix, Fig. S4). Similar phenomena have been observed in other SMEs containing algae or ciliates (18–21).

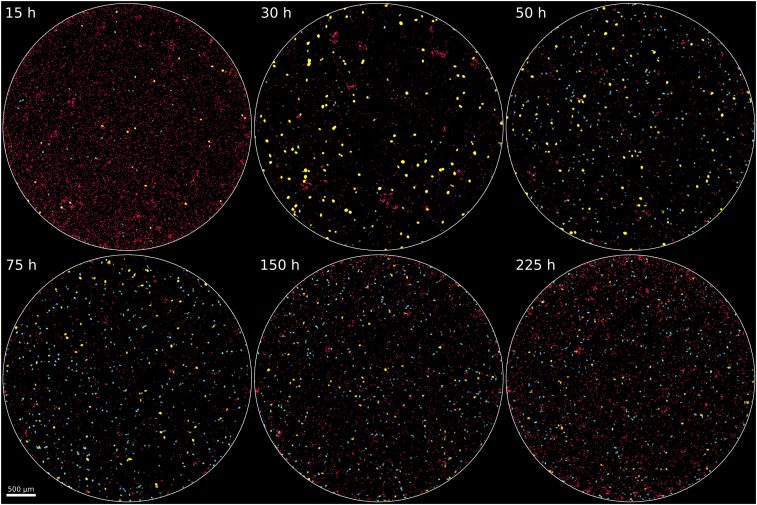
Fig. 2.

Whole-chamber time-lapse images from a single ecosystem. Six images from different times show overall changes in a replicate ecosystem. With regard to timing, there is a mix of many Cr (red cells) and some Tt (cyan and yellow cells) at 15 h, followed by the temporary increase in abundance of l-Tt (yellow cells) which phagocytose Cr cells at 30 h, leading to a large reduction in Cr by 50 h, followed by persistence of both Cr and Tt (mainly s-Tt; cyan cells) through 225 h. In other replicates, similar changes occur, but at different times (Figs. 3 and 5).

Population Variables and Their Time Series.

An exhaustive description of the dynamics of microbial ecosystems lies well beyond reach, even for ecosystems as simple as ours. It would have to include quantitative time series of internal variables of individual cells (e.g., gene expression, cellular morphologies, and metabolite concentrations), of their behavior (swimming, division, and death), of their mutual interactions (collisions, adhesion, predation, and chemical inhibition), and of their spatial distributions, as well as time series of the chemical composition of the surrounding media. Dynamical data which can be collected in practice remain quite sparse relative to the hypothetical full description. For example, in our case, we can only measure the location, size, shape, and motility of individual cells. However, as we will see below, such data can reveal rich phenomena, provided that quantitative measurements can be performed on replicate ecosystems in well-controlled conditions. In particular, we readily found that the observed microbial dynamics were very different from the simplistic trophic interactions usually discussed in textbooks, such as predator–prey or primary producer–consumer relationships (22).

Motivated by previous work on SMEs containing three species (15, 16), we sought to quantify the dynamics of abundances, morphologies, and aggregation. We separated Tt cells into two classes, based on their size, shape, and intensity—larger, rounder cells and cells with significant fluorescence in the red channel, presumably due to chlorophyll from ingested Cr, were called “l-Tt,” and smaller, more eccentric cells, with low intensity in the red channel, were called “s-Tt” (SI Appendix). We found that the logarithmic abundance of small Tt, $\log N_{\text{s}-\text{Tt}}\left(t\right)$, and that of large Tt, $\log N_{\text{l}-\text{Tt}}\left(t\right)$, were not strongly correlated ($r=0.57$), so these were treated as independent dynamical variables. We also quantified the number of Tt participating in swarms, $N_{\text{swarm}-\text{Tt}}\left(t\right)$, by considering the spatial density of Tt (SI Appendix).

To quantify abundances of Cr, which were found both as single cells and in dense clumps, and in both motile and nonmotile forms, we estimated the number of cells within each clump, and the abundance of clumped cells was calculated as the sum over estimated counts per clump (SI Appendix). The log abundance of Cr singlets was highly correlated with that of all clumped cells ($r=0.85$), so we decided to sum the two abundances at each time point, giving the total abundance of Cr, $N_{\text{Cr}}\left(t\right)$. Considering Cr counted in all replicates over time, roughly half were motile and half were nonmotile, and the counts in each motility class were not strongly correlated ($r=0.58$). We did not consider the motility dynamics in our primary analysis.

The population-abundance data thus consisted of counts in three primary classes (s-Tt, l-Tt, and Cr), estimated at single-cell resolution over the entire ecosystem, for each of 23 replicates, sampled every 5 min over week-long timescales (see SI Appendix for analysis which identified 2 outliers out of 25 measured replicates). We filtered high-frequency noise present in raw counts by taking a moving average over 15 frames (75 min). These data are denoted, for replicate $i$ at time $t$, as $N_{\text{s}-\text{Tt}}^{\left(i\right)}\left(t\right)$, $N_{\text{l}-\text{Tt}}^{\left(i\right)}\left(t\right)$, and $N_{\text{Cr}}^{\left(i\right)}\left(t\right)$. Time series of abundances are shown in Fig. 3, Left.

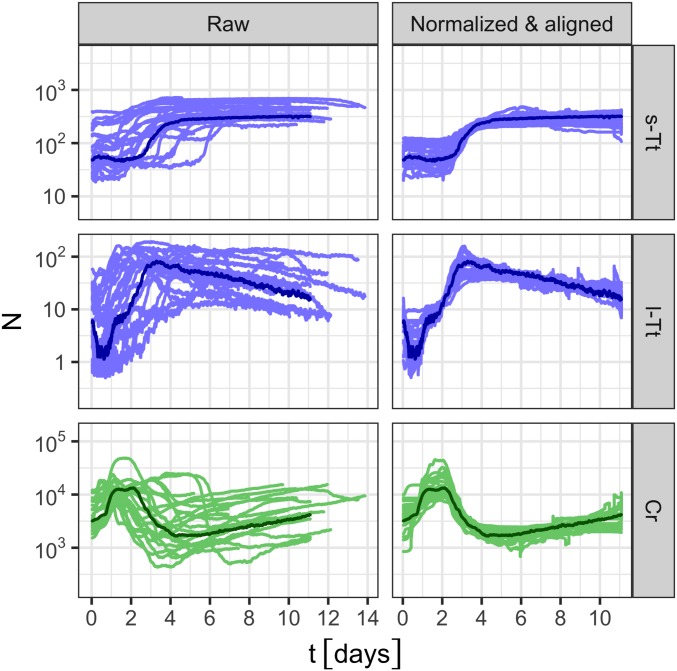
Fig. 3.

The abundances of each class of organism [Top, small T. thermophila (“s-Tt”); Middle, large T. thermophila (“l-Tt”); Bottom, C. reinhardtii (“Cr”)] from 23 replicate ecosystems are plotted as time series. The abundance estimates $N_c\left(t\right)$ are plotted in Left, and the temporally aligned, normalized abundances ${Ñ}_c\left(t\right)$ are plotted in Right (Materials and Methods). In all panels, data from the reference replicate used for temporal alignment is plotted in a darker color. All counts are incremented by $\frac{1}{2}$ to avoid divergence of zero counts on the log scale.

The gathered data include more information than temporal variations of abundances. We could follow at the same time changes of the cell morphologies and the swimming or aggregating behavior. However, our idea was to first analyze the data using the abundance dynamics as the primary variables and then look for the possible influence of other phenotypic characteristics.

Abundance Variations in Time and across Replicates.

The abundance dynamics of each class exhibit considerable variation over time. In all replicates, the abundance dynamics of small Tt, $N_{\text{s}-\text{Tt}}^{\left(i\right)}\left(t\right)$, had a sigmoidal appearance; the abundance of large Tt, $N_{\text{l}-\text{Tt}}^{\left(i\right)}\left(t\right)$, peaked, then slowly declined; and the abundance of Cr, $N_{\text{Cr}}^{\left(i\right)}\left(t\right)$, peaked early, declined, and then increased slowly until the end of the acquisition (Fig. 3). The dynamic range of the abundances spanned at least one order of magnitude for each class.

The abundance dynamics also varied significantly across replicates. These variations can be quantified by the geometric SD ${\sigma }_g$, which measures the typical fold change of a multiplicative process (15), as explained in Materials and Methods. The geometric SD ${\sigma }_g$ is calculated for each class and can be calculated over any time interval, including a single time point. The values of ${\sigma }_g$ calculated over replicates and the duration of data acquisition, were ∼1.9-fold for small Tt, 2.7-fold for large Tt, and 2.3-fold for Cr (Table 1).

Table 1.

Geometric SDs of abundance dynamics and their 90% confidence intervals

Symbol	Abundance type	Time interval	Class	Estimated value (fold change)	90% Conf. interval (fold change)
${\sigma }_{g,N_{\text{s}-\text{Tt}}}\left(t=0\right)$	Raw	Initial time	Small Tt	2.2	$\left[1.9,2.8\right]$
${\sigma }_{g,N_{\text{l}-\text{Tt}}}\left(t=0\right)$	Raw	Initial time	Large Tt	3.4	$\left[1.7,5.1\right]$
${\sigma }_{g,N_{\text{Cr}}}\left(t=0\right)$	Raw	Initial time	Cr	1.9	$\left[1.7,2.4\right]$
${\sigma }_{g,N_{\text{s}-\text{Tt}}}\left(T_3\right)$	Raw	All times	Small Tt	1.90	$\left[1.86,1.93\right]$
${\sigma }_{g,N_{\text{l}-\text{Tt}}}\left(T_3\right)$	Raw	All times	Large Tt	2.68	$\left[2.61,2.76\right]$
${\sigma }_{g,N_{\text{Cr}}}\left(T_3\right)$	Raw	All times	Cr	2.31	$\left[2.26,2.37\right]$
${\sigma }_{g,{Ñ}_{\text{s}-\text{Tt}}}\left(T_3\right)$	Aligned and normalized	All times	Small Tt	1.29	$\left[1.28,1.30\right]$
${\sigma }_{g,{Ñ}_{\text{l}-\text{Tt}}}\left(T_3\right)$	Aligned and normalized	All times	Large Tt	1.32	$\left[1.31,1.33\right]$
${\sigma }_{g,{Ñ}_{\text{Cr}}}\left(T_3\right)$	Aligned and normalized	All times	Cr	1.31	$\left[1.31,1.32\right]$

T₃ represents time points for which at least three replicates were measured. See Materials and Methods for details.

It seemed that much of the variation across replicates arose from two factors—the timing of events, such as rapid population increases and decreases, differed by up to several days, and the time-averaged abundances, around which the dynamics fluctuated, varied among different replicates by several fold.

The effect of variation in timing was considered by temporally aligning the abundance dynamics. Temporal alignment, described in detail in Materials and Methods and used previously to analyze similar phenomena (16), is a particular instance of dynamic time warping [originally called dynamic-programming matching (23)]. The method involves finding a mapping from time in a reference replicate to time in each other replicate, so as to minimize the differences between the abundances at these times. These mappings define “aligned times.” The minimization was performed under natural constraints, which assured that no portion of the dynamics was omitted and that the aligned times did not proceed backward in physical time. The time mapping was determined and applied independently for each replicate, but was the same for each class of organism. Summary statistics of the temporal alignments are shown in SI Appendix, Fig. S5.

The differences in time-averaged abundances of each organism class were removed through normalization, applied individually to each replicate and organism class (Materials and Methods). We found that temporal alignment and normalization accounted for the majority of the abundance variations over replicates; the typical deviation in aligned, normalized abundances across replicates was ∼1.3-fold for all three classes (Fig. 3 and Table 1).

To quantify the degree of homeorhesis, we can also consider how the variation in initial abundances among the replicates compares to and influences the later variations. The geometric SD of abundances at the beginning of data acquisition, ${\sigma }_g\left(t=0\right)$, was 2.2-fold for small Tt, 3.4-fold for large Tt, and 1.9-fold for Cr, compared with the time-averaged values of ∼1.3 for each class (Table 1). The influence of initial abundances on the subsequent dynamics decayed over time and explained only $\sim$30% of the variance over the last 7 d of the aligned experiments (SI Appendix, Fig. S6).

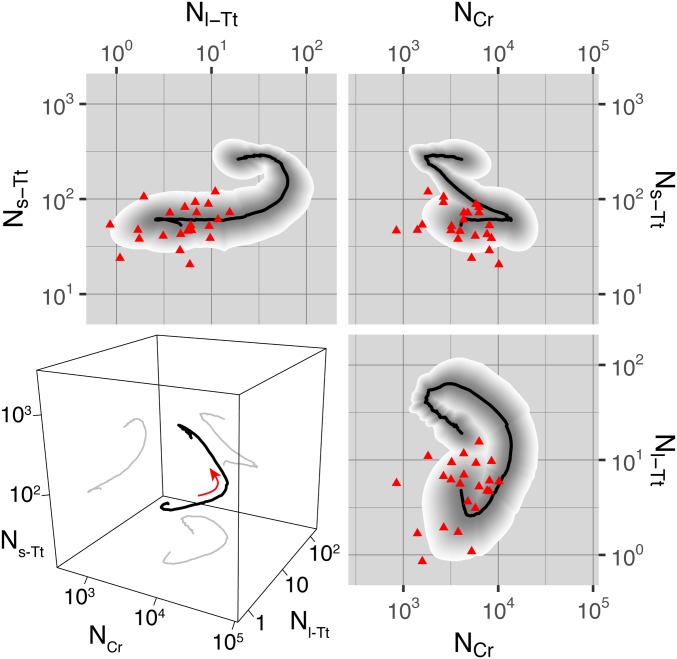
Temporal alignment also allowed us to consider statistics in the phase space of abundances, effectively projecting out differences in timing while preserving the temporal ordering. These trajectory statistics, as shown in Fig. 4, demonstrate (i) the sequence of events in abundance space, revealing a complexity beyond simple models such as predator–prey or consumer–producer; and (ii) the amount of variation over replicates, which clearly decreases significantly from the broad distribution of initial abundances and remains small compared with the range of abundance space explored by each trajectory.

Fig. 4.

Statistics of phase-space trajectories. In the 2D panels, population dynamics are plotted as trajectories in the space of one class’s normalized abundance vs. another’s. Black curve, geometric mean over replicates; shaded region, 68% quantile over replicates, with quantiles colored as a gradient from gray to white to show structure; red triangles, initial abundance for each replicate. The 3D panel at Lower Left shows the mean trajectory as a black curve in the space of normalized abundance of each class, with projections to each 2D subspace shown as gray curves. The red arrow indicates the direction along which the dynamics proceed with time. The classes are denoted as in the text: small T. thermophila, “s-Tt”; large T. thermophila, “l-Tt”; C. reinhardtii, “Cr.”

In summary, despite the broad distribution of initial abundances, normalized and aligned abundance dynamics in replicates of the microbial ecosystems rapidly converged to the same temporal patterns, changing by 10-fold over the course of the experiments, while fluctuating by only 30% over replicates.

Variations in Morphology and Behavior.

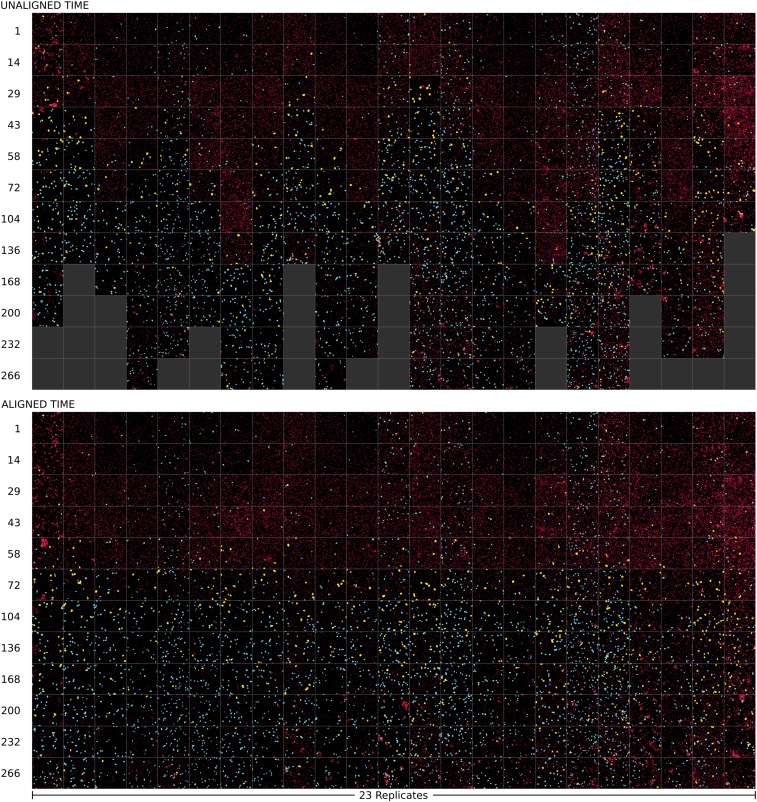
Given the rich structure of the dynamics of replicate ecosystems, involving not just abundances but also cell morphology and spatial distributions, we sought in addition to visualize the comprehensive dynamics, as has been done in a study of ecological succession in a network of forest plots studied after glacial retreat (24). This was achieved by applying the temporal alignment to images taken from each replicate at a subset of times, sampling the trajectories in approximately uniform intervals of phase-space arc length, providing “key frames” for the large datasets (SI Appendix). The result, shown in Fig. 5, summarizes the patterns of succession we observed in microbial ecosystems.

Fig. 5.

Time course of images from 23 replicates of the synthetic Tt/Cr ecosystem. In both Upper and Lower, each column represents the same replicate ecosystem. Each row corresponds to 12 different time points, where images are taken from the raw time (Upper) or from the aligned time (Lower) relative to a reference experiment. To show sufficient detail, we selected the most representative subimage of size $912\times 912\mu$m for that replicate and time (SI Appendix). To account for slight differences in fluorescence intensity across replicates, Cr singlets are shown by a circle of fixed size, and to allow visual identification of cell classes, all cells are pseudocolored by class (Cr in red, s-Tt in cyan, and l-Tt in yellow). Filled dark gray boxes in Upper indicate that data acquisition for that particular replicate had ended before that time. Times are indicated in hours to the left of each row (Upper, raw time; Lower, aligned time).

Examining these images, which were temporally aligned by using the abundance variables, one could ask whether phenotypic variables, such as cell morphologies or motility behavior, all follow the temporal pattern of abundances. By quantitatively analyzing the dynamics of such variables, we found that while some phenotypic variables closely followed the dynamics of microbial abundances, others did not exhibit any correlated temporal pattern.

For instance, the fraction of Cr existing in different phenotypic states—individual cells, motile clumps, and nonmotile clumps—varied significantly over time and was similar over replicates after temporal alignment (SI Appendix, Fig. S7).

In contrast, the number of Tt participating in swarms showed no clear temporal pattern across replicates, with some replicates lacking any swarming for the entire experiment and others exhibiting highly motile swarms of tens of cells for several days (SI Appendix, Figs. S4 and S8). The degree of swarming did not correlate with variations in abundance of any class—abundance deviations were regressed on the number of individuals in swarms and compared with shuffled data for significance, with no significant explanatory power found (14% of aligned abundance variance, compared with 12% of variance for 90% quantile of shuffled data). Therefore, the homeorhesis observed in the dynamics of abundances and the phenotypic distributions of Cr were apparently independent of the swarming dynamics of Tt.

Discussion

To explicitly investigate the phenomena of homeorhesis and succession, we have simplified the SMEs studied in earlier work (15, 16), to allow quantitation of the temporal dynamics of the whole population at single-cell resolution. The resulting ecosystems consisted of populations of freely swimming, interacting, and dividing T. thermophila and C. reinhardtii and were studied through fluorescence microscopy in multiple replicates over week-long periods. The main finding of our experiments was that trajectories of microbial abundances were tightly distributed (Fig. 4 and Table 1), and this despite the large variations in the initial abundances. Furthermore, the trajectories were tightly distributed along a highly dynamic path, rather than simply localized around a steady state, as seen for systems exhibiting homeostasis. Therefore, we conclude that the population dynamics of our SMEs clearly exhibit homeorhesis.

Although, to our knowledge, there is no accepted unique way to measure the extent of homeorhesis, we have confirmed the existence of this phenomenon by showing that: (i) The variations in the abundance trajectories across replicates are more than one order of magnitude smaller than the extent of the temporal variations during the course of the experiments; (ii) trajectories from replicates with initial conditions distributed through a large volume of phase space rapidly converged to a single path, with significantly smaller variations; and (iii) variations between replicates do not show any systematic trend to increase in time. This surprising degree of determinism seems to extend also to some phenotypic variables, such as the separation of Tetrahymena into two size classes or to the clumping behavior of the Chlamydomonas. However, other phenotypic variables, such as those describing swarming of Tetrahymena, differed significantly across replicates, and their dynamics did not significantly affect the microbial abundance dynamics themselves.

The origin of homeorhesis in our SMEs is not obvious. It is highly unlikely that the particular strains of two microbial species, which have been axenically cultured and studied in laboratories for many generations, have been selected for their quasideterministic dynamics or any other similar coexistence properties. The lack of an obvious selection pressure is in contrast to usual arguments evoked to explain homeorhesis observed in organismal development, first defined and studied by C. H. Waddington 70 years ago. In other words, we do not expect homeorhesis exhibited by SMEs to be the result of natural selection for resistance to noise in any specific conditions or in the presence of any particular interactions. However, it is possible that the species used in our experiments, as well as other species in naturally occurring communities, have evolved homeorhetic control of their internal states, with respect to a broad set of possible external conditions. Homeorhesis of each species’ internal states would then naturally extend to mutual interactions in communities of diverse compositions, resulting in homeorhetic abundance dynamics of the whole ecosystem, as observed here. Such a scenario could be tested by measuring time series of organisms’ internal variables, such as gene expression or metabolic rates, along with abundance dynamics, in response to external perturbations.

At this point, we would like to stress several important general points about homeorhesis, or canalization: (i) The observed homeorhesis in abundance dynamics does not mean that these ecological systems are not sensitive to changes in the environment or other possible perturbations. For instance, change of illumination intensity or external temperature can induce drastic changes in the population dynamics of microbial ecosystems (16). The presence of homeorhesis signifies only that the trajectories converge to similar trajectories in different replicates. (ii) The extent of homeorhesis may vary along the phase-space trajectory. In some regions, the trajectories can be more canalized than in others—i.e., the variations between the replicates can be more pronounced in different phase-space regions (as can be seen in Fig. 4). (iii) The extent of homeorhesis may depend on the initial conditions. For example, in our ecosystems, although homeorhesis was observed for a rather broad distribution of initial abundances, it is likely that more extreme initial abundances would result in qualitatively different trajectories, such as extinction of a species or absence of the large class of ciliates. And (iv) in general, one could expect the existence of other dynamical structures, such as homeorhesis with alternative paths (fourth example in Box 1). In this case, different replicates of the ecosystem would follow one of two or more possible groups of canalized trajectories, and the proportion of replicates in each group can form the characteristic of the given ecosystem. This would be analogous to branching in developmental dynamics, which can lead to phenotypic polymorphism present even in genetically homogenous populations (25). In fact, 2 of the replicate ecosystems measured in this work differed significantly from the other 23—we do not know if the two outlying trajectories represent alternative paths which are also homeorhetic, an escape from the homeorhetic region, or some other phenomenon. Further experiments, possibly studying a larger ensemble of replicate ecosystems, could investigate the statistical nature of alternative paths.

One consequence of the observed phenomenon of homeorhesis is reproducible patterns of marked changes of abundances, or of particular morphological and behavioral variables. This is somewhat similar to the phenomenon of succession observed and intensively studied in ecology for >100 years. There is no consensus as to how to define succession. A traditional definition, originating in the pioneering work of F. E. Clements, emphasizes the deterministic component of the ecological dynamics: its directionality, the reproducibility of trajectories, and the existence of a stable endpoint (8, 26). Such ecological successions have been observed in numerous studies of forest and marine ecosystems after a large perturbation—e.g., clearing of a large forest area due to fire or logging or abandonment of agricultural fields, followed by “return to the original ecosystem” (27, 28). Despite many observations, however, it is fair to say that there is no clear consensus in the quantitative understanding of the conditions, the mechanisms, and the extent of ecological successions. We would like to propose that synthetic ecological systems, such as those studied here, could play an important role to help clarify both the phenomena of biological homeorhesis and ecological succession.

More generally, the phenomenon of temporally ordered events with significant variability in timing arises in other domains of science—e.g., in physics or physical chemistry in the study of deterministic dynamical systems, such as intermittency or itinerancy associated with chaotic attractors (29, 30), or for stochastic dynamical systems, when the deterministic trends drive trajectories between local traps, and escape from the traps occurs only due to random fluctuations (31). However, in these examples, the dynamics are not necessarily robust to perturbations and therefore do not exhibit homeorhesis. On the other hand, the phenomenon of homeorhesis seems to be particularly prevalent in biology. The processes of DNA replication, transcription, translation, protein folding, assembly of macromolecular complexes, cell division, and embryogenesis all exhibit temporal ordering, despite variations in timing and the influence of perturbations at many levels. The phenomenon is also central to higher levels of biological organization, such as encountered in neuroscience. For instance, our recognition of speech or music is based mainly on the temporal order of sounds rather than their precise timing (32). The prevalence of such phenomena in biology should motivate further development of new theoretical ideas, possibly expanding the language of dynamical systems to a more algorithmic formulation. We hope that our experiments could also contribute to these potentially important theoretical developments.

Materials and Methods

Strains and Media.

Ecosystems consisted of two species: (i) the ciliate T. thermophila (strain CU428.2 mating type VII, SD00178 from the Cornell University Culture Collection), and (ii) the alga C. reinhardtii (strain CC-125, mating type +, from the Chlamydomonas Resource Center). Tt cells were grown in SPP medium (33) [2% proteose peptone, 0.1% yeast extract, 0.2% glucose, and 0.003% sequestrene (Fe-EDTA)] without shaking at room temperature, and Cr cells were grown with shaking at 200 rpm at 25 ^○C with ∼7,500 lx of illumination in SGHT medium (16), which is modified Sager–Granick medium (https://chlamycollection.org/SG.html) composed of 1.7 mm sodium citrate (dihydrate), 37 $\mathrm{\mu }$M ${\text{FeCl}}_3\cdot 6{\text{H}}_2\text{O}$, 0.36 mM ${\text{CaCl}}_2\cdot 2{\text{H}}_2\text{O}$, 1.22 mM ${\text{MgSO}}_4\cdot 7{\text{H}}_2\text{O}$, 11.2 mM ${\text{NH}}_4\text{Cl}$, 0.4 mM ${\text{KH}}_2{\text{PO}}_4\cdot 7{\text{H}}_2\text{O}$, and 0.4 mM ${\text{K}}_2{\text{HPO}}_4\cdot 7{\text{H}}_2\text{O}$, with standard trace elements replaced by Hutner’s trace elements (34). Hutner’s trace elements, composed of 134 $\mathrm{\mu }$M EDTA disodium salt, 77 $\mathrm{\mu }$M ${\text{ZnSO}}_4\cdot 7{\text{H}}_2\text{O}$, 184 $\mathrm{\mu }$M ${\text{H}}_3{\text{BO}}_3$, 26 $\mathrm{\mu }$M ${\text{MnCl}}_2\cdot 4{\text{H}}_2\text{O}$, 7 $\mathrm{\mu }$M ${\text{CoCl}}_2\cdot 6{\text{H}}_2\text{O}$, 6 $\mathrm{\mu }$M ${\text{CuSO}}_4\cdot 5{\text{H}}_2\text{O}$, 1 $\mathrm{\mu }$M ${\left({\text{NH}}_4\right)}_6{\text{Mo}}_7{\text{O}}_{24}\cdot 4{\text{H}}_2\text{O}$, and 18 $\mathrm{\mu }$M ${\text{FeSO}}_4\cdot 7{\text{H}}_2\text{O}$, was purchased from the Chlamydomonas Resource Center (https://www.chlamycollection.org/methods/media-recipes/hutners-trace-elements/).

Microfluidic Chamber Fabrication.

Polydimethylsiloxane (PDMS) microfluidic chamber (Fig. 1A) design and fabrication were similar to those described by Jordan et al. (33), except that the chamber dimensions in this work are 4.3 mm in diameter and 110 $\mathrm{\mu }$m in depth. This depth was selected to match the depth of field of the imaging setup, so that all of the cells in the chamber would remain in focus. The circular ring wall surrounding the central chamber was covered with scotch tape during plasma treatment, to prevent that section from permanently bonding to the cover glass, which, after removal of the tape, allowed it to be opened (for cell loading) and closed (for cell trapping) by using changes in pressure.

Ecosystems.

Ecosystems were prepared by centrifuging and washing separately grown Cr and Tt cultures with SGHT and then mixing the cells (in SGHT) before loading into the microfluidic chambers. The inlet and outlet ports of the PDMS device were connected to syringes fitted with three-way Luer valves and Tygon tubing attached to a blunt needle. Chambers were loaded by flowing medium containing the cell mixture into the inlet port of the microfluidic device, closing the outlet port, and adding slight pressure to raise the ring valve, then releasing the pressure to trap cells in the chamber. Ecosystems were kept at room temperature during imaging. The environmental conditions during data acquisition were not logged, but their statistics were estimated by measuring environmental conditions in the setup over a separate interval of 182 d (Table S1).

Time-Series Analysis.

Geometric SD quantifies variation in abundance dynamics.

Abundances $N_c\left(t\right)$ sampled from replicate microbial ecosystems have been found to vary on a logarithmic scale, following an approximately log-normal distribution and having a SD that scales linearly with the mean (15, 16). These properties are to be expected, as branching processes universally exhibit the same scaling (35). Therefore, it is natural to perform statistical analysis on log-transformed abundances, $\log N_c\left(t\right)$, for which distributions are approximately Gaussian and are thus well-described by their mean (over $n$ replicates)

$${\mu }_{\log N_c}\left(t\right)=\frac{1}{n}\sum _{i=1}^n\log N_c^{\left(i\right)}\left(t\right),$$ [1]

and SD

$${\sigma }_{\log N_c}\left(t\right)=\sqrt{\frac{1}{n-1}\sum _{i=1}^n{\left(\log \left(N_c^{\left(i\right)}\left(t\right)/{\mu }_{\log N_c}\left(t\right)\right)\right)}^2}.$$ [2]

The mean and SD of the log abundance depend on the base of the logarithm, obscuring their interpretation. Thus, a better alternative is the geometric mean ${\mu }_g$ and geometric SD ${\sigma }_g$ of $N_c\left(t\right)$, which are simply the exponential function of the mean and SD of $\log N_c\left(t\right)$, respectively:

$$\begin{array}{ll}\hfill {\mu }_{g,N_c}\left(t\right)& =e^{{\mu }_{\log N_c}\left(t\right)}=\exp \left(\frac{1}{n}\sum _{i=1}^n\log N_c^{\left(i\right)}\left(t\right)\right)\hfill \\ \hfill {\sigma }_{g,N_c}\left(t\right)& =e^{{\sigma }_{\log N_c}\left(t\right)}\hfill \\ \hfill & =\exp \left(\sqrt{\frac{1}{n-1}\sum _{i=1}^n{\left(\log \left(N_c^{\left(i\right)}\left(t\right)/{\mu }_{g,N_c}\left(t\right)\right)\right)}^2}\right).\hfill \end{array}$$ [3]

The geometric SD ${\sigma }_g$ represents the typical fold change around the geometric mean ${\mu }_g$ observed in a set of samples. For example, in a large set of samples drawn from a log-normal distribution with ${\mu }_g=100$ and ${\sigma }_g=1.3$, $\sim$68% fall between values of $\frac{{\mu }_g}{{\sigma }_g}\approx 77$ and ${\mu }_g{\sigma }_g$ = 130, $\sim$95% fall between values of $\frac{{\mu }_g}{{\sigma }_g^2}\approx 59$ and ${\mu }_g{\sigma }_g^2$ = 169, etc. The smallest possible value of ${\sigma }_g$ is 1, representing samples with identical values—i.e., samples drawn from a delta function distribution.

To consider the typical size of replicate-to-replicate fluctuations over a time interval $T$, the geometric SD is calculated as

$${\sigma }_{g,N_c}\left(T\right)=\exp \left(\sqrt{\frac{1}{mn-1}\sum _{i=1}^n\sum _{t\in T}{\left(\log \left(N_c^{\left(i\right)}\left(t\right)/{\mu }_{g,N_c}\left(t\right)\right)\right)}^2}\right),$$ [4]

where $m$ is the number of time points in the interval $T$.

The geometric SD for each class was calculated over all time points, for which at least three replicates were measured ($T_3=\left\{t:n_t\ge 3\right\}$). This quantifies the typical fold-change variation in abundance across replicates throughout the duration of the experiments (Table 1). The geometric mean and SD for normalized and temporally aligned abundances, ${Ñ}_c$ (see below), were calculated in the same way.

Temporal alignment and normalization.

Temporal alignment is achieved by choosing one replicate $i$ as the “target” and for each other replicate $j$, calculating a monotonic map between times in target replicate $i$ and times in replicate $j$. Denoting the duration of experiment $j$ by $T_j$, and the space of nondecreasing functions from the unit interval to itself by $\mathcal{T}$, we calculated temporal deformations ${\tau }_j$ and ${\upsilon }_j$ minimizing the aligned variance over functions in $\mathcal{T}$:

$$\begin{array}{ccc}\hfill {\tau }_j,{\upsilon }_j& =\hfill & \underset{\tau ,\upsilon \in \mathfrak{T}}{arg\; min}{\int }_0^1\sum _c\left(\log \left(N_c^{\left(i\right)}\left(T_i\tau \left(l\right)\right)\right)\right.\hfill \\ \hfill & \hfill & -\log {\left.\left(N_c^{\left(j\right)}\left(T_j\upsilon \left(l\right)\right)\right)\right)}^2\text{d}l.\hfill \end{array}$$ [5]

Normalization amounts to a scaling of abundances of each replicate by a constant. This scaling removes the zero-frequency component of the variability over replicates, analogous to the mean subtraction operation typically performed in time-series analysis (36). The scaling transforms $N_c^{\left(j\right)}\left(t\right)$ to ${\gamma }_c^{\left(j\right)}{N}_c^{\left(j\right)}\left(t\right)$. Thus, Eq. 5 is modified:

$$\begin{array}{ll}\hfill {\mathit{\gamma }}^{\left(\mathit{j}\right)},{\tau }_j,{\upsilon }_j\hspace{0.17em}& =\hfill \\ \hfill \underset{\begin{array}{c}\mathit{\gamma }\in {\mathbb{R}}_{>0}^3\\ \tau ,\upsilon \in \mathfrak{T}\end{array}}{arg\; min}{\int }_0^1& \sum _c{\left(\log \left(N_c^{\left(i\right)}\left(T_i\tau \left(l\right)\right)\right)-\log \left({\gamma }_c{N}_c^{\left(j\right)}\left(T_j\upsilon \left(l\right)\right)\right)\right)}^2\text{d}l.\hfill \end{array}$$ [6]

The minimization was carried out as described (16). The geometric SD of normalization constants was 1.5-fold for small T. thermophila, 1.9-fold for large T. thermophila, and 1.8-fold for C. reinhardtii. The normalization constants of the three classes were only significantly correlated for large T. thermophila and C. reinhardtii ($\text{cor}\left({\gamma }_{\text{l}-\text{Tt}},{\gamma }_{\text{Cr}}\right)=0.61$, P = 0.002), but not for the other two pairs of organism classes ($\text{cor}\left({\gamma }_{\text{s}-\text{Tt}},{\gamma }_{\text{l}-\text{Tt}}\right)=0.19$, P = 0.4; and $\text{cor}\left({\gamma }_{\text{s}-\text{Tt}},{\gamma }_{\text{Cr}}\right)=-0.15$, P = 0.5).

We can consider the temporally aligned, normalized abundances as time series by mapping to the physical time of the target replicate, $i$:

$${Ñ}_c^{\left(j\right)}\left(t\right)={\gamma }_c^{\left(j\right)}{N}_c^{\left(j\right)}\left(T_j{\upsilon }_j\left({\tau }_j^{-1}\left(t/T_i\right)\right)\right).$$ [7]

The results of normalization and temporal alignment are shown in SI Appendix, Fig. S9.