Significance
Spatial gradients of phosphatidylinositol phosphate (PIP) lipids in the cell membrane regulate a variety of cellular processes, including endocytosis, phagocytosis, and cell migration. The molecules that control these cellular processes must navigate a diverse range of geometric constraints, including membrane sheets, blebs, vesicles, and tubules. Stochastic geometry sensing provides a mechanism for controlling spatial patterning of molecules on cellular membranes, by exploiting differences in molecular copy number and kinetic asymmetries between opposing enzymatic reactions. The generality of the stochastic geometry-sensing mechanism suggests that such effects are likely to occur in cellular signaling systems.
Keywords: bistability, stochastic, polarization, kinase, phosphatase
Abstract
Phosphorylation reactions, driven by competing kinases and phosphatases, are central elements of cellular signal transduction. We reconstituted a native eukaryotic lipid kinase–phosphatase reaction that drives the interconversion of phosphatidylinositol-4-phosphate [PI(4)P] and phosphatidylinositol-4,5-phosphate [PI(4,5)P2] on membrane surfaces. This system exhibited bistability and formed spatial composition patterns on supported membranes. In smaller confined regions of membrane, rapid diffusion ensures the system remains spatially homogeneous, but the final outcome—a predominantly PI(4)P or PI(4,5)P2 membrane composition—was governed by the size of the reaction environment. In larger confined regions, interplay between the reactions, diffusion, and confinement created a variety of differentially patterned states, including polarization. Experiments and kinetic modeling reveal how these geometric confinement effects arise from a mechanism based on stochastic fluctuations in the copy number of membrane-bound kinases and phosphatases. The underlying requirements for such behavior are unexpectedly simple and likely to occur in natural biological signaling systems.
Phosphatidylinositol phosphate (PIP) lipids are an important class of membrane constituents that function in signal transduction. Inositol head groups are chemically modified by lipid kinases and phosphatases, generating various PIP lipid species that have distinct and dynamic cellular localization patterns (1). Specific PIP lipid compositions are thought to establish cellular zip codes for organelle identity and signaling activity. Many cytosolic proteins are selectively recruited to intracellular membranes based on PIP composition, and the PIP lipids are also direct modulators of protein function at the membrane (2, 3). Although spatial patterning is well documented in biological systems (4), the physical mechanisms by which these enzymatic reactions establish spatial composition patterns in the membrane and how the membrane shape may influence this remains poorly understood.
In the case of PIP lipid organization, much attention has been directed toward how lipid kinase and phosphatase activities are spatially controlled during endocytosis (5), phagocytosis (6, 7), and polarized cell migration (8, 9). Critical for all of these cellular processes is the production of PI(4,5)P2 at the plasma membrane, which is predominantly controlled by phosphatidylinositol-4-phosphate 5-kinase (PIP5K) (10). Opposing PIP5K activity are 5′-phosphatases (5′-PPtases), such as Lowe oculocerebrorenal syndrome protein (OCRL) and phosphatidylinositol polyphosphate 5′-phosphatase type IV (INPP5E), which catalyze the dephosphorylation of PI(4,5)P2 into PI(4)P (11). Membrane-associated adaptors and scaffolding proteins potentially modulate lipid kinase and phosphatase activities by regulating their membrane localization and binding kinetics (11–14). The range of PIP5K and 5′-PPtases activity states, however, is sparsely documented and warrants comprehensive analysis.
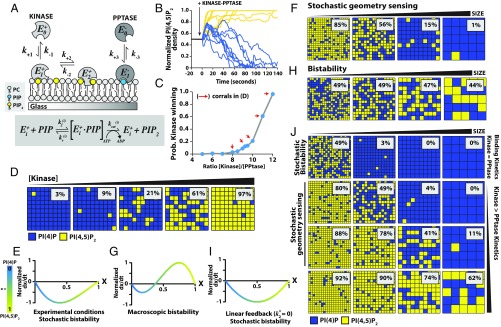
Here, we describe the reconstitution of a lipid kinase–phosphatase competitive reaction that drives the interconversion of phosphatidylinositol-4-phosphate [PI(4)P] and phosphatidylinositol-4,5-phosphate [PI(4,5)P2] lipids in supported membranes. We discovered an intrinsic positive-feedback mechanism in PIP5K. Binding of the kinase to PI(4,5)P2, at sites that do not interfere with catalytic activity, modulated localization of the kinase at the membrane surface, where it could efficiently access its substrate. Using a panel of 5′-PPtases with varying degrees of positive feedback, we added competitive lipid phosphorylation reactions against PIP5K activity, which could be tuned over a wide range. We observed a variety of responses, including formation of bistable PIP lipid compositional patterns and spontaneous polarization on geometrically confined membranes.
An entirely different phenomenon emerged when competitive reactions were adjusted outside the range of the intrinsically bistable behavior. Under such conditions, 1 enzyme reaction was more favorable and a spatially homogeneous membrane composition reflecting the dominant reaction resulted in unconstrained supported membrane. However, when the reaction was geometrically confined, the final composition of the membrane—beginning from identical starting conditions—was governed by the size and shape of the reaction environment. This effect, which we refer to as stochastic geometry sensing, arises from the system’s asymmetric response to stochastic fluctuations in the copy number of enzymes on the membrane surface. Although the geometry sensing stems from an intrinsically stochastic process, experiments revealed that the response to different membrane geometries can be almost entirely deterministic. The minimal requirements for stochastic geometry sensing are significantly less restrictive than those for the formation of widely discussed Turing patterns in reaction diffusion systems (4, 15, 16). We propose that stochastic geometry sensing may be a general mechanism by which membrane structures in living cells (e.g., vesicles, tubules, and blebs) can establish spatially distinct compositions in a dynamic fluid membrane environment.
Results
Kinetic Analysis PIP Lipid Reactions on Membrane Surfaces.
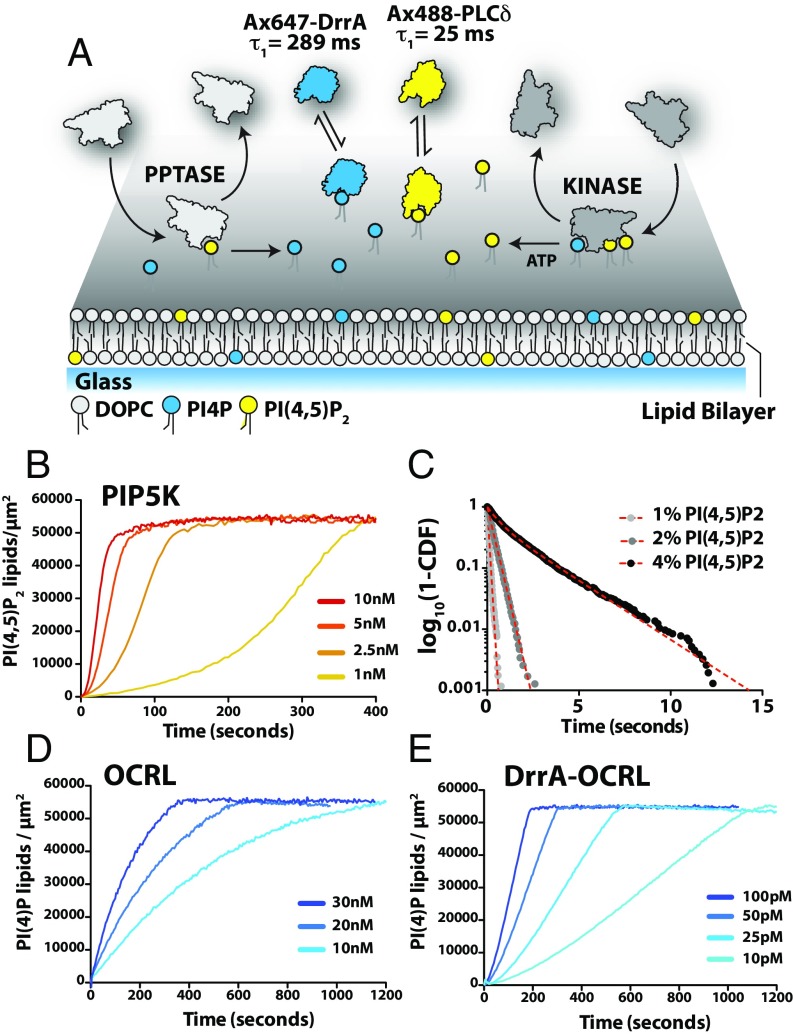
We first developed an experimental system to measure the kinetics of PIP lipid phosphorylation and dephosphorylation on supported lipid bilayers (SLBs). Fluorescently labeled protein constructs of defects in Rab recruitment protein A (DrrA) (17–19) and a pleckstrin homology (PH) domain derived from phospholipase C δ (PLCδ) (20) were used to selectively visualize PI(4)P and PI(4,5)P2 lipids in real time by total internal reflection fluorescence (TIRF) microscopy (Fig. 1A and SI Appendix, Fig. S1). Single-molecule binding-desorption measurements confirmed that both PIP lipid sensors exhibit single-exponential membrane dwell time distributions (corresponding to first-order dissociation kinetics) with mean dwell times of 25 ms (Alexa488-PLCδ) and 289 ms (Alexa647-DrrA) (Fig. 1A and SI Appendix, Fig. S2 A–F). Both PIP lipid sensors were highly mobile with diffusion coefficients of 2.2 to 2.4 µm2/s and exhibited negligible amounts of nonspecific binding on supported membranes (SI Appendix, Fig. S2 G and H). Probe concentrations were adjusted so that only a minor fraction (<0.1%) of membrane PIP lipid was bound to the probe, ensuring that the probes had minimal interference with the enzymatic reactions. Evaluating the fluorescence intensity of membrane-bound sensors over a range of PIP lipid concentrations (i.e., 0 to 4% molar) established a linear relationship between these parameters (SI Appendix, Fig. S2 I and J). This system provides a readout of membrane PI(4)P and PI(4,5)P2 lipid composition with subsecond time resolution and submicron spatial resolution.
Fig. 1.
Enzymology of phosphatidylinositol lipid kinase and phosphatases. (A) Schematic of PIP lipid-modifying reactions reconstituted on a supported lipid bilayer (SLB). Enzymes associate with membranes containing PI(4)P and PI(4,5)P2 lipids, catalyze PIP lipid phosphorylation or dephosphorylation, and then dissociate. Product formation was monitored using soluble Alexa647-DrrA and Alexa488-PLCδ, which transiently associate with PIP lipid-containing membranes. (B) Phosphorylation of PI(4)P to generate PI(4,5)P2 monitored in the presence of 20 nM Alexa488-PLCδ and varying concentrations of PIP5K. Initial membrane composition: 96% DOPC and 4% PI(4)P. (C) Single-molecule dwell-time distribution of Alexa647-PIP5K measured on SLBs containing 1% (τ1 = 88 ± 1 ms; n = 1,709 events), 2% (τ1 = 344 ± 4 ms; n = 2,347), or 4% PI(4,5)P2 (τ1 = 625 ± 1 ms [42%]; τ2 = 2.25 ± 0.01 s [58%]; n = 1,544). CDF = cumulative distribution frequency. (D and E) Dephosphorylation of PI(4,5)P2 was monitored in the presence of 20 nM Alexa647-DrrA and varying concentrations of (D) OCRL or (E) DrrA-OCRL. Initial membrane composition: 96% DOPC and 4% PI(4,5)P2.
Using this system, we first analyzed the kinetics of isolated PIP lipid-modifying reactions. Visualizing PIP5K-dependent phosphorylation of PI(4)P to generation of PI(4,5)P2 revealed reaction kinetics with a high degree of positive feedback (Fig. 1B). For soluble enzymes acting on membrane substrates, product binding independently of the catalytic site can promote positive feedback by retaining more enzyme on the membrane surface (21–23). Consistent with this notion, the amount of Alexa647-PIP5K localized to the membrane surface increased with increasing PI(4,5)P2 membrane density (SI Appendix, Fig. S3A). Additionally, the mean dwell time of Alexa647-PIP5K, determined from single-molecule imaging experiments, also increased with PI(4,5)P2 membrane density (Fig. 1C). This implicates multivalent PI(4,5)P2 interactions as a source of the observed PIP5K positive feedback. In contrast, we found that the 5′-PPtase domains derived from OCRL and INPP5E exhibited no feedback and catalyzed PI(4)P synthesis with simple bimolecular reaction kinetics (Fig. 1D and SI Appendix, Fig. S4). The activity of OCRL was ∼100-fold greater than INPP5E. Single-molecule dwell times for both 5′-PPtases were faster than our instrumental resolution of 8 ms per frame.
Several proteins have been reported to regulate membrane recruitment of 5′-PPtases in living cells. These include small GTPases and the AP1/AP2 adaptor protein complexes that regulate clathrin-mediated endocytosis (24, 25). To access the broad range of 5′-PPtase activities that arise from interactions with membrane-associated signaling proteins, we designed chimeric phosphatases with engineered membrane targeting domains. The simplicity of the 5′-PPtase domains facilitated linkage of a PI(4)P lipid binding domain to the N terminus of either OCRL or INPP5E. Compared with the bare 5′-PPtase domains, the engineered DrrA-INPP5E and DrrA-OCRL were much more active (Fig. 1E and SI Appendix, Fig. S5). The kinetic traces for both chimeric phosphatases were fit by a kinetic model with first-order positive feedback based on lipid product recognition (SI Appendix, Enzyme Kinetics). Overall, the chimeric 5′-PPtases expanded our repertoire of enzymes to span the broad range of activities that potentially exist in this ubiquitous signaling pathway under physiological conditions.
Kinetic Bistability in a Lipid Kinase–Phosphatase Competitive Reaction.
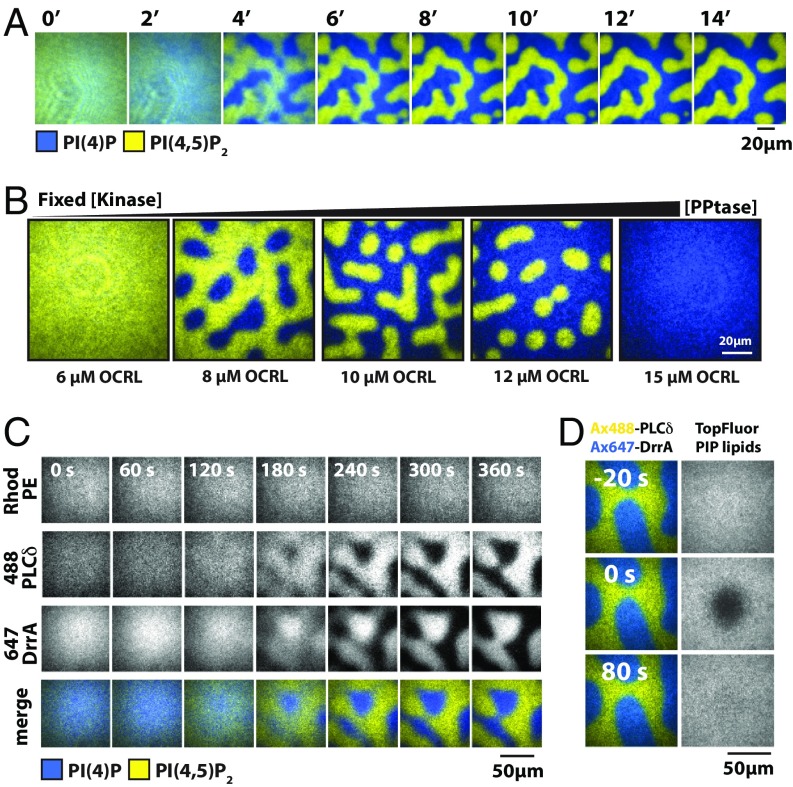
Using our panel of lipid-modifying enzymes, we reconstituted a range of PIP lipid kinase–phosphatase competitive reaction systems driving the interconversion of PI(4)P and PI(4,5)P2 lipids in supported membranes. Based on the nonlinear positive feedback we measured for PIP5K, we anticipated that it would be possible to tune this system to exhibit kinetic bistability, in which the overall reaction rate could go to zero at 2 different PIP lipid compositions (26, 27). For these studies, reactions were initiated on membranes containing 2% molar fraction of PI(4)P and PI(4,5)P2 lipids by flowing in a mixture of lipid sensors, ATP, and the opposing kinase and phosphatase enzymes. By varying the kinase–phosphatase ratio, the final reaction outcome could be tuned to favor either PI(4)P- or PI(4,5)P2-dominated states as a final outcome. When the overall kinase and phosphatase reactions are relatively balanced, however, much more interesting behavior ensued. Within a matter of minutes, we observed the reaction environment to split into regions that were enriched in either PI(4)P or PI(4,5)P2 (Fig. 2A, SI Appendix, Fig. S6, and Movie S1). PIP lipid patterns emerged on membranes lacking any preexisting patterns or positional information and amplified and coarsened over time. The surface area of steady-state patterns could also be changed by varying the initial kinase–phosphatase concentration ratio (Fig. 2B and SI Appendix, Fig. S6) or by flowing in new ratios of kinase and phosphatase (SI Appendix, Fig. S7 A–C). We note that this is a dissipative reaction system that continuously consumes ATP; steady-state conditions require a constant supply of ATP (SI Appendix, Fig. S8). The signature features of this reaction system—bistability and formation of compositional pattern—proved to be rather general properties that could be reconstituted using a variety of kinase–phosphatase combinations, including both native and engineered enzymes (SI Appendix, Fig. S6). The only basic requirement was that the competing reactions were roughly balanced on the membrane surface and at least 1 enzyme has a positive-feedback loop based on product recognition. From a practical perspective, the chimeric 5′-PPtases balanced the native PIP5K reaction kinetics at similarly low concentrations in solution, facilitating experiments.
Fig. 2.
Reconstitution of PIP lipid compositional patterns. (A) Time dependence of PIP lipid composition pattern formation reconstituted on SLBs in the presence of 50 nM PIP5K and 30 nM DrrA-OCRL. (B) The surface area of PIP composition patterns varies based on kinase–phosphatase concentration ratio. Kinase–phosphatase competitive reactions reconstituted in the presence of 50 nM PIP5K and varying concentrations of OCRL. (C) Rhodamine PE lipid (0.1% molar percentage) localization remains unchanged during spatial pattern formation. (D) FRAP of TopFluor PIP lipid (0.1% molar percentage) in composition patterns. TopFluor fluorescence represents the spatial distribution of both PI(4)P and PI(4,5)P2. (A–D) Initial membrane composition: 96% DOPC, 2% PI(4)P, 2% PI(4,5)P2, and 0.1% indicated fluorescent lipid. All competitive kinase–phosphatase reactions contained 20 nM Alexa488-PLCδ and 20 nM Alexa647-DrrA PIP lipid sensors.
Individual lipids and proteins remained highly dynamic throughout the reaction process, irrespective of composition patterns. Bulk imaging and single-molecule tracking of rhodamine-labeled phosphatidylethanolamine lipids in the membrane demonstrated that only the distribution of the PIP lipid phosphorylation state was spatially modulated; the membrane was otherwise homogeneous and fluid (Fig. 2C and SI Appendix, Fig. S9). Additionally, fluorescence recovery after photobleaching (FRAP) of a TopFluor tail-labeled PIP lipid confirmed uniform distribution and mobility of PIP lipids (Fig. 2D and SI Appendix, Fig. S9D). Individual PIP lipid molecules diffused rapidly into and out of the PI(4)P and PI(4,5)P2 regions, with their phosphorylation state changing as a result of the locally prevailing enzymatic reaction. Kinase and phosphatase membrane localization was governed by the local PIP composition (SI Appendix, Fig. S10). All enzymes were laterally mobile on the membrane surface during periods of association, but diffused more slowly than did individual lipids, which is consistent with multivalent binding of PIP lipids (SI Appendix, Fig. S11 C and D). FRAP analysis of Alex647-PIP5K and Cy5-DrrA-OCRL localized to compositional patterns indicated that these enzymes rapidly exchanged between the membrane and solution (SI Appendix, Fig. S11 A and B). Overall, both lipids and proteins in the reaction diffused and exchanged much faster than the timescale (minutes) at which the composition patterns evolved.
Bistability and Stochastic Fluctuations in Spatially Homogeneous Systems.
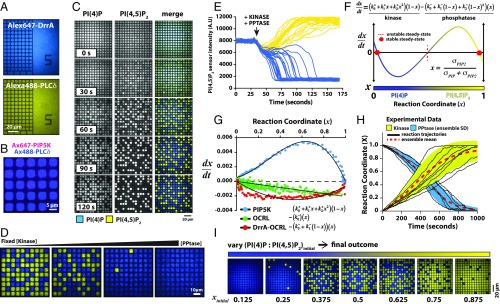
Kinetic bistability fundamentally results from positive feedback in the underlying enzymatic reactions. For this system, kinetic observations revealed distinctively asymmetrical behavior between the kinase and phosphatase reactions. PIP5K exhibited at least second-order positive feedback with increasing reaction rate as PI(4,5)P2 membrane concentration increased (SI Appendix, Effective Mean Rate Equation). In contrast, the native and engineered 5′-PPtases catalyzed the dephosphorylation of PI(4,5)P2 with simple bimolecular or linear positive-feedback kinetics, respectively (SI Appendix, Figs. S4 and S5 and Enzyme Kinetics). Comparing the association rate constants for Alexa647-PIP5K and Cy5-DrrA-OCRL revealed that the phosphatase binds to membranes approximately twice as fast as PIP5K (SI Appendix, Fig. S11 E–H). To further investigate the origins of kinetic bistability in this reaction system, and to separate this from the secondary process of spontaneous pattern formation, we ran the reactions on supported membrane microarrays (Fig. 3A). Metal structures fabricated onto the underlying glass substrate impose barriers to lateral diffusion within the membrane. Lipids and membrane-associated proteins diffuse freely within each confined corral but cannot cross the barriers (21, 28). However, at only ∼10 nm high, these barriers pose no impediment to diffusion or exchange of proteins within the adjoining 3D solution. Arrays of geometrically defined membrane corrals, all in contact with an identical 3D solution, can be studied in parallel.
Fig. 3.
Kinetic asymmetry and compositional fluctuations regulate kinase–phosphatase competitive reaction. (A) Chromium pattern SLBs incubated with 20 nM Alexa647-DrrA (blue, Top) and 20 nM Alexa488-PLCδ (yellow, Bottom). (B) Soluble enzymes bind stochastically to membrane corrals. Image of Alexa647-PIP5K (magenta) bound to membrane corrals containing PI(4,5)P2. (C) Kinase–phosphatase reaction exhibits bistability when reconstituted in 5 × 5-µm corrals in the presence of 50 nM PIP5K and 30 nM DrrA-OCRL (SI Appendix, Movie S2). (D) Final reaction outcome is regulated by the kinase–phosphatase concentration ratio. Competitive reactions reconstituted in the presence of 30 nM PIP5K and 6, 10, 12, or 15 µM OCRL (Left to Right). (E) Reaction trajectories for the bistable kinase–phosphatase reaction reconstituted in 5 × 5-µm corrals in the presence of 50 nM PIP5K and 30 nM DrrA-OCRL. Trajectories color reflects final reaction outcome—PI(4)P (blue) or PI(4,5)P2 (yellow). (F) Kinetic phase space for an intrinsically bistable kinase–phosphatase competitive reaction (SI Appendix, Enzyme Kinetics). (G) Experimental feedback profiles for the various enzymes measured in the presence of OCRL, DrrA-OCRL, and PIP5K. The following equations were used for curve fitting: for OCRL, for DrrA-OCRL, and for PIP5K. . (H) Reaction trajectories independently measured in 5 × 5-µm corrals in the presence of either 2.5 nM PIP5K or 10 pM DrrA-OCRL (n = 256 corrals; yellow or blue shading equals SD). Initial membrane compositions: 96% DOPC, plus 4% PI(4)P for PIP5K or 4% PI(4,5)P2 for DrrA-OCRL reaction. (I) Images of the final configuration for a series of membrane microarray reactions beginning at different starting PIP compositions (xinitial). Initial membrane composition: 96% DOPC, 2% PI(4)P, and 2% PI(4,5)P2 for reactions in C, D, and E. All competitive reactions contained 20 nM Alexa488-PLCδ, and 20 nM Alexa647-DrrA to visualize PIP lipids.
We focus initially on the reaction system in confined membrane corrals of 5 × 5 µm. At this size scale, lateral diffusion within the membrane is sufficiently fast for all components that no PIP lipid patterns form and each corral provides a spatially homogeneous reaction system. All corrals initially had the same lipid composition and were in contact with the same enzyme solution. The copy number of enzymes on the membrane surface at any moment varied as a function of PIP composition and could be less than 1 molecule per square micrometer in some cases (Fig. 3B). As such, the behavior of PIP lipid phosphorylation reactions in confined corrals exhibits significant effects from stochastic fluctuations in enzyme copy number resulting from membrane binding and unbinding events. As the reactions progressed, compositions of individual corrals initially tracked similarly, until variations caused them to diverge, and ultimately converge onto 1 of the 2 final composition states (Fig. 3C and SI Appendix, Fig. S12 and Movie S2). Varying the kinase–phosphatase concentration ratio and enzyme type influenced the final reaction outcome, but bistability is robust (Fig. 3D). Reaction trajectories from an array of 5 × 5-µm membrane corrals illustrating this kinetic bistability are plotted in Fig. 3E. After steady state was reached, further changes in composition were not observed in corrals, even though individual reactions remained active and all individual components continued to turn over. No communication between corrals was observed (SI Appendix, Fig. S12).
To quantitatively analyze bistability in this system, we defined the reaction coordinate, x, as , where and represent the membrane surface densities of PI(4)P and PI(4,5)P2, respectively. The effective mean reaction rate can be expressed as follows:
In this representation, and are functions that characterize the mean reaction rate per molecule of the forward and reverse reactions; their values depend on the concentrations of enzymes in solution and the PIP lipid composition (SI Appendix, Effective Mean Rate Equation). Feedback exhibited by the enzymatic reactions is reflected in the x dependence of and . At least second-order feedback [e.g., in a power series representation of ] is necessary for macroscopic kinetic bistability (intrinsic bistability), in which 2 different lipid compositions exhibit stable steady states (Fig. 3F) (29). However, apparently bistable behavior can result even with only linear feedback due to stochastic fluctuations. This phenomenon is sometimes referred to as stochastic bistability (30–32). We examined the origin of the experimentally observed bistability by analyzing the feedback profiles of the enzymes.
We measured individual enzymatic reaction rates over the full range of PIP lipid compositions to experimentally map the functional forms of and for the various enzymes. The native phosphatases, OCRL and INPP5E, exhibited linear scaling of reaction rate with x, indicating is a constant; these enzymes exhibit no feedback (Fig. 3G and SI Appendix, Fig. S4). For phosphatases engineered with a single PI(4)P product-binding domain, the reaction rate was nearly parabolic and was fit by , where first-order positive feedback in the PI(4)P product is represented by the term (Fig. 3G and SI Appendix, Fig. S5). Fitting 5′-PPtase kinetic traces using a model with higher order positive feedback did not improve the overall fit (SI Appendix, Fig. S5H). In contrast, the reaction rate for PIP5K was highly asymmetrical and required terms up to second order, , to fit kinetic data (Fig. 3G). In the case of the PIP5K, binding at least 2 PI(4,5)P2 lipids in the membrane establishes strong second-order positive feedback. The enzymes used in these experiments exhibit sufficient nonlinear feedback to enable macroscopic bistability in the mean reaction rate. However, for many of the experimental enzyme concentrations studied here, macroscopic bistability was not achieved and the system exhibited only stochastic bistability, which turns out to be an important distinction to which we return later.
In Fig. 3I, the final states of several membrane corral arrays are depicted for reactions starting from a range of initial PIP membrane compositions. Although the relative probability of reaching the PI(4)P- or PI(4,5)P2-enriched steady states clearly depended on starting composition, both states were still accessible from a wide range of initial PIP lipid compositions. This rules out the possibility that the final state of an individual reaction corral is dictated by subtle variations in its starting lipid composition. Instead, the system experiences large fluctuations in PIP composition, and these were observed in the individual reaction trajectories (Fig. 3H). Such large composition fluctuations could not arise from intrinsic noise in PIP lipid copy number because there were ∼108 PIP lipids in even the smallest (∼4 µm2) membrane corrals; intrinsic PIP lipid copy number fluctuations would not exceed ∼0.01% (33, 34). The observed large fluctuations in composition stem from stochastic binding and desorption of enzymes on the membrane surface and the resulting fluctuations in reaction velocity.
Geometric Constraints Regulate Reaction Outcome.
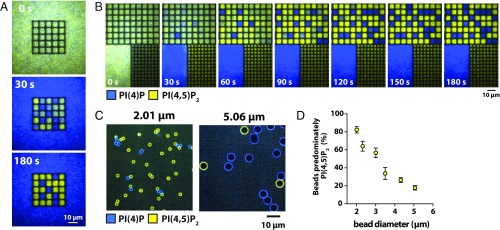
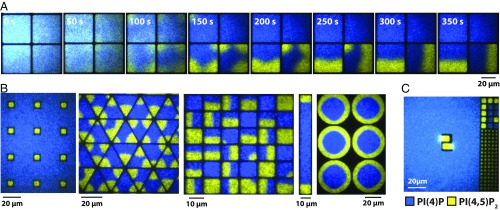
A distinct feature of this kinase–phosphatase competitive reaction, which we term geometry sensing, is that the final outcome is strongly dependent on the geometric confinement of the membrane reaction environment. The reaction system depicted in Fig. 4 A and B is tuned such that it universally converges on the PI(4)P-dominated state in large areas; this system is not macroscopically bistable. However, the array of 5 × 5-µm corrals clearly exhibits bistability, which we can now identify must be stochastic bistability. Perhaps most surprisingly, in the smallest corrals (∼2 × 2 µm), the system deterministically reached the PI(4,5)P2-dominated state (Fig. 4B, SI Appendix, Fig. S13 A and B and Movie S3), rather than converge on a 50–50 outcome. This dynamic configuration could be actively maintained over a period of several minutes. The geometry-sensing effect was also evident on membrane-coated microbeads of different sizes (Fig. 4 C and D and SI Appendix, Fig. S13C and Movie S4) (35), affirming that it resulted from the size and shape of the membrane regions, rather than boundary effects. This was further supported by the uniform binding and diffusivity of kinase and phosphatase enzymes on the membranes within corrals (SI Appendix, Fig. S14). This general phenomenon was observed for all kinase–phosphatase combinations, both native and engineered.
Fig. 4.
Size of membrane environment modulates kinase–phosphatase competitive reaction outcome. (A) Time sequence of the kinase–phosphatase reaction in a matrix of 5 × 5-µm corrals surrounded by free bilayer. The reaction is tuned for phosphatase to dominate on average on free bilayer, while reaction exhibits stochastic bistability in corrals. (B) Time sequence showing stochastic geometry sensing in the kinase–phosphatase competitive reaction in 4- and 25-µm2 corrals with adjacent free bilayer. (C) Representative images of lipid kinase–phosphatase competitive reaction reconstituted on 2- and 5.06-µm lipid-coated beads. (D) Frequency of predominantly PI(4,5)P2 final steady state for the kinase–phosphatase reaction reconstituted on lipid-coated beads with different diameters. Bars equal SD (n = 3). Competitive reactions (A–D) reconstituted in the presence of 50 nM PIP5K, 40 nM DrrA-OCRL, 20 nM Alexa488-PLCδ, and 20 nM Alexa647-DrrA. Initial membrane composition: 96% DOPC, 2% PI(4)P, and 2% PI(4,5)P2.
Stochastic Geometry Sensing Based on Kinetic Asymmetry.
One feature of any molecular reaction system that is intrinsically dependent on system size is the spectrum of stochastic composition fluctuations generated by the reaction (33, 34). Thus, rather than responding to geometric size per se, we propose that this kinase–phosphatase reaction is differentially governed by stochastic fluctuations within the reaction system itself. Under conditions of stochastic geometry sensing, the average reaction is tuned such that the phosphatase has a slight kinetic advantage. In large regions, where the individual reaction trajectories track much closer to the ensemble average, the final result of a PI(4)P-dominated membrane composition is observed with high probability. In smaller membrane corrals, fluctuations in composition are relatively larger and individual reaction trajectories explore a wider range of compositions. If a particular reaction reaches high enough PI(4,5)P2 density, then the kinase reaction begins to dominate and drives the system to the PI(4,5)P2-dominated steady state. The observed system behavior is determined by a first-passage probability rather than the mean kinetic rate. The apparent final state is thus not necessarily formally stable, but it is metastable for experimentally long periods of time.
We tested this hypothesis with stochastic kinetic modeling of a simple kinase–phosphatase reaction system (Fig. 5A). In this model, the kinase exists in 1 of 3 states, , corresponding to solution, singly, and doubly bound to PI(4,5)P2 lipids in the membrane. The phosphatase is treated similarly, although with only 2 states, , mimicking the single PI(4)P lipid binding of the engineered phosphatase construct. Conversion among these states is governed by mass action with kinetic rate constants and is modeled stochastically using a Gillespie algorithm (36) (SI Appendix, Stochastic Simulations). Similar to the corral experiments, the system exhibited kinetic bistability (Fig. 5B) and the reaction outcome was directly related to the ratio of kinase and phosphatase (Fig. 5 C and D). When modeling parameters were based on measured membrane binding kinetics and catalytic rates for the enzymes, this model reproduced the basic features of stochastic geometry sensing (Fig. 5 E and F). Under these conditions, the mean reaction rate (Fig. 5E) did not exhibit bistability; the behavior of the model system resulted from stochastic bistability only. When model parameters are adjusted to strengthen positive feedback and achieve macroscopic bistability in the mean reaction rate (Fig. 5G), the final reaction outcome was invariant with membrane corral size and stochastic geometry sensing was lost (Fig. 5H). Geometry sensing is thus not a simple by-product of bistability.
Fig. 5.
Stochastic geometry sensing based on kinetic asymmetry between opposing enzymes. (A) Scheme of kinase (3-state) and phosphatase (2-state) membrane binding mechanism was modeled stochastically using a Gillespie algorithm, while enzyme activity was modeled continuously following a Michaelis–Menten reaction mechanism (SI Appendix, Effective Mean Rate Equation). (B) Kinetic traces from a stochastic simulation of the reaction mechanism described in A. (C and D) Kinetic phase for stochastic simulations performed with different kinase–phosphatase concentrations. (E) Plot of kinetic phase space for experimentally measured parameters. (F) Final reaction outcomes for stochastic simulations shown for system (E) performed on a variety of corral sizes. System exhibits basic features of stochastic geometry sensing. (G) Kinetic phase space plot for a macroscopically bistable kinase–phosphatase competitive reaction. (H) Final reaction outcomes for stochastic simulations of system (G). (I) Kinetic phase space plot for kinase–phosphatase competitive reaction with only linear positive feedback, lacks macroscopic bistability and exhibits stochastic bistability. (J) Final reaction outcomes for stochastic simulations of system shown in I using enzymes with different binding kinetics. In all cases, the overall affinity of the enzymes for the membrane is identical, and correspondingly, they all have the same kinetic phase (G). (F, H, and J) Simulations were performed on membranes with dimensions 0.25, 0.5, 1, and 2 µm2. The initial membrane composition x = 0.5 [i.e., 50% PI(4)P and 50% PI(4,5)P2]. Percentages represent PI(4,5)P2-dominated corrals for n = 2,000 simulation per corral size. For parameters, see SI Appendix, Stochastic Simulations, Table S1, and Supporting Code S1.
Geometry sensing with essentially deterministic outcome, such as we experimentally observe, requires that the system exhibit strongly asymmetrical response to fluctuations in composition. Binding kinetics of enzymes to the membrane provides a source of temporal asymmetry in this system. This binding kinetics establishes a response time for the density of enzymes recruited to the membrane based on the changing membrane PIP composition. We examined the effect of this temporal asymmetry by simulating a series of reaction systems that have identical mean reaction velocity functions (Fig. 5I and SI Appendix, Fig. S15), but differ in the ratios of membrane binding kinetics between kinase and phosphatase. For this calculation, we chose a minimal model system in which both kinase and phosphatase exhibit only linear feedback; both were modeled with the 2-state mechanism as depicted for the phosphatase (Fig. 5A) with the kinase having a membrane binding rate equal to or faster than the opposing phosphatase (Fig. 5J). This system exhibits stochastic bistability under conditions in which the enzymes exhibited similar membrane binding kinetics (Fig. 5J, top row). Stochastic geometry sensing with the kinase reaction favored in smaller corrals, however, was only observed when the kinase exhibited faster membrane binding kinetics than the phosphatase (Fig. 5J, middle 2 rows). In the case where the kinase bound overwhelmingly fast (Fig. 5J, bottom row), the competitive reactions were no longer kinetically balanced and the phosphorylation reaction dominated in all sizes—geometry sensing was also lost.
Polarization under Spatial Confinement.
The reactions remained spatially homogeneous within corrals smaller than ∼10 µm, due to rapid lateral diffusive mixing within the membrane. However, under larger-scale geometric constraints, the system adopted spatially defined patterns in response to the constraint geometry. Increasing the size of the corrals to ≥10 × 10 µm allowed the competitive membrane reaction to spontaneously polarize into coexisting regions enriched in PI(4)P and PI(4,5)P2 (Fig. 6A). The process of polarization is revealed in a time sequence of images (Fig. 6A). The kinase reaction initially gained a foothold in the partially confined corners of the corral (Movie S5). Eventually the PI(4,5)P2 enrichment in 2 adjacent corners merged and the system evolved to a relatively stable polarized state. Thus, polarization appears to result from a combination of geometry sensing, to first locate corners, followed by pattern evolution through a reaction diffusion process consisting of enzymatic reactions and lipid diffusion within the membrane. Many different reproducible patterned states resulted from different types of spatial confinement (Fig. 6B). These effects did not require that the membrane region be entirely contained. The PI(4,5)P2 membrane composition dominated within a semibounded feature that was in open, diffusive contact with the surrounding phosphatase-dominated PI(4)P membrane (Fig. 6C).
Fig. 6.
Polarization and geometry sensing of spatially confined kinase–phosphatase competitive reactions. (A) Time sequence showing polarization of 20 × 20-µm corrals in the presence of 50 nM PIP5K, 200 nM DrrA-INPP5E, 20 nM Alexa488-PLCδ, and 20 nM Alexa647-DrrA. (B) Examples of stochastic geometry sensing and polarization in corrals. (C) Semibound corral supports stochastic geometry sensing that favors kinase reaction. Competitive reactions (B and C) reconstituted in the presence of 50 nM PIP5K, 40 nM DrrA-OCRL, 20 nM Alexa488-PLCδ, and 20 nM Alexa647-DrrA. Initial membrane composition: 96% DOPC, 2% PI(4)P, and 2% PI(4,5)P2.
Discussion
Symmetry breaking and the establishment of spatial patterns of molecules in a dynamic, fluid membrane environment is a hallmark of cellular organization in living systems. The physical basis of these phenomena has attracted scientific attention for decades. Alan Turing’s landmark paper (16), which highlighted the formation of stable patterns in reaction–diffusion systems, has been influential on our understanding of how biological signaling systems may self-organize (4, 15). Turing patterns are deterministic solutions to continuum differential equations describing the distribution of molecular species in a reaction–diffusion system. The requirements under which such stable solutions can be achieved are restrictive, and only a handful of systems exhibiting Turing patterns have been experimentally realized (37–39).
One prominent example of a biological pattern forming system that operates on the membrane surface is the bacterial Min protein oscillator. This system produces propagating waves (39) and standing oscillatory patterns (40) that self-organize on membrane surfaces in vitro and in vivo. The Min system also responds to geometric confinement (41), albeit in distinctively different ways than we observe in the kinase–phosphatase reactions. For example, when the Min oscillator is geometrically constrained on membranes that are smaller than its characteristic wavelength, Min waves can cross 2D geometric boundaries on the membrane, allowing patterns to remain spatially coupled with neighboring membrane corrals (41). This feature stems from the fact that the Min waves are a reaction diffusion process that includes a spatially inhomogeneous diffusive component both on the membrane surface and in the adjoining solution. In contrast, no such correlation is observed in the kinase–phosphatase experimental system (SI Appendix, Fig. S12). Additionally, kinetic modeling of the kinase–phosphatase system reproduced geometry sensing under strictly homogeneous solution conditions. The formation of Min protein patterns also requires a molecular timing mechanism that is regulated by the local accumulation of the MinE ATPase, followed by a MinD-induced conformational change in MinE that drives dynamic instability of their membrane interaction (42). The kinase–phosphatase system is far simpler, with only a local dynamic equilibrium between solution and membrane-associated enzymes determining the prevailing reaction. We speculate that the phosphatidylinositol 3-kinase (PI3K) and phosphatase and tensin homolog (PTEN) may function in a similar manner to regulate cell polarity in eukaryotic cells.
In Dictyostelium and hematopoietic cells, PTEN and PI(3,4,5)P3 lipids exhibit mutually exclusive localization at the plasma membrane (8, 9, 43, 44). This consists of PIP3-enriched/PTEN-excluded and PTEN-enriched/PIP3-excluded states that are strikingly similar to the reciprocal localization of PIP5K and 5′-PPtases observed in the PIP compositional patterns reported in this study. This reciprocal localization pattern arises from at least 2 opposing positive-feedback loops: (i) Ras(GTP)-PI3K-PIP3 and (ii) PTEN-PIP2 (45, 46). Similar to the enzymes described in our system, PTEN localization and activity are thought to be directly regulated by compositional sensing of PI(4,5)P2 lipids, as well as PI(4,5)P2 independent mechanisms that remain unknown (47). Concerning the PI3K branch of this polarity pathway, compositional sensing is generally thought to be indirect in the form of interactions between PIP3 and guanine nucleotide exchange factors (GEFs) that regulate small GTPase activity and consequently PI3K activation (48).
For the system described here, both PIP5K and the 5′-PPtases display a continuum of membrane binding affinities that depend on the local PIP lipid composition [e.g., 0 to 4% PI(4,5)P2]. The kinase transiently associates with the lipid bilayer containing low densities of PI(4,5)P2, while higher PIP2 densities support long-lived membrane interactions. Although compositional sensing of PIP lipids may underlie the complex network of positive- and negative-feedback loops the control the PI3K-PTEN polarity pathway, further biochemical characterization of those enzymes is required.
Early studies of stochastic effects on bistable reaction systems have identified system size effects (49) in the time-averaged probability distribution. Thus, although geometry sensing is in principle possible for systems with macroscopic bistability, we note that our experimental system behavior does not reflect the infinite time-averaged distribution. It is evident from the experimental data that the timescale to first reach a steady state is much faster than the time to switch between states. As such, the experimental system behavior is dominated by first-passage probabilities and we observe that such geometry sensing is effectively achieved primarily for systems that are macroscopically monostable.
The stochastic geometry sensing effect we describe here is not the result of a Turing instability in a reaction–diffusion system (16). We make this distinction to emphasize the fact that stochastic geometry sensing is simpler to achieve than a true Turing instability (4) and may therefore be more widespread in biology. The distinction between stochastic geometry sensing and Turing instability is most easily seen by noting that the geometry-sensing effect exists in spatially homogeneous reaction systems. As highlighted in Fig. 4 A and B, the reaction tends uniformly to the PI(4)P dominated state in larger regions and tends uniformly to the PI(4,5)P2 state in the smallest corrals. The underlying mechanism for this differential response, confirmed by kinetic modeling, is intrinsically stochastic; it has no analog in a mean or continuum model for such a system.
The experiments and modeling presented in this work establish a distinct mechanism for stochastic geometry sensing under spatially homogenous conditions. Our experimental results further illustrate how partial confinement can produce similar effects to complete confinement (e.g., Fig. 6C). One of the more striking, and perhaps biologically significant, effects we observed is the tendency for the system to polarize in slightly larger confined regions (e.g., 20 × 20 µm). In Fig. 6A of the main text, a series of images tracking the development of a polarized pattern reveals that the PI(4,5)P2 initially becomes enriched in corral corners. This process resembles the stabilized PI(4,5)P2 domain observed under partial confinement (Fig. 6C) mentioned above. In both cases, partial confinement hinders escape of PI(4,5)P2 as it is produced by membrane-bound kinase, thus triggering the kinase positive-feedback loop. This allows PI(4,5)P2 concentrations to grow higher than average, which in turn favors recruitment of more kinase to that location. This is the stochastic geometry-sensing mechanism. In the case of polarization, however, the confinement is too large to be entirely homogenized by diffusion. Instead, the evolution of the system involves an additional reaction–diffusion process. Stochastic geometry-sensing effects appear to be able to nucleate a pattern [e.g., PI(4,5)P2 enrichment in the corners], which then seeds a reaction–diffusion process that further evolves the pattern into the polarized state. With respect to a Turing instability, for polarization and other more complex patterns, in which stochastic geometry sensing seeds a reaction–diffusion process, it is possible that a Turing instability is achieved at some point. However, we do not currently have sufficient information about these processes to make definitive distinctions. What is certain is that stochastic geometry sensing can be achieved within isolated regions of membranes as well as partially confined regions based only on the fluctuation mechanism, without need for a Turing instability.
The basic requirements for stochastic geometry sensing are reaction feedback, at least stochastic bistability, and temporal asymmetry in membrane binding kinetics of the competing enzymes. These basic properties are shared by other kinase–phosphatase reaction systems and are also found in other biological signaling processes, such as Ras activation by GEFs and deactivation by GTPase-activating proteins (GAPs) (21, 50–52). The environment inside a living cell is subject to a diverse range of geometrical confinements (53), including membrane sheets, blebs, tubules, vesicles, and organelles (54–56). Additionally, the actin cytoskeleton can impose barriers that confine the diffusive movement of proteins and lipids laterally in the plasma membrane (57, 58). Basic membrane structures, such as a filopodium, produce a geometrical constraint on the cell membrane reaction environment that resemble some experimental conditions studied here (e.g., Fig. 6C). We suggest that stochastic geometry sensing is likely to contribute to the spatial patterning of molecules, such as PIP lipids, in cellular membranes.
Materials and Methods
Molecular Biology.
Genes coding for Legionella pneomophila DrrA/SidM (accession number Q5ZSQ3.1), human phosphatidylinositol 4,5-bisphosphate phosphodiesterase delta-1 PH domain (PLCδ; accession number P51178.2), human inositol polyphosphate-5-phosphatase E (INPP5E; accession number Q9NRR6), human oculocerebrorenal syndrome of Lowe inositol polyphosphate 5-phosphatase (OCRL; accession number Q01968), and human phosphatidylinositol 4-phosphate 5-kinase type-1β (PIP5Kβ; accession number O14986) were synthesized by GeneArt (Invitrogen) as codon-optimized open reading frames (ORFs). Gene encoding enzymes and lipid binding domains were subcloned into bacterial or baculovirus protein expression vectors containing coding sequences with different solubility and affinity tags. PIP5Kβ was cloned into a modified FAST Bac1 vector using ligation-independent cloning (59, 60). The complete ORFs of all vectors used in this study were sequenced by the University of California, Berkeley, DNA sequence facility to make sure no deleterious mutations were acquired during cloning. We screened protein expression conditions to maximize yield and solubility in both bacteria (BL21 DE3 Star, pRARE, Rosetta, etc.) and Spodoptera frugiperda (Sf9) insect cells.
Protein Expression and Purification.
See SI Appendix.
Preparation of Small Unilamellar Vesicles.
The following lipids were used to generated small unilamellar vesicles (SUVs): 1,2-dioleoyl-sn-glycero-3-phosphocholine (18:1 DOPC; Avanti; 850375C), l-α-phosphatidylinositol-4-phosphate [brain PI(4)P; Avanti; catalog number 840045X], l-α-phosphatidylinositol-4,5-bisphosphate [brain PI(4,5)P2; Avanti; 840046X], 1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine-N-(lissamine rhodamine B sulfonyl) (16:0 Liss Rhod PE; Avanti; 810158C), 1,2-dioleoyl-sn-glycero-3-phospho-l-serine (18:1 DOPS; Avanti; 840035C). In the main text, 16:0 Liss Rhod PE is referred to as Rhod PE. Brain PI(4)P and PI(4,5)P2 were purchased as 0.25 mg/mL stocks dissolved in chloroform:methanol:water (20:9:1).
To make liposomes, we combined 2 µmol of total lipids in a 35-mL glass round-bottom flask containing 2 mL of chloroform. Lipids were dried to a thin film using rotary evaporation with the glass round-bottom flask submerged in a 42 °C water bath. After evaporating all of the chloroform, the round-bottom flask was flushed with nitrogen gas for at least 30 min. The lipid film was hydrated and resuspended in 2 mL of PBS (pH 7.2), making a final concentration of 1 mM total lipids. All lipid mixtures mentioned in the manuscript are expressed as molar percentages [e.g., 98% DOPC, 2% PI(4)P]. For example, a 1 mM lipid mixture containing 98% DOPC and 2% PI(4)P is equivalent to 0.98 mM DOPC and 0.02 mM PI(4)P. To generate 30- to 50-nm SUVs, we extruded 1 mM total lipid mixtures through a 0.03-µm pore size 19-mm polycarbonate membrane (Avanti; 610002) with filter supports (Avanti; 610014) on both sides of the PC membrane.
Preparation of Supported Lipid Bilayers.
We created SLBs on 25 × 75-mm cover glass (IBIDI; 10812). Cover glass was first cleaned with 2% Hellmanex III (Fisher; catalog number 14-385-864) heated to 60 to 70 °C in a glass Coplin jar for 30 min. We then extensively washed the cover glass with MilliQ water, before etching the cover glass with Pirahna solution (1:3, hydrogen peroxide:sulfuric acid) for 10 to 15 min the same day SLBs were formed. Etched cover glass, in water, was rapidly dried with nitrogen gas before adhering to a six-well sticky-side chamber (IBIDI; catalog number 80608). To form a SLB, we flowed 100 to 150 µL of 0.25 mM SUVs diluted in PBS (pH 7.2) into the dry chamber. After 30 min, IBIDI chambers are washed with 5 mL of PBS (pH 7.2) to remove nonabsorbed SUVs. Membrane defects are blocked for 5 min with a 1 mg/mL β-casein (Thermo Fisher Science; catalog number 37528) diluted in 1× PBS (pH 7.4). Before using β-casein, frozen aliquots of 10 mg/mL β-casein were thawed, centrifuged for 30 min at 21,370 × g, and 0.22-µm syringe filtered. After blocking SLBs with β-casein, membranes were washed with 2 mL of PBS. Right before our experiments, SLBs were washed with 1 mL of kinase buffer.
Kinetics Measurements.
The kinetics of PI(4)P phosphorylation and PI(4,5)P2 dephosphorylation was measured on SLBs using TIRF microscopy. The following reaction buffer was used for all of our experiments: 20 mM Hepes (pH 7.0), 150 mM NaCl, 1 mM ATP, 5 mM MgCl2, 0.5 mM EGTA, 200 µg/mL β-casein, 20 mM BME, and 20 mM glucose. For all experiments, we monitored the change in PI(4)P or PI(4,5)P2 membrane density using a solution concentrations of 20 nM Alexa647-DrrA(544-647) or 20 nM Alexa488-PLCδ, respectively. The concentration of lipid sensor used for the kinetic assays does not interfere with the kinase or phosphatase activity. By comparing the intensity of fluorescence lipid sensors measured by TIRF microscopy in the presence of both 20 nM and near-saturating micromolar concentrations (SI Appendix, Fig. S1), we estimate that <0.1% of the PIP lipids are bound to a lipid sensor at any point during the kinetic experiments. Assuming a footprint of 0.72 nm2 for DOPC lipids (61, 62), we calculated a density of 2.8 × 104 lipids/µm2 for 2% PI(4)P or 2% PI(4,5)P2.
Reconstitution of PIP Lipid Compositional Pattern.
Liposomes containing an initial lipid composition of 96% DOPC, 2% PI(4)P, and 2% PI(4,5)P2 were used to make SLBs on Piranha etched glass coverslips. Visual inspection of both PIP lipid sensors showed highly dynamic membrane-bound proteins that rapidly diffused on the 2D membrane surface before dissociating. Before initiating reaction with lipid-modifying enzymes, 20 nM Alexa488-PLCδ and 20 nM Alexa647-DrrA(544-647) were added to the flow cells and imaged using TIRF microscopy. To initiate PIP kinase–phosphatase competitive reactions, PIP5K and a 5′-PPtase were flowed into the reaction chamber. PIP lipid sensors at concentrations of 20 nM Alexa488-PLCδ and 20 nM Alexa647-DrrA(544-647) were included with the catalytic domains to maintain the initial PIP lipid sensor concentrations. By systematically testing different combinations and concentrations of lipid-modifying enzymes, we established conditions that allow the balanced activities of PIP5K and a 5′-PPtase (native and engineered) to drive bistability and spatial patterning of PI(4)P and PI(4,5)P2 lipids of supported membranes. Compositional patterns were typically visualized using a 60× TIRF objective at a rate of four frames per minutes. Experiments were performed at 21 to 23 °C.
Bistable Competition Reactions Reconstituted on Chromium Pattern Membranes.
Kinase–phosphatase competitive reactions were reconstituted on chromium-patterned membrane surfaces using balanced in PIP5K and OCRL (or DrrA-OCRL) activity such that the resulting final reaction outcome was ∼50% PI(4)P and 50% PI(4,5)P2 on 5 × 5-µm corrals. These conditions served as a reference to reactions reconstituted on smaller (2 × 2 µm) or larger patterns (>10 × 10 µm). The experiment presented in Fig. 3C, for example, was designed to achieve a ∼50–50 reaction outcome beginning with the following membrane composition: 96% DOPC, 2% PI(4)P, and 2% PI(4,5)P2. The initial membrane composition [i.e., PI(4)P:PI(4,5)P2 ratio] was also varied to determine how the final reaction outcome was altered (Fig. 3I). Following injection of the enzymes into the reaction chambers, we typically observed a subtle change in the PIP lipid sensor intensities. This was due to a variety of factors, including (i) reequilibration of the lipid sensors, (ii) competition between the enzymes and sensors, and (iii) 1 enzyme functioning faster than the opposing enzyme.
Microscope Hardware and Imaging Acquisition.
Single-molecule imaging experiments were performed on an inverted Nikon Eclipse Ti microscope using a 100× Nikon objective (1.49 N.A.) oil-immersion TIRF objective. Macroscopic spatial patterning of PIPx lipid domains and the chromium-patterned SLB were visualized using a 60× Apo TIRF oil-immersion objective (1.45 N.A.). We manually controlled the x-axis and y-axis positions using an ASI stage and joystick. All images were acquired on an iXon Ultra EMCCD camera (Andor Technology). Fluorescently labeled proteins were excited with either a 488-, 561-, or 637-nm diode laser (OBIS laser diode; Coherent) controlled with a Solemere laser driver using analog and digital modulation (0 to 5 V). The power output measured through the objective for single-particle imaging was 1 to 3 mW. For dual-color imaging of spatial PIP lipid patterns on SLBs, samples were excited with 0.2- to 0.5-mW 488-nm and 0.2- to 0.5-mW 637-nm light, as measured through the objective. Excitation light was passed through the following dichroic filter cubes before illuminating the sample: (i) ZT488/647rpc and (ii) ZT561rdc (ET575LP) (Semrock). Fluorescence emission was detected on an ANDOR iXon Ultra EMCCD camera position after a Sutter emission filter wheel housing the following emission filters: ET525/50M, ET600/50M, and ET700/75M (Semrock). All experiments were performed at 21 to 23 °C. All microscope hardware was controlled using Micro-Manager, version 4.0 (63). Note that the nonuniform field of illumination observed in low-magnification images acquired using a 60× objective results from the high-power density of focused light created by the optics used for TIRF microscopy. This does not represent nonuniform binding the PIP lipid sensors (see Fig. 1C for example). For quantitative analyses, the nonuniform field of illumination is always corrected (using the ImageJ/Fiji plugin called shading corrector). However, we considered the raw images preferable since they convey the point without any need for illumination scaling.
Stochastic Simulations.
We used Gillespie-based stochastic simulations to evaluate the stochastic effect of enzyme binding kinetics on the bistable kinase–phosphatase reaction outcomes. The membrane composition, , within a small corral (approximately square micrometer) was approximated to be homogeneous (the diffusion coefficient of lipids in supported membranes is ∼3 µm2/s). Since the stochastic fluctuations in this system are primarily due to low number of membrane-bound enzymes (∼1 to 10 molecules per µm2 in the initial reaction), the protein copy number on membranes was simulated stochastically using the Gillespie algorithm (36). Each molecular species was expressed as the number of molecules. Both unimolecular and bimolecular reactions were expressed as the probabilities of the reaction occurring in the next time interval, , such that the rate parameters listed in SI Appendix, Table, have units of seconds−1. The processive catalysis by membrane-bound enzymes (as analyzed in Fig. 5A and SI Appendix, Effective Mean Rate Equation) was approximated with a deterministic chemical flux described by a mean rate equation: , where and is defined similarly (solution enzyme activities are considered to be negligible for enzymes that are processive only on membranes). In these simulations, all stochastic effects are therefore coming from enzyme recruitments, dissociations, and transitions into higher-order feedback complexes. All simulations began with and all enzymes in the solution unless stated otherwise. Simulations ended when the reaction time reached 30 unit time (which was usually sufficient for a trajectory to reach either or ). Statistics were collected from at least 2,000 simulations. All simulations were performed in Matlab R2016a.
Data and Materials Availability.
All of the information needed for interpretation of the data is presented in the manuscript or SI Appendix. Plasmids are available through Addgene.
Supplementary Material
Acknowledgments
We thank Scott Gradia (University of California, Berkeley, MacroLab) for plasmids and protocols for ligation-independent cloning. We thank Michael Vahey and Matt Bakalar (University of California, Berkeley) for critical reading of our manuscript. Funding was provided by National Institutes of Health U01 (CA202241) (to J.T.G.) and P01 (AI091580) (to J.T.G.), and National Research Service Award Postdoctoral Fellowship (F32 GM111010-02) (to S.D.H.). Additional support was provided by the Novo Nordisk Foundation Challenge Program under the Center for Geometrically Engineered Cellular Systems.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1901744116/-/DCSupplemental.
References
- 1.Di Paolo G., De Camilli P., Phosphoinositides in cell regulation and membrane dynamics. Nature 443, 651–657 (2006). [DOI] [PubMed] [Google Scholar]
- 2.Lassing I., Lindberg U., Specific interaction between phosphatidylinositol 4,5-bisphosphate and profilactin. Nature 314, 472–474 (1985). [DOI] [PubMed] [Google Scholar]
- 3.Ma L., Cantley L. C., Janmey P. A., Kirschner M. W., Corequirement of specific phosphoinositides and small GTP-binding protein Cdc42 in inducing actin assembly in Xenopus egg extracts. J. Cell Biol. 140, 1125–1136 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kondo S., Miura T., Reaction-diffusion model as a framework for understanding biological pattern formation. Science 329, 1616–1620 (2010). [DOI] [PubMed] [Google Scholar]
- 5.Wenk M. R., De Camilli P., Protein-lipid interactions and phosphoinositide metabolism in membrane traffic: Insights from vesicle recycling in nerve terminals. Proc. Natl. Acad. Sci. U.S.A. 101, 8262–8269 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Botelho R. J., et al. , Localized biphasic changes in phosphatidylinositol-4,5-bisphosphate at sites of phagocytosis. J. Cell Biol. 151, 1353–1368 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Scott C. C., et al. , Phosphatidylinositol-4,5-bisphosphate hydrolysis directs actin remodeling during phagocytosis. J. Cell Biol. 169, 139–149 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Servant G., et al. , Polarization of chemoattractant receptor signaling during neutrophil chemotaxis. Science 287, 1037–1040 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Arai Y., et al. , Self-organization of the phosphatidylinositol lipids signaling system for random cell migration. Proc. Natl. Acad. Sci. U.S.A. 107, 12399–12404 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Rameh L. E., Tolias K. F., Duckworth B. C., Cantley L. C., A new pathway for synthesis of phosphatidylinositol-4,5-bisphosphate. Nature 390, 192–196 (1997). [DOI] [PubMed] [Google Scholar]
- 11.Pirruccello M., De Camilli P., Inositol 5-phosphatases: Insights from the Lowe syndrome protein OCRL. Trends Biochem. Sci. 37, 134–143 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Mao Y., et al. , A PH domain within OCRL bridges clathrin-mediated membrane trafficking to phosphoinositide metabolism. EMBO J. 28, 1831–1842 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chao W. T., Daquinag A. C., Ashcroft F., Kunz J., Type I PIPK-alpha regulates directed cell migration by modulating Rac1 plasma membrane targeting and activation. J. Cell Biol. 190, 247–262 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lacalle R. A., et al. , Type I phosphatidylinositol 4-phosphate 5-kinase controls neutrophil polarity and directional movement. J. Cell Biol. 179, 1539–1553 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gierer A., Meinhardt H., A theory of biological pattern formation. Kybernetik 12, 30–39 (1972). [DOI] [PubMed] [Google Scholar]
- 16.Turing A. M., The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. B Biol. Sci. 237, 37–72 (1952). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Brombacher E., et al. , Rab1 guanine nucleotide exchange factor SidM is a major phosphatidylinositol 4-phosphate-binding effector protein of Legionella pneumophila. J. Biol. Chem. 284, 4846–4856 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Schoebel S., Blankenfeldt W., Goody R. S., Itzen A., High-affinity binding of phosphatidylinositol 4-phosphate by Legionella pneumophila DrrA. EMBO Rep. 11, 598–604 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hammond G. R., Machner M. P., Balla T., A novel probe for phosphatidylinositol 4-phosphate reveals multiple pools beyond the Golgi. J. Cell Biol. 205, 113–126 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lemmon M. A., Ferguson K. M., O’Brien R., Sigler P. B., Schlessinger J., Specific and high-affinity binding of inositol phosphates to an isolated pleckstrin homology domain. Proc. Natl. Acad. Sci. U.S.A. 92, 10472–10476 (1995). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Iversen L., et al. , Molecular kinetics. Ras activation by SOS: Allosteric regulation by altered fluctuation dynamics. Science 345, 50–54 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gureasko J., et al. , Membrane-dependent signal integration by the Ras activator Son of Sevenless. Nat. Struct. Mol. Biol. 15, 452–461 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bandaru P., Kondo Y., Kuriyan J., The interdependent activation of Son-of-Sevenless and Ras. Cold Spring Harb. Perspect. Med. 9, a031534 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Erdmann K. S., et al. , A role of the Lowe syndrome protein OCRL in early steps of the endocytic pathway. Dev. Cell 13, 377–390 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ungewickell A., Ward M. E., Ungewickell E., Majerus P. W., The inositol polyphosphate 5-phosphatase Ocrl associates with endosomes that are partially coated with clathrin. Proc. Natl. Acad. Sci. U.S.A. 101, 13501–13506 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Qian H., Cooperativity in cellular biochemical processes: Noise-enhanced sensitivity, fluctuating enzyme, bistability with nonlinear feedback, and other mechanisms for sigmoidal responses. Annu. Rev. Biophys. 41, 179–204 (2012). [DOI] [PubMed] [Google Scholar]
- 27.Murray J. D., Mathematical Biology (Springer, New York, ed. 3, 2002). [Google Scholar]
- 28.Groves J. T., Ulman N., Boxer S. G., Micropatterning fluid lipid bilayers on solid supports. Science 275, 651–653 (1997). [DOI] [PubMed] [Google Scholar]
- 29.Qian H., Bishop L. M., The chemical master equation approach to nonequilibrium steady-state of open biochemical systems: Linear single-molecule enzyme kinetics and nonlinear biochemical reaction networks. Int. J. Mol. Sci. 11, 3472–3500 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Artyomov M. N., Das J., Kardar M., Chakraborty A. K., Purely stochastic binary decisions in cell signaling models without underlying deterministic bistabilities. Proc. Natl. Acad. Sci. U.S.A. 104, 18958–18963 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bishop L. M., Qian H., Stochastic bistability and bifurcation in a mesoscopic signaling system with autocatalytic kinase. Biophys. J. 98, 1–11 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.To T. L., Maheshri N., Noise can induce bimodality in positive transcriptional feedback loops without bistability. Science 327, 1142–1145 (2010). [DOI] [PubMed] [Google Scholar]
- 33.Schrödinger E., What Is Life? The Physical Aspect of the Living Cell (The University Press; The Macmillan Company, Cambridge, UK, New York, 1944) p. viii, 91 p. [Google Scholar]
- 34.Reif F., Fundamentals of Statistical and Thermal Physics (McGraw-Hill, New York, 1965). [Google Scholar]
- 35.Baksh M. M., Jaros M., Groves J. T., Detection of molecular interactions at membrane surfaces through colloid phase transitions. Nature 427, 139–141 (2004). [DOI] [PubMed] [Google Scholar]
- 36.Gillespie D. T., General method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 22, 403–434 (1976). [Google Scholar]
- 37.Zaikin A. N., Zhabotinsky A. M., Concentration wave propagation in two-dimensional liquid-phase self-oscillating system. Nature 225, 535–537 (1970). [DOI] [PubMed] [Google Scholar]
- 38.Ouyang Q., Swinney H. L., Transition from a uniform state to hexagonal and striped Turing patterns. Nature 352, 610–612 (1991). [Google Scholar]
- 39.Loose M., Fischer-Friedrich E., Ries J., Kruse K., Schwille P., Spatial regulators for bacterial cell division self-organize into surface waves in vitro. Science 320, 789–792 (2008). [DOI] [PubMed] [Google Scholar]
- 40.Vecchiarelli A. G., et al. , Membrane-bound MinDE complex acts as a toggle switch that drives Min oscillation coupled to cytoplasmic depletion of MinD. Proc. Natl. Acad. Sci. U.S.A. 113, E1479–E1488 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Schweizer J., et al. , Geometry sensing by self-organized protein patterns. Proc. Natl. Acad. Sci. U.S.A. 109, 15283–15288 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Loose M., Fischer-Friedrich E., Herold C., Kruse K., Schwille P., Min protein patterns emerge from rapid rebinding and membrane interaction of MinE. Nat. Struct. Mol. Biol. 18, 577–583 (2011). [DOI] [PubMed] [Google Scholar]
- 43.Li Z., et al. , Regulation of PTEN by Rho small GTPases. Nat. Cell Biol. 7, 399–404 (2005). Erratum in: Nat. Cell Biol.8, 1038 (2006). [DOI] [PubMed] [Google Scholar]
- 44.Devreotes P., Janetopoulos C., Eukaryotic chemotaxis: Distinctions between directional sensing and polarization. J. Biol. Chem. 278, 20445–20448 (2003). [DOI] [PubMed] [Google Scholar]
- 45.Chen L., et al. , PLA2 and PI3K/PTEN pathways act in parallel to mediate chemotaxis. Dev. Cell 12, 603–614 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Veltman D. M., Keizer-Gunnik I., Van Haastert P. J., Four key signaling pathways mediating chemotaxis in Dictyostelium discoideum. J. Cell Biol. 180, 747–753 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Matsuoka S., Ueda M., Mutual inhibition between PTEN and PIP3 generates bistability for polarity in motile cells. Nat. Commun. 9, 4481 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Welch H. C., et al. , P-Rex1, a PtdIns(3,4,5)P3- and Gbetagamma-regulated guanine-nucleotide exchange factor for Rac. Cell 108, 809–821 (2002). [DOI] [PubMed] [Google Scholar]
- 49.Ebeling W., Schimansky-Geier L., Stochastic dynamics of a bistable reaction system. Physica A 98, 587–600 (1979). [Google Scholar]
- 50.Vetter I. R., Wittinghofer A., The guanine nucleotide-binding switch in three dimensions. Science 294, 1299–1304 (2001). [DOI] [PubMed] [Google Scholar]
- 51.Scheffzek K., et al. , The Ras-RasGAP complex: Structural basis for GTPase activation and its loss in oncogenic Ras mutants. Science 277, 333–338 (1997). [DOI] [PubMed] [Google Scholar]
- 52.Margarit S. M., et al. , Structural evidence for feedback activation by Ras.GTP of the Ras-specific nucleotide exchange factor SOS. Cell 112, 685–695 (2003). [DOI] [PubMed] [Google Scholar]
- 53.Vahey M. D., Fletcher D. A., The biology of boundary conditions: Cellular reconstitution in one, two, and three dimensions. Curr. Opin. Cell Biol. 26, 60–68 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.McMahon H. T., Gallop J. L., Membrane curvature and mechanisms of dynamic cell membrane remodelling. Nature 438, 590–596 (2005). [DOI] [PubMed] [Google Scholar]
- 55.Schmick M., Bastiaens P. I. H., The interdependence of membrane shape and cellular signal processing. Cell 156, 1132–1138 (2014). [DOI] [PubMed] [Google Scholar]
- 56.Fritz-Laylin L. K., et al. , Actin-based protrusions of migrating neutrophils are intrinsically lamellar and facilitate direction changes. eLife 6, e26990 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Golebiewska U., et al. , Evidence for a fence that impedes the diffusion of phosphatidylinositol 4,5-bisphosphate out of the forming phagosomes of macrophages. Mol. Biol. Cell 22, 3498–3507 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Fujiwara T., Ritchie K., Murakoshi H., Jacobson K., Kusumi A., Phospholipids undergo hop diffusion in compartmentalized cell membrane. J. Cell Biol. 157, 1071–1081 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Aslanidis C., de Jong P. J., Ligation-independent cloning of PCR products (LIC-PCR). Nucleic Acids Res. 18, 6069–6074 (1990). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Stols L., et al. , A new vector for high-throughput, ligation-independent cloning encoding a tobacco etch virus protease cleavage site. Protein Expr. Purif. 25, 8–15 (2002). [DOI] [PubMed] [Google Scholar]
- 61.Galush W. J., Nye J. A., Groves J. T., Quantitative fluorescence microscopy using supported lipid bilayer standards. Biophys. J. 95, 2512–2519 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Vacklin H. P., Tiberg F., Thomas R. K., Formation of supported phospholipid bilayers via co-adsorption with beta-d-dodecyl maltoside. Biochim. Biophys. Acta 1668, 17–24 (2005). [DOI] [PubMed] [Google Scholar]
- 63.Edelstein A., Amodaj N., Hoover K., Vale R., Stuurman N., Computer control of microscopes using µManager. Curr. Protoc. Mol. Biol. Chapter 14, Unit 14.20 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.