Dynamic allostery-based molecular workings of kinase:peptide complexes

Significance

Internal dynamics underlies the working of proteins, including kinases. Here we explain the role of dynamics-based allostery that orchestrates kinase:peptide complex recognition and formation. Substrate peptides have a distinct allosteric response from the kinase, as opposed to the product and inhibitor peptides. Internal dynamics of the entire kinase molecule is modulated in a global context, as opposed to previously speculated domino paths. Molecular dynamics simulations, in combination with the violin model of protein allostery for identifying communities, allows for exact mapping of allosterically coupled groups of residues throughout the kinase. Because the response from the substrate, product, and inhibitor peptides are distinct, these studies exemplify the power of computational methods to explore protein allostery in a previously unappreciated way.

Abstract

A dense interplay between structure and dynamics underlies the working of proteins, especially enzymes. Protein kinases are molecular switches that are optimized for their regulation rather than catalytic turnover rates. Using long-simulations dynamic allostery analysis, this study describes an exploration of the dynamic kinase:peptide complex. We have used protein kinase A (PKA) as a model system as a generic prototype of the protein kinase superfamily of signaling enzymes. Our results explain the role of dynamic coupling of active-site residues that must work in coherence to provide for a successful activation or inhibition response from the kinase. Amino acid networks-based community analysis allows us to ponder the conformational entropy of the kinase:nucleotide:peptide ternary complex. We use a combination of 7 peptides that include 3 types of PKA-binding partners: Substrates, products, and inhibitors. The substrate peptides provide for dynamic insights into the enzyme:substrate complex, while the product phospho-peptide allows for accessing modes of enzyme:product release. Mapping of allosteric communities onto the PKA structure allows us to locate the more unvarying and flexible dynamic regions of the kinase. These distributions, when correlated with the structural elements of the kinase core, allow for a detailed exploration of key dynamics-based signatures that could affect peptide recognition and binding at the kinase active site. These studies provide a unique dynamic allostery-based perspective to kinase:peptide complexes that have previously been explored only in a structural or thermodynamic context.

The expanse of structural information for protein kinases is defining, yet limiting, in its analysis of dynamic signatures that control their function. Indeed, its limitations are apparent most in the lack of understanding of how regions away from the kinase active site affect its function and regulation. In this context, we previously explored the dynamic action by an allosteric site Y204A in regulation of activity of protein kinase A (PKA) (1). Our community map approach allowed for defining kinase dynamics as a cohesive network of amino acids that make the conserved kinase domain. Signatures of dynamic allostery found direct correlations in the biochemical functioning of the kinase active site. In the present study we are extending our community map analysis to understand the dynamic signatures of kinase:peptide complexes. This study focuses on the role of protein internal motions in forming allosteric networks allowing for peptide recognition by the kinase domain. The inhibitor pseudosubstrate peptide from protein kinase inhibitor (PKI) and its nonnative substrate form PKS, differing by only 2 amino acids, allow for understanding community redistributions when the peptide changes from an inhibitor to substrate. Similarly, comparison between the RIα and RIIβ inhibitory-segments reveals the dynamic changes that contribute to isoform-specific regulation. We also use a peptide from the physiological substrate phospholamban (PLN) to assess the changes in dynamic signatures when peptide changes from substrate to product at the active site. This is a distinctive perspective to understanding dynamic signatures of binding and processing by the kinase domain that is previously unexplored.

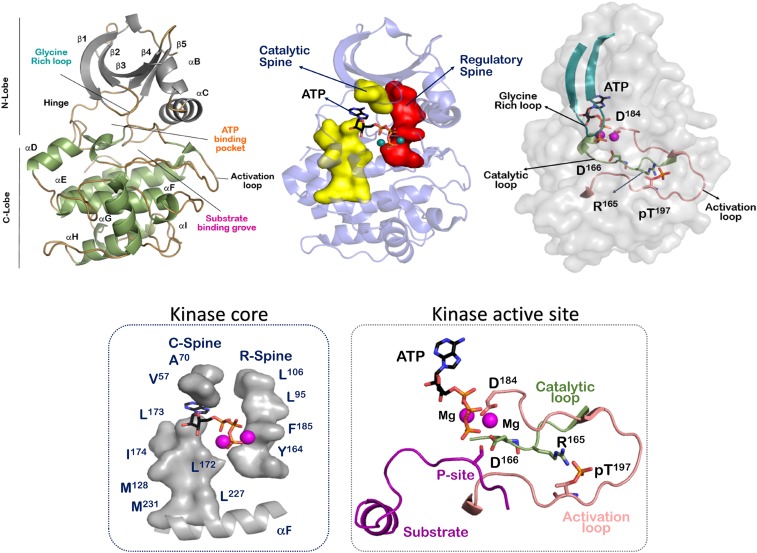
The active state of the kinase requires optimal arrangement of its key structural elements (2). A thorough analysis of kinase activation is available in literature that describes the plasticity of these structural elements (3, 4). The kinase active site is a wide cleft between its 2 lobes connected by a hinge region (5) (Fig. 1). The smaller N-lobe is predominantly made of β-strand elements that allow for optimized nucleotide binding. The glycine-rich loop located between the β2-β3 strands form a lid that contacts the γ-phosphate of ATP to prime it for phosphotransfer. A conserved lysine (Lys72 in PKA) located in the β3 strand makes contacts with the α- and β-phosphates of ATP. This lysine is also engaged in a signature salt bridge to a conserved glutamate in the αC-helix (Glu91 in PKA) (4, 6). Movement of the αC-helix and formation of the Lys72-Glu91 salt bridge is a unique feature used to characterize many kinases and their active sites (7). The most important catalytic residue of kinases is a conserved aspartate (Asp184 in PKA) in the Asp-Phe-Gly (DFG) motif. This aspartate makes functional contact with phosphates of ATP and also contacts the divalent magnesium ions at the active site. Effectively, the DFG motif and the following 2 residues are known as the magnesium-binding loop. The phenylalanine residue of the DFG motif is a part of the regulatory R-spine, whose assembly is the structural signature of an active kinase conformation (8). Rotational conformations of this phenylalanine are implicated in maintaining the optimal orientation of the catalytic aspartate and also form the basis of design of distinctive kinase inhibitors (9). The DFG motif extends into an activation loop of about 20–30 amino acids, culminating in a conserved APE (Ala-Pro-Glu) motif. This APE motif anchors the activation segment to the αF helix via an APE-αF linker. The activation loop is the most diverse segment in the kinome and contains the primary sites required for activation-based phosphorylation (10). This phosphorylation allows for the rearrangement of the loop to accommodate both nucleotide and substrate peptide binding (11). The β9 strand following the magnesium binding loop makes an antiparallel sheet with the β6 strand preceding the catalytic loop. This catalytic loop contains another kinase-specific motif called the HRD (His-Arg-Asp). The histidine of the HRD motif is a part of the R-spine and serves as a central hydrophobic core residue that combines with the DFG motif at the active site (8). The Aspartate of the HRD motif (Asp166 in PKA) is the most crucial residue of the motif and is responsible for optimal preorganization of the phospho-acceptor site (P-Site) of the substrate at the kinase active site for phosphotransfer (12). The arginine of the HRD motif supports the optimal configuration of the activation segment and connects the phosphorylation site with the magnesium binding loop (13). There are few kinases that lack this arginine, and these typically do not require phosphorylation of their activation segment (14).

Fig. 1.

Structural elements of the conserved protein kinase domain. The protein kinase domain is defined a bilobal structure that includes the active site in-between. The conserved kinase core has 2 hydrophobic spines, called the R-spine and C-spine, respectively. The activation segment forms the functional region of the kinase domain.

Kinases are molecular switches that are rapidly activated/inactivated in response to cell-specific cues. Processes that allow for activation are highly regulated and usually complex (14). There are diverse inactive configurations of the inactive state and multiple modes are required to stabilize these forms (4). A consistent feature of the inactive structure is a collapsed activation segment that is averse to substrate binding (3). Also, at the core of the kinase, the R-spine is seen to be disassembled. Alignment of the R-spine that allows for dynamic-driven interaction between the N- and C-lobes of the kinase at the hydrophobic core is a signature of the active conformation (8). The essential activated conformation has 2 main features: (i) The αC helix is optimally placed alongside the activation segment to allow for the opening and closing of the N-lobe through the catalytic cycle (6), and (ii) the glycine-rich loop is able to shield the nucleotide ATP and optimize its γ-phosphate for phosphotransfer (3). Once these 2 specifications are met, another hydrophobic spine assembles at the kinase core, called the catalytic or C-spine (15). Nucleotide bound in the kinase cleft completes the C-spine and primes the kinase for catalysis. Dynamic opening and closing of kinase active site orchestrates nucleotide binding, substrate binding, phosphotransfer, and release of ADP and product. A wide range of structural information is available for a molecular description of these catalytic events (16).

As more and more kinase structures become available, it becomes imperative to understand that these X-ray structures are snapshots of the protein’s dynamic ensemble. These snapshots are spatially averaged data that are themselves biased by experimental errors. While the structures’ B-factor (also called temperature factor) provides a mean square atomic displacement around the averaged structure, it is reflective of both dynamic fluctuations in the crystal and static disorder provided by multiple protein conformations trapped in the crystal lattice (17). Catalysis and turnover are defined less by the rigid structures and more by the molecular motions of the said structure in the pico-to-millisecond time scales (18–20). It is worth appreciating how nonrandom large-scale and small-scale motions of the enzymes preferentially modulate proficient catalysis at the enzyme active site (21, 22). The most comprehensive description of an enzyme’s mechanics requires consolidating information from different amplitudes and timescales of protein motion. In other words, the complete understanding of the structure–function relationship of any enzyme, including kinases, will require interpolating the role of dynamics. This said dynamics will influence the stability of the active kinase conformation (23), the transition state complex (24), and also the product complex (25). Currently, molecular dynamics (MD) force-fields provide accurate parametrization of the protein–solvent system (26), and indeed computational analysis has a remarkable edge in describing protein dynamics and its correlation with protein energy landscapes. A unified free-energy landscape theory describes how dynamics defines a protein’s conformational landscape with both thermodynamic (various populations or protein states) and kinetic (transitions from one protein state to another) parameters (27). This energy landscape of the protein defines its dynamic signature in binding ligands, substrates, or activity modulators (18).

Exploring dynamics-based explanations for protein function has been on-going for more than 4 decades, but suffers from lack of clarity of its specific explanations (28, 29). Underlying these efforts has been an interest to correlate conformational changes of the enzyme:substrate and enzyme:product complexes with the rate-limiting step, as well as with chemical mechanics and acceleration of reaction rates at the enzyme active site. Enzyme efficiency comes from optimized binding between the enzyme:substrate that enhances the energy of the complex in the direction of the chemical reaction (30). In the dynamic context, the interactions between the enzyme and substrate are recognized by each via a dynamic footprint. Changes in an enzymes’ dynamic footprint as it interacts with a distinct substrate is a necessary (although not sufficient) condition for optimized enzyme function (31). In the present study we use mutual-information and Girvan–Newman algorithm-derived “community networks” to understand the dynamic footprint of PKA-nucleotide-peptide inhibitory, substrate, and product complexes. In accordance with the violin model of protein allostery (32), this design and analysis allows us to understand the role of entropy-based protein allostery in kinase:peptide complexes. These complexes and their dynamic explorations provide a highly detailed understanding of how dynamics-based allostery is finely tuned based on a given ligand context in the eukaryotic protein kinase superfamily that has been unresolved.

Results and Discussion

Communities as the Dynamic Signature Elements of the Conserved Eukaryotic Kinase Domain.

Inner workings, as well as the structural stability of proteins, relies on its complex network of inter-amino acid interactions. Understanding of these interactions and their networks provides for a systems-based powerful analysis of protein mechanics that is largely independent of constraints imposed by secondary structures or topological protein folds. Dynamic plasticity defines the inner working of the kinase domain. Hence, dynamics-based network analysis is presently one of the most comprehensive tools used to explore allosteric modulation of kinases. MD simulations provide a robust dataset for all-atomic fluctuations that can be analyzed for allosteric dynamics (33–35). Two key issues were kept in mind while searching for functionally relevant networks of correlated motions in our unbiased simulations: (i) that network analysis is dependent on the length of the simulation trajectory (36), wherein the description of conformational ensembles must adequately sample the free-energy landscape of the desired allosteric process; (ii) that it is more relevant to understand these inner amino acid motions in the context of experimentally verifiable observables that can corroborate the role of said dynamics in the kinase structure–function relationship. In our mutual information-based community structures we have demonstrated that the present analysis blends seamlessly into explanations of biochemical function of PKA with respect to certain allosteric mutation sites (1). Finally, we take measures to ensure adequate and equivalent sampling of conformational space between complexes in this comparative study.

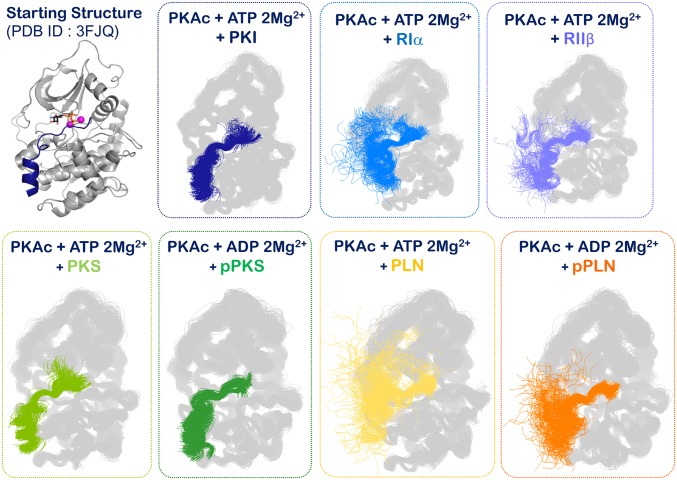
In the present report we describe a prudent understanding of PKA’s community networks and their detailed comparative analysis. We have undertaken multimicrosecond simulations of 7 kinase:nucleotide:peptide complexes to understand the dynamics-based signatures of their molecular interaction. All complexes have been simulated in triplicate for the same aggregate length (5.40 µs) to capture comparable representative conformational ensembles and dynamic timescales, ensuring that protein conformations explored for all 7 complexes are unbiased by topological effects (SI Appendix, Fig. S1). The peptides, although modeled onto the crystal structure of the PKI peptide, are unrestrained. As seen in Fig. 2 and SI Appendix, Fig. S1, while the protein samples a conformational space around the active closed kinase structure, greater conformational space is explored by the peptides. Because the PLN and regulatory subunit-derived peptides lack the sticky α-helix, they explore multiple conformations characteristic of unstructured peptides. This observation is in accordance with the conformation of the PLN peptide as seen in a conformation distinct from the PKI peptide in a reported crystal structure (SI Appendix, Fig. S2) (37). Conservation of overall protein topology with variation in peptide degree of flexibility is also apparent in the contact maps derived from the trajectories of each complex (SI Appendix, Fig. S3). Except for the regions of the peptide, essentially contact maps of each complex appear identical and are indicative of their comparable PKA topology. The protein ensemble sampled in each simulation is, hence, very similar and with subtle ligand-dependent changes in the free-energy landscape.

Fig. 2.

Simulation snapshots of the 7 kinase:peptide complexes. The simulation snapshots allow for visualization of the conformational sampling of the protein vs. the peptide. The protein maintains an overall conformation (also see SI Appendix, Fig. S1), while the peptides are free to explore more degrees-of-freedom in accordance with their sequence and structure.

Mutual information matrices derived from trajectories of the 7 simulations of kinase complexes explore the correlations in amino acid conformations in their equilibrium ensembles over multiple microseconds (38). This approach identifies amino acids with shared configurational entropy, or dependent conformational distributions. Cartesian coordinates for representative main-chain and side-chain atoms are used in the calculations because these provide a good descriptor of the low-frequency motions of semirigid bodies that are relevant to biological processes. Cartesian-based mutual information of MD simulations has been seen to agree well with extracted parameters from NMR relaxation experiments (39). This approach works optimally when conformational changes are subtle, as in our case where the perturbations in sampling the free-energy wells of the protein are minimal. Mutual-information matrices of all of the 7 complexes are shown in SI Appendix, Fig. S4. A comparison between these matrices and the contact map matrices (SI Appendix, Figs. S3 and S4) of the same datasets shows the relevance of the use of these calculations.

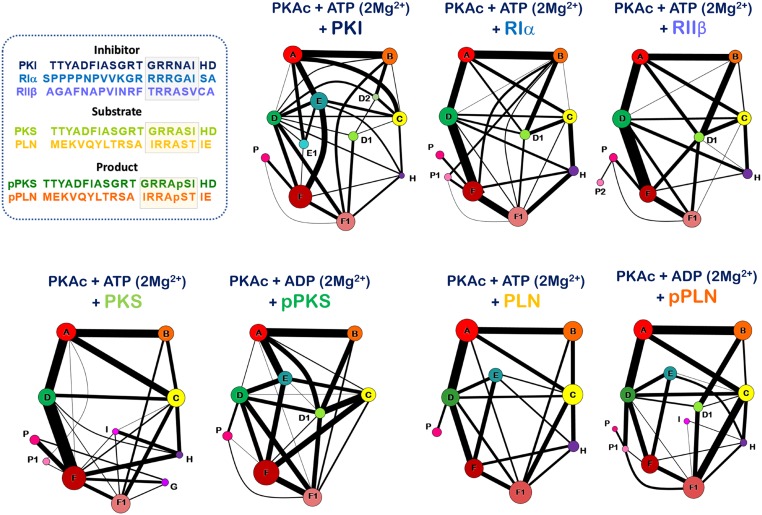
Community networks for the 7 complexes were determined using the Girvan–Newman approach (40) on the mutual information matrices (Figs. 3 and 4 and Movies S1–S7). The algorithm finds communities of correlated atoms by progressively removing edges between nodes, or atoms, at network interfaces, effectively identifying the remaining divided clusters of atoms. Essentially, betweenness of all of the edges is calculated and edges with the highest betweenness are removed to construct a hierarchal network. Iteration of this step reveals the underlying community network, a fundamental description of the correlated dynamics of the system. These communities have been mapped back onto the crystal structure of the kinase to allow for biochemical/biological relevant explanations (1, 41). The community map analysis effectively goes beyond traditional descriptions of secondary structure and tertiary elements, defining the eukaryotic protein kinase domain. Each community is a set of contiguous amino acids that participate in similar biochemical functions and exhibit correlated motions. The main chains and side chains of each residue are annotated/treated separately, and indeed for a subset of residues, the main chain and side chains participate in separate communities. In general, the active PKA conformation can be described by 10 communities that we label ComA through ComI (Fig. 3).

Fig. 3.

Community maps networks of the 7 kinase:peptide complexes, part I. This figure shows the community maps of the 7 complexes mapped into the secondary structural elements of the complex.

Fig. 4.

Community maps networks of the 7 kinase:peptide complexes, part II. This figure shows the community maps of the 7 complexes as a network drawing of nodes and edges. Each community is represented by a circle, whose size is reflective of the number of residues forming a part of the said community. The width of the edges joining the communities are indicative of the edge weights that connect these communities.

Communities ComA and ComB are limited to the N-lobe and divide the 5-stranded β-sheet into 2 dynamic groups. ComA includes residues that interact with the nucleotide with the exception of parts of the glycine-rich loop that behave as a separate dynamic entity. ComB is localized around the FxxF hydrophobic motif that binds the C-tail of AGC kinases and is a known kinase hotspot (42). ComC, ComD, and ComE are the most fluid of the communities and are most accommodating to reorganization. ComC includes elements from the αC helix and parts of the activation segment. Communities ComD and ComE (and their subsets ComD and ComE1) encompass the active site and cleft between the N- and C-lobes. Community ComD is most inclusive of the active site residues. The C-lobe is predominantly a single rigid-body that is defined by ComF. The frontal peptide binding region of the C-lobe is seen to develop as subset ComF1 from the ComF community. Three types of small communities arise in specific cases; these are ComG, ComH, and ComI. ComG includes the αG helix that participates in regulatory subunit binding (12). ComH and ComI are centered around previously described small-molecule binding or protein–protein interaction sites in the kinase domain (43–45). The general outlook of this community structure of the Eukaryotic kinase domain indicates 2 essential dynamic signatures: (i) The N-lobe is dynamically responsible for positioning the nucleotide, while (ii) the C-lobe dynamically couples the kinase active site to long-distance allosteric modulators. The fluidity of the community structure between the 2 lobes is a reminder of kinase plasticity and the biological role of its activation segment.

The present analysis of kinase:peptide complexes also allows for exploration of 2 more communities: ComP and ComP1. These communities arise from the binding peptides (Fig. 5). The complete peptide displays correlated dynamic participation with the kinase domain and peptide residues that directly bind into the active site cleft are seen to integrate into the community network of the kinase itself (Figs. 5 and 6). The remaining peptide behaves as an individual unit comprising of communities ComP and ComP1, but also bridging residues that allow ComP1 and ComP2 to communicate with the communities of the catalytic domain. A direct validation of this community map approach is seen in the bridging residues of these communities. These residues have their main chains as a part of one community, while the side chains are participating with another community. These bridging residues serve as important communication points for integrating and communications between the communities. One such bridging residue seen in the kinase:PKI and kinase: RIIβ complex is Y204 (SI Appendix, Tables S1–S3). Y204 serves as a bridge between ComF1 and ComF, both communities participating in peptide binding. Mutation of Y204 to alanine disrupts the synchronization between the nucleotide and substrate at the active site and decreases the catalytic efficiency of PKA by several-fold (1). ATP-ase activity of Y204A is comparable to wild-type PKA, and the mutant also binds the substrate with a good efficiency. However, because the bridge between the communities is lost, the dynamic network is redistributed and catalytic efficiency is compromised.

Fig. 5.

Community network of the 7 peptides. The interacting peptides also dynamically participate in the allosteric working of the kinase:peptide complex. Region corresponding to the PKA recognition sequence (RxxS/T) is coupled closely with the communities of the protein peptides, which also have their own ComP and ComP2 communities that are distinct from the communities of PKA.

Fig. 6.

Community network at the activation segment of the 7 kinase:peptide complexes. The community network at activation segment is seen to vary in the 7 kinase:peptide complexes in accordance with the signatures of their molecular recognition.

Dynamic Signatures of the Kinase:Nucleotide:Inhibitor Ternary Complexes.

In the present study we have explored complexes of the catalytic subunit of PKA bound to ATP and 2 Mg²⁺ ions in complex with 3 peptide inhibitor sequences. These peptides code for regions 5–24 of PKI, 82–101 of PKA regulatory subunit RIα, and 95–114 of the PKA regulatory subunit RIIβ (Fig. 4). Briefly, to emphasize, the catalytic activity of PKA is tightly regulated in cells by extensive protein–protein interactions. High-affinity binding of the catalytic subunit of PKA with its regulatory subunit creates an inactive holoenzyme (3). While 2 types of catalytic subunits exist (Cα and Cβ), a total of 4 regulatory subunits (RIα, RIβ, RIIα, and RIIβ) are expressed by the mammalian genome. Both type I and type II regulatory subunits (and their α- and β-isoforms) have 2 tandem conserved cAMP binding domains that allow for association–dissociation of the PKA holoenzyme in response to cAMP cues (43). The N terminus corresponds to a small dimerization domain, which is joined to the cAMP binding domains by a diverse linker segment. The linker includes an inhibitor sequence that binds into the active site cleft of the PKA catalytic domain. The sequence of the inhibitor segment corresponds to a PKA-specific phosphorylation recognition motif, which includes 2 arginine residues at the P-2 and P-3 positions and a hydrophobic residue at the P+1 site (Fig. 4). Sequences flanking this consensus region are diverse, and it has been speculated previously that these flanking regions may play a role in catalytic subunit and regulatory subunit association/recognition (46). The type I regulatory subunit inhibitor segment behaves like a perfect inhibitor because the phosphorylation (P-site) acceptor residue is naturally replaced by an alanine; it is thus a pseudosubstrate. In contrast, the type II regulatory subunit inhibitor segment is actually a substrate that harbors a phosphorylation amicable serine residue at the P-site. An intense interplay between the kinase activity of the catalytic subunit and the cAMP binding properties of the regulatory subunit allow the type II holoenzymes to oscillate between phosphorylated and nonphosphorylated forms (47). The type II holoenzymes is a unique example of a single turnover reaction wherein the nonphosphorylated inhibitor segment of the regulatory subunit occupies the active site of the catalytic subunit as a substrate. Once phosphorylated, the inhibitor segment is unable to dissociate fully from the catalytic subunit as the physical constraints holding the holoenzyme do not allow for its dissociation in the absence of cAMP. When the holoenzyme unleashes the active site following cAMP activation, phosphatase activity is required to dephosphorylate the type II inhibitor segment and allow for its reassociation with the catalytic subunit. In the case of the type I holoenzyme, this oscillation is achieved in trans, where-in PKG phosphorylates a serine located at the P+2 position in its inhibitor segment (48).

An additional layer of regulation of kinase activity of the catalytic subunit of PKA is provided by binding of the PKI protein. Unlike the association of the regulatory subunit, PKI binding to the catalytic subunit is insensitive to cAMP and low expression levels of PKI are speculated to maintain a basal active pool of PKA (49). The mammalian genome codes for 3 PKI isoforms (PKIα, PKIβ, and PKIγ). PKIα is expressed in the brain, heart, and skeletal muscle, while PKIβ is expressed in the testis. PKIγ, which is only about 30% similar in sequence to PKIα and PKIβ, is expressed in predominantly in the heart, skeletal muscles, and the testis (49). Binding of PKI to the catalytic subunit of PKA is reported to regulate its shuttling in-and-out of the nucleus via the export signal contained in the PKI protein (50). Region 5–24 of PKI contains the PKA recognition motif (Arg18-Arg19-Asn20-Ala21) that allows for its tight binding (K_D ∼ 2.0 nM) into the active-site cleft (1).

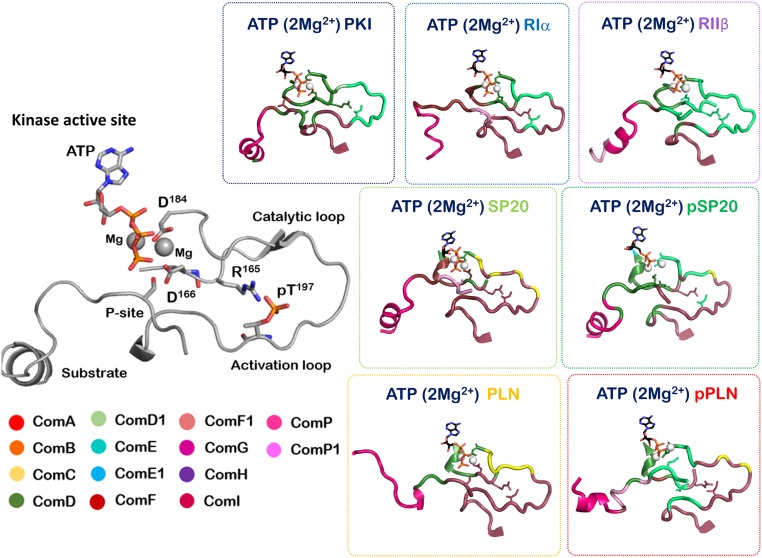
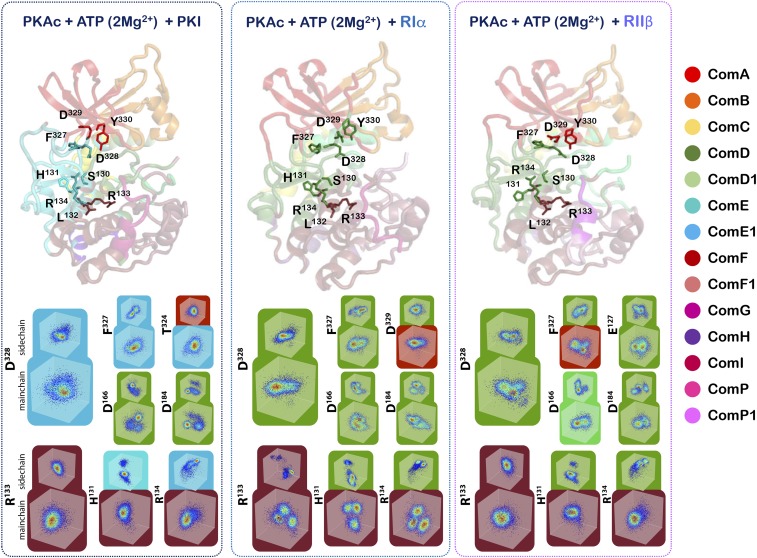
Interestingly, 2 mutations in the kinase domain of PKA are reported to affect these protein–protein interactions with the regulatory subunit and PKI without affecting much the catalytic properties of its phosphorylation reaction. The R133A mutation reduces the affinity of binding of the catalytic subunit for RIIβ and PKI with no effect on the interaction with RIα (46). In contrast, the D328A mutation affects the kinase domain interaction with RIα without altering the interaction with either RIIβ or PKI (46). These biochemical experiments have provided compelling first hints for a dynamics-based signature of the catalytic-subunit recognition mechanisms for its inhibitor peptides. Because the direct observations of the above-described experiments were focused on enthalpic and structural interactions, it was difficult to provide dynamic contributions to the interactions at that time. Our dynamics-based allostery maps now allow for exploration of these complexes from a mechanics-based entropic perspective, and we can visualize the residue networks of the catalytic subunit that underlie these recognition patterns. The community maps of the kinase:nucleotide:inhibitor complexes are shown in detail in Movies S1–S7. As can be seen in Fig. 7 and SI Appendix, Fig. S6, these community maps provide a dynamics-based explanation to the perplexing workings of these 2 amino acids. The R133 residue lies in a hotspot for distinct dynamics in the αD helix. While the αD helix is predominantly coupled to the C-lobe and is a part of ComF, the R133 residue is strongly coupled to “bridging residues” that participate with ComF, as well as communities associated with the active site. In the case of the PKA:PKI and PKA:RIIβ complexes, peptide binding stabilizes R133, as illustrated by those residues’ Cα and side-chain atom distribution in Cartesian space (Fig. 7). This stabilized dynamics propagates through ComF, including bridging residues that link ComF to ComE and ComD. Conversely, in the PKA:RIα complex, an increase in distribution of conformations is observed for R133 and this increase in dynamics is shared throughout ComF. Representative residues from ComF with high mutual information with R133 are shown in Fig. 7. The increase in disorder of R133 and ComF must reflect the reduced role of R133 in RIα binding relative to RIIβ and PKI. Similarly, D328 that is a part of the C-tail wrapping around the N-lobe of PKA, shows distinct dynamic behavior dependent on peptide recognition (Fig. 7 and SI Appendix, Fig. S6).

Fig. 7.

Bridging residues and the conformational distribution of residues surrounding R133 and D328. The distribution of backbone and side-chain conformations and resultant community maps for PKA:PKI, PKA:RIα, and PKA:RIIβ complexes reflect each inhibitor peptide’s specific binding mode. Bridging residues, where the backbone and side chain of a single residue is split between 2 communities, act as physical linkages between communities. The distribution of Cα and representative side-chain atoms for each residue is shown in normalized Cartesian coordinate space, colored by their probability density estimate. Representative residues with high mutual information with D328 or R133 are shown, except for PKA:PKI active site residues. D166 and D184, have low mutual information with D328 and are shown for illustrative purposes.

In the PKA:RIα and PKA:RIIβ complexes, D328 is a part of ComD that includes active-site residues. Opposite the effect observed with R133, D328 is stabilized in the PKA:RIα complex and destabilized in the PKA:RIIβ complex (Fig. 7). Again (de)stabilization is propagated throughout ComD and into active-site residues in the YRD and DFG motifs, (e.g., D166 and D184 in Fig. 7 and SI Appendix, Tables S1–S3). In the PKA:RIα complex this dynamic signature is also shared by a bridging residue, D329, that links ComD to ComA, a community associated with nucleotide interaction. However, in the PKA:PKI complex D328 also appears stabilized, as does the rest of the ComE1 community. Interestingly, in PKA:PKI D328 no longer has correlated motions with the active site, the residues of which have drastically different conformational distribution than D328 (Fig. 7 and SI Appendix, Tables S1–S3). T324 also acts as a bridging residue between ComE1 and ComA in the PKA:PKI complex; however, unlike in the other inhibitory complexes, ComA has weak correlation with active-site residues in ComD. The consequence of this loss of mutual information is a fragmented community map with weak correlation between communities. This explains how mutation in D328 affects the interaction of PKA with RIα differently from PKI and RIIβ and through vastly different dynamic mechanisms.

Dynamic Signatures of the Kinase:Nucleotide:Substrate/Product Ternary Complexes.

For the kinase:nucleotide:substrate complex, 2 peptides have been considered. These include the regions 1–20 from the physiological PKA substrate PLN that regulates calcium-pumps in the mammalian cardiac muscle (51), and a nonnative substrate created by substituting the P-site of the inhibitor segment of PKI to a phosphoacceptor serine (52). Both peptides contain the PKA recognition sequence as R-X-X-R-X-X-S/T-ϕ, where X is variable and ϕ is any hydrophobic amino acid. Both peptides show an optimal affinity for the catalytic subunit of PKA but with their turnover rates for phosphorylation differing by an order-of-magnitude (PLN: 20 s⁻¹; PKS: 1 s⁻), a consequence of the nonnatural heritage of PKS (51–53). Because the sequences flanking the PKA consensus sequence of these peptides are widely different, their different degrees-of-freedom in the kinase ternary complex are understandable (Fig. 2).

Nonetheless a comparison of their community network in the ternary complex and the comparison of these complexes with those of the phosphoproduct peptides provide us with some valuable insights. The community structure of the kinase:substrate complex links the communities at the core of the kinase to the surface providing for a cumulative effect of orchestrated response from the entire protein for phosphotransfer. As seen in Figs. 5 and 6 (and SI Appendix, Fig. S5), the activation segment and the kinase spines involve the synchronized working of ComC, ComD, and ComE. These 3 communities contain residues from the αC helix, the active-site residues that chelate the metals, and also the catalytic residues crucial for phosphotransfer. The autophosphorylation site pThr197 and Cys199 are included in ComF and coordinate with the C-lobe for long-distance communication with the active site. The C-tail contains 3 segments: The C-lobe tether, active site tether (AST), and the N-lobe tether (54). In our simulations, the AST is synchronized with the active site by ComD (Fig. 3). The ternary complex creates a small-molecule binding site at ComH (55) to allow for manipulation of this complex and its consequent regulation. The lack of interaction between this ComH community and ComF1 in the PKS complex resembles the lack of interaction between these communities in the RIIβ complex. This subtle reorganization of dynamics details how the RIIβ peptide functions as a substrate, much like the PKS peptide.

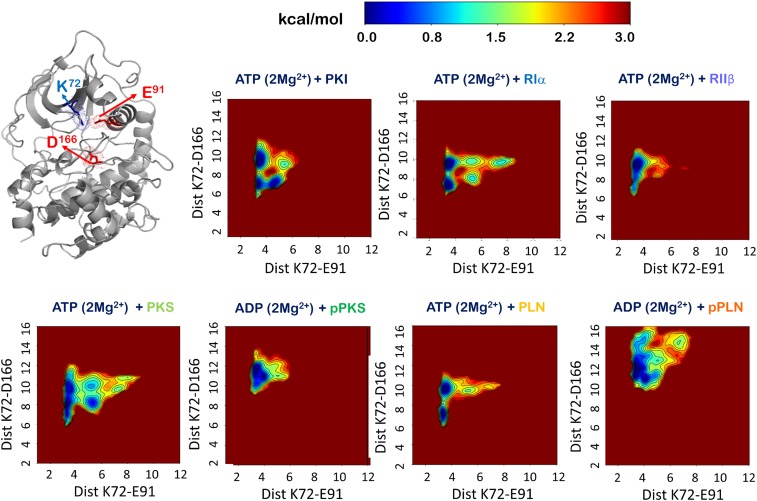
Strikingly, the kinase bilobal open-to-close and αC conformational landscape of the PKS complex resembles the PKI complex as well as the RIα complex more so than the RIIβ and PLN complexes, reflecting PKS’s pseudosubstrate origin and inhibitory properties, which include high-affinity binding as well as low catalytic rate (Fig. 8). In these 3 complexes the open–close dynamics is convoluted by catalytically nonproductive αC fluctuations. Still, as described above, the distribution of correlated dynamics seen in the community map of the PKS complex reflects the substrate’s phospho-acceptor properties, similar to RIIβ. In comparison, the physiological substrate PLN in complex with PKA exhibits a committed open–close conformational landscape, with little of the tertiary or higher-order substates observed in the PKS complex. This result agrees well with the synchronous global process measurable by NMR relaxation dispersion only for PKA:PLN but not for PKA:PKS (56). The observed free-energy landscape of the PKA:PLN complex most resembles the PKA:RIIβ complex, highlighting that both substrates are native phospho-acceptor sequences. However, again, the distribution of mutual information in the PKA:PLN complex, with strongly connected and unsegregated communities, compared with the inhibitory and nonnative substrate complexes, demonstrates the recognition of PLN by the kinase domain as a bona fide substrate.

Fig. 8.

Free-energy landscape of the MD simulations of the 7 kinase:peptide complexes. Open-to-close dynamics of the kinase are measured (Å) between K72- Nζ of the β3 strand and D166- Cγ of the YRD motif. The αC dynamics are measured (Å) by the distance between K72-Nζ and E91-Cδ of the αC helix.

In contrast to the kinase:substrate complexes, the kinase:product complexes are reminiscent of properties of products that behave more like inhibitors (Fig. 4). The dynamic coupling between the active site is broken to create a subcommunity ComD1. The crucial dynamics between ComC and the N-lobe communities, ComA and ComB, are reorganized to enhance coupling with the C-lobe ComF. The overall effect of the reorganized communities is to create a more dispersed set of residues with mutual information that do not participate in the phosphotransfer event. The product blocks the active site and shows a stronger affinity for the active site and a smaller root mean square fluctuation (Fig. 2 and SI Appendix, Figs. S1 and S7). The C-lobe now involves the peptides from the ComF1 community for aid in dissociation and consequent cycling of the kinase domain. The correlated dynamics associated with the pPKS peptide shows its closest similarity with the PKI peptide in concentrating all of the community coupling via the N-lobe and C-lobe cleft (Figs. 3 and 4). Interaction between ComA and ComB in the N-lobe and ComF and ComF1 in the C-lobe are at their strongest. Interactions of communities are intense yet dispersed around the active site, indicating the inhibitory effect of the peptide on the dynamics of the active site. The pPKS complex couples the ComC community tightly to ComD1 and ComF. In this way the αC helix is engaged with the C-lobe and its movement alongside the C-lobe is critical for product release. At the same time, the pThr197 site in the pPKS complex becomes a bridging residue and has its main chain as a part of ComF and side chain as a part of ComD1. Both product peptide complexes have shifted to a more open conformation relative to the substrate and inhibitor complexes (Fig. 8), potentially promoting nucleotide and product release. The PKA:pPLN complex populates both a more open and αC-perturbed conformation compared with PKA:pPKA, possibly contributing to the efficient product dissociation of the native product pPLN in comparison with the slow release of pPKS.

Conclusion

This study provides for dynamics-based signatures of kinase:inhibitor, kinase:substrate, and kinase:product complexes. This study explores the yet undeciphered role of dynamics-based allostery that allows enzymes to distinguish between inhibitor and substrates and allows for manipulation of the free-energy landscape to tune affinity and catalytic rate. In accordance with the violin model of allostery, these studies enhance the entropy-driven understanding of kinases and their workings in the biochemical context. We speculate that these studies will pave the way for further correlated dynamics-based studies on the Eukaryotic protein kinases, allowing us to perhaps create a dynamics-based map of the kinases in the coming decades.

Materials and Methods

System Preparation.

All complexes were prepared from the crystal structure of PKA in a closed ternary conformation bound with PKI5-23 inhibitor peptide, ATP, and 2 Mn⁺² ions (PDB ID code 3FJQ). Residues Thr197 and Ser338 were both taken in the phosphorylated phosphothreonine and phosphoserine forms, as seen in the crystal structure. For generating the various different complexes, Mn⁺² ions were changed to Mg⁺² and the inhibitor peptide mutated to the desired sequence. A total of 7 peptides were used to generate kinase:nucleotide:peptide ternary complexes. Three complexes were with inhibitor peptides, PKI (region 5–23) (TTYADFIASGRTGRRNAIHD), inhibitor region of RIα (SPPPPNPVVKGRRRRGAISA), and an inhibitor region of RIIβ (AGAFNAPVINRFTRRASVCA). The substrate complexes used PKS (modified from PKI) (TTYADFIASGRTGRRASIHD) and the physiological phospholamban (PLN region 1–20) (MEKVQYLTRSAIRRASTIE). In the phospho-product complexes, the phospho-acceptor site of the peptides were included as the phosphoserine and a phosphate was removed from ATP to make the kinase:ADP:phosphoproduct complex. Sequences used were pPKS (TTYADFIASGRTGRRApSIHD) and pPLN (MEKVQYLTRSAIRRApSTIE). All models were processed in Maestro (Schrodinger), where counter ions and ioniziable side chains were modeled in the Protein Preparation Wizard, as previously described (41). Hydrogens were added and the models were solvated in a cubic box of TIP4P-EW water (57) with a 10 A buffer in AMBERtools (58). Parameters from the Bryce AMBER Parameter Database were used for ATP (59), ADP (59), phosphothreonine (60), and phosphoserine (60). Protonation states of histidines and Cys199 were optimized for neutral pH and established reactivity as reported in literature. Finally these were included as HIP for His87, HIE for His142, and HID for the remaining histidines. Cys199 was used as the CYM negatively charged form.

MD Simulations and Preliminary Analysis.

AMBER16 (58) was used for energy minimization, heating, and equilibration, using the CPU code for minimization and heating and GPU code for equilibration. Five-hundred steps of hydrogen-only minimization was followed by 500 steps of solvent minimization, 500 steps of side-chain minimization, and 5,000 steps of all-atom minimization. Systems were heated and equilibrated as previously described (41). Briefly, the systems were heated from 0 K to 300 K over 500 ps with 2-fs timesteps and 10.0 kcal⋅mol⋅Å position restraints on protein and ligand. Temperature was maintained by the Langevin thermostat. Constant pressure equilibration with a 10 Å nonbonded cutoff was performed with 100 ps of protein and ligand restraints followed by 100 ps without restraints. An 8 Å cutoff for nonbonded interactions with particle mesh Ewald was used for a final 50 ns of simulation. Production simulations were performed on GPU-enabled AMBER16 as above in triplicate for a total aggregate simulation time of 5.4 μs for each complex. The first 100 ns of each simulation were removed before analysis. GROMACS (Groingen Machine for Chemical Simulations) tools were used to analyze the triplicate trajectories for properties of root mean square fluctuation, contact maps generation and RMSD, and so forth (61). Xmgrace was used for graphical visualization of data.

Mutual Information and Community Analysis.

Mutual information between pairs of backbone and side-chain atoms was calculated as described previously (41) for the triplicate trajectories. Cartesian mutual information was calculated for Cα atoms and representative side-chain atoms for each residue after alignment to PKA C-lobe residues 128–300 for each complex’s triplicate trajectories sampled at 120-ps intervals. The configurational entropy based approach finds shared entropy or mutual information between atoms using a 24-binned histogram entropy estimation with corrections for conformational undersampling (38, 41). Each triplicate data were divided evenly into 6 “independent” trajectories for undersampling correction of the estimated mutual information, as described previously (41). Main-chain and side-chain conformational distributions were plotted in 3D Cartesian coordinate space following normalization of each atom. KDE was used to determine a probability density function for each distribution. The Girvan–Newman algorithm (40) was used to determine the network graph of the representative atoms with mutual information as edge weights (41). Briefly, Girvan–Newman analysis is a divisive top-down hierarchal method that attempts to build a community structure by separating clusters of vertices through iterative removal of edges connecting vertices that display the most betweenness: That is, which are at the interface of communities, quantified by the number of shortest paths over them. The resulting network structure has communities of atoms with high mutual information or correlated motions and edges between communities as the summation of mutual information between those communities’ members. A contact cutoff, where pairs of atoms within 10 Å of each other for 75% of the trajectory, was used to include only short-range correlated configurational distributions. The representative community map shows each communities’ membership population by the size of the node and the shared information between communities are shown as edge thickness. All structural representations were made using PyMOL. Movies were made using PyMol and ImageJ (62).