Significance
Universals in language are hard to come by, yet one candidate is that words across the lexicons of the world’s languages are, by and large, connected: When a word applies to two objects, it also applies to any objects “between” those two. A natural hypothesis is that the source of this regularity is a learning bias for connected patterns, a hypothesis supported by recent experimental studies. Is this learning bias typically human? Is it language related? We ask whether other animals show the same bias. We present an experiment that reveals that learning biases for connectedness are present in baboons, suggesting that the shape of the world’s languages (both content and logical words) has roots in general, nonlinguistic, cognitive biases.
Keywords: connectedness, human languages and their lexicons, primate semantics
Abstract
Using a pattern extraction task, we show that baboons, like humans, have a learning bias that helps them discover connected patterns more easily than disconnected ones—i.e., they favor rules like “contains between 40% and 80% red” over rules like “contains around 30% red or 100% red.” The task was made as similar as possible to a task previously run on humans, which was argued to reveal a bias that is responsible for shaping the lexicons of human languages, both content words (nouns and adjectives) and logical words (quantifiers). The current baboon result thus suggests that the cognitive roots responsible for regularities across the content and logical lexicons of human languages are present in a similar form in other species.
Humans and animals categorize objects in the world into natural classes based on various criteria. A prominent example of a criterion that has been hypothesized for humans is “connectedness.” Informally, connectedness requires that whenever two objects and belong to a certain class, and a third object is “between” and , then must also belong to that class. The traces of connectedness are twofold. First, content words (nouns and adjectives) in the world’s natural languages are generally connected (1). For example, the set of all flying, feathered animals is a natural, connected class, for which many languages have a single word (e.g., “bird”). However, the set of all objects that are either red or a bird is not a natural class—it is too disconnected (e.g., it includes both raspberries, which are red, and blue jays, which are birds, but not blueberries, even though blueberries are, intuitively, “between” raspberries and blue jays)—and indeed no language has a single word meaning “red or bird.” Second, connectedness creates a learning bias: New nouns are more readily associated with connected meanings than with nonconnected ones (2, 3).
Recently, Chemla et al. (4) have generalized the notion of connectedness from the domain of content words (in which the relevant notion of betweenness is often difficult to specify; see ref. 5) to the domain of logical words, specifically, quantifiers (in which a precise, canonical notion of betweenness naturally arises based on the mathematical subset relation between sets).* They show that connectedness is a weak version of monotonicity, a classic notion in formal semantics: A quantifier is monotonic just in case both and its negation are connected. Examples of monotonic quantifiers include “somebody,” “everybody,” and “more than five people.” Connected but nonmonotonic quantifiers include “some but not all people” and “between three and five people.” Nonconnected quantifiers include “all or no people” and “fewer than three or more than five people.” As in the domain of content words, connected quantifiers appear to be privileged across the lexicons of the world’s languages: Most lexicalized quantifiers are connected, if not monotone, and, conversely, nonconnected concepts generally require compositional machinery to be expressed (e.g., via overt disjunction or with the help of a nonconnected content word, as in “an odd number of people;” see ref. 6 for a survey). Furthermore, Chemla et al. (4) show that humans have corresponding learning biases favoring connected quantifiers, as evidenced by performance on rule learning, or pattern extraction, tasks: It is easier to discover connected rules than nonconnected ones, and easier still to discover monotone ones.
A natural hypothesis is that the source of the regularity of the world’s lexicons, for both content and logical words, is a learning bias for connectedness. Indeed, Chemla et al. (4) argue that their experimental results with humans support this hypothesis: “[C]onnectedness may be an active constraint during language acquisition, biasing the learning device to search for connected meanings first, and thereby biasing the lexicon of natural languages to preferentially contain words with connected meanings.” There are numerous reasons to inquire about the source and status of this preference and to ask, in particular, whether it is present in other species, such as baboons. First, previous results showing a preference for connected patterns by humans could have been the result of their language (these patterns are easier to talk about); thus, replicating the result with baboons, who do not have a language as we know it (certainly not one with function words like “somebody” and “everybody”), would be significant. It would strongly suggest that the relevant logico-linguistic facts have been shaped by general cognitive preferences, and not the other way around. Second, this would show not only that the connectedness preference is separate from our language faculty, but also that it is a “deep” one. If the connectedness preference is found in other species, it could be because it arose in an ancient common ancestor of these species (“common evolution”) and was preserved in its lineage since then, or it could be because connectedness has evolved several times in evolution (“convergent evolution”). Either way, this would suggest that connectedness is a fundamentally useful and natural part of living creatures’ notion of complexity and of the way they understand and organize the world around them. Overall, then, replicating the result with baboons would strongly suggest that the fact that languages of the world typically have a word for “all” and “none,” and not one for “all or none,” is not (just) a logical curiosity about language, per se, but rather is a fact about cognition and some of its most stable aspects: Such lexical patterns may be the fossils of cognitive constraints that emerged repeatedly in evolution or was preserved across millions of years.
The contribution of this study, then, is one about language: Can the roots of humans’ bias for connectedness be found independently of language proper, and do other animals show the same bias? The object/noun version of the connectedness constraint has been explored with animals, often under the name of “pseudocategorization” (e.g., refs. 7–9). Here, we report on an experiment that explores a variation on these experiments, to prompt more directly the quantifier version of connectedness with animals. We presented baboons with a pattern-extraction task, which is as close as possible to the task used to argue for a human learning bias favoring connected quantifiers. We do not ask whether this requires high-level reasoning abilities (10, 11), and surely we make no claim that a “word”-like element has this high logical type in an animal’s repertoire. Instead, our empirical question is whether the connectedness constraint can be detected in nonhuman animals, just as well as it had been in humans, in such a way that it could affect these animals’ potential “functional vocabulary.” If the answer is positive, it may suggest that the shape of the world’s lexicons, including logical lexicons, has roots in general, nonlinguistic cognitive biases, which may have evolved in other animals, too, independently of language.
Methods
The data and the script for the analysis in this paper are available at https://doi.org/10.17605/OSF.IO/U72H3.
Ethical Standards.
This research conformed to the Standard of the American Psychological Association’s Ethical Principles of Psychologist and Code of Conduct and received ethical approval from the French Ministry of Education (approval APAFIS 2717-2015111708173794 v3).
Participants and Apparatus.
A total of 14 Guinea baboons (Papio papio; 11 females; age range: 2–20 y) from the CNRS primate facility (Rousset-sur-Arc, France) participated in the study. The participants were tested by using 10 automatic computerized learning devices for monkeys (12), each comprising a touch screen and food dispenser, which were freely accessible from the baboons’ living enclosures. The procedure used an automated radio-frequency identification of the subjects within each test system, making it possible to test the individuals without capturing them. Use of this procedure improves animal welfare in experimental research (13).
The experiment was made available to all 23 animals in our facility, who participated in the study on a voluntary basis. Of the 23 participants, 9 failed to complete the first condition they were assigned to (Procedure and Learning Criteria). We thus tested the maximal number of participants that we could test. The participation rate (14 of 23) mostly reflects the global ability of the experiment to motivate participants and is standard for this type of binary response task.
Stimuli.
There were three sets of six stimuli, represented in Table 1. A stimulus was a picture of a circle filled by % of a color and by % of a color on a black background. had six possible values (0, 20, 40, 60, 80, or 100), such that each stimulus in its set could be described by its proportion of color . The three stimuli sets differed in the / colors they featured (purple/white, blue/orange, or gray/pink), in the orientation of the line separating the two colors (horizontal, diagonal, or vertical), and in the set of two response buttons provided to the participants to arrange the stimuli in two groups. Each response button featured a yellow digit on a black background. All participants saw the three sets of stimuli in the same order, but associated with different conditions. Each image was created as a bitmap file with 250 250 pixels and presented on the screen as a square of 6 cm, corresponding to a visual angle of 11.4° at a distance of 30 cm.
Table 1.
Stimuli and responses
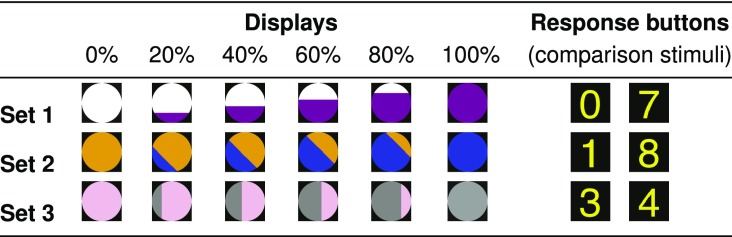 |
Each stimulus was a circle characterized by the proportion of color (e.g., for set 1, white vs. purple) of its total area, varying from 0% to 100% by increments of 20. Each set was presented with a different pair of response buttons (i.e., arbitrary digits).
Task and Conditions.
Participants were tested in a matching-to-sample task: In each trial, an item selected from a given stimulus set was used as a sample, and two distinctive shapes A and B (i.e., digits) as comparison stimuli. The task was to learn a rule where half of the six stimuli in a set correspond to a response A and the other half to a response B. At this stage, we use the term “rule” in a weak sense: A rule is simply the association between stimuli and responses A and B to be learned in one condition of this task (see, e.g., ref. 14 for discussion). There were three conditions (or rules), described schematically in Table 2. In the “monotone” condition, the three stimuli associated with A were clustered at one extreme (and the stimuli associated with B were thus clustered at the other extreme). In the “connected” condition, the three stimuli associated with A were all contiguous, but not clustered at an extreme. Finally, in the “nonconnected” condition, the three stimuli associated with A were spread noncontinuously, and so were the stimuli associated with B.
Table 2.
Conditions
 |
The three conditions were determined by whether a particular stimulus should be matched with the first response button (A) or the second response button (B). Monotonicity and connectedness of the resulting pattern are determined based on the way the A’s and B’s are entangled.
The three conditions were implemented in a different order to three different groups of participants. The order of the conditions was determined such that group 1 saw the conditions in increasing order of difficulty (a priori), group 2 in decreasing order, and group 3 started with the connected condition so that all conditions occurred first across groups. The stimuli sets were implemented in the same order to the different participants (so that they would be matched with different conditions across groups).
Procedure and Learning Criteria.
Stimuli were presented in blocks of six trials containing all proportions, with random order within each block. A trial started with the presentation of a stimulus centered in the middle of the screen. Once participants touched the stimulus picture, the two response buttons A and B appeared on each side of the screen. The left–right location of the response buttons was fixed within each learning condition. Touching the correct button cleared the screen and delivered a food reward. Touching the incorrect button triggered a 3-s timeout indicated by a green screen. Participants were allowed a maximum of 5 s to respond. The intertrial interval was set to 3 s. A condition was considered to be learned when the participants made no more than 1 error per block for three consecutive blocks (a general accuracy criterion), and no two of such errors were on the same stimulus (to ensure that each item could be counted as learned). Once these criteria were reached, the experiment would progress to the next condition.
Inclusion Criterion.
All conditions for which the learning criteria were reached were included in the analysis. Of the 14 participants included in our sample, 9 participants (3 per group) learned the three proposed rules (one in each condition), 2 learned two rules (connected and monotone), and 2 learned a single rule (one in the nonconnected condition and the other in the monotone condition). Excluding participants who did not finish the experiment (i.e., who could not reach the learning criteria in all of the three proposed conditions) does not change the pattern of results.
Results
We reproduced the two analyses already used in a human version of the task (4).
Analysis 1: Learning Performance.
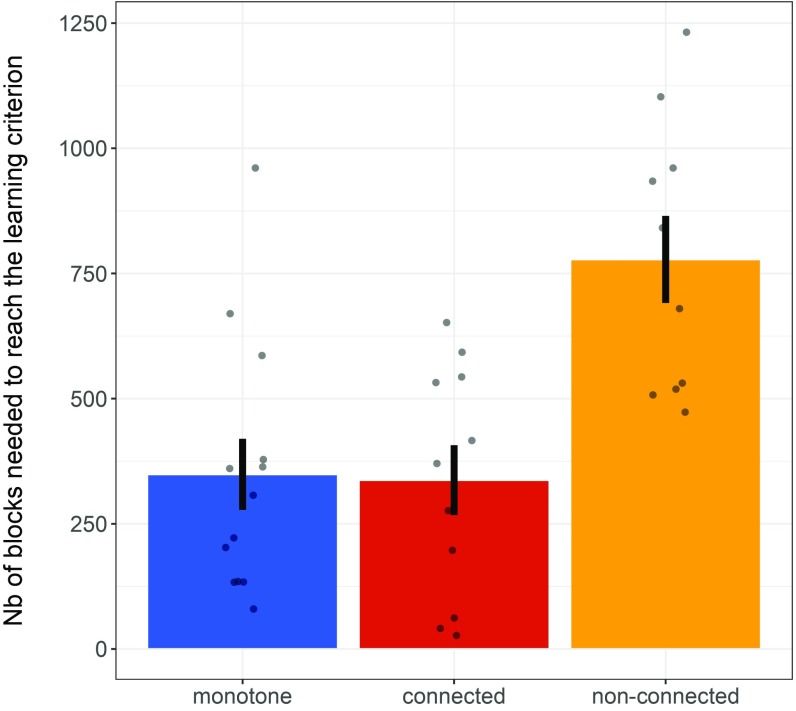
Participants took on average 2,826 trials to reach the learning criteria across conditions (; ; and ). Fig. 1 reports the average number of blocks of trials needed to learn a rule per condition (monotone, connected, and nonconnected).
Fig. 1.
Results corresponding to analysis 1: The figure represents the average number (Nb) of blocks needed to reach the learning criterion for each connectedness condition (monotone, connected, and nonconnected). Error bars indicate SEM. Dots represent individual data points.
To quantify the ease with which different conditions are mastered, we fit the number of blocks of six trials needed to attain the learning criterion using a mixed model in R (lme4 package; ref. 15). The model included a categorical predictor Condition (monotone, connected, nonconnected) as well as a random intercept for each participant. The model was specified as: Nblocks ∼ Condition + (1 Participant) and compared with a model without the predictor Condition to establish the effect of connectedness on learning difficulty.† Condition was a significant predictor of learning performance [; P < 0.001] with the monotone and the connected conditions learned the fastest ( blocks; ; blocks; and ) and the nonconnected condition learned the slowest ( blocks; and ).‡
Analysis 2: Bias for Connectedness.
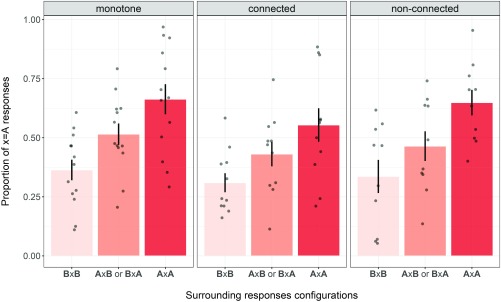
We explore here the role of a bias for connectedness in the course of learning: Do responses adhere to connectedness, whether or not these responses adhere to the underlying rule we imposed in each condition? For this, we abstracted away from the conditions we tested and looked at whether a participant’s response for a given stimulus (characterized by % of its area colored in one way) is dependent on this participant’s preceding responses for the two “surrounding” stimuli (filled by % and % of the same color). The responses to the surrounding stimuli define the following configurations: Either participants responded A to both surrounding stimuli (a configuration we refer to as AxA, in which represents the response to be looked at and the two A’s represent the responses given to the surrounding stimuli), B to both surrounding stimuli (BxB), or A to one of them and B to the other (AxB or BxA). The idea then is that when participants responded in one way to both % and %, they should respond in the same way to the central case %. We modeled participants’ responses (coded as 1 for A responses, and 0 for B responses) using a mixed logit model specified as responseSurroundingResponses * Condition+(SurroundingResponses * Condition Participant). Here, SurroundingResponses is a numerical predictor set to 0 in the baseline (i.e., mixed configurations AxB and BxA), to in AxA configurations (where we expect a bias toward A responses), and to −1 in BxB configurations (where we expect a bias toward B responses).
As can be seen in Fig. 2, participants’ responses were modulated by the responses they gave to surrounding stimuli [; P < 0.001]. Participants were at chance between responding A and B when they responded A to one of the two surrounding stimuli and B to the other. However, they were more likely to answer A when they responded A to both surrounding stimuli (AxA configurations) and more likely to answer B when they responded B to both surrounding stimuli (BxB configurations). There was no interaction between condition and participants’ SurroundingResponses [; P = 0.51], nor an effect of Condition [; P = 0.14].
Fig. 2.
Results corresponding to analysis 2: The figure represents the proportion of A responses as a function of the responses given to the contiguous stimuli: either participants responded A to both contiguous stimuli (AxA), only to one of them (AxB or BxA), or to none of them (BxB). Error bars indicate SEM. Dots represent individual data points.
We can refine the above analysis to rule out alternative interpretations.§ The analysis above may conflate a genuine bias for connectedness with a side effect of the structure of the material. To see this, consider triplets of contiguous stimuli in the various conditions and their expected responses (Table 2). It could be that triplets with similar correct responses at the edges (AxA or BxB) more often than not impose the same response to the middle condition. This in a sense would be a form of (probabilistic) local connectedness in our material, and surely the monotone and connected conditions are locally connected, by construction. If we assume that, sooner or later, participants provide correct responses, one expects the analysis of triplets above to reveal what we described as a bias for connectedness, but this bias would simply be reflecting the fact that the rules to be learned are (probabilistically) locally connected and that the participants eventually learn them. The nonconnected condition thus becomes crucial: By construction, it was not connected, and it was also not locally connected in that sense (there is simply no AxA or BxB configuration). However, the analysis above yields the same result when restricted to this nonconnected condition [; P < 0.01].
One can dig more deeply into similar issues with two further analyses. First, one can restrict the above type of analysis to incorrect responses, so that effects coming from correct responses to underlyingly locally connected triplets are taken out of the picture. However, one may argue that such an analysis could be subject to a backfiring sampling bias, depending on the actual structure of the material: If there were many triplets with correct responses ABA in the material, filtering out correct responses to the middle stimulus would generate a spurious effect of (local) connectedness. Concretely, if one rule had been of the form ABABAB, all triplets could have created an effect of local connectedness when filtering out correct responses in the middle of the triplets. Second, then, we ran the same analysis now restricted to correct responses. These additional analyses confirmed the presence of a bias for connectedness, whether the analysis was restricted to incorrect responses [; P < 0.01] or to correct responses [; P < 0.001].¶ Overall, whether one focuses on all responses, only on incorrect responses, or only on correct responses, the analyses all reveal a bias for connectedness in all conditions. The effect thus arguably goes beyond any of the structural regularities imposed by the material.
Finally, we tested whether the evidence for a connectedness bias is also robust with respect to participants’ own biases. In particular, a connected response pattern of the form AAA could result from a mere response bias in favor of A (note that giving the same answer throughout the experiment or throughout a block is not worse than answering at random, since stimuli were divided in half among the two categories). We therefore conducted the analysis above excluding blocks where participants gave the same response to all stimuli (categorizing them all as A or all as B). A bias for connectedness was again found across all conditions [; P < 0.01] and in particular in the critical nonconnected condition [; P < 0.01].
Discussion
A deflationary description of our results may say that the patterns we described as connected (and monotonic) are intuitively less “complex” than those we described as nonconnected, and so perhaps all that we have shown is that baboons learn less complex patterns more easily. However, it is important to establish an independently motivated metric of complexity to evaluate such a statement: In precisely what sense is one pattern more or less complex than another? Complexity measures may be more or less easy to design objectively, and surely they should eventually be arbitrated based on empirical data of the type provided here (see, e.g., ref. 16). One way of interpreting our results, then, is to say that the complexity to which baboons are sensitive, in pattern-extraction tasks like the ones we used, involves connectedness, since what distinguishes the different conditions is whether it is possible to describe the sorting pattern with a connected rule. Thus, and crucially for our enterprise, we conclude that baboons have learning biases that favor connectedness (be it for complexity reasons that can be independently assessed or not), just like humans.
The present results closely follow and resemble well-established results about so-called “pseudocategorization” (7–9), which has been explored very broadly, with very consistent findings. On this basis, we trust that the effects are reliable. We see our contribution as showing that what has been said for pseudocategorization and object concepts can be extended to logical concepts. We furthermore hope that our results are framed in a way that may open up interesting developments, in particular the possibility of exporting many discussions about object concepts to logical concepts in the animal kingdom.
Finally, returning to our starting point, we reiterate that the meanings of words in natural languages are, by and large, subject to a connectedness constraint. This constraint could be the fossilization in language of more general, nonlinguistic biases: In a large hypothesis space for the meaning of a new word, connected meanings are at an advantage because the patterns they correspond to are more salient to humans. These biases may not have a linguistic source, however, and they could thus be present even in nonhuman animals without an extended lexicon. Strikingly, even if both content words and logical words may show the traces of these biases for humans, the biases themselves may be found in species without a communication system like human language, certainly not one with logical words. The evidence shows that indeed baboons, just like humans, find it easier to discover connected patterns than nonconnected patterns. The connectedness constraint is thus active in these species in a form that can explain how the referential and functional lexicons of human languages are shaped.
Acknowledgments
The research leading to these results has received funding from the European Research Council (ERC) under the European Union’s Seventh Framework Programme (FP/2007-2013)/ERC Grant Agreement 313610; from the Agence Nationale de la Recherche (ANR-17-EURE-0017); from the Economic and Social Research Council (ES/N017404); and from the Excellence Initiative of Aix-Marseille University (A*MIDEX).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
Data deposition: The data and the script for the analysis in this paper are available at https://doi.org/10.17605/OSF.IO/U72H3.
*For instance, the set of all Berliners () is a subset of the set of all Germans (), which in turn is a subset of the set of all Europeans (); thus, is between and in the sense that . To check whether a quantifier is connected, one can therefore check whether the truth of and ( applied to the extreme sets) entails the truth of ( applied to the in-between set). Take, for example, “between three and five people” (assume that “people” refers to the people here in this room). If between three and five people here are Berliners, and moreover, between three and five people here are Europeans, then it follows that between three and five people here are Germans. (The smallest possible number of Germans is three, since there are at least three Berliners, and the largest possible number of Germans is five, since there are at most five Europeans.) Thus, “between three and five people” is connected. By contrast, “fewer than three or more than five people” is nonconnected: If fewer than three or more than five people here are Berliners, and, moreover, fewer than three or more than five people here are Europeans, it does not follow that fewer than three or more than five people here are German. (A counterexample: Exactly two people here are Berliners, exactly two people here are Hamburgers, exactly two people here are Parisians, and nobody else is European. Then, there are exactly two Berliners, exactly six Europeans, but exactly four Germans.)
†Since adding a predictor condition order (and its interaction with condition) did not improve the model fit significantly [; P = 0.31], this predictor was removed from the final model.
‡In some cases, the nonconnected rule could not be learned at all: Two participants did not succeed in reaching the learning criteria in the nonconnected condition, despite receiving a high number of blocks (>1,675) and despite succeeding in learning in the two other conditions. Note that these two unfinished learning conditions are not included in our analysis (see Inclusion Criterion).
§We thank an anonymous reviewer for encouraging us to present the following conservative and exhaustive analyses.
¶For both analyses, an additional effect of condition was found [on incorrect responses: ; P < 0.01; on correct responses: ; P < 0.001], reflecting that the rate of A responses differed between the connected condition on the one hand and the monotone and the nonconnected conditions on the other hand. This is a consequence of the specific connected rule chosen, which contains more triplets of stimuli with A, rather than B, in the middle, while the number of A-middle and B-middle stimuli in all possible triplets is balanced in the monotone and the nonconnected conditions.
For the analysis based on incorrect responses, we also found a marginal interaction between Condition and participants’ SurroundingResponses [; P = 0.07], reflecting that the effect of participants’ surrounding responses on their middle response was stronger in the nonconnected condition than in the monotone and connected conditions when focusing on errors only. This is expected if there is a sampling bias of the form mentioned above: Correct responses exhibit local connectedness in the monotone and connected conditions; filtering out correct responses therefore artificially hides local connectedness in these conditions.
References
- 1.Gärdenfors P., Conceptual Spaces: The Geometry of Thought (MIT Press, Cambridge, MA, 2004). [Google Scholar]
- 2.Xu F., Tenenbaum J. B., Word learning as Bayesian inference. Psychol. Rev. 114, 245–272 (2007). [DOI] [PubMed] [Google Scholar]
- 3.Dautriche I., Chemla E., What homophones say about words. PLoS ONE 11, e0162176 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Chemla E., Buccola B., Dautriche I., Connecting content and logical words. J. Semantics, 10.1093/jos/ffz001 (2019). [DOI] [Google Scholar]
- 5.Murphy G. L., Medin D. L., The role of theories in conceptual coherence. Psychol. Rev. 92, 289–316 (1985). [PubMed] [Google Scholar]
- 6.Keenan E. L., Paperno D., Handbook of Quantifiers in Natural Language: Volume II (Springer, New York, NY, 2017), Vol. 97. [Google Scholar]
- 7.Zentall T. R., Wasserman E. A., Lazareva O. F., Thompson R. K. R., Rattermann M. J., Concept learning in animals. Comp. Cogn. Behav. Rev. 3, 13–45 (2008). [Google Scholar]
- 8.Wasserman E. A., Kiedinger R. E., Bhatt R. S., Conceptual behavior in pigeons: Categories, subcategories, and pseudocategories. J. Exp. Psychol. Anim. Behav. Process. 14, 235–246 (1988). [Google Scholar]
- 9.Huber L., “Visual categorization in pigeons”, in Avian Visual Cognition, Cook R. G., Ed. (Comparative Cognition Press, 1999). http://www.pigeon.psy.tufts.edu/avc/. Accessed 24 April 2019.
- 10.Call J., “Descartes’ two errors: Reason and reflection in the great apes”, in Rational Animals?, Hurley S., Nudds M., Eds. (Oxford University Press, Oxford, UK, 2006), pp. 219–234. [Google Scholar]
- 11.Tomasello M., A Natural History of Human Thinking (Harvard University Press, Cambridge MA, 2014). [Google Scholar]
- 12.Fagot J., Bonté E., Automated testing of cognitive performance in monkeys: Use of a battery of computerized test systems by a troop of semi-free-ranging baboons (Papio papio). Behav. Res. Methods 42, 507–516 (2010). [DOI] [PubMed] [Google Scholar]
- 13.Fagot J., Gullstrand J., Kemp C., Defilles C., Mekaouche M., Effects of freely accessible computerized test systems on the spontaneous behaviors and stress level of Guinea baboons (Papio papio). Am. J. Primatol. 76, 56–64 (2013). [DOI] [PubMed] [Google Scholar]
- 14.ten Cate C., Assessing the uniqueness of language: Animal grammatical abilities take center stage. Psychon. Bull. Rev. 24, 91–96 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bates D., Mächler M., Bolker B., Walker S., Fitting linear mixed-effect models using lme4. J. Stat. Softw. 67, 1–48 (2015). [Google Scholar]
- 16.Feldman J., Minimization of Boolean complexity in human concept learning. Nature 407, 630–633 (2000). [DOI] [PubMed] [Google Scholar]