Conflicting functional effects of xylem pit structure relate to the growth-longevity trade-off in a conifer species

Significance

Understanding life history trade-offs is important because they present limits to adaptation in organisms. Life history trade-offs are usually thought to result from resource allocation conflicts among multiple traits, but functional constraints based on individual morphological traits can also contribute. We show that a fundamental life history trade-off between growth and longevity in a conifer species is related to a single morphological trait in the xylem that has conflicting functional effects. Our results demonstrate that, in addition to resource allocation trade-offs among multiple traits, functional constraints based on individual morphological traits provide mechanistic insight into how and when life history trade-offs arise.

Abstract

Consistent with a ubiquitous life history trade-off, trees exhibit a negative relationship between growth and longevity both among and within species. However, the mechanistic basis of this life history trade-off is not well understood. In addition to resource allocation conflicts among multiple traits, functional conflicts arising from individual morphological traits may also contribute to life history trade-offs. We hypothesized that conflicting functional effects of xylem structural traits contribute to the growth-longevity trade-off in trees. We tested this hypothesis by examining the extent to which xylem morphological traits (i.e., wood density, tracheid diameters, and pit structure) relate to growth rates and longevity in two natural populations of the conifer species Pinus ponderosa. Hydraulic constraints arise as trees grow larger and xylem anatomical traits adjust to compensate. We disentangled the effects of size through ontogeny in individual trees and growth rates among trees on xylem traits by sampling each tree at multiple trunk diameters. We found that the oldest trees had slower lifetime growth rates compared with younger trees in the studied populations, indicating a growth-longevity trade-off. We further provide evidence that a single xylem trait, pit structure, with conflicting effects on xylem function (hydraulic safety and efficiency) relates to the growth-longevity trade-off in a conifer species. This study highlights that, in addition to trade-offs among multiple traits, functional constraints based on individual morphological traits like that of pit structure provide mechanistic insight into how and when life history trade-offs arise.

Life history trade-offs are important because they present adaptive constraints on the most proximal components of fitness (1). A ubiquitous life history trade-off across organisms is that between growth and life span; organisms that grow slowly tend to live longer than those with faster growth, indicating that rapid growth is associated with reduced longevity (2). Consistent with the growth-longevity trade-off, slow early growth in trees has been associated with longer life spans in several species (3–9). However, in trees, fast growth rates and large size also provide fitness benefits via increased competitive ability, faster time to reproduction, and increased chances of early survival (10). Yet, selection for fast growth rates early in life can conflict with selection for slow growth at mature stages, as shown in adult Pinus ponderosa during a bark beetle outbreak (11). Although resource allocation conflicts have been shown to drive life history trade-offs (2), we know less about how morphological traits contribute. Nonetheless, understanding the functional trade-offs of specific morphological traits can enhance our ability to predict when and how life history trade-offs arise.

Life history trade-offs are usually interpreted as trade-offs that result from resource allocation conflicts among multiple traits that enhance fitness (12). Indeed, life history traits such as growth, reproduction, and survival require large investments in available resources and depend on a complex network of interrelated morphological and functional traits. Constraints imposed by individual traits and among multiple traits can therefore influence life history trade-offs. Multiple- and single-trait trade-offs can be distinguished on the basis of the underlying selection regime. Multiple-trait trade-offs arise when two or more fitness-enhancing traits are favored by selection but compete for a limiting resource and/or share a genetic correlation (12). Examples include flower size versus number (13), offspring size versus number (14), and growth versus defensive mechanisms in plants (15). On the other hand, single-trait trade-offs arise due to opposing selection by different selective agents, such as different environments or different components of fitness (12). Coat color in animals is an example of a single-trait trade-off: darker or lighter coat color is favored to match different seasonal background environments with dramatic consequences on fitness (16). Although trade-offs among multiple traits have been the focus of many life history studies, the contribution of single-trait trade-offs warrants further attention.

In trees, competing functional demands on stem xylem morphological traits may lead to a growth-longevity trade-off. Stem xylem performs several physiological functions critical to tree growth and survival, including efficient water transport, embolism resistance, and mechanical safety (17, 18). Trees require water to assimilate carbon and to maintain cellular turgor to promote tissue growth and function; therefore, water transport efficiency is positively related to growth rate (19–22). Embolism resistance, or the ability to tolerate high tensions in the xylem without hydraulic failure, allows for the maintenance of water transport and survival during drought (23, 24). Mechanical safety provides protection against physical damage, such as that caused by wind, pests, or pathogens, and cellular implosion under high xylem tension, and thus it is also related to survival (18, 25).

When multiple critical functions depend on the same xylem morphological traits, functional conflicts can arise with important consequences for tree growth and survival. This pattern may be more prevalent in conifers compared with angiosperm trees due to fundamental differences in xylem structure. In angiosperms, specialized cell types perform distinct functions. For example, vessels transport water while fibers provide biomechanical support. The physical separation between biomechanical support and water transport in angiosperms allows vessels to reach large dimensions, thus decreasing resistance to water flow (26). However, large vessels have disadvantages, such as reduced resistance to freeze-induced embolism (27). Furthermore, storage in parenchyma tissue may also trade off with hydraulic and biomechanical functions (28, 29). Thus, in angiosperm xylem, functional trade-offs involve the complex interplay between morphological characteristics of different cell types and their respective functional consequences (29). In contrast, in the conifer xylem, tracheid cells perform both water transport and biomechanical support functions. Tracheid cells are much smaller than vessels and the corresponding higher cell-wall thickness-to-span (lumen) ratio provides biomechanical support (26).

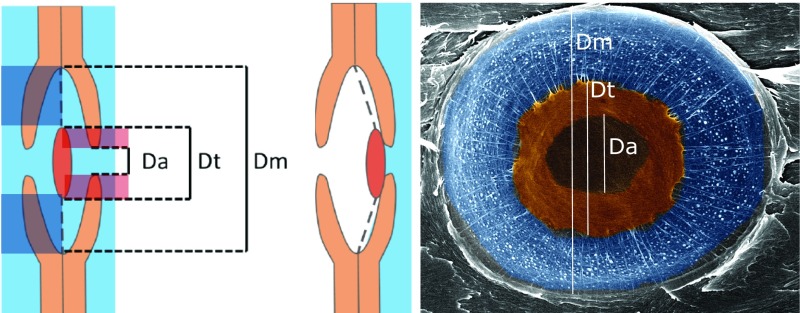
Another distinction between angiosperm and conifer xylem morphology is pit structure. Water movement between tracheids occurs only through pit openings and not perforations, as occurs in vessel elements. The larger size of conifer pit membranes and pores compared with the pore openings of angiosperms reduces resistance to water flow to compensate for increased resistance imposed by the small diameters of tracheids (30). Conifer pits also have a specialized form, with a torus-margo structure (Fig. 1) in which water flows through the porous margo, and the thickened torus in the center acts as a valve, sealing the opening when embolism occurs, thus preventing air spread throughout the rest of the xylem and increasing embolism resistance (31). However, all else being equal, a pit structure that enhances embolism resistance with a larger overlap between the torus and aperture (i.e., opening) would limit water transport efficiency by reducing the space for water flow through the margo and aperture (Fig. 1; Discussion). Therefore, torus-margo pit structure may play a pivotal role in a functional trade-off between water transport efficiency and safety in the conifer xylem.

Fig. 1.

Schematic of an unaspirated torus-margo pit structure (Left) and an aspirated pit (Center) as viewed from a radial cut between two tracheids, showing measurements of pit membrane (D_m), torus (D_t), and aperture diameters (D_a). Torus overlap (D_t-D_a/D_m-D_a) is shown in red and margo space (D_m-D_t/D_m-D_a) is shown in dark-blue shading. Scanning electron microscope image (colorized with Adobe Photoshop) of aspirated torus-margo pit surface (Right) showing measured pit dimensions.

We hypothesized that conflicting functional effects of xylem traits contribute to the growth-longevity trade-off in the temperate conifer species ponderosa pine (P. ponderosa Lawson and C. Lawson var. ponderosa C. Lawson). We tested this hypothesis by examining the extent to which xylem morphological traits (i.e., wood density, tracheid diameters, and pit structure) relate to growth rates and longevity in two natural populations. By focusing on a single conifer species we were able to examine the role of each xylem trait in growth and longevity while minimizing the types of variation in xylem structure observed among species. Hydraulic constraints arise as trees grow taller, with xylem anatomical traits expected to adjust to compensate for these constraints (32, 33). We therefore disentangled the effects of size through ontogeny in individual trees and growth rates among trees on xylem traits by retrospectively sampling each tree at multiple trunk diameters. We found that the oldest trees had slower lifetime growth rates compared with younger trees in the populations that we studied, indicating a growth-longevity trade-off. Furthermore, we provide evidence that a single xylem trait, pit structure, relates to the growth-longevity trade-off in a conifer species due to its conflicting effects on hydraulic safety and efficiency.

Results

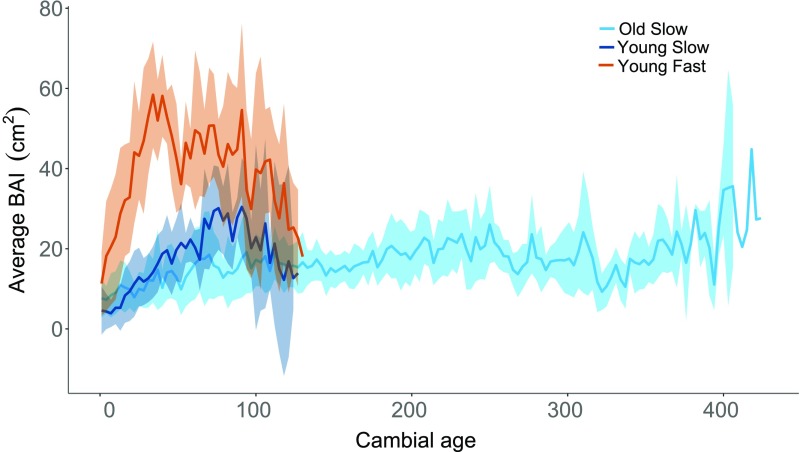
The oldest trees had slower average lifetime growth rates than all young trees combined (F_1,19 = 5.839, P = 0.026). Slow-growing young trees had similar average lifetime growth rates compared with the old trees, but old trees did not grow as quickly as fast-growing young trees even early in life (F_2,18 = 51.87, P < 0.0001; Fig. 2). Although not included in this study, differences in lifetime growth rates among age classes were also significant with larger sample sizes of trees from the same sites (34), even after correcting for climatic differences between the early-life growth periods of old and young trees (see SI Appendix, Fig. S1 for growth rates by calendar year of selected trees for this study).

Fig. 2.

Average annual basal area increment (BAI) growth rate over cambial age (years) for each class of trees from both sites (n = 7 trees per class, 21 total). Shaded bands represent 95% confidence intervals. The oldest trees had slower average lifetime growth rates than all young trees combined (F_1,19 = 5.839, P = 0.026). Slow-growing young trees had similar average lifetime growth rates compared with the old trees, but old trees did not grow as quickly as fast-growing young trees even early in life (F_2,18 = 51.87, P < 0.0001).

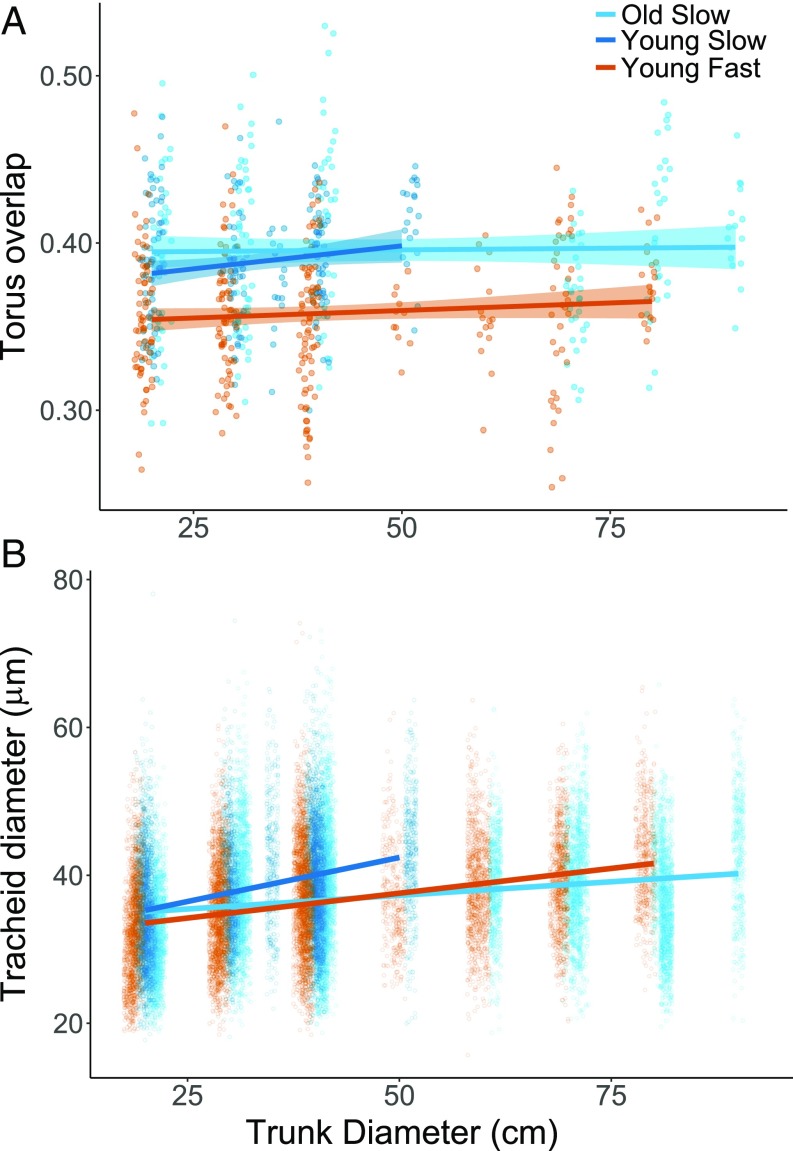
Torus overlap (the width of pit border covered by the torus; Fig. 1) was larger in slow-growing trees (both young and old) compared with fast-growing young trees at the single site sampled (F_1,11.57 = 6.199, P = 0.029; Fig. 3A) and was primarily achieved by smaller pit aperture diameters (F_1,9.61 = 4.0859, P = 0.07; SI Appendix, Fig. S2). There is an inverse relationship between torus overlap and margo space (the fraction of pit border width leftover for margo; Fig. 1); thus margo space was smaller in slow-growing trees compared with fast-growing trees (F_1,11.57 = 6.2154, P = 0.029; SI Appendix, Fig. S3). Torus overlap did not change with trunk size through ontogeny (F_1,33.51 = 0.407, P = 0.528; Fig. 3A), although all raw pit dimensions increased with trunk size (SI Appendix, Fig. S2). Tracheid diameters did not differ with growth rates (F_1,52.08 = 0.492, P = 0.486) but increased with trunk size through ontogeny (F_1,45.55 = 26.626, P < 0.0001; Fig. 3B). Tracheid diameters did not differ with trunk size between classes (F_2,42.21 = 1.855, P = 0.1689; Fig. 3B). Correspondingly, we found no differences in heartwood or sapwood density due to growth rates among trees (SI Appendix, Fig. S4).

Fig. 3.

Torus overlap (A) and tracheid diameters (B) by individual trunk diameter through ontogeny for each age-growth class at the Mackay Bar site (n = 4 trees per class, 12 trees total). Shaded bands represent 95% confidence intervals but are too narrow to be visible in B due to large tracheid sample size. Points represent individual pit (n = 708) and tracheid measurements (n = 24,989). Torus overlap was larger in slow-growing trees (both young and old) compared with fast-growing young trees (F_1,11.57 = 6.199, P = 0.029). Tracheid diameters increased with trunk size through ontogeny (F_1,45.55 = 26.626, P < 0.0001).

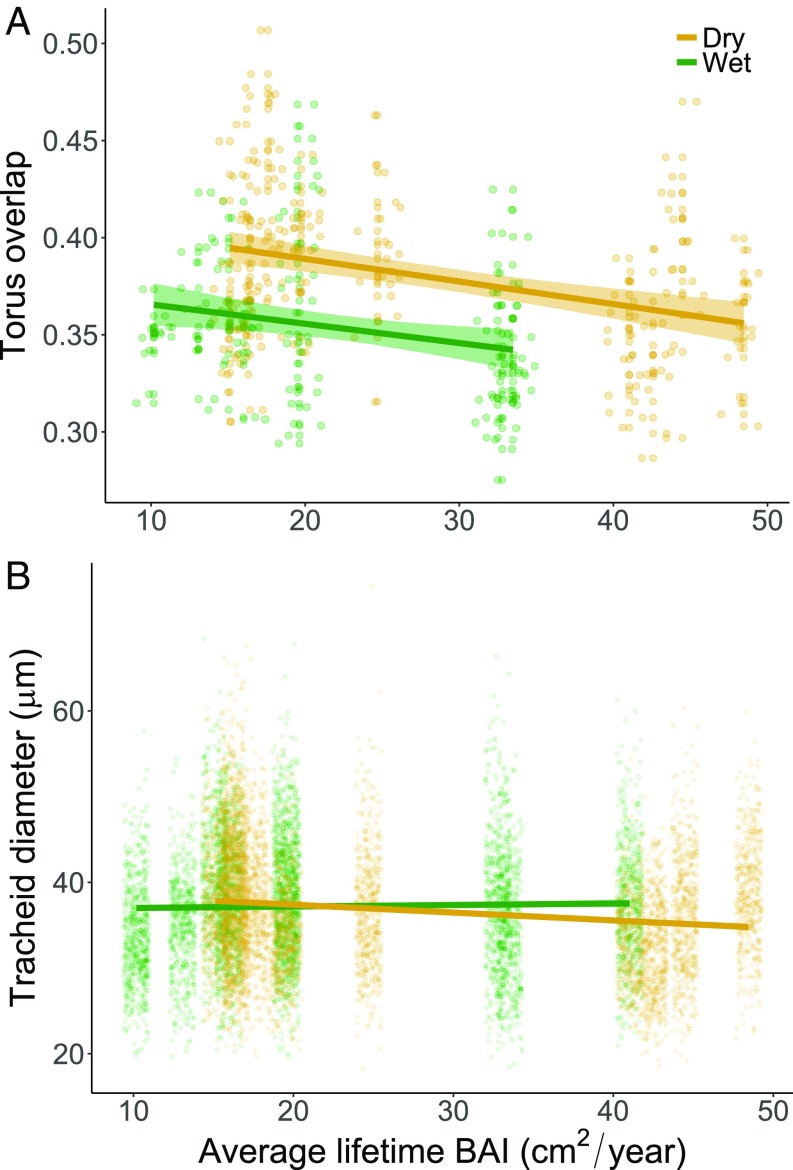
Torus overlap was also negatively related to average lifetime growth rates among trees at both sites when sampled at a fixed trunk diameter (F_1,21.59 = 7.189, P = 0.0138; Fig. 4A). While there was no significant interaction effect between growth rate and site, average torus overlap was larger in trees from the drier site (F_1,22.19 = 11.902, P = 0.0023; Fig. 4A). On the other hand, tracheid diameters sampled at given trunk size did not vary with average lifetime growth rates (F_1,20.95 = 1.516, P = 0.2319), site (F_1,20.94 = 0.933, P = 0.7631), or their interaction (F_1,20.92 = 0.780, P = 0.3873) when sampled at a fixed trunk diameter (Fig. 4B).

Fig. 4.

Torus overlap (A) and tracheid diameters (B) by average lifetime annual BAI (cm²/y) for each site: Mackay Bar (Dry) and Bullion Ridge (Wet). Xylem traits were sampled at a fixed trunk diameter of 30 cm for all trees (n = 7 trees per class, 21 total). Shaded bands represent 95% confidence intervals, but are too narrow to be visible in B due to large sample size. Points represent individual pit (n = 322) and tracheid measurements (n = 10,470). Torus overlap was negatively related to average lifetime growth rates among trees at both sites (F_1,21.59 = 7.189, P = 0.0138) and was larger in trees from the drier site (F_1,22.19 = 11.902, P = 0.0023).

Discussion

This study provides evidence that pit structure, a xylem morphological trait with conflicting functional effects on hydraulic safety versus efficiency, relates to the growth-longevity trade-off in natural populations of a conifer species. In the mixed-age ponderosa pine populations that we studied, the oldest trees grow slower compared to younger trees, a pattern found in several other studies (3–9) that is consistent with a growth-longevity trade-off. Slow-growing trees from these populations have intertracheid pits with larger torus overlap compared to fast-growing trees. Torus overlap enhances embolism resistance in conifers (35, 36), and it can also limit water transport efficiency of the xylem (below). A growth-safety trade-off based on pit structure is consistent with the growth-longevity trade-off found in these populations: trees with less efficient xylem grow more slowly but may reach older ages in part because their xylem is more drought-resistant. Although the basis of any life history trade-off is inherently complex, this study highlights that the growth-longevity trade-off in natural populations of a conifer species relates to a single morphological trait with conflicting functional effects.

The negative correlation that we found between torus overlap and growth rates among trees at both sites (Fig. 4A) is consistent with a trade-off between hydraulic safety and efficiency based on pit structure. First, it is well documented that a larger torus overlap provides greater embolism resistance among conifer species by creating a stronger seal with the pit aperture that prevents air spread to adjacent xylem cells when embolism occurs (35, 36). Many temperate conifers such as ponderosa pine live in environments that are seasonally dry (37), and embolism resistance conferred by larger torus overlap likely contributes to their ability to survive droughts and consequently live longer. Moreover, while the slope of the negative correlation between torus overlap and growth rate is consistent across sites, torus overlap was larger on average for a given diameter growth rate in trees from the drier site (Fig. 4A), suggesting an advantage for larger torus overlap and increased embolism resistance in dry environments.

As trees require water when stomata open to allow carbon assimilation and to maintain cellular turgor for cell expansion (growth) and function, water transport efficiency is positively related to growth rate (19–22). In conifers, pits are unavoidably involved in water transport efficiency because water transport from cell to cell up the tree can occur only through pits. However, the contribution of pit structure alone to water transport efficiency at the tissue or whole-plant level is very difficult to quantify and not well resolved because factors such as pathway length, conduit size, and pit density are also involved (38). In light of this complexity, the correlation between torus overlap (yet no other xylem trait) and growth rates at two different sites is remarkable. It suggests that our focus on natural populations of a single species and sampling at similar trunk sizes reduced variability in other xylem traits and unmasked the functional conflicts of pit structure and its relationship to life history patterns. Variability in xylem traits across species, plant size, and environments, along with the relative contribution of each xylem trait to hydraulic function, may explain the lack of a clear trade-off between hydraulic safety and efficiency when tested among a broader set of conifer species (38).

At the pit level, the effect of torus overlap on water transport efficiency is not empirically resolved either. Consistent with previous studies (35, 39), we found that increases in torus overlap were mostly due to a decrease in pit aperture diameter. The extent to which pit aperture contributes to whole-pit resistance to water flow likely depends on the pore area of the margo. If the margo pore area is small compared with the aperture size, most of the resistance to water flow will be due to the margo and the aperture will have less influence (40, 41). However, if the margo pore area is large, as is the case in ponderosa pine (35) (Fig. 1), it would contribute less resistance and a greater portion of whole-pit resistance will shift to the aperture (42, 43). Ultimately, smaller pit aperture (SI Appendix, Fig. S2) and less margo space (SI Appendix, Fig. S3) associated with larger torus overlap would unavoidably constrain flow through the pit membrane, leading to a trade-off between hydraulic safety and efficiency at the pit level. This conclusion is in line with previous studies that find a strong correlation between pit hydraulic resistance and embolism pressure for Northern Hemisphere conifers (31, 44) and a strong relationship between P₅₀ and pit hydraulic resistance in Pseudotsuga menziesii as torus overlap increases with height (45).

Surprisingly, we did not detect a correlation between tracheid diameters and growth rates among trees in our study. We expected that the strong influence of tracheid diameter on water transport efficiency (Hagen–Poiseuille equation; ref. 46) would lead to a positive correlation between tracheid diameters and growth rates. Instead, we found that tracheid diameters scaled strongly and positively with individual trunk size through ontogeny, but not with growth rates among trees (Fig. 3B). This result is consistent with recent studies showing that the primary driver of conduit diameters in woody plants is the scaling effect of conduit tapering as the hydraulic pathway lengthens with stem height (47).

Motivated by several studies that report a strong correlation between wood density and tree demographics (48–50), an emergent hypothesis from the wood economics spectrum posits that denser wood is related to slow growth and higher survival (18). In conifer xylem, the tracheid cell-wall thickness-to-span ratio determines wood density (51). Thus, consistent with the lack of relationship between tracheid diameters and growth rates among trees, we did not detect a correlation between wood density and growth rates (SI Appendix, Fig. S4). These results indicate that cell-wall thickness does not differ between fast and slow-growing trees, consistent with previous studies that show low variability in cell-wall thickness in conifer tracheids (26, 51) and a recent study on the kinetics of tracheid development that demonstrated that cell-wall thickness is driven mainly by changes in cell size (i.e., duration of cell enlargement) in conifers (52).

We were surprised to find that tracheid diameters did not vary with site moisture, although both of these sites are relatively dry; interpolated climate data (53) indicate mean annual precipitation of 693 and 863 mm at the drier versus wetter site. However, we did find an effect of site dryness on the relationship between tree height and diameter; trees at the drier site were shorter for a given trunk diameter (SI Appendix, Fig. S5). Furthermore, in cold climates, small conduit diameters provide a selective advantage because smaller cells reduce the occurrence of freeze–thaw embolism (54–56). This may be a factor constraining tracheid diameters at a given tree height in these populations that experience regular freeze–thaw events. Protection from freeze–thaw embolism could also explain larger torus overlap for a given growth rate in trees at the Mackay Bar site, which is colder and drier (Fig. 4A). Therefore, we speculate that tree height, site dryness, and freezing temperatures impose selection pressures that constrain variation in tracheid diameters and wood density in these populations. These constraints on tracheid dimensions could explain the pivotal role of pit structure in water transport efficiency and growth rates in the studied trees. We conclude that variation in pit structure with diameter growth rate may be favored due to conflicting hydraulic demands depending on competition and differences in site climate among these populations.

Conclusions

Here we provide evidence that pit structure, a single morphological trait in the xylem with conflicting functional effects on hydraulic safety versus efficiency, relates to the growth-longevity trade-off in a conifer species. Our results support the profound consequences of torus-margo pit structure for conifer evolution (30). In light of the evolutionary and ecological relevance of a growth-safety trade-off based on pit structure in conifers, future research should focus on determining how this trade-off operates in natural populations of other species. Further research is also needed to quantify the contribution of pit structural variation to total xylem hydraulic resistance and efficiency through computational and physical models. Another research priority should be to determine the relevance of pit structure to drought survival by testing for differences between live and dead trees following drought events (57). To determine the adaptive potential of pit structure, genetic differentiation and developmental plasticity of the trait could be evaluated using common garden studies (58). However, these research goals will necessitate advances in efficient and reliable methods of measuring pit structure; currently, these measurements are prohibitively time-consuming at the sample sizes necessary for genetic or ecological studies. Importantly, if the growth-safety trade-off based on xylem structure that we found in ponderosa pine is common, it provides a mechanistic basis for declines in coniferous forest productivity as drought becomes more prevalent with climate change (59). Finally, this study highlights that, in addition to trade-offs among multiple traits, functional constraints based on individual morphological traits like that of pit structure provide mechanistic insight into how and when life history trade-offs arise.

Materials and Methods

Site and Tree Sampling.

We selected two sites for sampling, originally for a study of the long-term effects of wildfire frequency on tree growth (60). The sites were in remote areas with no history of logging and were located on ridges above the Salmon River in Idaho; one site near Mackay Bar and the other site near Bullion Ridge about 40 km downriver (SI Appendix, Fig. S6) (61). All sites had a mixture of old (>350 y old) and younger trees. At each site, we sampled relatively open-grown ponderosa pine trees in a range of size classes from a specified area of similar topography. For smaller size classes, trees experiencing obvious suppression from neighboring trees were avoided. At each tree, we recorded tree diameter at breast height. Based on needle carbon isotope ratios and vegetation structure, we determined that Mackay Bar was drier than Bullion Ridge (62). Furthermore, we interpolated normal climate data for the 1961–1990 period with the software ClimateWNA (53), which indicates that mean annual temperature and precipitation at the Mackay Bar site was 5.0 °C and 693 mm and at Bullion Ridge, 5.7 °C and 864 mm.

Growth Rates, Age Estimation, and Tree Classes.

We collected two cores from each tree and recorded tree diameter at coring height at 50 cm from the ground. We measured tree heights using a laser range-finder (Impulse 200). Cores were prepared using standard techniques (mounted and sanded until cellular structure was visible through a binocular microscope) and visually cross-dated to assign a calendar year to each tree ring (63). We measured ring widths of all cores to the nearest 0.001 mm using an Acu-Gage micrometer and Measure J2X software version 3.1 (Voortech Consulting) and verified dating accuracy using COFECHA (64). We used standard techniques to correct age estimates on cores missing the pith and to correct for coring height (65).

To calculate basal area growth, we determined the inside-bark radius of each tree by dividing the measured diameter at coring height by two and subtracting the average bark depth. We converted annual radial growth increments to proportions of the total inside-bark radius (66) and then converted to annual basal area increments (BAI) by assuming circular basal area with the pith at the center (67). We calculated lifetime annual BAI as the average of all of the annual BAI values for each tree. We first divided trees based on cambial age: old trees were above 350-y-old cambial age and young trees were between 85 and 150 y old at sampling. We further selected a subset of young trees with the fastest growth (lifetime BAI > 30 cm²⋅y⁻¹) and slowest growth (lifetime BAI < 25 cm²⋅y⁻¹) for comparison at each site. We selected trees at the extremes of the distribution of growth rates to enhance the likelihood of detecting trade-offs. Combining across sites, we sampled a continuum of growth rates among trees (Fig. 4). We used three classes per site based on age and growth rates: old slow-growing trees, young slow-growing trees, and young fast-growing trees. Due to the intensive sampling for xylem traits with trunk size through ontogeny, we sampled four trees per class (12 total) at a single site, Mackay Bar. For comparison between sites (at the same trunk size for each tree), we sampled 4 trees per class (12 total) from Mackay Bar and 3 trees per class (9 total) from Bullion Ridge.

Xylem Morphological Traits.

We extracted cores from their original mounts by exposing them to steam. We visually distinguished heartwood and sapwood and separated them on each core with a razor blade. We measured wood density (g⋅cm⁻³) as the dry mass per saturated volume (after overnight rehydration, as cores were not freshly collected) following methods outlined in ref. 68. Wood densities based on saturated and fresh volume were strongly correlated when tested in a separate set of freshly collected ponderosa pine core samples.

Once wood density was determined, we extracted multiple segments from each core at selected sizes (trunk diameters) by cutting them carefully with a razor blade. Core segments ranged from three to five growth rings, depending on how much tissue was needed for a section at least 5 mm in length. We soaked segments in ethanol for at least an hour and then remounted and covered them with a waterproof, gap-filling glue. We cut transverse sections of ∼16 µm using a rotary microtome (Leica RM 2235). We brushed sample surfaces with a mixture of cornstarch, glycerol, and water, which act as a non-Newtonian fluid that maintains the cell-wall structure of softwoods when cut (69). We stained samples using a solution of astrablue and safranin for 10 min, rinsed with distilled water, and then gradually dehydrated with a 75%, then 95% ethanol rinse and finally an anhydrous alcohol solution of 95% ethanol + 2.2-dimethoxypropane. After dehydration, we fixed samples with a drop of Eukitt quick-hardening mounting medium and dried them in an oven at 60 °C for at least 12 h. We imaged samples using a light microscope (Amscope T700) connected to a digital camera. For each transversal section, mean tracheid diameters were calculated from at least 100 tracheids throughout the earlywood (SI Appendix, Fig. S7).

We cut core segments radially by hand with a razor blade for sampling pit structure. We mounted samples on aluminum stubs and coated them with gold in a vacuum using a sputter machine (Denton Vacuum Desk V model). We observed and imaged samples with a scanning electron microscope (Hitachi S-4700 cold field emission, EMtrix electron microscope facility at the University of Montana). We measured the following pit dimensions on horizontal and vertical axes of each image: pit membrane diameter (D_m), torus diameter (D_t), and pit aperture diameter (D_a) on 10–20 pits per earlywood segment (Fig. 1). We measured pit dimensions using ImageJ 1.48 (National Institutes of Health). We calculated torus overlap (O) as in Hacke et al. 2004 (31): O = (D_t − D_a)/(D_m − D_a). We chose Hacke et al.’s formula over alternatives (34) because it is relativized to pit membrane minus pit aperture diameter, making the calculation more relevant to water flow resistance, although the two calculations were strongly correlated. We calculated margo space as the following: M = (D_m − D_t)/(D_m − D_a) because it accounts for the distance between the pit membrane border and torus relativized to pit membrane minus pit aperture diameter (representing the space through which water must flow in the pit).

Data Analyses.

We tested differences in average lifetime growth rates and wood density between classes using a standard ANOVA. We tested relationships between xylem traits with trunk size through ontogeny between classes of trees sampled at the Mackay Bar site using a general linear mixed model (GLMM) with tree class and trunk diameter as fixed effects and tree and position nested within core as random effects. We modeled xylem traits with lifetime growth rates using GLMM with tree as a random effect. For models of tracheid diameters, we used a log-normal transformation to stabilize residuals. We compared the relationships between xylem traits and growth rates among trees between sites at a fixed trunk diameter of 30 cm, using GLMM with tree as random effect. We performed all statistical analyses using RStudio 1.0.136 (70). Data reported in this paper have been publicly archived in the Dryad Digital Repository (https://doi.org/10.5061/dryad.31ns53c).