Dynamic graphical models of molecular kinetics

Significance

Biomolecules, such as proteins or nucleic acids, can adopt a number of molecular configurations, which grow exponentially with their size. Since conformation change drives biological function, characterizing structural configurations is critical. However, exhaustively sampling an exponentially large number of states and the transitions in between these rapidly becomes difficult by explicit simulation. Here, we make significant strides toward the characterization conformations of such systems. To achieve this, we break molecular configurations into subsystems and model how the subsystems mutually affect the others’ dynamics. We show that this approach may accurately capture the molecular dynamics and systematically outperforms existing methodology by predicting unobserved molecular configurations.

Abstract

Most current molecular dynamics simulation and analysis methods rely on the idea that the molecular system can be represented by a single global state (e.g., a Markov state in a Markov state model [MSM]). In this approach, molecules can be extensively sampled and analyzed when they only possess a few metastable states, such as small- to medium-sized proteins. However, this approach breaks down in frustrated systems and in large protein assemblies, where the number of global metastable states may grow exponentially with the system size. To address this problem, we here introduce dynamic graphical models (DGMs) that describe molecules as assemblies of coupled subsystems, akin to how spins interact in the Ising model. The change of each subsystem state is only governed by the states of itself and its neighbors. DGMs require fewer parameters than MSMs or other global state models; in particular, we do not need to observe all global system configurations to characterize them. Therefore, DGMs can predict previously unobserved molecular configurations. As a proof of concept, we demonstrate that DGMs can faithfully describe molecular thermodynamics and kinetics and predict previously unobserved metastable states for Ising models and protein simulations.

How many states does a macromolecule have? When is a molecular dynamics (MD) simulation converged? State-based MD analysis methods, such as Markov state models (MSMs) (1–6) and related MD simulation methods (7–10), take a direct approach at these questions: map each macromolecular configuration to a single global state such that they distinguish between metastable states or macro states—sets of configurations that are separated by rare event transitions. The number of states of a macromolecule is then determined by the timescales that one wants to resolve (2), and an MD simulation can be considered converged when all of these metastable states have been found and the transitions between them have been sampled in both directions. This state-based view has enabled characterization of folding (11–13), conformation changes (14, 15), ligand binding (16–19), and association/dissociation (20) in small- to medium-sized proteins. Although seemingly conceptually different, reaction coordinate (RC)-based methods, such as umbrella sampling (21) and flooding/metadynamics (22, 23), are also state-based methods, where the state is characterized by the values of the chosen RCs. Still, with such methods, all rare events that are not statistically independent of the chosen RCs must be sampled, and the corresponding metastable states must be resolved.

Even with massive simulation power and enhanced sampling methods, a converged analysis in the state-based picture fundamentally relies on the fact that there are relatively few metastable states. This is the case for cooperative macromolecules, such as small- to medium-sized proteins, where the long-ranged interactions create relatively smooth free energy landscapes, explaining the success for these systems. However, almost all available MD simulation and analysis methods will break down for systems with many metastable states. The proliferation of metastable states can already be observed in nontrivial protein systems (24), but a more pathological example is nucleic acids, where the number of ways to pair bases grows exponentially in size with the system, creating highly rugged energy landscapes with many metastable states (25, 26). Even for protein systems, the ability to characterize the global system state by a single variable will break down at a certain size. Beyond the size of a few nanometers, electrostatic interactions are weak, and thus, large molecular machines, such as the ribosome and neuronal active zones, are expected to consist of dozens to thousands of sparsely coupled switchable units. Even if each of these units only has 2 possible states, the total number of global system states grows exponential with system size, and any simulation or analysis method that relies on all of these states to be sampled is doomed.

In this paper, we propose a change of perspective from a global approach to one based on local subsystems by introducing dynamic graphical models (DGMs). DGMs represent each molecular configuration by a concatenation of subsystem configurations and then, model how these subsystems evolve in time by a set of local rules, encoding how each subsystem behaves in the field of all of the other subsystems. Although conceptually more involved than models with a single global state, such as MSMs, the decision to model a system as many coupled subsystems is key in reducing the computational complexity for systems that have astronomically large numbers of states. To learn the rules according to which each subsystem $i$ switches its state, not all global system configurations need to be sampled but only the states of those other subsystems $j$ that are directly coupled to $i$.

DGMs have conceptual connections to prior work in time series modeling as well as in MD. One example is a recent Granger causality model, which captures the time evolution of several binary random variables (27). DGMs, however, are mathematically more similar to Ising models, which are graphical models widely used to describe equilibrium behavior of solid states but also have many other applications (28, 29). In MD, DGMs have conceptual connections with ultracoarse graining (UCG) (30), where coarse-grain beads are used represent large groups of atoms, such as protein domains. Similar to DGM subsystems, each bead can change its interactions with other beads by means of discrete switching events (30, 31). The main difference between these models is that UCG is a particle-based simulation model, where subsystem switches are added to represent a more complex Hamiltonian compared with purely bead-based coarse graining. With DGMs, we here aim to describe the global state space dynamics purely as a set of coupled discrete switches, and they are thus generalizations of MSMs.

The main difficulty in applying graphical models to MD is that it is not clear a priori what the subsystems are and how they are coupled. Estimating the structure of graphical models from data is an extensively studied machine learning problem (32–35). Here, we take a first step toward estimating DGMs from simulation data by using a dynamical version of Ising model estimators (36).

The property that not all global system configurations need to be sampled to parametrize a DGM implies that DGMs are generative models. This means that they should be able to predict previously unobserved molecular configurations and thus, promote the efficient discovery of conformation space. Here, we demonstrate that DGMs can indeed predict previously unobserved protein conformations and that protein thermodynamics and kinetics can be accurately captured as for MSMs.

Dynamic Graphical Models

General Model Structure.

Here, we propose DGMs as a method to model molecular kinetics and thermodynamics inspired by graphical models, a classical machine learning approach to encode dependencies between random variables (34). Instead of encoding the global molecular configuration in a single state variable, DGMs characterize the molecular configuration by a set of subsystems $\mathbf{s}={\left\{{\sigma }_i\right\}}_{i=1}^N$ that encode the states of local molecular features (Fig. 1). The coupling parameters $J_{ij}\left(\tau \right)$ of a DGM then encode how each subsystem switches in time as a result of the states of other subsystems at a previous time: that is, ${\left\{{\sigma }_i\left(t\right)\right\}}_{i=1}^N\stackrel{J_{ij}\left(\tau \right)}{\to }{\sigma }_j\left(t+\tau \right)$. Like MSMs, DGMs are Markovian models in which the current configuration only depends on the previous time step. In contrast to MSMs that encode transition probabilities of global system configurations, DGMs encode the transition probabilities of single subsystems dependent on the settings of all of the subsystems. In addition, each subsystem does not generally depend on all other subsystems but only on a local neighborhood of subsystems—in other words, the coupling parameters are generally sparse.

Fig. 1.

Illustration of molecular representations in MSMs and DGMs. (A) Cartoon representation of protein conformational states along a trajectory. (B) MSM with Markov states, $S_i$, and transition probabilities between states $S_i$ and $S_j$, $p_{ij}$. The number of different Markov states, $S_i$, may grow exponentially with the number of subsystems, and only subsystem combinations that have been observed can be encoded in Markov states. (C) DGMs, here illustrated using a DIM, represent the current state of the system via the states of its subsystems, ${\sigma }_i$, that are coupled by parameters $J_{ij}$. The DGM can encode exponentially many states, although the number of parameters grows only quadratically with the number of subsystems.

For illustration, consider a DGM of a one-dimensional (1D) Ising model (37) (Fig. 2A) consisting of $N$ subsystems on a ring, each of which adopts 1 of 2 configurations: 1 or −1. Each subsystem (or spin) interacts directly only with its nearest neighbors and possibly, an external field, resulting in 3 coupling parameters for each spin. Given a choice of the dynamics used to flip the spins, such as Metropolis, Glauber (Gibbs), or Kawasaki dynamics (38–40), a DGM that describes the probability of each spin’s state at time $t+\tau$ given the spin configuration at time $t$ will thus require $3N$ parameters. A direct MSM, however, distinguishes all $2^N$ global Markov states and needs to estimate an up to $2^N\times 2^N$ transition matrix from the data. More importantly, an MSM can only retrospectively describe the dynamics between states that have been observed in the simulation data. For example, an MSM is unable to predict that “spins up” and “spins down” are 2 different metastable states unless it has sampled transitions between them. A DGM can in principle be parameterized only using the spin fluctuations in 1 of 2 metastable states, and the global thermodynamics and kinetics can still be predicted. We intend to exploit this property for modeling biomolecular dynamics.

Fig. 2.

DGMs estimated for a 1D Ising model from equilibrium simulation data (ED) and from simulation data only containing configurations with negative net magnetization (NED). (A) Illustration of the circular Ising model. (B) Analytic stationary distributions of $⟨M⟩$ and empirical histograms NED dataset. Shown DGM predictions are for models where the local fields $\left\{h_i\right\}$ are not estimated. (C) Implied timescales of estimated models and the true reference.

When using DGMs to model biomolecular dynamics, we are not given the definition of subsystems and their couplings a priori, but we must rather estimate them from data. A subsystem could be something as complex as a protein domain (Fig. 1A) with multiple internal states or something as simple as a torsion angle rotamer or a contact between 2 chemical groups that each have only 2 settings, similar to spins. After the subsystems are defined, it must be estimated which of them are coupled. Estimating the coupling graph from data is a notoriously difficult problem, often referred to as the inverse Ising problem. (32, 33, 41). However, we have the advantage that modeling the dynamics via a DGM creates a directed dependency graph in time: the spin variables at time $t+\tau$ only depend on the spin variables at time $t$ (Fig. 1C). This makes the problem of estimating the coupling between subsystems tractable.

Dynamic Ising Models.

Here, we propose a first implementation of DGMs using a dynamic variant of the Ising models. Ising models consist of a set of $N$ spins with configuration $\mathbf{s}={\left\{{\sigma }_i\right\}}_{i=1}^N$. Each spin can be in 1 of 2 settings, ${\sigma }_i\in \left\{-\mathrm{1,1}\right\}$. The probability of a spin configuration is given by

$$p\left(\mathbf{s}\right)={\mathcal{Z}}^{-1}\exp \left(\sum _{i=1}^N\sum _{j\ne i}{J}_{ij}{\sigma }_i{\sigma }_j+h_i{\sigma }_i\right),$$ [1]

where the model parameters $J_{ij}=J_{ji}$ and $h_i$ describe the coupling strength between subsystems $i$ and $j$ and the local field of subsystem $i$, respectively, and $\mathcal{Z}$ is the partition function. The distribution (1) can be easily sampled (38, 39) given the parameters $\mathbf{J}$ and $\mathbf{h}$. The most common Ising models have spins arranged in a lattice, and only neighboring spins are coupled.

When modeling molecular kinetics, our data consist of (possibly short) time series rather than samples from the equilibrium distribution. Therefore, we use dynamic Ising models (DIMs) (36) that model the conditional distribution $p\left({\mathbf{s}}_t\mid {\mathbf{s}}_{t-\tau }\right)$ that governs how spin configuration—and thus, the configuration of our molecular system—changes in time. Note that, given a model $p\left({\mathbf{s}}_t\mid {\mathbf{s}}_{t-\tau }\right)$, we can simulate long trajectories and thus, also predict the equilibrium distribution, $p\left(\mathbf{s}\right)$. The DIM is given by

$$p\left({\mathbf{s}}_t\mid {\mathbf{s}}_{t-\tau }\right)={\mathcal{Z}}^{-1}\exp \left\{\sum _{i=1}^N{\sigma }_{t,i}\left(\sum _{j=1}^N{J}_{ij}\left(\tau \right){\sigma }_{t-\tau ,j}+h_i\left(\tau \right)\right)\right\},$$ [2]

where $\mathbf{J}\left(\tau \right)\in {\mathbb{R}}^{N\times N}$ is a matrix of coupling parameters, $\mathbf{h}\left(\tau \right)$ is a vector of local fields, and $\mathcal{Z}$ is the partition function. DIMs can readily be generalized to more than 2 states per subsystem ${\sigma }_i$, which we call dynamic Potts models (DPMs) (SI Appendix has details). Unlike in Eq. 1, the self-couplings $J_{ii}\left(\tau \right)$ are nonzero. The coupling matrix $\mathbf{J}\left(\tau \right)$ is not necessarily symmetric, and it does not have a specified topology. In this work, we use DIMs to implement all of the presented DGMs.

The DIM samples the current state of all subsystems given their configuration at a time $\tau$ prior. This is in contrast to Glauber dynamics, where only a single subsystem is allowed to change its state in some infinitesimal time $\delta t$. Consequently, if we use a $\tau$, which is larger than the characteristic timescale of 1 or more of the subsystems, the dynamics of these subsystems will not be resolved. This is analogous to how a lag time defines the temporal resolution in an MSM. More detailed analysis of DIM properties is in SI Appendix, section 1.3 and Fig. S1.

Results

Recovery of an Unobserved Phase and Its Thermodynamics and Kinetics in the Ising Model from Biased Data.

One of the most interesting properties of DGMs is that they make predictions for global system configurations that have not been observed in the training data. Here, we test whether a DGM trained with data from an Ising model confined to negative net magnetizations only can predict the existence of configurations with positive net magnetization, their equilibrium probabilities, and the timescale of remagnetizing the system.

As a first test, we simulate a 1D periodic Ising model with 9 spins using Glauber dynamics, which exhibit 2 metastable phases with negative and positive net magnetization, $⟨M⟩$. Nonequilibrium (NED) and equilibrium (ED) datasets are generated by simulating 16 trajectories with all subsystems initialized in state −1. NED simulations are terminated before the net magnetization becomes larger than 0 (i.e., the NED dataset has no configurations with more than 4 subsystems in the $+1$ configuration). Consequently, the entire metastable state with positive net magnetizations is missing. In the ED data, simulations are run with lengths to match the sampling statistics of the NED data, but trajectories are allowed to reach positive net magnetizations. DGMs are estimated by optimizing SI Appendix, Eq. S4. We find that both the ED and the NED DGMs converge to the correct subsystem couplings (SI Appendix, Fig. S2A) regardless of whether we choose to estimate the external field parameters, $h_i$, or not (SI Appendix, Fig. S3). This means that the unbiased subsystem couplings can be recovered from a biased dataset, in turn suggesting that global system characteristics can be estimated from incomplete data (Fig. 2).

To compute the overall thermodynamics and kinetics of the system and the estimated DGMs, we generate MSMs with all $2^9$ states and compute their transition probabilities using Eq. 2. Indeed, the distribution of the net magnetizations, $⟨M⟩$, predicted by the DGMs closely resembles the true distribution (SI Appendix, Fig. S1B). In contrast, an MSM estimated using the NED data only contains configurations contained in the data and therefore, fails to predict the existence of positive net magnetizations (SI Appendix, Fig. S1B).

Remarkably, DGMs can also predict the kinetics involving states that have not been observed. The DGM predicts a global $2^9\times 2^9$ transition matrix that correlates well with the reference, albeit with some biases (compare SI Appendix, Fig. S2B with SI Appendix, Fig. S3C). The true global relaxation timescales are recapitulated well by the DGMs (Fig. 1C)—however, for the NED DGM, the timescales are systematically overestimated, as some self-couplings are overestimated (SI Appendix, Fig. S2A). As expected, the NED MSM completely fails to capture the slowest relaxation timescale, as it corresponds to the inversion of net magnetization that has not been observed in the training data.

DGMs of MD.

We now turn to MD, where DGMs are built using a discretization of molecular features and hence, introduce a systematic modeling error. To this end, we model MD simulation data of a pentapeptide Trp-Leu-Ala-Leu-Leu (WLALL) and compare DGMs with MSMs that are well established for peptide simulation data (Fig. 3A).

Fig. 3.

Comparison of DGM and MSM describing backbone torsion dynamics of the peptide Trp-Leu-Ala-Leu-Leu (WLALL). (A) Molecular structure rendering of WLALL in stick representation. (B) Global-state distribution computed according to DGM and MSMs. (C) Torsion angles serve as binary subsystems with value that indicates the rotamer. Vertical and horizontal dotted lines indicate the boundaries of the −1 to 1 transition in the $\varphi$ and $\psi$ torsions, respectively. Reference density of ($\varphi ,\psi$) torsions in Leu-2 from the WLALL dataset. (D) The 95% confidence intervals of MSM-implied (orange) and DGM-implied (blue) timescales at $\tau =2\hspace{0.17em}\mathrm{n}\mathrm{s}$. Confidence intervals in B and D are computed using bootstrap with replacement. Markov states shown in B are those observed in all 24 trajectories; DGM state probabilities are renormalized to this set.

We model WLALL by 7 subsystems corresponding to its backbone torsions ($\varphi ,\psi$). Each subsystem ${\sigma }_i$ can assume 2 “spin” states $\left\{-\mathrm{1,1}\right\}$ defined by splitting $\varphi$ at $0^{○}$ and $180^{○}$ and $\psi$ at $80^{○}$ and $180^{○}$, thus discretizing the Ramachandran plane into 4 states (Fig. 3C and SI Appendix). Our state vector $\mathbf{s}$ is thereby a rotameric state vector encoding the current state of the subsystems. We stress that the subsystem representation is a modeling decision and will in general be different for different molecules. We estimate MSMs and DGMs using this representation. For the MSMs, all $2^7$ possible global configurations serve as possible Markov states, and the MSMs are estimated on the subset of observed Markov states. MSMs are computed from DGMs by enumerating all possible global-state transitions. We find that the implied timescales of DGMs match those of the MSMs well (Fig. 3D and SI Appendix, Fig. S4). Additionally, the Markov state probabilities of the DGMs match closely those of the MSM, in particular for high probability states (Fig. 3B).

The DGMs only use 56 parameters but predict equilibrium probabilities for all 128 possible states and all $\mathrm{16,384}$ possible transitions. Thus, DGMs are statistically much more efficient than MSMs. MSMs directly estimate a transition matrix for all states that have been observed—for WLALL, 45 states (35.16%) and 337 state-to-state transitions (2.06%) have been observed ($\tau =2\hspace{0.17em}\mathrm{n}\mathrm{s}$). Enumerating all possible system configurations is not scalable to larger systems. For larger systems, MSMs are built by clustering states, preferentially by grouping states that are quickly exchanging (42–45). Still, this approach requires all long-lived sets of configurations to be sampled in the data.

Prediction of Unobserved Metastable Molecular Configurations.

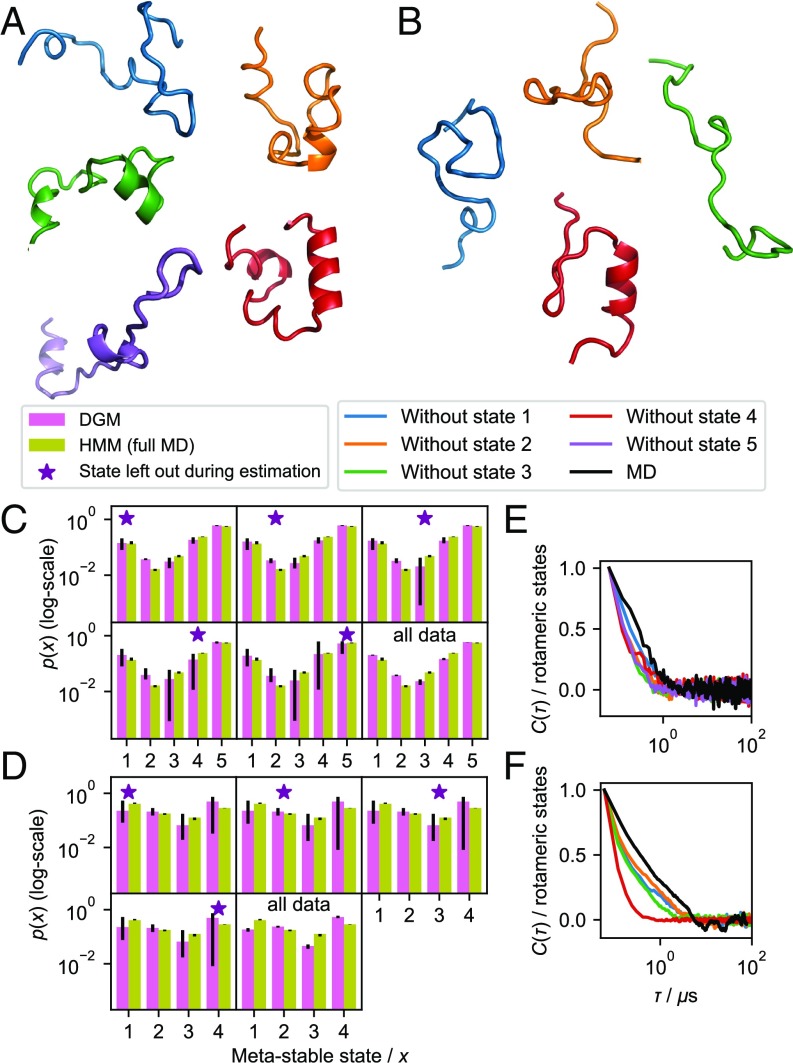
To more systematically test the performance of DGMs in predicting metastable states not observed during training, we estimated several DGMs (Materials and Methods) designed to be selectively blind toward a particular metastable state. We used simulation data previously published of 2 fast-folding proteins villin ($\alpha$-helical) and BBA ($\alpha /\beta$-fold) (46). As for WLALL above, we use the backbone torsion rotameric state vector to represent these proteins.

For villin and BBA, we built hidden Markov models (HMMs) (47) that resolves 5 and 4 metastable states, respectively (structures are in Fig. 4 A and B). We then estimated DGMs using the same data and confirmed that they qualitatively reproduce the equilibrium probabilities of the HMMs (Fig. 4 C, last panel, and D, last panel). Using the HMMs, we assign the MD data to metastable states and generate 5 and 4 sets of training data for the 2 proteins, where each set is missing 1 of the states. These subsampled datasets are used for estimating “one-blind” DGMs that are each “blind” to 1 metastable configuration (SI Appendix has details). From the estimated DGMs, we simulate synthetic trajectories of the subsystems to test whether these one-blind DGMs can recover the unobserved states and their statistics.

Fig. 4.

Prediction of macroscopic stationary and dynamic properties of fast-folding proteins villin and BBA with DGMs. (A and B) Molecular renderings of metastable configurations identified by HMMs of villin (A) and BBA (B) using a ribbon representation. Color/metastable state relationship: blue/1, orange/2, green/3, red/4, and purple/5. (C and D) Metastable state distributions sampled by DGMs were estimated leaving data from 1 of 4 metastable state out during estimation and using the full dataset (yellow). Reference distribution estimated using an HMM was estimated with the full MD dataset (magenta). (E and F) Normalized TCF of the rotameric-state vector in villin (E) and BBA (F) as sampled by the DGMs and in the simulation data.

We find that the one-blind DGMs sample the same configurational space as the full MD simulations, although the predicted equilibrium distributions differ (SI Appendix, Fig. S5). This suggests that, although the predicted thermodynamics in the one-blind DGMs are not quantitatively accurate, they are able to predict relevant states that have not been included in the training data. This is mirrored at the microscopic level: configurations sampled by the DGM closely agree with their MD counterparts (SI Appendix, Figs. S6–S8).

Next, we compare the macroscopic stationary and dynamic properties predicted by the one-blind DGMs with the full-data HMMs (Fig. 4). Indeed, all one-blind DGMs predict the existence of the state missing in the training data and in most case, with a population comparable with the MD simulation (Fig. 4 C and D). For visualization, we have reconstructed molecular trajectories from the subsystem trajectories simulated from a select set of one-blind DGMs (SI Appendix, Fig. S9 and Movies 1 and 2).

Finally, we compare the kinetics predicted by the one-blind DGMs with those of the original simulation. We use the time correlation function (TCF) of the rotameric state vector in the reference simulations of villin and BBA and compare them with corresponding TCFs from the DGM trajectories (Fig. 4 E and F). The TCFs are computed as $C\left(\tau \right)=ĉ\left(\tau \right)/ĉ\left(0\right)$ with $ĉ\left(\tau \right)={\sum }_i^N⟨\left({\sigma }_{i,t+\tau }-\overline{{\sigma }_i}\right)\left({\sigma }_{i,t}-\overline{{\sigma }_i}\right)⟩$, where $⟨\cdot ⟩$ is the time average and $\overline{{\sigma }_i}$ is the mean value of ${\sigma }_i$. We find that these generally agree well, although the DGMs tend to somewhat overestimate the relaxation rates, in particular the DGMs that were blind to the folded configurations (fourth [red in Fig. 4] state in both cases).

Metastability in One-Blind DGMs.

The analysis above shows that the conformational space sampled by the one-blind DGMs is realistic and recapitulates the conformational space sampled in the full MD datasets. However, whether metastable states predicted by the one-blind DGMs indeed are identical to the metastable states identified in the MD is not clear from this analysis alone. In other words, although we sample a conformational space, which is realistic, it is unclear whether information about slow conformational transitions is captured. To more quantitatively assess this, we estimated HMMs trained on datasets generated using the one-blind DGMs (SI Appendix). In half of the cases, the number of metastable states identified from the one-blind DGM datasets matches the corresponding numbers from the full MD dataset (SI Appendix, Table S1). In most of the remaining cases, 1 metastable state is missing, and in a single case, 1 extra metastable state is identified, closely resembling another metastable state (SI Appendix).

To better understand the identity of the metastable states observed in the one-blind DGMs, we assigned them to corresponding metastable states from the full MD dataset to minimize the total assignment error (SI Appendix). We find that the metastable states sampled by the one-blind DGMs can be unambiguously assigned to a corresponding metastable state observed in the MD dataset, and their sampling statistics correlate well with their MD counterparts (SI Appendix, Fig. S10 A and C). The average lifetimes of these metastable states qualitatively correlate with those of the reference MD dataset but generally are too short as already indicated above (SI Appendix, Fig. S10 B and D).

Discussion and Conclusions

The ability to simulate a molecular system to convergence depends critically on how the simulation is analyzed and how the quantities of interest are computed. Most current simulation and analysis methods use the idea that the molecule is a single global state—most explicitly, MSMs make that assumption. However, this picture leads to a sampling problem that does not scale to large molecular systems. A molecule with $N$ independent subunits with $M$ metastable states each will have an exponential number, $M^N$, of states.

In this paper, we introduce the concept of DGMs and their utility to model molecular kinetics. In DGMs, the global configurational state is encoded as a vector of states of its subsystems. As DGMs only model the pairwise interactions between subsystems, an exponential number of global configurations can be represented with a quadratic number of parameters. We illustrate DGMs using the DIM—and its generalization, the DPMs (SI Appendix).

In general, we find that the DGMs—despite their compact parametric form—can approximate well the dynamic behavior of several molecular systems. When gauged against MSMs, DGMs predict similar characteristic timescales and stationary distributions. Beyond the capabilities of MSMs, DGMs also allow for the prediction of transitions to and from unobserved molecular conformations and their stationary probabilities. Specifically, we found that DGMs can predict the presence of metastable configurations, which have not been observed during model estimation, although their absolute probabilities are not always accurately captured.

The representation of a molecule in the DGM framework gives rise to technical challenges that need to be addressed in future studies. (i) How can the subsystems of a molecule be learned from simulation data? Here, we have defined these subsystems a priori by choosing dihedral rotamers, but general optimization principles are needed (e.g., the variational approach for Markov processes) (48–50). (ii) How do we reconstruct molecular configurations from a subsystem-encoded representation? Going from an encoded representation back to a molecular configuration (decoding) is generally a difficult problem. (iii) How do we optimally choose regularization strategy and strength? While several options are available choosing the most appropriate combination remains heuristic. (iv) What are the limits of DGMs? The compact parametric comes with limited expressive power, and it is assumed that the subsystem couplings are not a function of the global configuration—if the latter is violated, we cannot expect quantitative predictions by DGMs. (v) How can we reconcile DGMs with experimental observables? Unlike for MSMs (51), the integration of experimental data into the estimation of DGMs is currently not possible. While in MSMs, experimental observables can be directly expressed in terms of transition matrix properties (52, 53), in DGMs we do not have direct access to these properties, and reconstructing them may be prohibitively expensive.

Machine learning has had a significant impact on molecular modeling in recent years (54–63). In particular, deep learning with its ability to learn complicated nonlinear functions given sufficient available data (64) has seen multiple applications. Problems faced here, including identification of subsystems and their discretization, are highly nonlinear and may benefit from these properties as well. Indeed, the variational approach for Markov processes network (VAMPnets) approach recently illustrated how the featurization, projection, and discretization pipeline of MSM building could be replaced by a deep neural network (54). We envision that a related approach can be taken in the context of identifying subsystems in molecular systems for DGMs and thereby, side step this currently cumbersome and manual process.

We anticipate DGMs and follow-up methods to be broadly applicable in biophysics. The compact parametric form allows us to model molecular systems that are significantly larger than what would be tractable using for example MSMs. Furthermore, a sparse subsystem coupling matrix $\mathbf{J}\left(\tau \right)$ could enable a spatial decomposition of large molecular systems into conditionally independent fragments, which are more amenable for simulation. The ability of DGMs to predict unobserved global configurations could further be used in an adaptive simulation setting, where previously unobserved states are reconstructed and used to seed new molecular simulations.

Materials and Methods

As we show in SI Appendix, section 1, the estimation of the DGM parameters $\mathbf{J}\left(\tau \right)$ and $\mathbf{h}\left(\tau \right)$ is tractable and factorizes into $N$-independent logistic regression problems. Here, we maximize the posterior distribution (SI Appendix, Eq. S4) using the SAGA optimization algorithm (65) as implemented in the scikit-learn python library (66). Additional details are given in SI Appendix, section 2. An open source library (LGPL-3.0 license) for estimation and analysis of DGMs along with example notebooks is available at http://www.github.com/markovmodel/graphtime/.