How lovebirds maneuver through lateral gusts with minimal visual information

Significance

Pilots need complex instruments and training to safely fly through gusts when their vision is deprived. In contrast, birds fly reliably over open water and at night, despite being more susceptible to gusts due to their much lower flight speeds. We found that even inexperienced lovebirds can navigate through strong opposing gusts in the dark, with only a faint point light source as a beacon. Their ability is surprising, because it was previously thought that diurnal animals needed a visual horizon and image features moving over their retina to maneuver. Instead, lovebirds fixate their head on the beacon while reorienting their body into the gust like a weathervane, enabling them to infer gust angle via neck twist and compensate accordingly.

Abstract

Flying birds maneuver effectively through lateral gusts, even when gust speeds are as high as flight speeds. What information birds use to sense gusts and how they compensate is largely unknown. We found that lovebirds can maneuver through 45° lateral gusts similarly well in forest-, lake-, and cave-like visual environments. Despite being diurnal and raised in captivity, the birds fly to their goal perch with only a dim point light source as a beacon, showing that they do not need optic flow or a visual horizon to maneuver. To accomplish this feat, lovebirds primarily yaw their bodies into the gust while fixating their head on the goal using neck angles of up to 30°. Our corroborated model for proportional yaw reorientation and speed control shows how lovebirds can compensate for lateral gusts informed by muscle proprioceptive cues from neck twist. The neck muscles not only stabilize the lovebirds’ visual and inertial head orientations by compensating low-frequency body maneuvers, but also attenuate faster 3D wingbeat-induced perturbations. This head stabilization enables the vestibular system to sense the direction of gravity. Apparently, the visual horizon can be replaced by a gravitational horizon to inform the observed horizontal gust compensation maneuvers in the dark. Our scaling analysis shows how this minimal sensorimotor solution scales favorably for bigger birds, offering local wind angle feedback within a wingbeat. The way lovebirds glean wind orientation may thus inform minimal control algorithms that enable aerial robots to maneuver in similar windy and dark environments.

When maneuvering toward a goal—such as during treetop landings—birds sense gusts and compensate. Over long ranges, birds compensate for crosswinds by fusing visual, olfactory, auditory, magnetic, and vestibular cues (1). In near-ground short-range navigation, it is thought that the velocity of image patterns (optic flow) over the retina (2) enables birds to compensate for lateral gusts (3). Clear vision in flight is made possible by head stabilization, which reduces retinal blur (4), stabilizes image features (5), and defines a clear gravity vector for the vestibular system (6). Birds stabilize their heads using complex neck motions to negate wind perturbations (7), wing flapping (8), and flight maneuvers (9) —even if the body is fully inverted, as it can be for geese (8). Human pilots cannot land safely at night without runway lighting, radio beacons, and guidance from air traffic controllers due to spatial disorientation (10). Birds have none of this technology yet maneuver easily even when visual cues are sparse. Frigate birds, for example, maintain their heading over open water, at times soaring in thick clouds (11), and specialist birds such as swiftlets and oilbirds fly in dark caves (12). What visual information birds need to stabilize their heads and compensate for lateral gusts without becoming disoriented is an open question.

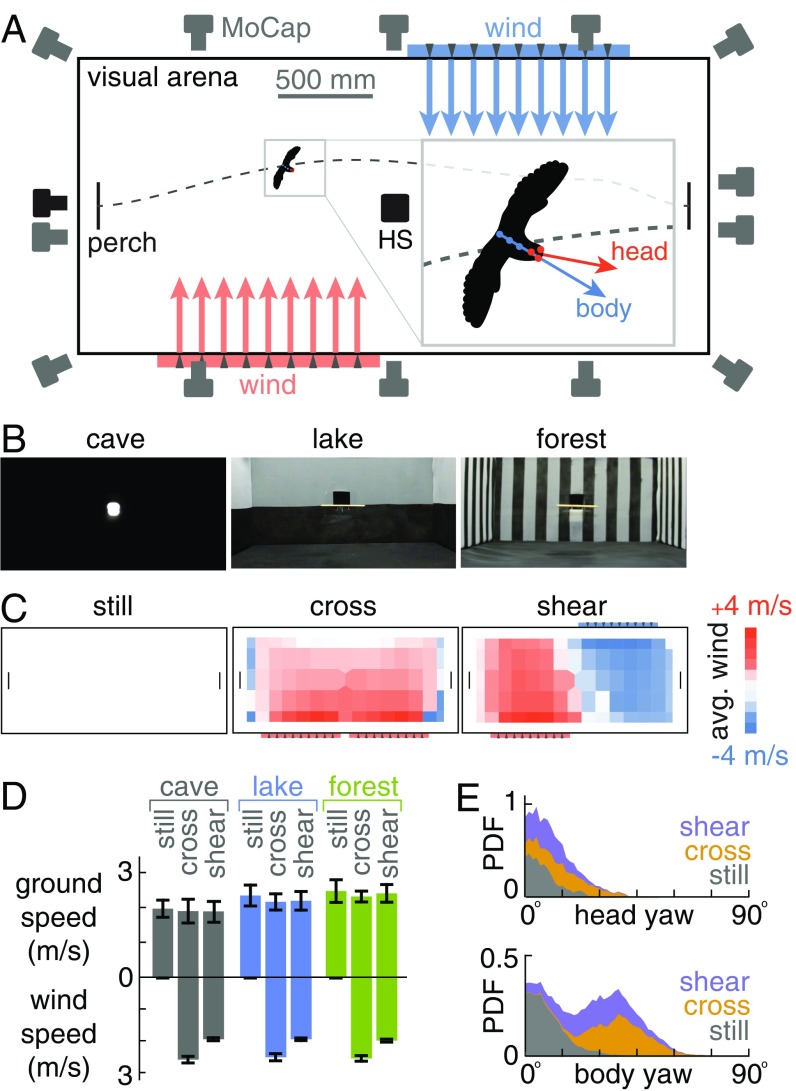
To determine what visual information birds need to maintain their heading in gusts, we manipulated the visual and gust environment in a 3.2-m-long arena in which 3 lovebirds (Agapornis roseicollis) flew between 2 perches (Fig. 1A). These generalist, diurnal, nonmigratory birds were raised in captivity, so they were naïve to lateral gusts. We simulated 3 visual environments: a cave, black walls with a small dim light behind the goal perch to simulate a narrow cave exit; a lake, a horizontal contrast line to simulate the wide-field horizon of open water; and a forest, vertical stripes optimized for optic flow perception (Fig. 1B and Materials and Methods). The global illumination in the cave was only 0.2 lx, similar to a full moon (13). We designed the cave (our control case) to give the minimum amount of visual information that still provided a heading to guide birds to a safe landing. In contrast, the illumination in the lake and forest was 160 lx, similar to a closed canopy during a clear sunny day (12). We used movable gust generators to simulate 3 gust environments: still, no gusts; cross, same-side gusts; and shear, opposing-side gusts (Fig. 1C). The gust speeds were comparable to the birds’ flight speeds, causing effective wind angles up to 45°. To determine how the birds flew in the 9 environmental permutations, we tracked 3D marker clusters on their head and body at 1,000 Hz over 366 flights. The differences between the marker cluster attitudes quantify the neck’s role in wind compensation.

Fig. 1.

Lovebirds fly at constant ground speed toward a goal irrespective of lateral gusts by turning their body into the gust. (A) Flight arena. Using IR light, 13 cameras automatically tracked marker clusters on the body and head (1,000 Hz); grayscale cameras recorded high-speed (HS) video (500 Hz). (B) Visual environments simulated a cave (uniform black), lake (horizontal stripe), and forest (vertical stripes). (C) The gust generators produced still (no gust), cross (side gust), and shear (opposing side gusts) environments. (D) The ground speed of lovebirds is somewhat higher in visually richer environments, but is not modified by gust condition (N = 3; separated by bird in SI Appendix, Fig. SF5). (E) Lovebirds orient their head toward the goal and their body into the gust across visual conditions (PDF = probability density function; histograms are stacked).

Results

Lovebirds Successfully Traverse the Arena in All Visual and Wind Environments.

The lovebirds easily traversed the arena in all 9 combinations of visual and wind environments. We only found small differences in the average ground speed (flight speed relative to the ground) between the visual conditions: lovebirds traversed the arena somewhat faster in the forest and somewhat slower in the cave (Fig. 1D). These findings agree with earlier observations that visual cues affect ground speed (2). The ground speed is not affected by wind environment; the birds reached the goal just as quickly in strong crosswinds as they did in still air (Fig. 1D), without being blown off course. Using a simple drag model, we estimate lateral displacements of 23 ± 11 cm based on measured gust speeds along the flight path (SI Appendix, section S1). Instead, the birds compensated for the gusts and landed near the center of the target perch (half-width 17 cm) across flights. They compensated by turning their body into the gust while directing their head toward the goal across visual conditions (Fig. 1E).

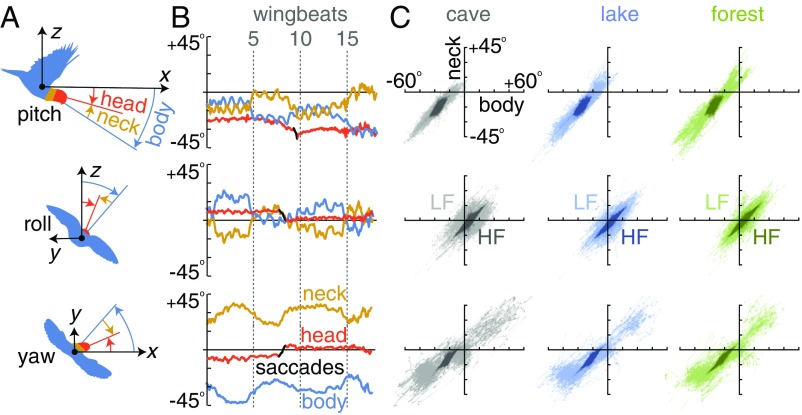
To fixate on their goal direction, the lovebirds use fast compensatory neck motions to stabilize their head—and thus their visual and vestibular system—even when their only visual cue is a dim point light (Fig. 1B and Movies S1–S3). We illustrate this ability with bird BB’s first flight in the cave–cross environment (Fig. 2B). BB’s head was stabilized over roughly 3 timescales: body oscillations during each wingbeat, body wobbling over several wingbeats, and body reorientations into the gust over approximately 10 wingbeats (Fig. 2B). Like the other 2 birds, BB showed no patterned changes in behavior with more time in the arena (SI Appendix, Figs. SF20–SF30). Across all flights, lovebirds used their necks to actively stabilize pitch, roll, and yaw relative to the body (Fig. 2 A and C). The stabilization was especially pronounced over wingbeat timescales, where the slope of neck versus body angles is nearly 1 (Fig. 2C). These neck motions must rely on vestibular and proprioceptive cues, because the point light in the dark cave provided very little roll information. Indeed, both the vestibulocollic and the cervicocollic reflex—which remained functional in the dark—underpin active head stabilization in vertebrates (6, 14). These findings are consistent with reports that body-fixed pigeons (15), free-standing pigeons (16), and hand-held owls (17) stabilize their head in the dark based on vestibular and proprioceptive feedback alone.

Fig. 2.

The neck isolates the head from body motion and orients it toward the goal based on minimal visual information. (A) The difference between head and body attitude determines neck pitch, roll, and yaw joint angles. Angles are defined by an arena-based inertial frame (x, y, z) that translates with the body. (B) The first flight by bird BB in the cave–cross environment shows how the neck isolates the head from body motion over multiple timescales. (C) For each bird (N = 3; separated by bird in SI Appendix, Figs. SF6–SF8), neck angle is correlated with body angle, which stabilizes the head in pitch, roll, and yaw over both low and high frequencies (LF, < 8.5 Hz; HF, > 8.5 Hz; Materials and Methods). Body–neck slopes are close to 1 at high frequencies (visual conditions pooled: pitch LF, 1.04, R² 0.90; pitch HF, 1.02 R² 0.76; roll LF, 0.87, R² 0.65; roll HF, 1.02, R² 0.90; yaw LF, 0.75, R² 0.76; yaw HF, 1.01, R² 0.81).

While compensating body oscillations, lovebirds also use their necks to stabilize head yaw and roll in a coupled fashion relative to the body (Fig. 3B). Head yaw and roll motion are coupled (Fig. 3B) such that the head yaws and rolls toward the goal, similar to how aircraft couple yaw and roll when turning (18). We did not observe a patterned coupling between pitch and other angular degrees of freedom (SI Appendix, Figs. SF31 and SF32). In contrast, yaw and roll are coupled by the neck as follows. The neck translates low-frequency body motions—which are weakly yaw–roll coupled (Fig. 3A)—into low-frequency head motions that are highly coupled (Fig. 3B). The neck does not couple yaw and roll over wingbeat timescales: high frequencies are as weakly yaw–roll coupled in the head as they are in the body (Fig. 3). However, roll and yaw saccades—which are directed gaze changes and not suppressed by head stabilization—show even stronger coupling than low-frequency motions (Figs. 3B and 2B). As with the body–neck coupling (Fig. 2C), the yaw–roll coupling must rely on vestibular and proprioceptive cues, because it persists in the dark cave over a range of timescales (Fig. 3B). Lovebirds seem to make larger saccades in the cave environment (Fig. 3B), probably because gaze slip is harder to detect by the eye. Pitch saccades are infrequent (SI Appendix, Fig. SF33), which helps the vestibular system sense the direction of gravity, according to a robot model of head stabilization (19). Motivated by the low residuals in high-frequency head motion (Fig. 3B), we further analyzed how the head is stabilized within a wingbeat.

Fig. 3.

Lovebirds coordinate yaw and roll simultaneously as they maneuver through the gust. (A) For each bird (N = 3; separated by bird in SI Appendix, Figs. SF9–SF14), body yaw and roll are coupled at high frequencies (HF pooled, slope −1.18, R² 0.51; LF, < 8.5 Hz; HF, > 8.5 Hz; Materials and Methods) with biases that depend on gust condition. The apparent coupling in LF shear is caused by the 2 gusts inducing different responses: first gust, negative yaw and positive roll; second gust, positive yaw and negative roll. (B) Head yaw and roll are coupled at low frequencies (LF, slope −0.66, R² 0.86) and weakly coupled at high frequencies (HF, slope −0.64, R² 0.32). The cross condition shows a bias toward negative yaw in combination with positive roll angles. (Inset) Simultaneous yaw–roll saccades (70% of saccades recorded) show strong yaw–roll coupling (slope −1.4; R² 0.98).

Lovebirds Attenuate 3D High-Frequency Head Oscillations with Their Necks.

The gain and phase of high-frequency neck motions reveal that wingbeat-driven linear body motion can be attenuated by the neck’s semipassive viscoelastic response. By highpass filtering the measured neck motions, we found that lovebirds attenuate lateral (y) and vertical (z), but not frontal (x) motions (Fig. 4A). The lateral and vertical residual head amplitudes are 20 ± 6% and 33 ± 9% of the eye diameter (5 mm), which reduces retinal image jitter (8). This reduction is probably not essential for frontal motion, where jitter will not substantially change motion parallax (20). Minimal frontal stabilization may be advantageous, because a force transmission ratio near 1 helps birds estimate speed and distance by integrating forward acceleration (21) using their otherwise stabilized vestibular system. By applying a semipassive neck suspension model, we found that the lovebird’s S-shaped neck acts like a tuned anisotropic viscoelastic beam. In the frontal direction, the head is nearly in phase with the body (phase lag: −0.02 ± 0.08 wingbeats), corresponding to either a strutlike stiff spring (high muscle tone) or a narrowly tuned spring (lower muscle tone) with almost no damping (Fig. 4B). The lateral and vertical directions (phase lag: −0.03 ± 0.20 wingbeats and 0.18 ± 0.09 wingbeats) correspond to underdamped and critically damped springs. Motivated by the larger vertical head-to-body ratios observed in lovebirds compared with whooper swans [0.52 vs. ∼0.2 (8); body mass 0.054 vs. 8.5 kg (22)], we analyzed how wingbeat-induced vertical body oscillations scale with body mass across flying animals. Using isometric scaling (SI Appendix, section S2), we predict that insects and hummingbirds experience minor vertical image jitter even without stabilizing their head, while larger birds experience major jitter that must be attenuated (Fig. 4C).

Fig. 4.

Lovebirds stabilize their head beat by beat in all directions except frontal. (A) Whereas motion in the frontal (x) direction is not stabilized (gain $\overline{a}\approx 1$), the neck stabilizes lateral (y), vertical (z), pitch, roll, and yaw motion for each bird (N = 3; separated by bird in SI Appendix, Fig. SF15). Head stabilization in each gust condition is similar across visual environments (underbars represent gust conditions). (B) A passive neck suspension model reveals ranges of natural frequency ratios $\left(f_{\text{n}}/f\right)$ and damping coefficients $\left(\zeta \right)$ corresponding to gains and phase lags observed in the head motion (circles, mean; contours, ±SD). (C) Smaller flying animals can maintain vertical image jitter less than eye diameter $\left({\Delta }_{z,\text{eye}}/d_{\text{eye}}<1\right)$ regardless of the head–body gain $\left(\overline{a}\right)$. Mean and SD by species group was derived from literature (58) for evaluating the scaling trend (light gray, insects; medium gray, hummingbirds; dark gray, other birds; SI Appendix, Fig. SF37 for all species). The Inset shows lovebird eye displacements are similar for each visual condition. See SI Appendix, section S2 for scaling details.

Whereas passive neck tensioning can provide and explain linear head stabilization, active stabilization is required to explain angular head stabilization according to our lovebird data. The pitch, roll, and yaw residual amplitudes are similar: 2.5° ± 0.6°; 1.9° ± 0.7°; and 1.9° ± 0.6°, which are 3 or more times greater than angular uncertainties in our marker constellations (SI Appendix, section S6). When applying our neck suspension model, the uncorrelated phase lags in head roll, pitch, and yaw (pitch, −0.20 ± 0.33; roll, −0.06 ± 0.39; yaw, 0.03 ± 0.32) correspond to an envelope of torsional spring-damper coefficients (Fig. 4B). The prevalent negative damping ratios represent active motorlike muscle function. Combined with the springlike properties of linear attenuation, these findings exhibit the known motor-, brake-, strut-, and spring-like functions of muscles (23). The maximum angular velocity of the head (residual amplitude × 2π × flapping frequency ∼ 250 °/s), is larger than what small parrots can resolve at full resolution [visual acuity (24) × flicker fusion frequency (25) ∼ 0.1° × 70 Hz = 7 °/s] (4). Lovebirds may therefore stabilize the image on their retina further by moving their eye via the vestibulo-ocular reflex (6, 26), though studies of pigeons suggest these attenuations may be limited to one-sixth those of head stabilization (26). By stabilizing their head within a wingbeat (Figs. 2 B and C and 4A), the lovebirds reduce the wingbeat-induced noise in the visual and vestibular cues that guide them toward their goal over many wingbeats.

Lovebirds Fixate Their Head on the Goal While Yawing Their Body into Gusts.

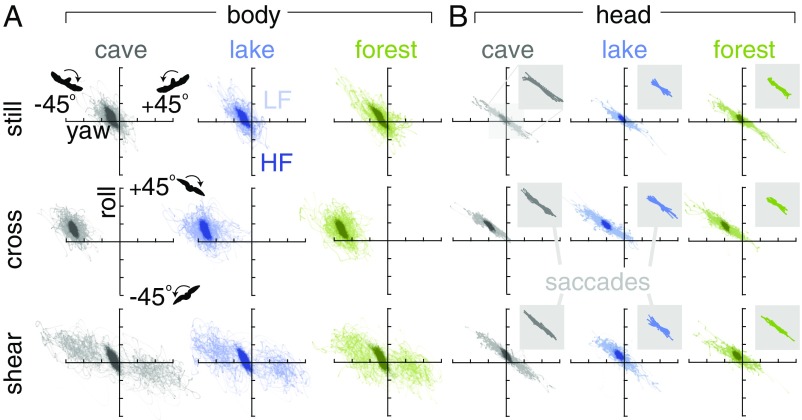
In each gust environment, lovebirds compensate as well in the dark cave as they do in well-lit environments with a wide-field horizon (lake) or strong optic flow (forest) (Fig. 5). Across all conditions, the lowpass-filtered flight paths (Fig. 5A) and body reorientations (Fig. 5 B–D) are similar. The most pronounced reorientation is in yaw: the body orients roughly 45° into the gust and reorients almost 90° midflight in the shear environment (Figs. 3A and 5D). The body also rolls into the wind, albeit over much smaller angles (Figs. 3A and 5C). In all conditions, head pitch remains constant while the body pitches up in preparation for landing (Fig. 5B). The lovebirds thus combine strategies of general aviation pilots, who pitch the fuselage up and trim their heading by using “crabbing” (yaw into the wind) or “wing-low” (roll into the wind) to compensate for strong crosswinds on final approach (18). Overall, the maneuvers to mitigate gusts are primarily performed in the horizontal plane (Fig. 5D). Motivated by the consistent yaw reorientations into the wind (Figs. 3A and 5D), we corroborated a yaw reorientation model to understand how the lovebirds might infer the local wind direction to negate the 45° cross and shear gusts.

Fig. 5.

Lovebirds traverse complex wind environments similarly well in forest, lake, and cave visual environments by fixating on a goal. (A) The average horizontal flight paths are similar across visual environments ($N=$ 3; separated by bird in SI Appendix, Figs. SF16–SF18). (B, C, and D) The pitch, roll, and yaw orientations of the head and body are similar across visual environments. Lovebirds pitch their body up gradually as they get closer to the landing perch while keeping their head level (B). In cross wind and shear conditions, lovebirds yaw their body into the gust while keeping their head fixated on the goal perch (D).

Discussion

Wind Angle Can Be Inferred by Fixating on the Goal While the Body Yaws into the Wind.

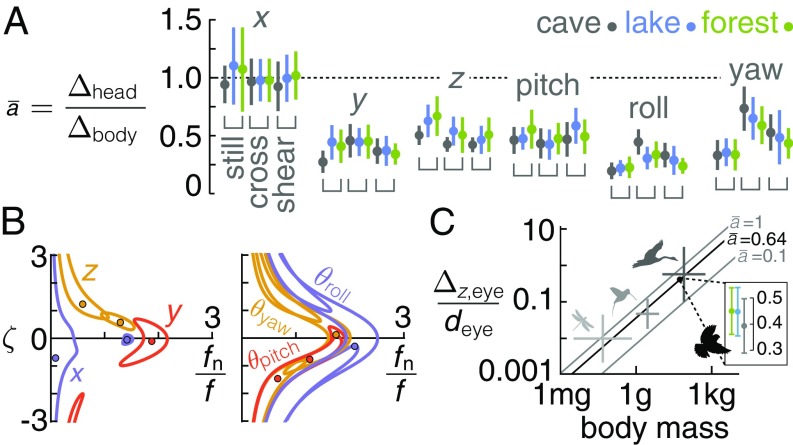
A 2D yaw reorientation and speed control model shows how lovebirds can compensate gusts by inferring the local wind direction via neck twist. Their neck is twisted by actively aligning their head with the goal direction, while aerodynamic torques work to align their body with the local wind direction. The local wind angle with respect to the goal direction can then be estimated via muscle proprioceptive cues encoding the angle over which the neck is twisted (Fig. 6 A and B). The twist angle feeds back into a basic proportional controller of body yaw, which responds fast enough to compensate for lateral gusts based on the measured flight paths. The ability of lovebirds to stabilize their head while maneuvering in gusts (Fig. 2–4) underpins this neck-informed gust compensation model. Stabilization enables the otoliths in the vestibular system (6) to reliably sense the direction of gravity (19), which provides an inertial horizon for performing horizontal (2D) compensation maneuvers in lateral gusts (Fig. 5D) without a visual horizon (Fig. 1B; cave). It also enables the lovebirds to stabilize their vision, which they need to keep their head fixated on the goal via neck twist (Figs. 2C and 4). The lovebirds fixate on the perch more often during the second half of the flight (Fig. 6B), presumably to provide the additional precision required for landing, similar to how raptors use straighter gaze angles when approaching a target (27).

Fig. 6.

Using an inertia-spring-damper model for body yaw, we infer that lovebirds combine passive and active control to reach the goal perch in gusts. (A) Slip angles range up to 30° in the cross environment ($N=$ 3; separated by bird in SI Appendix, Fig. SF19). Neck angles are sufficient for proprioceptive input (dark green, gaze aligns with perch; medium green, gaze within ±150% of the perch). (B) When landing in the shear environment (left side of plot), slip angles are larger and the head is fixated on the perch more often. (C) The slip angle passively goes to zero for an ornithopter, except for a small offset ($\approx$8°) due to minor wing asymmetries (Movie S4). (D) The nondimensional restoring torque on the ornithopter is proportional to slip angle over angles relevant to lovebirds (95% of lovebird data occurred between shaded boxes). Gray, tracking data; black, linear fit. (E) In our minimalistic model, body yaw is driven by a passive torque proportional to slip angle $\left({\theta }_{\text{slip}}\right)$ and an active torque proportional to neck angle $\left({\theta }_{\text{neck}}\right)$, and is dampened by a passive flapping counter torque. (F) The average corroborated coefficients in Eqs. 1 and 2 are similar across visual/gust environments, leading to similar damping coefficients $\left(\zeta \right)$ and yaw response times in wingbeats $\left(\tau \right)$. (G) A scaling analysis of the lovebird yaw gust response model applied for a steplike gust across animals in flapping flight shows they also can infer the direction of gusts based on neck twist within several wingbeats. Air density and nondimensional ratios can change the yaw response time in wingbeats up to an order of magnitude. See SI Appendix, section S5 for scaling details. Mean and SD by species group was derived from literature (58) for evaluating the scaling trend (light gray, insects; medium gray, hummingbirds; dark gray, birds; see SI Appendix, Fig. SF37 for all species). The Inset shows the corroborated lovebird response time varies little with visual condition.

Another essential building block of the compensation model is the aerodynamic restoring torque that orients the bird’s body into the wind. Our preliminary analysis of the bird’s yaw dynamics (Fig. 5D) suggested that this torque could be passive, like it is for a weathervane. Birds lack a vertical tail to generate this torque. However, when we used our wind tunnel to test a suspended mechanical flapping bird—which had no vertical tail—it passively reoriented into the wind as soon as it was released from a nonzero slip angle (the local wind angle minus body angle). When we removed the horizontal tail, the yaw dynamics still did not markedly change. These experiments show that flapping wings passively reduce slip angle effectively (Fig. 6C). The weathervanelike restoring torque generated by the flapping wings is approximately linearly proportional to the slip angle $\left({\theta }_{\text{slip}}\right)$ up to large angles (Fig. 6D). This is similar to the passive aerodynamic restoring torque generated by vertical tails (and to a much smaller degree, fuselages) of aircraft with nonzero slip angles (28).

The slip-reducing torque generated by flapping wings complements the previously discovered flapping counter torque, a passive torque proportional to body yaw velocity, ${\dot{\theta }}_{\text{body}}$, that dampens yaw motion in flapping wings (29). These 2 passive aerodynamic torques generated by a flapping wing sum together and determine the passive angular acceleration of the body yaw as follows (Fig. 6E):

$${\ddot{\theta }}_{\text{body}}=\left(k/I\right){\theta }_{\text{slip}}-\left(c/I\right){\dot{\theta }}_{\text{body}},$$ [1]

where $I$ is the animal’s yaw moment of inertia, $k$ is the aerodynamic restoring torque constant, and $c$ is the aerodynamic angular damper constant. By using the average corroborated $k/I$ and $c/I$ coefficient ratios based on the lovebird flight data, the model explains most of the yaw reorientation in the cross and shear condition (cross, R² 0.87, rms 12°; shear, R² 0.60, rms 16°; measurement uncertainty $\pm$2°, SI Appendix, section S6). The corroborated response time for the lovebird yaw model (Eq. 1 and Fig. 6F) is close enough to that of the mechanical bird model (Fig. 6 C and F; $\tau$ = 1.4 vs. 1.34 wingbeats) to support the idea that a passive aerodynamic restoring torque reduces slip. However, the residual error is still appreciable because the passive model predicts a 0° equilibrium slip angle, whereas lovebirds exhibit slip angles of 15° or more (Fig. 6 A, B, and E). Lovebirds must therefore actively control slip angle.

We inferred that a proportional (P) controller may be sufficient to explain how the lovebirds maintain nonzero slip angles, because P controllers produce offsets in their output when competing forces affect the system dynamics (28). Pigeons too have been found to use steering that resembles proportional control for close-range obstacle avoidance (30). In contrast to the passive body yaw response (Eq. 1), proportional yaw control requires wind slip angle feedback. Our recordings show that the birds fixate their gaze on the goal (Figs. 1E, 5 B–D, and 6 A and B) by actively contorting their neck up to 30$°$ or more in yaw and pitch (Figs. 2C, 5 B and D, and 6 A and B). Such angles are large enough to give yaw feedback via neck muscle proprioception (6) according to data for human necks (31). We also found that minor wing asymmetries in the mechanical bird model result in nonzero equilibrium slip angles of ≈8° (Fig. 6C), which is similar to the ≈15° recorded for lovebirds. Therefore, we hypothesized that neck angle times a constant P control stiffness, $k_{\text{P}}$, could predict the control torque that the birds apply using wing asymmetry:

$${\ddot{\theta }}_{\text{body}}=\left(k/I\right){\theta }_{\text{slip}}+\left(k_{\text{P}}/I\right){\theta }_{\text{neck}}-\left(c/I\right){\dot{\theta }}_{\text{body}}.$$ [2]

Indeed, adding the proportional controller enables the model to represent the data well (cross, R² 0.94, rms 9°; shear: R² 0.79, rms 13°). The goodness of fit especially improves in the shear case, where the 90° midflight yaw reorientations presumably require more active control. The fitted nondimensional damping coefficients, $\zeta \equiv c/\sqrt{4\left(k+k_{\text{P}}\right)I}=2.2\pm 2.0$, show that the response ranges from under to slightly overdamped (Fig. 6F) (28). To prevent drift while orienting in the wind, the lovebirds could also use their neck angle as feedback to modulate airspeed: we found that for each bird, lateral airspeed is indeed proportional to neck angle (R² = 0.77, 0.76, 0.52; SI Appendix, Figs. SF34 and SF35).

Neck Angle Gives Effective Gust Feedback and Scales Favorably with Body Mass.

When combined, the neck-informed proportional control models for body yaw and speed can explain most of the observed lateral-gust compensation behavior in lovebirds. The role of proprioception in flight control is also suggested by the observation that pigeons fly poorly when a paper collar blocks neck motion (9). Further refinement of the lateral-gust response model—e.g., by adding integral, differential, or other feedback terms informed by additional sensory inputs—is thus not essential according to the principle of parsimony. We expect, however, that fusing additional sensory feedback plays a role in making lateral-gust compensation more precise and robust. In addition to proprioceptive feedback, gusts may also be sensed by specialized feathers whose follicles encode feather vibration (32). These so-called filoplumes (33) are thought to inform behavioral changes when wind is blown at the breast of a fixed bird (34). In contrast, neck proprioception offers rapid, high-fidelity, directional feedback, as it does for the cervicocollic reflex (6). Lovebirds surely fuse other cues as well, such as expanding (looming) visual cues (35), parallax (36), or spatial memory cues (37). However, given the predictive strength of our simple model (Eq. 2), the most parsimonious explanation is that lovebirds compensate for gusts in the dark by using the dim point light source as a heading and reference for proprioceptive wind cues. Considering lovebirds are diurnal generalists, their innate ability may apply more generally to other birds, including those that fly in the dark with minimal visual information (12). To see if other birds could make use of proprioception-informed maneuvers, we calculated how the yaw angle response changes with body size according to our model (Eq. 2).

The rate at which the lovebirds can glean gust information from proprioception scales with the rate of the yaw reorientation into the wind. According to our model, the body yaw angle of lovebirds responds to a sharp lateral gust (step function) with a time constant $\tau =2fI/c=$ 1.4 $\pm$ 1.0 wingbeats (Fig. 6F and SI Appendix, section S4). Using isometric scaling, we find this time constant generally decreases with body size—ranging from around 10 wingbeats for insects to 1 wingbeat for large birds—showing that bigger animals could use proprioception to gather wind information over fewer wingbeats than lovebirds (Fig. 6G). Our model may therefore help to explain how birds migrate effectively even with minimal visual information, such as at night or in clouds and fog (11, 12, 38), or how blindfolded gulls can fly stably in crosswinds (39). However, the time constant is further modified by parameters such as air density, aspect ratio, and stroke amplitude within 1 order of magnitude (Fig. 6G), so further consideration is required for specific species (SI Appendix, section S5). Our model could also give mechanistic insight into why birds fly toward and crash into artificial light sources at night. These sources, which can be lighthouses (40), monuments (41), or skyscrapers (42), are estimated to lead to billions of bird deaths a year (43). Steady lights—like the one in our study—can be particularly attractive and thus disorienting for migrating birds (44).

Conclusion

Our corroborated control model can explain how lovebirds maneuver through 45° lateral gusts, without optic flow or a visual horizon, in visually poor conditions that cause spatial disorientation in pilots. By counteracting most of the low- and high-frequency body motions with their neck, lovebirds can infer the inertial horizon and reliably fixate on the light beacon. By comparing goal heading to body angle, which is driven into the gust by a weathervane-like aerodynamic torque generated by the flapping wings, lovebirds can estimate the local wind angle and proportionally control body slip and speed. The similarity in the proportional control model coefficients across environments (Fig. 6F) and consistent body kinematics (Fig. 5) show that this strategy is robust and works equally well in the dark with only a point light source as a beacon. The corresponding differences in ground speed are remarkably small across visual conditions (Fig. 1D), despite major gust speed differences. These results revise our understanding of the importance of optic flow in avian flight control. Optic flow is likely used to regulate ground speed (Fig. 1D) and vertical position—as it is with budgies (2) and hummingbirds (45) in corridors of still air—but is apparently not essential for dynamic flight control. Furthermore, a wide-field visual horizon may be replaced by a stabilized (Figs. 2 and 4) inertial horizon (46), in combination with a visual beacon, to navigate environments with 45° lateral gusts.

Our model explains how proprioceptive information related to flow direction is both available and functional in the lovebird’s gust compensation, whereas it was previously thought to be unimportant for wind orientation over longer flight distances in birds (3). Notably, our corroborated model performs better for the longer gust (Eq. 2; cross, R² 0.94, rms 9°) and converges over longer “crosswind” distances (SI Appendix, section S3) in a way that scales favorably with avian body mass (Fig. 6G). These findings suggest future movement ecological studies may find value in tracking both the body and head motion of birds [as recently pioneered in a pigeon navigation study (47)] to interpret atmospheric wind orientation in birds (SI Appendix, Fig. SF36). These studies will also benefit from more detailed laboratory studies that further dissect sensorimotor function in birds negating gusts and atmospheric turbulence across different length and timescales. Finally, the corroborated gust compensation model may inspire new minimal control algorithms that help aerial robots navigate dark and gusty environments as deftly as lovebirds (Movies S1–S3).

Materials and Methods

Experimental Setup.

We conducted flight experiments in a flight corridor (320 × 150 × 70 cm) surrounded by mesh walls, floor, and ceiling (CAD rendering in SI Appendix, Fig. SF38). The mesh type (Polyester Mesh 670 Μm - Open Area: 52%, ELKO Filtering) was chosen to be coarse enough for air from the gust generators to pass through, while fine enough that the generators were invisible from inside the arena. The floor was covered with a black rubber mat. Birch landing perches (34 cm long, 1.2 cm diameter) were mounted at the center of each end of the arena (equidistant from sidewalls and 33 cm from the floor). The perches were mounted on transparent acrylic bars set 10 cm off the wall to make them clearly visible (Fig. 1B) and allow safe landings. Birds entered the arena through entry windows (12.5 × 12.5 cm) cut out of the wall behind the perches.

We textured the white mesh walls in one of three ways: black vertical stripes 100 mm wide (forest), bottom half black and top half white (lake), and all black (cave). The vertical stripe dimensions (20 cm period, 10 cm black + 10 cm white) were tuned such that birds flying at 2 m/s in the center of the arena experienced a 10-Hz spatiotemporal frequency, a motion rate known to be well perceivable by small parrots (48, 49) like lovebirds. We chose the paint (black matte finish, Quick Color; Rust-Oleum) to provide high contrast: the average Michelson contrast measured from the center of the arena was 0.73 ± 0.03 between vertical stripes and 0.79 ± 0.004 across the horizon, which are perceivable contrasts for small parrots (49, 50). To provide sufficient ambient light for visual navigation (49, 50), we installed 2 large LED panels (120 × 120 cm; Samsung High CRI; illuminance: 600 cd/m²) 130 cm above the flight volume. The ambient light level was 155 ± 13 lx in the forest condition and 158 ± 12 lx in the lake condition (LX1330B; Dr.Meter), compared with 0.2 lx in the cave condition, where the only light source was a dim light behind the target perch (luminance 30 cd/m², LS-100; Konica Minolta). Black textile sheets prevented light from the LED panels from exiting the arena, and light sources in the surrounding room were shut off. As a result, no exterior visual cues were visible from within the flight arena (Fig. 1B).

Lateral gusts were produced by 2 custom-built gust generators outside the mesh sidewalls. Each generator consisted of 6 fans (12-in. diameter; 2931 CFM, Global Industrial) arranged in 2 rows within a wooden housing (CAD rendering in SI Appendix, Fig. SF39). Two mesh screens in front of the fans were designed to merge the individual air streams into a single uniform airflow (51). Each generator covered the entire height of the arena and one-third of the arena length. To create gust maps, we used a hot wire anemometer (CTM DT-8880) to measure airspeed at 135 perch-height locations (20 cm × 15 cm grid) (Fig. 1C). We placed noise-dampening foam pads on the room walls to reduce the noise to 94 dB (A-weighted; Velleman DVM805) when both gust generators were running. The birds spent no more than 2 h in the room when the generators were running, which is less than the 4 h allowed at these levels by California’s Occupational safety and health administration (52).

The lovebirds (Agapornis roseicollis) were hand-raised and housed in indoor social cages with at least 2 birds per cage in a 12-h night/day cycle. To habituate the lovebirds to the gust generator noise, we placed electric fans and speakers playing gust generator recordings in their holding room for 15 min at a time, up to 2 h a day, for a month before the experiments. To habituate the birds to the flight arena, we placed them in the arena for an hour at a time periodically during the 2 wk before the experiment. During the habituation, all lights were on, the visual environment had maximum richness (forest), the gust generators were off (still), and the birds were fed millet spray. Some habituation sessions included wearing tracking gear. Of 4 habituated birds, 3 showed no change in behavior when wearing the motion-tracking gear. The fourth bird was excluded from the experiment as it did not fly reliably wearing gear. The age of the 3 birds ranged from 14 to 36 mo, and their weights range from 53 to 55 g. Two birds were male (NN, RR); one was female (BB). All birds received food and water ad libitum, their cages were enriched, and all training and experimental procedures were approved by Stanford University’s Administrative Panel on Laboratory Animal Care.

To capture the positions/orientations of the bird’s head and body, we placed clusters of 3 retroreflective markers on a harness and thin goggle sockets worn by the bird (SI Appendix, Fig. SF40). The attitude (position and orientation) of each 3-marker cluster was tracked at 1,000 Hz by 13 infrared motion capture cameras (Qualisys Oqus 7+; 3 MP) mounted above the arena. The infrared light (880 nm) used by the cameras was outside the measured spectral sensitivity of the birds (53). During the calibration procedure, the tracking software (Qualisys Track Manager 2) reported positional tracking residuals of 0.1 to 0.3 mm. The harness and goggle sockets were custom fitted to the body shape of each bird to ensure a snug fit (54). The goggle sockets were made thin to ensure the visual field was not occluded (CAD rendering in SI Appendix, Fig. SF40). To minimize stress and avoid escape responses, we applied the tracking gear in complete darkness. To aid our vision and hand–eye coordination while applying the gear, we lit the room with 2 infrared LED lights (850 nm; Univivi U48R 48- LEDs WideAngle IR Illuminator) and wore custom-built infrared goggles (GoPro Hero3: Silver Edition with RipCage custom casing and 5.4 mm f/2.5 60d HFOV 10MP lens without IR filter mounted to high-definition video goggles; Dominator Revision A, Fat Shark).

Kinematic videos were made with 2 additional high-speed grayscale CMOS-cameras (Phantom Miro 310; Vision Research) mounted to the side and above the arena. The camera sensitivity in the infrared spectrum allowed us to make 500-Hz recordings in all visual environments, including the cave environment with the infrared motion capture cameras as the only light source. An external trigger was used to trigger the end of a 15-s ring buffer recording.

Data Capture.

The birds were exposed to the 9 visual and gust environments psuedorandomly (SI Appendix, Table ST3). For welfare reasons, and to reduce the probability that the birds used visual cues besides wall textures, we started with the bright environments (lake, forest), then finished with the cave (SI Appendix, Table ST3). Within each visual condition, we ordered gust environments for each bird in a Latin square fashion (SI Appendix, Tables ST3 and ST4) (55, 56). Before each set of flights, we put tracking gear on the bird, then transferred it in a covered transport box to 1 of the 2 entry windows of the unlit flight arena. We then slid open the door of the box and turned on the arena lights, prompting the bird to fly to the starting perch. Once the bird crossed the arena (either spontaneously or with a hand-wave cue), we saved data from the ring buffer. We only kept flights in which the takeoff direction was facing directly to the opposite perch ($\pm$30°). After each set of flights, birds were returned to their aviary and trained using positive reinforcement and handfed, so that all remained tame and voluntarily approached human hands.

After each flight, we cropped the kinematic video footage from takeoff until landing. After each set of flights, we checked the marker tracking data for quality. Frames with spurious rigid bodies were removed, and clear misidentifications of markers were corrected. These procedures were conducted in the Qualisys Track Manager (Qualisys AB) before exporting the position/orientation data as MAT files. Eight flights exported to MAT files were later discovered to have corrupt tracking data (clear misidentifications and/or blank datasets); these flights were not analyzed. During each flight, the birds flew across the arena in 1 of 2 directions: direction A and direction B. Of the 366 analyzed flights (BB, $n=$ 115; RR, $n=$ 127; NN, $n=$ 124), 187 were direction A and 179 were direction B. Analyzing both flight directions allowed us to ensure that the cross gusts were not always come from the same direction. Due to the symmetry of the arena and the lack of visible differences between direction A and B flights, we mirrored the kinematics of flights from B to A (SI Appendix, Fig. SF41). All data are publicly available online (57).

Data Processing.

The body and head attitude data were processed and filtered before subsequent analyses. Across all timesteps, 13% of the positions/orientations were missing due to markers temporarily being blocked by feathers or part of the bird’s body. Most of these missing data occur during takeoff and landing; for our analysis, we cropped out the takeoff/landing data (data where x was within 20 cm of the perches). The remaining data had 2% of values missing, and these values were omitted from subsequent analyses. Noise in the position/orientation data were filtered out using a lowpass filter at 6 times that trial’s flapping frequency (6$f$ = 102 ± 5 Hz). The position/orientation data were either analyzed with no additional filtering (Fig. 2B), an additional highpass filter [Fig. 2C (HF); Fig. 3 (HF); Fig. 4], or an additional lowpass filter [Fig. 2C (LF); Fig. 3 (LF); Fig. 5; Fig. 6 A, B, F, and G)]. The additional highpass filter was designed to isolate high-frequency head stabilization (cutoff frequency $f$/2 = 8.5 Hz). The additional lowpass filter was designed to isolate low-frequency head orientations (cutoff frequency $f$/2 = 8.5 Hz). We applied filters using Mathematica’s LowpassFilter and HighpassFilter functions (v11.0.1; Wolfram Research), which use Hamming windows for preprocessing and apply linear finite impulse response filters.

Wingbeat frequency and saccade data were extracted manually from kinematic video and tracking data. The ends of down- and up-strokes were defined as frames when wings were in their most anterior and posterior positions, respectively (5). We defined wingbeat frequency as the inverse of the average time between upstrokes ($f$ = 17.0 ± 1.0 Hz). Saccades were isolated by scanning the unfiltered head orientation data. A linear regression was applied to each extracted saccade to estimate the angular speed of the saccade.

To isolate the variation in yaw and roll (Fig. 3), we subtracted each trial’s average yaw and roll, then added in the ensemble-averaged yaw and roll. The same procedure was used to isolate variation in body–neck coupling (Fig. 2). To create smooth navigation traces (Fig. 5), we resampled the lowpass-filtered position/orientation data over the x domain of the arena such that the y, pitch, roll, and yaw data had the same input domain (−1.3 to 1.3 m with 0.01-m resolution; third-order polynomial fits between successive data points via Interpolation, Mathematica). The mean and SD of y, pitch, roll, and yaw were then calculated at each x value. We omitted averages at x values where more than 10% of the flights contained missing values (≈2% of x values at the beginning and end of the domain).

Data Analysis.

To analyze the passive role of the neck in head stabilization, we considered a 2-coefficient mass-spring-damper model for the highpass-filtered head kinematics:

$$m{\ddot{\xi }}_{\text{h}}=-c{\dot{\xi }}_{\text{h}}-k\left({\xi }_{\text{h}}-{\xi }_{\text{b}}\right),$$

where $m$ is the head mass, $c$ is a damping constant, $k$ is a spring constant, ${\xi }_{\text{h}}$ is the $x$/$y$/$z$/pitch/roll/yaw of the head, and ${\xi }_{\text{b}}$ is the corresponding measurement for the body. The coefficients are nondimensionalized as the damping coefficient, $\zeta \equiv c/\sqrt{km}$, and the natural frequency ratio, $f_{\text{n}}/f$, where $f_{\text{n}}$ is the natural frequency of the spring $\left(\sqrt{k/4{\pi }^{2}m}\right)$ and $f$ is the average wingbeat frequency.

The gain $G$ and phase lag $\varphi$ of the response $\left({\xi }_{\text{h}}\right)$ compared with the forcing $\left({\xi }_{\text{b}}\right)$ is a function of the natural frequency and damping coefficient. For harmonic forcing, the gain and phase lag have closed-form solutions $G=\sqrt{{\left(1-{\left(f_{\text{n}}/f\right)}^2\right)}^2+4{\zeta }^2{\left(f_{\text{n}}/f\right)}^2}$ and $\varphi ={\text{sin}}^{-1}\left(2\zeta \left(f_{\text{n}}/f\right)G\right)$. We inverted these functions to solve for the natural frequency ratio and damping coefficient given the measured average value and SD of the gain and phase offset. We calculated the gain and phase lag directly from experimental data: the gain as the ratio of the mean absolute value of the head signal to the body signal and the phase lag as the peak of the cross-correlation between head and body signal. Inverting the quartic gain function gives 4 solutions. We present the 2 real positive $f_{\text{n}}$ solutions, one of which often represents an inverse damper $\left(c<0\right)$ for the rotational degrees of freedom.

To test scaling predictions of the passive head stabilization model, we estimated vertical head displacements compared with eye diameter. We estimated body center of mass displacements to be $g/\left(4\text{π}{f}^2\right)$, where $g$ is the acceleration due to gravity (SI Appendix, section S2). We used published frequency versus body mass data to generate displacements as a function of body mass (58). The resulting head displacements are the body displacements times the gain we calculated for lovebirds. To estimate head displacements compared with eye diameter $\left(d_{\text{eye}}\right)$, we used an established power scaling for eye diameter as a function of body mass (59), $d_{\text{eye}}\sim m^{0.23}$, and passed the scaling through the average for our experiment (body mass = 54 g, eye diameter = 5 mm).

To analyze the role of body yaw in maneuvering through crosswinds, we fit a 3-coefficient inertia-damper-spring model with an active P-controller to the body yaw data (Eq. 2; derivation in SI Appendix, section S2). The aerodynamic stiffness term was corroborated from our ornithopter experiments in the wind tunnel, where the restoring torque was proportional to slip angle over the range of angles experienced by the lovebirds (Fig. 6D). Three scaled coefficients ($k/I$, $k_{\text{P}}/I$, and $\text{c}/I$) were fit using a gradient-descent scheme (ParametricNDSolveValue & FindFit in Mathematica) that minimized the squared residuals between the measured and modeled head data. To avoid sharp initial conditions, ${\theta }_{\text{slip}}$ and ${\theta }_{\text{neck}}$ were padded with smooth transitions to zero (transition duration = 10% of the flight time) before the beginning and after the end of each flight. The padding was to provide numerical stability; the goodness of fit is based on data during the true flight time and does not include the padded data. The fit was first computed without the active term $\left(k_{\text{P}}=0\right)$ and then with the active term $\left(k_{\text{P}}\ge 0\right)$. In nearly all (99%) of the flights, the coefficients quickly converged to stable averages; the remaining 1%, defined as cases where coefficients were more than 3$\sigma$ from the mean, were not included in the reported averages (Fig. 6F). We present 2 dimensionless outcomes of the fit:

$$\tau =\frac{2fI}{c}\hspace{0.17em}\text{and}\hspace{0.17em}\zeta =\frac{c}{\sqrt{4\left(k+k_{\text{P}}\right)I}}\hspace{0.17em},$$

where $\tau$ is the response time in wingbeats and $\zeta$ is the effective damping coefficient in a 2-spring system with spring constants $k$ and $k_{\text{P}}$; it quantifies whether the yaw response is underdamped $\left(\zeta <1\right)$, critically damped $\left(\zeta =1\right)$, or overdamped $\left(\zeta >1\right)$. To determine whether lovebirds could also use neck angle to regulate airspeed, we compared lateral airspeed (y ground speed minus local wind speed, $v_{\text{wind}}$) to neck angle and found they were proportional (SI Appendix, Fig. SF35).

We defined the goodness of fit based on the mean squared residuals compared with the variance of the signal,

$${\text{R}}^2=1-\frac{{\displaystyle \sum {\left({\theta }_{\text{body},\text{actual}}-{\theta }_{\text{body},\text{model}}\right)}^2}}{{\displaystyle \sum {\left({\theta }_{\text{body},\text{actual}}-\overline{{\theta }_{\text{body},\text{actual}}}\right)}^2}},$$

where ${\theta }_{\text{body},\text{actual}}$ is the measured body yaw, ${\theta }_{\text{body},\text{model}}$ is the modeled body yaw, and the overbar denotes time averaging. The goodness of fit runs from 0 (model is no closer to actual than the variance of the actual) to 1 (model is identical to actual).

To test scaling predictions of the body yaw model, we considered the response time of the yaw angle to changes in gust conditions. The model predicts step changes in ${\theta }_{\text{neck}}$ or ${\theta }_{\text{slip}}$ to result in oscillations that decay with the time constant $\tau$ (SI Appendix, section S4). Using isometric scaling, we predict that this time constant scales with $m/\rho {\ell }^3$ (SI Appendix, section S5), and we estimated the scaling coefficient using the measured point for our experiment (body mass $=$ 54 g, wing length = 120 mm, $\tau =$ 1.4 wingbeats) in Fig. 6G. We estimate that changes in nonisometric variables (air density, aspect ratio, nondimensional third moment of area, stroke amplitude, force coefficient, and wing path shape factor) could shift the trendline by a factor of 0.2 to 4 (SI Appendix, section S5). Given the multiple orders of magnitude spanned by the trendlines, the scaling predictions for hummingbirds and insects are robust based on reasonable estimates of error.

Mechanical Bird Model Experiments.

To determine how flapping wings passively orient in lateral gusts, we tested a free-flight ornithopter (Avitron v2.0) in a wind tunnel (60). The ornithopter started at 1 of 6 slip angles ($\pm$30°, $\pm$60°, $\pm$90°, 3 trials per angle) and then freely rotated on a custom mount that only allowed yaw motion. We removed the tail to isolate the contributions of the wings. The ornithopter was fixed at a stroke plane angle of 25° with the rotational axis intersecting the ornithopter’s center of gravity. The flow in the tunnel’s test section (0.8 × 1.0 × 1.73 m) was at a representative lovebird airspeed, 4 m/s. Turbulence intensity in the flow was 3.42%.

We measured the yaw angle with 2 markers tracked at 1,000 Hz by 7 infrared motion capture cameras (Qualisys Oqus 7+, 3 MP). From the calibration procedure, we estimated a positional tracking error of 0.1 to 0.3 mm. Our motion capture process yielded 100% tracking success with no lost frames. To remove wingbeat-driven oscillations, we lowpass filtered the yaw angle data (fourth-order Butterworth) with a cutoff frequency of half the wingbeat frequency. We took derivatives of the data using a central difference scheme and fit the resulting data (fitnml, MATLAB) to a 3-coefficient passive yaw model,

$${\ddot{\theta }}_{\text{body}}=\hspace{0.17em}\left(k/I\right)\left({\theta }_{\text{slip}}-{\theta }_0\right)-\left(c/I\right){\dot{\theta }}_{\text{body}}.$$

The model is identical to the passive model used for lovebirds (Eq. 1), except for a slip angle offset, ${\theta }_0$, used because of slight wing asymmetries in the ornithopter that caused an equilibrium slip angle of about −8°. The model captured most of the ornithopter yaw dynamics (R² 0.74) over the range of slip angles encountered by the lovebirds ($-50\mathrm{°}<{\theta }_{\text{slip}}<31\mathrm{°}$ for 95% of data). We nondimensionalized restoring torque (Fig. 6D) by using the yaw response time (SI Appendix, section S4).