Entropic colloidal crystallization pathways via fluid–fluid transitions and multidimensional prenucleation motifs

Significance

The transformation from a fluid to a crystal can be complicated and involve one or more precursors. Such multistep crystallization pathways occur in many chemical and physical systems, and the driving force for the appearance of the precursors has been explained by unique characteristics of the interactions among the system’s building blocks. Here we report 2-step crystallization pathways in hard particles, where interaction is dictated solely by building-block shape and thus entropy. We categorize our 2-step crystallization pathways based on the dimension of the prenucleation motifs, and discuss possible comparisons to other crystallization processes.

Abstract

Complex crystallization pathways are common in protein crystallization, tetrahedrally coordinated systems, and biomineralization, where single or multiple precursors temporarily appear before the formation of the crystal. The emergence of precursors is often explained by a unique property of the system, such as short-range attraction, directional bonding, or ion association. But, structural characteristics of the prenucleation phases found in multistep crystallization remain unclear, and models are needed for testing and expanding the understanding of fluid-to-solid ordering pathways. Here, we report 3 instances of 2-step crystallization of hard-particle fluids. Crystallization in these systems proceeds via a high-density precursor fluid phase with prenucleation motifs in the form of clusters, fibers and layers, and networks, respectively. The density and diffusivity change across the fluid–fluid phase transition increases with motif dimension. We observe crystal nucleation to be catalyzed by the interface between the 2 fluid phases. The crystals that form are complex, including, notably, a crystal with 432 particles in the cubic unit cell. Our results establish the existence of complex crystallization pathways in entropic systems and reveal prenucleation motifs of various dimensions.

Entropically stabilized colloidal crystals of hard particles exhibit a range of structures as diverse and complex as traditional crystals (1, 2). In these systems, entropic forces emerge as a consequence of a multiplicity of equivalent microscopic states, producing, effectively, entropic bonds (3, 4). The resulting entropic valence increases with density in both strength and directionality. There is now a preponderance of evidence that entropy is as versatile as chemical bonds in producing structural complexity. However, all crystallization pathways that have been reported for hard-particle systems are simple. For example, hard-sphere crystallization follows predictions of classical nucleation theory in simulation and experiment (5, 6). By contrast, fluid-to-solid transition scenarios well known for atomistic and molecular systems, including liquid–liquid phase separation (7–14), prenucleation cluster formation (15, 16), and particle attachment (17), have not been reported for purely entropic systems. In particular, in the absence of depletion interactions involving hard colloids with small molecule depletants, no fluid–fluid transitions are predicted or reported. Here, we present 3 hard-particle systems that exhibit entropically driven 2-step crystallization. Each 2-step process features, notably, first the transformation from a homogeneous low-density fluid (LDF) to an LDF phase coexisting, temporarily, with a high-density fluid (HDF) with more pronounced prenucleation order. This fluid–fluid transition is followed by a transformation to the final crystalline structure. Nucleation of the crystal is catalyzed by the LDF–HDF interface (18, 19), and the resultant crystal is an ordered variant of the HDF. We show that, despite the lack of explicit attractive forces, both the LDF-to-HDF transformation and the HDF-to-crystal transformation can be first-order phase transitions accompanied by structural, thermodynamic, and kinetic discontinuities.

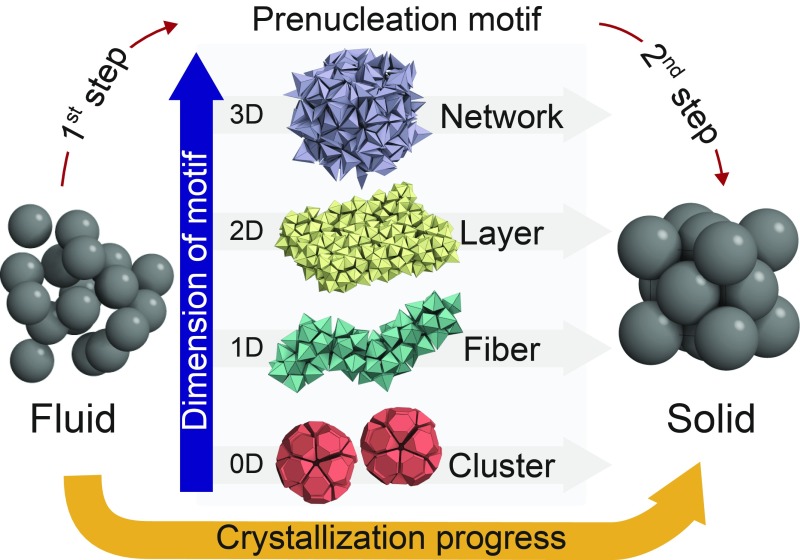
It is known that the geometry of phases involved in prenucleation depends on the specifics of the multistep nucleation pathway. For instance, calcium carbonate (CaCO₃) solutions favor compact prenucleation clusters at the early stage of nucleation (20). Amyloid fibrils crystallize via a hierarchical assembly of $\beta$-strands and $\beta$-sheets (21). And, in the crystallization of a gas hydrate, water molecules form amorphous frameworks around guest molecules before clathrate nucleation occurs (22, 23). Given the diversity in these examples, it appears natural to categorize multistage nucleation pathways according to prenucleation motif dimension. We report here that many of the possibilities suggested by dimension categorization are realized in hard-particle––that is, purely entropic––systems (Fig. 1). Each of the 3 particle shapes in this study is a polyhedron whose geometry favors certain prenucleation motifs via the maximization of face-to-face contacts. Truncated tetrahedra (TTs) crystallize into a complex cubic crystal via an HDF containing cluster-type motifs. Pentagonal bipyramids (PBPs) crystallize into a layered crystal via an HDF containing fiber-type and layer-type motifs. And, triangular bipyramids (TBPs) crystallize into a clathrate crystal via an HDF containing network-type motifs. All 3 crystals are highly complex compared with other known hard-particle crystals. Interestingly, the clathrate crystal is identical to that reported for TBPs linked together with DNA (24); here the crystal is obtained solely with entropy.

Fig. 1.

Categorization of 2-step nucleation pathways. Two-step nucleation pathways are mediated by precursors that can be categorized by the dimension of the prenucleation motif. We distinguish in our simulations of 3 different systems clusters (zero-dimensional motif), fibers (one-dimensional) and layers (2D), and networks (3D), respectively. The dimension of the motif is a direct consequence of geometrical frustration that builds up as prenucleation motifs grow (27).

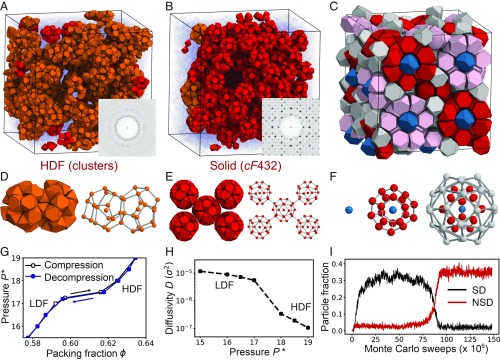
The TT particle is obtained by truncating the vertices and edges of a regular tetrahedron to create adequate space for 1 TT to fit at the center of an assembled dodecahedron cluster of 20 TTs (SI Appendix, Fig. S1 A and B). Our simulations demonstrate that the self-assembly of hard TTs is mediated by a metastable LDF-to-HDF phase transition and proceeds in 2 steps. In the first step, an isotropic fluid of hard TTs rapidly (within a few million Monte Carlo sweeps) separates into a coexistence of LDF and HDF at constant packing density $\varphi =0.615$ (Fig. 2A). At the beginning of HDF formation, individual clusters emerge from the LDF (SI Appendix, Fig. S2 A–C). As the number of clusters grows, they aggregate by sharing particles (Fig. 2D and SI Appendix, Fig. S2 D and E). In the HDF, about 27% of the TTs form cluster-type motifs while the rest remain weakly ordered with weaker face-to-face contacts (SI Appendix, Fig. S3 A–C). Clusters and aggregates of clusters continuously change position and morphology via particle exchange with the weakly ordered region in the HDF (SI Appendix, Fig. S3D). Clusters do not diffuse within the HDF as rigid units. In the second step, nucleation occurs and crystal growth proceeds isotropically (Movie S1). Unlike clusters in the HDF, clusters in the crystal are periodically arranged at larger separations without shared particles (Fig. 2E). During crystal growth the number of nonshared clusters rapidly increases, while the number of shared clusters decreases (Fig. 2I). After 1.50 × 10⁸ Monte Carlo sweeps, a single crystal coexists with the LDF fluid in equilibrium (Fig. 2B).

Fig. 2.

Crystallization of cF432 via cluster formation. Hard TTs self-assemble into the cF432 crystal at constant packing density $\varphi =0.615$. (A) In the early stage of crystallization, hard TTs separate into an LDF and an HDF. The HDF consists of cluster aggregates that share particles (orange in A and D) and individual clusters that do not share particles (red in A). (B) The crystal consists of clusters that are periodically arranged without sharing particles (red in B and E). (C) A unit cell of the cF432 crystal consists of a body-centered cubic packing of 3-shell truncated octahedron clusters (F). (G) Equation of state of hard TTs. Each data point is obtained by a single isobaric Monte Carlo run initialized in a disordered starting configuration for compression (black line) and initialized in an HDF configuration for decompression (blue line). (H) Diffusivity of the 2 fluids near the LDF-to-HDF transition. (I) Evolution of the number of shared dodecahedron (SD, shown in D) motifs and nonshared dodecahedron (NSD, shown in E) motifs during the crystallization trajectory. SDs are dominant until $75\times {10}^6$ Monte Carlo sweeps, and NSDs rapidly increase as nucleation occurs.

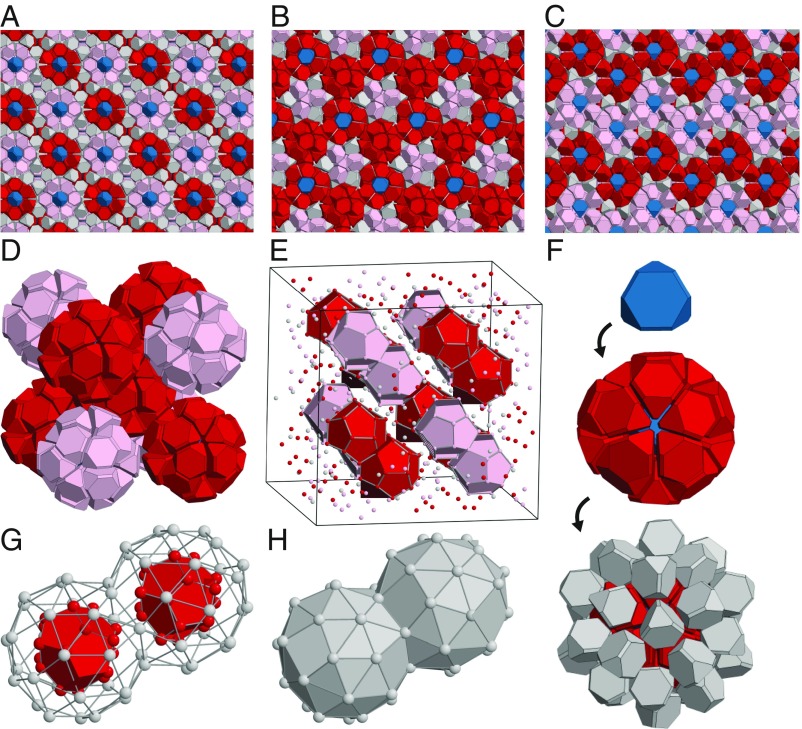
Structural analysis with sites placed at the centroid of each particle reveals that the unit cell of the crystal has Pearson symbol cF432, i.e., it contains 432 particles (Figs. 2C and 3) arranged with space group $Fd\overline{3}c$. This is the most complex crystal structure reported in any hard-particle system to date. The crystal can be described as a body-centered cubic packing of large truncated octahedral clusters of 3 successive shells: a TT in the center, a dodecahedron inner shell, and the truncated octahedral outer shell (Figs. 2F and 3 D–H). The large clusters tile space and describe the structure completely. The truncated octahedron is decorated with additional particles centered over its hexagonal faces and can be regarded as the union of a strongly distorted dodecahedron and a distorted icosahedron. If both of these polyhedral shells were regular, they would form a rhombic triacontahedron, which is a typical cluster shape found in metallic compounds, such as Bergman-type icosahedral quasicrystals and their approximants (25). The crystal reported here is equivalent in its structure to that of the clathrate-type compound cF432-Te_7+xSi_20−x (26).

Fig. 3.

Crystal structure of the cF432 crystal. Ideal structure model of cF432 constructed with hard TTs. Red and pink TTs represent dodecahedron clusters with different orientations. Blue TTs represent TTs at the cluster centers. All other TTs are colored gray. (A) View along 4-fold axis; (B) 3-fold axis; and (C) 2-fold axis. (D) Body-centered cubic packing of dodecahedron clusters extracted from the crystal. (E) The arrangement of dodecahedron clusters in the crystal. TTs are displayed by their centers and dodecahedron clusters are shown in polyhedron representation. (F) Three successive shells of the dodecahedron cluster: a single TT (blue), a dodecahedron inner shell (red), and a truncated octahedron outer shell (gray). (G and H) Clusters are arranged on a body-centered cubic lattice by sharing a hexagonal face. The outer shells cover space without gaps.

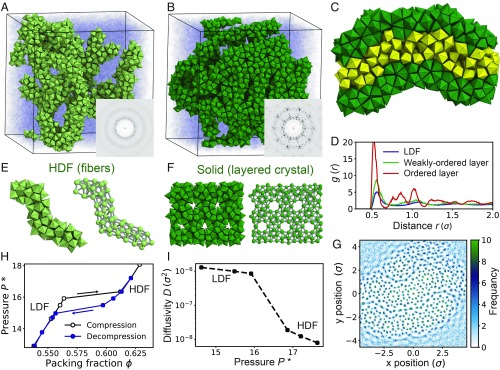
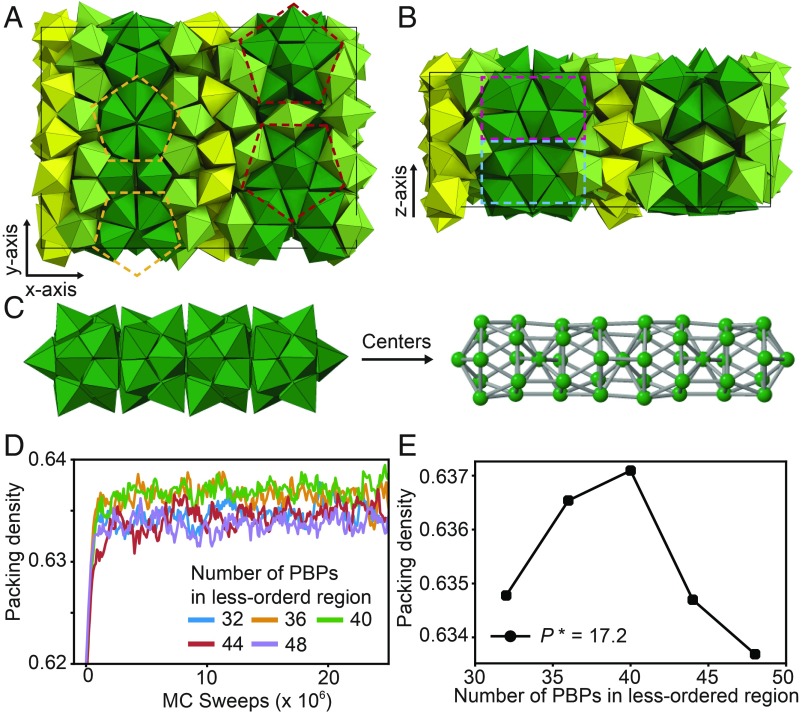
We next investigate the crystallization pathway of a system of hard PBPs. The aspect ratio of the PBP particle is set to 1.31, which is optimal for 12 PBPs to form a small stellated dodecahedron (SI Appendix, Fig. S1 C and D). We find that crystallization of hard PBPs is again mediated by a metastable LDF-to-HDF transition and follows 2 steps. In the first step, an isotropic fluid of hard PBPs separates into LDF and HDF phases at constant packing density $\varphi =0.58$ (Fig. 4A). The HDF possesses fiber-like prenucleation motifs, where small stellated dodecahedra are connected through shared PBPs (Fig. 4E) but cannot easily continue ordering perpendicular to these connections due to geometrical frustration (27). At the beginning of HDF formation, small fibers emerge and then grow into longer, interconnected fibers with various morphologies (SI Appendix, Figs. S4 A, B, D, and E). The fiber-type motifs continuously change their morphologies and locations by exchanging particles with weakly ordered regions within the HDF (SI Appendix, Fig. S3 E–H). In the second step, a decagonal quasicrystal approximant with Pearson symbol oF244 and containing 10-fold symmetric columns (Fig. 5) nucleates at the interface between the HDF and the LDF. Crystal growth proceeds into the LDF, reminiscent of the growth of certain protein crystals (28) (Fig. 4B and SI Appendix, Fig. S5 A–C). The approximant crystal is composed of multiple layers, where highly ordered layers and weakly ordered layers alternate (Fig. 4C). Highly ordered layers are fiber nets with periodic order within the layer (Fig. 4F and SI Appendix, Fig. S4 C and F), and their growth proceeds outwards (SI Appendix, Fig. S5 and Movie S2). Remarkably, the crystal grows in a zigzag pattern within a layer (Movie S2).

Fig. 4.

Crystallization of a layered crystal (oF244) via fiber formation. Hard pentagonal bipyramids (PBPs) self-assemble into a layered crystal (oF244) at constant packing density $\varphi =0.58$0. (A) In the early stage of crystallization, hard PBPs separate into an LDF (transparent blue) and an HDF that consists of fiber-like motifs (light green). (B) The obtained crystal consists of layers of parallel fibers (dark green). (C) A cross-section of the crystal phase shows that a crystal layer (dark green) and a weakly ordered layer (yellow) alternate within the crystal. (D) The radial distribution function $g\left(r\right)$ of the crystal layers, the weakly ordered layers, and the LDF. (E) A fiber-type prenucleation motif (Left) found in the HDF. (Right) Centers of PBPs and bonds (gray). (F) Part of a crystal layer with PBP representation (Left) and its centers (Right). (G) A density plot of particle centers for a cross-section of the crystal averaged over $200\times {10}^6$ Monte Carlo sweeps. See Movie S3 for the movement of particles in each layer. (H) Equation of state of hard PBPs. Each data point is obtained by a single isobaric Monte Carlo run initialized in a disordered starting configuration for compression (black line) and initialized in an HDF configuration for decompression (blue line). (I) Diffusivity of the 2 fluids near the LDF-to-HDF transition.

Fig. 5.

Crystal structure of the oF244 crystal. Ideal structure model of the oF244 crystal constructed with hard PBPs. (A) View along the z axis and (B) y axis of the orthorhombic unit cell. Dashed lines indicate different orientations and layers of the 10-fold symmetric column (C) within the unit cell. Dark-green PBPs (120 particles in the unit cell) represent highly ordered layers of the crystal. Yellow PBPs (40 particles) represent weakly ordered layers of the crystal. PBPs existing between the 2 layers (84 particles) are colored in light green. The configuration of the dark-green and the light-green PBPs is well defined in the unit cell, while the configuration of yellow PBPs cannot be determined unambiguously due to their diffusive motion. (D) To determine the most probable number of PBPs in the weakly ordered region, we compared packing density at constant pressure (P* = 17.2) as a function of the number of the weakly ordered PBPs in the unit cell. (E) The unit cell with 40 weakly ordered PBPs has the highest packing density, suggesting it corresponds to the most stable structure.

The structure and dynamics of the crystal phase of PBPs are highly anisotropic. Structural differences between the 2 distinct layers are apparent in the radial distribution function $g\left(r\right)$ (Fig. 4D). $g\left(r\right)$ in the weakly ordered layer is mostly similar to that of the LDF, and by contrast develops distinctive peaks in the highly ordered layer. Particle dynamics of the 2 layers are also distinct as evidenced by the particle density at a cross-section of the crystal averaged over $2\times {10}^8$ Monte Carlo sweeps (Fig. 4G). Particle positions in the highly ordered layer are sharp, while particle positions in the weakly ordered layer are smeared out, indicating the more diffusive nature of their motion. Movie S3 shows the difference in movement of 10 selected particles of each layer.

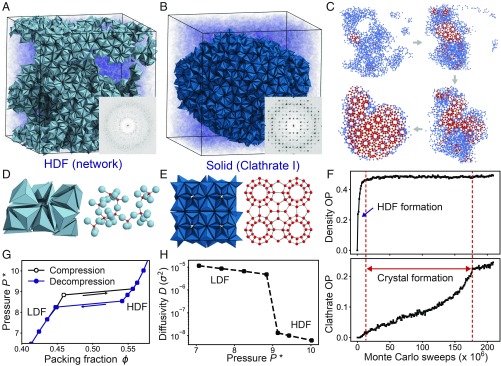
Finally, we investigate the crystallization pathway of a system of hard TBPs. The edge angle of the TBP particles is set to 109.5°, which allows groups of 4 TBPs to arrange into tetramers and eventually a tetrahedral network (24) (SI Appendix, Fig. S1 E–G). We observe that crystallization of hard TBPs is similar to the previous examples, except that the HDF of TBPs now has a network-like prenucleation motif. In the first crystallization step, an isotropic fluid of hard TBPs separates into an LDF and an HDF at constant packing density $\varphi =0.50$ (Figs. 6A and 7A). TBPs in the HDF prefer to form tetramers that are interconnected without long-range order (Fig. 6D). Centers of the tetramers can be mapped onto the nodes of a tetrahedral network. The prenucleation network spans the HDF isotropically and incorporates most of the HDF particles (SI Appendix, Fig. S3 I–K). Few particles can exchange between the network and the nonnetwork particles in the HDF (SI Appendix, Fig. S3L), resulting in much slower dynamics in the HDF of TBPs compared with the dynamics in the HDF of TTs or PBPs. In the second, slower step, a clathrate crystal with Pearson symbol cP92 nucleates and grows (Fig. 6B). We identified the clathrate structure as clathrate type I (Fig. 6E), where the tetramer centers (network nodes) are arranged in 2 types of clathrate cages, 5¹² and 5¹²6² (Fig. 7 B and C). Here, the notation $5^n{6}^m$ indicates that a cage has n pentagons and m hexagons as faces (24).

Fig. 6.

Crystallization of clathrate I (cP92) via network formation. Hard TBPs self-assemble into clathrate I at constant packing density $\varphi =0.500$. (A) A snapshot from the early stage of TBP crystallization, where an LDF (transparent blue) and an HDF (light blue) coexist. (B) A snapshot of the final stage of TBP crystallization, where the TBP clathrate (dark blue) coexists with the LDF (transparent blue). (Insets) Diffraction patterns. (C) Snapshots of the crystallization process using a network representation that connects TBP tetramer centers. The HDF is colored in blue and the clathrate is colored in red. (D) Local motifs found in the HDF (Left). Centers of tetramers (Right, red spheres) can be mapped onto nodes of a tetrahedral network. (E) Unit cell of the TBP clathrate crystal (Left). Centers of tetramers can be mapped onto an atomic clathrate I structure (Right, red spheres). (F) Evolution of the density order parameter (Top) and a clathrate order parameter (Bottom). Definitions for order parameters are found in Methods. (G) Equation of state of hard TBPs. Each data point is obtained by a single isobaric Monte Carlo run initialized in a disordered starting configuration for compression (black line) and initialized in an HDF configuration for decompression (blue line). (H) Diffusivity of the 2 fluids near the LDF-to-HDF transition.

Fig. 7.

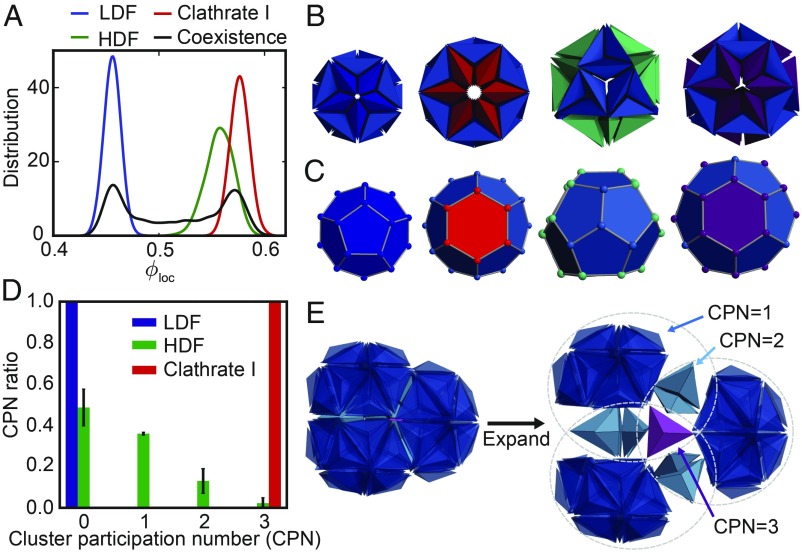
Order parameters of the TBP system. (A) Distribution of the local packing density ${\varphi }_{\text{loc}}$ at 4 subsequent stages. The LDF $\left(P^{\ast }=8.84\right)$, HDF $\left(P^{\ast }=9.43\right)$, and clathrate I $\left(P^{\ast }=9.43\right)$ are calculated under isobaric conditions, and the coexistence phase is calculated under isochoric conditions $\left(\varphi =0.50\right)$. (B) N = 30, 36, 39, and 42 TBPs form clathrate clusters that can be mapped onto C, clathrate cage A $\left(5^{12}\right)$, cage B $\left(5^{12}{6}^2\right)$, cage C $\left(5^{12}{6}^3\right)$, and cage D $\left(5^{12}{6}^4\right)$, respectively, by connecting the TBP tetramer centers (SI Appendix, Fig. S1G). (D) Distribution of the values for the CPN in the 3 observed phases of the TBP system. (E) The CPN is defined as the number of clathrate clusters a TBP participates in.

The snapshots in Fig. 6C and SI Appendix, Fig. S6 cover the complete crystallization process in the network representation obtained by connecting tetramer centers. A disordered network (HDF) is dominant in the early stage. The formation of the HDF from the LDF occurs spontaneously and, at early times, follows the prediction of the Cahn–Hilliard theory of spinodal decomposition (29), namely exponential growth of the first peak in the structure factor at constant wavevector (SI Appendix, Fig. S7). Two-step nucleation and growth in which the first step occurs through spinodal decomposition was recently reported in simulation of an aqueous NaCl solution (30). Clathrate nucleation occurs at the LDF–HDF interface and growth proceeds into the LDF (SI Appendix, Fig. S6). Depletion of LDF particles during clathrate growth is compensated by reduction of the HDF phase in directions distinct from the growth direction of the nucleus (Movie S4). The HDF region assumes a gradually more spherical shape during clathrate growth (SI Appendix, Fig. S8) suggesting an increase in surface tension during the second step of crystallization, as recently predicted (31). Two crystallization stages can be clearly distinguished by following the time evolution of appropriate order parameters (Figs. 6F and 7 D and E and Methods). In the HDF formation stage, a density order parameter rapidly increases while the clathrate order parameter remains small. Subsequently, the clathrate order parameter increases during clathrate crystal growth and finally reaches equilibrium.

The crystallization behavior of the TBP system mimics aspects of clathrate formation in water, for which an amorphous network has been identified as a crystallization precursor (22, 32). The nucleation behavior of TBPs is also similar to that found in simulation studies of some tetrahedral systems in the sense that a metastable liquid–liquid transition can occur before crystallization (9, 10, 12). In contrast, while the precursor of the TBP system is a high-density phase, precursors of many tetrahedral crystals are low-density phases (33). The tetrahedral networks of the molecular systems are open structures, while TBPs fill most of the space when forming a tetrahedral network (SI Appendix, Fig. S1G). In addition, the location of the TBP clathrate nucleus at the LDF–HDF interface and its growth direction into the LDF (SI Appendix, Fig. S6) are different from those observed in molecular models of water (33), where nucleation takes place within the low-density liquid. Such details of the nucleation process are affected by the diffusivity of the precursor phase, as discussed for protein crystallization (8, 28).

We find that the LDF-to-HDF transitions of TTs, PBPs, and TBPs are accompanied by thermodynamic and dynamic discontinuities. The thermodynamic first-order nature of the 3 transitions is confirmed by the equations of state calculated under isobaric condition (Figs. 2G, 4H, and 6G). A small increase of pressure around the phase-transition point results in an abrupt density increase of 5% (TT), 8% (PBP), and 16% (TBP) during the formation of the HDF. A dynamic discontinuity is identified via analysis of the diffusivity extracted as the slope of the mean-squared displacement (SI Appendix, Fig. S9). The diffusivity drops by around 1.5 (TT), 2.0 (PBP), and 2.5 (TBP) orders of magnitude across the LDF-to-HDF transition (Figs. 2H, 4I, and 6H). Although diffusivity of the HDF is comparably low, it remains nonzero, demonstrating that the HDF is a fluid rather than an amorphous solid in all 3 cases. We observe the density and diffusivity changes across the fluid–fluid transition are more pronounced if the prenucleation motif in the HDF has a higher dimension. Thus, the density and diffusivity change from the cluster formation within the HDF (TT) are smaller than the density and diffusivity change from the fiber formation within the HDF (PBP), which in turn are smaller than the density and diffusivity change from the network formation within the HDF (TBP). This suggests that particles in a motif with higher dimension are more strongly correlated and as a result produce a denser and less diffusive HDF. The effect of motif dimension on the LDF-to-HDF transition is reminiscent of micellization of amphiphiles, where the character of the phase transition depends in a similar fashion on the size and morphology of aggregates (34, 35).

Multistep nucleation and a second liquid phase have been reported in a variety of systems and explained by unique system properties including ion binding (15, 20, 36), molecular geometry (21, 37), and tetrahedral bonding (9, 12, 38). The fact that we observe 2-step nucleation mechanisms via a metastable fluid–fluid phase transition in our 3 model systems of anisotropic hard particles suggests that local order and the geometry of the nearest-neighbor shell play the central role in complex phase behavior and kinetics. Whether this geometry is a result of enthalpic bonds or entropic bonds is less important. In this work, we categorized 2-step nucleation pathways according to prenucleation motif dimension. It may be fruitful to apply this categorization to analyze the structure of precursors involved in other crystallization processes. If these ideas hold generally, then it may be possible to rationalize the appearance of liquid–liquid phase transitions and multistep nucleation pathways dominated by connectivity and strain in local particle clusters––2 quantities that contribute to motif dimensionality. Independent of this, our results add to the growing body of evidence that entropic bonds can be as effective as traditional chemical bonds in creating the necessary valence for producing nontrivial crystal structures (1–3).

Methods

Particle Geometry.

The TT shape (SI Appendix, Fig. S1A) is a member of the spherical triangle invariant 323 family, with truncation parameters $\left(a,b,c\right)=\left(1.10,1.00,1.44\right)$ according to previous convention (39). The PBP used in this work has aspect ratio 1.31 (SI Appendix, Fig. S1C). The TBP has edge angle 109.5° (SI Appendix, Fig. S1E) and aspect ratio 0.35. The aspect ratio of the 2 bipyramids is defined by the ratio of the height of the bipyramid to the diameter of the circumscribed circle of the base polygon (a regular pentagon for PBP and a regular triangle for TBP). The vertices of the bipyramids are classified as equatorial tips composing the base polygon and polar tips perpendicular to the base polygon. This classification is used when detecting local motifs of the bipyramids.

Cluster-Type Prenucleation Motif of TTs.

Twenty TTs form a dodecahedron cluster where an additional TT is located at the center of the cluster (SI Appendix, Fig. S1B). The cluster is detected by the number of nearest neighbors (NNs) of the central particle. At high enough pressure, when the TT system forms cluster motifs, most TTs prefer face-to-face contacts that allow them to have at most 4 NNs. On the other hand, TTs at the cluster center have 20 NNs that compose a dodecahedron cluster shell (SI Appendix, Fig. S1H). After detecting all clusters in the system, we checked if a cluster shares TTs with other clusters to distinguish between shared clusters (Fig. 2D) and nonshared clusters (Fig. 2E). The number of each type of cluster is an order parameter for the crystallization of TTs (Fig. 2I).

Fiber-Type Prenucleation Motif of PBPs.

Twelve PBPs form a small stellated dodecahedron (SSD) that is a unit of fiber-like motifs (Fig. 4E and SI Appendix, Fig. S1D). When PBPs align face to face, their polar tips come together at the center of the SSD (SI Appendix, Fig. S1D). The distribution of polar-tip cluster size in the HDF $\left(P^{\ast }=16.34\right)$ shows a peak at 12 (SI Appendix, Fig. S1I), indicating that a large number of SSDs exist within the phase. We used this structural characteristic to detect the SSDs in PBP systems. From the arrangement of the SSDs, we identified the fiber-like motifs (Fig. 4E and SI Appendix, Fig. S4 D and E) and the layered crystal (Fig. 4F and SI Appendix, Fig. S4F).

Network-Type Prenucleation Motif of TBPs.

Four TBPs form a tetramer without gaps by arranging in a face-to-face manner (SI Appendix, Fig. S1F). Each TBP arranged into a tetramer in this way can be part of 2 tetramers, a prerequisite for the formation of a tetrahedral network (SI Appendix, Fig. S1G). Because the 4 TBPs of a tetramer share a polar tip in the tetramer center, we can identify tetramers by detecting 4-member polar tip clusters. The distribution of TBP polar-tip cluster sizes in the HDF $\left(P^{\ast }=9.13\right)$ exhibits a peak at cluster size 4 (SI Appendix, Fig. S1J). We describe a configuration of many TBPs that are exclusively arranged face to face by connecting the centers of tetramers (red spheres as nodes in Fig. 6 D and E and SI Appendix, Fig. S1G). We call the resulting representation the network representation (Fig. 6C and Movie S4).

Highly Ordered and Weakly Ordered Regions in the HDF.

When the HDF is formed, locally highly ordered prenucleation motifs appear within the HDF and the rest of the HDF remains weakly ordered (SI Appendix, Fig. S3 A, E, and I). The relative number of particles in each of the 2 HDF regions depends on the dimension of the motif structure (cluster, fiber, and network). At a similar degree of supercompression $P^{\ast }/P_m^{\ast }\sim 1.05$, the HDFs of TTs, PBPs, and TBPs contain 27%, 33%, and 91% of particles in the highly ordered region, respectively (SI Appendix, Fig. S3 B, F, and J). Structural distinction between the highly ordered and the weakly ordered region is confirmed by the coordination number distribution calculated from NNs (SI Appendix, Fig. S3 C, G, and K). The coordination number distributions of TTs, PBPs, and TBPs in the highly ordered region show a sharp peak at 4, 10, and 6, respectively, corresponding to the number of faces of each particle. This indicates that the particles in the highly ordered region have greater local order with more pronounced face-to-face contacts than those in the weakly ordered region.

The highly ordered and the weakly ordered region in the HDF continuously exchange particles, and therefore the location where prenucleation motifs appear continuously changes within the HDF. The particle exchange between the 2 regions is verified by tracking the location of 5 randomly selected particles during $30\times {10}^6$ Monte Carlo sweeps (SI Appendix, Fig. S3 D, H, and L). In all 3 systems, the selected particles move between the highly ordered and the weakly ordered regions. The TBP system shows a less frequent exchange than the other systems due to the relative sparseness of its weakly ordered region.

Order Parameter for TBPs.

To identify each stage of TBP crystallization, we monitored 2 different order parameters: the local packing density (density order parameter shown in Fig. 6 F, Top) and the cluster participation number (clathrate order parameter shown in Fig. 6 F, Bottom). The former is used to identify phase separation between a low-density region (LDF) and a high-density region (HDF) in the first step. The latter is used to identify crystallization of clathrate from the HDF in the second step. For the second step, we could not use the density order parameter because the growth of the clathrate is accompanied by only a minor reorganization of the tetrahedral network and therefore is reflected weakly in local packing density (Fig. 7A).

For the density order parameter, the local packing density ${\varphi }_{\text{loc}}$ of a TBP is defined as the packing density around the TBP within a sphere of radius $1.5\sigma$, where $\sigma$ is the longest edge of a TBP. TBPs are identified as belonging to the low-density region (corresponding to the LDF) if ${\varphi }_{\text{loc}}\le 0.52$ and to the high-density region (HDF or clathrate) if ${\varphi }_{\text{loc}}>0.52$ (Fig. 7A). Therefore, the particle fraction in the high-density region is used as the density order parameter.

For the clathrate order parameter, we developed the cluster participation number (CPN) that is defined as the number of clathrate clusters that a given TBP participates in with its 3 equatorial tips. The clathrate clusters are cage-type clusters that 30, 36, 39, and 42 TBPs can form (Fig. 7B). They can be mapped onto clathrate cages by connecting polar tips (Fig. 7C) (24). Each clathrate cluster can be identified by counting the number of equatorial tips at the center of the cluster because an equatorial tip of each TBP points toward the center when forming the cluster. Therefore, a TBP that has 3 equatorial tips can participate in up to 3 clathrate clusters. This property is used to define the CPN of each TBP (Fig. 7E). From the distribution of CPN in each phase, we confirmed that TBPs in a clathrate have $\text{CPN}=3$ whereas TBPs in the HDF have $\text{CPN}<3$ (Fig. 7D). Therefore, the ratio of TBPs with $\text{CPN}=3$ is used as the clathrate order parameter.

Monte Carlo Simulations.

Simulations were performed using the hard-particle Monte Carlo (HPMC) (40) simulation code implemented in the HOOMD-blue simulation package (41, 42). The HOOMD-blue software suite is available at http://glotzerlab.engin.umich.edu/hoomd-blue/. HPMC is implemented on multiple central processing units (CPUs) or graphics processing units using message passing interface domain decomposition. The minimum system size with periodic boundary conditions depends on the size of the crystal unit cell. We used particle numbers of $N=\mathrm{8,000}$ for TT (Fig. 2 A and B), $N=\mathrm{10,000}$ for PBP (Fig. 4 A and B), and $N=\mathrm{20,000}$ for TBP (Fig. 6 A and B). Simulations with disordered starting configurations were initialized by placing particles randomly at very low packing density $\varphi =N{v}_0/V$ < 0.1% and compressing until the desired thermodynamic condition ($\varphi$ or reduced pressure $P^{\ast }=P{v}_0/k_{B}T$) was reached. Here, $v_0$ and $V$ are the volume of a particle and the volume of the simulation box, respectively. The unit length of all simulations is defined by $\sigma$. In this work, the particle volume of a TT is set to ${\sigma }^3$, the height of PBP is 0.9$\sigma$, and the largest edge length of TBP is $\sigma$. After initialization, each run was continued in the isochoric ensemble at constant packing density $\varphi$ or in the isobaric ensemble at constant pressure $P^{\ast }$ until equilibration was reached. Total simulation times reached $1.5\times {10}^8$ Monte Carlo sweeps for TT, $11.0\times {10}^8$ Monte Carlo sweeps for PBP, and $1.5\times {10}^8$Monte Carlo sweeps for TBP. Pressure or density was measured every ${10}^3$ Monte Carlo sweeps to confirm equilibration. Although the duration of crystallization in the present systems is slightly longer than the duration of hard polyhedron crystallization observed in past works [a few million to tens of millions of Monte Carlo sweeps close to coexistence (1)], self-assembly is robust, repeatable, and comparably fast given the degree of structural complexity of the crystal structures. Simulation parameters are listed in the text or figure legend. As an example of a typical compute time, a simulation with 20,000 TBPs at $\varphi =0.5$ run for $2.1\times {10}^8$ Monte Carlo sweeps required 20,570 CPU hours on Intel Xeon E5-2680v2 and E5-2680v3 CPUs.