Protein synthesis rates and ribosome occupancies reveal determinants of translation elongation rates

Significance

Although sequencing of ribosome footprints has uncovered aspects of mRNA translation, the determinants of ribosome flux remain incompletely understood. Combining ribosome footprint data with measurements of protein synthesis rates, we inferred transcriptome-wide rates of translation initiation and elongation in yeast strains with varying translation capacity. We found that the translation elongation rate varies up to ∼20-fold among transcripts and is significantly correlated with the rate of translation initiation. Our data indicate that the amino acid composition of the synthesized proteins impacts the rate of translation elongation to the same extent as measures of codon and transfer RNA (tRNA) adaptation. Elongation is slow on transcripts encoding ribosomal proteins, which have a lower protein output compared with other transcripts with similar ribosome densities.

Abstract

Although protein synthesis dynamics has been studied both with theoretical models and by profiling ribosome footprints, the determinants of ribosome flux along open reading frames (ORFs) are not fully understood. Combining measurements of protein synthesis rate with ribosome footprinting data, we here inferred translation initiation and elongation rates for over a 1,000 ORFs in exponentially growing wild-type yeast cells. We found that the amino acid composition of synthesized proteins is as important a determinant of translation elongation rate as parameters related to codon and transfer RNA (tRNA) adaptation. We did not find evidence of ribosome collisions curbing the protein output of yeast transcripts, either in high translation conditions associated with exponential growth, or in strains in which deletion of individual ribosomal protein (RP) genes leads to globally increased or decreased translation. Slow translation elongation is characteristic of RP-encoding transcripts, which have markedly lower protein output compared with other transcripts with equally high ribosome densities.

Gene expression analysis frequently relies on the high-throughput sequencing of cellular messenger RNAs (mRNAs). While the mRNA expression levels may be sufficient to decipher how cells respond to specific stimuli, they explain protein abundances only to a limited extent, with coefficients of determination R² in the range of 0.14 to 0.41 (1, 2). Protein levels vary over a much wider range than the levels of the corresponding mRNAs, indicating extensive regulation of protein metabolism, and especially synthesis (1). Translation is predominantly regulated at the initiation step (3), whose rate varies broadly between mRNAs, depending on the structural accessibility of the 5′-end to translation factors, and on the presence of upstream open reading frames. The latter generally hinder translation of the main open reading frame (ORF) (4). Translation elongation rates also differ between mRNAs, primarily due to codon biases and differences in the availability of cognate transfer RNAs (tRNAs). Whether and how the translation elongation rate is dynamically modulated is currently debated (2, 5–8). tRNA availability, translational cofolding of the polypeptide chain, and the presence of positively charged amino acids in the nascent peptide have all been linked to variation in elongation rate (5–8). Furthermore, it has been proposed that the codon usage is the substrate of “translational programs” that adjust the protein output of specific classes of mRNAs to the state (proliferation or differentiation) of the cell (9). However, explicit comparison of the coverage of 5′ and 3′ halves of ORFs by ribosome footprints did not reveal clear differences, indicating that bottlenecks in elongation along coding regions are uncommon (2).

Insights into the dynamics of translation and putative bottlenecks have emerged from theoretical studies, in particular of the totally asymmetric simple exclusion process (TASEP), introduced 5 decades ago (10). In a simple form of this model, ribosomes bind to mRNAs according to an initiation rate, move stochastically to downstream codons with an average elongation rate, if these codons are not already occupied by ribosomes, and are released at the end of the coding region with a given termination rate. The interplay of these rates gives rise to 3 distinct regimes. If initiation is infrequent, proteins are synthesized at a rate equal to the initiation rate and the ribosome density on ORFs is very low. As the initiation rate increases relative to the rate of elongation, the ribosome density on the ORF increases in parallel with the protein output. Finally, when the rate of initiation is too high, ribosomes start to “collide,” the ribosome density becomes very high, and the protein output drops markedly (11).

Currently available technologies enable predictions about the relationship between ribosome flux (corresponding to the protein synthesis rate) and ribosome density along ORFs to be tested. Ribosome density along ORFs can be studied with high resolution by sequencing of ribosome-protected mRNA footprints, a method known as ribosome footprinting or ribosome profiling (2). The approach has already uncovered novel principles of resource allocation and translation regulation (12, 13). Furthermore, model-based analyses of ribosome profiling data uncovered sources of local variation in ribosome densities and translation elongation along transcripts (14). However, the ribosome flux has rarely been measured directly, despite mass spectrometry-based methods being able to provide estimates of synthesis and degradation rates for a substantial fraction of eukaryotic proteomes (15). Direct measurement of protein synthesis rate is necessary to detect global changes in translation capacity between conditions (16) and for studying translation in an ORF-specific manner, because the protein synthesis rates can be inferred from ribosome profiles only up to a constant factor.

To fill this gap and further uncover factors that underlie variations in translation elongation rates between ORFs, we measured protein synthesis rates transcriptome-wide, by pulsed stable isotope labeling of amino acids in culture (pSILAC), in the widely studied experimental model of exponentially growing yeast cells. Combined analysis of pSILAC and ribosome footprinting data revealed the range of variation in translation elongation rates between yeast ORFs. Among broadly studied determinants of this rate, most indicative were the availability of cognate tRNAs and the frequency of positively charged amino acids in the synthesized protein. We found no evidence that translation is curbed by ribosome collisions either in exponentially growing wild-type yeast or in mutant strains with global alterations in translation. Rather, we found that translation elongation on mRNAs encoding positively charged proteins (particularly ribosomal proteins [RPs]) is slower compared with other mRNAs with similar ribosome densities.

Results

Ribosome Allocation Is Largely Explained by the Copy Number and Length of ORFs.

To uncover determinants of translation speed in exponentially growing yeast cells, we analyzed a recently published ribosome footprinting dataset obtained in this system (4), from the perspective of the TASEP model of translation (Fig. 1A). Denoting by $N$ the number of ribosomes bound to a coding region of $L$ codons, and assuming that the rate with which a ribosome completes the polypeptide chain is given by the product of the frequency of finding a ribosome at the stop codon $N/L,$ and the effective ribosome translocation (and termination) rate $k_{el}$, the change in the number of ribosomes bound on the mRNA is given by the differential equation $dN/dt=k_{in}m-\left(k_{el}/L\right)N$. Here, $m$ is the number of mRNA molecules, $k_{in}$ is the effective rate of translation initiation on an mRNA molecule, and we assume the broad region of parameter values where ribosome collisions are rare. This model predicts that the number of ribosome-protected fragments (RPFs) mapping to a specific mRNA is proportional to the mRNA abundance, the length of the ORF, and the ratio of the effective rates of initiation and elongation, $N\approx \left(k_{in}/k_{el}\right)Lm$.

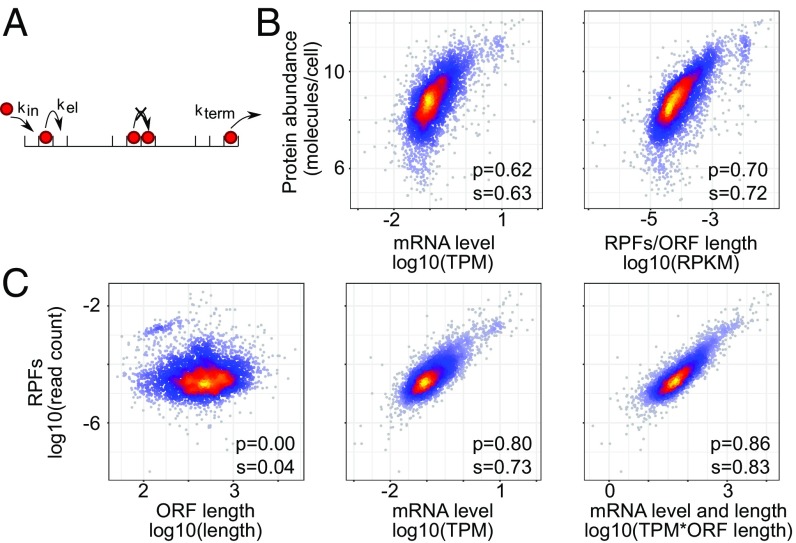
Fig. 1.

Predicted and observed relationships in gene expression in the BY4741 yeast strain. (A) Illustration of the classical totally asymmetric exclusion process (TASEP) with constant rates of initiation, elongation, and termination. (B) Relationship between protein abundance (ref. 18) and the density of RPFs on the ORF, or the mRNA abundance. (C) Relationship between the number of RPFs mapped to individual mRNAs and the corresponding ORF length, mRNA level, and both. p and s are Pearson’s and Spearman’s correlation coefficients, respectively.

Testing this prediction with the experimental dataset mentioned above (4), we found that the number of RPFs mapped to a specific mRNA indeed correlated very well with the relative abundance of the mRNA estimated by mRNA sequencing. However, further incorporating the ORF length slightly but significantly (z score = −4.74, Fisher z-transformation test) reduced the correlation, rather than improved it (SI Appendix, Fig. S1). As it was reported that the estimation of mRNA abundance by RNA sequencing is a critical aspect to control in the analysis of ribosome footprinting data (4), we repeated the analysis of the scaling behavior with estimates of mRNA abundance from another RNA-seq dataset, obtained by sequencing of RNAs purified directly with oligo(dT) from yeast cell lysates (17). The 3′-end bias in ORF coverage by RNA-seq reads, which strongly affects the accuracy of mRNA abundance estimates (4), was limited in this dataset, comparable with that inferred from the data obtained with a Ribo-zero protocol (SI Appendix, Fig. S2). We found that, when using the RNA samples obtained by oligo(dT)-based purification, both the mRNA level and ORF length contributed to the number of RPFs, as expected (Fig. 1C). We therefore used this mRNA-sequencing dataset for the analyses described below, but present similar results with the RNA-seq data from reference 4 in SI Appendix.

The mRNA levels alone explained 65% of the variance in RPF numbers. Further taking into account the ORF length increased this number to 74% (Fig. 1C), setting an upper bound of 25% on the variance in RPFs that could be due to differences in ribosome density along transcripts. From previously published measurements of protein levels in the same yeast strain (18), we further inferred that the number of RPFs explained ∼50% of the variance in protein levels, compared with only 38% explained by the mRNA abundance (Fig. 1B).

Ribosome Allocation Predicts Protein Synthesis Rates.

Theoretical analysis of the TASEP model showed that the main dynamical regimes are defined by the density and the flux of ribosomes on mRNAs (11), the latter corresponding to the protein synthesis rate. To infer the translation regime of individual yeast mRNAs, we determined relative ribosome densities on individual ORFs from the RPF and RNA-seq data, knowing the ORF lengths. The estimates that we obtained here correlated quite well (Fig. 2A; Spearman correlation coefficient, 0.46; P = 1.6e-194) with those from a much earlier study that determined the distribution of individual mRNA species across polysomal fractions corresponding to 1, 2, 3, etc., translating ribosomes, with microarrays (19). Having computed ribosome densities for each ORF, we used pSILAC to measure the corresponding protein synthesis rates.

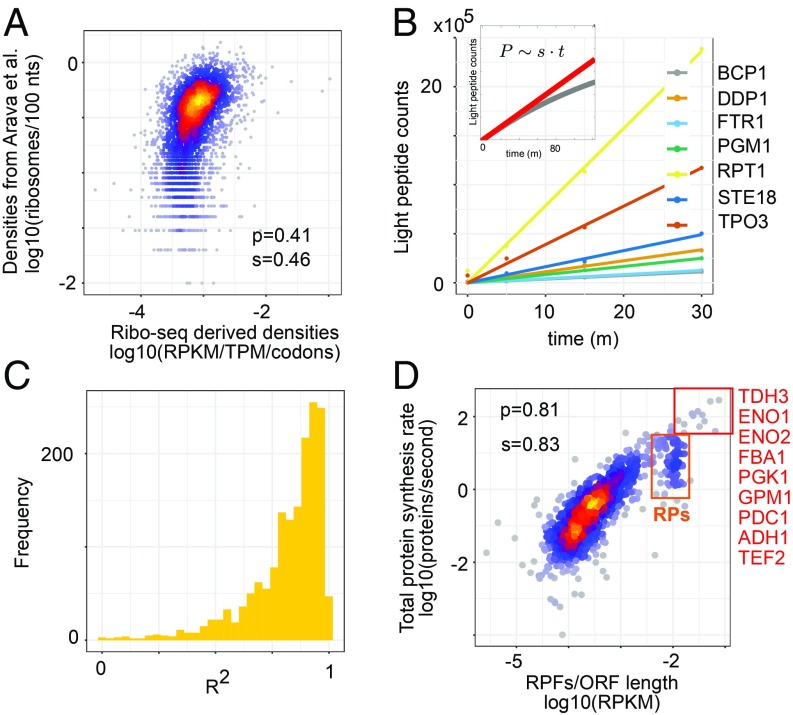
Fig. 2.

Analysis of protein synthesis rates. (A) Ribosome densities derived from the sequencing of RPFs (x axis) or estimated based on the relative abundance of RNAs across polysomal fractions in ref. 19 (y axis). (B) Protein synthesis rates s can be estimated from the dynamics of light peptide (P) accumulation within a short time interval t (in minutes) after medium change (Inset). Examples of linear fits to the peptide accumulation curves for the proteins indicated in the legend. (C) Histogram of R² values of the linear fit for all 1,616 measured proteins. (D) Relationship between ribosome allocation per codon and the protein synthesis rate. Highlighted in the red box are the proteins with highest synthesis rates. The orange box highlights the cluster of RPs. p and s are Pearson’s and Spearman’s correlation coefficients, respectively.

On a short timescale, upon shifting cells from a medium with heavy-isotope–containing amino acids to a medium with light-isotope–containing peptides, “light” peptides should accumulate proportionally to the protein synthesis rates (Fig. 2B). Indeed, we found that the light peptide accumulation in the first 30 min after the medium change was very well described by a linear model (R² for the linear fit >0.8 for 1,114 of the 1,616 proteins; Fig. 2C). Furthermore, the protein synthesis rates thus estimated correlated better with the density RPFs than the protein levels did (Pearson correlation coefficients of 0.81 and 0.7, respectively; Fig. 2D and Fig. 1C). This conforms to the expectation that RPFs reflect protein synthesis, while protein levels are set by the balance between synthesis and degradation.

Protein Synthesis Rates Are Not Limited by Ribosome Collisions in Exponentially Growing Yeast Cells.

Although protein synthesis rates increased linearly with the ribosome allocation over the entire range, a small cluster of ORFs did not conform to this relation but had distinctly lower protein output than other ORFs with similarly high numbers of allocated ribosomes (Fig. 2D, orange box). These ORFs encoded almost exclusively RPs, while other highly translated ORFs, with a single exception (the translation elongation factor 2 [TEF2]), encoded genes involved in sugar metabolism (Fig. 2D, red box). Indeed, Gene Ontology terms Glucose metabolic process and Gluconeogenesis and KEGG Glycolysis/Gluconeogenesis pathway were strongly enriched in this set (false discovery rate [FDR] for these biological processes: 1e-14 and 2e-12, respectively; Fig. 2D). To understand the dynamics of translation on individual ORFs, we then sought to infer their absolute rates of translation initiation and elongation.

A yeast cell needs about 2 h to divide (20) and contains about 5 × 10⁷ protein molecules (21), whose average half-lives are ∼8.8 h (22). These numbers define the total number of proteins produced by a yeast cell per unit time, allowing us to convert the relative protein synthesis rates inferred from the pSILAC time series to absolute rates of molecules per unit time. Further taking into account the estimated number of 40,000 (23, 24) mRNA molecules in a yeast cell, we obtained protein synthesis rates per mRNA (Methods). To directly compare the experimental data (Fig. 3B) with predictions of the TASEP model (Fig. 3A), we converted the relative ribosome densities that we obtained from sequencing of RPFs to absolute densities of ribosomes per codon (rpc) using the first principal component of the scatter of RPF-based densities as a function of absolute density measured in ref. 19 (Fig. 2A). Results of protein synthesis rate and ribosome density for individual ORFs, computed using either oligo(dT) or Ribo-zero RNA-sequencing datasets, are given in Datasets S1 and S2.

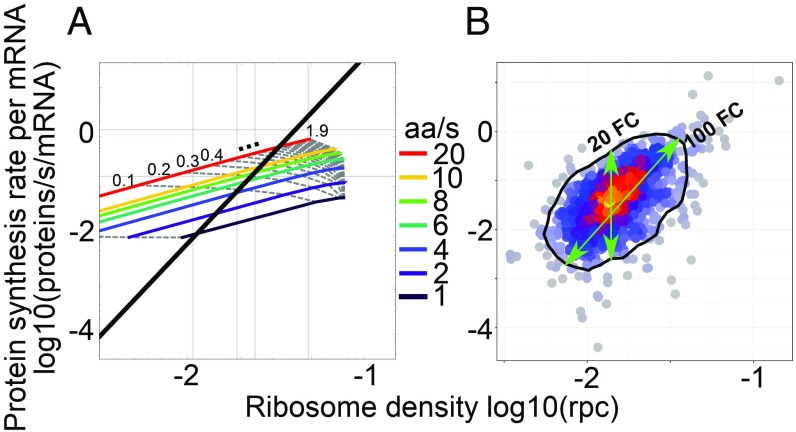
Fig. 3.

Predicted and observed relationship between the protein synthesis rate and the ribosome density on the corresponding ORF. (A) TASEP model predictions with isoclines corresponding to individual translation initiation (gray dotted lines; rate range, 0.01 to 1.9/s; increments of 0.1 starting from second line at 0.1; mean, 0.04/s) and elongation rates (colored lines; rate range, 1 to 20 aa/s). Superimposed is the first principal component of the experimental data shown in B, for which the mean initiation and elongation rates were 0.04/s and 2.63 aa/s, respectively. (B) Similar visualization of experimental results: protein synthesis rates were measured by pSILAC and converted to molecules per mRNA per second from the expected protein mass doubling time; ribosomes densities were obtained from the fit of ribosome footprint densities to numbers of ribosomes per codons (rpc) estimated by ref. 19. The black contour indicates 90% of the empirical distribution approximated through the 2D kernel density estimation from the R package “MASS.”

In the model, ORFs that initiate translation at very low rates have very low protein output and their ribosome coverage per codon reflects the rate of translation elongation (Fig. 3A). Although our dataset contained only few proteins with very low synthesis rate, the ∼10-fold range in ribosome coverage that we infer this way is comparable to the 20-fold range that we observed for ORFs with the same RPF density (Fig. 3B). The model also predicts that protein synthesis rate and ribosome coverage increase linearly with the initiation rate, as long as ribosome collisions do not halt elongation (Fig. 3A). The ∼100-fold range of variation in protein output in the experimental data corresponds to a similar range of variation in translation initiation rate. Thus, our analysis indicates that translation is primarily regulated at the level of initiation, as reported before (4). The regime of high ribosome density and low protein output exhibited by the model was not observed in our data (Fig. 3B). We also carried out simulations of the inhomogeneous TASEP model using the codon-specific speeds inferred from Ribo-seq codon densities (SI Appendix, Materials and Methods) and found that differences in elongation speed between codons are not sufficient to explain the observed variability in synthesis-density scatter (SI Appendix, Fig. S3). Furthermore, even in the inhomogeneous model, queued ribosomes only start to accumulate abruptly and limit protein output at very high ribosome densities (∼0.05 rpc).

An additional indication of evolutionary optimization of translation so as to avoid wasteful ribosome collisions comes from comparing the first principal component of the experimental data from Fig. 3B with the equal elongation rate isoclines from the simulation (black line in Fig. 3A). This comparison suggests that the rates of translation initiation and elongation are correlated, transcripts for which the initiation rate is high having also higher rate of elongation compared with transcripts for which the initiation rate and protein output are lower (SI Appendix, Fig. S3). Allowing for a 2-fold error in the estimation of protein synthesis rate or ribosome density, either due to experimental variability or to processes that we did not consider here such as sequestration or degradation of mRNAs with stalled ribosomes (25), does not destroy this correlation (SI Appendix, Fig. S4). Thus, although ribosome stalling may contribute to the variability in synthesis density scatter observed in Fig. 3B, it is unlikely that those ribosome collisions curb the rate of protein synthesis in the high protein output regime of exponentially growing yeast.

Combining Protein Synthesis Rate and Ribosome Footprint Density Reveals the Speed of Translation Elongation.

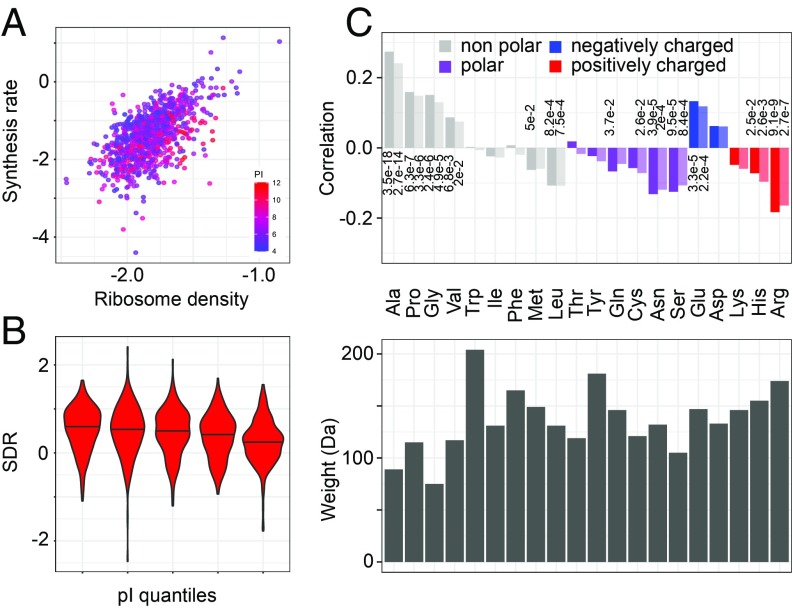
If ribosome queueing events are rare, proteins should be synthesized at the rate at which new chains are initiated $s\simeq k_{in},$ the ribosome density can be approximated as $\rho \simeq k_{in}/k_{el},$ and the ratio of protein synthesis rate to ribosome density (SDR) will be the effective translation elongation rate, $s/\rho \simeq k_{el}.$ We used this relationship to uncover features of the mRNA or of the corresponding protein that most strongly affect elongation (Fig. 4). The positive correlation of the SDR with the average speed of ribosomes, calculated from the normalized ribosome densities at individual codons, served as control (Fig. 4A). We found that all measures related to tRNA availability and codon usage [tRNA adaptation index (tAI) (26), “normalized tAI” (27), fraction of optimal codons (FOP) (28), and codon adaptation index (CAI) (29)] (see Methods for details) correlated positively with the SDR, as expected (30) (Fig. 4A). Interestingly, the ribosome density was also positively correlated with the SDR (Fig. 4A). This could be due to a correlation between initiation and elongation, but also to ribosomes promoting translation speed by resolving RNA secondary structure, consistent with the negative correlation between the average predicted propensity of 5-nt-long windows along the ORF to be in single-stranded conformation (“accessibility,” denoted as Acc5) and the SDR (see below). Participation of the newly incorporated amino acid in a protein domain was also associated with faster elongation, and this association was not due to a specific type of domain such as α-helix or β-sheet.

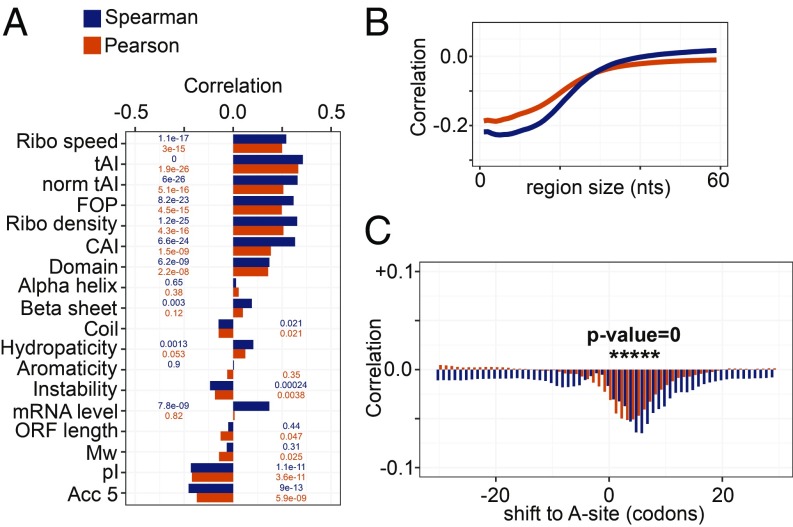
Fig. 4.

Determinants of translation elongation rate in yeast. (A) Correlation coefficients (P values indicated on the bars) of SDR with features related to codon speed, biochemical properties of the encoded protein, and RNA secondary structure accessibility. (B) Correlation coefficients of the average accessibility of regions in the ORF of length indicated by the x axis with SDR. (C) Correlation coefficients of SDR with the probability of regions of 20 nt starting at the position indicated on the x axis relative to the A site to be in single-stranded conformation. Positions where the correlation coefficients are highly significant (P value of 0) are marked by asterisk. In all panels, Spearman and Pearson correlation coefficients are shown in blue and orange, respectively.

Strikingly, the feature most strongly anticorrelated with SDR was the estimated isoelectric point (pI), reflecting the charge of the encoded protein. Other global features of the encoded protein such as the proportion of aromatic amino acids (aromaticity), hydropathicity [measured by the grand average of hydropathy (GRAVY) index (31)], molecular weight (Mw), and instability [measured by the instability index (32)] had much smaller correlation with SDR and thus with translation speed. Incorporating all of the features shown in Fig. 4A into a linear model predicted better the protein synthesis rate than the ribosome density alone (correlation coefficient, 0.69 vs. 0.49; Fisher’s Z test z score = −7.84). Using only the tAI from among the tRNA abundance-related features with high pairwise correlation (SI Appendix, Figs. S5 and S6) reduced the predictive power of the model only marginally (correlation coefficient, 0.65). The linear model also highlighted the most explanatory features, which were (in order of the significance of their correlation coefficient being different from zero) the ribosome density (P < 2e-16), isoelectric point pI (P = 3.64e-15), codon adaptation index (P = 1.22e-11), molecular weight of the encoded protein (P = 9.83e-05), ORF length (P = 0.000118), GRAVY index (P = 0.000256), tRNA adaptation index (P = 0.000977), domain coverage (P = 0.006493), and fraction of optimal codons (P = 0.009106). The weights of individual features in the linear model are shown in Dataset S3. Qualitatively similar but somewhat lower in magnitude correlation coefficients were obtained when the other RNA-seq dataset, from ref. 4, was used in the analysis (SI Appendix, Fig. S7).

Consistent with RPs being elongated relatively slowly (Fig. 2D), the set of 50 genes with greatest distance from PC1 in the direction of reduced elongation rate was strongly enriched in RPs (15 genes are in GO:CC ribosome; hypergeometric test FDR = 3e-8) but also contained other positively charged proteins such as histones HTA1 and HHF1, the INH1 inhibitor of F1F0-ATP synthase, and the SEC62 component of the Sec63 complex for protein targeting to the endoplasmic reticulum. No specific biological process or cellular component was preferentially represented among the genes with the highest elongation rates.

Complex Effect of RNA Secondary Structure on Translation Elongation.

Although it did not significantly contribute to the linear model, the structural accessibility of translated RNAs—measured by the average probability of windows of n nucleotides along the ORF of being predicted in single-stranded conformation—was anticorrelated with SDR for n up to 20 to 40 nt (Fig. 4B). This indicates that RNAs that are highly structured are also highly translated (33). Although this seems counterintuitive, a theoretical study proposed that structural rearrangements of the mRNA during translation may serve to maintain an optimal ribosomal flux for high protein output (34). On the other hand, structural accessibility of the RNA immediately ahead of the decoded codon was significantly anticorrelated with the ribosome density on the decoded codon, as found in vitro (35, 36) (Fig. 4C). Our results thus indicate that, although ribosomes progress faster through unstructured regions of the ORFs, unstructured RNAs ultimately have lower translational output.

Influence of Incorporated Amino Acids on Translation Speed.

A functional analysis uncovered sequence-dependent rearrangements of the nascent polypeptide in the ribosomal exit tunnel, suggesting that side-chain size and charge of the incorporated amino acid impact the rate of polypeptide chain elongation, as do cotranslational protein folding and interaction with chaperones (37). Indeed, our analysis provides evidence for both size and charge of amino acids affecting translation speed; negatively charged proteins are synthesized at up to ∼2-fold higher rates, on average (comparing first last pI quantile bins; Fig. 5 A and B), compared with positively charged proteins. Furthermore, among nonpolar amino acids, those with small side chains are associated with faster elongation, whereas the more voluminous ones have the opposite effect (Fig. 5C). The amino acid charge and relative abundance of cognate tRNAs impact translation elongation rate to a similar degree.

Fig. 5.

Influence of encoded amino acids on the translation elongation rate. (A) Positively charged proteins have low synthesis rate for the density of ribosomes on their corresponding ORFs. Each point represents an mRNA, with x and y coordinates corresponding to the ribosome density and protein synthesis rate, respectively, both on a log₁₀ scale. The color indicates the isoelectric point of the encoded protein, red indicating proteins with high pI (positively charged) and blue indicating proteins with low pI (negatively charged). (B) SDR distributions for increasing isoelectric point quantiles (left–right bins, t test, P = 2e-8). (C) Spearman (dark shade) and Pearson (light shade) correlation coefficients of SDR with amino acid frequencies in the encoded proteins (Top; only values of P < 0.05 are shown) and respective amino acids sizes (Bottom).

The explanatory power of linear models using relative frequencies of encoded amino acids or features related to tRNA abundance along with the ribosome density on the ORF were very similar (Pearson’s R, 0.69 vs. 0.68). The most informative amino acids were Arg (P value of the coefficient being different from zero in the linear fit = 2.35e-10), Pro (P = 1.68e-07), Ala (P = 1.87e-07), Glu (P = 1.14e-06), and Ser (P = 0.00861). See Dataset S3 for the inferred weights of these features.

Ribosomal Protein mRNAs Are Translated Slowly for Their Ribosome Densities.

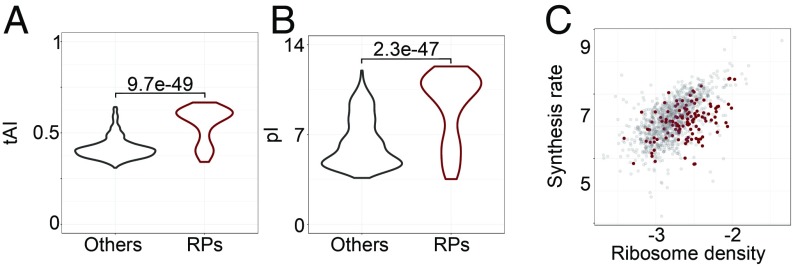
Assuming that all initiating ribosomes complete translation and that they elongate at similar rates across transcripts the ribosome footprint density is generally used as an estimate of the translation efficiency, defined as the number of protein molecules produced per mRNA molecule per unit time (12). As RPs represent a high translation burden for the cell, their transcripts should be highly optimized for translation. Indeed, RP-encoding genes have a significantly higher tRNA adaptation index than other genes (Fig. 6A; t test, P = 9.7e-49). However, the high ribosome density of the RP-encoding transcripts is not a simple reflection of high translation efficiency, because RPs also have a much higher isoelectric point than other proteins (Fig. 6B; t test, P = 2.3e-47). Visualizing the tAIs of the ORFs and the pIs of proteins along with the protein synthesis rate and ribosome allocation on individual ORFs, clearly illustrates that positively charged proteins stand out as having lower than expected protein output for the ribosome densities on the corresponding ORFs (Fig. 6C and SI Appendix, Fig. S8), or in other words, the ribosome density on their ORFs is higher compared with ORFs encoding other proteins that are synthesized at the same rate. These results suggest that the interaction of positively charged proteins, and in particular of RPs, with the negatively charged exit tunnel, slows down translation elongation, increasing the ribosome density on the ORF without a corresponding increase in protein output.

Fig. 6.

Properties of RPs (n = 122) compared with all other quantified yeast proteins (n = 992). Box plots of (A) tRNA adaptation index of individual ORFs and (B) isoelectric point for corresponding ribosomal and all other yeast proteins. (C) Protein synthesis rate [log₁₀(peptides/s/mRNA)] as a function of ribosome density [log₁₀(RPKM/TPM)] for transcripts encoding RPs (brown) and all other proteins (gray).

Perturbed Translation Dynamics in Ribosomal Protein Deletion Strains.

Deletion of specific RP genes has been associated with changes in translation and replicative life span (17, 38). In particular, deletion of rpl7a (Δrpl7a strain) led to ribosome assembly defects and overall decreased protein synthesis (measured by the incorporation of a methionine analog), whereas deletion of rpl6a (Δrpl6a strain) led to increased protein production (17). To determine how the translation parameters of individual ORFs are affected in these strains, we measured the protein synthesis rates by pSILAC and analyzed them jointly with ribosome profiling data obtained before (17). Results for individual ORFs are given in Datasets S4–S6, for the wild-type control, Δrpl6a, and Δrpl7a strains.

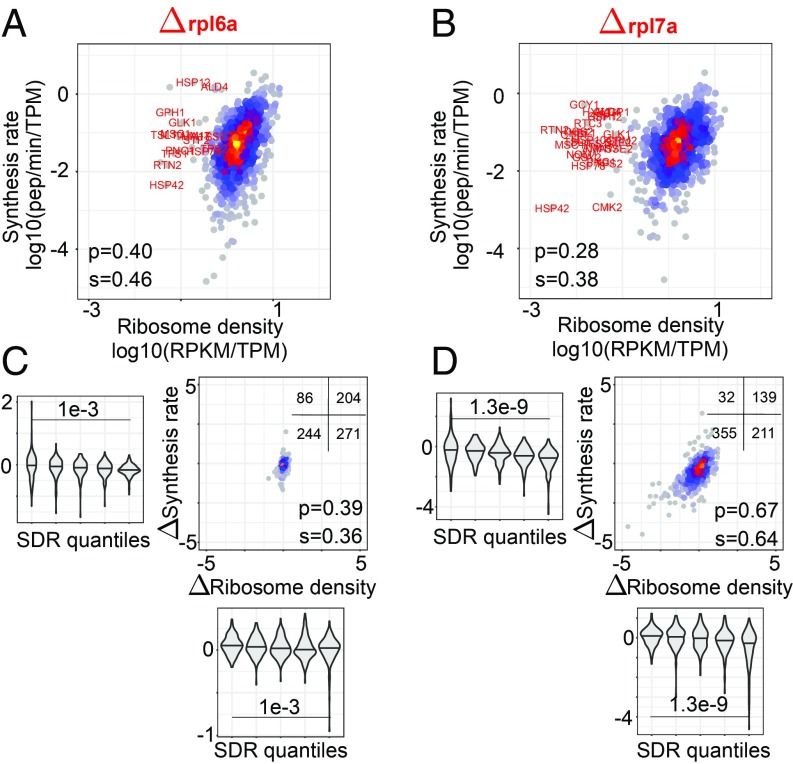
We found that accumulation of light peptides in the mutant strains was less well explained by a linear fit compared with the wild-type strain, especially for the high-translation Δrpl6a strain (SI Appendix, Fig. S9). In both mutant strains, the correlation between ribosome density and protein synthesis rates was lower (Fig. 7 A and B) compared with the wild type maintained in the same conditions (SI Appendix, Fig. S10). For the Δrpl7a strain, the decrease was due, in large part, to ORFs encoding proteins involved in starch and sucrose metabolism (FDR = 1.86e-6), glycolysis and gluconeogenesis (FDR = 0.00389), whose protein output was higher than expected for their observed ribosome densities in all of the strains (Fig. 7B and SI Appendix, Fig. S10). Excluding the 31 ORFs with a log₁₀ ribosome density lower than −1 led to correlation coefficients comparable with those obtained for the Δrpl6a strain (both Pearson and Spearman correlation coefficients = 0.41). We then compared the synthesis rate–density relationship of these strains with that of the wild-type strain analyzed in the same study (17) (SI Appendix, Fig. S10). The ribosome density changed very little in the Δrpl6a strain (Fig. 7C), and large, correlated changes in density and flux (more than 2-fold in either direction) were only observed for 11 ORFs. Furthermore, we did not find any ORF that was highly translated in the wild-type strain and whose protein output collapsed in the high-translation Δrpl6a strain, as would be expected if ribosome collisions occurred in this high-translation strain. This was not due to missing protein synthesis rate data, because the large majority (25 of 31) of ORFs with highest ribosome density and measured output in the wild type were also measured in the Δrpl6a strain.

Fig. 7.

Translation parameters in yeast strains with deletions in RP genes, Δrpl6a and Δrpl7a. (A and B) Ribosome density–protein synthesis rate plots for the 2 strains; highlighted in red are outliers (having ribosome density of <0.1 RPKM/TPM; Dataset S7) in the Δrpl7a strain. (C and D) Change in the ribosome density vs. change in the synthesis rate in the Δrpl6a and Δrpl7a strains compared with wild type. The Insets show the number of transcripts in each of the 4 quadrants of the plots. In the violin plots, the distributions of density and synthesis rate changes are shown for 5 bins of SDR values (20% of transcripts in each bin), from the lowest SDR (left-most bin) to the highest (right-most bin). P values of the t test comparing the mean density and synthesis rate changes between 20% transcripts with highest and lowest SDR values, respectively, are shown.

In contrast, hundreds of proteins had reduced synthesis rates in the Δrpl7a strain relative to wild type, with correspondingly reduced ribosome densities along ORFs (Fig. 7D). The change in ribosome density was well correlated with the change in protein output (correlation coefficients = 0.64 [Spearman, P < 2e-16] and 0.67 [Pearson, P < 2e-16]). However, ORFs with high SDR had a higher reduction in output compared ORFs with low SDR. This is indeed the behavior expected upon a global reduction in translation that comes with reduced ribosome biogenesis in the Δrpl7a strain. Namely, ORFs on which elongation is relatively slow and are in the elongation-limited regime of translation in the wild-type strain will not undergo as large a change in protein output upon the reduction of translation initiation rate as ORFs that are in the initiation-limited regime already in the wild-type strain. This can be inferred from the size of the intervals between 2 lines of distinct translation initiation rates (dashed lines in Fig. 3B) along 2 lines of high and low elongation rates (colored lines in Fig. 3B). These results demonstrate that the analysis of protein synthesis rates and ribosome densities enables the inference of translation initiation and elongation parameters for individual genes and that these parameters can be used to uncover elements that regulate translation in individual strains and conditions.

Discussion

Protein synthesis is a central activity in all cells, which has to be appropriately adjusted to resources and to the signals that a cell receives. The overall ribosome content of mammalian cells is strongly linked to their proliferation rate, in actively dividing cells ribosomal RNAs (rRNAs) taking up ∼80% of all nucleic acids and ∼15% of the biomass (39). Understanding how translation is regulated in relation to the cellular state is important, as changes in the protein synthesis capacity can lead to both cancers (40, 41) and changes in organism life span (17, 38, 42). Although theoretical models of biosynthetic processes have been proposed and studied for decades (10, 11, 43–46), measurements of translation dynamics across a large fraction of the transcriptome became possible only recently. Taking advantage of abundant data generated for the yeast Saccharomyces cerevisiae and measuring protein synthesis rates with the high transcriptome coverage afforded by currently available methods, we evaluated the translation initiation and elongation rates for individual yeast ORFs.

Using additional datasets to estimate absolute protein synthesis rates as well as ribosome densities per codon, we found that the translation initiation rate varies over a ∼100-fold range among yeast transcripts (Fig. 3). This is consistent with an initial estimation of translation efficiency based on ribosome profiling (2) as well as with the results of a study that used these data to parametrize a whole-cell model of translation, which found that the time between initiation events on individual mRNAs (5th to 95th percentile) is from 4 to 293 s (45). However, a narrower range of variation, ∼11-fold (1st to 99th percentile), was reported based on the initial analysis of the ribosome profiling data that we also used here (4), as well as in a subsequent study of a more limited set of proteins (14). It was suggested that inaccuracies in estimation of mRNA expression levels could account for discrepancies in estimates of translation efficiency from ribosome profiling (4). However, here we found that to explain the direct measurements of protein synthesis rates, the wider range of variation (∼150-fold; SI Appendix, Fig. S11) in translation initiation rates was indeed necessary. This was the case irrespective of the protocol used to prepare the mRNA-sequencing samples that were used in the analysis of ribosome densities. The similar results obtained based on mRNA level estimates with 2 sequencing protocols is perhaps not surprising, as the 3′-end bias of these mRNA-sequencing data was similar (SI Appendix, Fig. S2) and the transcript abundance estimates showed limited systematic differences between the 2 datasets (SI Appendix, Fig. S12). However, it is interesting to note that the data obtained with the optimized Ribo-zero protocol did not yield the expected scaling of RPFs with mRNA length and abundance, even though the mRNA abundances inferred from these data were very highly correlated with the number of RPFs. In the future, it will be interesting to determine the translation status of mRNA species that are preferentially enriched by different protocols. It is also unlikely that the wider range in translation initiation rate is due to error in estimating the protein synthesis rates because our analysis only included ORFs for which peptide accumulation was well described by a constant accumulation rate. The selection of transcripts for analysis in different studies may account for some of the reported differences in the range of rate variation, as the study of ref. 14, for example, used only ORFs of at least 200 codons and with a minimum ribosome density of 10 per site. This amounted to 894 ORFs, of which 826 are also covered by our analysis. However, our analysis includes 290 additional ORFs, some with relatively low translation. Despite this, the mean initiation and elongation rates in our data are quite close to those reported before, namely mean waiting time between initiation events of ∼25 s compared with a median of 8 s reported by ref. 14, and elongation rates of 2.63 aa/s compared with the 5.6 aa/s reported for mouse peptides by ref. 47, based on a ribosome runoff assay. More importantly, previous studies did not measure protein synthesis rates directly, but rather estimated initiation and elongation rates from ribosome densities. This can be done up to a constant scale factor, which was assumed to be identical between genes and set such as to achieve a specific target elongation rate toward the 3′-end of the ORF (14). Our data indicate, however, that there are substantial differences in protein output of ORFs with similar ribosome densities, underscoring the importance of direct measurements of protein synthesis rates to analyze the dynamics of translation.

The translation parameters of short ORFs, many of which encode RPs, have been the topic of much discussion (4, 45). The high ribosome density observed on short ORFs (19) has been attributed to their being evolutionarily optimized for protein output through high rate of translation initiation (45). As the high codon adaptation index exhibited by these ORFs would predict fast elongation and thereby low ribosome density (45), high ribosome density on short ORFs has also been interpreted as evidence for initiation being the main determinant of ribosome density. Consistently, we also found a small but significant correlation between ORF length and the principal component of the protein synthesis rate—ribosome density scatter, which is indicative of the translation initiation rate (Fig. 3 and SI Appendix, Fig. S13). However, our results reveal a more complex picture, which suggests that the charge of the encoded protein is an important determinant of ribosome flow. ORFs with similar overall ribosome density differ by up to ∼20-fold in protein output. This effect is not captured by models that assume that the rate of elongation depends only on the tRNA availability-dependent decoding speed at the A site of the ribosome. Indeed, we demonstrated that protein synthesis rates can be predicted with significantly higher accuracy when taking into account global features of the encoded protein such as the pI than when using solely the ribosome density.

Dissecting the independent contributions of various features to the rate of elongation is nontrivial because these features are not uniformly represented among various classes of proteins. RPs, in particular, tend to be short, positively charged, and enriched in amino acids such as lysine and arginine, which are targeted by enzymes such as trypsin, used during sample preparation for mass spectrometry. These are also the amino acids that are isotope labeled for pSILAC. Although we cannot completely exclude these confounding factors influencing our estimates of elongation rates, we did try to minimize their effect. In particular, we estimated the protein synthesis rates by measuring the accumulation of light peptides, after switching the cells from a medium with heavy isotopes to a medium with light isotopes so as to not impair protein synthesis. Furthermore, although the frequency of lysines and arginines in RPs is higher compared with other proteins, RPs do yield peptides that are sufficiently long and amenable to quantification. Finally, the estimated “rate” with which a given RP-derived peptide accumulates as a function of time should not be affected by the enzymatic digestion during samples preparation.

Overall, we found that the rate of elongation varies up to ∼20-fold among yeast ORFs, less than the rate of initiation. As the determinants of translation elongation rate are actively debated (9, 30, 45, 48, 49), we evaluated their relative contributions in our data. We further included in our study yeast strains with globally perturbed translation through RP gene deletions. We found no evidence that translation elongation severely curbs protein output, either in the exponentially growing BY4741 yeast strain, or in the Δrpl6a and Δrpl7a deletion strains, the first with higher and the second with lower overall protein synthesis rate compared with the BY4741 wild type. Rather, several lines of evidence point to evolutionary optimization of ORF sequences to maintain appropriate ribosome flux and minimize the chance of ribosome collision. For instance, ORFs with high protein output have high rates of translation initiation and at the same time a high codon adaptation index. This is predicted to enable fast elongation, as optimal codons will be rapidly found by cognate tRNAs that are in highest abundance. Our data provide transcriptome-wide evidence for the high elongation rates of highly expressed ORFs. Thus, although initiation rates vary over a wide range, the protein output increases in parallel with the ribosome density, without the latter reaching saturation. Moreover, the density of RNA secondary structure predicted in the ORF was positively correlated with the translation elongation rate, not negatively correlated, as would be expected if RNA structure were to hinder translation. This indicates that the RNA structure may also help maintaining the flux of ribosomes along the ORF to minimize ribosome collisions, as proposed in a previous study (34). Interestingly, we were able to confirm the positive influence of RNA secondary structure using dimethyl sulfate-sequencing–based measurements of secondary structure density (50) rather than computational predictions; despite the experimental dataset being sparser than our computational predictions (only 231 ORFs for which we had protein synthesis and ribosome density data also had experimental data on secondary structure), the density of secondary structure (measured by a Gini index; see ref. 50 and Dataset S8) correlated positively with our SDRs (Pearson correlation coefficient = 0.17; P = 0.007). Our results do not exclude “controlled” ribosome stalling at specific positions, such as on upstream ORFs (51), or at codons for which cognate tRNAs are limiting in specific conditions, where active regulatory mechanisms are used to modulate the output of specific ORFs (49). They also do not exclude that slow clearance of the ribosomes from the 5′-end of transcripts reduces the initiation rate to some extent [the concept of 5′-ramp (14)]. Rather, our data support the notion that ORFs have undergone evolutionary selection to minimize the chance of ribosome stalling due to imbalanced initiation and elongation rates.

That the charge of the translated protein affects the rate of translation elongation has been observed before (7, 8, 14, 52) and has been attributed to variation in the “friction” of the polymeric chain with the ribosomal exit tunnel. This effect is most marked for the positively charged RPs, whose elongation rate is low relative to other proteins whose transcripts have similar ribosome densities, and also in comparison with negatively charged RPs (SI Appendix, Fig. S14). Furthermore, even considering only transcripts whose codon usage is not optimal (CAI < 0.5), the vast majority of which encode non-RPs, the SDR is significantly lower when comparing encoded proteins with high predicted pI (>7.5) with those with low predicted pI (<7.5) (SI Appendix, Fig. S14). Our results thus provide a rationale for the previous observation that the ratio of protein to mRNA molecules is lower for RP-encoding compared with other genes (53). It is important to note that establishing a causal role of protein charge on elongation rate remains a big challenge. RPs are unusual in many respects that could affect or feedback on translation. They are very small, very abundant, under very strong selection, etc. Among all of the features of transcripts and proteins that we have tested, the pI had one of the highest correlations with the elongation rate, which argues for a more direct contribution of this parameter to the elongation rate. However, a causal effect will need to be established through additional experiments. A very exciting possibility would be to apply the recently developed nascent polypeptide chain tracking technique to a variety of constructs, engineered to vary in one specific aspect such as the pI. Although the data available to date are very limited, one study reported average translation elongation rates of ∼8, 10, and 12 aa/s for 3 very distinct proteins, histone H2B, lysine demethylase KDM5B, and actin (54), whose pIs (from GeneCards, http://www.genecards.org/) are 10.32, 6.26, and 5.29, respectively. Thus, albeit extremely sparse, these data are consistent with our finding that the pI of the protein is anticorrelated with the average speed with which the ribosome elongates the polypeptide chain, a finding that extends beyond the unusual class of RPs.

The interaction of RPs with the negatively charged rRNAs likely imposes a strong selection pressure for positive charge on RP genes (55), which in turn sets an upper bound on the rate of translocation of the polypeptide chain through the ribosome channel. It will be interesting to explore whether this slower elongation rate may have as side effect an increased translation fidelity of these very abundant proteins (56).

Over 10 y ago it was discovered that protein folding takes place already cotranslationally and that helices can fold within the ribosome exit tunnel (57). A recent study further suggested that nonoptimal codons drive effective cotranslational folding of α-helices and β-sheets (27). Although our results are consistent with these conclusions, they indicate that the positive correlation of translation speed with high density of protein domains is not limited to particular secondary-structure elements.

All of the distinct features that we analyzed here, namely tRNA/codon usage, structure accessibility of the RNA and protein charge, have small and comparable correlation with elongation rate. Altogether, they explain approximately one-half of the variance in elongation rate. This indicates that more detailed models that also include positional features (14) as well as more accurate ribosome coverage profiles (58) will be necessary to improve the prediction of translation dynamics. Our measurements of protein synthesis rates in multiple yeast strains with different translation capacity provide an ideal test bed for new models.

Materials and Methods

Simulations.

All simulations of the TASEP model have been performed with C++ code developed in-house and available in the github repository at the following link: https://github.com/andreariba/codon_TASEP. The size of the ribosome footprint has been set to 10 codons.

Analysis of Poly-A Selected RNA-Seq.

Reads from the fastq files associated with the publication of ref. 17 have been trimmed with cutadapt (59) with parameters “–error-rate 0.1 –minimum-length 15 –overlap 1,” first of the 3′ adapter (TGGATTCTCGGGTGCCAAGG) and then of the poly-A tail [“adapter” = (A)₅₀]. Resulting sequences of at least 15 nt were then mapped to yeast ORFs obtained from the yeastgenome.org (60) database (https://downloads.yeastgenome.org/sequence/S288C_reference/orf_dna/), with the bowtie2 (61) aligner, version 2.2.9, with parameter “-q” (fastq format). For each read, the best alignment reported by bowtie2 was used, and expression levels for each ORF, expressed in reads per kilobase per million (RPKM) were calculated by dividing the number of reads mapped to the ORF by library size and ORF length, then multiplying by 10⁶. For each ORF, the expression level used in the analysis was the average computed from 3 replicates.

Analysis of Ribosome Profiling Data.

Ribo-seq data have been downloaded from the Gene Expression Omnibus database (62) (accession number GSE53313). Reads from raw fastq files were trimmed with cutadapt (3′ adapter: TCGTATGCCGTCTTCTGCTTG) with parameters “–error-rate 0.1 –minimum-length 15 –overlap 1.” The first 8 nt corresponding to random barcodes were then trimmed as well and the remainder of the sequence was first aligned to rRNAs with bowtie2, version 2.2.9, parameters “-q” and “–un” to indicate the fastq format of the input file and to obtain also the unmapped reads. The latter were then aligned to a database consisting of all yeast ORFs extended by 200 nt upstream and downstream, to be able to reconstruct full-length ribosome profiles along the ORFs. To allow for the possibility of closely spaced ORFs which would lead to reads mapping in an overlapping manner to the 2 genes, we extracted up to 2 best mappings, with bowtie2 parameter “-k 2.” The positions of the “A” site of ribosomes in individual reads were inferred as in ref. 4.

Codon densities have been estimated as in ref. 4 by considering only ORFs with more than 1 read per codon and removing the first 200 codons. For each ORF, deviations were computed relative to the average number of reads per codon. These relative densities of reads were then collected for individual codons and averaged to get the estimated residence time of the ribosome in each codon.

Analysis of Protein Synthesis Rates.

For the pSILAC experiment, the S. cerevisiae strain BY4741 was grown as described (22). Briefly, synthetic medium containing 2% glucose, yeast nitrogen base (6.7 g/L), and dropout medium (2 g/L) containing all of the amino acids except l-lysine was prepared. Initially, a preculture of yeast was grown at 30 °C, 200 rpm, in 3 biological replicates obtained by inoculating 3 different colonies in 5 mL of heavy SILAC synthetic medium containing heavy l-lysine-2HCl, ¹³C₆, ¹⁵N₂ (Thermo Fisher; 88209) at a final concentration of 30 mg/L. The preculture step was repeated one more time so that all of the proteins became tagged with heavy isotope. The preculture thus obtained was used to grow cells at optical density of A600 = 0.4 in 200 mL. At this point, cells were centrifuged, washed twice with light SILAC synthetic medium containing light l-lysine-2HCl (Thermo Fisher; 89987) at concentration of 30 mg/L and transferred to 200 mL of light SILAC media. Cells were harvested at 0, 5, 15, 30, 60, 120, and 180 min for the mass-spectrometric analysis.

Cells were lysed in a buffer containing 1% sodium deoxycholate, 0.1 M ammonium bicarbonate, and 10 mM TCEP using strong ultrasonication (Bioruptor; 10 cycles, 30 s on/off; Diagenode). Samples were heated to 95 °C for 10 min, and after cooling, the protein concentration was determined by the BCA assay (Thermo Fisher Scientific), using a small sample aliquot. Fifty micrograms of protein were alkylated with 15 mM chloroacetamide for 30 min at 37 °C and incubated with sequencing-grade modified trypsin (1/50 [wt/wt]; Promega) overnight at 37 °C. After acidification using 5% TFA, precipitated detergent was removed by centrifugation (14,000 rpm, 5 min). Peptides were desalted on C18 reversed-phase spin columns according to the manufacturer’s instructions (Microspin; Harvard Apparatus) and dried under vacuum.

The setup of the μRPLC-MS system was as described previously (63). Chromatographic separation of peptides was carried out using an EASY nano-LC 1000 system (Thermo Fisher Scientific), equipped with a heated reversed-phase–high-performance liquid chromatography column (75 μm × 37 cm) packed in-house with 1.9-μm C18 resin (Reprosil-AQ Pur; Dr. Maisch). Aliquots of 1-μg total peptides were analyzed per liquid chromatography–tandem mass spectrometry run using a linear gradient ranging from 95% solvent A (0.15% formic acid, 2% acetonitrile) and 5% solvent B (98% acetonitrile, 2% water, 0.15% formic acid) to 30% solvent B over 90 min at a flow rate of 200 nL/min. Mass spectrometry analysis was performed on Q-Exactive HF mass spectrometer equipped with a nanoelectrospray ion source (both Thermo Fisher Scientific). Each MS1 scan was followed by high-collision–dissociation of the 10 most abundant precursor ions with dynamic exclusion for 20 s. Total cycle time was ∼1 s. For MS1, 3 × 10⁶ ions were accumulated in the Orbitrap cell over a maximum time of 100 ms and scanned at a resolution of 120,000 full width at half-maximum (FWHM) (at 200 m/z). MS2 scans were acquired at a target setting of 10⁵ ions, accumulation time of 50 ms, and a resolution of 15,000 FWHM (at 200 m/z). Singly charged ions and ions with unassigned charge state were excluded from triggering MS2 events. The normalized collision energy was set to 27%, the mass isolation window was set to 1.4 m/z, and 1 microscan was acquired for each spectrum.

The acquired raw files were imported into the Progenesis QI software (version 2.0; Nonlinear Dynamics, Limited), which was used to extract peptide precursor ion intensities across all samples applying the default parameters. The generated mgf files were searched using MASCOT using the following search criteria: full tryptic specificity was required (cleavage after lysine or arginine residues, unless followed by proline); 3 missed cleavages were allowed; carbamidomethylation (C) was set as fixed modification; oxidation (M) and heavy SILAC (K8) were applied as variable modifications; mass tolerance of 10 ppm (precursor) and 0.02 Da (fragments). The database search results were filtered using the ion score to set the FDR to 1% on the peptide and protein level, respectively, based on the number of reverse protein sequence hits in the datasets. The relative quantitative data obtained were normalized and statistically analyzed using our in-house script (SafeQuant) as above (63). The mass spectrometry proteomics data have been deposited to the ProteomeXchange Consortium via the PRIDE (64) partner repository with the dataset identifier PXD014357.

The protein synthesis rates have been obtained from the slope of linear regression constrained to 0 at time point 0. This analysis was performed with the lm() function of R (version 3.4.2). For each regression, R² values have been recorded for further analysis (Fig. 2C).

Scaling mRNA Copy Numbers, Protein Synthesis Rates, and Ribosome Densities.

To obtain absolute protein synthesis rates, the relative rates obtained from pSILAC were scaled, using the known values of the number of protein molecules per yeast cell (21), the doubling time of yeast, and the average half-life of yeast proteins (22). Furthermore, as the proteomics experiment does not capture all proteins, the uncaptured fraction had to be taken into account. The fraction of captured proteins has been approximated as follows: reads from ribosome footprints were used to compute normalized ORF abundances in the Ribo-seq data (RPKMs). The total abundance of translated ORFs that were not captured in the proteomics data, relative to all of the ORFs captured in Ribo-seq, was used as the fraction of uncaptured protein. The steady-state level of protein per cell should be given by the ratio of synthesis and degradation rates. The synthesis rate can thus be calculated as the product of the steady-state level of protein per cell and the degradation rate. The latter is the result of 2 processes, protein degradation and dilution due to cell growth. This leads to the following expression for the average synthesis rate of the captured fraction:

$$k_p=\mathrm{captured}\hspace{0.17em}\mathrm{fraction}\ast \mathrm{protein}\hspace{0.17em}\mathrm{per}\hspace{0.17em}\mathrm{cell}\ast \ln \left(2\right)\ast \left(\frac{1}{\mathrm{doubling}\hspace{0.17em}\mathrm{time}}+\frac{1}{\mathrm{average}\hspace{0.17em}\mathrm{protein}\hspace{0.17em}\mathrm{half-life}}\right).$$

To obtain synthesis rates for individual ORFs, we multiplied the total synthesis rate of the captured fraction by the relative synthesis rate inferred by fitting the light peptide accumulation in pSILAC:

$$k_{p_i}=k_p\ast \mathrm{normalized}\hspace{0.17em}\mathrm{protein}\hspace{0.17em}\mathrm{synthesis}\hspace{0.17em}\mathrm{rate}\hspace{0.17em}{\mathrm{p}}_{\mathrm{i}}.$$

To infer absolute densities of ribosomes per codon, we determined the first principal component of the absolute ribosome densities from ref. 19 relative to our estimates based on RPFs (Fig. 2A). We used this first principal component to map relative densities we obtained based on RPF and mRNA-seq reads to ribosomes densities per codon for each ORF.

Absolute abundances of mRNA molecules per cell were obtained by rescaling the relative numbers inferred from RNA-seq to obtain a total of 40,000 transcripts per cell, as found in previous work (23, 24).

Computation of mRNA/Protein Features.

Protein features used in the analysis of translation elongation rate have been downloaded from the yeast genome database at the following link: https://downloads.yeastgenome.org/curation/calculated_protein_info/protein_properties.tab.

The tRNA adaptation index (tAI) and normalized tAI (ntAI) have been computed as in refs. 26 and 27 with a custom Python script. The RNAplfold tool from ViennaRNA package (65) (version 2.1.8) was used with default parameters to estimate structural accessibility along ORFs. For each ORF, the average accessibility of windows of a specified size has been calculated.

We analyzed the following features:

• •Molecular weight (Mw) of the protein in daltons;
• •Isoelectric point (pI): the pH at which the protein does not carry net electric charge;
• •Grand average of hydropathicity (GRAVY score): the average of hydropathy values of all amino acids in the protein (31);
• •Aromaticity score: the frequency of aromatic amino acids, Phe, Tyr, and Trp;
• •Codon adaptation index (CAI): measure of the bias of codon usage in a coding sequence with respect to a reference set of genes (29). It is defined as the geometric mean of the weights over all codons in the sequence $\left(L\right)$:

$$\mathrm{CAI}={\left({\displaystyle {\prod }_{i=1}^L{w}_i}\right)}^{\frac{1}{L}},$$

• where the weight of each of codon is computed from the reference sequence set, as the ratio between the observed frequency of the codon $f_i$ and the frequency of the most frequent synonymous codon $f_j$ for that amino acid:

$$w_i=\frac{f_i}{\max \left(f_j\right)},$$

• with $i,j$ synonymous codons.

• •tRNA adaptation index (tAI): measure of the adaptation of each transcript to the pool of tRNAs (26). Similarly to CAI, tAI is the geometric mean of weights associated to each codon:

$$\mathrm{tAI}={\left({\displaystyle {\prod }_{i=1}^L{w}_i}\right)}^{\frac{1}{L}},$$

• where

$$w_i=\left\{\frac{W_i}{W_{\max }}\mathrm{if}{W}_i\ne 0,w_{\mathrm{mean}}\mathrm{else}\right\},$$

• and

$$W_i={\displaystyle \sum _{j=1}^{n_i}\left(1-s_{ij}\right)tGC{N}_{ij}},$$

• with $n_i$ as number of tRNA isoacceptors, $tGC{N}_{ij}$ as gene copy number of tRNA jth recognizing ith codon, and $s_{ij}$ as a selective constraint of codon–anticodon coupling.

• •Normalized tRNA adaptation index (ntAI): normalized version of tAI based on the codon usage in the transcriptome (27), it has a similar form to tAI, but with $W_i$ being scaled by the normalized codon expression in the following way: $U_i$ is the usage of codon $i$ taking into account the abundance of individual transcripts:

$$U_i={\displaystyle \sum _{j=1}^g{a}_j{c}_{ij}},$$

• with $a_j$ being the transcript abundance of gene $j$ and $c_{ij}$ as the number of occurrences of codon $i$ within the ORF of the gene $j.$ The usage of codon $i$ is then defined as follows:

$$c{u}_i=U_i/U_{\max },$$

• and finally the weights that used in the calculation of the tAI are defined as follows:

$$W_i\text{'}=W_i/c{u}_i,$$

$$W_i\text{'}\text{'}=W_i\text{'}/W_i^{\max }.$$

• The factor $W_i\text{'}\text{'}$ substitutes $W_i$ in the formula for tAI.

• •Fraction of optimal codons (FOP): fraction of optimal codons in the ORF (28). The optimal codon for an amino acid is the codon most used to encode the amino acid in the ORFs encoding the top expressed proteins;
• •Instability index: measure of protein half-life estimated based on the dipeptide composition of the protein (32);
• •Domain coverage: fraction of protein covered by Pfam domains predicted by InterPROScan (66);
• •α-Helix, β-sheet, coil: fraction of the protein sequence involved in the indicated types of secondary structures predicted by PSIPRED (67);
• •Accessibility, 5 nt: average probability of finding a window of size 5 nt in an open conformation predicted with RNAplfold from ViennaRNA package (65).

Enrichment Tests.

Gene ontology and KEGG pathway enrichments have been performed through the STRING database (68).