Leveraging device-arterial coupling to determine cardiac and vascular state

Abstract

Objective:

Limitations in available diagnostic metrics restrict the efficacy of managing therapies for cardiogenic shock. In current clinical practice, cardiovascular state is inferred through measurement of pulmonary capillary wedge pressure and reliance on linear approximations between pressure and flow to estimate peripheral vascular resistance. Mechanical circulatory support devices residing within the left ventricle and aorta provide an opportunity for both determining cardiac and vascular state and offering therapeutic benefit. We leverage the controllable mode of operation and transvalvular position of an indwelling percutaneous ventricular assist device to assess vascular and, in turn, cardiac state through the effects of device-arterial coupling across different levels of device support.

Methods:

Vascular state is determined by measuring changes in the pressure waveforms induced through intentional variation in the device generated blood flow. We evaluate this impact by applying a lumped parameter model to quantify state-specific vascular resistance and compliance and calculate beat-to-beat stroke volume and cardiac output in both animal models and retrospective patient data without external calibration.

Results:

Vascular state was accurately predicted in patients and animals in both baseline and experimental conditions. In the animal, stroke volume was predicted within a total RMS error of 3.71 mL (n=482).

Conclusion:

We demonstrate that device-arterial coupling is a powerful tool for evaluating patient and state specific parameters of cardiovascular function. Significance: These insights may yield improved clinical care and support the development of next generation mechanical circulatory support devices that determine and operate in tandem with the supported organ.

I. INTRODUCTION

Cardiogenic shock, defined as impaired cardiac function leading to inadequate end-organ perfusion, is a highly morbid condition with mortality rates exceeding 40% despite prompt medical therapy [1]–[5]. Treatment is impeded by the lack of sufficient tools to aid the clinician in performing timely diagnosis, determining the severity of dysfunction, and accurately titrating support to physiologic demand [6], [7]. Laboratory data are intermittently obtained at significant delay while practical considerations limit the frequent use of echocardiography to assess cardiac function. Indwelling catheters, such as those that reside in the pulmonary artery [8], provide real-time measures of central venous pressure and pulmonary artery pressure and can be used to periodically measure the pulmonary capillary wedge pressure – considered an estimate of the left ventricular end-diastolic pressure. Pulmonary artery catheters (PACs) can also estimate cardiac output (CO) using Fick’s laws through measures of systemic oxygen consumption or the bolus thermodilution method [9]–[11] By applying linear Ohmic relationships of systemic pressure and flow, these pressure measurements and cardiac output estimates are clinically used to derive additional metrics such as systemic vascular resistance (SVR), pulmonary vascular resistance, and the transpulmonary gradient [12], [13].

Though heralded when first introduced into clinical practice, PAC use has dropped precipitously [9], [14], [15]. Burdened by the required assumptions used to arrive at metrics and the corresponding lack of fidelity with more invasive measurements, PACs have been unable to establish reliable association with clinical outcomes [9], [16]. For example, PCWP is only intermittently obtained because inflation of the occlusive balloon can affect the pulmonary vasculature and the underlying simplifications for PCWP measurements can lead to inaccurate quantification [17], [18]. Furthermore, measurements obtained by PACs discount dynamic changes in cardiac function and the non-linear aspects of systemic ventricular-vascular coupling are lost by quantification to a single number. This dynamic information may hold valuable insights into cardiovascular performance. For example, observations that variation in the LV stroke volume over the respiratory cycle leads to corresponding changes in systemic pulse pressure indicative of intravascular volume status demonstrate that clinically important metrics can be derived from measurement of dynamic changes [19], [20].

Mechanical circulatory support (MCS) devices have the potential to fill this information gap while providing means of maintaining systemic perfusion and restoring homeostasis during cardiogenic shock [21]–[26]. Percutaneous ventricular assist devices (pVADs) that reside within the left ventricle and pass across the aortic valve present an opportunity to directly assess their local environment and to use the interaction between these devices and the heart to characterize further cardiovascular state. Indeed, use of insights drawn from these interactions to guide titration of support may lead to improved outcomes that have yet to be realized in the clinical trials of mechanical support performed to date [27], [28].

Employing a transvalvular intraventricular pVAD (Impella CP, Abiomed, Danvers, MA) as our paradigmatic device, we previously described leveraging heart-device interactions to determine the left ventricular end diastolic pressure [29] - quantifying ventricular pressure by using intrinsic device performance, i.e. motor current patterns, at a set support level. Here, we investigate how variable levels of support subsequently impact vascular hemodynamics in a way that can be used to characterize the vasculature and to then predict the dynamic cardiac functional state through application of a model of the cardiovascular system. The presented approach, which is independent of the intrinsic device-heart interactions, demonstrates a method that purposefully uses extrinsic device effects to continuously calculate diagnostic patient-specific vascular state and thus make predictions about cardiac state. Notably, this is all done without additional intervention or external calibration and relies only on existing technology readily capable of clinical implementation. We apply a lumped parameter model of the vascular system to improve on traditional linear approximations and provide measurement of dynamic variation in the vascular response. From this model, we introduce and measure the results from controlled perturbations of the vascular system through an MCS device to continuously calculate vascular resistance and compliance from which we calculate cardiac stroke volume.

The effects of an MCS device can be leveraged to provide additional clinical data to aid in titration of appropriate device support. Here, we demonstrate how these effects can be used to continuously measure vascular and cardiac performance in a way that provides information that is directly relevant to the clinician and easily translatable to the clinic. More importantly, use of MCS devices for otherwise invasively obtained metrics demonstrates the impact and potential of device-arterial coupling to determine cardiac and vascular state.

II. METHODS AND MATERIALS

A. Mechanical Circulatory Support Device

We employ the Impella CP as our paradigmatic MCS device. The device is mounted at the end of a 9-French catheter introduced percutaneously via the femoral or axillary artery and advanced retrograde until the pump inlet resides within the left ventricle with the outlet in the aorta (Fig. 1A) [30]. The device controller is connected to the external end of the catheter and functions to maintain an operator determined fixed rotor speed (RPM) by modulating power delivered to the pump (Fig. 1B). This power modulation is necessary as pump operation changes with load variations induced by left ventricular contraction [31]. Importantly for the purpose of the method described here, the pump experiences minimal load variability during diastole when the aortic valve is closed so that the flow rate remains steady and time-independent during this phase.

Fig. 1. Impella device with controller and lumped parameter approximation of the cardiovascular system.

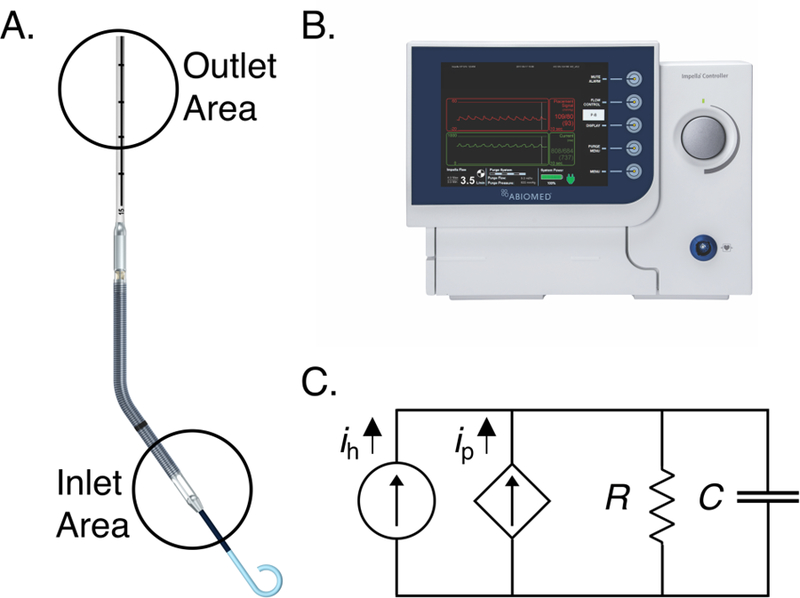
(A) The Impella is a catheter mounted axial flow mechanical support device that is inserted transvalvularly into the left ventricle to pull flow across the aortic valve and into the aorta. The inlet area resides in the left ventricle and the outlet resides in the ascending aorta. (B) The external Impella controller used to set Impella speeds and estimate and record operational data including aortic pressure and flow rate. (C) A 2-element lumped parameter approximation of the cardiovascular system with an additional source from the Impella pump.

The controller measures and records motor current and aortic pressure and also records real motor speed by measuring the frequency of polarity changes by each rotation of the rotor. Speed-specific determination of the pump-performance curve for each device allows for estimation of device flow output derived from the device motor current at each speed. This relationship is the basis of the displayed estimated flow on commercially available Impella controllers [30]. Flow estimation is most accurate during diastole as there is minimal Impella load variation and nearly all forward flow into the aorta is device generated.

B. Model to Evaluate Device-Arterial Coupling

Lumped parameter models relying on electrical circuit analogs of resistors, capacitors, inductors, and current or voltage sources are well-established means of simulating the cardiovascular system [32]–[34]. While increased model complexity is used to gain insight into intricate cardiovascular phenomena, simpler models are appealing and used here for ease of understanding and decreased quantitative burden allowing for clinical use [35]. Otto Frank popularized a simple yet robust model in the 1800s, inspired by the hand-powered fire engine pump, in which the heart is modeled as a flow source and the impedance of the arterial system is represented by parallel lumped resistance and compliance [36]. Impulses from the simulated heart correspond to stroke volume and generate an arterial blood pressure waveform. This model has been extensively adapted and expanded upon in numerous physiological applications. Addition of new components to the model allows more refined results for a specific physiological state or cardiovascular interaction. However, this is at the expense of computational complexity and the need to define values for each newly added component.

Determination of appropriate values for model elements is a significant barrier to accurate implementation of lumped parameter models and has limited the utility of simpler models. Each element has significant inter- and intra-patient variability. Systemic vascular resistance and compliance in humans can nominally vary between 700–1600 $\frac{dyns}{c{m}^5}$ [37] and between 0.4–1.5 $\frac{mL}{mmHg}$ respectively, with wider ranges in disease [38]. To address this variability, complex methods have been developed to estimate values using intra-waveform analysis and other forms of calibration with questionable accuracy and usability [35], [39].

Here we present a method to estimate vascular lumped parameter values without any additional modeling or methods by leveraging the unique coupling effects that occur during MCS. While others have studied how MCS alters models of the cardiovascular system, they were not implemented as a clinically deployable method to assess the state of patient values [40]–[42]. Rather than demonstrate a novel model of the unique physiology introduced during MCS, we employ a model in a unique way to assess patient and state specific parameters in a manner readily applicable to patient care.

We use a two-element lumped parameter model to maintain simplicity and focus on creating a tool that is both relevant and accessible to clinicians (Fig. 1C). Lumped systemic resistance and compliance are conceptually familiar to clinicians and are relatable to current clinical estimation methods. In the device-heart system, the addition of the Impella adds a parallel constant flow source that can be controlled by setting different RPM values. The general governing equation for this resulting circuit is:

$$C\frac{dP}{dt}+\frac{P}{R}=i_h+i_p$$ (1)

Where P is the aortic pressure waveform, R is the systemic vascular resistance, C is the systemic vascular compliance, i_h is the flow from the native heart, and i_P is the flow from the Impella. This equation can be simplified through consideration of the physiological state during diastole. The aortic valve is closed during diastole resulting in elimination of the i_h term while the output of the Impella is fixed, fully-developed, and known. Equation (1) is then expressed and solved as follows:

$$P=P_0{e}^{-\frac{t}{RC}}+i_{p}R$$ (2)

Where P₀ is the initial aortic pressure during diastole. Using (2), vascular state can be determined through analysis of the aortic pressure waveform measured by the Impella.

Vascular state is determined by measuring the difference in aortic pressure induced by Impella speed changes with the underlying assumption that the vascular state remains stable over this minute-long interval for a given speed. Systemic vascular resistance, R, is determined by using the above equation at two different Impella operating points and the difference in estimated Impella flow rate. Beats at end expiration are used to reduce respiratory variation effects. We average three end-expiratory beats to improve signal fidelity. Systemic compliance, C, is determined using the mean time constant for the exponential decay of aortic pressure during diastole and the calculated systemic vascular resistance. Cardiac performance can then be determined by using these vascular state values in (1), the general governing equation, with the measured aortic pressure to calculate flow from the heart. The pulsatile ejection component of the flow rate waveform is numerically integrated using trapezoidal Riemann sums over the ejection phase of the cardiac cycle to estimate stroke volume and thereby obtain CO. These calculations were performed using custom scripts and built-in functions in MATLAB (MathWorks, Natick, MA).

C. Animal Models

We investigated the effects of the Impella CP on cardiovascular function in a porcine model of acute pharmacological and mechanical intervention [29]. Experimental procedures were conducted on four young adult castrated male Yorkshire swine (45–80 kg) in accordance with NIH and AAALAC guidelines (CBSET, Lexington MA). Animals were sedated with an intramuscular injection of Telazol (6 mg/kg), endotracheally intubated, and maintained under general anesthesia with inhaled isoflurane while continuously monitoring oxygen saturation, core body temperature, and electrocardiography.

Vascular access was obtained at each femoral artery and vein. The Impella was introduced via the left femoral artery over a wire and advanced into the left ventricle. A Millar Pressure-Volume Loop conductance catheter (Millar, Houston, TX, USA) was introduced via the right femoral artery and advanced into the left ventricle parallel to the Impella to obtain continuous measurement of left ventricular volume and pressure. Continuous stroke volume estimation was obtained through calculation of the change in left ventricular volume measured by the Millar catheter over the cardiac cycle. A PAC was introduced in the right femoral vein and advanced into the pulmonary artery to obtain a cardiac output estimation via thermodilution for validation and calibration of the Millar system. Three sequential thermodilution measurements were performed at the beginning of each experimental condition and averaged. Ultrasound and fluoroscopy were used to guide and confirm placement of the Impella and catheters and confirm absence of aortic regurgitation. The Impella was operated at varying speeds commonly used clinically with continuous measurement of motor speed, motor current, and aortic pressure. Only steady state conditions were considered after waiting at least 10 seconds after speed changes. Invasive blood pressure transducers were used to record femoral arterial and venous pressures. An animal received a 25-µg bolus of norepinephrine to achieve a change in vascular state from baseline to demonstrate ability to determine change in cardiovascular state.

Resulting data was registered and analyzed using MATLAB and compared using correlation and Bland-Altman plots with calculations of root mean square error and mean absolute error [43]. For validation purposes, systemic vascular resistance was calculated using (3):

$$SVR=80\frac{MAP-CVP}{CO}$$ (3)

Where SVR is systemic vascular resistance in units $\frac{dyns}{c{m}^5}$, 80 is a unit conversion factor from Wood units to $\frac{dyns}{c{m}^5}$, MAP is the mean arterial pressure, CVP is the central venous pressure, and CO is the cardiac output measured via thermodilution.

D. Patient Data

Anonymized retrospective patient data were used for validation and to demonstrate method applicability. These data were obtained using IRB approval from acute cardiogenic shock patients treated with the Impella CP at the Brigham and Women’s Hospital (Boston, MA). The chart recorded CO, heart rate, and hemodynamic pressures were obtained for validation purposes. Impella motor speed, motor current, and aortic pressure were obtained from the Impella controller and were analyzed with the same methodology as was developed from the animal model.

E. Statistical Analysis

Correlation and Bland-Altman plots were used to confirm validity of estimation by comparing measured and calculated stroke volume using ± 2 standard deviation confidence intervals [44]. Differences between calculated and measured values are found for each trial using mean absolute error and expressed in whole via root-mean-square difference. Statistical analysis was conducted using MATLAB and the Statistics and Machine Learning Toolbox from MATLAB.

III. RESULTS

We assessed vascular state from animal and patient data obtained from indwelling Impella CPs as our paradigmatic MCS device. These results were applied to a lumped parameter model of the cardiovascular system to estimate vascular parameters and cardiac performance without need for any measurements or estimations of cardiac output for calibration.

A. Animal Data

The method was tested in an experimental animal model at baseline and with an acute intervention. An Impella was implanted and maintained at either 33,000 or 44,000 RPM. These speeds were selected to ensure a measurable impact on aortic pressure, while minimizing any changes in vascular state. Changes in aortic pressure by this speed variation of the Impella are measurable with distinctive differentiation of relaxation post-aortic valve closure under all conditions (Fig. 2A). There was close agreement between systemic vascular resistance calculated by our method, R, (Table 1), and the value determined by the traditional CO thermodilution estimation method, SVR, across all the animals. This agreement between the vascular resistance calculated by our method and through thermodilution estimation was maintained during a change in vascular state induced through the administration of a 25-µg bolus of norepinephrine. As expected, our model predicted the observed vasoconstrictive effects of norepinephrine as an increase in resistance and reduction in vascular compliance, C (Table 1).

Fig. 2. Changes in aortic pressure waveform from variation in mechanical support device operating speed.

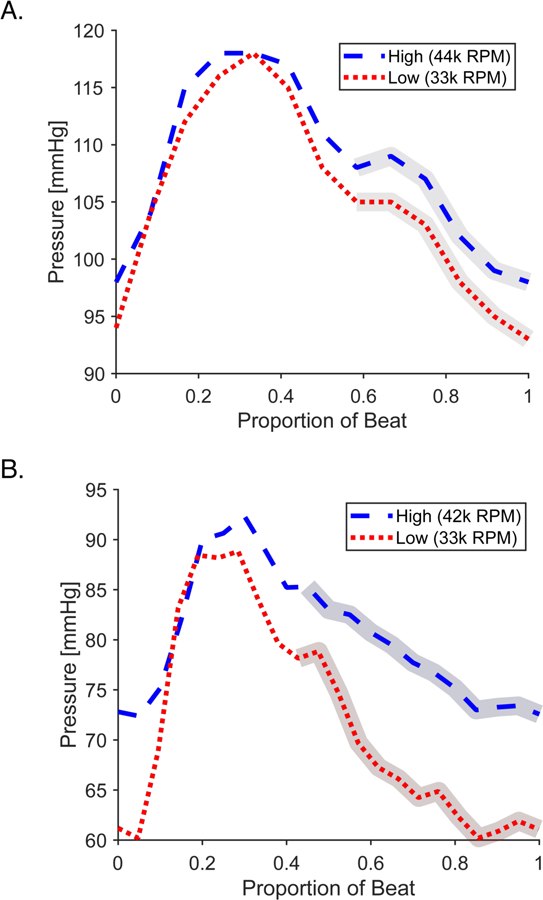
(A) Representative beat from animal model showing a high Impella speed at 44,000 RPM (blue dashed) and a low Impella speed at 33,000 RPM (red dotted). (B) Representative beat from patient data showing a high Impella speed at 42,000 RPM (blue dashed) and low Impella speed at 33,000 RPM (33k RPM). For both, the identified regions of isovolumetric relaxation used for calculation of vascular parameters is highlighted. The variation from the animal is smaller despite a larger speed change because of healthier cardiac state.

TABLE I.

BASIC HEMODYNAMICS FOR EACH ANIMAL AT BASELINE AND DURING INTERVENTION.

	Animal 1	Animal 1 Intervention	Animal 2	Animal 3	Animal 4
Mass [kg]	77.3	77.3	79.4	48.6	58
Heart Rate [bpm]	92	112	97	104	79
MAP [mmHg]	82.4	106.0	64.2	54	90.6
CVP [mmHg]	18.4	18.9	9.1	13.6	15.8
Measured CO (SV) [LPM (mL)]	6.6 (71.7)	6.6 (58.9)	7.4 (76.3)	2.3 (22.0)	3.9 (49.3)
Measured SVR [dyn s/cm5]	775	1055	595	1405	1534
Mean Calculated SV [mL]	70.5	58.5	76.1	21.2	48.7
Calculated R [dyn s/cm5]	718	1019	575	1287	1313
SV Data Points	155	71	54	115	91
Mean Absolute Error [mL]	2.9	2.5	4.0	3.1	3.7

Each animal trial was performed independently with the first animal also undergoing a pharmaceutical intervention via bolus of norepinephrine. CO measurements are based off thermodilution calibration of a Millar catheter. SVR measurements are based off hydraulic resistance calculation using thermodilution CO estimation, mean arterial pressure, and mean central venous pressure. ^aMAP = mean arterial pressure, CVP = central venous pressure, CO = cardiac output, SV = stroke volume, SVR = systemic vascular resistance, R = resistance, kg = kilograms, bpm = beats per minute, mmHg = millimeter of mercury, LPM = liters per minute, mL = milliliters, dyn = dynes, s = second, cm = centimeter.

We applied the calculated resistance and compliance values in our lumped parameter model of the cardiovascular system by using aortic pressure (Fig. 3A) to determine flow (Fig. 3B) and subsequent estimation of a continuous stroke volume. In our first representative animal, the output averaged over 150 heart beats (~100 seconds) yields a mean stroke volume value of 70.5 mL; similar to the stroke volume of 71.7 mL derived from the thermodilution estimated cardiac output of 6.6 L/min divided by a heart rate of 92 bpm (Table 1). Data from a second representative animal are shown yielding a mean stroke volume of 76.1 mL calculated by our method compared to 76.3 mL derived from the thermodilution estimated cardiac output of 7.4 L/min divided by the heart rate of 97 bpm. Subsequent animals also had similar results with though with a range of stoke volume values due to the variability in size and cardiac output of the animals (Table 1). As predicted, stroke volume was decreased following norepinephrine administration in the setting of increased afterload. The stroke volume directly after peak effect over 70 beats was 58.5 mL, nearly identical to calibrated Millar stroke volume measurement over the same period of 58.9 mL.

Fig. 3. Aortic pressure waveform and corresponding flow rate prediction in an animal model.

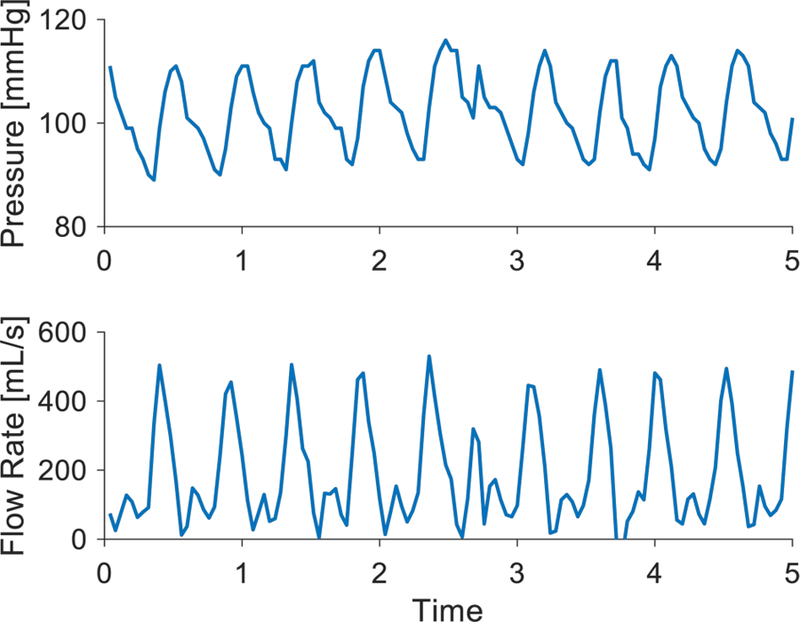
(A) Aortic pressure measured from the placement signal of the Impella is shown with an artifact. (B) Calculated flow rate waveform of the heart using the 2-element lumped parameter model and corresponding aortic pressure waveform. The effect of the aortic pressure artifact can be seen at the corresponding time point.

For all cases, the beat-to beat stroke volume calculation compared favorably with a Millar stroke volume measurement calibrated via thermodilution, demonstrating stroke volume oscillation that occurs with respiratory variation (Fig. 4). Combining all cases with the animals (n = 482) resulted in a stroke volume RMS error of 3.71 mL and a correlation between Millar measured and calculated SV with R² = 0.96 (Fig. 5).

Fig. 4. Beat-to-beat stroke volume prediction compared to Millar catheter measurement in an animal model.

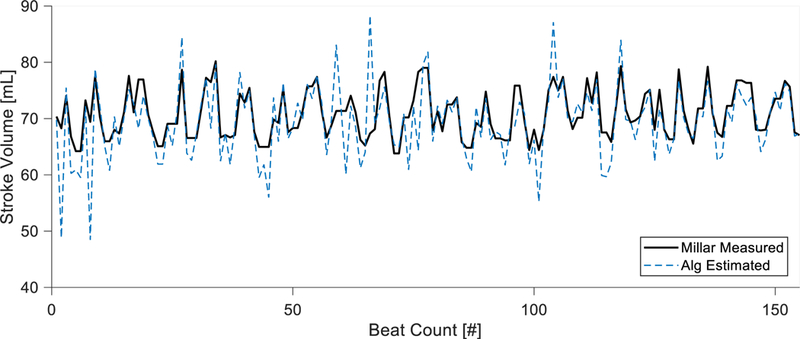
The stroke volume predicted from the algorithm is compared with direct measurement via Millar catheter. The Millar catheter is calibrated by cardiac output found via three averaged thermodilution measurements. The algorithm is able to track accurate mean stroke volume as well as native respiratory variation. Algorithm estimations are made without any calibrations and only use estimated vascular parameters.

Fig. 5. A correlation and Bland-Altman plot to show accuracy of stroke volume estimation compared to direct Millar catheter measurement over multiple animal trials.

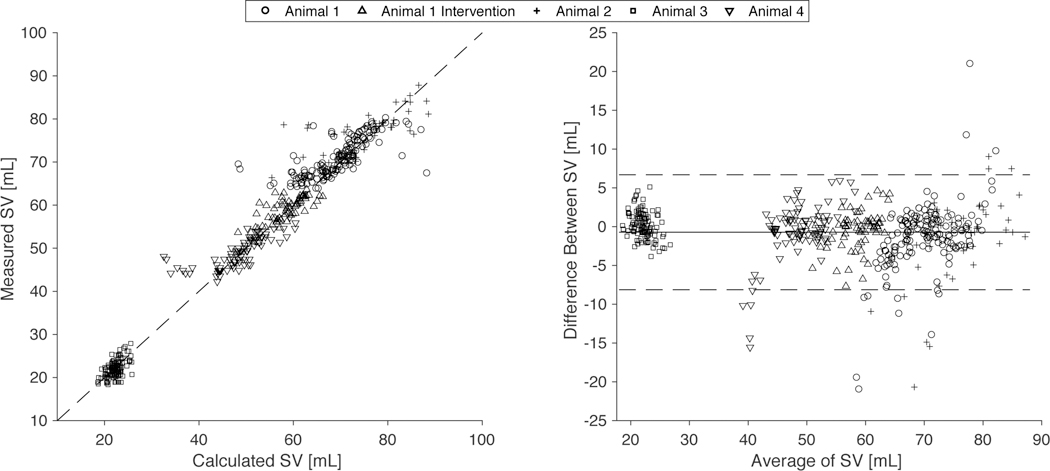
Data from 4 pig animals with an implanted Impella are shown at varying baseline values and with a pharmaceutical intervention of norepinephrine bolus totaling 482 observations. (A) The correlation plot comparing estimated and directly measured stroke volume for all cases as indicated. (B) The Bland-Altman plot for all cases as indicated with standard confidence intervals using ± 2 standard deviations of the difference between the estimated and directly measured stroke volume over the average result of both methods.

B. Patient Data

Retrospective Impella patient data provided clinical validation of this method with motor speed variation from 39,000 to 42,000 RPM. Changes in aortic pressure by this speed variation of the Impella are measurable with distinctive differentiation of relaxation post-aortic valve closure (Fig. 1B). Using beats from these two operating states with the same simplified model of the cardiovascular system, a patient specific vascular resistance and compliance were 1130 $\frac{dyns}{c{m}^5}$ and 0.61 $\frac{mL}{mmHg}$ and SV was 42.6 mL. The latter compared with a chart reported SV of 45 mL determined from a thermodilution estimation of CO and recorded heart rate (Table 2). In a second patient with motor speed variation from 31,000 to 39,000 RPM, the model calculated patient specific vascular resistance and compliance were 964 $\frac{dyns}{c{m}^5}$ and 0.75 $\frac{mL}{mmHg}$ and SV was 40.6 mL. This is compared with a chart reported SVR of 1021 $\frac{dyns}{c{m}^5}$ and SV of 44.3 mL determined from a thermodilution estimation of CO and recorded heart rate (Table 2).

TABLE II.

BASIC HEMODYNAMICS FOR EACH PATIENT AT AVAILABLE CLINICAL DATA POINT

	Patient 1	Patient 2
Measured SV [mL]	45	44.3
Measured SVR [dyn s/cm5]	-	1021
Mean Calculated SV [mL]	42.6	40.6
Calculated R [dyn s/cm5]	1130	964
Calculated C [mL/mmHg]	0.61	0.75

Retrospective review of patients on Impella CP support was centered around available clinical data. For two patients, there were clinical measurements of stroke volume done around the time of a performance-level change. Chart reported stroke volume and systemic vascular resistance is compared with algorithm calculations. ^aMAP = mean arterial pressure, CVP = central venous pressure, CO = cardiac output, SV = stroke volume, SVR = systemic vascular resistance, R = resistance, kg = kilograms, bpm = beats per minute, mmHg = millimeter of mercury, LPM = liters per minute, mL = milliliters, dyn = dynes, s = second, cm = centimeter.

IV. DISCUSSION

The high morbidity of cardiogenic shock despite prompt medical treatment and use of intra-aortic counterpulsation therapy [28] motivated the development of sophisticated new MCS technologies, such as pVADs, capable of delivering increased perfusion support [45], [46]. However, the realizable benefit of these devices is limited by lack of reliable markers of patient state to guide initiation, titration, and weaning of support. While PACs are presently relied on to provide metrics of cardiac function and vascular state, the metrics they provide are indirect. Left ventricular filling pressures inferred from the pulmonary capillary wedge pressure or estimates of cardiac output and systemic vascular resistance calculated from the thermodilution method, are intermittently obtained, assume no losses at different sites in the vascular circuit, and use linear time-invariant Ohmic relationships of pressure and flow [9], [14], [47]. The practical effect of these limitations is that decisions on the management of patients in cardiogenic shock are made based on data that is overly simplified, too coarse to provide meaningful insight, or may be obsolete and no longer representative of the patient’s present state by the time it is available to the clinician. Diagnostic tools capable of continuously tracking cardiac and vascular state based on accurate time-varying models that capture physiological responses are vitally needed to more effectively use advanced therapies to improve clinical outcomes.

We previously described how the interactions between a transvalvular intraventricular MCS device and the heart during normal device operation create a device-heart system that can be used to determine left ventricular end diastolic pressure (LVEDP), a key physiological parameter that provides clinically useful information of cardiac state [29]. We now describe how intentional variation of the operational state of the MCS device in the combined device-heart system can be leveraged to affect cardiac dynamics, i.e ventricular-vascular coupling and thereby interrogate the physiological state of the cardiovascular system. The addition of MCS allows controlled variation of the ventricular inputs to ventricular-vascular coupling with measurable results. We use these perturbations to continuously generate reliable clinically useful metrics of cardiac and vascular state. To accomplish this, we employ a time-variant non-linear model of the vascular system and exploit device-arterial coupling, a well-controlled analog to ventriculo-vascular coupling, to continuously determine systemic vascular resistance and compliance and quantify cardiac stroke volume without need for additional external measurements. The Impella is an ideally suited MCS device to demonstrate this as the device operates at user-defined fixed speeds, provides physiologic antegrade flow into the aorta, and provides aortic pressure and flow estimations through the pump. These measurements are obtained throughout MCS support with negligible impact on therapeutic function.

We employ a two-element lumped parameter model of the vascular system to model the dynamic and non-linear cardiac and vascular interactions more accurately than is provided by typical Ohmic relationships. Using known terms to approximate these element values allows this method to be readily validated and utilized in clinical applications. While others have used lumped parameter models for estimations, they are limited due to reliance on direct calibrations and other external methods to determine patient and state specific variables [32]–[35], [39]. Here, our method is able to provide these patient and state specific variables by leveraging the operation of an indwelling mechanical circulatory support device without need for additional measurements or catheters.

We evaluated our method and model under baseline physiological conditions and assessed its performance following pharmaceutical intervention in a swine model of cardiovascular intervention to precisely investigate its response to changes in vascular tone. As a whole, this demonstrates the ability of the model to track a change in both cardiac and vascular state. Similar results across all the animals demonstrate not only repeatability but validity even in vastly different physiologic baselines (Table 1). The Bland-Altman plot has fewer than 5% of the nearly 500 observed values outside of the expected significance bounds with no discernable trends and patterns, thus indicating a good agreement between the measurement techniques (Fig 5.). We choose to directly compare stroke volume because its current clinical measurement techniques are more direct and rely on fewer underlying assumptions than systemic vascular resistance, making it a more accurate validation metric.

Our model’s ability to continuously and accurately track changes in systemic vascular resistance and compliance as well as estimate cardiac stroke volume mark a significant advancement over traditional measures obtained from a PAC or other diagnostics readily deployed in clinical practice. At present, clinicians titrate inotropic medications or mechanical support based on intermittent and coarse metrics of cardiac contractility. Vasopressors and vasodilators are routinely adjusted based on pressure measurements without real-time insight into how these changes affect cardiac function. An accurately estimated cardiac stroke volume reported in real-time has the potential to radically transform present clinical practice and would provide near-immediate feedback on titration of inotropic support. Knowledge of the systemic vascular resistance and compliance would further guide clinical management of vasopressors and vasodilators and would provide a continuous metric of the vascular state. These parameters taken together provide clinicians with the previously unobtainable capability of titrating cardiac function and vascular state in concert to optimize ventriculo-vascular coupling and thereby provide a means of improving clinical outcomes. The novelty and advantages of our method are highlighted by the need to rely on invasive research-grade measures of cardiovascular function through the use of conductance catheters placed into the left ventricle to validate our model’s findings.

In addition to the bulk estimation over a given time, cardiac performance is continuously measured by integrating pressure and flow waveforms over the ejection phase of each beat to determine a nearly beat-to-beat stroke volume (Fig. 4). The calculated stroke volume closely agreed with mean stroke volume estimates obtained from thermodilution-based CO measurements while also providing the temporal resolution to reflect the effect of respiratory variation on left ventricular function as observed by direct measurements with the Millar catheter. Averaging the output of 50–150 beats provides an accurate mean stroke volume output without sacrificing fidelity. Even greater accuracy may be realized through improvements in the Impella pressure transducer. Intermittent speed variations will be necessary to determine changes in the lumped parameter values (R and C) that are likely to occur with changing patient state and therapeutic interventions. This re-querying of vascular state can be manually triggered with change in therapy or be automatically triggered with a timer or rapid changes in aortic pressure or stroke volume prediction. Due to the short time needed at each speed, ease of re-querying lumped parameters will result in a nearly beat-to-beat estimation.

Retrospective patient data analysis demonstrates clinical applicability and validity with ready implementation using current clinically deployed technology. Results from both patients yielded results similar to those clinically reported using additional pulmonary artery catheter measurements, with differences that are comparable to that seen with our animal studies (Table 2). Differences in values between patients may demonstrate not only normal physiologic variation between individuals, but also the concomitant effect of differential manifestation of disease and compensatory mechanisms. While these estimations may be improved by specific changes in pump control, they can nonetheless be made with current clinically deployed devices.

A. Limitations and Future Work

Our method relies on accurate flow prediction by the Impella controller and precise measurement of changes in pressure waveform. Improved flow prediction accuracy will yield better estimation of vascular characteristics. However, we hypothesize that improved characterization of variation in Impella load due to cardiac ejection will not be as impactful, because our method relies on estimates obtained during diastole. Our method also assumes negligible impact on vascular state from device flow changes. While vascular state is dependent on pressure and volume, close agreement with our calculated resistances and stroke volume and validation measurements at different speeds validates in part the absence of significant effects of variation in motor speed. Yet, we cannot exclude that such effects are the source of our small errors and future work will continue to minimize speed changes to mitigate this potential source of variability. Vascular parameters calculated through pressure waveform is complicated by the limited sampling frequency of the current pressure transducers. Many individual beats are not of sufficient fidelity to provide meaningful data. Even with sufficient fidelity, multiple beats are required to construct a meaningful waveform. Consequently, fully developed and steady Impella flow conditions must be present for the model to be applied. The model creates near beat-to-beat predictions that are otherwise not able to be clinically estimated, however it does so assuming a fixed value for the lumped parameter values due to limitations in pressure sampling to recreate a simple vascular impedance. Higher fidelity pressure sensors may allow for more sophisticated analysis because averaging is no longer necessary to create values that are gated to respiration. In addition to these considerations, noise from the pressure transducer may lead to inaccurate calculations of flow rate and thus stroke volume in an amplified manner since they rely on calculation of the derivative (Fig. 2). While not evaluated here, drift in the pressure sensor may affect results over significant timescales that can be mitigated by recalibration of the pressure sensor. Because the Impella is a transvalvular device, there is a risk for aortic insufficiency during its use. While we confirmed the absence of valvular regurgitation in our studies, it may be present in future clinical use-cases. Any retrograde flow may affect the aortic pressure signal and consequently impact estimation of vascular characteristics. Understanding this phenomenon will be an important part of future work, however, its impact can be mitigated by evaluation for regurgitation during Impella placement.

Future work will evaluate use of the Impella to generate stochastic impulse-like inputs to determine systemic impedance responses with the goal providing improved understanding of cardiovascular physiology while furthering the development of clinically deployable diagnostic devices.