A Luminescent Thermometer Exhibiting Slow Relaxation of the Magnetization: Toward Self-Monitored Building Blocks for Next-Generation Optomagnetic Devices

Abstract

The development and integration of Single-Molecule Magnets (SMMs) into molecular electronic devices continue to be an exciting challenge. In such potential devices, heat generation due to the electric current is a critical issue that has to be considered upon device fabrication. To read out accurately the temperature at the submicrometer spatial range, new multifunctional SMMs need to be developed. Herein, we present the first self-calibrated molecular thermometer with SMM properties, which provides an elegant avenue to address these issues. The employment of 2,2′-bipyrimidine and 1,1,1-trifluoroacetylacetonate ligands results in a dinuclear compound, [Dy₂(bpm)(tfaa)₆], which exhibits slow relaxation of the magnetization along with remarkable photoluminescent properties. This combination allows the gaining of fundamental insight in the electronic properties of the compound and investigation of optomagnetic cross-effects (Zeeman effect). Importantly, spectral variations stemming from two distinct thermal-dependent mechanisms taking place at the molecular level are used to perform luminescence thermometry over the 5–398 K temperature range. Overall, these properties make the proposed system a unique molecular luminescent thermometer bearing SMM properties, which preserves its temperature self-monitoring capability even under applied magnetic fields.

Short abstract

A Dy^III dinuclear complex with single-molecule magnet behavior can act as a self-calibrated luminescent thermometer, providing information about its temperature under applied magnetic fields.

Introduction

The realization of atomic and nanoscale electronic devices remains a formidable technological challenge. The ever-growing need for faster and lower-power electronics as well as higher density data storage continues to stimulate the synthesis and study of new materials. To that end, molecular nanomagnets termed Single-Molecule Magnets (SMMs) are anticipated to revolutionize spintronic applications as their magnetic properties are intrinsic to the molecule, allowing for an unprecedented level of device miniaturization.¹⁻⁶ The recent development of lanthanide (Ln^III)-based SMMs with record-breaking operating temperatures, reaching and surpassing that of liquid nitrogen, supports their potential for commercialization.^7,8 Furthermore, promising achievements in the fabrication of molecular spin valves and transistors testify to the viability of SMMs as ideal materials for the nanofabrication of next-generation devices.³

With that said, there are many exciting challenges to overcome such as addressability (i.e., readout). Often, small electrical fields have been envisioned as a method of choice for the addressability of nanoscale devices.³ In that regard, when an electric current is conducted through a material, it generates heat.⁹ Understanding heat distribution in an electronic device is critical for its efficient engineering and for preventing catastrophic failure. Heat generation on larger circuit boards is now well-understood; however, at the nanoscale, the relationship between heat and electricity remains unanswered due to lack of appropriate thermometers capable of thermal monitoring without perturbing the system. Unfortunately, temperature measurement at the submicrometer spatial range is not possible with conventional contact thermometers.¹⁰ A way to overcome this impasse is building microdevices with materials capable of also acting as in situ thermometers having submicrometric spatial resolution. Herein, the use of self-calibrated thermometers (i.e., not requiring an external reference system) relying on ratiometric approaches is essential to avoid any influence stemming from fluctuations of absolute signal intensity (e.g., due to concentration and excitation power variability). It is thus clear that the combination of luminescence thermometry and SMM properties in the very same compound will not only open a new dimension in understanding the fundamentals of heat generation in devices but also enable in operando temperature monitoring of future SMM-based devices.

The concept of luminescence thermometry has been widely applied in Ln^III-doped inorganic materials¹⁰⁻¹⁶ and metal–organic frameworks (MOFs).¹⁷⁻¹⁹ Recently, molecular Ln^III compounds acting as luminescent thermometers have also attracted much interest.²⁰⁻²⁹ In this regard, SMM-based luminescence thermometry is yet to be reported. Herein, we present a unique dual-functional {Dy₂} complex bearing SMM properties while simultaneously being a molecular luminescent thermometer. The temperature readout was achieved over the 5.4–398 K range exploiting the thermally promoted electron population redistribution within Stark sublevels and energy transfer between the metal center and the ligand scaffold. Importantly, this temperature range encompasses the superparamagnetic SMM range (<12 K) to the application range of electronic devices (up to 398 K) with a high relative thermal sensitivity. The retaining of the luminescent thermometer behavior by the compound under applied magnetic fields paves the way toward optomagnetic studies on future innovative devices.

Results and Discussion

Crystal Structure

To couple photoluminescence (PL) with SMM properties, we have combined Dy^III ions with efficient light harvesting β-diketonate (1,1,1-trifluoroacetylacetonate (tfaa^–)) and 2,2′-bipyrimidine (bpm) as chelating and bridging ligands to promote the formation of a {Dy₂} molecule. The complex was isolated in excellent yield as colorless air-stable crystals. The molecular structure of the dinuclear centrosymmetric [Dy₂(bpm)(tfaa)₆] (1) complex is composed of two Dy^III ions bridged by a neutral bpm ligand (Figure 1, Table S1 for structural information). Three bidentate tfaa^– ligands complete the coordination environment of each metal center. The octa-coordinate Dy^III ions adopt a distorted square antiprismatic (SAP) configuration, similarly to several well-studied mononuclear Dy^III β-diketonate complexes.^30,31 More specifically, four oxygen atoms from the tfaa^– ligands form one square plane (O8, O10, O18, and O20) while the other plane is formed by two tfaa^– oxygen and two bpm nitrogen atoms (O13, O15, N1, N5). These planes are nearly parallel to each other (1.68°) and separated by a distance of 2.58 Å. The skew angle Φ of 45.61° for 1 deviates slightly from the ideal angle of 45° for a SAP polyhedron with maximum D_4d symmetry. The intramolecular Dy···Dy distance within the molecule of 6.7 Å is well within the range of other neutral bpm bridged {Dy₂} complexes.³²⁻³⁵ Inspection of the packing arrangement reveals the closest Dy···Dy intermolecular distance of 7.89 Å. To provide a magnetostructural correlation, ab initio calculations at the CASSCF/SO-RASSI level of theory were performed on 1 (Tables S2 and S3). Calculations revealed that for both Dy^III ions the principal magnetic axes of the ground Kramers doublet (KD) are oriented at an angle of 77° with respect to the plane of the bpm ligand. Thus, the tfaa^– O-donor atoms control the crystal field of the Dy^III ions over the bridging bpm N-donor atoms (Figure S1).

Figure 1.

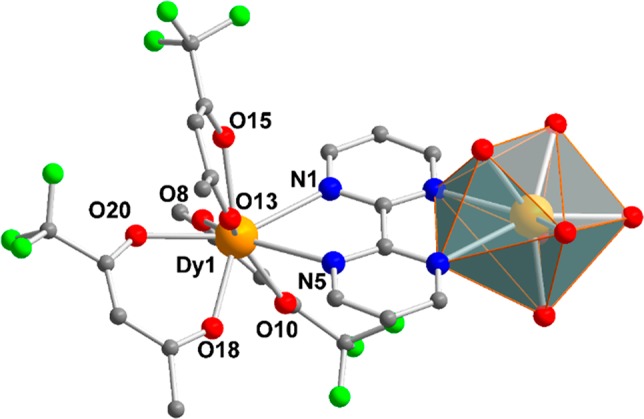
Partially labeled molecular structure of the centrosymmetric [Dy₂(bpm)(tfaa)₆] complex (1). The distorted square antiprismatic configuration is highlighted as a gray coordination polyhedron. Disordered groups and hydrogen atoms are omitted for clarity. Color code: Dy, orange; C, gray; O, red; N, blue; F, lime green.

Magnetic Properties—Slow Relaxation Dynamics

With the aim of probing the magnetic properties of 1, direct current (dc) magnetic susceptibility measurements were performed to learn about its static behavior. Under an applied field of 1000 Oe at room temperature, the χT value (χ is the molar magnetic susceptibility and T the temperature) of 27.42 cm³ K mol^–1 is close to the predicted value of 28.34 cm³ K mol^–1 for two noninteracting Dy^III ions (⁶H_15/2, S = 5/2, L = 5, g = 4/3) (Figure S2a). The downturn of the χT product at low temperatures (T ≤ 20 K) can be attributed to a combination of thermal depopulation, spin–orbit contribution, and weak antiferromagnetic coupling between the metal ions.

The intramolecular exchange interaction was estimated using the Lines model via ab initio calculations, which yielded a small exchange coupling constant of J = −0.046 cm^–1 indicative of the weak antiferromagnetic coupling between the metal ions. Hence, any SMM behavior, should it arise, will originate from “single-ion” behavior. This is not surprising given the core nature of the 4f orbitals and the significant separation (6.7 Å) between the metal centers. At low temperatures (below 7 K), the field dependence of the magnetization was also probed up to 7 T, reaching saturation at 10.5 μ_B at 7 T and 1.8 K (Figure S2b). The splitting of the m_j sublevels determined through the ab initio calculations suggests that 1 may exhibit SMM behavior. To validate this, the slow magnetic relaxation dynamics were probed with alternating current (ac) magnetic susceptibility measurements within the range 0.1–1500 Hz. In the absence of the applied dc field, a single frequency-dependent signal is observed in the ac data (Figure 2a). The χ″ plot reveals frequency-dependent shifting, indicative of slow relaxation of the magnetization from 12 to 6 K, below which deviation from the Arrhenius law is observed due to quantum tunneling of the magnetization (QTM). The low-symmetry coordination environment of the Dy^III ions introduces small transverse components to the g-tensor of the ground KD (g_x = 0.008, g_y = 0.026, g_z = 19.281, see Table S2), which in turn promotes QTM. The decomposition of the SO-RASSI wave function showed strong mixing between states that is also the result of the aforementioned low symmetry (Table S3). The transition probabilities of the calculated energy barrier to spin-reversal of 1 (Figure S3) for direct vertical transitions and Orbach processes are more significant than the value of the matrix element of the ground KD. However, this value (0.57 × 10^–2 μ_B) is 2 orders of magnitude larger than that obtained for Dy^III-based SMMs, in which the ground-state QTM is fully quenched due to the highly axial (g_x = g_y = 0.0, g_z ≈ 20.0) g-tensor of the ground state.^36,37 Unfortunately, given the weak intramolecular exchange parameter in 1, the ground-state QTM cannot be suppressed.

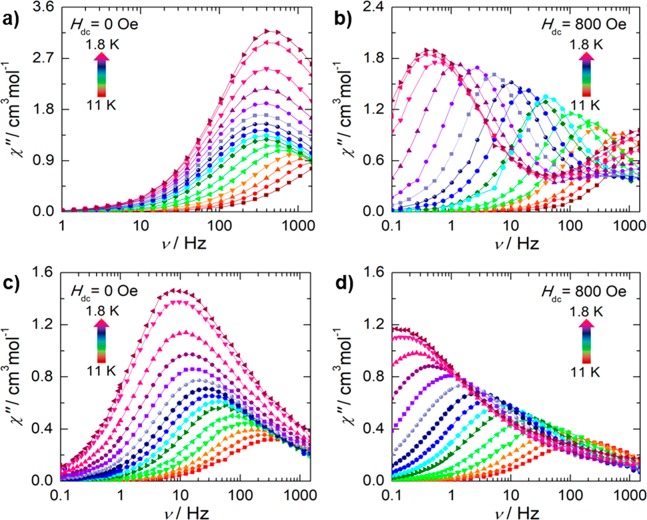
Figure 2.

Frequency dependence of the out-of-phase (χ″) magnetic susceptibility for 1 in the absence of an applied static field [H_dc = 0 Oe: (a) solid-state; (c) solution] and under an applied 800 Oe static field [(b) solid state; (d) solution] as a function of temperature.

To probe the mechanisms to spin-reversal, we examined the field dependence on the relaxation dynamics of 1 (Figure S4). The field-dependent χ″ revealed two frequency-dependent peaks, respectively dominant in the low-frequency (LF; 0.1–20 Hz) and in the high-frequency (HF; 20–1500 Hz) regimes. The relaxation times (τ) obtained from the generalized Debye model³⁸ were subsequently fitted (eq 1, Figures S5 and S6) including both the field-dependent direct and tunneling mechanisms, which accurately reproduce both the LF and HF behavior individually.

1

The direct parameters for the LF and HF processes are relatively small (2.586 × 10^–14 and 2.070 × 10^–8 s^–1 Oe^–4 K^–1), indicating negligible contributions from the direct pathway even upon application of higher fields. The B₁ and B₂ terms reflect the degree of mixing between the m_j levels and are indicative of the magnitude of the QTM process (for summary of parameters, see Table S4).³⁹ The fitting of τ^–1 versus H dependence of the LF process reveals that application of a static field above 1400 Oe results in the direct process being the dominant pathway as indicated by the decrease of the obtained relaxation time upon increasing fields.⁴⁰ This coincides with the suppression of the HF peak with increasing static field strength. Therefore, to ensure negligible contributions from the field-dependent components (QTM, direct) and to prevent the use of excessive fields, the ac susceptibility was collected at 800 Oe where the effects of both pathways are minimized (Figure S7).

To elucidate the contributions of the various relaxation pathways, the temperature-dependent relaxation times in both the absence and presence of an applied field (0 and 800 Oe) were determined by fitting the out-of-phase susceptibility with the generalized Debye model.²¹ Due to the rapid spin-reversal through the ground-state KD, minimal magnetization reversal through thermally activated KDs is expected. Thus, the τ^–1 versus T plot can be fitted considering only Raman and QTM processes (eq 2, Figure S8e).

2

This fit reproduces the data successfully, revealing best fit parameters of C = 0.0132 s^–1, n = 6.53, and τ_QTM^–1 = 3.65 × 10^–4 s. In the absence of an applied field, the QTM rate is 3 orders of magnitude faster than what was observed when a static field was applied (vide infra). When such an efficient relaxation process is operable, there is minimal contribution from the thermally activated pathways (two phonon Orbach and thermally assisted QTM). Attempts to incorporate the field-dependent τ data obtained from the fit parameters presented in Table S5 into eqs 2 and 3 did not provide physically meaningful parameters presumably due to overparametrization. Therefore, the tunneling component was defined as the rate constant of QTM (τ_QTM^–1). Additionally, the Raman exponent (n = 6.53) is smaller than expected for a Kramers ion (n = 9);⁴¹ however, it does fall within the range for Raman processes with optical acoustic phonons (n = 1–6).^42,43

Comparatively, with the application of a static field of 800 Oe (Figure 2b,d), the crystal field microstates are shifted out of resonance with one another, leading to a thermally activated relaxation regime. This has been accounted for by the inclusion of an Orbach term in the model for the relaxation rate (eq 3, Figure S8f).

3

Once again, the fit to eq 3 reproduces the data successfully, yielding the best fit parameters found in Table S5. By application of the static field, relaxation through the ground state (QTM) is minimized, allowing for the observation of a modest effective energy barrier (U_eff) of 33 K. The largely linear regime of the temperature-dependent relaxation times (Figure S8e,f) implies that the dominant pathway is Raman. Under an applied field, a Raman exponent of n = 5.35 is achieved, marginally smaller than the best fit parameters obtained in the absence of a field (n = 6.53). Attempts to restrain the exponent to n = 6.53 failed to reproduce the data well. The difference may be a result of field-induced mixing of excited crystal field states (vide supra).⁴⁰

To better understand the crystal lattice effects on the slow relaxation dynamics of 1, and to mitigate any contribution from intermolecular interactions to the magnetic inversion pathways, solution-state measurements were performed in a frozen matrix of CH₂Cl₂ (Figure 2c,d and Figure S9). Remarkably, a significant enhancement of the slow relaxation behavior of 1 at 0 Oe static dc field upon dilution of the crystal lattice was observed, particularly in the lower temperature regime (below 6 K), where the relaxation times are longer than those collected in the absence of applied field in the solid state (Table S5). This phenomenon is expected due to decreased intermolecular interactions, which lead to the observation of reduced phonon-assisted spin-reversal of the magnetization. This results in a tunneling rate, which is 2 orders of magnitude slower than in the solid state, further supporting that QTM is rendered less efficient when 1 is embedded in a frozen solvent matrix. This allows for the observation of a thermally activated regime, not previously observed in the absence of the dc field in the solid state for this system. Nevertheless, a U_eff of 53 K is obtained, demonstrating that overbarrier mechanisms—e.g., Orbach—are likely not the dominant pathway as the U_eff is smaller than the CASSCF/SO-RASSI calculated energy of the first excited state of 1. Likewise, when the frozen solution of 1 was subjected to a static field of 800 Oe, the ac susceptibility showed the near total suppression of the HF process. Under these conditions, the relaxation times are longer (Table S5), thus indicating that the QTM effects are minimized under applied static field.

Interestingly, regardless of the experimental conditions, 1 displayed large relaxation times consistent with Raman relaxation. The solution measurements completed in the absence of and under a 800 Oe dc field revealed Raman exponents significantly smaller (n = 2.39 and 3.50) than those obtained from the solid state (n = 6.53 and 5.35). While smaller than T⁹ dependences are readily observed for SMMs,⁴²⁻⁴⁵ the exceptionally small n-values have been used to describe spin-reversal via a phonon-bottleneck.^46,47 The smaller n-values may also be a consequence of the rate of energy exchange between the spin and the lattice in the frozen matrix compared to the solid and would suggest that the rate in the solution state is much faster. Lastly, an additional explanation for the smaller than expected Raman exponent (n) may be a result of the field-induced mixing of excited states.⁴⁰ This is not overly surprising as the CASSCF/SO-RASSI calculations on 1 clearly demonstrate that the purity of the m_j states is not maintained in the excited states (Table S3).

In sum, these studies reveal that we can effectively promote SMM behavior of 1 in the absence of the dc static field upon dilution of the crystal lattice, indicating a significant contribution of dipolar interactions to the spin-reversal behavior of 1. Frozen solution measurements demonstrate the inherent slow relaxation of the magnetization rather than stemming from dipolar mediated relaxation, confirming the importance of solid-state effects in promoting different spin–lattice relaxation mechanisms over others.⁴⁸

Optical Properties—Luminescence Thermometry

The employment of bpm and tfaa^– ligands not only allows for the observation of SMM behavior but also fosters PL (Figure S10). The emission displayed by 1 upon UV excitation is appealing from both fundamental and application viewpoints. Significant fundamental value arises from the possibility to optically probe the fine structure of the electronic ground state of Dy^III (⁶H_15/2), which in turn determines the magnetic performances of an SMM.⁴⁹ In addition, the sensitivity of the spectral features toward temperature endows compound 1 with thermal sensing capabilities.

The ligand-sensitized PL emission of 1 stems from the favorable relative position of the tfaa^– triplet state (T₁—obtained from the phosphorescence signal of the Gd^III analog (2), Figure S11) and the emitting Dy^III 4F_9/2 level. The energy difference of approximately 2050 cm^–1 ensures an efficient ligand-to-Dy^III energy transfer (ET),^50,51 while limiting—yet not entirely eliminating—back-ET from Dy^III to the ligands, which is of interest for thermal sensing purposes (vide infra). Deconvolution of the visible high-resolution PL spectrum recorded at 14 K reveals the expected eight and seven components for the ⁴F_9/2 → ⁶H_15/2 and ⁴F_9/2 → ⁶H_13/2 transitions—in good agreement with the results from ab initio calculations—along with contributions stemming from the electron population redistribution among ⁴F_9/2 Stark sublevels (Figure S12 and Table S6). Most importantly, the optical properties of 1 can be exploited for luminescence thermometry (Figure 3). Usually, thermal sensing is achieved in a molecule-based system by the interaction between different moieties⁵² or Ln^III ions.^23,53 Instead, in 1, thermometry is enabled by two mechanisms (Figure 3d), each predominant in different temperature ranges: (i) an increased probability of back-ET from Dy^III to the ligands above room temperature (double-band thermometry) and (ii) the thermally induced electron population redistribution between Dy^III 4F_9/2 Stark sublevels at low temperature, down to the cryogenic regime (single-band thermometry).

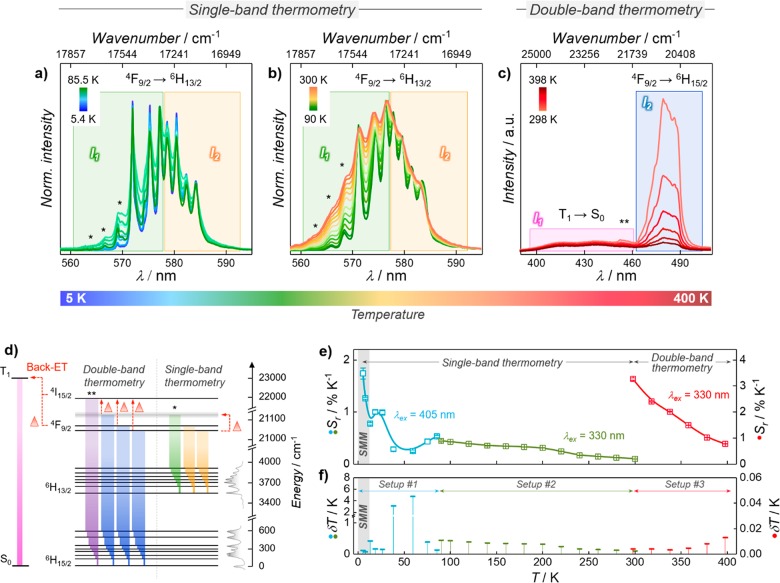
Figure 3.

(a, b) ⁴F_9/2 → ⁶H_13/2 emission band used for single-band thermometry (*, hot-bands). (c) ⁴F_9/2 → ⁶H_15/2 Dy^III emission and T₁ → S₀ ligand emission used for double-band thermometry (**, Dy^III 4F_9/2 → ⁶H_15/2 transition). (d) Partial energy diagram for 1 including transitions relevant for thermometry. Red Δs denote processes favored by a temperature increase. The gray rectangle represents a generic m_j level. (e) Relative thermal sensitivities (S_r). Lines are guides for the eye. (f) Uncertainties (δT) associated with temperature readout. The detailed description of the different setups used to acquire the optical data (here indicated as Setup #1, #2, and #3) is provided in the Methods section.

In this context, the use of a metal–organic system is favorable, allowing the exploitation of the emission from the ligand scaffold along with the signal from the Ln^III ion. As demonstrated for MOFs,⁵⁴ a temperature increase leads to a higher probability of back-ET from the metal center to the ligand. This behavior is also showcased by 1, which ultimately results in temperature-dependent spectral variations that can be readily exploited for thermal sensing. Here, back-ET is enhanced by the increased population of the Dy^III 4I_15/2 level, which is thermally coupled with the ⁴F_9/2 level. Such coupling is usually employed in Dy^III-based luminescent thermometers at high temperature.^12,13,19,22 However, only a weak signal ascribed to the ⁴I_15/2 → ⁶H_15/2 transition was detected (marked with ** in Figure 3a–c), the intensity of which decreases as the temperature increases. This behavior stems from an energy difference between the Dy^III 4I_15/2 level and T₁ of only 1150 cm^–1, a situation that favors, particularly at high temperature, back-ET to tfaa^– over radiative de-excitation to Dy^III lower states. Given that the ⁴I_15/2 → ⁶H_15/2 emission was not directly accessible, we considered the ligand’s phosphorescence (T₁ → S₀) in the wavelength region 385–462 nm. Overall, the effect of a temperature increase is a more marked quenching of the Dy^III emission compared to that of the ligand scaffold. Hence, the ratio between the ligands’ phosphorescence (T₁ → S₀) and the PL signal of Dy^III (⁴F_9/2 → ⁶H_15/2) was used to obtain a ratiometric thermometer (Figure S13) with a relative sensitivity⁵⁵ of S_r = 3.3% K^–1 at room temperature (Figure 3e). This value is in line with similar molecular systems reported in the literature (for a comparison see, for instance, the recent review from Brites et al.⁵⁶).

A major merit of the presented system is its thermal sensing capability below room temperature, endowed by electron population redistribution between the Dy^III 4F_9/2 Stark sublevels (Figure 3a–c). This translates to an intensity increase of the signals stemming from transitions (“hot-bands”—marked with * in Figure 3a–d) located at energies higher than the ⁴F_9/2 → ⁶H_13/2 0–0 line. Therefore, the ratio between the integrated signal at the high-energy (560–577 nm) and low-energy (578–592 nm) side can be exploited as a thermometric parameter (luminescence intensity ratio—LIR) down to 5.4 K (Figure 3c, Figure S13). Between 90 and 300 K, the calculated S_r ranges between 0.10% K^–1 and 0.45% K^–1 (Figure 3e). 1 retains this behavior even when homogeneously dispersed in a polymeric film (Figure S14), which demonstrates a thermometric performance truly inherent of the system at a molecular level. It has to be noted that an increase of the temperature brings a higher phonon density. This translates to more sizable contributions of vibronic components, also expected to contribute to the emission profile of 1 along with electron population redistribution (“hot-bands”). The interplay between the two effects (electron population redistribution and intermixing of vibro-electronic levels) is not trivial and prevents the unambiguous separation of their respective influence on the Dy^III emission profile. Specifically, the nonmonotone trend of the LIR in the 5.4–85.5 K temperature range (Figure S13) could be a consequence of such interplay. Even though this may lead to an ambiguous temperature readout in the range 30–85.5 K, univocal thermal sensing with a relative sensitivity of S_r > 1% K^–1 and an associated uncertainty δT < 1 K (Figure 3e,f) is obtained in the working temperature range of the SMM (below 12 K). Notably, the luminescence thermometric approaches feature a repeatability⁵⁷ around 99% throughout the whole studied temperature range (Figure S15). The described thermometry works well over an extended temperature interval. However, a better performance of the luminescent thermometer in the temperature range of SMM operation is achieved considering the LIR between the integrated intensity of the multiplet corresponding to the 0–1 line (575.1–575.6 nm) and a so-called “hot-band” arising from the thermally induced population of high-energy ⁴F_9/2 Stark sublevels (568.2–570.5 nm, Figure S16). The presence of a double signal in the “hot-band” range could be ascribed to the presence of vibro-electronic contributions.

Overall, this approach (hereafter, the “narrow-bands approach”) yields a more linear LIR trend below 40 K and an S_r as high as 14% K^–1 between 5 and 8 K, among the highest values reported so far for luminescent thermometers.⁵⁶ Also, the associated uncertainty and repeatability remained, respectively, smaller than 0.4 K and higher than 99%. It is important to mention that caution has to be exercised in the latter case. The fine structure observed in the emission multiplets of Dy^III (and Ln^III in general) is influenced by the detection system employed. Specifically, the width of the emission lines is dependent upon the measurement conditions (e.g., slit width). Therefore, Ln^III-based luminescent thermometers relying on the integration of the signals over narrow wavelength ranges are more prone to repeatability and reproducibility issues. In contrast, methods based on the use of wider integration ranges mitigate the fluctuations of the calculated thermal parameters associated with experimental conditions’ variations, averaging them out. They are also more reliable in the case of the application of an external magnetic field, which induces spectral shifts according to the Zeeman effect (vide infra).

Luminescence Thermometry under Applied Magnetic Fields

To further support our envisioned use of SMMs with temperature self-monitoring capabilities in real-world applications, we evaluated the performance of 1 as a luminescent thermometer under externally applied magnetic fields (Figure 4).

Figure 4.

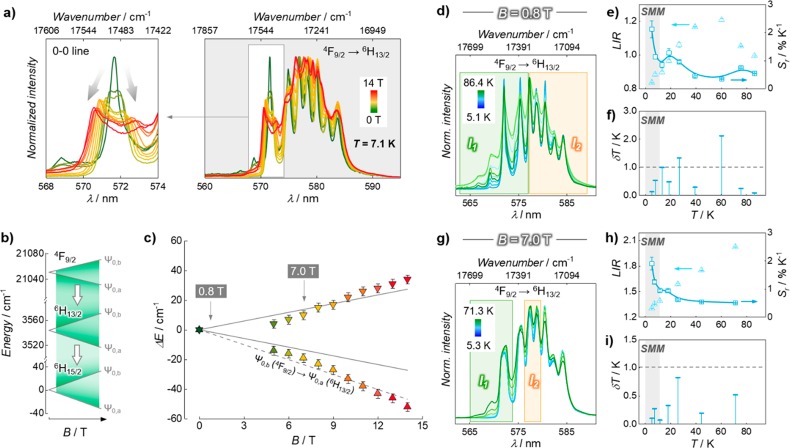
Effect of magnetic fields on the luminescence of 1 and its performance as a luminescent thermometer. (a) Variation of the emission profile of the ⁴F_9/2 → ⁶H_13/2 Dy^III transition under different applied fields. (b) Calculated Zeeman splitting of the lowest m_j levels of ⁴F_9/2, ⁶H_13/2, and ⁶H_15/2 Dy^III electronic levels. (c) Zeeman splitting of the lowest ⁶H_13/2m_j level as obtained from spectroscopy (points) and as estimated from eq 4 (solid lines). The dashed line shows the expected trend considering the Zeeman splitting of the emitting level (⁴F_9/2). Points in part c are color-coded according to the spectra in part a. Luminescence thermometry under applied magnetic fields of (d–f) 0.8 T and (g–i) 7.0 T. (d, g) Emission spectra with the shaded areas indicating the range used for the integration procedure to obtain I₁ and I₂; (e, h) LIR and corresponding S_r values (light and dark cyan points, respectively). (f, i) Uncertainties. Dashed lines in parts f and i mark the δT = 1.0 K threshold.

We first observed the influence that externally applied magnetic fields have on the emission arising from the ⁴F_9/2 → ⁶H_13/2 transition (Figure 4a–c, see Figure S17 for the case of ⁴F_9/2 → ⁶H_15/2). Although the Zeeman effect (i.e., magnetically induced splitting of the electronic levels) starts occurring already at weak applied fields, it was experimentally observable only from 4 T, similarly to what was reported for an analogous system.⁵⁸ An increase of the applied field to higher values (up to 14 T) determined a broadening of the profile. Moreover, pronounced splitting of the 0–0 line was observed (zoom-in in Figure 4a). The total Zeeman splitting energy can be calculated from the equation

4

where μ_B is the Bohr magneton (0.467 cm^–1 T^–1), g_L is the Landé factor for the considered ^2S+1L_J electronic level, m_j is the total angular momentum of the Stark sublevel, and B is the applied magnetic field.⁵⁹ For the lower-lying levels of ⁴F_9/2, ⁶H_13/2, and ⁶H_15/2, m_j and g_L are, respectively, 9/2 and 4/3, 13/2 and 9/7, and 15/2 and 4/3.⁵⁸ The use of these values allowed a calculation of the opening of the Zeeman levels as shown in Figure 4b. The Zeeman splitting for the level ⁶H_13/2 was experimentally evaluated from the position of the split 0′–0 line. The position of the maxima (experimental points in Figure 4c) follows the theoretical trend (solid gray lines) obtained from eq 4. Small deviations could be rationalized taking into account the splitting of the emitting level (⁴F_9/2, dashed line).

With this knowledge in hand, we tested the thermometric capability of 1 under two magnetic fields (0.8 and 7 T) to probe any difference that might arise at different applied dc fields and the overall performance of the system (Figure 4d,g). Due to the negligible Zeeman effect induced by the 0.8 T field, we could perform luminescence thermometry using the same single-band approach presented above (Figure 3). Unsurprisingly, the relative sensitivity and associated uncertainty are comparable to those found in the absence of an applied field (Figure 4e,f). The “narrow-band approach” was also attempted, but large fluctuations of the LIR values were obtained. This is likely due to slight variations of the applied field and/or temperature during the measurements, which result in small changes of the spectral profile but have a great impact in the case of small integration ranges. It is also noteworthy that, envisioning the exploitation of the magnetic behavior of the system concomitantly with the use of the luminescence properties for sensing purposes, magnetically induced variations of the energy state population could result in changes of the spectral profile. Depending on the time scale of both magnetic relaxation phenomena and probing of the luminescent signal, the interferences might be relevant. Hence, although the investigated system seems insensitive to these effects under an applied static field of 0.8 T, this fine interplay has to be kept in mind for future studies and applications.

When a stronger field (7 T) was applied, the so-far-discussed single-band thermometric approach did not yield equally satisfying results (Figure S18). This can be rationalized by observing how the spectral profile is modified by the magnetic field, due to the splitting of the m_j states. Such a spectral variation imposes the selection of more suitable wavelength integration ranges, i.e., 565–574 nm (I₁) and 576.5–580 nm (I₂). From the obtained LIR (I₁/I₂), a sensitivity above 1.5% K^–1 and an uncertainty well below 1 K were calculated in the range of operation of the SMM behavior (Figure 4h,i). The choice of the integration interval I₁ stems from the appearance of hot-bands at those wavelengths upon increasing the temperature (Figure 4g). Instead, the selection of the integration range I₂ was more arbitrary and was performed with the pragmatic aim of maximizing the performance of the luminescent thermometer. Although the use of a deconvolution procedure often returns higher sensitivities,⁵⁷ the use of fixed integration ranges is more straightforward and desirable in foreseeable everyday applications. This is particularly true in situations like the one under study, where the deconvolution of the signal over a broad range is made challenging by the presence of competing effects (thermal population of electronic levels, Zeeman splitting, vibronic contributions).

It is important to note that the dynamic magnetic properties of 1 were probed at magnetic fields (up to 3000 Oe) well below the lowest value tested for luminescent thermometry (0.8 T = 8000 Oe). Therefore, the observation that even under these conditions it is still possible to obtain good relative thermal sensitivity (S_r > 1% K^–1) and temperature uncertainty (δT < 0.5 K) represents an invaluable feature of the system.

Conclusions

We reported a dinuclear Dy^III complex [Dy₂(bpm)(tfaa)₆] simultaneously featuring magnetic and temperature-dependent photoluminescent properties. This system constitutes an example how the merge of magnetism and optics contributes to the gaining of fundamental knowledge at the molecular level (optomagnetic correlation of Ln^III Stark sublevels and investigation of the Zeeman effect). On a practical side, we demonstrated the successful alliance of cutting-edge magnetic features (slow relaxation of the magnetization) with advanced optical approaches (self-calibrated luminescence thermometry). Indeed, we harnessed the luminescence of the complex to probe temperature at the scale of a single molecule over a broad temperature range spanning from approximately 5 to 398 K. We confirmed the retained operativity of the luminescent thermometer simultaneously under applied magnetic fields and in the temperature range where 1 displays SMM behavior. This observation opens exciting avenues for the foreseeable implementation in electromagnetic devices of SMMs with built-in luminescence thermometry capabilities. In fact, the use of these molecules would endow such potential devices with unrivalled properties in terms of data storage, SMM, and submicrometer temperature monitoring, luminescence thermometry, both features of exceptional benefit in miniaturized electromagnetic devices.

Methods

Chemicals

All chemicals were purchased from Alfa Aesar, STREM Chemicals, Ark Pharm, and Sigma-Aldrich and were used as received without further purification.

No unexpected or unusually high safety hazards were encountered during the below-described experimental procedures.

Synthesis of [Dy₂(bpm)(tfaa)₆] (1) and [Gd₂(bpm)(tfaa)₆] (2)

The ligand 2,2′-bipyrimidine (bpm) was prepared as per the established synthetic method described elsewhere,⁶⁰ while the complexes were synthesized following a procedure previously reported.⁶¹ A saturated ammonia solution (1.2 mL, 1.62 mmol) was added to a stirring solution of 1,1,1-trifluoroacetylacetone (197 μL, 1.62 mmol) in 5 mL of ethanol. The resulting mixture was allowed to stir for 15 min after which a 5 mL ethanol solution of 2,2′-bipyrimidine (42.7 mg, 0.27 mmol) followed by DyCl₃·6H₂O (99.9%, 204 mg, 0.54 mmol) was swiftly added. The resulting mixture was allowed to stir for 1 h after which the solution was filtered and allowed to evaporate in open air. The resulting solid was washed with a small amount of chloroform, and the crude product was suspended in 15 mL of dichloromethane and stirred for 30 min. The resulting solution was allowed to evaporate slowly to yield 1 as clear, colorless crystals (yield ∼79%). Elemental Anal. Calcd: C, 32.56%; H, 2.16%; N, 4%. Found: C, 32.18%; H, 1.98%; N, 3.7%. IR (ATR cm^–1, 1): 554s, 605w, 663m, 690w, 723s, 757s, 783s, 831w, 852m, 946w, 1003w, 1018w, 1073w, 1130vs, 1185s, 1219s, 1292vs, 1365w, 1407m, 1478w, 1528m, 1575w, 1620s. DSC (5 °C min^–1): 191 °C (melt.), 299 °C (sublim., onset).

Synthesis of [Gd₂(bpm)(tfaa)₆] (2) was achieved following the same procedure as described for 1, whereas GdCl₃ (99.9%, 142 mg, 0.54 mmol) was used in place of DyCl₃·6H₂O (yield ∼75%). Elemental Anal. Calcd: C, 32.81%; H, 2.17%; N, 4.03%. Found: C, 32.5%; H, 1.92%; N, 3.88%. IR (ATR cm^–1, 2): 555s, 605w, 663m, 690w, 724s, 758s, 784s, 832w, 852m, 946w, 1003w, 1018w, 1077w, 1128vs, 1183s, 1215s, 1288vs, 1363w, 1407m, 1475w, 1530m, 1572w, 1617s. DSC (5 °C min^–1): 189 °C (melt.), 300 °C (sublim., onset).

Characterization Methods

Infrared (IR) spectra were obtained on a Nicolet Nexus 550 FT-IR spectrometer equipped with an ATR using transmission mode in the 4000–600 cm^–1 range. Differential scanning calorimetry (DSC) was performed using a TA Instruments DSC Q2000 calorimeter. Measurements were carried out with a constant heating rate of 5 K min^–1 and a nitrogen flow of 10 L h^–1 using 2–3 mg of sample within a sealed Tzero aluminum pan and lid. The crystals were mounted on a thin glass fiber, affixed using paraffin oil, and cooled to 200.15 K. Data were collected on a Bruker AXS SMART or KAPPA single-crystal diffractometer equipped with a sealed Mo tube source (λ = 0.710 73 Å) and APEX II CCD detector. The data reduction included multiscan absorption correction (SADABS). Raw data collection and processing were performed with the APEX II software package from BRUKER AXS.⁶² The crystal structures were solved and refined using the SHELXTL program suite (v. 2012, A. S. S.; Bruker AXS: Madison, WI, 2005). Direct methods were used yielding all non-hydrogen atoms, which were refined with anisotropic thermal parameters. All hydrogen atom positions were calculated on the basis of the geometry of their respective atoms. Structures for 1 and 2 obtained are isostructural to those reported previously for the Tb analog.^61,63 Crystallographic data are summarized in Table S1.

The magnetic susceptibility measurements were obtained on a Quantum Design SQUID magnetometer MPMS-XL7 operating between 1.8 and 300 K. Direct current (dc) susceptibility measurements were performed on finely ground polycrystalline samples of 1 restrained in a matrix of vacuum grease and wrapped in a polyethylene membrane. The magnetization data were collected at 100 K to check for ferromagnetic impurities. Diamagnetic corrections were applied for the sample holder, and the inherent diamagnetism of the prepared sample was estimated with the use of Pascal’s constants.

The photoluminescence data were obtained on a Fluorolog-3 spectrofluorometer (Horiba FL3-22-iHR320), with double-gratings (1200 g mm^–1, 330 nm blaze) in the excitation monochromator and double-gratings (1200 g mm^–1, 500 nm blaze) in the emission monochromator. A 450 W ozone-free xenon lamp (Ushio) was used as a radiation source. The excitation spectra were corrected in real time according to the lamp intensity and the optical system of the excitation monochromator using a silicon diode as a reference. The emission spectra were recorded using the front face mode at 22.51° and corrected according to the optical system of the emission monochromator and the photomultiplier response (Hamamatsu R928P). The emission decay curves were obtained with a flash 150 W xenon lamp using a time-correlated single photon counting (TCSPC) system. The 14 K PL spectra and emission lifetime data were obtained using a cryostat (Janis Research Company CCS-450), controlled by a Lakeshore 335 temperature controller, and the accessory was coupled to the spectrofluorometer via optical fiber. For liquid-N₂-to-room-temperature thermometry, the measurements were performed on the system described above with an excitation wavelength of 330 nm. The temperature was lowered to 77 K and increased stepwise to 300 K. For each step, upon reaching the target temperature, 10 min passed to guarantee thermal stabilization. This is indicated as Setup #2 in Figure 3d. For high-temperature thermometry, the sample was placed in a platinum crucible inside a Linkam TS1500 stage coupled with a Linkam T95-HT controller. The accessory was coupled via optical fiber to a Fluorolog-3 spectrofluorometer (Horiba FL3-22-iHR320) as reported above. A 450 W ozone-free xenon lamp (Ushio) was used as a radiation source. The temperature was increased from 298 to 398 K with a 20 K step. For each step, upon reaching the target temperature, 10 min were waited to guarantee thermal stabilization. This is indicated as Setup #3 in Figure 3d. The measurements at the cryogenic range were performed on a homemade setup. A powder of the sample was placed in a silicon wafer coated with aluminum and mounted in an Oxford helium magneto-optical cryostat equipped with a three-axis Attocube stepper nanopositioner to control the sample position. The samples were excited using a 405 nm laser (PicoQuant LDH-D-D-405) focused with a 50× objective, and the detection was performed with a 0.5 m spectrometer (Shamrock SR500) coupled with a CCD detector. These spectra were obtained at different temperatures under a magnetic field of variable intensity from no field to 14 T. This is indicated as Setup #1 in Figure 3d.

The luminescence intensity ratio (LIR) for the explored thermometric approaches was obtained as

5

where the following applies:

• In the single-band thermometry, I₁ and I₂ are, respectively, the integrated signal at the high-energy side (560–577 nm) and low-energy side (578–592 nm) of the ⁴F_9/2 → ⁶H_13/2 Dy^III emission.

• In the double-band thermometry, I₁ and I₂ are, respectively, the integrated signal of the ligand’s phosphorescence (T₁ → S₀) and ⁴F_9/2 → ⁶H_13/2 Dy^III emission.

• In the thermometric approach exploiting narrower wavelength ranges (narrow-bands approach), I₁ and I₂ are, respectively, the integrated signal between 568.2 and 570.5 nm and 575.1 and 575.6 nm of the ⁴F_9/2 → ⁶H_13/2 Dy^III emission.

• In the thermometric approach used under an applied magnetic field of 7 T, I₁ and I₂ are, respectively, the integrated signal between 565 and 574 nm and 576.5 and 580 nm of the ⁴F_9/2 → ⁶H_13/2 Dy^III emission.

The relative thermal sensitivity (S_r) of the different approaches proposed in this paper was evaluated using the expression⁵⁵

6

The uncertainty on the temperature was calculated as

7

where the error on the thermometric parameter LIR was obtained through standard error propagation—considering the error associated with each integrated area as the standard deviation obtained from the elaboration of the data from three independent measurements.

The repeatability was calculated as⁵⁷

8

where LIR_mean is the mean value of the thermometric parameter as obtained from the calibration curve, and LIR_i is the value of the thermometric parameter obtained for each considered measurement.

The geometry of 1 was obtained from the crystal structure. Prior to ab initio calculations, the positions of hydrogen atoms were optimized at the DFT level of theory while the positions of heavier atoms were fixed to their respective crystal structure coordinates. Moreover, Dy^III ions were substituted for Y^III ions to avoid convergence problems. The pure GGA PBE functional in conjunction with the def2-TZVP basis was used in the DFT calculation.^64,65 The core electrons of Y^III ions were treated with an effective core potential,⁶⁶ and the resolution of identity approximation was used to speed up the calculation.^67,68 The DFT calculation was performed using the Turbomole V7.1 quantum chemistry program.⁶⁹

The multireference ab initio calculations were calculated by MOLCAS 8.0 and 8.2 ab initio software packages.⁷⁰ The standard CASSCF/SO-RASSI methodology was employed to obtain the spin–orbit states for each Dy^III ion separately while the other one was replaced with the Lu^III ion. In all ab initio calculations, the following basis sets were used: the ANO-RCC-VTZP basis set for the Dy^III ion and the ANO-RCC-VDZP basis set for all other atoms (H, C, N, O, F, Lu).⁷¹⁻⁷³ The scalar relativistic effects were treated employing the exact two component (X2C) transformation.⁷⁴⁻⁷⁶ The Cholesky decomposition was used for two electron integrals with the threshold value of 10^–8. In the state-averaged CASSCF^77,78 calculations, all 21 sextet, 224 quartet, and 490 doublet states, arising from the complete active space of 9 electrons and seven 4f orbitals, were included in orbital optimization. Of all these spin-free states, 21 spin sextets, 128 spin quartets, and 130 spin doublets were then mixed by spin–orbit coupling using the SO-RASSI procedure.⁷⁹ The local magnetic properties (g-tensors, transition magnetic moments, and orientation of magnetic axis) were then extracted from the SO-RASSI wave functions using the SINGLE_ANISO routine.⁸⁰ The intramolecular exchange interaction between the Dy^III ions was modeled using the Lines model and POLY_ANISO routine.⁸¹⁻⁸³ The exchange parameter was obtained by fitting the calculated susceptibility and magnetization to the experimental data by scanning the exchange parameter with increments of 0.001 cm^–1 and including only the ground Kramers doublets of both Dy centers into the exchange interaction. During the fitting procedure the dipolar interaction between the Dy^III ions was calculated as implemented in the POLY_ANISO routine.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.9b00288.

• Summary of crystallographic data and additional magnetic and optical characterization (PDF)

Author Present Address

^⊥ D.A.G.: Department of Chemistry and Biomolecular Sciences, University of Ottawa, Ottawa, Ontario K1N 6N5, Canada.

Author Contributions

^# D.E. and R.M. contributed equally. E.H., F.A.S., and M.M. conceived and supervised the work. D.E., R.M., E.H., and M.M. prepared the manuscript. D.E. and A.P. synthesized the compounds. D.E., K.L.M.H., and M.M. performed magnetic measurements and analyzed the data. B.G. performed single-crystal X-ray diffraction measurements. J.O.M. performed theoretical calculations. D.A.G. and R.M. performed spectroscopic measurements and analyzed the data. F.I. and O.D.D.C.J. provided the infrastructure for thermometry measurements below 80 K, helped with the optimization of the optical system, and provided support during the measurements. All authors have given approval to the final version of the manuscript.

M.M., E.H., D.E., R.M., K.L.M.H., A.P., and B.G. gratefully acknowledge the financial support provided by the University of Ottawa, the Canadian Foundation for Innovation (CFI), and the Natural Sciences and Engineering Research Council of Canada (NSERC). J.O.M. gratefully acknowledges the Academy of Finland (Projects 315829, 320015, and 285855). F.A.S., D.A.G., F.I., and O.D.D.C.J. gratefully acknowledge the São Paulo Research Foundation FAPESP (Projects 2013/22127-2, INOMAT: 2014/50906-9, 2012/11382-9, and 2016/16365-6), the Brazilian National Research Council CNPq (Project 305769/2015-4), and CAPES.

The authors declare no competing financial interest.

Notes

Crystallographic data for compounds 1 (CCDC 1859276) and 2 (CCDC 1859277) can be obtained from the Cambridge Crystallographic Data Centre (https://www.ccdc.cam.ac.uk) upon request.