A convolutional autoencoder approach for mining features in cellular electron cryo-tomograms and weakly supervised coarse segmentation

Abstract

Cellular electron cryo-tomography enables the 3D visualization of cellular organization in the near-native state and at submolecular resolution. However, the contents of cellular tomograms are often complex, making it difficult to automatically isolate different in situ cellular components. In this paper, we propose a convolutional autoencoder-based unsupervised approach to provide a coarse grouping of 3D small subvolumes extracted from tomograms. We demonstrate that the autoencoder can be used for efficient and coarse characterization of features of macromolecular complexes and surfaces, such as membranes. In addition, the autoencoder can be used to detect non-cellular features related to sample preparation and data collection, such as carbon edges from the grid and tomogram boundaries. The autoencoder is also able to detect patterns that may indicate spatial interactions between cellular components. Furthermore, we demonstrate that our autoencoder can be used for weakly supervised semantic segmentation of cellular components, requiring a very small amount of manual annotation.

1. Introduction

Recent developments in cellular electron cryo-tomography (CECT) have enabled the three-dimensional visualization of cellular organization in the near-native state and at submolecular resolution. Subcellular components can be systematically analyzed at unprecedented levels of detail. This in situ 3D visualization has made possible the discovery of numerous important structural features in both prokaryotic and eukaryotic cells as well as in viruses (Grunewald and Desai, 2003; Bartesaghi et al., 2007; Delgado et al., 2015; Jasnin et al., 2016). As the approach develops, high quality CECT data will continue to yield valuable insights into the structural organization of the cell. In principle, a tomogram of a cell contains structural information of all cellular components within the field of view. However, cellular structures are densely packed within a small volume, which makes it challenging to systemically extract cellular structural information from tomograms. Imaging limitations, such as low signal-to-noise ratio (SNR) and missing wedge effects, further complicate the systematic recovery of such information. Currently, many CECT structural identification, characterization and segmentation tasks are performed by visual inspection and manual annotation, which can be very laborious. Consequently, the labor-intensive nature of these analyses has become a major bottleneck in CECT studies.

Structural separation approaches for macromolecules may be used for facilitating the systematic and automatic characterization of structural or image features. Inside a tomogram, a macromolecule can be extracted and represented as a subtomogram, which is a 3D small subvolume (3D analog of a 2D image patch) of cubic shape. Reference-free subtomogram classification (e.g. Bartesaghi et al., 2008; Xu et al., 2012; Chen and Pfeffer, 2014; Scheres et al., 2009) has been developed for the structural separation of macromolecules. Such approaches are designed for recovering structures of large macromolecular complexes. Nevertheless, the steps for subtomogram alignment or integration over all rigid transformations in those approaches are computationally intensive, and therefore limit the scalability of these approaches. To increase scalability, we and others have developed 3D rotational invariant feature (Xu et al., 2009, 2011; Chen et al., 2012) approaches. Recently, we developed a supervised deep structural feature extraction approach (Min et al., 2017) that can be used for the characterization of structural or image features. Nevertheless, this method employs a supervised approach that requires data annotation for training.

In this paper, we complement existing approaches by developing an unsupervised approach for automatic characterization of tomogram features. Automatic characterization of image features (represented as 3D small subvolumes) is very useful for separating heterogeneous small subvolumes into homogeneous small subvolume sets, which simplifies the structural mining process by separating structures with different shapes or orientations. Although resulting small subvolume sets are not labeled, image feature clues are provided to guide the identification of representative structures. Unknown structures of the same type and orientation are likely to be clustered in the same small subvolume set, which helps the identification of the structure and spatial organization in a systematic fashion.

Specifically, we propose a 3D convolutional autoencoder model for efficient unsupervised encoding of image features (Fig. 1a). A convolutional autoencoder is a type of Convolutional Neural Network (CNN) designed for unsupervised deep learning. The convolutional layers are used for automatic extraction of an image feature hierarchy. The training of the autoencoder encodes image features (represented as 3D small subvolumes) into compressed representations. The encoded image features are then clustered using k-means clustering. a small subvolume set is characterized by the decoded cluster center. With an optional fast preprocessing step of pose normalization, and with GPU acceleration, the separation process is significantly more scalable than the subtomogram classification (e.g. Xu et al., 2012) and pattern mining (Xu et al., 2015a) approaches. As a result, it is particularly suitable for unsupervised structural mining among large amounts of small subvolumes and identifying representative structures with representative orientations. Through testing our approach on experimental cellular cryo-tomograms (Section 3.3), we are able to efficiently encode and cluster tens of thousands of small subvolumes using a single GPU. We identified (1) surface features such as membranes, carbon edges, and tomogram boundaries of certain orientations and (2) large globular features corresponding to macromolecular complexes likely to be ribosomes. Both the surface features and the large globular features were qualitatively validated by embedding these patterns back into the tomograms. Interestingly, we further identified a spatial interaction pattern between cellular components which is difficult to identify through visual inspection of the tomogram. Moreover, we performed a numerical study on simulated data to analyze the accuracy of our autoencoder model on detecting surface features and ribosome structures, and to assess the missing wedge effect (Supplementary Section S3).

Fig. 1.

Conceptual diagrams of (a) Autoencoder for characterization of small subvolumes (Section 2.2). (b) Encoder-decoder network for small subvolume semantic segmentation (Section 2.4).

To reduce the dependence of our convolutional autoencoder model to the variation in orientation and translation of image features, as an optional step, we further adapted a pose normalization approach (Xu et al., 2015a) to normalize the location and orientation of image features. After pose normalization, the image features of similar structure have similar orientation and location. Therefore, unknown structures of similar shape are more likely to be clustered in the same small subvolume set, which assists the characterization of the image features in a less orientation dependent fashion. Our tests on both experimental and simulated tomograms demonstrate the efficacy of the combination of pose normalization and convolutional autoencoder (Fig. 7 and Supplementary Sections S3).

Fig. 7.

Isosurfaces of decoded pose normalized small subvolumes of selected clusters embedded to the COS-7 tomogram 1. Surface features (yellow) and large globular features (red) are annotated in the tomogram. Green arrows indicate horizontal surface regions that were not detected without pose normalization. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Manual segmentation of tomograms is a laborious task. To facilitate structural segmentation, automatic or semi-automatic approaches have been developed for segmenting specific structures. Such approaches use manually designed rules for (1) extraction of image features characterizing the specific ultrastructure and (2) segmentation based on combinations of extracted image features. Often, feature extraction and segmentation rules are specifically designed for particular types of image features or ultrastructures, such as membranes (e.g. Bartesaghi et al., 2005; Martinez-Sanchez et al., 2011, 2013; Collado and Fernandez-Busnadiego, 2017) or actin filaments (e.g. Rigort et al., 2011; Xu et al., 2015b). Only very few generic and unified approaches exist for segmenting various structures (e.g. Chen et al., 2017; Luengo, 2017). Generic and unified approaches come with the advantage of being easily extended to segmenting new types of structures through automatic learning rules, which is often done in a supervised fashion. In recent years, deep learning-based approaches (e.g. Long et al., 2015) have emerged as dominant approaches for supervised generic segmentation in computer vision applications due to their superior performance in the presence of large amounts of training data. Deep learning has also been used for generic segmentation of ultrastructures (Chen et al., 2017) in cellular tomograms. Since supervised segmentation approaches often rely on training data prepared through manual segmentation of images, it is beneficial to develop approaches to reduce the amount of supervision (in terms of manual annotation) to facilitate the automation of training data preparation.

To complement existing approaches through reducing the amount of supervision, in this paper, we demonstrate that the cluster groups generated from our autoencoder can be used to train a 3D CNN model for semantic segmentation in a weakly supervised fashion. In particular, after simple manual selection and grouping the clusters, the cluster groups are used to train dense classifiers for the voxel-level classification and to semantically segment tomograms. In the whole segmentation pipeline, the amount of manual voxel-wise segmentation of 3D images can be dramatically reduced. The only step that requires manual intervention is the selection and grouping of image feature clusters among a number (such as 100) of candidate clusters, based on the decoded cluster centers. Therefore, the whole pipeline is weakly supervised and requires only a small amount of human intervention. Our preliminary tests and qualitative assessments on experimental tomograms demonstrate the efficacy of our approach (Section 3.3).

Our contributions are summarized as follows:

1. We designed a deep autoencoder network for unsupervised clustering of CECT small subvolumes to provide a fast and coarse mining and selection of CECT small subvolumes without any annotated training data. Specifically, we adapted 2D autoencoder networks to 3D networks for CECT data. Also, we combined k-means clustering algorithms with autoencoder networks to provide clustering of CECT small subvolumes into sets with homogeneous image features.

2. To merge small subvolumes of similar image features but different orientation together, we adopted a pose normalization approach for normalizing the location and orientation of structures in a small subvolume. As a result, small subvolumes of similar image features with different orientations are more likely to be grouped into the same image feature cluster.

3. We designed an encoder-decoder semantic segmentation network for weakly supervised coarse segmentation of tomograms. This approach can effectively reduce the amount of manual voxel-wise segmentation of simple image features.

2. Methods

2.1. Background

Deep learning is one of the most popular computer vision techniques used today across a broad spectrum of applications (LeCun et al., 2015). Convolutional Neural Networks (CNN) (LeCun et al., 1998), an artificial neural network inspired by the hierarchical organization of animal visual cortex, have achieved high performance and accuracy in computer vision tasks such as image classification (e.g. Alex and Ilya, 2012) and semantic segmentation (e.g. Long et al., 2015). A CNN model is a combination of layers in sequence and each layer consists of a certain number of neurons with receptive fields on the previous layer. In this paper, we employ CNN to encode CECT small subvolumes to low dimensional vectors for clustering. The use of a stack of convolution layers has the advantage of learning the inherent structure of local correlations and hierarchical organization of correlations in images. The details of different types of CNN layers, activation functions, and the optimization techniques are introduced in Supplementary Section S1.

2.2. Autoencoder3D network for unsupervised image feature characterization

A typical autoencoder (Goodfellow et al., 2016) consists of two main components, the encoder ø: X → F, which encodes the input X to a representation F, usually in the form of low dimensional vector, and the decoder$\psi :F\to \widehat{X}$, which decodes the F to a reconstruction of X,$\widehat{X}$. The autoencoder network is trained to minimize the difference between input X and reconstruction output$\widehat{X}$. Normally, the goal of the autoencoder network is to reduce the dimension of input and to characterize image features with high precision.

We propose a 3D convolutional autoencoder model, denoted as Autoencoder3D. Our model consists of four types of layers: convolution, pooling, fully connected, and softmax (Supplementary Section S1 for details). The body of standard CNN models for computer vision tasks is designed to have alternating convolutional layers and pooling layers. We adopted such design into our Encoder3D network. Following standard convolutional autoencoder models, we use fully connected layers to encode the features extracted from previous layer into a 32-dimensional vector. Since the Encoder3D network encodes an input small subvolume to a 32-dimensional vector and the Decoder3D network decodes the encoded vector to reconstruct the input image, the architecture of Decoder3D network is a mirror reversal of the Encoder3D network, with up-sampling layers replacing max-pooling layers. The input of Autoencoder3D network is a 3D small subvolume extracted from a tomogram, represented as a 3D array A of ${ℝ}^{m\times n\times p}$. The En-coder3D network encodes the small subvolume A as an encoding vector v of $ℝ$ ³². The Decoder3D network decodes the encoding vector v to a reconstruction $\widehat{A}$ of the same size ${ℝ}^{m\times n\times p}$ .

The architecture of the Autoencoder3D model is shown in Fig. 2a. The Encoder3D part contains two convolutional layers with 3 × 3 × 3 3D filters, two 2 × 2 × 2 3D max pooling layers, and one fully connected output layer outputting vector v of length 32. We use L1 norm regularization to encourage sparsity in the encoded features. Previous work (Ng, 2011) shows that sparsity regularization improves autoencoder performance. The Decoder3D part contains one fully connected layer with the same output shape as the input shape of the Encoder3D fully connected output layer, two convolutional layers with 3 × 3 × 3 3D filters, two 2 × 2 × 2 3D upsampling layers, and one convolutional output layer with 3 × 3 × 3 3D filters. All hidden layers and the En-coder3D fully connected output layer are equipped with the rectified linear (ReLU) activation. The Decoder3D convolutional output layer is equipped with a linear activation.

Fig. 2.

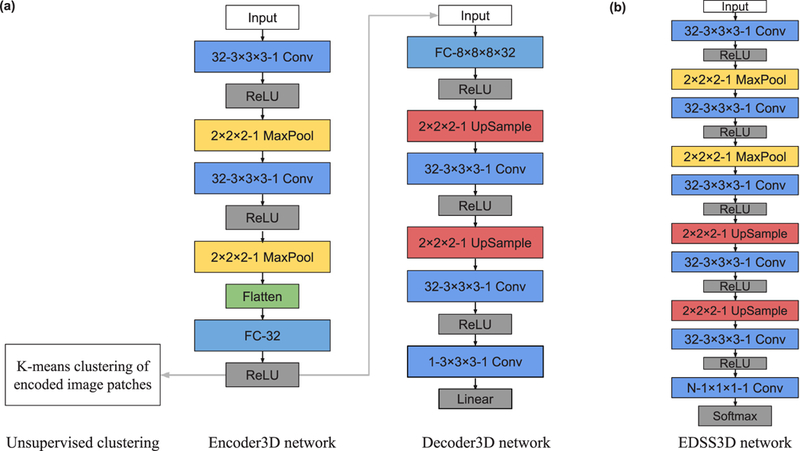
The network architecture of our CNN models. All three networks have multiple layers. Each colored box represents one layer. The type and configuration of each layer are shown inside each box. For example, ‘32–3 × 3 × 3–1 Conv’ denotes a 3D convolutional layer with 32 filters, 3 × 3 × 3 kernel size, and 1 stride. ‘2 × 2 × 2–1 MaxPool or UpSample’ denotes a 3D max pooling or upsampling layer over a 2 × 2 × 2 region with 1 stride, respectively. ‘FC-8 × 8 × 8 × 32’ denotes a fully connected layer with neurons of size 8 × 8 × 8 × 32, where every neuron is connected to every output of the previous layer. ‘Flatten’ denotes a layer that flattens the input. N is the number of classes in the semantic segmentation training set. ‘ReLU’, ‘Linear’, ‘Softmax’ denote different types of activation layers. See Supplementary Section S1 for details of different layers.

Simple CNNs with less number of layers and neurons are faster to train and compute. Increasing the number of layers and neurons may increase the capacity and accuracy of predictions, but can be prone to issues such as over-fitting. Over-fitting occurs when a model fits too close to the training data that cannot perform well for testing data. We have tried different autoencoder networks with a range of layer numbers and neuron numbers. We designed the current CNN networks by balancing the efficiency, validation accuracy, and training speed. The user can directly apply our networks to their CECT small subvolumes data. Our networks were optimized to have high validation accuracy and fast training speed. The networks can be further optimized based on the same guideline.

The autoencoder follows a similar principle as sparse coding (Lee et al., 2007). Studies have shown that a small subvolume can be effectively represented by a linear combination of a small number of basis vectors (Lee et al., 2007). When designing our Autoencoder3D model, we have tried different encoding vector length, from 16, 32, to 128. By visually comparing the decoded images patches with the corresponding input small subvolumes, we observed that, when using encoding vector of length 32, several elements in the encoding became zeros for all small subvolumes. Increasing the encoder vector length further will not change the results much. A 32-dimensional encoding vector was enough for our task. The rationale behind the deep autoencoder is that images can be compressed to a very simple vector, which can be decoded to reconstruct the original image. An element in the encoding vector does not mean to encode only one feature. Since there are millions of parameters in the decoding network, 32 elements in combination can already encode and produce a large number of features.

The Encoder3D network contains two 2 × 2 × 2 3D max pooling layers whereas the Decoder3D network contains two 2 × 2 × 2 3D up-sampling layers. Therefore, to have the subvolume reconstruction output the same size as the input, all three dimensions of the input subvolume must be extracted to be a multiple of 4. For example, after two rounds of 2 × 2 × 2 max pooling, a subvolume of size 40³ will become an array of size 10³. Then, a flattening layer is applied, which will flatten the 10³ array to a one dimensional vector of length 1000. Then a fully connected layer, which can take inputs of arbitrary length, will process the one dimensional vector of length 1000 to be an encoding of length 32. This encoding will be used for clustering. Every neuron in the fully connected layer is connected to all 1000 elements of the input vector. This is why a fully connected layer can take inputs of arbitrary length. We note here the encoding vector length 32 is not related to the size of the input subvolume.

2.3. Unsupervised learning for grouping of small subvolumes

Clustering is a necessary step for collecting relatively homogeneous groups of small subvolumes from heterogeneous inputs. However, due to the high dimensionality of the samples, it is extremely difficult to discriminate two small subvolumes only based on simple distance measures (Min et al., 2017; Aggarwal et al., 2001). Therefore, we propose an unsupervised small subvolume clustering approach based on encoded features of substantially lower dimensions. Using the Auto-encoder3D network, each small subvolume is encoded into a vector of real numbers that represent features of the original small subvolume. K-means clustering is then applied to group similar small subvolumes together based on the encoding.

We note here that after k-means clustering, a simple step of manually selecting interested clusters is needed to further supervise semantic segmentation of new datasets in Section 2.4. So, the decoded cluster centers are plotted to guide the user to select and group clusters of interest. Selected and grouped clusters are used as positive samples in a dataset for training a semantic segmentation model defined in Section 2.4. An example of selecting and semantic segmentation model training is described in 3.3 and 3.4. The segmentation used for training in the training set is obtained by thresholding the decoded 3D images at a certain mask level.

2.4. EDSS3D network for weakly supervised semantic segmentation

In this section, we propose a 3D encoder-decoder semantic segmentation network (EDSS3D) to perform supervised segmentation of new small subvolume data based on previous unsupervised learning results. The design of the model is inspired by Badrinarayanan et al. (2015). The input of EDSS3D network is a 3D small subvolume, represented as a 3D array B of size ${ℝ}^{m\times n\times p}$ , extracted from a testing dataset tomogram. The EDSS3D network outputs L number of 3D arrays $B_l^{\prime }$ of the same size ${ℝ}^{m\times n\times p}$, where L is the number of semantic classes and each voxel in $B_l^{\prime }$ denotes the segmentation probability of this voxel belonging to the lth semantic class.

In particular, the decoded 3D images of selected clusters are used as training data. The architecture of EDSS3D model is shown in Fig. 2b. The architecture consists of five convolutional layers with 3 × 3 × 3 3D filters, two 2 × 2 × 2 3D max pooling layers, two 2 × 2 × 2 3D upsampling layers, and one convolutional 3D output layer with the number of filters equal to the number of segmentation classes. All hidden layers are equipped with ReLU activation layer. The convolutional 3D output layer is equipped with a softmax activation layer.

We adopted the standard CNN model design into our EDSS3D network. Similar to the Autoencoder3D model, our EDSS3D model is an encoder-decoder bottleneck-type model with same-size output as the input for each class. However, the Autoencoder3D model performs image encoding for unsupervised image feature characterization whereas EDSS3D model performs supervised image semantic segmentation. Accordingly, the EDSS3D model is not broken into two parts. Also, for multi-class classification, the EDSS3D has an output softmax activation layer rather than a linear activation layer.

2.5. Optional preprocessing step: pose normalization of small subvolumes

CECT small subvolumes contain image features of different orientations. The similar image feature of different orientations often cannot be clustered together. Previously, we have developed level set based pose normalization for pre-filtering of subtomograms (Xu et al., 2015a). We adapted this method as an optional step for preprocessing small subvolumes by directly normalizing the orientation and location of image features.

Specifically, before the small subvolumes are used to train the Autoencoder3D model, the center of mass and principal direction of each small subvolume are calculated. The principal direction of a small subvolume is computed as the directions of the first two principal components in principal component analysis (Wold et al., 1987). Each small subvolume is translated and rotated according to its center of mass and principal directions. Therefore, the orientation and location of a feature inside a small subvolume are normalized for better clustering. Some voxel values of a rotated and translated small subvolume may be missing due to rotation and translation operation. Those missing values are filled using the corresponding image intensities from the original tomogram.

In a small subvolume, voxels with negative values of high magnitude correspond to regions with high electron density. Before pose normalization, we normalize small subvolume values so that all values are positive and the signal regions have higher values. We note here that the value normalization is only used for calculating the center of mass and the principle component. Rotated and translated small subvolumes will still have negative values of high magnitude corresponding to regions with high electron density. Let $\overrightarrow{r}={[x,y,z]}^{\top }$ denote the locations of voxels in a small subvolume and $f(\overrightarrow{r})$ denote the normalized value at location $\overrightarrow{r}$. First, we calculate a center of mass $\overrightarrow{c}$ of x:

$$\overrightarrow{c}=\frac{{\int }_{\overrightarrow{r}}f(\overrightarrow{r})\overrightarrow{r}}{{\int }_{\overrightarrow{r}}f(\overrightarrow{r})}.$$ (1)

Then, we calculate

$$W={\int }_{\overrightarrow{r}}{[f(\overleftrightarrow{r})]}^2(\overrightarrow{r}-\overrightarrow{c}){(\overrightarrow{r}-\overrightarrow{c})}^{\top }.$$ (2)

We apply the eigen decomposition $W=Q\Lambda Q^T$ of W where Q is an orthogonal matrix of eigenvectors and $\Lambda$ is a diagonal matrix of eigenvalues in descending order by their magnitude. Pose normalization is performed on a small subvolume by first translating the center of mass to the center and then rotating the small subvolume using Q as the rotation matrix. Examples of pose normalization on surface small subvolumes are shown in Fig. 3. After pose normalization, the surface small subvolumes are normalized to be horizontal orientation located in the center.

Fig. 3.

Examples of surface small subvolumes (2D slices) before and after pose normalization. For better visualization, small subvolumes are Gaussian smoothed with δ = 2.0. See Supplementary Section S2 for details of Gaussian smoothing. Isosurface views are plotted below the 2D slices.

Remark: Convolutional neural networks can input image of arbitrary size. Therefore, it is a potential advantage of handling non-cubic small subvolumes. However, if the optional pose normalization preprocessing step is applied, it is preferable for the input small subvolumes to be cubic shape to facilitate rotation operation.

2.6. Implementation details

The training and testing of our CNN models were implemented using Keras (François Chollet, 2015) and Tensorflow (Abadi et al., (2016). Image processing suite EMAN2 was used for reading tomograms (Tang et al., 2007). A variant of our Tomominer library was used for data preparation and image display (Frazier et al., 2017). K-means clustering was performed using the Sklearn toolbox (Pedregosa et al., 2011). Pettersen et al. (2004) and Ramachandran and Varoquaux (2011) were used to generate the embedded tomogram figures. The experiments were performed on a computer equipped with Nvidia GTX 1080 GPU, one Intel Core i5–5300U CPU, and 128 GB memory.

3. Results

3.1. Acquisition of experimental tomograms

To test our implementation, we used two cellular tomograms of COS-7 (Cercopithecus aethiops kidney) cells. Cells were grown on c-flat gold mesh carbon-coated holey carbon grids to a density of 1–2 cells/ grid square. Cells were maintained at 37 °C, 5% CO₂ in Dulbecco’s modified Eagle’s medium supplemented with L-glutamine, nonessential amino acids, and 10% fetal bovine serum. Prior to freezing, BSA-conjugated 10-nm gold fiducial markers were added to grids, which were then blotted manually from the backside for 4 s, and plunged into a liquid ethane/propane mixture cooled to liquid N₂ temperature. Tilt series were collected on a Tecnai TF30 “Polara” electron microscope equipped with a Quantum postcolumn energy filter (Gatan) operated in zero-loss imaging mode with a 20-eV energy-selecting slit. All images were recorded on a postfilter ≈4000 × 4000 K2-summit direct electron detector (Gatan) operated in counting mode with dose fractionation. Tilt series were collected using SerialEM at a defocus of –6 μm. Tilt series covered an angular range of –60° to +50° in increments of 4°. Tomograms were reconstructed in IMOD using weighted back-projection, with a voxel size of 0.355 nm. The tomograms are not collected for the purpose of subtomogram averaging, therefore they are not CTF corrected. They were further binned four times to reduce size. The resulting two tomograms were termed COS-7 tomogram 1 and COS-7 tomogram 2.

3.2. Data preparation and autoencoder training

To collect small subvolumes, we performed a template-free Difference of Gaussian (DoG) particle picking process as described in Pei et al. (2016). The COS-7 tomogram 1 was convolved with a Gaussian Kernel of σ = 2 voxelmissins in radius for smoothing and then with a 3D DoG function with scaling factor of σ = 5 voxels in radius and scaling factor ratio K =1.1 for small subvolume extraction. Potential macromolecules detected as peaks in the DoG map were filtered so that the distance between peaks were at least 10 voxels. 38112 small subvolumes of size 32³ voxels were extracted for autoencoder network training. In principle, one can also use a sliding window to extract small subvolumes. However, a sliding window on a 3D image would produce a substantially larger amount of small subvolumes that would introduce a substantially larger amount of computational burden.

We randomly split the 38112 small subvolumes into a training set of size 34300 and a validation set of size 3812. The Autoencoder3D model was trained using optimizer Adaptive Moment Estimation (Adam) with exponential decay rates β₁= 0.9 and β₂ = 0.99 to minimize the mean squared error loss function (Kingma and Adam, 2014) (see Supplementary Section S1 for details of Adam). After one epoch training, the model was saved only if there was an improvement in validation dataset loss compared to the previous epoch. Adam training was performed with learning rate 0.001 and a batch size of 8 until the validation dataset loss did not improve for 20 consecutive epochs. The learning rate in CNNs defines the “step size” of a gradient update. When the learning rate is too high, such as 1, the output truth over-corrects the model output and overshoots the optima that we are trying to converge to, which will make the CNN training highly unstable. When the learning rate is too low, steps are too small and training will take much longer to converge. To find the optimal learning rate, we started with an initial value of 0.1, and decreased it until the training began to stably converge.

We measured the computation speed of Autoencoder3D network. On average, the training took 0.013 s per small subvolume per epoch for Autoencoder3D. Given the trained Autoencoder3D model, on average, the encoding of a small subvolume took 0.0012 s and the decoding of an encoded small subvolume took 0.0023 s. Therefore, our model can be used to quickly process large amounts of small subvolumes. Computing times and environments of all steps can be found in Supplementary Table S2.

3.3. K-means clustering of encoded features

After training, the Autoencoder3D network was used to encode each small subvolume as a 32-dimensional vector. Then, we performed k-means clustering with k = 100 on the encoded small subvolumes to group similar small subvolumes together. The cluster center of each group, a 32-dimensional vector, was decoded to a 3D small subvolume reconstruction by the Decoder3D network. Fig. 4 shows examples of decoded cluster centers.

Fig. 4.

Four decoded cluster centers obtained from COS-7 tomogram 1. For each cluster center, 2D slices of the decoded 3D images are shown. The slices are 32 images representing 32² voxels, representing a decoded 3D image of size 32³. Cluster 39 and 43 are selected surface feature clusters. Cluster 98 is a selected large globular feature cluster. Cluster 41 is an example of a non-selected cluster that contains small globular image feature. The majority of non-selected clusters look like this small globular image feature.

It is evident that clusters 39 and 43 represent parts of surface fragments seen in different orientations. Cluster 98 represents globular macromolecules with sizes similar to that of established ribosomal macromolecules; as such the characteristic structures contained in this cluster are likely ribosomes (termed ribosome-like structures). A further inspection of ‘large globule’ small subvolumes by template searching and reference-free subtomogram averaging can be found in Supplementary Section S4. The majority of non-selected classes look like ‘small globule’ structure as in cluster 41.

After manually labeling these 100 clusters, we selected 10 clusters of 500 small subvolumes that represented surface features of different orientations and 7 clusters of 308 small subvolumes that represented large globular features. The total 808 small subvolumes of surface and large globular features were used to annotate the COS-7 tomogram 1 (Fig. 5). In Fig. 5, parts of membranes, carbon edge, and tomogram boundary regions are automatically annotated based on our cluster results. Large globular features are annotated across a large region in the tomogram.

Fig. 5.

Isosurfaces of decoded small subvolumes of selected clusters embedded to the COS-7 tomogram 1. Surface features (yellow) and large globular features (red) are annotated in the tomogram. A long carbon edge and a tomogram boundary, annotated in yellow, are indicated by red arrows. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

We also explored the impact of pose normalization on model training and clustering. After the small subvolumes were extracted from the COS-7 tomogram 1, images patches values were normalized by taking the inverse and subtracting the minimum value. Each small subvolume was then pose normalized (Section 2.5) and used for Au-toencoder3D training (Section 3.2). Then, the encoded small subvolumes were clustered using k-means clustering with k = 100. Fig. 6 shows examples of decoded cluster centers of surface features. After pose normalization, surface features of different orientations were normalized to the horizontal orientation, which made it easier to cluster surface features even if of different orientations.

Fig. 6.

Three decoded cluster centers of surface features. Surface features of different orientations were pose normalized to the horizontal orientation. All 12 cluster centers of surface features resulted are of the horizontal orientation as these three clusters.

We selected 12 clusters of 900 small subvolumes that represented surface features of different orientations and 5 clusters of 370 small subvolumes that represented large globular features. The total 1270 small subvolumes of surface and large globular features were used to annotate the COS-7 tomogram 1 (Fig. 7). We note here that after pose normalization, more surface features and large globular structures are selected and annotated. This could be due to the fact that pose normalization improves the clustering ability to group features of different orientations. In Fig. 7, differently oriented surface features are clearly annotated.

3.3.1. Image features that may indicate spatial interaction

Interestingly, we detected small subvolumes that may indicate spatial interactions between cell components. By visual inspection of the location of the spatial interaction patterns, we found clusters 6, 64, and 85 to represent macromolecules that are enriched in membraneproximal regions (Fig. 8). We averaged the original small subvolumes of each of the three clusters. Fig. 8 shows the 2D slices of the averaged small subvolume of the three clusters of such spatial interaction pattern (Fig. 8). We are able to identify a macromolecule in the middle and some spatial interaction (likely to be membrane and macromolecule associations). To better visualize the averaged small subvolumes of this spatial interaction pattern between membrane and macromolecule, the 2D slices of images with Gaussian smoothing of σ = 3 are shown in 8. These clusters present clear evidence of such spatial interaction. The decoded cluster centers of these three clusters are also plotted, which provide additional evidence of spatial interaction enriched in membrane-proximal regions. The Gaussian smoothed averages are very consistent with the decoded cluster centers. Such consistency provides a strong evidence of the fidelity of the decoded cluster centers in representing the small subvolumes of the corresponding clusters. The validity and biological implication of this pattern remain to be further investigated.

Fig. 8.

The 2D slices of average small subvolumes of spatial interaction pattern detected in COS-7 tomogram 1. Gaussian smoothed averages of σ =3 are shown in the middle. The decoded cluster centers are shown on the right.

3.4. Semantic segmentation

3.4.1. Construction of testing dataset from COS-7 tomogram 2

A similar data preparation procedure was carried out on COS-7 tomogram 2. 42,097 small subvolumes of size 32³ voxels were extracted. The small subvolumes were then filtered to reduce the probability of obtaining false-positive results. The 42,097 small subvolumes were encoded by the trained Encoder3D network from Section 3.2. The 42,097 encoded small subvolumes were mapped to its nearest cluster centroid from Section 3.3. Only the 312 small subvolumes mapped to surface feature clusters or large globular feature clusters were kept for semantic segmentation. Encodings mapped to other clusters were filtered out as they were less likely to contain any surface or large globular feature. Such filtering may also be performed through our recently developed 3D sub-volume classification approach (Min et al., 2017).

3.4.2. Construction of training dataset from COS-7 tomogram 1

We used the k-means clustering results as a training dataset for the Encoder-decoder semantic segmentation network (EDSS3D) and then applied the trained EDSS3D network on the testing dataset.

First, the 100 decoded cluster centers were manually labeled with the two most recognizable cellular structures: surface features (membrane, carbon edge, or tomogram boundary) and electron-dense structures with the same general appearance as large globular features (termed ribosome-like structures). These structures were grouped into two classes for training. The surface feature class consisted of 10 clusters with 500 small subvolumes in total. And the large globular feature class consisted of 7 clusters with 308 small subvolumes in total. We added a third class, the background class, to denote the background regions where there was no target structure present. The segmentation ground truth was obtained by masking each decoded small subvolume in the training dataset with image intensity level 0.5. Voxels with signal greater than 0.5 were segmented as the background region and voxels with signal less than or equal to 0.5 were segmented as either the surface region or large globular region as determined by the cluster label.

3.4.3. Training

We randomly split the 808 small subvolumes into a training set of size 727 and a validation set of size 81. The encoder-decoder network model was trained using Adam with exponential decay rates β₁= 0.9 and β₂ = 0.99 to minimize the categorical cross-entropy loss function. After one epoch training, the model was saved only if there was an improvement in validation dataset loss compared with previous epoch. Adam training was performed with learning rate 0.001 and a batch size of 128 until the loss for validation dataset did not improve for 20 consecutive epochs.

3.4.4. Segmentation

The trained EDSS3D network was applied to the testing dataset of 312 small subvolumes. 2D slices of the original testing small subvolumes and the resulting three class segmentation probability results were plotted. Fig. 9 and 10 show the segmentation of two example small subvolumes. An overall visual inspection of the segmentation results on the test dataset shows that our unsupervised Autoencoder3D network and weakly supervised EDSS3D network can successfully segment this dataset into semantically meaningful classes and structures.

Fig. 9.

2D slices of an example small subvolume (in COS-7 tomogram 2) being segmented to a surface fragment.

Fig. 10.

2D slices of an example small subvolume (in the COS-7 tomogram 2) being segmented to a large globule.

Fig. 11 shows an embedding of segmented small subvolumes to COS-7 tomogram 2. In Fig. 11, some membrane regions, including many vesicular membranes, are successfully segmented and annotated in yellow. Carbon edge and tomogram boundary regions were also segmented as surface regions in yellow. Large globular features that may indicate ribosome-like structures are segmented and annotated in red across a large region in the tomogram. We note here that only a small number of small subvolumes were selected after the filtering for semantic segmentation. Some false-negative results were obtained due to the filtering. However, of the selected small subvolumes, surface regions and large globular macromolecules were successfully segmented.

Fig. 11.

Annotated COS-7 tomogram 2 based on segmentation. Surface feature segmentation (yellow) and large globular macromolecules segmentation (red) are annotated in the tomogram. A tomogram boundary, annotated in yellow, and a long carbon edge, partly annotated in yellow, are indicated by red arrows. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

We measured the computation speed of the EDSS3D network. On average, the training took 0.011s per small subvolume per epoch. Given the trained EDSS3D model, the segmentation took 0.011 s for one small subvolume. Therefore, our model can be used to quickly segment large mount of small subvolumes. Computing times and environments of all steps can be found in Supplementary Table S2.

4. Discussion

CECT has emerged as a powerful tool for 3D visualization of the cellular organization at submolecular resolution and in a near-native state. However, the analysis of structures in a cellular tomogram is difficult due both to the high complexity of image content and imaging limits. To complement existing approaches, in this paper, we proposed a convolutional autoencoder approach for the fast and coarse characterization of image features among small subvolumes. We further proposed a weakly supervised semantic segmentation approach by combining the convolutional autoencoder and the full convolutional network, which only involves a very small amount of manual annotation. The preliminary tests of our approaches on experimental and simulated tomograms demonstrate the efficacy of our approaches. This proof-of-principle work presents a useful step towards the automatic and systematic structural characterization in cellular tomograms. To our knowledge, our work is the first application of convolutional autoencoder and CNN based weakly supervised semantic segmentation to the analysis of CECT data. Our methods are useful complements to current techniques.

Potential uses of our method include facilitating in silico structural purification and pattern mining in tomograms of intact cells, cell lysates (Kemmerling, 2013), or purified complexes, and using selected image feature clusters of the same type (but possibly in different orientations) to train semantic segmentation. Moreover, template search approaches can also be facilitated by our method. In cases where the user is looking for a specific structure matched to a template, the user can ignore the resulting small subvolume sets whose cluster centers are vastly different from the template. In addition, once the feature clusters are obtained by our Autoencoder3D network, they can then be used to extract, recognize, filter, or to enhance specific types of image features. Selected small subvolume clusters grouped by different types of features can be directly used to train a classifier to recognize these features in a similar way as our recent work (Min et al., 2017).

The main motivation of our use of convolutional autoencoder is as follows: First, direct classification (clustering) of 3D CECT small subvolumes is challenging because the distance measures calculated on such high dimensional data as 3D images have poor discrimination ability (Min et al., 2017; Aggarwal et al., 2001). On the other hand, our previously developed supervised dimension reduction approach (Min et al., 2017) relies on the availability of training data in form of labeled subtomograms. Therefore, we employ the convolutional property of CNN to perform unsupervised feature extraction and dimension reduction. As small subvolumes are projected to a lower dimension, the distance between vectors is significantly more discriminative and faster to compute.

In principle, besides convolutional autoencoder, other alternative encoding approaches can also be employed, such as sparse coding (Lee et al., 2006), dictionary learning (Tosic and Frossard, 2011) and nonlocal means (Chatterjee and Milanfar, 6814). However, unlike convolutional autoencoder, these alternative approaches do not take the advantage of the inherent structures inside images such as local correlations and hierarchical organization of correlations. Also, some of these alternative approaches use linear representation models. Such approaches may fail to encode when the linearity assumption is invalid for certain data.

Data preparation and clustering processes still require the user to choose proper parameters such as the small subvolume size, the scale factor of Difference of Gaussian particle picking, and the number of k-means clusters. Currently we set an arbitrary number of 100 for clustering. We have tested Gap Statistic (Tibshirani et al., 2001) and the Calinski-Harabasz index (Maulik and Bandyopadhyay, 2002) for automatically choosing the cluster number. Both methods fail to converge to a certain cluster number. Since a simple manual grouping of resulting clusters is required, the impact of cluster number on the results is generally reduced. How to automatically determine the cluster numbers for encoded highly heterogeneous macromolecules from cellular tomograms remains as an open problem. Additionally, k-means clustering generates different cluster labels for each run, and thus the manual selection needs to be redone. A more user-friendly clustering procedure would be beneficial to further reduce the amount of manual work required.

Future works include (1) adapting the methods to take into account missing wedge effects; and (2) systematically optimize the metaparameters of the autoencoder and semantic segmentation models through various combinatorial optimization techniques (Ngiam et al., 2011), such as a line search, to further improve the performance of the models in terms of validation accuracy and training speed.