Abstract
Nonaqueous polyelectrolyte solutions have been recently proposed as high Li+ transference number electrolytes for lithium ion batteries. However, the atomistic phenomena governing ion diffusion and migration in polyelectrolytes are poorly understood, particularly in nonaqueous solvents. Here, the structural and transport properties of a model polyelectrolyte solution, poly(allyl glycidyl ether-lithium sulfonate) in dimethyl sulfoxide, are studied using all-atom molecular dynamics simulations. We find that the static structural analysis of Li+ ion pairing is insufficient to fully explain the overall conductivity trend, necessitating a dynamic analysis of the diffusion mechanism, in which we observe a shift from largely vehicular transport to more structural diffusion as the Li+ concentration increases. Furthermore, we demonstrate that despite the significantly higher diffusion coefficient of the lithium ion, the negatively charged polyion is responsible for the majority of the solution conductivity at all concentrations, corresponding to Li+ transference numbers much lower than previously estimated experimentally. We quantify the ion–ion correlations unique to polyelectrolyte systems that are responsible for this surprising behavior. These results highlight the need to reconsider the approximations typically made for transport in polyelectrolyte solutions.
Short abstract
Molecular dynamics simulations reveal the mechanisms governing charge transport in nonaqueous polyelectrolyte solutions for application in Li ion batteries.
Introduction
The performance of conventional lithium ion batteries (LIBs) is limited by their low cation transference number (t+), defined as the fraction of ionic conductivity imparted by the lithium ion rather than its counterion.1 These low t+ values (typically about 0.4)2 correspond to electrolytes in which the anion is highly mobile, whereas the electrochemically active Li+ moves more sluggishly as a result of its bulky solvation shell.3 As a result, concentration gradients form in the electrolyte, which limit material utilization, promote lithium plating, and generate concentration overpotentials, all of which contribute to a lower power density, energy density, and lifetime of the cell.4−6
Strategies toward increasing t+ typically focus on immobilizing the anion, for example, via lithium-conducting ceramics7−10 or single-ion conducting solid polymer electrolytes.11−14 However, the mechanical properties of ceramics make thin film processing difficult, and polymer electrolytes suffer from poor conductivity, particularly at room temperature and below. Alternatively, it has recently been proposed that t+ could be increased by covalently appending the anion to the backbone of a polymer, which is then dissolved in nonaqueous solvent to form a lithium-neutralized polyelectrolyte solution.15−18 This approach slows anion motion without substantially impacting conductivity and is compatible with current cell designs.
Initial efforts have suggested that these polyelectrolyte solutions are promising, with transference numbers (approximated on the basis of self-diffusion coefficient measurements) of as high as 0.8 to 0.98 depending on the polymer chemistry, solvent, and ion concentration.15,16 Further development of these systems, however, is limited by a lack of fundamental understanding of ion transport phenomena in these solutions. Many of the properties which most strongly govern battery performance, such as ion speciation, diffusion mechanisms, and the true transference number are challenging to precisely access experimentally.19 Moreover, the majority of theoretical work on polyelectrolyte solutions has focused on the properties of the polyion chain alone, rather than the behavior of the counterion, which is the electroactive species of interest for batteries.20,21
Simulation techniques such as molecular dynamics (MD) are well-suited to address many of the unanswered questions surrounding these nonaqueous polyelectrolytes. As the time and length scales associated with ion transport are compatible with those accessible by MD, this technique has been used extensively to gain insight into the properties of conventional binary lithium salts such as lithium bis(trifluoromethanesulfonyl)imide (LiTFSI) or lithium hexafluorophosphate (LiPF6)22,23 as well as solid polymer electrolytes.24−28 MD has also been successfully applied to polyelectrolytes, although these studies have been performed almost exclusively in aqueous systems,29−31 for example, on biological polyelectrolytes such as DNA32,33 or in solvent-free ionomer melts.34−37 Others have performed polyelectrolyte simulations in nonexplicit continuum solvents,38−40 but this approach often fails to adequately capture trends in chain conformation and ion dissociation.16,41 Of the MD simulations in explicit nonaqueous solvents,17,42 we are unaware of any which characterize the battery-relevant transport properties (such as t+) of the solution.
Herein, we employ all-atom classical MD simulations of a model polyelectrolyte system for battery applications, poly(allyl glycidyl ether-lithium sulfonate) (PAGELS) in dimethyl sulfoxide (DMSO). This polymer consists of a poly(ethylene oxide) backbone with side chains terminated in sulfonate anions (schematic in Figure S5). Several of the most important transport properties of this system have been investigated experimentally,15 enabling validation of the computational model. We characterize the structural properties of a single chain in solution, demonstrating the intuitive connection between ion pairing behavior and polyion conformation. Next, we explore the dynamic mechanisms for lithium ion diffusion and migration, focusing specifically on ion–ion correlations and their impact on conductivity and transference number. This work illuminates some of the fundamental atomistic processes governing transport in these nonaqueous polyelectrolyte solutions, which has implications not only for the design of enhanced LIB electrolytes but also for improved understanding of polyelectrolyte dynamics in general.
Results and Discussion
Structural Properties
Ion Speciation
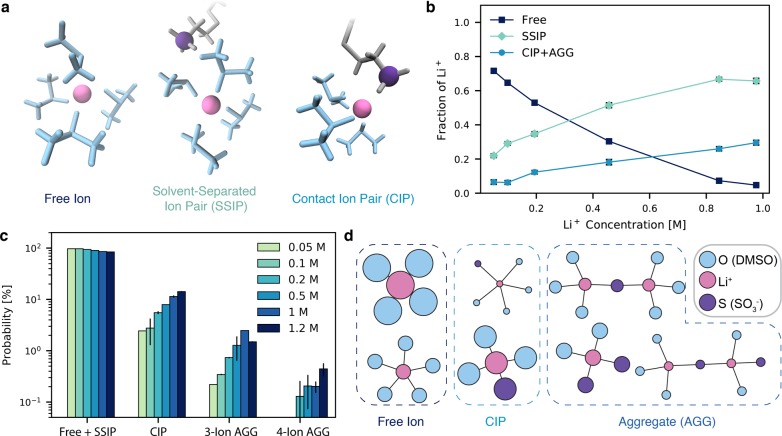
One of the most deciding aspects of the performance of a battery electrolyte is ion speciation: the extent of ion pairing in an electrolyte governs the number of charge-carrying species, thereby directly influencing the conductivity, transference number, and other crucial electrolyte properties.43−45 Using a distance criterion obtained from the cation–anion radial distribution function (RDF), we classify each Li+ ion as either free, in a solvent-separated ion pair (SSIP), or in a contact ion pair (CIP) or a larger aggregate (AGG) with the sulfonate ions, the anionic moiety of the polyion (Figure 1a). The nomenclature used here is common in the field of battery electrolytes, but in the polyelectrolyte literature, this phenomenon is typically referred to as counterion condensation.46 The CIPs referred to here are analogous to Manning’s “site” bound ions, whereas SSIPs are similar to “territorially” bound condensed counterions.47 Consistent with the various theories of counterion condensation in polyelectrolytes,48,49 here we observe that the fraction of free Li+ ions (Figure 1b) decreases as the concentration increases, ranging from 72% at 0.05 M down to 5% at 1.0 M, while the extent of ion pairing and aggregation increases. The coordination number of anions within the first Li+ shell (plotted in Figure S1) yields a similar trend.
Figure 1.
Ion speciation trends. (a) Schematics of the three most common states of ion speciation: free ions, solvent-separated ion pairs (SSIPs), and contact ion pairs (CIPs). (b) Fraction of lithium ions in each speciation state as a function of concentration. (c) Probability of observing ion clusters of different sizes. (d) Most commonly observed topologies representing the connectivity of Li+ to neighboring sulfur (SO3–) and oxygen (DMSO) atoms, averaged over all concentrations. The node area is proportional to the logarithm of the probability of observing each topology.
While this initial analysis provides a general picture of ion speciation trends in the polyelectrolyte, the data in Figure 1b does not distinguish between CIPs and AGGs. We quantify the relative significance of these AGGs in Figure 1c, which gives the probability of observing aggregates of different sizes for each concentration. We observe that the probability of ion aggregates to form decreases approximately exponentially with aggregate size, a trend which has been observed for conventional LIB electrolytes.23 Because fewer than 2.5% of the observed aggregates consist of three or more ions, we expect the bulk behavior of the system to be dictated primarily by the free ions, SSIPs, and CIPs.
To further visualize the most prevalent solvation structures and aggregate types in the polyelectrolyte solution, we employ a graph theory approach analogous to that of Tenney et al.50 in which we translate the positions of the system’s atoms at any given time into a graph composed of nodes and vertices. The nodes in this case represent Li+, S (SO3–), or O (DMSO) atoms, and the edges give connectivity between Li+-S (SO3–) or Li+-O (DMSO) pairs which are coordinated in their first solvation shell. An analysis of the connectivities at each time step allows for determining the most common topologies observed over the course of the simulation, as shown in Figure 1d. The area of the nodes in this figure is proportional to the logarithm of the frequency at which the topology appears in the system, averaged over all concentrations. As expected, the most frequently observed topologies are the free ion and CIP (SSIPs are not captured in this analysis), while clusters with more ions are significantly less common.
Polymer Conformation
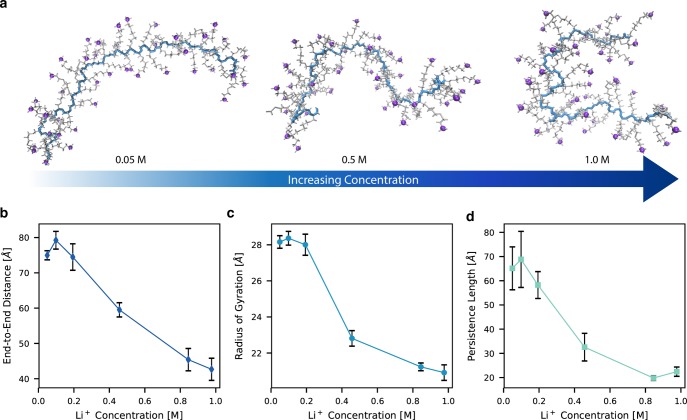
In this section, we focus on the polymer conformation, which is closely tied to ion speciation. At low concentrations, when contact ion pairing is negligible, the polymer chain is highly charged. In this state, electrostatic repulsion between charged monomers extends the chain into a predominantly linear conformation. As the concentration increases and more counterions (Li+) bind to the chain, the repulsion between the monomers decreases and the polymer adopts a more entropically favorable, globular conformation.19 This trend is apparent in the snapshots shown in Figure 2a. The linear-to-coiled transformation with concentration can be observed quantitatively in both the end-to-end distance (Figure 2b) and the radius of gyration (Figure 2c), which both decrease as concentration increases.
Figure 2.
Polymer structure as a function of concentration. (a) Example configurations of polymer conformation at 0.05, 0.5, and 1.0 M. (b) End-to-end distance, (c) radius of gyration, and (d) persistence length at each concentration. Sulfur atoms on the sulfonate anion are depicted in purple, the chain backbone is blue, and the side chains are gray. Solvent molecules and lithium ions are omitted for clarity.
Changes in the polyion’s persistence length (Figure 2d) are also consistent with our trends in ion pairing described in the previous section. The persistence length reflects the extent of orientational correlation along the backbone of the chain. For polyelectrolytes, the overall persistence length is a combination of orientational correlations from the inherent flexibility of the uncharged backbone as well as electrostatic correlations induced by repulsion of the charged monomers.51 Hence changes in electrostatic correlations dictate the trend in persistence length with concentration, such that the highly charged chains at lower concentrations yield the greatest persistence lengths. Our results are in qualitative agreement with the classical Odijk–Skolnick–Fixman (OSF) theory,52,53 which predicts that persistence length should be proportional to κ–2, where κ–1 is the Debye screening length, or inversely proportional to the solution ionic strength. Quantitative agreement with this model should not be expected, however, given the oligomeric nature of the chain (here 43 monomers, chosen to match available experimental data; see the Methods section for details on system setup) as well as the presence of the long side chains, which render the distribution of anionic charges on the chain somewhat irregular. Similar limitations prevent us from comparing other structural or dynamic properties of the polyion to known polyelectrolyte scaling laws, which typically assume infinitely long chains with uniform charge distributions.54
Dynamic Properties
Before extracting atomistic transport motifs for the PAGELS polyelectrolyte, we validate the dynamics produced by our MD force field against experimental data.15 The calculated self-diffusion coefficients and those measured experimentally in previous work using pulsed-field gradient nuclear magnetic resonance (PFG-NMR) are given in Figure 3a. In addition to reproducing the experimental trend in which both the lithium ions and polyion diffuse more slowly as concentration increases, the diffusion coefficients match to within less than half of an order of magnitude, well within the errors commonly observed for MD simulations using nonpolarizable force fields.55,56 Some of the observed discrepancy, particularly for the polyion, may be attributed to finite size effects from our simulations of a single polymer chain. These effects are well known to result in slower diffusion relative to an infinitely large simulation box.57 Although we have performed simulations with two chains at the highest concentrations that suggest these finite size effects are relatively small (Figure S6), it is possible that significantly larger simulation sizes could yield better agreement with experimental diffusion data. The experimental ionic conductivity σ is also reproduced within reasonable error (Figure 3b). Our overestimation of the total conductivity suggests that the force field may underestimate the effects of ion pairing in the actual system. However, the relative changes in conductivity with concentration show excellent agreement with experimental trends (Figure S7).
Figure 3.
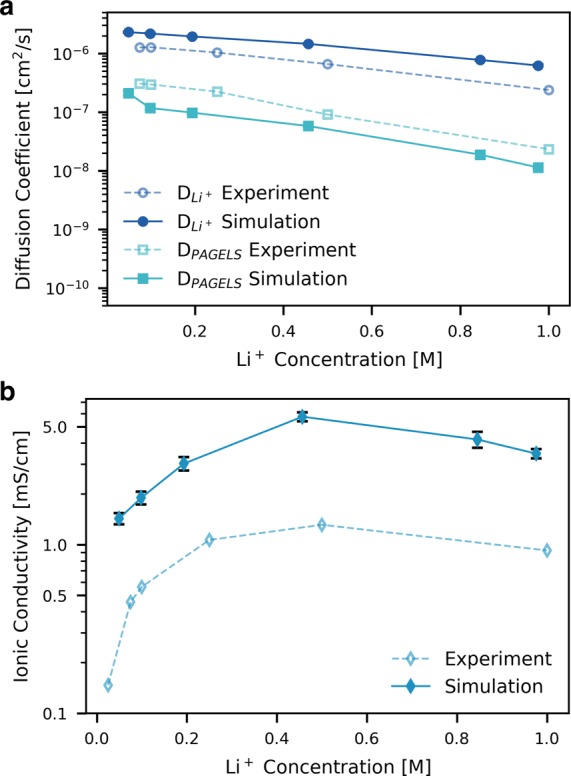
Comparison of calculated dynamic properties with experimental values. (a) Diffusion coefficients of Li+ and the polyelectrolyte (PAGELS) center of mass. (b) Ionic conductivity. Experimental values are taken from Buss et al.15
Lithium Diffusion Mechanisms
To characterize lithium ion transport within this polyelectrolyte system, we consider not only the static picture of the lithium ion coordination environments but also the dynamic trends governing the motion of Li+ relative to its surroundings. The diffusion of Li+ relative to another species can be characterized as either vehicular, in which Li+ diffuses together with its solvation shell as a single complex, or structural, where neighboring species do not move together for appreciable distances. In the latter case, the Li+ solvation shell molecules are frequently exchanged.58 Identification of these mechanisms has been shown in previous works to be crucial to fully understanding trends in ionic conductivity.59,60
The diffusion mechanism of one species relative to another can be distinguished quantitatively by calculating the residence time (τ) for two neighboring species to move together.61,62 Herein we have evaluated residence times for Li+ with respect to DMSO and SO3– (both CIPs in the first solvation shell and SSIPs in the second solvation shell) as well as for SO3– with respect to DMSO in its first solvation shell.
The residences
times alone, however, cannot be used to compare
diffusion mechanisms because overall diffusion slows down at higher
concentrations as a result of increased solution viscosity. Indeed,
we observe that the residence times calculated for each pair of species
(Figure S8) generally increase as concentration
increases. Because the overall changes in system viscosity will be
reflected in the solvent (DMSO) diffusion coefficient, we use this
quantity to convert from residence time to diffusion length, L, where 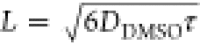 . The calculated diffusion lengths (Figure 4a) enable a systematic
comparison of changing diffusion mechanisms across concentration.
This analysis demonstrates that the diffusion length generally decreases
as concentration increases, corresponding to a shift in the diffusion
mechanism toward more structural diffusion for all lithium species.
The SO3–-DMSO diffusion length, which stays relatively constant across concentration,
is the only exception to this trend. The Li+-SO3– (CIP)
trend here is of particular interest. Although more ion pairs exist
at higher concentrations (as shown by our static coordination environment
analysis), the change in the diffusion mechanism indicates that each
of these ion pairs will travel a shorter distance as neighbors. We
note that this observation has important implications for our analysis
of cation–anion correlations and ionic conductivity in the
following section.
. The calculated diffusion lengths (Figure 4a) enable a systematic
comparison of changing diffusion mechanisms across concentration.
This analysis demonstrates that the diffusion length generally decreases
as concentration increases, corresponding to a shift in the diffusion
mechanism toward more structural diffusion for all lithium species.
The SO3–-DMSO diffusion length, which stays relatively constant across concentration,
is the only exception to this trend. The Li+-SO3– (CIP)
trend here is of particular interest. Although more ion pairs exist
at higher concentrations (as shown by our static coordination environment
analysis), the change in the diffusion mechanism indicates that each
of these ion pairs will travel a shorter distance as neighbors. We
note that this observation has important implications for our analysis
of cation–anion correlations and ionic conductivity in the
following section.
Figure 4.
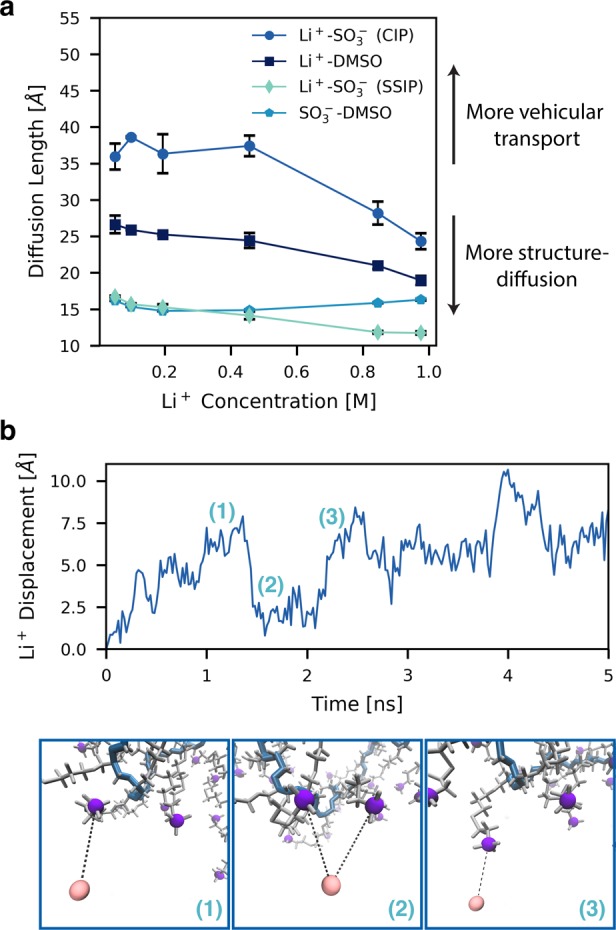
Characterization of lithium ion diffusion mechanisms. (a) Diffusion length as a function of concentration for various species. (b) Sample Li+ trajectory with snapshots depicting the solvent-separated ion-hopping process. Sulfur atoms on the sulfonate anion are depicted in purple, the lithium ion is pink, the chain backbone is blue, and the side chains are gray. Solvent molecules are omitted for clarity.
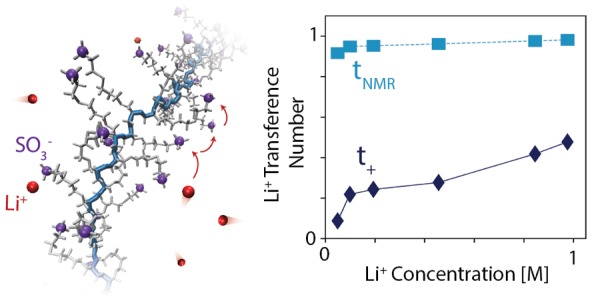
While the aforementioned diffusion mechanism analysis has dealt exclusively with the average behavior of all lithium ions, we gain additional insight from analyzing the trajectories of individual Li+. When mapping a given Li+ trajectory over the scale of a few nanoseconds (shown for a representative Li+ atom in Figure 4b), we observe discrete jumps of approximately 4 to 5 Å overlaid on the typical noise associated with molecular diffusion. Visualization of the lithium ion and its surroundings over this period reveals that these jumps correspond to ion-hopping events between solvent-separated lithium and sulfonate ions, as pictured in Figure 4b. The average time between these hops is consistent with the residence time analysis of solvent-separated Li+-SO3– pairs, as shown in Figure S8. The residence time provides a quantitative measure of the average rate of hopping events, which can be interpreted as inversely proportional to τ.63
This mechanism is reminiscent of the ion-hopping behavior postulated for transport in solid polymer electrolytes26,64 as well as organic liquid electrolytes at high concentration.65,66 In this polyelectrolyte, however, solvent-separated ion hopping is observed for all concentrations simulated, suggesting that hopping events may be facilitated by the presence of the polymer. Indeed, recent work67 has generated evidence for the substantial migration of territorially bound counterions (SSIPs) along polyelectrolyte backbones. It is possible that constraining the anion positions through their attachment to the chain backbone generates favorable anion–anion separation distances for the hopping to occur. Importantly, however, we emphasize that the ion-hopping diffusion mechanism is not the only process governing overall Li+ motion. In addition to these hopping events, full trajectory inspection (Figure S9) reveals that the overall movement of the ions is heavily influenced by free diffusion in DMSO as well as codiffusion of CIPs with the polymer.
Ionic Conductivity and Transference Number
Given that the main motivation for polyelectrolyte solutions as battery electrolytes is their predicted high lithium transference number, in this section we aim to evaluate the transference number as well as elucidate the physical mechanisms which govern it. The transference number is defined as the fraction of current carried by a given species in a system with no concentration gradients.1,68 On the basis of Ohm’s law (i = σE, where i is current density, σ is conductivity, and E is the electric field), we can equivalently interpret the transference number as the fraction of conductivity which can be attributed to a given species. The conductivity is often written in terms of the electrophoretic mobilities of the ionic species in the electrolyte, where the mobility μi describes how quickly a species i migrates in response to an electric field (vi = μiE, where vi is the species velocity).69 For a binary salt system,
| 1 |
where F is Faraday’s constant, zi is the charge of species i, and ci is the concentration of species i. Thus, the transference number of the cation species can be written as
| 2 |
Assuming electroneutrality (∑izici = 0), this expression reduces to
| 3 |
In nondilute solutions, t+ is challenging to determine unequivocally from experiments. Most reported electrochemical t+ measurements, namely, those using the Bruce and Vincent method,70 assume ideal solutions of noninteracting ions, while those that incorporate the effects of nonidealities are typically challenging to execute experimentally. Balsara and Newman’s71 generalization of the Bruce and Vincent method to concentrated solutions, for example, requires a restricted diffusion experiment as well as the determination of the salt activity coefficient. Other techniques, such as the Hittorf or Tubandt method,72 are associated with large statistical uncertainties due to noisy data.2,73 As a result, true transference numbers are rarely measured directly.5 Instead, the transference number is usually approximated using self-diffusion coefficients obtained from PFG-NMR. Assuming entirely uncorrelated ion motion corresponding to an infinitely dilute, ideal solution, the electrophoretic mobility can be related to the diffusion coefficient using the Nernst–Einstein equation1
| 4 |
where Di is the self-diffusion coefficient of species i, R is the ideal gas constant, and T is temperature. Substitution into eq 3 for a binary electrolyte yields the most frequently cited equation for determining the transference number:
| 5 |
Here we denote this quantity as tNMR to emphasize the requirement of ideality in order to employ diffusion coefficients rather than mobility values. In this work, we use the notation tNMRexp and tNMR to distinguish between transference numbers calculated using experimentally measured diffusion coefficients and those using diffusion coefficients computed from MD simulations, respectively. We also note that tNMR is sometimes referred to as a transport number rather than a transference number.74 The choice of z+ and z–, while trivial for conventional electrolytes, is arguably ambiguous for a polyelectrolyte solution. Noting that all anions on the chain must move collectively over long time scales, one may interpret z– as the net charge of the polymer (zpolymer). However, experimental work on these systems thus far has exclusively used z– = −1,15,16 considering each of the anionic moieties on the chain independently. When analyzed accordingly, the transference number of the PAGELS system is found to be significantly higher than that of conventional electrolytes: tNMRexp and tNMR are both greater than 0.8 for all concentrations studied (Figure S10).
MD trajectories afford us the ability to calculate t+ without having to make any assumptions about the ideality of the solution. To obtain t+ as well as gain more insight into the physical processes governing the ionic conductivity trends as a whole, we decompose the total ionic conductivity into separate contributions from the various types of correlated and uncorrelated ion motion in the system:75−78
| 6 |
The cation-self (σcats), anion-self (σan), cation-distinct (σcatd), anion-distinct(σan), and cation–anion-distinct (σcat,and) conductivities are defined in the SI. The two self-conductivity terms (σcat and σans) yield the conductivity from completely uncorrelated ion motion. The distinct terms (σcat, σand, and σcat,an) capture ion–ion correlations between pairs of cations, pairs of anions, and cation–anion pairs, respectively. If the sum of all of the distinct terms is zero, then the resulting conductivity follows Nernst–Einstein or ideal solution behavior. In this case, tNMR will correspond to the true transference number. However, the distinct terms typically decrease both the conductivity and cation transference number relative to the ideal case.78,79
While an analysis of the conductivity in this manner is more common for conventional, low-molecular-weight salt electrolytes, the framework here is consistent with that often used in the polyelectrolyte community in which the total conductivity is expressed as the product of the ideal solution conductivity and an interaction parameter capturing interionic friction and ion pairing effects.80 It has been shown by Vink81 that these expressions for polyelectrolyte conductivity can be derived from linear irreversible thermodynamics, the same starting point for deriving the Green–Kubo relations on which the conductivity analysis in this work is based. The analysis here, however, allows us to calculate the relative contribution of each type of ion–ion interaction to the total conductivity rather than only a single interaction parameter, an analysis which to the best of our knowledge has not been previously applied to any polyelectrolyte system. Note that in this analysis we are considering the behavior of each individual sulfonate anion rather than the center-of-mass motion of the entire polyelectrolyte chain. We have verified that equivalent results for the computed total ionic conductivity, electrophoretic mobilities, and transference number were obtained by analyzing either the polyion as a single unit or as individual anions (Figure S11).
Figure 5a shows the contribution of each of the terms in eq 6 to the overall molar conductivity in this system. The two self-conductivity terms are closely related to the cation and anion self-diffusion coefficients, and thus their contribution to the total molar conductivity decreases as concentration increases. The Li+-distinct conductivity is approximately zero at all concentrations, corresponding to uncorrelated ion motion, although at higher concentrations the relative contribution of σcatd slightly decreases to become negative. Negative conductivity contributions signify anticorrelated motion, as Li+ ions within close proximity repel each other. This trend is more apparent when plotting the fractional contribution of each conductivity term to the total conductivity (Figure S12) rather than the molar conductivity.
Figure 5.
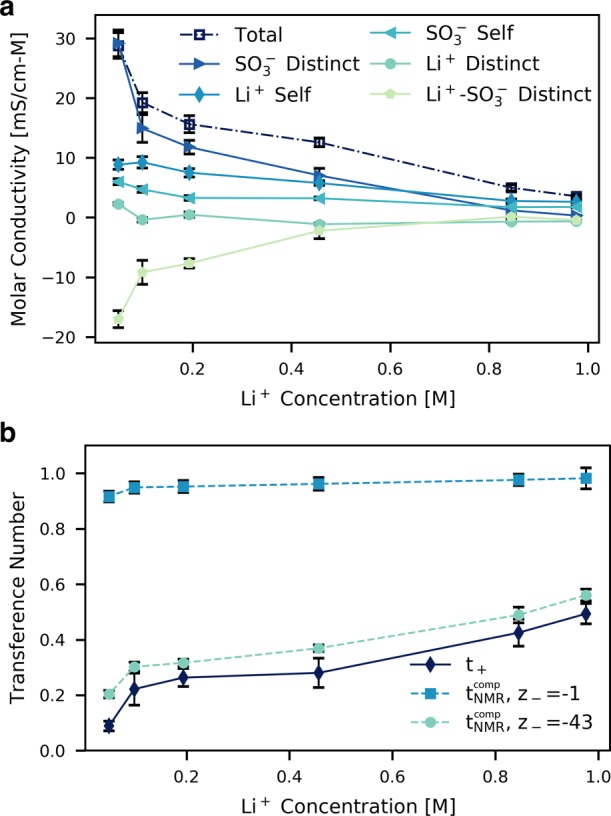
(a) Contributions of each type of uncorrelated (self) or correlated (distinct) ion motion to the total molar conductivity. (b) Transference number as a function of concentration. The true transference number (t+) calculated from ionic conductivity data is plotted along with the transport number (tNMRcomp, an approximation of t+ for ideal systems). Values for the charge of the anionic species (z–) of both −1 and zpolymer = −43 are used in calculating the transport number.
Li+-SO3– distinct conductivity impacts the overall conductivity much more significantly. We find the calculated σcat,and for the PAGELS in DMSO system to be negative for all concentrations. The anion and cation are oppositely charged, so a negative σcat,an corresponds to correlated ion motion, for example, through the joint movement of an ion pair. This negative contribution coincides with our intuitive understanding of ion pairing lowering the overall conductivity relative to the ideal case. Surprisingly, the negative contribution of σcat,and decreases in magnitude, signifying less correlated cation–anion motion as concentration increases, despite the fact that the fraction of paired Li+ ions increases with concentration. We rationalize this behavior at least in part through the aforementioned trends in the diffusion mechanism. While the percentage of CIPs is higher at high concentrations, these ion pairs exhibit shorter diffusion lengths such that they diffuse through a more structural mechanism than ion pairs at low concentration. Indeed, shorter distances traveled as a single correlated entity are consistent with smaller contributions to σcat,an. We speculate that changes in the Li+-SO3– correlation with concentration may also be related to the decreased charge screening length at high concentrations, which limits electrostatic attraction between ions to shorter distances.
These results suggest that a purely static analysis of ion pairing, simply the spatial arrangement of atoms at any given time, is inadequate to fully understand trends in ionic conductivity. Importantly, this finding conflicts with the underlying assumptions of many polyelectrolyte conductivity theories in which the fraction of uncondensed (free) counterions is often included as an adjustable parameter by which the entire conductivity is scaled.80,82
We further note that the trend of increasingly negative σcat,and at lower concentrations has been observed in MD simulations of systems other than polyelectrolytes, such as superconcentrated LiTFSI in tetraglyme as well as 1-butyl-3-methylimidazolium tetrafluoroborate ([BMIM+][BF4–]) electrolytes in a variety of solvents.75,76 Similarly, Haskins et al.83 noted that the fraction of uncorrelated ionic motion (σNE/σ, where σNE is the Nernst–Einstein conductivity) increases with concentration for Li+-doped ionic liquid electrolytes (i.e., the distinct conductivity terms decrease as concentration increases). In agreement with our observations, they attribute this trend to a change in the diffusion mechanism from vehicular to more structural as concentration increases.
While the aforementioned trends in self, cation–cation, and cation–anion conductivities are not unique to polyelectrolytes, the anion–anion correlation term introduces complexities not seen in conventional salt solutions. Typically, σand does not contribute substantially to the overall conductivity,75,76 analogous to σcat. In anionic polyelectrolytes, however, each of the anions on a given chain is highly correlated to the others through their connection to the same polymer backbone. This correlated motion results in substantial positive contributions to the total ionic conductivity, which have important implications for the analysis of the transference number (vide infra).
In addition to providing information on the mechanisms dictating ionic conductivity, dividing the conductivity into its constitutive elements also enables facile computation of the electrophoretic mobility of the ionic species:
| 7 |
| 8 |
We note that the choice of z– will not impact the final mobility because product c–z– is constant regardless of whether the individual anionic moieties or the polymer chain as a whole is considered. The mobilities of both the polyion and Li+ are shown in Figure S13. As concentration increases, the mobility of both the polyelectrolyte chain and Li+ decreases. As before, because of the short length of the polyion chain, the results do not coincide with the classical polyelectrolyte scaling laws, which predict that polyelectrolyte mobility should be independent of concentration.84 The mobilities can be converted to transference numbers using eq 3. In Figure 5b, the calculated true transference numbers (denoted as t+) are overlaid with the diffusion-coefficient-based transport numbers (tNMRcomp) calculated from eq 5 using both z– = −1 and z– = zpolymer = −43. As mentioned previously, tNMR calculated using z– = −1 is in agreement with the commonly employed experimental analyses15,16 and yields very high transference number estimates which are relatively constant with concentration. The true transference number, however, is significantly lower, ranging from 0.09 to 0.49; only the highest concentrations studied are predicted to exhibit transference numbers appreciably greater than those of conventional LIB electrolytes.
These results demonstrate that the use of z– = −1 in eq 5 severely overestimates the true transference number and that the only correct interpretation of eq 5 is that using z– = zpolymer. Choosing z– = −1 in the Nernst–Einstein equation assumes that all ions in the system are completely uncorrelated, which simply cannot be true when all ions on a given chain are constrained to move together. In fact, anion–anion correlations (σand) constitute the largest portion of the nonideal distinct conductivity terms and are responsible for the majority of the discrepancy between tNMR (z– = −1) and t+. In contrast, tNMRcomp (z– = zpolymer) treats the polymer collectively as a single unit and thus eliminates the need to account for anion–anion correlations within a given chain, effectively combining the SO3– self- and distinct contributions into a single term, the PAGELS self-conductivity. This data is in much closer agreement with the true t+. In this case, the only component of the overall conductivity which is not accounted for is the cation–anion distinct conductivity (σcat,an). We note, however, that the calculated t+ could be influenced by finite size effects. Our single-chain simulations may fail to capture important interchain interactions which may contribute to the overall distinct conductivity, although our preliminary tests using two chains (Figure S6) suggest that these effects are unlikely to impact our main conclusions. Although we have modeled one specific polyelectrolyte system, the ion correlation and transference number analysis presented here have not made any assumptions regarding the chain length or charge distribution of the polyelectrolyte and should thus be generally applicable. Hence, we recommend that experimentalists employing the Nernst–Einstein approximation and eq 5 to estimate the transference number use z– = zpolymer in future work rather than z– = −1. This applies not only to polyelectrolyte systems but also to those which tether the anions together through other means, for example, in polyoligomeric silsesquioxanes (POSS) functionalized with anionic moieties.85
Although the cation transference number of the PAGELS in DMSO polyelectrolyte is not as promising as originally thought, optimization of the chain length, concentration, and polymer chemistry may still yield systems with significantly higher t+. Furthermore, the wide range in the true transference number as a function of concentration suggests that polyelectrolyte systems present an interesting means of tuning transference number in ways which cannot be accomplished in more conventional systems. Preliminary simulations suggest that decreasing polymer charge density (i.e., reducing the fraction of monomers with anionic moieties) may be a promising means of decreasing anion–anion correlations and thus increasing the transference number. The complex balance among charge density, total lithium concentration, viscosity, conductivity, and transference number in these solutions is the subject of future work.
Conclusions
In this work, the structural and transport properties of a model nonaqueous polyelectrolyte solution, PAGELS in DMSO, were investigated through all-atom MD simulations. To validate the model, the calculated diffusion coefficients and ionic conductivity values were benchmarked against experimental results. We characterized the solvation structure and ion speciation behavior of the Li+ in the electrolyte and demonstrated the clear relationship between ion pairing and polymer structure. Furthermore, analysis of the ion transport mechanisms in the solution revealed a shift toward more structural diffusion as concentration increases as well as the presence of a solvent-separated ion-hopping motif. Finally, we deconvoluted the total ionic conductivity into contributions from each type of correlated and uncorrelated ion motion to demonstrate the substantial impact of cation–anion and anion–anion correlations. These nonideal ion correlations substantially decrease the cation transference number relative to estimates based on experimentally measured diffusion coefficient data. We envision that the ion-transport mechanisms elucidated in this work will inform the design of improved polyelectrolyte systems for LIBs and enhance our understanding of charge transport in polyelectrolyte solutions in general.
Methods
All-atom classical molecular dynamics (MD) simulations were performed using the LAMMPS86,87 code. Simulations were carried out on the anionic polymer poly(allyl glycidyl ether-lithium sulfonate) (PAGELS, see Figure S5 for structural schematic) in dimethyl sulfoxide (DMSO). Each simulation consisted of one polyion chain with a degree of polymerization of 43, 43 lithium counterions, and a variable number of DMSO molecules, chosen to adjust the concentration of Li+ in the system from 0.05 to 1 M. See Table S1 for details on the exact concentrations, numbers of solvent molecules, and simulation box sizes used. Although these simulations would ideally consist of many polymer chains to fully capture the effects of interchain interactions, we are limited by the large computational cost of these multichain simulations. To evaluate the impact of using just one chain, we have performed preliminary simulations with two chains at the two highest concentrations studied. (These are the concentrations at which we would expect interchain interactions to be most significant.) As shown in Figure S6, the transport properties of the solution (diffusion coefficients, conductivity, and transference number) are not significantly altered between the one- and two-chain simulations, suggesting that our single-chain study here has adequately captured the most important physics underlying transport in these systems.
The molecules of each simulation were randomly packed into a cubic box using PACKMOL,88 with the polymer chain prepared in a linear conformation. This initial configuration was first relaxed using a conjugated-gradient energy-minimization scheme with a convergence criterion, defined as the energy change between successive minimization iterations divided by the magnitude of the energy, of 1.0 × 10–4. The system was then equilibrated in the isothermal–isobaric (NPT) ensemble at a pressure of 1 atm and a temperature of 298 K for 3 ns, followed by simulated annealing at 400 K for 2 ns and then cooling back to 298 K over 3 ns.56 A Nosé–Hoover-style thermostat and barostat with damping parameters of 0.1 and 1 ps, respectively, were used. Production runs were subsequently carried out in the canonical (NVT) ensemble at 298 K using the Nosé–Hoover-style thermostat and a time step of 2 fs. Simulations were carried out for 50 ns with the last 40 ns used for analysis.
In each simulation, the equations of motion were numerically integrated using the velocity-Verlet algorithm. Each system was periodic in the x, y, and z directions and incorporated the PPPM method89 with an accuracy of 1.0 × 10–5 to compute long-range Coulombic interactions. A cutoff of 15 Å was used in computing short-ranged potentials. The length of the C–H bonds of the PAGELS chain was fixed by implementing the SHAKE algorithm.90,91
All force field parameters were taken from the OPLS_2005 force field,92 where atom type and partial charge assignment were automated using MacroModel and the Maestro graphical interface (Schrödinger).93 Partial charges of the ionic species were scaled by a factor of 0.7 to account for the fact that ion–ion interactions are typically overestimated in nonpolarizable force fields.94 Trajectories were analyzed using an in-house code (available upon request) built with the help of MDAnalysis software.95,96 Errors for reported data were obtained primarily through block averaging, as described in the SI.
No unexpected or unusually high safety hazards were encountered.
Acknowledgments
K.D.F. acknowledges support from NSF GRFP under grant no. DGE 1752814. This work was supported by the Assistant Secretary for Energy Efficiency and Renewable Energy, Vehicle Technologies Office, U.S. Department of Energy under contract DE-AC02-05CH11231 under the Advanced Battery Materials Research (BMR) Program. This research used resources of the National Energy Research Scientific Computing Center (NERSC) as well as the Savio computational cluster resource provided by the Berkeley Research Computing program at the University of California, Berkeley (supported by the UC Berkeley Chancellor, Vice Chancellor for Research, and Chief Information Officer).
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.9b00406.
Additional data analysis methods to analyze ion speciation, polymer conformation, diffusion coefficients, ionic conductivity, diffusion mechanisms, and statistical errors; PAGELS schematic; and additional transport data including residence times and electrophoretic mobilities (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Newman J.; Thomas-Alyea K. E.. Electrochemical Systems, 3rd ed.; John Wiley & Sons: Hoboken, NJ, 2004. [Google Scholar]
- Valoen L. O.; Reimers J. N. Transport properties of LiPF6-based Li-ion battery electrolytes. J. Electrochem. Soc. 2005, 152, A882. 10.1149/1.1872737. [DOI] [Google Scholar]
- Gering K. L. Prediction of electrolyte conductivity: results from a generalized molecular model based on ion solvation and a chemical physics framework. Electrochim. Acta 2017, 225, 175–189. 10.1016/j.electacta.2016.12.083. [DOI] [Google Scholar]
- Doyle M.; Fuller T. F.; Newman J. The importance of the lithium ion transference number in lithium/polymer cells. Electrochim. Acta 1994, 39, 2073–2081. 10.1016/0013-4686(94)85091-7. [DOI] [Google Scholar]
- Diederichsen K. M.; McShane E. J.; McCloskey B. D. Promising routes to a high Li+ transference number electrolyte for lithium ion batteries. ACS Energy Letters 2017, 2, 2563–2575. 10.1021/acsenergylett.7b00792. [DOI] [Google Scholar]
- Lu Y.; Tikekar M.; Mohanty R.; Hendrickson K.; Ma L.; Archer L. A. Stable cycling of lithium metal batteries using high transference number electrolytes. Adv. Energy Mater. 2015, 5, 1402073. 10.1002/aenm.201402073. [DOI] [Google Scholar]
- Murugan R.; Thangadurai V.; Weppner W. Fast lithium ion conduction in garnet-type Li7La 3Zr2O12. Angew. Chem., Int. Ed. 2007, 46, 7778–7781. 10.1002/anie.200701144. [DOI] [PubMed] [Google Scholar]
- Aono H. Ionic conductivity of the lithium titanium phosphate (Li1+XMXTi2–X(PO4)3, M = Al, Sc, Y, and La) systems. J. Electrochem. Soc. 1989, 136, 590. 10.1149/1.2096693. [DOI] [Google Scholar]
- Kamaya N.; Homma K.; Yamakawa Y.; Hirayama M.; Kanno R.; Yonemura M.; Kamiyama T.; Kato Y.; Hama S.; Kawamoto K.; Mitsui A. A lithium superionic conductor. Nat. Mater. 2011, 10, 682–686. 10.1038/nmat3066. [DOI] [PubMed] [Google Scholar]
- Kato Y.; Hori S.; Saito T.; Suzuki K.; Hirayama M.; Mitsui A.; Yonemura M.; Iba H.; Kanno R. High-power all-solid-state batteries using sulfide superionic conductors. Nature Energy 2016, 1, 16030. 10.1038/nenergy.2016.30. [DOI] [Google Scholar]
- Matsumi N.; Sugai K.; Ohno H. Ion conductive characteristics of alkylborane type and boric ester type polymer electrolytes derived from mesithylborane. Macromolecules 2003, 36, 2321–2326. 10.1021/ma021734u. [DOI] [Google Scholar]
- Zhang H.; Li C.; Piszcz M.; Coya E.; Rojo T.; Rodriguez-Martinez L. M.; Armand M.; Zhou Z. Single lithium-ion conducting solid polymer electrolytes: Advances and perspectives. Chem. Soc. Rev. 2017, 46, 797–815. 10.1039/C6CS00491A. [DOI] [PubMed] [Google Scholar]
- Kobayashi N.; Uchiyama M.; Tsuchida E. Poly[lithium methacrylate-co-oligo(oxyethylene)methacrylate] as a solid electrolyte with high ionic conductivity. Solid State Ionics 1985, 17, 307–311. 10.1016/0167-2738(85)90075-X. [DOI] [Google Scholar]
- Klein R. J.; Welna D. T.; Weikel A. L.; Allcock H. R.; Runt J. Counterion effects on ion mobility and mobile ion concentration of doped polyphosphazene and polyphosphazene ionomers. Macromolecules 2007, 40, 3990–3995. 10.1021/ma070357o. [DOI] [Google Scholar]
- Buss H. G.; Chan S. Y.; Lynd N. A.; McCloskey B. D. Nonaqueous polyelectrolyte solutions as liquid electrolytes with high lithium ion transference number and conductivity. ACS Energy Letters 2017, 2, 481–487. 10.1021/acsenergylett.6b00724. [DOI] [Google Scholar]
- Diederichsen K. M.; Fong K. D.; Terrell R. C.; Persson K. A.; McCloskey B. D. Investigation of solvent type and salt addition in high transference number nonaqueous polyelectrolyte solutions for lithium ion batteries. Macromolecules 2018, 51, 8761–8771. 10.1021/acs.macromol.8b01696. [DOI] [Google Scholar]
- Smiatek J.; Wohlfarth A.; Holm C. The solvation and ion condensation properties for sulfonated polyelectrolytes in different solvents - A computational study. New J. Phys. 2014, 16, 025001. 10.1088/1367-2630/16/2/025001. [DOI] [Google Scholar]
- Kreuer K. D.; Wohlfarth A.; De Araujo C. C.; Fuchs A.; Maier J. Single alkaline-ion (Li+, Na+) conductors by ion exchange of proton-conducting ionomers and polyelectrolytes. ChemPhysChem 2011, 12, 2558–2560. 10.1002/cphc.201100506. [DOI] [PubMed] [Google Scholar]
- Marcus Y.; Hefter G. Ion pairing. Chem. Rev. 2006, 106, 4585–4621. 10.1021/cr040087x. [DOI] [PubMed] [Google Scholar]
- Muthukumar M. 50th Anniversary perspective: A perspective on polyelectrolyte solutions. Macromolecules 2017, 50, 9528–9560. 10.1021/acs.macromol.7b01929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dobrynin A. V.Polymer Science: A Comprehensive Reference; Elsevier, 2012; Vol. 1, pp 81–132. [Google Scholar]
- Borodin O.; Smith G. D. Quantum chemistry and molecular dynamics simulation study of dimethyl carbonate: Ethylene carbonate electrolytes doped with LiPF6. J. Phys. Chem. B 2009, 113, 1763–1776. 10.1021/jp809614h. [DOI] [PubMed] [Google Scholar]
- Borodin O.; Smith G. D. LiTFSI structure and transport in ethylene carbonate from molecular dynamics simulations. J. Phys. Chem. B 2006, 110, 4971–4977. 10.1021/jp056249q. [DOI] [PubMed] [Google Scholar]
- Savoie B. M.; Webb M. A.; Miller T. F. Enhancing cation diffusion and suppressing anion diffusion via Lewis-acidic polymer electrolytes. J. Phys. Chem. Lett. 2017, 8, 641–646. 10.1021/acs.jpclett.6b02662. [DOI] [PubMed] [Google Scholar]
- Müller-Plathe F.; Van Gunsteren W. F. Computer simulation of a polymer electrolyte: Lithium iodide in amorphous poly(ethylene oxide). J. Chem. Phys. 1995, 103, 4745–4756. 10.1063/1.470611. [DOI] [Google Scholar]
- Webb M. A.; Jung Y.; Pesko D. M.; Savoie B. M.; Yamamoto U.; Coates G. W.; Balsara N. P.; Wang Z. G.; Miller T. F. Systematic computational and experimental investigation of lithium-ion transport mechanisms in polyester-based polymer electrolytes. ACS Cent. Sci. 2015, 1, 198–205. 10.1021/acscentsci.5b00195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diddens D.; Heuer A. Simulation study of the lithium ion transport mechanism in ternary polymer electrolytes: The critical role of the segmental mobility. J. Phys. Chem. B 2014, 118, 1113–1125. 10.1021/jp409800r. [DOI] [PubMed] [Google Scholar]
- Webb M. A.; Yamamoto U.; Savoie B. M.; Wang Z. G.; Miller T. F. Globally suppressed dynamics in ion-doped polymers. ACS Macro Lett. 2018, 7, 734–738. 10.1021/acsmacrolett.8b00237. [DOI] [PubMed] [Google Scholar]
- Ennari J.; Elomaa M.; Sundholm F. Modelling a polyelectrolyte system in water to estimate the ion-conductivity. Polymer 1999, 40, 5035–5041. 10.1016/S0032-3861(98)00731-9. [DOI] [Google Scholar]
- Carrillo J. M. Y.; Dobrynin A. V. Detailed molecular dynamics simulations of a model NaPSS in water. J. Phys. Chem. B 2010, 114, 9391–9399. 10.1021/jp101978k. [DOI] [PubMed] [Google Scholar]
- Wohlfarth A.; Smiatek J.; Kreuer K.-D.; Takamuku S.; Jannasch P.; Maier J. Proton dissociation of sulfonated polysulfones: Influence of molecular structure and conformation. Macromolecules 2015, 48, 1134–1143. 10.1021/ma502550f. [DOI] [Google Scholar]
- Lyubartsev A. P.; Laaksonen A. Molecular dynamics simulations of DNA in solution with different counter-ions. J. Biomol. Struct. Dyn. 1998, 16, 579–592. 10.1080/07391102.1998.10508271. [DOI] [PubMed] [Google Scholar]
- Yang L.; Weerasinghe S.; Smith P.; Pettitt B. Dielectric response of triplex DNA in ionic solution from simulations. Biophys. J. 1995, 69, 1519–1527. 10.1016/S0006-3495(95)80022-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frischknecht A. L.; Winey K. I. The evolution of acidic and ionic aggregates in ionomers during microsecond simulations. J. Chem. Phys. 2019, 150, 064901. 10.1063/1.5085069. [DOI] [PubMed] [Google Scholar]
- Ting C. L.; Stevens M. J.; Frischknecht A. L. Structure and dynamics of coarse-grained ionomer melts in an external electric field. Macromolecules 2015, 48, 809–818. 10.1021/ma501916z. [DOI] [Google Scholar]
- Hall L. M.; Seitz M. E.; Winey K. I.; Opper K. L.; Wagener K. B.; Stevens M. J.; Frischknecht A. L. Ionic aggregate structure in ionomer melts: Effect of molecular architecture on aggregates and the ionomer peak. J. Am. Chem. Soc. 2012, 134, 574–587. 10.1021/ja209142b. [DOI] [PubMed] [Google Scholar]
- Ma B.; Nguyen T. D.; Pryamitsyn V. A.; Olvera De La Cruz M. Ionic correlations in random ionomers. ACS Nano 2018, 12, 2311–2318. 10.1021/acsnano.7b07432. [DOI] [PubMed] [Google Scholar]
- Micka U.; Holm C.; Kremer K. Strongly charged, flexible polyelectrolytes in poor solvents: molecular dynamics simulations. Langmuir 1999, 15, 4033–4044. 10.1021/la981191a. [DOI] [Google Scholar]
- Liao Q.; Dobrynin A. V.; Rubinstein M. Molecular dynamics simulations of polyelectrolyte solutions: Nonuniform stretching of chains and scaling behavior. Macromolecules 2003, 36, 3386–3398. 10.1021/ma025995f. [DOI] [Google Scholar]
- Stevens M. J.; Kremer K. The nature of flexible linear polyelectrolytes in salt free solution: A molecular dynamics study. J. Chem. Phys. 1995, 103, 1669–1690. 10.1063/1.470698. [DOI] [Google Scholar]
- Chremos A.; Douglas J. The influence of polymer and ion solvation on the conformational properties of flexible polyelectrolytes. Gels 2018, 4, 20. 10.3390/gels4010020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burlatsky S.; Darling R. M.; Novikov D.; Atrazhev V. V.; Sultanov V. I.; Astakhova T. Y.; Su L.; Brushett F. Molecular dynamics modeling of the conductivity of lithiated Nafion containing nonaqueous solvents. J. Electrochem. Soc. 2016, 163, A2232–A2239. 10.1149/2.0461610jes. [DOI] [Google Scholar]
- Johansson P. Electronic structure calculations on lithium battery electrolyte salts. Phys. Chem. Chem. Phys. 2007, 9, 1493–1498. 10.1039/B612297C. [DOI] [PubMed] [Google Scholar]
- Xu K. Nonaqueous liquid electrolytes for lithium-based rechargeable batteries. Chem. Rev. 2004, 104, 4303–4418. 10.1021/cr030203g. [DOI] [PubMed] [Google Scholar]
- France-Lanord A.; Grossman J. C. Correlations from ion pairing and the Nernst-Einstein equation. Phys. Rev. Lett. 2019, 122, 136001. 10.1103/PhysRevLett.122.136001. [DOI] [PubMed] [Google Scholar]
- Manning G. S. Limiting laws and counterion condensation in polyelectrolyte solutions I. Colligative properties. J. Chem. Phys. 1969, 51, 924–933. 10.1063/1.1672157. [DOI] [Google Scholar]
- Manning G. S. Counterion binding in polyelectrolyte theory. Acc. Chem. Res. 1979, 12, 443–449. 10.1021/ar50144a004. [DOI] [Google Scholar]
- Nyquist R. M.; Ha B. Y.; Liu A. J. Counterion condensation in solutions of rigid polyelectrolytes. Macromolecules 1999, 32, 3481–3487. 10.1021/ma9811021. [DOI] [Google Scholar]
- González-Mozuelos P.; De La Cruz M. O. Ion condensation in salt-free dilute polyelectrolyte solutions. J. Chem. Phys. 1995, 103, 3145–3157. 10.1063/1.470248. [DOI] [Google Scholar]
- Tenney C. M.; Cygan R. T. Analysis of molecular clusters in simulations of lithium-ion battery electrolytes. J. Phys. Chem. C 2013, 117, 24673–24684. 10.1021/jp4039122. [DOI] [Google Scholar]
- Ullner M.; Woodward C. E. Orientational correlation function and persistence lengths of flexible polyelectrolytes. Macromolecules 2002, 35, 1437–1445. 10.1021/ma010863s. [DOI] [Google Scholar]
- Odijk T. Polyelectrolytes near the rod limit. J. Polym. Sci., Polym. Phys. Ed. 1977, 15, 477–483. 10.1002/pol.1977.180150307. [DOI] [Google Scholar]
- Skolnick J.; Fixman M. Electrostatic persistence length of a wormlike polyelectrolyte. Macromolecules 1977, 10, 944–948. 10.1021/ma60059a011. [DOI] [Google Scholar]
- Hara M.Polyelectrolytes: Science and Technology; Marcel Dekker: New York, 1993. [Google Scholar]
- Salanne M. Simulations of room temperature ionic liquids: From polarizable to coarse-grained force fields. Phys. Chem. Chem. Phys. 2015, 17, 14270–14279. 10.1039/C4CP05550K. [DOI] [PubMed] [Google Scholar]
- Rajput N. N.; Murugesan V.; Shin Y.; Han K. S.; Lau K. C.; Chen J.; Liu J.; Curtiss L. A.; Mueller K. T.; Persson K. A. Elucidating the solvation structure and dynamics of lithium polysulfides resulting from competitive salt and solvent interactions. Chem. Mater. 2017, 29, 3375–3379. 10.1021/acs.chemmater.7b00068. [DOI] [Google Scholar]
- Dünweg B.; Kremer K. Molecular dynamics simulation of a polymer chain in solution. J. Chem. Phys. 1993, 99, 6983–6997. 10.1063/1.465445. [DOI] [Google Scholar]
- Castiglione F.; Ragg E.; Mele A.; Appetecchi G. B.; Montanino M.; Passerini S. Molecular environment and enhanced diffusivity of Li+ ions in lithium-salt-doped ionic liquid electrolytes. J. Phys. Chem. Lett. 2011, 2, 153–157. 10.1021/jz101516c. [DOI] [Google Scholar]
- Sorte E. G.; Paren B. A.; Rodriguez C. G.; Fujimoto C.; Poirier C.; Abbott L. J.; Lynd N. A.; Winey K. I.; Frischknecht A. L.; Alam T. M. Impact of hydration and sulfonation on the morphology and ionic conductivity of sulfonated poly(phenylene) proton exchange membranes. Macromolecules 2019, 52, 857–876. 10.1021/acs.macromol.8b02013. [DOI] [Google Scholar]
- Kreuer K.-D.; Paddison S. J.; Spohr E.; Schuster M. Transport in proton conductors for fuel-cell applications: simulations, elementary reactions, and phenomenology. Chem. Rev. 2004, 104, 4637–4678. 10.1021/cr020715f. [DOI] [PubMed] [Google Scholar]
- Solano C. J.; Jeremias S.; Paillard E.; Beljonne D.; Lazzaroni R. A joint theoretical/experimental study of the structure, dynamics, and Li+ transport in bis([tri]fluoro[methane]sulfonyl)imide [T]FSI-based ionic liquids. J. Chem. Phys. 2013, 139, 034502. 10.1063/1.4813413. [DOI] [PubMed] [Google Scholar]
- Borodin O.; Smith G. D.; Henderson W. Li+ cation environment, transport, and mechanical properties of the LiTFSI doped N-methyl-N-alkylpyrrolidinium+TFSI– ionic liquids. J. Phys. Chem. B 2006, 110, 16879–16886. 10.1021/jp061930t. [DOI] [PubMed] [Google Scholar]
- Druger S. D.; Nitzan A.; Ratner M. A. Dynamic bond percolation theory: A microscopic model for diffusion in dynamically disordered systems. I. Definition and one-dimensional case. J. Chem. Phys. 1983, 79, 3133–3142. 10.1063/1.446144. [DOI] [Google Scholar]
- Borodin O.; Smith G. D. Mechanism of ion transport in amorphous poly(ethylene oxide)/ LiTFSI from molecular dynamics simulations. Macromolecules 2006, 39, 1620–1629. 10.1021/ma052277v. [DOI] [Google Scholar]
- Reger A.; Peled E.; Gileadi E. Mechanism of high conductivity in a medium of low dielectric constant. J. Phys. Chem. 1979, 83, 873–879. 10.1021/j100470a023. [DOI] [Google Scholar]
- Hwang S.; Kim D. H.; Shin J. H.; Jang J. E.; Ahn K. H.; Lee C.; Lee H. Ionic conduction and solution structure in LiPF6 and LiBF4 propylene carbonate electrolytes. J. Phys. Chem. C 2018, 122, 19438–19446. 10.1021/acs.jpcc.8b06035. [DOI] [Google Scholar]
- Kamcev J.; Paul D. R.; Manning G. S.; Freeman B. D. Ion diffusion coefficients in ion exchange membranes: significance of counterion condensation. Macromolecules 2018, 51, 5519–5529. 10.1021/acs.macromol.8b00645. [DOI] [Google Scholar]
- Wright M. R.An Introduction to Aqueous Electrolyte Solutions; John Wiley, 2007. [Google Scholar]
- Yeh I.-C.; Hummer G. Diffusion and electrophoretic mobility of single-stranded RNA from molecular dynamics simulations. Biophys. J. 2004, 86, 681–689. 10.1016/S0006-3495(04)74147-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bruce P. G.; Vincent C. A. Steady state current flow in solid binary electrolyte cells. J. Electroanal. Chem. Interfacial Electrochem. 1987, 225, 1–17. 10.1016/0022-0728(87)80001-3. [DOI] [Google Scholar]
- Balsara N. P.; Newman J. Relationship between steady-state current in symmetric cells and transference number of electrolytes comprising univalent and multivalent ions. J. Electrochem. Soc. 2015, 162, A2720–A2722. 10.1149/2.0651514jes. [DOI] [Google Scholar]
- Bruce P. G.; Hardgrave M. T.; Vincent C. A. The determination of transference numbers in solid polymer electrolytes using the Hittorf method. Solid State Ionics 1992, 53–56, 1087–1094. 10.1016/0167-2738(92)90295-Z. [DOI] [Google Scholar]
- Fritz H. P.; Kuhn A. Comparative determination of effective transport numbers in solid lithium electrolytes. J. Power Sources 1993, 41, 253–261. 10.1016/0378-7753(93)80043-O. [DOI] [Google Scholar]
- Walls H. J. Anion and cation transference numbers determined by electrophoretic NMR of polymer electrolytes sum to unity. Electrochem. Solid-State Lett. 1999, 3, 321. 10.1149/1.1391136. [DOI] [Google Scholar]
- Dong D.; Bedrov D. Charge transport in [Li(tetraglyme)][bis(trifluoromethane) sulfonimide] solvate ionic liquids: insight from molecular dynamics simulations. J. Phys. Chem. B 2018, 122, 9994–10004. 10.1021/acs.jpcb.8b06913. [DOI] [PubMed] [Google Scholar]
- McDaniel J. G.; Son C. Y. Ion correlation and collective dynamics in BMIM/BF4– based organic electrolytes: From dilute solutions to the ionic liquid limit. J. Phys. Chem. B 2018, 122, 7154–7169. 10.1021/acs.jpcb.8b04886. [DOI] [PubMed] [Google Scholar]
- Kashyap H. K.; Annapureddy H. V. R.; Raineri F. O.; Margulis C. J. How is charge transport different in ionic liquids and electrolyte solutions?. J. Phys. Chem. B 2011, 115, 13212–13221. 10.1021/jp204182c. [DOI] [PubMed] [Google Scholar]
- Dong D.; Sälzer F.; Roling B.; Bedrov D. How efficient is Li+ ion transport in solvate ionic liquids under anion-blocking conditions in a battery?. Phys. Chem. Chem. Phys. 2018, 20, 29174–29183. 10.1039/C8CP06214E. [DOI] [PubMed] [Google Scholar]
- Molinari N.; Mailoa J. P.; Kozinsky B.. General trend of negative transference number in Li salt/ionic liquid mixtures. 2019, 1–21, 10.26434/chemrxiv.7728545. [DOI] [Google Scholar]
- Vink H.Physical Chemistry of Polyelectrolytes; CRC Press: Boca Raton, FL, 2001; Chapter 7, pp 225–244. [Google Scholar]
- Vink H. The dynamic frictional theory of transport processes in relation to nonequilibrium thermodynamics. J. Colloid Interface Sci. 1993, 160, 51–58. 10.1006/jcis.1993.1366. [DOI] [Google Scholar]
- Colby R. H.; Boris D. C.; Krause W. E.; Tan J. S. Polyelectrolyte conductivity. J. Polym. Sci., Part B: Polym. Phys. 1997, 35, 2951–2960. . [DOI] [Google Scholar]
- Haskins J. B.; Bennett W. R.; Wu J. J.; Hernández D. M.; Borodin O.; Monk J. D.; Bauschlicher C. W.; Lawson J. W. Computational and experimental investigation of Li-doped ionic liquid electrolytes: [pyr14][TFSI], [pyr13][FSI], and [EMIM][BF4]. J. Phys. Chem. B 2014, 118, 11295–11309. 10.1021/jp5061705. [DOI] [PubMed] [Google Scholar]
- Muthukumar M. Dynamics of polyelectrolyte solutions. J. Chem. Phys. 1997, 107, 2619–2635. 10.1063/1.474573. [DOI] [Google Scholar]
- Chatare V.; Chereddy S.; Gobet M. P.; Wunder S. L.; DiLuzio S. P.; Greenbaum S. G.; Chinnam P. R. An alternative route to single ion conductivity using multi-ionic salts. Mater. Horiz. 2018, 5, 461–473. 10.1039/C7MH01130J. [DOI] [Google Scholar]
- Plimpton S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. 10.1006/jcph.1995.1039. [DOI] [Google Scholar]
- http://lammps.sandia.gov (accessed Aug 11, 2017).
- Martínez L.; Andrade R.; Birgin E. G.; Martínez J. M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. 10.1002/jcc.21224. [DOI] [PubMed] [Google Scholar]
- Toukmaji A. Y.; Board J. A. Ewald summation techniques in perspective: a survey. Comput. Phys. Commun. 2003, 95, 73–92. 10.1016/0010-4655(96)00016-1. [DOI] [Google Scholar]
- Andersen H. C. Rattle: A ”velocity” version of the shake algorithm for molecular dynamics calculations. J. Comput. Phys. 1983, 52, 24–34. 10.1016/0021-9991(83)90014-1. [DOI] [Google Scholar]
- Ryckaert J. P.; Ciccotti G.; Berendsen H. J. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. 10.1016/0021-9991(77)90098-5. [DOI] [Google Scholar]
- Banks J. L.; et al. Integrated modeling program, applied chemical theory (IMPACT). J. Comput. Chem. 2005, 26, 1752–1780. 10.1002/jcc.20292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schrödinger. MacroModel, 2018.
- Leontyev I.; Stuchebrukhov A. Accounting for electronic polarization in non-polarizable force fields. Phys. Chem. Chem. Phys. 2011, 13, 2613–2626. 10.1039/c0cp01971b. [DOI] [PubMed] [Google Scholar]
- Michaud-Agrawal N.; Denning E. J.; Woolf T. B.; Beckstein O. MDAnalysis: A toolkit for the analysis of molecular dynamics simulations. J. Comput. Chem. 2011, 32, 2319–2327. 10.1002/jcc.21787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gowers R.; Linke M.; Barnoud J.; Reddy T.; Melo M.; Seyler S.; Domański J.; Dotson D.; Buchoux S.; Kenney I.; Beckstein O. MDAnalysis: A Python package for the rapid analysis of molecular dynamics simulations. Proceedings of the 15th Python in Science Conference 2016, 98–105. 10.25080/Majora-629e541a-00e. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.