Abstract
This work examined in detail the a priori prediction of the axial dispersion coefficient from available correlations versus obtaining both it and mass transfer information from experimental breakthrough data and the consequences that may arise when doing so based on using a 1-D axially dispersed plug flow model and its associated Danckwerts outlet boundary condition. These consequences mainly included determining the potential for erroneous extraction of the axial dispersion coefficient and/or the LDF mass transfer coefficient from experimental data, especially when nonplug flow conditions prevailed in the bed. Two adsorbent/adsorbate cases were considered, i.e., CO2 and H2O vapor in zeolite 5A, because they both experimentally exhibited significant nonplug flow behavior, and the H2O-zeolite 5A system exhibited unusual concentration front sharpening that destroyed the expected constant pattern behavior (CPB) when modeled with the 1-D axially dispersed plug flow model. Overall, this work showed that it was possible to extract accurate mass transfer and dispersion information from experimental breakthrough curves using a 1-D axial dispersed plug flow model when they were measured both inside and outside the bed. To ensure the extracted information was accurate, the inside the bed breakthrough curves and their derivatives from the model were plotted to confirm whether or not the adsorbate/adsorbent system was exhibiting CPB or any concentration front sharpening near the bed exit. Even when concentration front sharpening was occurring with the H2O-zeolite 5A system, it was still possible to use the experimental inside and outside the bed breakthrough curves to extract fundamental mass transfer and dispersion information from the 1-D axial dispersed plug flow model based on the systematic methodology developed in this work.
Graphical Abstract
1. INTRODUCTION
A major issue associated with achieving a fully predictive simulation of gas adsorption in fixed beds is finding values for the free (i.e., unknown) parameters in either the mass balance or energy balance partial differential equations. It is thus advantageous to reduce the number of free parameters by using verified correlations to determine the mass and heat transfer coefficients a priori. However, when parameters cannot be determined a priori, simplifications are utilized that lump multiple heat or mass transfer mechanisms together, with the corresponding coefficients (i.e., lumped free parameters) potentially losing their meaning. These coefficients are necessarily determined empirically by fitting to experimental data.
One such simplification is the one-dimensional (1-D) axially dispersed plug flow model that is frequently used to simulate fixed-bed adsorption processes.1–5 The axial dispersion term in this model leads naturally to the ubiquitous use of the Danckwerts boundary condition at the outlet of the bed. This is a Neumann boundary condition that can be derived rigorously when pure axial molecular diffusion is accounted for with continuity of concentration and mass flux across the outlet boundary.6 Two issues arise from the use of this simplified 1-D model that limit its utility.
The first issue is associated with the a priori prediction of the axial dispersion coefficient from available correlations. Numerous correlations are available based on the particle Peclet number, velocity, and pellet diameter.4,7–10 In principle, these correlations should work fine, but in practice they do not. The actual mechanisms that contribute to axial and radial mixing in fixed beds are necessarily lumped into the axial dispersion term. These mechanisms include turbulence, flow splitting and rejoining around particles, Taylor dispersion, channeling, and wall effects.11–13 Not only do none of these correlations account for all the different dispersion mechanisms mentioned above, but also there is considerable variance in the values obtained from them. To make matters even worse, the 1-D axially dispersed plug flow model only accounts for dispersion mechanisms that fall within the framework of the plug flow condition.
Nevertheless, axial dispersion in a fixed-bed adsorber cannot be ignored because it reduces the adsorption process efficiency. To capture its influence, the axial dispersion coefficient is typically considered an adjustable parameter in the 1-D model and fit to experimental breakthrough curves. Although this approach is sound in principle and widely adopted, if the experiments are not designed properly the information obtained from them may be erroneous.
The second issue concerns the development of constant pattern behavior (CPB) inside the bed, wherein the concentration front (i.e., concentration bed profile) propagates through the bed without changing its shape. CPB has been widely established theoretically4,14 and confirmed experimentally for systems with favorable Type I isotherms.12,15 However, an unusual situation may arise when modeling a fixed-bed adsorber with the 1-D axially dispersed plug flow model because of its inherent assumptions. For example, when used to analyze experimental data, solutions obtained for fixed-bed adsorption with axial diffusion described by the Fickian model may produce breakthrough curve sharpening for both shallow and deep beds.6,16 While this concentration front sharpening effect is appropriate for axial molecular diffusion under plug flow conditions, it fails to correctly capture the more complicated dispersive dynamics present in many adsorption systems. In other words, if an experiment could be designed that was described perfectly well by the 1-D axial dispersed plug flow model with axial dispersion described by Fickian molecular diffusion, then experimentally concentration front sharpening would indeed be observed at the end of the bed and thus it is a real phenomenon. The inherent problem lies in the fact that it would be difficult, if not impossible, to design such an experiment in fixed-bed adsorption.
This concentration front sharpening effect has been largely ignored in the literature, except for a few studies.6,12 In many simulation studies, neither the internal concentration histories nor the bed concentration profiles are shown to verify CPB. Quite possibly, the breakthrough curve from the model is blindly fitted to the experimental breakthrough curve to obtain mass transfer information, like the linear driving force (LDF) mass transfer coefficient, while perhaps limiting itself to dispersion coefficients predicted from known correlations.17–21 The results obtained in such cases may be erroneous because they may have been obtained from experimental results dominated by nonplug conditions or from simulated breakthrough curves that deviated from the expected and real CPB physics due to concentration front sharpening occurring near the exit of the bed.
The objective of this work is to examine in detail the issues described above. These issues are the a priori prediction of the axial dispersion coefficient from available correlations versus obtaining it and also the LDF mass transfer coefficient from experimental breakthrough data and the consequences that may arise when doing so based on using the 1-D axially dispersed plug flow model and its associated Danckwerts outlet boundary condition. Two adsorbent/adsorbate cases are considered, i.e., CO2 and H2O vapor in zeolite 5A, which illuminate these issues.
2. EXPERIMENTAL SECTION
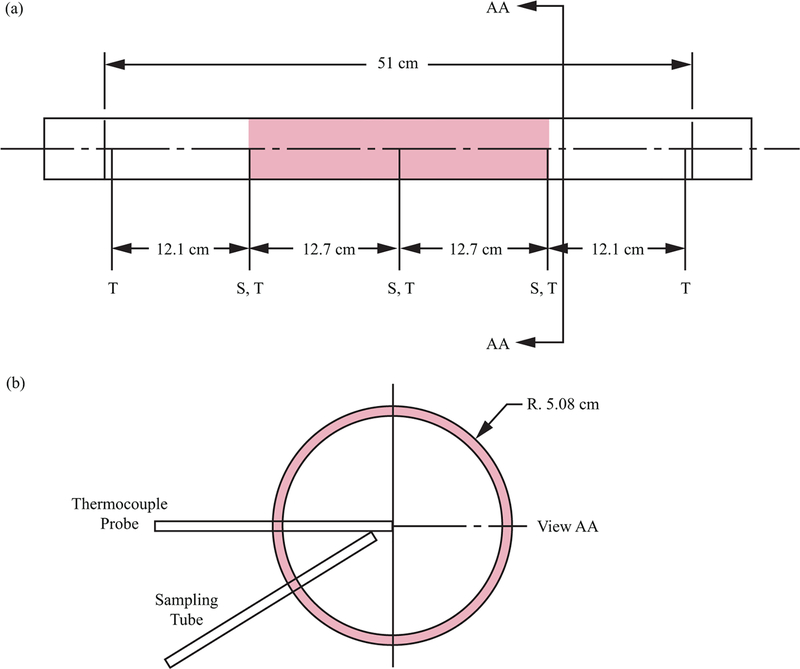
The fixed-bed adsorption breakthrough experiments analyzed and discussed in this work were extracted from the work of Knox.22 The fixed-bed adsorption breakthrough apparatus used is shown in Figure 1; its properties are listed in Table 1. The center of a roughly 51 cm long × 5.08 cm outer diameter tube was used to house a packed bed of adsorbent 25.4 cm in height. The remainder of the column was packed with glass beads. Temperatures were measured at the packed bed section inlet, midpoint, and exit. As in typical breakthrough test setups, concentration was measured downstream of the tube outlet. In addition, gas samples were taken at the centerline of the packed bed at the inlet, midpoint, and exit. As shown in the figure, gas sample lines were located as close as possible to the centerline of the column and the thermocouple junction. In order to prevent disturbing the downstream flow, a gas chromatograph was used to measure internal concentrations, thus allowing for the sample flow volume to be a small fraction of the overall flow. The zeolite 5A adsorbent was obtained from Grace Davison (Grade 522) in bead form. The adsorbent properties23,24 are also listed in Table 1. The experimental procedure that describes how a typical breakthrough experimental was carried out is given in Knox.22
Figure 1.
(a) Breakthrough test apparatus of Knox22 and (b) cross-sectional view of a typical temperature measurement and gas sampling location. “T” indicates thermocouple probe location, and “S” indicates sampling tube location. Shading in (a) indicates location of sorbent packing.
Table 1.
Properties of the Zeolite 5A Adsorbent and Fixed-Bed Adsorption Breakthrough Apparatus
| 5A adsorbent | fixed-bed apparatus | ||
|---|---|---|---|
| pellet radius (spherical) | Rp = 1.16 mm | bed height | L = 0.254 m |
| particle density | ρs = 1180 kg m−3 | void fraction | e = 0.35 |
| skeletal density | ρsk = 2040 kg m−3 | bed internal diameter | D; = 47.6 mm |
| heat capacity | Cps = 920J kg−1 K−1 | column wall thickness | I = 1.59 mm |
| wall density | ρw = 7833 kg m−3 | wall heat capacity | Cpw = 475 J kg−1 K−1 |
| wall conduction | kw = 14.2 Wm−1 K−1 | ||
3. MATHEMATICAL MODEL
3.1. Gas-Phase Mass Balance.
The commonly employed 1-D axially dispersed plug flow model is shown in eq 1
| (1) |
where DL is the axial dispersion coefficient, x is the axial coordinate, υi is the interstitial velocity, t is the time, ε is the bulk void fraction, is the average adsorbed-phase concentration of the adsorbate, and c is the gas-phase concentration of the adsorbate defined according to the ideal gas law, i.e.
| (2) |
where p is the partial pressure of the adsorbate, Tf is the fluid (gas phase) temperature, and R is the universal gas constant.
Eq 1 is derived from a differential mass balance based on the following assumptions: All mechanical dispersion effects are lumped together with molecular diffusion in the axial dispersion term. Plug flow is assumed, i.e., there is no gradient of velocity, concentration, temperature, or porosity in the radial direction. Velocity in the axial direction is not compensated for loss of adsorbate since the adsorbate gas-phase mole fraction is ≪1. Velocity is temperature compensated per the ideal gas law.
The boundary conditions are shown in eq 3. A constant flux boundary condition is used for the inlet concentration, and the Danckwerts boundary condition is used for the outlet25
| (3) |
where co is the concentration and υs is the superficial velocity (both far upstream), and L is the bed height.
3.2. Adsorbed-Phase Mass Balance.
The transport of the adsorbate from the gas phase to the adsorbed phase is described by a linear driving force (LDF) approximation,26 as shown in eq 4
| (4) |
where kn is the LDF mass transfer coefficient, and q* is the equilibrium adsorbed-phase concentration that corresponds to the adsorbate gas-phase partial pressure p at the sorbent temperature Ts based on the equilibrium adsorption isotherm shown later. The LDF approximation is frequently used with the 1-D axially dispersed plug flow model in the analysis of adsorption processes. All the transfer resistances, including micropore and macropore resistances and surface diffusion, are lumped into the LDF mass transfer coefficient. If the mass transfer resistance is assumed to be a single mass transfer mechanism that is dominant and constant throughout the adsorption process, then this approach is valid. Moreover, it is well-known that the LDF approximation incurs little error for most commercial gas phase cycle adsorption processes when empirically derived.5,27
3.3. Energy Balance.
For the adsorbent/adsorbate systems and concentrations studied, significant deviations from isothermal conditions were observed.22,28 Therefore, energy balance equations for the gas (fluid), adsorbent, and column wall are included in the model. The gas-phase energy balance is provided in eq 5. This equation includes transient heat storage, gas conduction, gas convection, and heat transfer from the adsorbent to the column wall via Newton’s law of cooling29
| (5) |
where af is the superficial free flow area, ρf is the gas-phase density, cpf is the gas-phase heat capacity, keff is the effective gas-phase conductivity, as is the pellet external surface area per unit volume, hs is the adsorbent to gas heat transfer coefficient, Ts is the adsorbent temperature, Pi is the inner perimeter of the column, hi is the heat transfer coefficient between the column wall and the gas-phase, and Tw is the column wall temperature.
The boundary conditions for the gas-phase energy balance are shown in eq 6. A constant flux boundary condition is used for the gas inlet, and a Danckwerts-type boundary condition is used for the outlet that specifies no thermal dispersion
| (6) |
where T0, ρf0, and cpf0 are the temperature, density, and heat capacity far upstream.
The adsorbent energy balance is provided in eq 7. This equation includes transient energy storage, heat conduction, and heat transfer from the gas phase via Newton’s law of cooling and the heat of adsorption
| (7) |
where ρs is the adsorbent density, cps is the adsorbent heat capacity, and λ is the isosteric heat of adsorption.
The column wall energy balance is similar and provided in eq 8. This equation includes transient energy storage, heat conduction, and heat transfer from the internal gas phase to the ambient environment via Newton’s law of cooling
| (8) |
where aw is the cross-sectional area of the column, ρw is the column wall density, cpw is the column wall heat capacity, kw is the column wall conductivity, Po is the column wall outer perimeter, Ta is the ambient temperature, and ho is the column wall to ambient heat transfer coefficient.
3.4. Equilibrium Adsorption Isotherms.
The Toth equilibrium adoption isotherm is used to calculate the equilibrium adsorbed-phase loading corresponding to the adsorbate gas-phase partial pressure. The single gas Toth isotherm is shown in eq 9
| (9) |
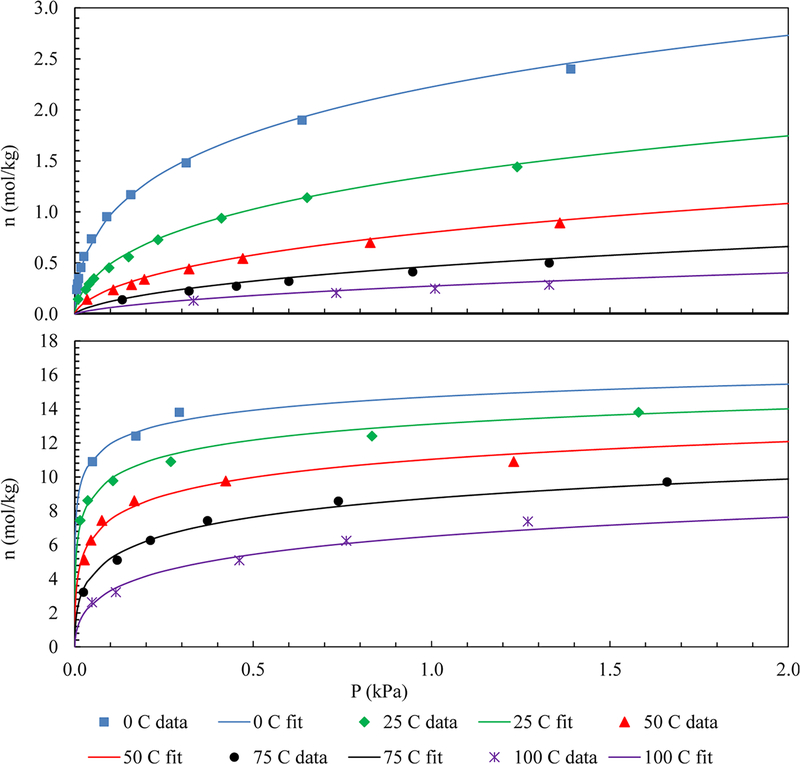
where n is the loading of the adsorbate in the adsorbed phase, a is the saturation capacity, b is an equilibrium constant, and t is the heterogeneity parameter. Parameters a, b, and t are temperature dependent as shown, whereas a0, b0, and t0 are system dependent adsorption isotherm parameters. A comparison of the Toth equation and the experimental data are shown in Figure 2; the corresponding adsorption isotherm parameters were obtained from Wang and LeVan30 and given in Table 2.
Figure 2.
Equilibrium adsorption isotherms for CO2 (top) and H2O vapor (bottom) on zeolite 5A.30 Symbols: experimental data. Lines: Toth equation.
Table 2.
Toth Equation Equilibrium Adsorption Isotherm Parameters for CO2 and H2O Vapor on Zeolite 5A30
| System | a0 (mol·kg−1·kPa−1) | b0 (kPa−1) | E (K) | t0 | c (K) |
|---|---|---|---|---|---|
| CO2/5A | 9.875 × 10−7 | 6.761 × 10−8 | 5.625 × 103 | 2.700 × 10−1 | −2.002 × 101 |
| H2O/5A | 1.106 × 10−8 | 4.714 × 10−10 | 9.955 × 103 | 3.548 × 10−1 | −5.114 × 101 |
3.5. Axial Dispersion Coefficient.
Five different correlations that describe axial dispersion in packed beds based on the pellet Peclet (Pe) number as a function of the product of the Reynolds (Re) and Schmidt (Sc) numbers are shown in eq 10a per Wakao and Funazkri,7 eq 10b per Edwards and Richardson,8 eq 10c per Wicke,9 eq 10d per Ruthven4, and eq 10e per Wen and Fan10
| (10a) |
| (10b) |
| (10c) |
| (10d) |
| (10e) |
The definitions of the Re, Sc, and Pe numbers are provided in eq 11
| (11) |
where Rp is the pellet radius, D is the fluid diffusion coefficient determined with the Fuller method described by Poling31, and μ is the fluid viscosity determined with the Lucas corresponding states method also described by Poling.31 As mentioned above, the large variation in the ranges of values and the trends provided by these five different correlations is well-known.
3.6. Gas-Phase Properties: Heat Transfer.
The gas-phase heat capacity (cp) is calculated based on parameters obtained from Reid.32 The polynomial equation used is shown in eq 12
| (12) |
where a0–a3 are the four parameters fitted to experimental heat capacity values. The mixture gas heat capacity was obtained via a weighted average on a molar basis.
3.7. Correlations for Heat Transfer Coefficients.
The heat transfer coefficient hs from the gas phase to the pellet is calculated using a film diffusion relationship developed for mass transfer by Wakao and Funazkri7 and a similarity expression given by Ruthven.4 These relationships are given in eqs 13 and 14, respectively. Eqs 13 and 14 have been verified experimentally for fluid-to-particle heat transfer4,7
| (13) |
| (14) |
where Sh is the Sherwood number defined in eq 14.
The heat transfer coefficient hi from the gas phase to the interior wall of the column is calculated based on the correlation of Li and Finlayson33 for 1-D models, as shown in eq 15
| (15) |
where Nu is the Nusselt number.
3.8. Effective Thermal Conductivity.
The Krupickzka equation, given by eq 16, is used to calculate the effective thermal conductivity (ke) of a quiescent bed of spherical particles34,35
| (16) |
The effective axial thermal conductivity for a fixed bed of spherical particles with flow is calculated from the correlation of Yagi,36 as shown in eq 17; it was verified against test data by Kaviany35
| (17) |
where Pr is the Prandtl number. The gas-phase conductivity (kf) is calculated based on the analogy between mass and heat transfer and the fluid diffusivity, as shown in eq 18
| (18) |
4. RESULTS AND DISCUSSION
The 1-D axial dispersed plug flow model equations described in Section 3 were solved using the COMSOL Multiphysics software package (Version 5.1). The initial conditions for the gas and adsorbed phases in the bed were each set to values 3 orders of magnitude lower than their corresponding inlet equilibrium states. This means the bed was not clean at time equal to zero. It also means the bed was not in an equilibrium state at time equal to zero. The effect of this initial state of the bed was inconsequential because the concentrations in both phases were very small.
Two of the three free (unknown) parameters, which included one of the heat transfer coefficients (ho) and the axial dispersion coefficient (DL), were determined either a priori using the correlations described in Section 3 or by fitting the model to the experimental data. The LDF mass transfer coefficient (kn) was determined by fitting the model to the experimental data. In all cases, when determining a free parameter by fitting the model to experimental data, the sum of squared residuals (SSR) was minimized. When comparing simulated breakthrough curves to experimental data, the SSR was minimized between 25 and 75% of the inlet concentration to focus the fit on the midheight slope of the breakthrough curve.
The heat transfer properties of the experimental apparatus were determined first. Then, the mass transfer properties of each adsorbent/adsorbate system were determined in terms of finding kn for each adsorbent/adsorbate system by fitting the model to experimental data with DL determined a priori from the correlations in Section 3. Finally, it was necessary to re-evaluate the DL for each system by fitting the model to experimental data while using the value of kn just found for each adsorbent/adsorbate system. The features of each adsorbent/adsorbate system are discussed in detail throughout this systematic analysis that was developed to determine their heat and mass transfer properties.
4.1. Thermal Characterization Tests and Verification of Heat Transfer Parameters.
To determine and verify the heat transfer parameters, the model was compared to a thermal characterization experimental test that was performed by introducing heated nitrogen to the inlet of the column. The adsorbent was regenerated prior to the test, as described elsewhere.22 The test conditions are shown in Table 3.
Table 3.
Test Conditions for Thermal Characterization, Breakthrough Tests with CO2 on Zeolite 5A, and Breakthrough Tests with H2O Vapor on Zeolite 5A
| parameter | thermal characterization | CO2/5A | H2O/5A |
|---|---|---|---|
| flow rate, L min−1 at STP | 28.0 | 28.3 | 28.3 |
| initial temp, K | 297 | 299 | 297 |
| initial inlet temp, K | 297 | 298 | 297 |
| inlet pressure, kPa | 107 | 106 | 107 |
| inlet partial pressure, kPa | n/a | 0.819 | 0.805 |
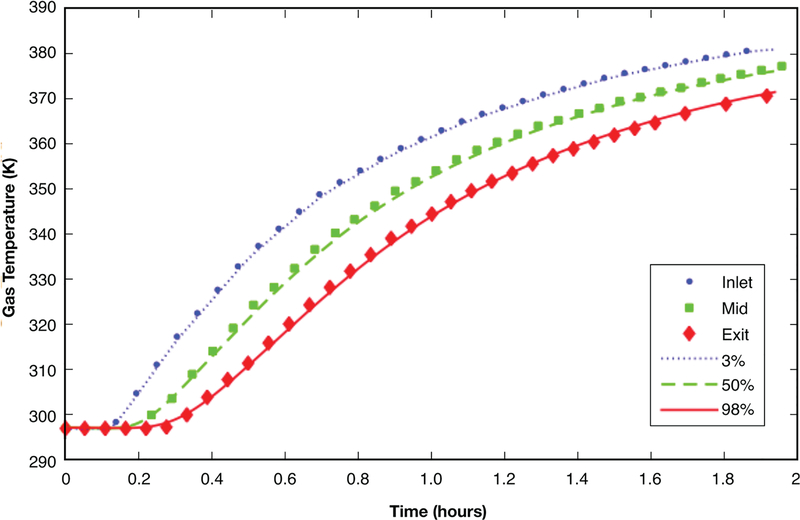
Figure 3 shows a comparison of the thermal characterization test data and the corresponding model results. Measurement uncertainty for a 95% confidence interval was determined to be ±0.4 K for temperature readings.37 The inlet temperature provided the boundary condition for the simulation. The only adjustable parameter was the heat transfer coefficient (ho) from the column wall to the surroundings; all the other parameters were obtained from the heat transfer correlations given in Section 3. A value of ho = 1.685 Wm−1 K−1 provided the best fit to the thermal characterization test data, with the resulting simulated temperatures closely matching the experimental temperatures measured at the inlet (2.5%), middle (50%), and exit (97.5%) of the bed. On the basis of these favorable results, the heat transfer correlations and ho = 1.685 Wm−1 K−1 were used for all the breakthrough tests discussed below.
Figure 3.
Comparison of thermal characterization test data (symbols) and simulation (lines) at three locations in the bed (% from feed end).
4.2. Experimental Breakthrough Tests for CO2 and H2O Vapor on Zeolite 5A.
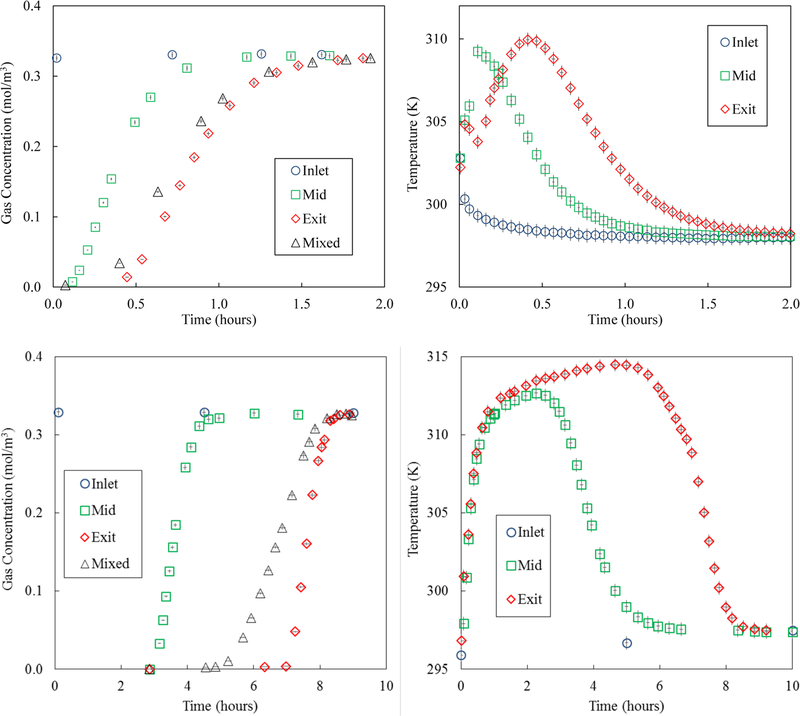
The experimental breakthrough test conditions for CO2 and H2O vapor on zeolite 5A are provided in Table 3. In preparation for these tests, the adsorbent was purged with helium gas heated to 590 K to ensure starting with a fully regenerated bed. Nitrogen was used as the carrier gas for these breakthrough tests. The breakthrough test results for both CO2 and H2O vapor are shown in Figure 4 in terms of the resulting experimental gas-phase concentration and temperature profile histories. The centerline gas-phase concentration profile histories were measured just inside the bed (2.5% into the bed), in the middle of the bed (50% into the bed), and just inside the exit of the bed (97.5% into the bed). The typical gas-phase concentration breakthrough curve was also measured just outside the bed. Measurement uncertainty for a 95% confidence interval was determined to be ±0.4 K for temperature readings, ±1.3% of reading for water vapor concentrations, and ±1.2% of reading for carbon dioxide concentrations. Uncertainty in time was determined to be ±1.3% of reported time.37
Figure 4.
Left panels: Experimental gas-phase concentration profile history breakthrough curves for CO2 (top) and H2O vapor (bottom) on zeolite 5A at 3 centerline locations in the bed (circles: 2.5%, squares: 50%, and diamonds: 97.5%) and just outside the bed (triangles). Right panels: Corresponding experimental temperature profile histories for CO2 (top) and H2O vapor (bottom) on zeolite 5A at 3 centerline locations in the bed (circles: 2%, squares: 50%, and diamonds: 98%). Error bars show experimental uncertainty.
The early peaks in the experimental temperature profile histories observed for CO2 (Figure 4 top) at the 97.5% location were due to the initial adsorption of N2. Recall the bed was filled with He at the start of a run. This feature was not observed with the H2O vapor-zeolite 5A system (Figure 4 bottom) simply due to the much longer time scale of that run.
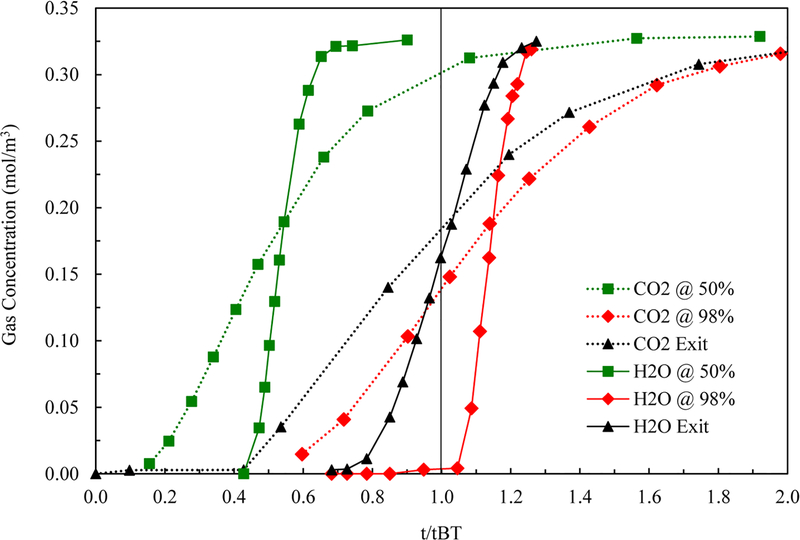
The discrepancies between the gas-phase concentration profile histories for both adsorbates at the 97.5% location, which are not generally available in breakthrough studies in the literature, and those just outside the bed provided insight into the nature of the actual, nonplug flow conditions existing in the bed. The earlier breakthroughs observed with the outside bed profiles indicated that channeling was probably occurring along the inner wall of the column. This nonplug flow behavior was most readily observed for H2O vapor.
Channeling is generally known to occur due to a higher near-wall gas flow rate that is associated with a lower packing density (i.e., higher void fraction) close to the wall. This was a surprising result, especially when considering that the ratio of the bed to pellet diameter for this packed bed was around 20. A value of 20 is generally considered to be large enough to obviate the wall effects due to the near-wall lower packing density.38
The analyses in Figure 5 and Table 4 show that the origin of this nonplug flow condition was independent of the adsorbates involved. This was expected, but only if the dispersion for each system was the same and derived from a mechanical phenomenon like that associated with near-wall channeling. To prove this supposition, the same experimental gas-phase concentration profiles histories are shown in Figure 5 for the 50%, 97.5%, and just outside the bed locations for both CO2 and H2O vapor but now plotted against a dimensionless time (t/tBT) defined relative to the respective breakthrough time for each adsorbate for the breakthrough curve measured just outside the bed, i.e., tBT. Table 4 shows the dimensionless breakthrough times for both species at the 50% and 97.5% locations relative to tBT, where was evaluated based on the formulation for dilute systems, i.e.
| (19) |
The relative temporal locations of the breakthrough curve times at the 50% and 97.5% locations were nearly identical for both CO2 and H2O vapor, as expected for a mechanical dispersion phenomenon that should be independent of the adsorbate. It is also worth pointing out the self-consistency of the experimental outside the bed breakthrough curves for the CO2 and H2O vapor systems. When plotted as shown in Figure 5, the two curves should cross at t/tBT = 1. A vertical line was drawn at t/tBT = 1 in Figure 5 to emphasize this point. Clearly, only a slight vertical difference existed between the two curves at the crossing point.
Figure 5.
Experimental gas-phase concentration profile history breakthrough curves for CO2 (dotted lines) and H2O vapor (solid lines) on zeolite 5A at 2 centerline locations in the bed (squares: 50%, and diamonds: 97.5%) and just outside the bed (triangles) plotted against dimensionless time defined relative to the respective breakthrough time for each adsorbate for the breakthrough curve measured just outside the bed, i.e., tBT.
Table 4.
Center of Mass Gas-Phase Concentration Profile History Breakthrough Curve Time Ratios for CO2 and H2O Vapor on Zeolite 5A at 2 Centerline Locations in the Bed (from Figure 5)
| CO2 on zeolite 5A | H2O vapor on zeolite 5A | % difference | ||
|---|---|---|---|---|
| 97.5% to outside | 1.144 | 97.5% to outside | 1.140 | 0.34% |
| 50% to outside | 0.5422 | 50% to outside | 0.5396 | 0.48% |
4.3. Empirical Determination of the LDF Mass Transfer Coefficient kn.
The determination of a mass transfer parameter, like kn, is commonly accomplished by fitting the 1-D axial dispersed plug flow model to an experimental breakthrough curve measured at a location outside the bed, just like those shown in Figure 4. From the analysis provided so far it should be clear that even for a proper bed to pellet diameter ratio of 20, a breakthrough curve obtained just outside the bed may not be providing fundamental mass transfer information, because it may be strongly subjected to nonplug flow effects that are most likely due to near-wall channeling. It is shown below that this dilemma can be resolved by using the experimental centerline gas-phase concentration profile histories to determine kn, as the nonplug flow, near-wall channeling effects should not exist along the centerline of the column.
First, the dispersion coefficients were predicted for each adsorbate/adsorbent system from the five correlations given in eq 10. The results are summarized in Table 5. The dispersion coefficients predicted from the Edwards and Richardson correlation (eq 10b) were within 2% of the smallest values obtained from the Wen and Fan correlation (eq 10e), and those from the Wakao and Funazkri correlation were (eq 10a) the largest values. The dispersion coefficients predicted from the other two correlations fell in between. Between the largest and smallest values, there was a factor of 2 for CO2 on zeolite 5A and a factor of nearly three for H2O vapor on zeolite 5A. Based on these findings, both the Edwards and Richardson (eq 10b) and Wakao and Funazkri (eq 10a) correlations (which encompass the extremes) were used in the determination of kn to see if there was any effect of the magnitude of the predicted dispersion coefficient.
Table 5.
Axial Dispersion Coefficients Predicted from the Five Correlations Given in Eq 10 and the Resulting LDF kn Values Obtained from Fitting the 1-D Axial Dispersed Plug Flow Model to the 97.5% Location Experimental Centerline Gas-Phase Concentration Breakthrough Curves for CO2 and H2O Vapor on Zeolite 5A Using Only the Top Two Dispersion Coefficient Correlations Listed
| CO2 on zeolite 5A | H2O on zeolite 5A | ||||
|---|---|---|---|---|---|
| kn,s−1 | Dl correlation | DL, m2 s−1 | kn,s−1 | Dl correlation | Dl, m2 s−1 |
| 2.2 × 10−3 | Edwards and Richardson | 8.99 × 10−4 | 8.8 × 10−4 s−1 | Edwards and Richardson | 8.62 × 10−4 |
| 2.3 × 10−3 | Wakao and Funuzkri | 1.89 × 10−3 | 9.8 × 10−4 s−1 | Wakao and Funazkri | 2.40 × 10−3 |
| Wicke | 9.91 × 10−4 | Wicke | 9.91 × 10−4 | ||
| Ruthven | 9.72 × 10−4 | Ruthven | 9.63 × 10−4 | ||
| Wen and Fan | 8.93 × 10−4 | Wen and Fan | 8.47 × 10−4 | ||
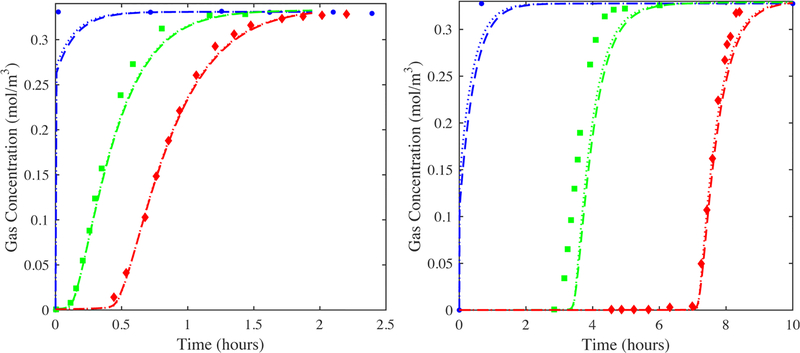
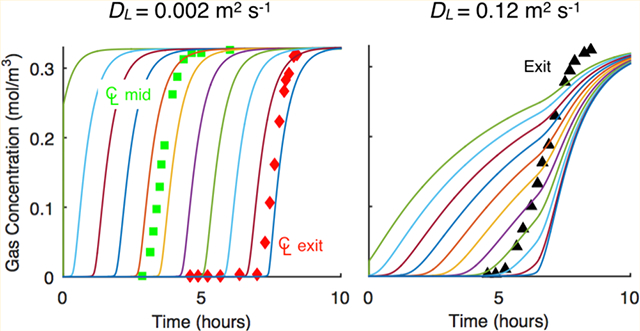
Figure 6 shows fits of the model to the 97.5% location experimental gas-phase concentration breakthrough curves for both adsorbate/adsorbent systems using axial dispersion coefficients predicted from the Edwards and Richardson (eq 10a) and Wakao and Funazkri (eq 10b) correlations. The corresponding LDF kn values, the only adjustable parameter, are listed in Table 5. In all cases, the saturation terms of the isotherms for both CO2 and H2O were adjusted to make the model agree with the location of the experimental results along the x-axis. These capacity adjustments were inconsequential to the resulting kn values and were done to show how well the model fitted the data. Figure 6 also shows predictions from the model at the 2.5% and 50% experimental locations for both systems using the resulting kn values.
Figure 6.
Fits of the 1-D axial dispersed plug flow model to the 97.5% location (diamonds) experimental centerline gas-phase concentration breakthrough curves for CO2 (left) and H2O vapor (right) on zeolite 5A and corresponding predictions from the model of the 2.5% (circles) and 50% (squares) locations. Diamonds: experimental data; dashed lines: simulations with the Edwards and Richardson correlation for axial dispersion (eq 10a) and corresponding kn values (Table 5); dotted lines: simulations with the Wakao and Funazkri correlation for axial dispersion (eq 10b) and corresponding kn values (Table 5). The saturation term in the CO2-zeolite 5A isotherm was increased by 15%. The saturation term in the H2O vapor-zeolite 5A isotherm was decreased by 3%. The void fraction was reduced to 0.33 based on the Cheng distribution39 with C = 1.4 and N = 5, as recommended by Nield and Bejan.40
The fitted and predicted modeling results in Figure 6 show good agreement with the experimental data. The modeling results in Figure 6 also show essentially no effect of using extreme values of the predicted dispersion coefficients on the resulting values of kn, as the results in Table 5 show that similar values of kn were obtained for CO2 (0.0022 vs 0.0023 s−1) and H2O vapor (0.00088 vs 0.00098 s−1) regardless of the dispersion coefficient correlation. These results further show that particle-scale dispersion stemming from bed packing (i.e., turbulence and flow splitting), which are the only types of dispersions accounted for with these correlations, had a negligible influence on the breakthrough results, corroborating what has been known for some time.5,38 Consequently, these results show that it was indeed possible to extract fundamental adsorbate/adsorbent mass transfer information from these well-designed breakthrough experiments using the 1-D axial dispersed plug flow model with DL predicted from a common correlation. This was the case because the experimental center line gas-phase concentration breakthrough curves, as alluded to earlier, experienced conditions very far removed from any near-wall channel effects, thereby allowing them to be described well by such a 1-D model. It was surmised that the consistent displacement between model and experiment at the 50% location for both CO2 and H2O vapor perhaps indicated a misplacement of the gas sampling lines.
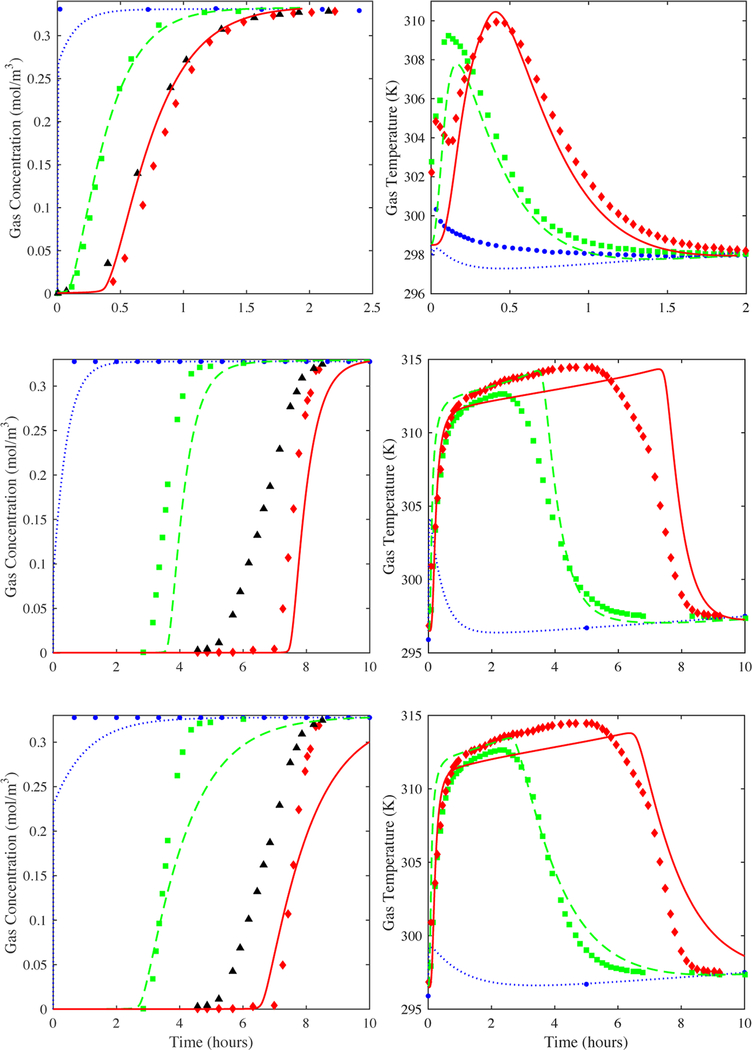
Figure 7 compares the experimental gas-phase concentration breakthrough curves at the three inside centerline bed locations with those from the model for both CO2 and H2O vapor but now without any adjustments to the saturation terms of the isotherms and using the largest dispersion coefficients predicted from the Wakao and Funazkri correlation (eq 10a). The agreement was still quite good, especially in terms of shape, but not so much in terms of capacity, as expected without any adjustments. Notice that the shape and location of the experimental breakthrough curve obtained just outside the bed for CO2 was only slightly more dispersed than the one at the 97.5% location, so the model also coincidently predicted it well; this was not the case for H2O vapor. These interesting observations are addressed in more detail below after the temperature profile histories are discussed.
Figure 7.
CO2 on zeolite 5A (top panels): Predictions from the model (lines) shown in Figure 6 of the 2.5% (circles), 50% (squares), and 97.5% location (diamonds) experimental center line gas-phase concentration breakthrough curves but now using the reported saturation term for the CO2-zeolite 5A isotherm (no adjustment), a void fraction of 0.33, the Wakao and Funazkri correlation (eq 10a) for axial dispersion and LDF kn = 0.0023 s−1. The experimental outside the bed (triangles) breakthrough curve is shown for comparison. Predictions from the model (lines) of the 2.5% location (circles), 50% location (squares), and 97.5% location (diamonds) experimental center line temperature profile histories. H2O on zeolite 5A (middle panels): Predictions from the model (lines) shown in Figure 6 of the 2.5% location (circles), 50% location (squares), and 97.5% location (diamonds) experimental center line gas-phase concentration breakthrough curves but now using the reported saturation term for the H2O-zeolite 5A isotherm (no adjustment), a void fraction of 0.33, the Wakao and Funazkri correlation (eq 10b) for axial dispersion and LDF kn = 0.0008 s−1. The experimental outside the bed (triangles) breakthrough curve is shown for comparison. Predictions from the model (lines) of the 2.5% location (circles), 50% location (squares), and 97.5% location (diamonds) experimental center line temperature profile histories. H2O on zeolite 5A (bottom panels): same as middle but now with LDF kn adjusted to kn = 0.0002 s−1 to match the slope of the experimental outside the bed (triangles) breakthrough curve.
Figure 7 also compares the experimental centerline temperature profile histories at the three locations in the bed with those predicted from the model. In terms of shape, the model and experiment agreed quite well, especially for CO2 and despite the fact that for H2O vapor the model did not match the location of the experimental breakthrough curve just outside the bed as it did for CO2. Notice how below 307 K in the cooling branch of the temperature profile histories for H2O vapor both the model and experiment tracked parallel to each other, as they should in this mass transfer dominated region of the temperature profile histories. This result indicated that the correct mass transfer information was extracted from the model by fitting it to the experimental center line gas-phase concentration breakthrough curves. To exemplify this point, the LDF kn was purposely adjusted to match the slope of the concentration breakthrough curve just outside the bed (this is what is typically done in the literature to obtain kn), which required decreasing it by a factor of 4 compared to the supposedly correct value. This result is shown in the bottom two panels of Figure 7. Notice how the model and experiment now deviated significantly from each other in the mass transfer limited region of the temperature profile histories. The point being made here is that the experimental centerline temperatures in the bed and the experimental concentration breakthrough curve measured just outside the bed did not reflect the same phenomena, the former being dominated by adsorbate/adsorbent mass transfer and the latter being dominated by mechanical dispersion. As for the differences observed between the model and experiment above 307 K in the temperature profile histories for H2O vapor, it was surmised that this was most likely due to the same nonplug flow near-wall channeling phenomena that most certainly could not be predicted by the 1-D axial dispersed plug-flow model.
As an aside, it is noted that the differences between model and experiment measured just outside the bed (black triangles), which represent the capacity of the bed, differ for the two systems under consideration. Two factors that in combination may be responsible for the observed differences are (1) lower CO2 and H2O capacity for the lot of zeolite 5A used in the experiment than that used by Wang and LeVan30 and (2) incomplete desorption of water off the 5A prior to measurement of isotherms by Wang and LeVan (regeneration was performed overnight at 175C at vacuum). For the CO2/5A system, the two factors appear to cancel, resulting in a good agreement between model and experiment. In this case even a minute amount of water remaining on the 5A after regeneration can significantly reduce CO2 adsorption. For the H2O/5A system, the lower H2O capacity for the lot of zeolite 5A used in the experiment is not canceled by the incomplete regeneration, since if only a minute amount of water remained, the impact on the measured capacity would be small.
4.4. Nonplug Flow Axial Dispersion Coefficient Determination on Zeolite 5A.
As shown above, the DL values predicted from two correlations representing the extreme high and low values did not have a significant influence on the simulation results and thus the resulting kn values. It was also shown above that the breakthrough curves obtained just outside the bed were subjected to a nonplug flow, mechanical dispersion mechanism. This mechanical dispersion mechanism was most likely due to near-wall channeling associated with higher velocities that naturally occur due to higher porosities near the wall.
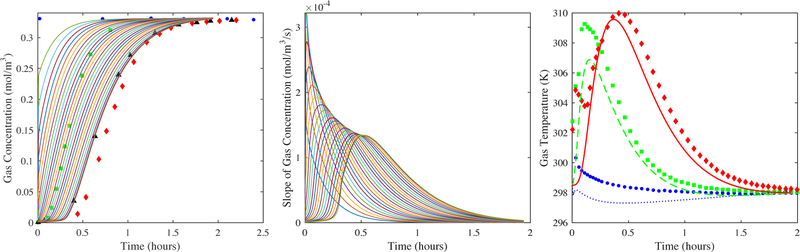
Figure 8 compares the model to experiment for CO2 on zeolite 5A using the fitted kn = 0.0023 s−1 and a value of the dispersion coefficient that was 7 times larger than that predicted from the Wakao and Funazkri correlation (eq 10a). It displays the modeling and experimental gas-phase concentration breakthrough curves at several locations in the bed and just outside the bed, the corresponding derivatives or slopes of the concentration breakthrough curves from the model, and the modeling and experimental centerline temperature profile histories within the bed. Notice how the model now captured very well the contour of the experimental breakthrough curve just outside the bed. To do this, it took a value of DL that was 7 times larger than the largest value predicted from any of the correlations. This substantiated the fact that the dominant dispersion mechanism in the experimental data was not the same as any of those accounted for in any of the correlations. It was also interesting that the slopes of the concentration breakthrough curves did not show any sign of concentration front sharpening at the end of the bed, and they indicated that CPB was just approached near the end of the bed. This was not the case for the H2O vapor system, as shown later.
Figure 8.
CO2 on zeolite 5A: Fit of the 1-D axial dispersed plug flow model to the outside bed (triangles) experimental breakthrough curve using a value of DL 7 times greater than that from the Wakao and Funazkri correlation and the fitted LDF kn = 0.0023 s−1 (left panel). The reported saturation term for the CO2-zeolite 5A isotherm was used, along with the reported void fraction of 0.35. Predictions from the model (lines) of the gas-phase concentration breakthrough curves at 0, 4, 8, 12, …, 92, 96, and 100% locations in the bed are also shown in the left panel, along with the 2.5% (circles), 50% (squares), and 97.5% location (diamonds) experimental center line gas-phase concentration breakthrough curves (left panel). The corresponding derivative (or slope) of the predicted gas-phase concentration breakthrough curves in the bed is shown in the middle panel. Predictions from the model (lines) of the 2.5% (circles), 50% (squares), and 97.5% location (diamonds) experimental center line temperature profile histories are shown in the right panel.
Figure 9 compares the model to experiment for H2O vapor on zeolite 5A using the fitted kn = 0.00098 s−1 and values of the dispersion coefficients that were 7, 30, 50, and 70 times larger than that predicted from the Wakao and Funazkri correlation (eq 10a). These results show that it took a dispersion coefficient value ~50 times larger than the value predicted by the Wakao and Funazkri correlation to reasonably fit the slope and shape of the experimental concentration breakthrough curve just outside the bed. However, as the axial dispersion coefficient increased, the shape of the temperature profile histories increasingly deviated from the experimental results. These results again clearly show that the experimental temperature profile histories and the experimental concentration breakthrough curve obtained just outside the bed did not reflect the same dominating mechanism: as mentioned above, the experimental temperatures reflected the mass transfer process taking place, while the experimental concentration breakthrough curve measured outside the bed reflected mechanical dispersion caused by nonplug flow conditions due to near-wall channeling effects.
Figure 9.
H2O vapor on zeolite 5A: Predictions from the 1-D axial dispersed plug flow model of the outside bed (triangles) experimental breakthrough curve when varying the value of DL. DL = 10 (dotted lines), 30 (dashed lines), 50 (solid lines), and 70 (dash-dot lines) times greater than Wakao and Funazkri correlation with the LDF kn = 0.00083 s−1 (left panel). The reported saturation term for the H2O-zeolite 5A isotherm was used, along with the reported void fraction of 0.35. The corresponding predictions from the model (lines) of the 2.5% (circles), 50% (squares), and 97.5% location (diamonds) experimental center line temperature profile histories are shown in the right panel.
Furthermore, the fact that H2O vapor required such a large value of the dispersion coefficient (~50 times the value from the Wakao and Funazkri correlation) to capture the shape of the experimental concentration breakthrough curve measured just outside the bed was inconsistent with the value required by the CO2 system, which was only 7 times the value from the Wakao and Funazkri correlation. If the dispersion mechanism explaining these deviations was indeed the same for both adsorbate/adsorbent systems, then the respective deviations from the Wakao and Funazkri correlation should have also been about the same. The explanation to this apparent conflict was associated with the breakdown of the 1-D axially dispersed plug flow model, wherein its inherent limitations prevented it from accounting for dispersion phenomena beyond that associated with molecular diffusion, especially for systems with highly nonlinear Type I isotherms.6,16
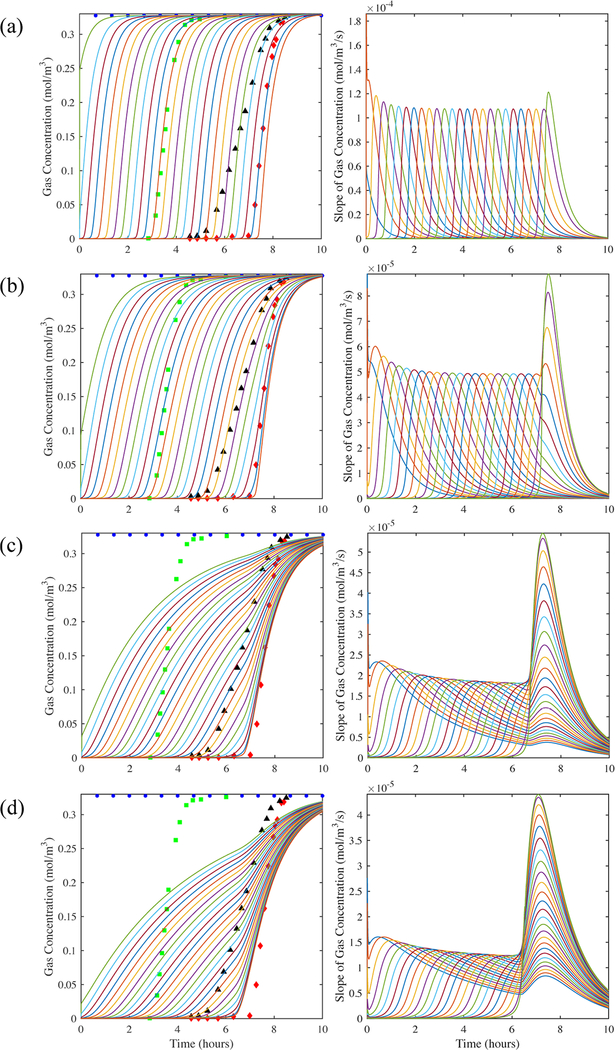
Figure 10 again compares the model to experiment for H2O vapor on zeolite 5A using the fitted kn = 0.00098 s−1 and for values of the dispersion coefficient that were 1, 7, 30, and 50 times larger than that predicted from the Wakao and Funazkri correlation (eq 10a). Both the gas-phase concentration profile histories at numerous locations in the bed and the corresponding slopes of them are displayed, along with the experimental gas-phase concentration breakthrough curves within and just outside the bed. There are a number of characteristic features in this set of graphs that revealed the issues associated with the use of the 1-D axial dispersed plug flow model with this adsorbate/adsorbent system. First, note that the results in Figure 10a correspond to those used to obtain the kn. As such, the shapes of the experimental gas-phase concentration profiles in the bed matched quite well with those predicted from the model. Also, note that the model clearly predicted CPB, as observed by the maximum in the slopes gradually approaching a constant value, except just at the end of the bed where the onset of concentration front sharpening was predicted by the model. This phenomenon was revealed by the maximum in the slope increasing slightly beyond that clearly associated with CPB. However, in this case the concentration front sharpening was not enough to distort the internal gas-phase concentration profiles predicted from the model, thereby resulting in a reasonable value for kn when the model was fitted to the experimental centerline gas-phase concentration profile at the 97.5% location. Despite these insignificant effects on the gas-phase concentration profile histories and also on the temperature profile histories (Figure 7), the results in Figure 10a began to expose the fact that the 1-D axial dispersed plug flow model might predict erroneous results for some systems. The results in Figures 10b, 10c, and 10d were even more revealing.
Figure 10.
H2O vapor on zeolite 5A: Predictions from the model (lines) shown in Figure 9 of the gas-phase concentration breakthrough curves at 0, 4, 8, 12, …, 92, 96, and 100% locations in the bed (left panels). The 2.5% (circles), 50% (squares), and 97.5% location (diamonds) experimental centerline gas-phase concentration breakthrough curves are also shown for comparison in the left panels. The corresponding derivatives (or slopes) of the gas-phase concentration breakthrough curves in the bed are shown in the right panels. (a) DL = Wakao-Funazkri correlation, and (b) DL = 7, (c) 30, and (d) 50 times greater than Wakao and Funazkri correlation.
Figures 10b, 10c, and 10d show increasingly worse distortions of the gas-phase concentration profile histories and corresponding slopes predicted from the model near the exit of the bed when using values of DL = 7, 30, and 50 times that predicted by the Wakao and Funazkri correlation. It was interesting that when the value of DL was just 7 times greater (Figure 10b), the shapes of the internal gas-phase concentration profiles predicted from the model agreed quite well with the experimental concentration profile obtained just outside the bed. The fact that a value 7 times greater was required by CO2 to fit the experimental breakthrough curve outside the bed (Figure 8) was not a coincidence and further substantiated that the same nonplug flow dispersive mechanism prevailed for both the CO2 and H2O vapor systems, independent of the adsorbate. The reason the model required a value ~50 times greater to fit the H2O vapor experimental breakthrough curve outside the bed (Figure 9) was due to extensive concentration front sharpening occurring for the H2O vapor system, as shown especially in Figures 10c and 10d. To overcome it and make the concentration front more dispersed, an artificially large value of the dispersion coefficient was required.
The results in Figure 10 further show that at such large values of DL the concentration front sharpening actually propagated all the way to the entrance of the bed, as observed in Figure 10d. In this case, not only was CPB clearly not preserved anywhere in the bed but also, and more importantly, the predicted breakthrough curves outside the bed no longer provided any useful fundamental information. Evidence for this supposition was provided by the experimental nonplug flow dispersive behavior of the bed being predicted very well by a value of DL that was only 7 times greater, not 50 times greater, than that from the Wakao and Funazkri correlation.
The problem with the correctly derived Danckwerts boundary condition at the exit of the bed for the Fickian axial diffusion model (eq 3) stems from its inability to correctly describe the dispersive or nonconvective aspect of the flux, even under a plug flow regime, as was just observed. The resulting mathematically derived zero slope, as required by the satisfaction of the continuity of both concentration and flux in the Fickian diffusion model, is not preserved experimentally when breakthrough takes place at the boundary because of the complicated dispersive dynamics. However, forcing the slope of the concentration front to be zero at the exit of the bed for a system with a steep Type I isotherm, like the H2O vapor-zeolite 5A system, has such a large influence on the mass balance that it causes unusually large changes in the gas-phase concentration near the exit of bed. This results in concentration front sharpening and loss of CPB near the exit of bed that may propagate throughout the entire bed, as clearly revealed in the modeling results in Figure 10 for this system. If an adsorbate/adsorbent system was accurately described by such a model, then this phenomenon would be observed experimentally. The problem lies not within the model and its physics but with trying to build a fixed bed adsorption experiment that only exhibits dispersion based purely on molecular Fickian diffusion.
5. CONCLUSIONS
This work with CO2 and H2O vapor on zeolite 5A revealed that special caution must be taken when using typical experimental breakthrough curves measured just outside the bed to extract mass transfer and dispersion information from a fixed-bed adsorber based on the widely utilized 1-D axial dispersion plug flow model; otherwise, the resulting information may be erroneous. An experimental breakthrough curve measured just outside the bed, as commonly practiced, should, in principle, provide fundamental adsorbate/adsorbent mass transfer information when such a model is fitted to the data. This is because the dispersion coefficient predicted from known correlations does not have a significant impact on the model results.
However, this work showed that to use these correlations the design of the fixed-bed adsorber must satisfy the plug-flow condition. This work also showed that the only way to verify when the plug flow condition was satisfied was to compare experimental breakthrough curves obtained outside the bed with those obtained inside the bed along its axial center. From this comparison it was determined that even a well-accepted bed diameter to pellet ratio of about 20 was not large enough to ensure plug-flow conditions prevailed in the bed. The experimental outside of bed and inside of bed centerline breakthrough curve results consistently revealed that the bed was experiencing considerable near-wall channeling, i.e., mechanical dispersion phenomena.
Because of the presence of mechanical dispersion, the 1-D axial dispersed plug flow model could not simultaneously predict the experimental concentration profile histories obtained just outside the bed and the experimental centerline temperature profile histories measured inside the bed for either adsorbate/adsorbent system. It was deduced that the temperature profile histories reflected the adsorbate/adsorbent mass transfer process involved, while the outside of bed concentration profile histories reflected a mixing process akin to a nonplug flow pattern existing in the bed that was independent of the adsorbate, i.e., near-wall channeling. It was nevertheless shown that the sought after fundamental mass transfer information could still be obtained, in this case an LDF kn for each adsorbent/adsorbate system, when experimental centerline gas-phase concentration and temperature profile histories were measured somewhere in the bed. It is therefore strongly recommended that this be the preferred method for obtaining experimental mass transfer information from a 1-D axial dispersed plug flow model.
Moreover, despite the alluded to limitations of the 1-D axial dispersed plug flow model, an effort was put forth to extract a dispersion coefficient from the model using the experimental outside the bed breakthrough curves that inherently included the nonplug flow dispersion taking place. In this case, the s values obtained by fitting the experimental inside the bed breakthrough curves were used. The resulting DL values for CO2 and H2O vapor were both 7 times greater than the largest value predicted from five established DL correlations. This analysis confirmed the unique nature of the nonplug flow mechanical dispersion phenomena taking place in the bed, and it correctly showed that such phenomena should be independent of the adsorbate. However, while obtaining DL significant differences were observed between the CO2 and H2O vapor systems. Extracting DL from the experimental data for CO2 was straightforward but not for H2O vapor.
The process of extracting DL from the experimental data for H2O vapor revealed the mathematical inability of the 1-D axial dispersed plug flow model to obtain such information at the exit of the bed. Depending on the value of DL, significant concentration front sharpening occurred for this system. This concentration front sharpening is an unusual but real phenomenon that is scarcely known and a consequence of the limited ability of the 1-D axial dispersed plug flow model and its Danckwerts boundary condition to represent nondiffusive dispersive mechanisms for very rectangular Type I isotherms, such as H2O vapor in zeolite 5A. To obtain a DL value for H2O vapor that was consistent with that obtained for CO2, the predicted inside the bed centerline breakthrough curves, necessarily chosen from a location unaffected by any concentration front sharpening, were matched to the experimental outside the bed breakthrough curve. Otherwise, the DL value obtained for H2O vapor when using the experimental outside the bed breakthrough curves was 50 times greater, as opposed to 7 times greater, due to compensating for the significant concentration front sharpening that the model predicted for this system.
Overall, this work clearly showed that it was possible to extract accurate mass transfer and dispersion information from experimental breakthrough curves using a 1-D axial dispersed plug flow model when they were measured both inside and outside the bed. To ensure the extracted information was accurate, the inside the bed breakthrough curves and their derivatives from the model were plotted to confirm whether or not the adsorbate/adsorbent system was exhibiting CPB or any concentration front sharpening near the bed exit. Even when concentration front sharpening was occurring, like with the H2O vapor-zeolite 5A system, it was still possible to use the experimental inside and outside the bed breakthrough curves to extract fundamental mass transfer and dispersion information from the 1-D axial dispersed plug flow model based on the systematic methodology developed in this work.
NOMENCLATURE
- a
saturation capacity in Toth equation, mol kg−1 kPa−1
- a0
Toth equation parameter, mol kg−1 kPa−1
- af
superficial free flow area, m2
- as
pellet external surface area per unit volume, m−1
- aw
column cross-sectional area, m2
- b
equilibrium constant in Toth equation, kPa−1
- b0
Toth equation parameter, kPa−1
- c
concentration, mol m−3: also parameter in Toth equation, K
- co
inlet concentration, mol m−3
- cpg
gas heat capacity, J kg−1 K−1
- cps
sorbent heat capacity, J kg−1 K−1
- cpw
column wall heat capacity, J kg−1 K−1
- hs
sorbent to gas heat transfer coefficient, W m−2 K−1
- D
fluid-phase diffusion coefficient, m2 s−1
- DL
axial dispersion coefficient, m2 s−1
- E
Toth equation parameter, K−1
- hi
column wall to gas heat transfer coefficient, W m−2 K−1
- ho
column wall to ambient heat transfer coefficient, W m−2 K−1
- hs
sorbent to gas heat transfer coefficient, W m−2 K−1
- ke
quiescent bed gas conductivity, W m−1 K−1
- keff
effective axial thermal conductivity, W m−1 K−1
- kf
gas conduction, W m−1 K−1
- kn
LDF mass transfer coefficient, s−1
- ks
sorbent conduction, W m−1 K−1
- kw
column wall conduction, W m−1 K−1
- L
bed height, m
- LDF
linear driving force
- n
sorbent loading, mol kg−1
- p
partial pressure in Toth equation, kPa
- Pe
particle Peclet number
- Pi
column inner perimeter, m2
- Po
column outer perimeter, m2
average adsorbed concentration, mol m−3
- q*
equilibrium adsorption concentration, mol m−3
- Rp
pellet radius, m
- t
time, seconds; also heterogeneity parameter in Toth equation
- t0
Toth equation parameter
- Tf
fluid (gas) temperature, K
- Ts
adsorbent temperature, K
- Tw
column wall temperature, K
- T0
inlet temperature, K
- x
axial coordinate, m
- λ
isosteric heat of adsorption, kJ mol−1
- ε
void fraction
- μ
gas viscosity, micropoise
- υi
interstitial velocity, m s−1
- ρf
gas density, kg m−3
- ρs
sorbent density, kg m−3
- ρw
column wall density, kg m−3
Footnotes
The authors declare no competing financial interest.
REFERENCES
- (1).Beeyani AK; Singh K; Vyas RK; Kumar S; Kumar S Parametric studies and simulation of PSA process for oxygen production from air. Pol. J. Chem. Technol. 2010, 12 (2), 18–28. [Google Scholar]
- (2).Ahn H; Lee CH Adsorption dynamics of water in layered bed for air-drying TSA process. AIChE J. 2003, 49 (6), 1601–1609. [Google Scholar]
- (3).Chou CT; Chen CY Carbon dioxide recovery by vacuum swing adsorption. Sep. Purif. Technol. 2004, 39 (1–2), 51–65. [Google Scholar]
- (4).Ruthven DM Principles of Adsorption and Adsorption Processes; 1984; p 433. [Google Scholar]
- (5).Yang RT Gas Separation by Adsorption Processes; Imperial College Press: London, 1997; Vol. 1. [Google Scholar]
- (6).Coppola AP; LeVan MD Adsorption with Axial Diffusion in Deep Beds. Chem. Eng. Sci. 1981, 36 (6), 967–971. [Google Scholar]
- (7).Wakao N; Funazkri T Effect of fluid dispersion coefficients on particle-to-fluid mass transfer coefficients in packed beds: Correlation of Sherwood numbers. Chem. Eng. Sci. 1978, 33 (10), 1375–1384. [Google Scholar]
- (8).Edwards MF; Richardson JF Gas dispersion in packed beds. Chem. Eng. Sci. 1968, 23 (2), 109–123. [Google Scholar]
- (9).Wicke E Phys. Chem. 1973, 77, 160. [Google Scholar]
- (10).Wen CY; Fan LT Models for flow systems and chemical reactors; Marcel Dekker: New York, 1975; Vol. 20, 570 pages. [Google Scholar]
- (11).Aviles BE; LeVan MD Network Models for Nonuniform Flow and Adsorption in Fixed-Beds. Chem. Eng. Sci. 1991, 46 (8), 1935–1944. [Google Scholar]
- (12).Mahle JJ; Friday DK In Axial Dispersion Effects on the Breakthrough Behavior of Favorably Adsorbed Vapors; Recents Progres en Genie Des Procedes, France, Meunier F, LeVan MD, Eds.; Groupe Francais de Genie des Procedes: France, 1991. [Google Scholar]
- (13).Russell BP; LeVan MD Nonlinear adsorption and hydrodynamic dispersion in self-similar networks. Chem. Eng. Sci. 1997, 52 (9), 1501–1510. [Google Scholar]
- (14).LeVan DM; Carta G Adsorption and Ion Exchange In Perry’s Chemical Engineer’s Handbook, 8th ed ed.; McGraw-Hill: New York, 2008. [Google Scholar]
- (15).Mohamadinejad H; Knox J; Smith J Experimental and numerical investigation of adsorption/desorption in packed sorption beds under ideal and nonideal flows. Sep. Sci. Technol. 2000, 35 (1), 1–22. [Google Scholar]
- (16).Coppola AP; LeVan MD Adsorption with Axial Diffusion in Shallow Beds. Chem. Eng. Sci. 1983, 38 (7), 991–997. [Google Scholar]
- (17).Jee J-G; Kim M-B; Lee C-H Pressure swing adsorption processes to purify oxygen using a carbon molecular sieve. Chem. Eng. Sci. 2005, 60 (3), 869–882. [Google Scholar]
- (18).Nastaj J; Ambrozek B Analysis of gas dehydration in TSA system with multi-layered bed of solid adsorbents. Chem. Eng. Process. 2015, 96, 44–53. [Google Scholar]
- (19).Park J-H; Kim J-N; Cho S-H Performance Analysis of Four-Bed H2 PSA Process Using Layered Beds. AIChE J. 2000, 46 (4), 790. [Google Scholar]
- (20).Rouf SA; Eic M Adsorption of SO2 from Wet Mixtures on Hydrophobic Zeolites. Adsorption 1998, 4, 25–33. [Google Scholar]
- (21).Soares J; Casarin GL; José HJ; Moreira RDFPM; Rodrigues AE Experimental and Theoretical Analysis for the CO2 Adsorption on Hydrotalcite. Adsorption 2005, 11, 237–241. [Google Scholar]
- (22).Knox JC Finite Difference Modeling and Experimental Investigation of Carbon Dioxide Adsorption on a Molecular Sieve Sorbent Material Used in Spacecraft Carbon Dioxide Removal Systems: A Thesis. University of Alabama, Huntsville, 1992. [Google Scholar]
- (23).Finn JE; Ho EC Progress Report on the 4BMS Adsorption Characterization Study; Ames Research Center: 1995. [Google Scholar]
- (24).Radenburg E Particle Size Analysis; National Aeronautics and Space Administration, Marshall Space Flight Center: 2013. [Google Scholar]
- (25).Danckwerts PV Continuous flow systems. Distribution of residence times. Chem. Eng. Sci. 1995, 50 (24), 3857–3866. [Google Scholar]
- (26).Glueckauf E Theory of chromatography. Part 10.—Formulæ for diffusion into spheres and their application to chromatography. Trans. Faraday Soc. 1955, 51, 1540–1551. [Google Scholar]
- (27).Sircar S; Hufton JR Why does the linear driving force model for adsorption kinetics work? Adsorption 2000, 6 (2), 137–147. [Google Scholar]
- (28).Mohamadinejad H; Knox JC; Finn JE; Smith JE Hardware-Independent Mathematical and Numerical Modeling of a Four-Bed Molecular Sieve--Part 1: Modeling and Verification of Gas Adsorption on Zeolite 5A In International Conference on Environmental Systems; SAE: Monterey, CA, 1996. [Google Scholar]
- (29).Bird RB; Stewart WE; Lightfoot EN Transport Phenomena, 2nd ed; John Wiley & Sons, Inc: New York, 2002. [Google Scholar]
- (30).Wang Y; LeVan MD Adsorption Equilibrium of Carbon Dioxide and Water Vapor on Zeolites 5A and 13X and Silica Gel: Pure Components. J. Chem. Eng. Data 2009, 54 (10), 2839–2844. [Google Scholar]
- (31).Poling BE; Prausnitz JM; O’Connell JP The Properties of Gases and Liquids, 5th ed; McGraw-Hill: New York, 2001. [Google Scholar]
- (32).Reid RC; Prausnitz JM; Poling BE The Properties of Gases and Liquids, 4th ed; McGraw-Hill: 1987. [Google Scholar]
- (33).Li C; Finlayson B Heat transfer in packed beds –a re-evaluation. Chem. Eng. Sci. 1977, 32, 1055–1066. [Google Scholar]
- (34).Wakao N; Kaguei S Heat Transfer in Packed Beds; 1982.
- (35).Kaviany M Principles of Heat Transfer in Porous Media, 2nd ed; Springer-Verlag: New York, 1995; p xxii, 708 p. [Google Scholar]
- (36).Yagi S; Kunii D; Wakao N Studies on axial effective thermal conductivities in packed beds. AIChE J. 1960, 6 (4), 543–546. [Google Scholar]
- (37).Knox JC A Deterministic Approach Towards Predictive Simulation of Gas Adsorption in Fixed Beds and its Practical Limitations due to the Inappropriate Danckwerts Boundary Condition. University of Alabama, Huntsville, 2016. (submitted). [Google Scholar]
- (38).Richardson JF; Harker JH; Backhurst JR; Coulson JM Coulson and Richardson’s chemical engineering Vol. 2 Particle technology and separation processes, 5th ed; Butterworth-Heinemann: Oxford, 2002. [Google Scholar]
- (39).Nield DA; Bejan A Convection in Porous Media. Springer-Verlag: New York, 1992. [Google Scholar]
- (40).Cheng P; Chowdhury A; Hsu CT Forced Convection in Packed Tubes and Channels with Variable Porosity and Thermal Dispersion Effects In Convective Heat and Mass Transfer in Porous Media, Kakaç S, Kilkiş B, Kulacki FA, Arinç F, Eds. Springer Netherlands: Dordrecht, 1991; 625–653. [Google Scholar]