Known-Component Model-Based Material Decomposition for Dual Energy Imaging of Bone Compositions in the Presence of Metal Implant

Abstract

Dual energy computed tomography (DE CT) is a promising technology for the assessment of bone compositions. One of potential applications involves evaluations of fracture healing using longitudinal measurements of callus mineralization. However, imaging of fractures is often challenged by the presence of metal fixation hardware. In this work, we report on a new simultaneous DE reconstruction-decomposition algorithm that integrates the previously introduced Model-Based Material Decomposition (MBMD) with a Known-Component (KC) framework to mitigate metal artifacts. The algorithm was applied to the DE data obtained on a dedicated extremity cone-beam CT (CBCT) with capability for weight-bearing imaging. To acquire DE projections in a single gantry rotation, we exploited a unique multisource design of the system, where three X-ray sources were mounted parallel to the axis of rotation. The central source provided high energy (HE) data at 120 kVp, while the two remaining sources were operated at a low energy (LE) of 60 kVp. This novel acquisition trajectory further motivates the use of MBMD to accommodate this complex DE sampling pattern. The algorithm was validated in a simulation study using a digital extremity phantom. The phantom consisted of a water background with an insert containing varying concentrations of calcium (50 – 175 mg/mL). Two configurations of titanium implants were considered: a fixation plate and an intramedullary nail. The accuracy of calcium-water decompositions obtained with the proposed KC-MBMD algorithm was compared to MBMD without metal component model. Metal artifacts were almost completely removed by KC-MBMD. Relative absolute errors of calcium concentration in the vicinity of metal were 6% – 31% for KC-MBMD (depending on the calcium insert and implant configuration), compared favorably to 48% – 273% for MBMD. Moreover, accuracy of concentration estimates for KC-MBMD in the presence of metal implant approached that of MBMD in a configuration without implant (6%–23%). The proposed algorithm achieved accurate DE material decomposition in the presence of metal implants using a non-conventional, axial multisource DE acquisition pattern.

1. INTRODUCTION

Evaluations of fracture healing could benefit from accurate measurements of callus mineralization and mechanical stability of the injured bone. Recently developed dedicated extremity cone-beam CT (CBCT)¹ (Fig. 1A) provides an attractive platform for the development of such biomarkers. It acquires volumetric images under physiological weight-bearing, thus enabling direct assessments of mechanical properties of the fracture. To achieve a comprehensive evaluation of the healing bone, this capability should be augmented with accurate quantifications of bone mineralization, which could be achieved using dual energy (DE) imaging with calcium (bone mineral) and water (soft tissues) as base materials².

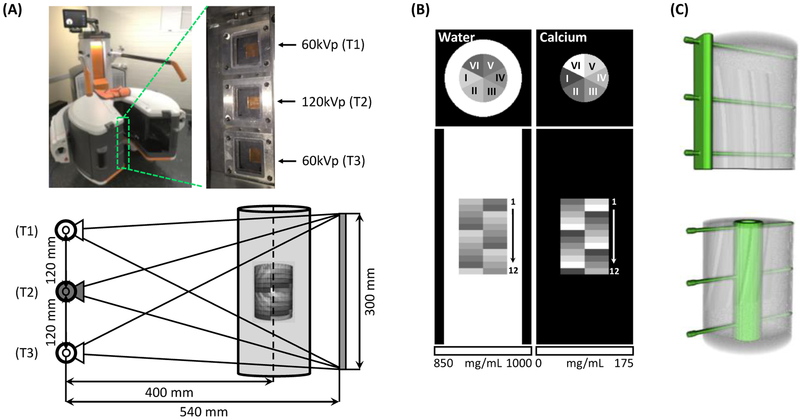
Fig.1.

(A) Extremity CBCT system with an axial multi-source x-ray unit. System geometry and source firing sequence for a single-scan DE acquisition is shown. (B) Digital multi-material phantom (axial and coronal view) used in validation studies. The phantom consisted of an outer water container with an inner insert containing water-Ca mixtures of varying Ca concentration. (C) The placement of metal implants (top: plate, bottom: intramedullary nail) with respect to the inner insert of the phantom.

The extremity CBCT system employs a unique multisource X-ray unit³ shown in Fig. 1A. Three X-ray sources are arranged parallel to the axis of rotation. Each source can be operated at a different tube potential, thus enabling DE acquisition in a single gantry rotation. For example, the central source can be used to generate a high energy (HE) beam, while the peripheral sources provide low energy (LE) projections. However, conventional projection-based methods⁴ for DE decomposition cannot be applied to such data, as no matching HE and LE ray paths are available.

We have recently proposed a model-based algorithm for simultaneous DE reconstruction and material decomposition (i.e. Model-Based Material Decomposition, MBMD)⁵. The algorithm can perform decompositions directly from the projections, but, unlike conventional methods, does not require matching LE and HE ray paths. MBMD is hence well-suited for the proposed multisource DE acquisition protocol.

Internal fixation hardware is commonly used in lower extremity fractures. The presence of metal components may cause artifacts that will affect the accuracy of MBMD estimates of bone composition. In this work, we develop a novel approach to mitigate the effects of metal implants in DE material decomposition. The new algorithm integrates MBMD with the Known-Component (KC) framework⁶, which incorporates prior knowledge of implant’s shape and composition into the model-based iterative reconstruction process.

We present the mathematical derivation of the proposed Known-Component Model-Based Material Decomposition (KC-MBMD). The performance of the algorithm in decomposing three-source DE data acquired on the extremity CBCT is investigated in simulation studies with two titanium implant configurations. Accuracies of water and calcium concertation estimates are compared to MBMD without implant model and MBMD of a metal-free phantom.

2. METHOD

2.1. Known-Component Model-Based Material Decomposition (KC-MBMD)

The forward model for the DE acquisition with K base materials can be written as:

$$\overline{y}=\int S(\epsilon )\exp \left(\sum _{k=1}^K-A{m}^{\left\{k\right\}}(\epsilon ){\rho }^{(k)}\right)\text{d}\epsilon$$ (1)

where S(ε) is the spectral response of the system (including energy-weighting, polyenergetic X-ray spectrum, and detector response). m^{k}(ε) is the energy-dependent mass-attenuation coefficient of the base material k, and ρ^{k} is the unknown local density (concentration). We have shown that this forward model can be written in a general matrix form⁵:

$$\overline{y}=B\exp (-Mx)$$ (2)

where x is the vector of unknown densities of two base materials. M combines a standard projection matrix with energy-dependent attenuations of base materials m^{k}(ε). B is a matrix that applies the spectral response S(ε). Assuming that the measurement y follows Gaussian distribution with mean ȳ and covariance Ky, the representation in Eq. 2 permits the use of a previously developed generalized nonlinear PWLS algorithm with the following objective function^5,7:

$$\Phi ={[y-B\exp (-Mx)]}^T{K}_y^{-1}[y-B\exp (-Mx)]+\beta R(x)$$ (3)

We have demonstrated that MBMD using the PWLS objective in Eq. 3 yields accurate material concentrations in a variety of DE acquisition scenarios5. To address metal artifacts, we assume a priori knowledge of implant shape and composition. The implant is specified by known spatial density distribution ρ_I, known mass-attenuation coefficient m_I(ε), and unknown pose described by a transformation operator T. The resulting KC-MBMD forward model is:

$$\overline{y}=\int S(\epsilon )\exp \left(\sum _{p=1}^P-A{m}_I^{\left\{p\right\}}(\epsilon )T^{\left\{p\right\}}{\rho }_I^{\left\{p\right\}}\right)\exp \left(\sum _{k=1}^K-A{m}_{*}^{\left\{k\right\}}(\epsilon ){\rho }_{*}^{\left\{k\right\}}\right)\text{d}\epsilon$$ (4)

where we assumed P implants presenting in the field-of-view, and ${\rho }_{*}^{\left\{k\right\}}$ denotes the unknown density of the base material k excluding the voxels belonging to the metal implants (i.e. ‘masked’ by the implants’ shape).

We note that terms related to the forward model of the implants can be factored into spectral response matrix S(ε), as all of them are independent from the unknown base material density ρ_* (the unknown poses of the implants can be determined prior to reconstruction using a standard 3D-2D registration⁶). The forward projection of the implant can thus be considered as a spatial filter applied onto the X-ray spectrum. This allows incorporating the known components into the B matrix term in Eq. 3 and 4. The same optimization framework as in MBMD can thus be used, yielding the KC-MBMD algorithm.

2.2. Axial Multisource Dual Energy CBCT Acquisition Protocol

Fig. 1(a) illustrates the multisource configuration of the dedicated extremity CBCT system. Three X-ray tubes are mounted along the axis of rotation of the scanner with a spacing of 120 mm. This also implies that the sources are arranged vertically in the weight-bearing configuration of the gantry. We denote the superior tube as T1, the central one as T2, and the inferior one as T3. The source-axis distance of the scanner is 400 mm, source-detector distance is 540 mm, and the detector field-of-view is 300 × 300 mm². Investigations in this work utilize the following single-scan, multisource DE protocol: T1 and T3 deliver LE beams at 60kVp (+0.2 mm Cu, +2.0 mm Al filtrations), while T2 delivers HE beams at 120 kVp (+0.2 mm Cu, +2.0 mm Al filtrations). We assume a circular scan orbit with an angular view distance of 1°. The sources are energized sequentially from view-to-view as follows: T1, T2, T3, T2, T1, …, T2. This protocol thus yields 180 HE projections and 180 LE projections in total (i.e. 90 for T1 and 90 for T3).

2.3. Simulation Study

The proposed KC-MBMD algorithm and DE acquisition pattern were validated in a polyenergetic simulation study using a digital extremity phantom with metal implants (Fig. 1B & C). The diameter of the outer water cylinder was 80 mm, and the height was 225 mm (extending beyond the field-of-view of the system). The simulated bone insert was 50 mm in diameter and 78 mm in height, which was then divided into 12 levels with 6.5 mm thickness each. Each section contained water-calcium mixtures of varying calcium concentration arranged in six sectors. The compositions of the sectors ranged from 50 mg/mL to 175 mg/mL of calcium in 25 mg/mL steps. Each level of the phantom contained the same six sectors, but the pattern was rotated by 60° compared to the previous level.

Two configurations of titanium implants were studied: a fixation plate (5 mm thickness) mounted using three screws (3 mm diameter), and an intramedullary nail (15 mm outer dimeter and 3 mm wall thickness) mounted with the same three screws. Implants were affixed to the inner bone cylinder as shown in Fig. 1C. The digital phantom was generated using a 0.5 × 0.5 × 0.5 mm³ voxels. The simulated flat-panel detector (FPD) had 0.278 mm pixels. Poisson noise was added onto the projection data (assuming a photon flux of 1.4 × 10⁴ counts/pixel).

Simultaneous image reconstruction-decomposition was performed with both MBMD and KC-MBMD. MBMD used a water-calcium base material set, meaning that the implant was also reconstructed as a mixture of these two materials. In KC-MBMD, in contrast, the implant registration was assumed to be known (given by the phantom design). Both methods were initialized by an empty matrix for the calcium volume and a uniform cylinder for water (obtained by segmentation of an initial reconstruction). The same quadratic regularization was used for all reconstructions, with penalty strengths for water and calcium at 10⁸ and 2 × 10⁹, respectively. This choice reflects the ratio between the minimum calcium concentration (i.e. 50 mg/mL) and the maximum water concentration (i.e. 1,000 mg/mL) in the phantom⁵. Detector pixels were binned by 6 × 6 during projection postprocessing before reconstructions. Data was reconstructed onto 0.5 × 0.5 × 0.5 mm³ voxels for both MBMD and KC-MBMD methods using Nesterov acceleration with 300 iterations and 45 subsets. Estimated water and calcium concentrations in the region where all three beams covered were further analyzed.

3. RESULTS

Fig. 2 shows the reconstructed water and calcium concentrations. MBMD decompositions of the phantom without implant is shown on the left column. The rest four columns display the decompositions where the implant is present. Dramatic reduction of metal-induced biases with KC-MBMD is apparent for both materials and both implant configurations. Edge artifacts in the water decompositions for both methods will likely be resolved with further optimization of regularization and relative penalty strengths⁵.

Fig.2.

Water (top) and calcium (bottom) concentrations obtained from multisource DE CBCT data for various phantom configurations (with and without implants). Coronal and axial views are shown for both material concentration volumes.

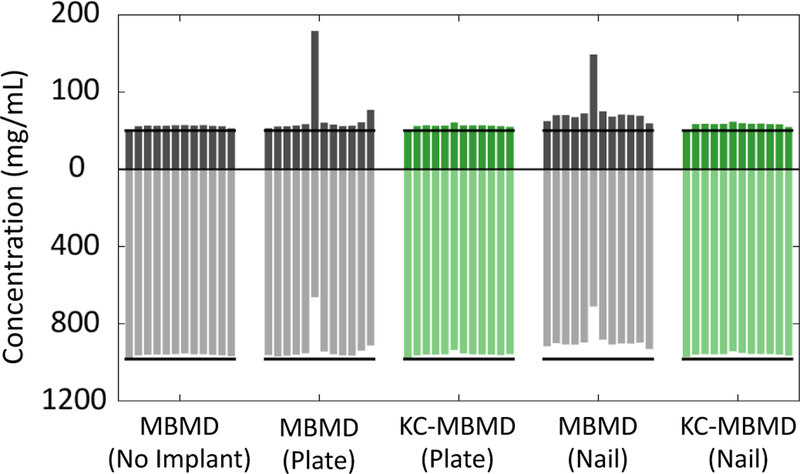
Estimated calcium and water concentrations for sector I of all vertical sections of the phantom are shown in Fig. 3. Individual bars (from left to right) represent the consecutive 12 levels of the phantom. Overall, concentrations estimated using KC-MBMD are much closer to the metal-free reference case than those estimated by MBMD. Biases in MBMD estimates are particularly evident in the sections where the sector-of-interest was penetrated by the titanium screw. Overall, proposed KC-MBMD achieved a fairly stable performance across all vertical sections of the phantom.

Fig.3.

Estimates of water (lower half) and calcium (upper half) concentrations obtained for various phantom configurations, shown for one example sector of the digital phantom (50 mg/mL calcium). Individual bars represent vertical sections of the phantom.

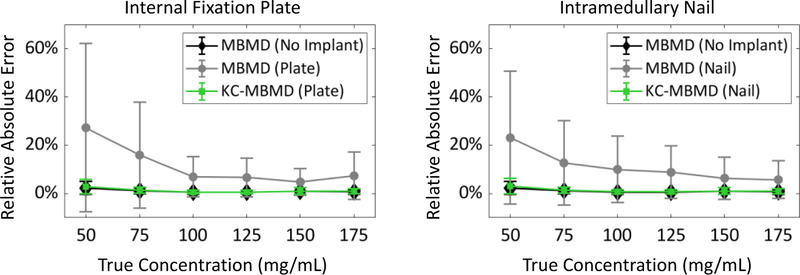
Fig. 4 investigates the errors of calcium concentration estimates. From all calcium insert levels, we chose the 6 sectors of the phantom penetrated by the screw. Fig. 4 shows the distribution of errors across all voxels belonging to those sectors normalized by their nominal concentrations. At the low calcium concentrations, KC-MBMD reduces relative percentage errors from >100% to 30% or less. Such level of errors is similar to that of MBMD in the metal-free scenario.

Fig.4.

Relative absolute errors of MBMD and KC-MBMD, measured in sectors-of-interest directly adjacent to metal hardware (screws) in the two implant configurations (i.e. internal fixation plate and intramedullary nail).

4. DISCUSSION & CONCLUSION

The proposed KC-MBMD approach yielded accurate estimates of calcium concentrations in the presence of metal implants using a novel axial multisource DE CBCT protocol. The algorithm naturally handles the unconventional sampling pattern of the multisource system by utilizing an appropriate projection matrix in the forward model. Matching LE and HE ray paths are therefore not required to obtain base material decompositions directly from the projections. By incorporating the KC framework, metal artifacts and their associated decomposition errors are greatly reduced without the need of including implants among the DE base materials. Ongoing work includes experimental validations using an extremity CBCT scanner. When deployed on the weight-bearing system, KC-MBMD will enable simultaneous monitoring of callus mineralization and mechanical stability in the healing fracture with internal metal fixators.