α-Synuclein pathology spread through the brain connectome is modulated by selective vulnerability and predicted by network analysis

Abstract

Studies of patients afflicted by neurodegenerative diseases suggest that misfolded proteins spread through the brain along anatomically-connected networks, prompting progressive decline. Recently, mouse models have recapitulated the cell-to-cell transmission of pathogenic proteins and neuron death observed in patients. However, factors regulating spread of pathogenic proteins remain a matter of debate due to an incomplete understanding of how vulnerability functions in the context of spread. Here, we use quantitative pathology mapping in the mouse brain combined with network modeling to understand the spatiotemporal pattern of spread. α-Synuclein pathology patterns are well-described by a network model based on two factors—anatomical connectivity and endogenous α-Synuclein expression. The map and model allow assessment of selective vulnerability to α-Synuclein pathology development and neuron death. Finally, we use quantitative pathology to understand how the G2019S LRRK2 genetic risk factor impacts the spread and toxicity of α-Synuclein pathology.

INTRODUCTION

The synaptic protein α-Synuclein misfolds in Parkinson’s disease (PD)^1–3 and related diseases and aggregates into large intraneuronal inclusions known as Lewy bodies (LBs)⁴. Recent evidence suggests that α-Synuclein not only accumulates in LBs, but can itself act as an agent of disease, templating the aggregation of α-Synuclein in anatomically connected neurons throughout the brain⁵. While the cell-to-cell transmission of α-Synuclein explains much of the pathology and symptom progression seen in PD and related synucleinopathies, certain neuron populations are clearly more vulnerable than others⁶, resulting in specific degeneration of certain neurons while sparing others nearby⁷. Therefore, the extent to which intrinsic cell vulnerability or cell-to-cell spread of α-Synuclein pathology drive of PD pathogenesis is still a matter of debate.

Exogenous misfolded α-Synuclein injected into wildtype mice induces misfolding of endogenous α-synuclein into phosphorylated, aggregated inclusions resembling human LBs^8,9. These inclusions are found in many brain regions directly or indirectly connected to the injection site, and the inclusions induce a time-dependent degeneration of the inclusion-bearing neurons^8,10,11. Previous work has demonstrated that pathogenic α-Synuclein is transmitted extracellularly since spread can be blocked by an anti-α-Synuclein antibody¹², or by blocking a receptor for misfolded α-Synuclein¹³. Thus, injection of misfolded α-Synuclein into mice is an ideal model to understand the spatiotemporal pattern of pathogenic protein spread and how network connectivity and neuronal vulnerability affect spreading dynamics.

In this study, we used quantitative assessment of α-Synuclein pathology in non-transgenic (NTG) mice injected with α-Synuclein pre-formed fibrils (PFFs) to generate a spatiotemporal map of pathology spread and neuron death. A network diffusion model based on anatomical connectivity explains much of the variation in pathological burden. Further, α-Synuclein gene (Snca) expression correlates well with the differential vulnerability observed between regions, suggesting that anatomical connectivity and α-synuclein protein expression are major contributors to pathogenic protein spread. Finally, we sought to determine how genetic risk factors affect network dynamics of pathological α-Synuclein spread. We performed quantitative pathology mapping in transgenic mice carrying the Gly2019Ser (G2019S) leucine-rich repeat kinase (LRRK2) risk factor for PD¹⁴ and assessed how transgene expression affects network properties of α-Synuclein spread, neuron vulnerability and neuron toxicity. The quantitative pathology maps and network model presented here represent an important framework for understanding and treating progressive neurodegenerative diseases.

RESULTS

Brain-wide quantification of α-Synuclein pathology

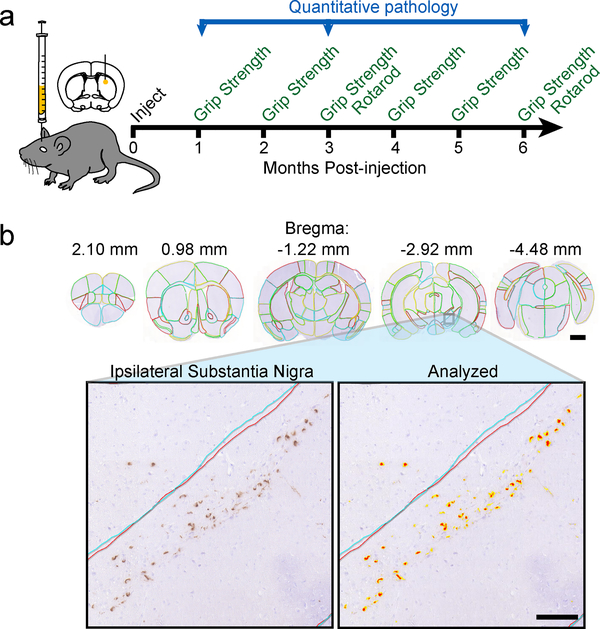
A model for PD pathogenesis has recently been described in which α-Synuclein pathology can be induced in non-transgenic mice following a single injection of α-Synuclein pre-formed fibrils (PFFs)⁸ but pathology is not induced by injection of either monomeric α-Synuclein or PBS⁸. While the α-Synuclein pathology in these mice has been described qualitatively, we sought to understand the spatiotemporal spread of α-Synuclein pathology quantitatively and to use this data to develop a network model of spread. To accomplish these aims, we injected 3-month-old NTG (C57BL/6J) mice in the dorsal striatum with 5 μg α-Synuclein PFFs and allowed them to age 1, 3 or 6 months post-injection (MPI, Fig. 1a). Brains embedded in paraffin were sectioned and stained using traditional immunohistochemical techniques for pathological misfolded (Syn506) and phosphorylated (pS129) α-Synuclein. These sections were then scanned into a digitized format, allowing for automated quantitation of α-Synuclein pathology burden. An expert in mouse neuroanatomy, but blinded to treatment, manually annotated 172 regions in 5 coronal slices for each mouse (Fig. 1b, Supplementary Fig. 1). These anatomical regions were selected to encompass all major regions in which α-Synuclein pathology appears. Regions with little α-Synuclein pathology but a large number of nuclei, such as the thalamus and mesencephalon, were grouped so as to minimize error in annotation and to maximize efficiency.

Fig. 1. Quantitation of α-Synuclein pathology allows for brain-wide analysis of pathology spread.

a, Experiment schematic: mice were injected in the dorsal striatum with α-Synuclein at 3 months of age. The mice were then aged 1, 3 or 6 months post-injection and assessed for motor behaviors during that time period. The brains of mice were used for quantitative pathology analysis. b, Representative images of brain sections (similar for 16 wildtype mice) with manual annotation of 172 regions displayed (scale bar=1mm). The ipsilateral SN of this brain is shown below with and without an analysis mask overlaid (scale bar=100 μm).

A simple quantitative algorithm identified the percentage of each region occupied with α-Synuclein pathology above a threshold 0.157 optical density (Fig. 1b). To minimize sampling bias, a completely separate set of sections flanking the original sections was immunostained, annotated and analyzed in a similar manner. Representative sections for all regions can be found in Supplementary Fig. 17. The mean of the two sets is reported in Supplementary Table 1 and is used in all subsequent analysis (n, 1 MPI=4, 3 MPI=6, 6 MPI=6).

Dynamic spread patterns in non-transgenic mice

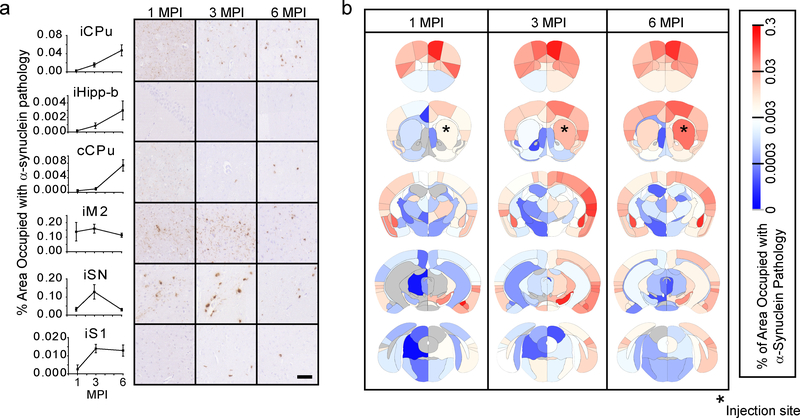
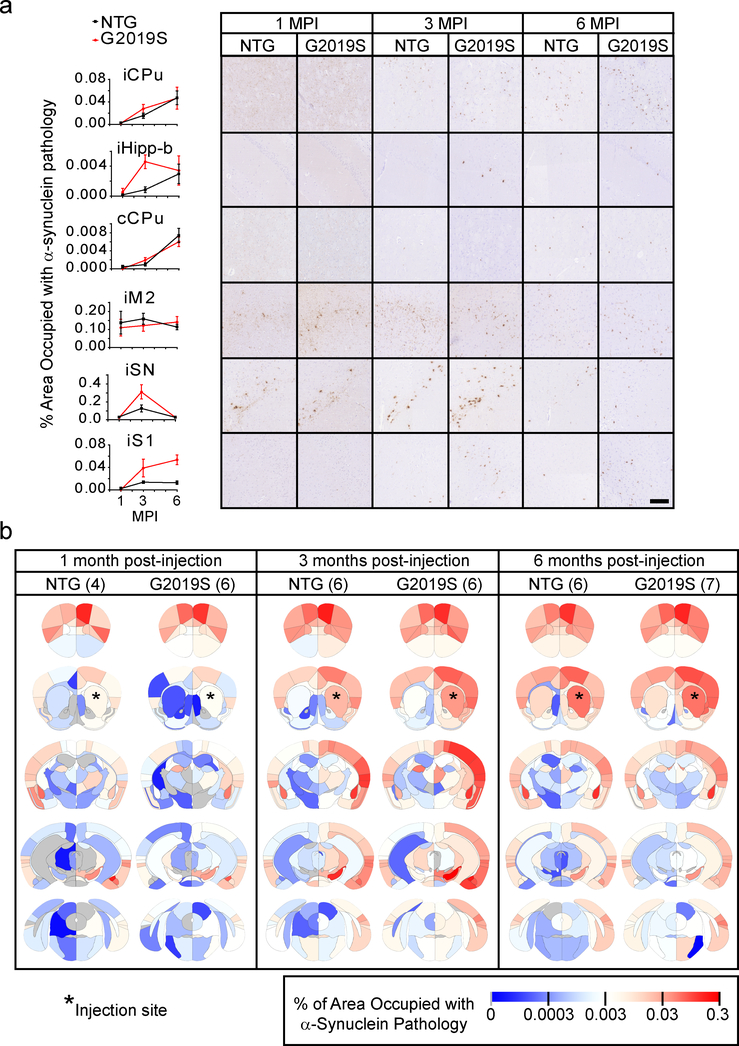
Regional pathological burden values differed by greater than 1000-fold and revealed dynamic patterns of regional α-Synuclein pathology spread over time. Several distinct patterns of spread were observed that are consistent with pathological progression and neuron death (Fig. 2a): 1) Slow initiation of pathology, but constant progression after initiation as seen in the ipsilateral caudoputamen (iCPu) and hippocampus (iHipp-b). 2) Delayed initiation, constant progression as seen in the contralateral caudoputamen (cCPu), likely due to the trans-synaptic nature of pathology spread. 3) Rapid initiation, slow progression as seen in the directly-connected ipsilateral secondary motor cortex (iM2) cortex. 4) Rapid initiation, rapid decrease as seen in the vulnerable ipsilateral substantia nigra (iSN)^8,15 which has robust cell death by 6 MPI, causing a commensurate reduction in pathology. 5) Constant initiation, slow progression as seen in the ipsilateral primary somatosensory cortex (iS1). The pathological burden of each region at all three timepoints can be displayed as a heat map overlaid onto the brain anatomy (Fig. 2b) or in a region by time graph (Supplementary Fig. 2). Whole-brain quantitation of α-Synuclein pathology facilitates macroscopic observation of network patterns, including the overall increase in pathology over time and most substantial spread to highly connected ipsilateral regions. While pathological α-Synuclein load in informative, we also sought to develop a brain-wide measure of neuron death.

Fig. 2. α-Synuclein spreads in a dynamic spatiotemporal pattern throughout the mouse brain.

a, Representative quantitative pS129 α-Synuclein pathology plots and images are shown for 1-, 3- and 6-month timepoints (scale bar=50 μm). Plots display mean +/− standard error. b, Heat map of regions affected with α-Synuclein pathology. The names of the associated areas are plotted onto identical maps in the supplementary material. The color scale represents log-transformed mean percentage area occupied with α-Synuclein pathology. n (number of mice), 1 MPI=4, 3 MPI=6, 6 MPI=6.

Estimating neuron death

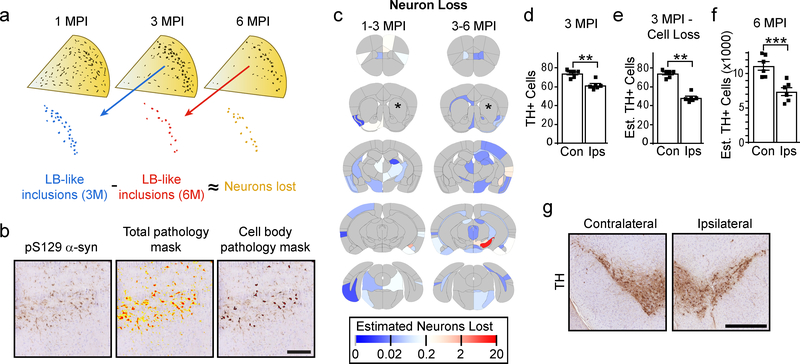
α-Synuclein pathology can take multiple morphological forms. Soon after injection, the majority of pathology is neuritic (Fig. 3a). By 3 MPI, much of the pathology has consolidated into large LB-like cell body inclusions. By 6 MPI, some regions have diminished pathology possibly due to consolidation of neuritic pathology into cell body inclusions and neuron death. Previous work has demonstrated that in the substantia nigra (SN)⁸, cortex¹⁰ and accessory olfactory nucleus¹¹ loss of cell body pathology is indicative of the death of the inclusion-bearing neurons. Therefore, we proposed to obtain estimates of neuron loss in each region by measuring cell body inclusions throughout the brain and using the difference between timepoints as an estimate of neuron loss (Fig. 3a).

Fig. 3. Select quantification of cell body pathology allows for assessment of neuron loss.

a, Theoretical framework for assessing neuron loss. Pathology appears at 1 month as primarily neuritic pathology, which consolidates over time into large LB-like inclusions. If these large inclusions can be measured as sequential timepoints, it would allow an approximation of the number of neurons that are lost during that time period. b, An example of a region that has both high neuritic and cell body pathology burden. The total pathology mask identifies both forms of pathology, while the cell body pathology mask excludes neuritic pathology and identifies only cell body pathology (scale bar = 100 μm). c, Heat map of the estimated number of neurons lost in each anatomical region. The color scale represents log- transformed mean number of neurons lost between 1 and 3 (1–3 MPI) and between 3 and 6 (3–6 MPI) months post-injection. d, One section in between the two sections used for pathology quantitation was stained with an anti-TH antibody and used for quantification of substantia nigra neurons in each 3 month post-injection mouse (two-tailed paired t-test, p=0.0026). e, The mean estimated neuron loss between 3 and 6 months from the SN was subtracted from the TH cell counts in 3 MPI mice (two-tailed paired t-test, p=0.0075). f, Every 10^th section through the SN was stained with an anti-TH antibody and SN neurons were counted to estimate the total number of neurons present in NTG mice 6 months after injection (two-tailed paired t-test, p=0.0003). g, Representative images of the contralateral and ipsilateral substantia nigra from NTG mice 6 months post-injection (scale bar = 500 μm). (Plots display mean +/− standard error with individual values plotted) n (number of mice), 1 MPI=4, 3 MPI=6, 6 MPI=6.

To exclude neuritic pathology, we developed a second algorithm to measure only cell body inclusions based on size (40–400 μm²), shape (round) and texture (thick) (Fig. 3b). After optimizing the ability of the algorithm to identify exclusively cell body pathology throughout the brain, the algorithm was applied to all annotated sections. The difference between the number of cell body inclusions at sequential timepoints was used to give an estimate of neuron loss (Fig. 3c). The highest observed neuron loss was in the SN between 3 and 6 MPI, consistent with the SN’s high vulnerability in PD.

To validate the neuron loss measure, sections from 3 MPI mice between the two sections used for pathology quantitation were stained for tyrosine hydroxylase (TH) and the number of neurons in the SN were counted (Fig. 3d). The mean estimated neuron loss for this region from 3 to 6 MPI was then subtracted from the TH cell counts to give an estimated 35% neuron loss on the side ipsilateral to the injection side compared to the contralateral side (Fig. 3e). To test the accuracy of this estimate, every 10^th section through the midbrain of 6 MPI mice was stained for TH, and the number of TH cells was counted (Fig. 3f, 3g). The actual TH cell loss in the ipsilateral SN of 6 MPI mice was 34% compared to the contralateral side. The concordance of the estimated and actual neuron loss suggests that loss of cell body inclusions is a valid proxy for neuron loss.

Network model of pathological α-Synuclein spread

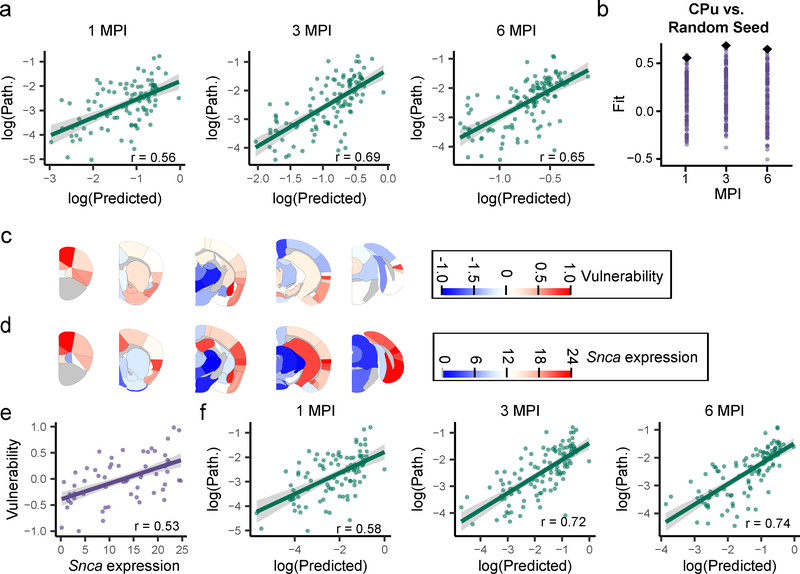
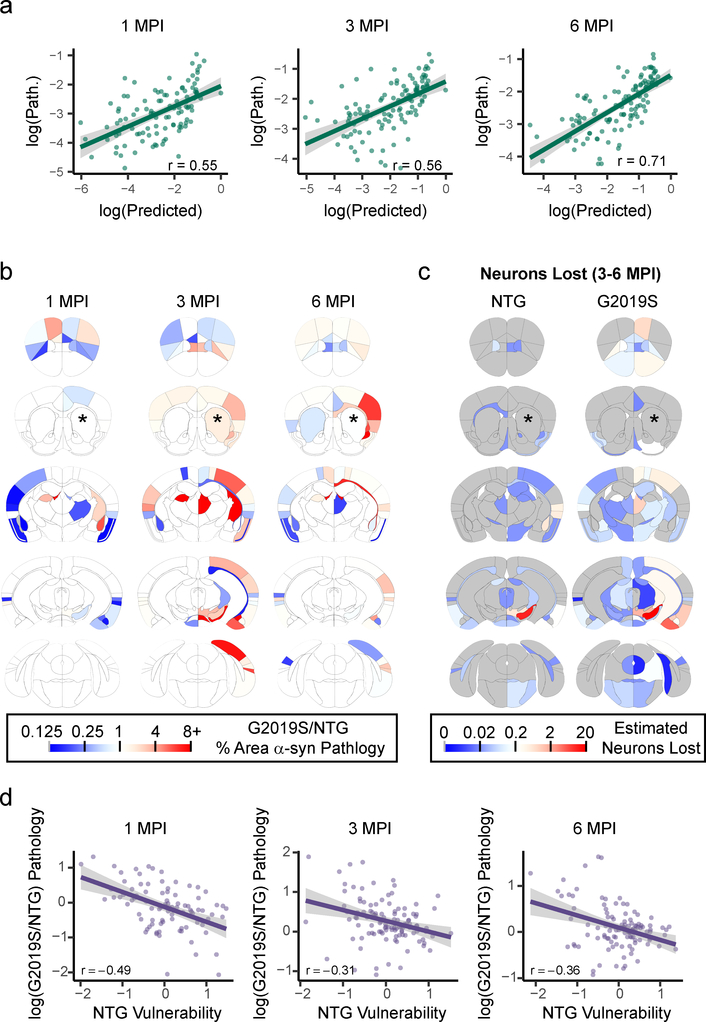
Observationally, many of the regions to which α-Synuclein spreads have high direct anatomical connectivity to the injected CPu¹⁶ (Supplementary Fig. 3). However, this connectivity hypothesis has not been tested using quantitative pathology data. Here, we experimentally validated a network diffusion model based on anatomical connectivity (Supplementary Fig. 4, see Methods for details). Using this model, we estimated pathology as a function of time given the introduction of misfolded protein into the iCPu. The model specified that pathological α-Synuclein would propagate retrogradely along synapses at a rate proportional to the density of axonal projections, and explained much of the overall variability in the mean regional pathology across all mice at 1, 3 and 6 MPI (Fig. 4a). These results suggest that linear dynamics imposed on a network of synaptic connections can explain pathological α-synuclein spread over time.

Fig. 4. Network diffusion model based on anatomical connectivity explains pathological α-Synuclein spread.

a, Scatterplots and Pearson correlation coefficients (r) of log predicted pathology based on anatomical connectivity versus actual pathology values for each region are shown for 1 (df = 95, p_corr = 9.85×10⁻⁹), 3 (df = 111, p_corr = 1.66×10⁻¹⁶) and 6 (df = 111, p_corr = 2.64×10⁻¹⁴) MPI (two-tailed t-tests). p-values were Bonferroni-corrected over the 3 time points. The green line represents the line of best fit, and the shaded ribbon represents the 95% prediction interval. b, Each different brain region was seeded and pathology propagation was modeled from each site. The fit of each of these sites is plotted for 1, 3, and 6 MPI (purple dots). The CPu seed (black diamond) produced either the best fit (3 and 6 MPI, 100^th percentile of fits) or second best fit (1 MPI, 99^th percentile of fits). c, Heat map of the residuals between the log(predicted) and log(pathology) are plotted on an anatomical mouse brain as a measure of the relative vulnerability of regions. d, Heat map of the Snca mean expression energy values from the Allen Brain Atlas in situ hybridization data for each of the designated regions. e, Scatterplots and Pearson correlation coefficients (r) of Snca expression energy and vulnerability estimates for each region. The two values show a positive Pearson correlation of r = 0.53 (two-tailed t-test, df = 114, p = 1.08×10⁻⁹). The purple line represents the line of best fit, and the shaded ribbon represents the 95% prediction interval. f, Scatterplots and Pearson correlation coefficients (r) of log predicted pathology based on anatomical connectivity and Snca expression vs. log actual pathology values for each region are shown for 1 (df = 95, P_corr = 1.85×10⁻⁹), 3 (df = 111, p_corr = 5.84×10⁻¹⁹) and 6 (df = 111, p_corr = 1.34×10⁻²⁰) MPI (two-tailed t-tests). p-values were Bonferroni-corrected over the 3 time points. The green line represents the line of best fit, and the shaded ribbon represents the 95% prediction interval. n (number of mice): 1 MPI=4, 3 MPI=6, 6 MPI=6).

To further test the ability of anatomical connectivity to predict the spread of pathology, each of the other brain regions was used as the seed region, and the model was propagated forward to generate predictions of pathological spread at 1, 3 and 6 MPI. The fit of the predicted pathology to the actual pathology displayed a range of accuracies, but an iCPu seed produced either the best or second-best fit at all time points (Fig. 4b). The other seed regions that showed a high fit to the empirical data had high in-projection similarity to the CPu (Supplementary Fig. 5), suggesting that seed regions exhibiting high degrees of topological similarity yield similar predictions.

To explore the directionality of spread, retrograde and anterograde connectivity values were inserted into the model separately. While retrograde connectivity had r=0.56–0.69 (Fig. 4a), anterograde alone gave r=0.32–0.43 (Supplementary Fig. 6), suggesting that α-Synuclein spreads primarily in a retrograde manner or that retrograde spread to cell bodies is more easily detected than anterograde spread to nerve terminals.

We further tested the specificity of the network diffusion model by evaluating the ability of proximity to the injection site and higher-order topological features to explain the observed α-Synuclein pathology. A network defined by the Euclidean distance between regions poorly explains the observed pathology (Pearson’s r=−0.066–0.1, Supplementary Fig. 7a), and disruption of higher-order topological features also abrogates the predictive capabilities of the model (Pearson’s r=0.14–0.18, Supplementary Fig. 7b).

Notably, the model requires only a single parameter to be fit, which is a time constant that simply scales the location of the observed time points along the trajectory of the model. We selected the time constant that produced the best mean fit across all time points with the empirical data. To ensure that the time constant we selected was externally valid, we performed split reliability tests. Specifically, we fit the time constant on a random sample composed of half of the mice, and tested its ability to explain the mean regional α-Synuclein pathology values in the remaining half of the mice. This procedure was repeated 100 times, and the fits observed when using every mouse (Fig. 4a) did not lie outside of the distribution of out-of-sample fits (Supplementary Fig. 8). These results suggest a high reliability of the estimated time constants, and low variability between mice in the time course of the spread of pathological α-Synuclein.

Differential vulnerability of regions is correlated with α-Synuclein expression

Intrinsic vulnerability is postulated to be a critical factor that impacts the development of pathology at any given time⁶, and the network model provides a framework to understand which regions are more or less vulnerable than expected if anatomical connectivity were the sole driver of pathological spread (Supplementary Fig. 9). We therefore define the difference, or residual, between the connectivity-based prediction and observed pathology to be a measure of relative vulnerability. Regions wherein the a- synuclein pathology is exactly predicted by the model have a vulnerability value of 0. Regions that have more pathology than predicted have vulnerability values greater than 0; regions that have less pathology than predicted have vulnerability values less than 0 (Supplementary Fig. 10a).

In order to account for noise in the estimation of intrinsic neuron vulnerability, we computed a summary measure of vulnerability based on two principles that can be enforced on the residuals between the model and the empirical data: 1) Intrinsic vulnerability should not change over time and 2) intrinsic vulnerability should not be different on the ipsilateral and contralateral sides. Accordingly, we averaged the residuals for each region across all timepoints (Supplementary Fig. 10b) and both hemispheres (Fig. 4C). We posit that these two assumptions bring us closer to an estimation of the true regional vulnerability to pathological α-Synuclein spread. It is interesting to note that the basolateral amygdala, rostral cortical regions and piriform cortex are the most vulnerable, while thalamic and mesencephalic nuclei are largely resilient to α-Synuclein pathology (Supplementary Fig. 11a, 11b).

While incorporating relative vulnerability values into the network model would improve the predictive ability of the model for a CPu injection, we sought to identify a factor which would explain the regional vulnerability without any reliance on the empirical data set. We hypothesized that one factor which should influence the development of α-Synuclein pathology is α-Synuclein expression. We used α-synuclein gene (Snca) expression energy values¹⁷ from the Allen Brain Atlas (Fig. 4d, Supplementary Fig. 11a, 11c, brain-map.org) to examine the relationship of Snca expression to regional vulnerability. In support of our hypothesis, Snca expression is highly correlated with vulnerability values (Fig. 4e, Supplementary Fig. 11a, 11d).

While Snca expression explained variance in vulnerability (Supplementary Fig. 12), we also sought to explicitly incorporate Snca expression levels into our network diffusion model. We accomplished this aim by weighting the outgoing connections of every node by its respective Snca expression value, based on the notion that retrograde propagation of misfolded α-Synuclein will lead to greater pathological accumulation in regions with greater endogenous Snca expression. Indeed, incorporation of Snca expression into the model in this fashion improved the ability of the model to accurately predict the burden of α-Synuclein pathology (Fig. 4f). Together, these data suggest that Snca expression is an important factor in determining the vulnerability of regions to developing α-Synuclein pathology. Importantly, our network diffusion model is based only on factors intrinsic to the brain, i.e. anatomical connectivity and Snca expression, and can therefore be used as a powerful tool to model spread from other sites and investigate the role of network topology in pathological protein spread.

Model Applications

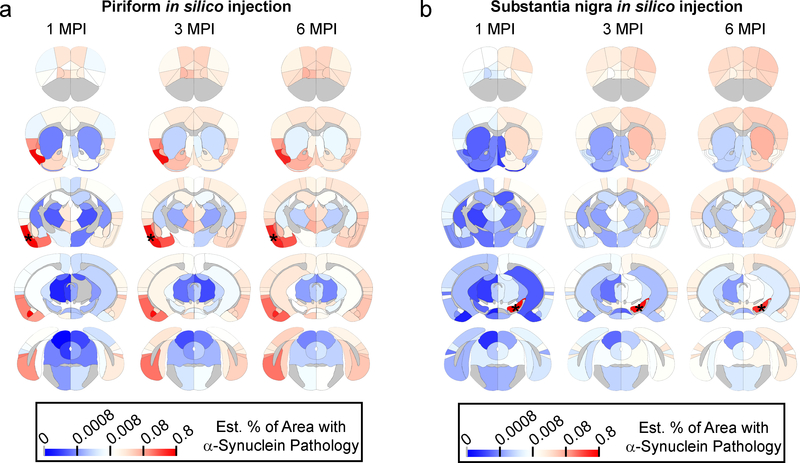
To demonstrate the generalizability of our model, we placed seeds in alternate sites and propagated the model forward in time to observe pathological α-Synuclein spread in silico. One of the most comprehensive assessments of α-Synuclein pathology spread to date used injections of α-Synuclein PFFs into the olfactory bulb of wildtype mice followed by semi-quantitative pathology grading through the mouse brain at 1, 3, 6 and 12 months post-injection¹⁸. To replicate this injection in silico, we seeded pathology in the piriform cortex and propagated the model 1, 3 and 6 MPI (Fig. 5a). The model shows a remarkable visual correspondence to the scoring previously reported¹⁸, suggesting our model is generalizable to different injection sites.

Fig. 5. In silico seeding of alternate regions in mouse brain.

Heat map of regions affected with α-synuclein pathology with in silico propagation of α-Synuclein pathology after seeding in either a, the piriform cortex or b, the substantia nigra. The color scale represents log-transformed mean percentage area occupied with α-Synuclein pathology.

LB staging from human PD and preclinical patients has led to a hypothesized neuroanatomical pathway by which pathology spreads from the brainstem or olfactory bulb up through the midbrain and limbic structures to cortical regions^19–21. Portions of this hypothesis can be tested by placing a seed in midbrain regions, including the SN (Fig. 5b). The seeding of α-Synuclein pathology in the SN results in slow propagation through the CPu to cortical regions, analogous to what has been observed in the staging of human cases. Seeding other regions including the hippocampus and secondary motor cortex (M2) (Supplementary Fig. 13) shows very distinct patterns of spread. Intriguingly, injections into M2 result in rapid decreases in pathology in frontal cortical structures in conjunction with progressive increases in pathology in subcortical structures (Supplementary Fig. 13b). In silico injection into the caudoputamen demonstrates the ability of the network model to recapitulate the empirical spread pattern, but also highlights regions in which spread is not fully recapitulated by the model (Supplementary Fig. 13c). Future in vivo injections at other sites will be important to quantitatively validate this model and determine other factors influencing pathological protein spread.

Understanding changes in network parameters due to G2019S LRRK2 expression

While theoretical manipulations of the network model can provide a powerful means of hypothesis testing, we sought to directly assay how a genetic risk factor for PD alters the spread of pathogenic a- synuclein and to use network modeling to understand properties underlying these alterations. While most cases of PD are idiopathic, autosomal dominant mutations in LRRK2 are responsible for 1–2% of all PD cases²². PD patients with LRRK2 mutations have a similar onset and somewhat slower progression of disease than idiopathic patients²³ and a similar incidence of pathological α-Synuclein inclusions²². The most common mutation Gly2019Ser (G2019S) leads to elevated kinase activity^24–26, and a recent report has suggested that LRRK2 kinase activity is elevated even in idiopathic PD patients²⁷. Despite the strong evidence implicating LRRK2 in PD pathogenesis, only 25–42.5% of G2019S carriers will get disease²⁸, suggesting that mutations in LRRK2 modulate pathogenesis of PD. We therefore hypothesized that while G2019S LRRK2 expression may not initiate α-Synuclein pathogenesis in mice, it may alter the vulnerability of neurons, alter the toxicity of α-Synuclein pathology and/or change the rate of pathology progression. Using the approach described thus far for NTG mice, we quantitatively measured and modeled α-Synuclein pathology spread in the brains of G2019S LRRK2 mice to understand the contribution of this genetic risk factor to disease.

The BAC transgenic G2019S LRRK2 mice used for this study have similar expression of α-Synuclein as wildtype (NTG) mice (Supplementary Fig. 14a, 14b) and show no accumulation of pathogenic α-synuclein without α-Synuclein PFF injection up to at least 12 months of age (Supplementary Fig. 14c, 14d). Interestingly, G2019S mice weigh less than NTG (Supplementary Fig. 14e) but show similar grip strength (Supplementary Fig. 14f) and enhanced motor performance on rotarod at early ages (Supplementary Fig. 14g), consistent with previous reports²⁹.

G2019S LRRK2 mice were injected with the same α-Synuclein PFFs in the dorsal striatum at the same time as C57BL/6J mice, so the two groups of mice could be directly compared. α-Synuclein PFF injection causes reduced grip strength in both NTG and G2019S mice compared to uninjected controls, but no difference between the genotypes (Supplementary Fig. 14f). α-Synuclein PFF injection did not cause a change in the latency to fall in the rotarod assay for NTG mice, but abrogated the enhanced performance seen in G2019S mice (Supplementary Fig. 14g).

The overall pattern of pathological spread in NTG and G2019S is similar (Fig. 6, N, 1 MPI-NTG=4, 1 MPI-G2019S=6, 3 MPI-NTG=6, 3 MPI-G2019S=6, 6 MPI-NTG=6, 6 MPI-G2019S=7). In fact, the spread pattern in many regions is nearly identical (Fig. 6a, iCPu, cCPu, iM2) validating the replicability of this quantitative pathology method. However, there are large regional differences in the degree and rate of α-Synuclein pathology accumulation (iHipp-b, iSN, iS1). These regional differences lead to an overall alteration in the dynamics of pathological α-Synuclein spread (Fig. 6b) which is best understood at the network level.

Fig. 6. Quantitative α-Synuclein pathology mapping allows a direct comparison between NTG and G2019S LRRK2 mice.

a, Representative quantitative pS129 α-Synuclein pathology plots and images are shown for 1-, 3- and 6-month timepoints for both NTG and G2019S mice (scale bar = 100 μm). Plots display mean +/− standard error. b, Heat map of regions affected with α-Synuclein pathology. The names of the associated areas are plotted onto identical maps in the supplementary material. The color scale represents log-transformed mean percentage area occupied with α-Synuclein pathology. n (number of mice), 1 MPI-NTG=4, 1 MPI-G2019S=6, 3 MPI-NTG=6, 3 MPI-G2019S=6, 6 MPI-NTG=6, 6 MPI-G2019S=7.

We first fit the G2019S pathology data with the same network model as we had done previously for NTG mice. Specifically, we used a network based on anatomical connectivity weighted by Snca expression and fit a time constant to the G2019S pathology data. The model showed similar predictive power for the G2019S mice as we have already established for the NTG mice (Fig. 7a), suggesting that anatomical connectivity and Snca expression are powerful predictors of pathological spread. The model including Snca expression also had similarly elevated fit over a model only incorporating anatomical connectivity (Supplementary Fig. 15). However, the mean of the bootstrapped time constants was lower for G2019S than for NTG mice. This finding suggests that the rate of connectivity-based spread of α-Synuclein pathology is globally reduced in G2019S mice.

Fig. 7. α-Synuclein pathology shows enhanced spread and toxicity in resilient regions in G2019S LRRK2 mice.

a, Scatterplots and Pearson correlation coefficients (r) of log predicted pathology based on anatomical connectivity and Snca expression versus actual pathology values for each region are shown for 1 (df = 104, p_corr = 2.00×10⁻⁹), 3 (df = 112, p_corr = 2.39×10⁻¹⁰) and 6 (df = 113, p_corr = 9.07×10⁻¹⁹) MPI (two-tailed t-tests). p-values were Bonferroni-corrected over the 3 time points. The green line represents the line of best fit, and the shaded ribbon represents the 95% prediction interval. b, Heat map of regional ratios of pathology in G2019S/NTG mice. Warm colors represent areas with more pathology in G2019S mice, while cooler colors represent regions with less pathology in G2019S mice. c, Heat map of the estimated number of neurons lost in each anatomical region in NTG and G2019S mice. The color scale represents log-transformed mean number of neurons lost between 3 and 6 (3–6 MPI) months post-injection. d, Scatterplots and Pearson correlation coefficients (r) of timepoint-specific NTG regional vulnerability measures versus log G2019S/NTG pathology, showing a negative correlation between the two variables at 1 (df = 89, p_corr = 2.88×10⁻⁶), 3 (df = 109, p_corr = 0.0027) and 6 (df = 110, p_corr = 0.00035) MPI (two-tailed t-tests). p-values were Bonferroni-corrected over the 3 time points. The purple line represents the line of best fit, and the shaded ribbon represents the 95% prediction interval. n (number of mice), 1 MPI=6, 3 MPI=6, 6 MPI=7.

To test the hypothesis that the G2019S mutation would systematically affect vulnerability to connectivity-based spread, we visually compared the difference in α-Synuclein pathology between the NTG and G2019S plotted out on anatomical coordinates (Fig. 7b) to vulnerability values in NTG mice (Fig. 4c). It appeared that many of the regions with elevated pathology in G2019S are those that were resilient in NTG mice. Further, many of these regions also undergo enhanced neuron loss in the G2019S mice (Fig. 7c), including the ipsilateral SN, a phenomenon which was confirmed by TH cell counts (Supplementary Fig. 16). To further explore the relationship between the vulnerability of regions to α-synuclein pathology as established in NTG mice and the pathology observed in G2019S mice, we plotted vulnerability values against the difference in log(pathology), i.e. log(G2019S/NTG pathology) (Fig. 7d) for each timepoint. There was a negative correlation at all timepoints, suggesting that G2019S expression selectively enhances α-Synuclein pathology in otherwise resilient populations of neurons.

DISCUSSION

With limited neuropathology data, there appear to be islands of vulnerable neurons that are susceptible to developing pathogenic protein inclusions. However, meticulous neuropathological examination throughout the brain at different stages of disease has revealed patterns that suggest pathology spreads between anatomically-connected regions over time^19–21. Mouse models have further indicated that exogenous misfolded proteins can be taken up by neurons and induce the misfolding of endogenous protein, eventually leading to neuron death. Here, we employed absolute quantification paired with network diffusion modeling to explore the factors that dictate the rate and severity of pathogenic α-synuclein spread.

The current study takes advantage of several features of pathological protein spread in mice. First, the disease factor (pathological α-Synuclein) can be directly imaged in tissue. Second, the origin and timing of the disease factor is known since α-Synuclein PFFs were injected in the dorsal striatum at 3 months of age and allowed to age a further 1, 3, or 6 months. Third, anatomical connectivity of the mouse brain has been extensively characterized at a similar scale¹⁶, providing accurate antero- and retrograde connectivity measures for the model. Comparison of the network diffusion model developed in this study to the empirical data set found that anatomical connectivity is a major pathway of pathogenic protein spread. Studies using human imaging datasets have demonstrated the utility of similar network diffusion models to explain the degree of atrophy seen in human patients and even to extrapolate an initiation site for the observed atrophy^30–32. Future development of ligands which bind misfolded proteins in the human brain will allow longitudinal in vivo imaging of pathogenic protein and direct comparison between mouse and human neuropathology.

We were particularly interested in regions that showed higher or lower pathology than would be expected given the anatomical connectivity-based prediction, which may represent vulnerable and resilient populations of neurons, respectively. We found that Snca gene expression showed a remarkably similar pattern to inferred vulnerability, suggesting that resilient regions are those with very low α-Synuclein expression and vulnerable regions have relatively higher α-Synuclein expression. This finding is consistent with work from human brains showing that regions with low α-Synuclein expression are resilient to LB pathology³³. While other factors such as neurotransmitter type, spike rate, reactive oxygen species production and hyperbranching axons may shape the susceptibility of neurons to cell death⁶, much of the variance in α-Synuclein spread was explained purely by anatomical connectivity and α-Synuclein expression. It should be noted that Snca mRNA expression was utilized due to the public availability of this data and the correspondence of in situ hybridization data to neuronal cell bodies. Future studies should confirm whether other pathogenic proteins, such as tau, may spread based on anatomical connectivity and endogenous protein expression and whether incorporating other factors such as neuron type into the network model can explain even more of the variance in pathological protein spread.

The current study also found a high correspondence between clearing of LB-like inclusions and neuron death in the substantia nigra, confirming previous studies which found that neurons bearing LB-like inclusions eventually die^8,10. This observation allows us to use LB-like inclusion loss as a proxy for neuron loss. Measurement of LB-like inclusion number through the brain of mice at different timepoints indicates that neuron loss mostly occurs after long time periods and is related to the pathological burden in that region.

Though the data presented here are based on a single injection site, the factors dictating the network diffusion model are independent of the pathology data set. As intrinsic components of the network, these factors can be applied similarly to any injection site. Future empirical data is necessary to fully assess the generalizability of the model. In the interim, we believe that modulation of the factors controlling pathogenic protein spread will allow the assessment of the likely efficacy of therapeutic treatments and will aid understanding of the impact of genetic risk factors. This method can be merged with tools from network control theory^34,35 to analytically identify the optimal approach to effect a targeted change in the progression of pathology, either by modifying network nodes³⁴ (therapies targeted to regions) or edges³⁶ (therapies targeted to connections).

The current study found that G2019S mice exhibit higher pathology in some regions, yet lower pathology at other regions relative to NTG mice, perhaps explaining some of the conflicting data suggesting that either increases^37–39 or decreases^40,41 in LRRK2 activity can lead to α-Synuclein aggregation and dopaminergic neuron death. The increase in α-Synuclein pathology in the SN at 3 MPI and increased neuron death at 6 MPI in G2019S mice are consistent with what has been observed in G2019S BAC mice injected with PFFs⁴² or G2019S knock-in mice overexpressing A53T α-Synuclein via AAV⁴³. However, our work reveals that broader network dynamics of pathogenic protein spread are changed. The global rate of pathogenic α-Synuclein spread is reduced in G2019S mice, and resilient populations of neurons show enhanced α-Synuclein pathology and toxicity. It will be interesting to integrate these novel findings relating G2019S LRRK2 to pathological α-Synuclein network spread with the known involvement of LRRK2 in vesicle trafficking and network physiology⁴⁴.

One limitation of the data and model presented here is the mesoscale of analysis, which was chosen to allow comparison to anatomical connectivity data. Pathology in cortical regions shows a clear laminar distribution and the closer investigation of the layer and neuron types affected in the future will provide additional information about pathology spread. Another limitation is the sparseness of the regions sampled. Given current technological limitations, it was not possible to map quantitative pathology in the whole brain. However, the sparse data provides sufficient constraints of the network model to allow remarkably accurate reconstruction of pathological α-Synuclein spread. The further ability of in silico injection in an independent brain region to capture the spread pattern suggest that the data captured is sufficient to develop highly informative predictions. Possible differences in anatomical connectivity between strains of mice is also an important caveat to keep in mind in future modeling studies. Future work will also focus on improving performance of the model by incorporating factors such as regional protein turnover rate, neuron type and functional connectivity.

The network model presented here is informed by quantitative empirical data, but it is simple and uses only intrinsic network properties including anatomical connectivity and gene expression for its predictions. Therefore, the model is also easily manipulated by seeding in different regions, predicting the effects of known genetic risk factors and modeling therapeutic intervention by changing parameters of the model (e.g. reducing diffusivity to mimic α-Synuclein immunotherapy).

METHODS

Animals

All housing, breeding, and procedures were performed according to the NIH Guide for the Care and Use of Experimental Animals and approved by the University of Pennsylvania Institutional Animal Care and Use Committee. C57BL/6J (NTG, JAX 000664, RRID: IMSR_JAX:000664) and B6.Cg-Tg(Lrrk2*G2019S)2Yue/J (G2019S, JAX 012467, RRID: IMSR_JAX:012467) mice have been previously described¹⁴. The current G2019S BAC line was backcrossed to C57BL/6J mice for >10 generations and bred to homozygosity at loci as determined by quantitative PCR and outbreeding. The expression level of G2019S LRRK2 was thereby stabilized in this line of mice. All experiments shown use homozygous G2019S mice. Both male and female mice were used for this study.

Behavior

Mouse all-limb grip strength was measured using the animal grip strength test (IITC 2200). For this test a grid mesh is attached to a digital force transducer. Mice are moved to a quiet behavioral testing suite and allowed to acclimate for 1 hour. Each mouse was held by the base of the tail and allowed to grasp the grid mesh. Once the mouse clasps the grid, the mouse is slowly moved backwards, in line with the force transducer until the mouse released the grid. The maximum grip force was recorded. The mouse was allowed to rest for several seconds, and then was placed on the grid again. The maximum grip strength of 5 tests was recorded. No fatigue was observed during the test period, so the average of all 5 measures is reported.

An accelerating rotarod (MED-Associates) was used to assess motor coordination. Mice received two training sessions and two tests sessions. During the training sessions, mice were placed on a still rod. The rod then began to accelerate from 4 rotations per minute (rpm) to 40 rpm over 5 minutes. Mice were allowed to rest at least one hour between training and testing sessions. During the testing sessions, mice were treated as before, and the latency to fall was recorded. Time was also stopped if a mouse gripped the rod and rotated with it instead of walking. Mice were allowed a maximum of 10 minutes on the rod.

α-Synuclein PFF Stereotaxic Injections

Purification of recombinant α-Synuclein and generation of α-Synuclein pre-formed fibrils (PFFs) was conducted as described elsewhere ^45–47. All of the surgery or experiments were performed in accordance with protocols approved by the Institutional Animal Care and Use Committee (IACUC) of the University of Pennsylvania. Mouse α-Synuclein PFFs, which were generated at a concentration of 5 mg/mL were vortexed and diluted with Dulbecco’s phosphate-buffered saline (DPBS) to 2 mg/mL. They were then sonicated on high for 10 cycles of 30 seconds on, 30 seconds off (Diagenode Biorupter UCD-300 bath sonicator).

Mice were injected when 3–4 months old. Mice were evenly assigned to one of two surgeons at random. Even groups of NTG and G2019S mice were injected concurrently to minimize any differences due to surgery date or α-Synuclein PFF preparation. Mice were injected unilaterally by insertion of a single needle into the right forebrain (coordinates: +0.2 mm relative to Bregma, +2.0 mm from midline) targeting the dorsal striatum (2.6 mm beneath the dura) with 5 μg α-Synuclein PFFs (2.5 μL). Injections were performed using a 10 μL syringe (Hamilton, NV) at a rate of 0.4 μL/minute. After 1, 3 or 6 months, mice were perfused transcardially with PBS, brains were removed and underwent overnight fixation in 70% ethanol in 150 mM NaCl, pH 7.4.

Immunohistochemistry

After perfusion and fixation, brains were embedded in paraffin blocks, cut into 6 μm sections and mounted on glass slides. Slides were then stained using standard immunohistochemistry as described below. Slides were de-paraffinized with 2 sequential 5-minute washes in xylenes, followed by 1-minute washes in a descending series of ethanols: 100%, 100%, 95%, 80%, 70%. Slides were then incubated in deionized water for one minute prior to antigen retrieval as noted. After antigen retrieval, slides were incubated in 5% hydrogen peroxide in methanol to quench endogenous peroxidase activity. Slides were washed for 10 minutes in running tap water, 5 minutes in 0.1 M tris, then blocked in 0.1 M tris/2% fetal bovine serum (FBS). Slides were incubated in primary antibodies overnight. The following primary antibodies were used. For misfolded α-Synuclein, Syn506⁴⁸ was used at 0.4 ug/mL final concentration with microwave antigen retrieval (95°C for 15 minutes with citric acid based antigen unmasking solution (Vector H-3300). For pathologically-phosphorylated α-Synuclein, pS129 α-Synuclein (EP1536Y; Abcam ab51253) was used at 1:20,000 with microwave antigen retrieval. To stain midbrain dopaminergic neurons, Tyrosine hydroxylase (TH-16; Sigma-Aldrich T2928) was used at 1:5,000 with formic acid antigen retrieval.

Primary antibody was rinsed off with 0.1 M tris for 5 minutes, then incubated with goat anti-rabbit (Vector BA1000) or horse anti-mouse (Vector BA2000) biotinylated IgG in 0.1 M tris/2% FBS 1:1000 for 1 hour. Biotinylated antibody was rinsed off with 0.1 M tris for 5 minutes, then incubated with avidin-biotin solution (Vector PK-6100) for 1 hour. Slides were then rinsed for 5 minutes with 0.1 M tris, then developed with ImmPACT DAB peroxidase substrate (Vector SK-4105) and counterstained briefly with hematoxylin. Slides were washed in running tap water for 5 minutes, dehydrated in ascending ethanol for 1 minute each: 70%, 80%, 95%, 100%, 100%, then washed twice in xylenes for 5 minutes and coversliped in Cytoseal Mounting Media (Fisher 23–244-256).

All mice were initially stained with Syn506 for quantification of pathology. It was noted that several mice had perfusion artifacts which were recognized by secondary antibody staining of Syn506 due to the fact that Syn506 is a mouse antibody. Since absolute quantification relies on no background staining these mice were excluded from analysis. The recently developed pS129 α-Synuclein antibody (EP1536Y) is a rabbit monoclonal antibody, and using anti-rabbit secondary antibody prevents recognition of endogenous mouse antibodies present in perfusion artifacts. After direct comparison of EP1536Y staining to Syn506 staining revealed a high correspondence of the two stains, the remaining mice were stained with EP1536Y. The fact that analyzing mice in iterative groups finds good correspondence of time constant fitting (Supplementary Fig. 8) also supports the high congruence of the two stains.

Slides were scanned into digital format on a Lamina scanner (Perkin Elmer) at 20× magnification. Digitized slides were then used for quantitative pathology.

Quantitative pathology

All section selection, annotation and quantification was done blinded to genotype. For quantification of α-Synuclein pathology, coronal sections were selected to closely match the following coordinates, relative to bregma: 2.10 mm, 0.98 mm, −1.22 mm, −2.92 mm and −4.48 mm. The digitized images were imported into HALO software to allow annotation and quantification of the percentage area occupied by α-Synuclein pathology and the number of cell body inclusions. Standardized annotations were drawn to allow independent quantification of 172 regions throughout the brain. Each set of annotations was imported onto the desired section and modified by hand to match the designated brain regions. After annotation, the analysis scripts were applied to the brain to make sure that no non-pathology signal was detected. After annotation of all brains, analysis algorithms were applied to all stained sections and data analysis measures for each region were recorded.

Two analysis algorithms were applied to the tissue. The first detects total signal above a minimum threshold. Specifically, the analysis included all DAB signal that was above a 0.157 optical density threshold, which was empirically determined to not include any background signal. This signal was then normalized to the total tissue area. A minimal tissue optical density of 0.02 was used to exclude any areas where tissue was split, and a tissue edge thickness of 25.2 μm was applied to exclude any edge effect staining. The second analysis was designed to detect only cell body inclusions. This analysis first classified staining into two broad classes: thin versus thick pathology based on size and texture inputs. The analysis used only the class of thick pathology and excluded objects smaller than 40 μm² and greater than 400 μm² to remove small inclusions and to separate multiple inclusions from each other.

Every 10^th slide through the midbrain was stained with tyrosine hydroxylase (TH). TH-stained sections were used to annotate the substantia nigra, and cell counting was performed manually in a blinded manner for all sections. The sum of all sections was multiplied by 10 to estimate the total count that would be obtained by counting every section.

Computational Model

To generate a computational model of pathological spread, we required anatomical connectivity, gene expression and α-Synuclein pathology measures that were in the same anatomical space. We used the previously-generated data set¹⁶ for synaptic connectivity and Snca gene expression¹⁷ (brain-map.org). Snca gene expression values were recorded as 200 μm² pixel expression energy values (Snca-RP_071218_03_E03 (coronal)). The mean value for all pixels in a given region was taken as the expression energy for that region. α-Synuclein pathology measures generated for this study were calculated as described above and reported in Supplementary Table 1. The anatomical regions largely corresponded between the three data sets, but in cases where they did not, the average for the regions in the corresponding atlas was taken to create an accumulated score for that region. For example, the thalamus was broken into several large regions for α-Synuclein pathology analysis due to the fact that there is little pathology there and the several nuclei that encompass it are difficult to manually demarcate. Therefore, the ventromedial thalamus (VMThal) in the pathology data actually encompasses the following nuclei from the connectivity data: Ventral anterior-lateral (VAL), ventral posteromedial (VPM), ventral medial (VM), ventral posterolateral (VPL) and reticular (RT) nuclei of the thalamus. In the other direction, the piriform area, while only having one connectivity value, actually spans several of the sections in which pathology was quantified. Therefore, the mean of all piriform α-Synuclein pathology values was used to compare to the connectivity of the piriform area.

Linear diffusion model of pathological spread

Previous studies have used linear diffusion models to predict patterns of atrophy observed in various neurodegenerative diseases^30,31, supporting a mechanism of prion-like spread of misfolded proteins along large white matter fibers. In the present work, we aimed to validate the ability of these linear diffusion models to predict the spread of misfolded α-Synuclein throughout the mouse brain from an injection site in the right caudate-putamen (iCPu).

We model pathological spread of α-Synuclein as a diffusion process on a directed structural brain network G = {V, E} whose nodes V are N cortical and subcortical grey matter regions and whose edges e_ij ∈ E represent an axonal projection initiating in V_i and terminating in V_j, where e_ij ≥ 0 for all E. Edge strength was quantified by the Allen Brain Institute using measures of fluorescence intensity from retrograde viral tract tracing¹⁶. We define the weighted adjacency matrix of G as A = [A_ij]. Rows and columns of A were averaged to generate a final parcellation of 116 regions, in accordance with our quantitative measurements of regional synuclein pathology at time t, which were obtained at t = [1 3 6] months.

We represent the magnitude of observed α-Synuclein pathology of all N nodes at time t as the vector x(t). We compute the predicted regional α-synuclein pathology $\widehat{\mathit{x}}(t)$ as a function of A and seed region s ∈ V:

$$\widehat{\mathit{x}}(t)=e^{-c\mathit{L}t}{\mathit{x}}_o,$$

where ${\mathit{L}}_{ij}=\{\begin{array}{c}-{\mathit{A}}_{ij}\text{for}i\ne j\\ {\sum }_{j=1}^N{\mathit{A}}_{ij}\text{for}i=j\end{array}$, ${\mathit{x}}_{o_i}=\{\begin{array}{l}0\text{for}i\ne s\hfill \\ 1\text{for}i=s\hfill \end{array}$, and c is a constant to tune the time scale of the system. We selected the time constant c which maximized the model fit f, defined as Pearson correlation between log₁₀ x(t) and log₁₀ $\widehat{\mathit{x}}(t)$ for all non-zero values of x(t), averaged over t = [1 3 6]. Note that L is the out-degree Laplacian, a version of the well-characterized graph Laplacian designed for directed graphs⁴⁹. This model posits that the rate of change of in pathology at region i is proportional to a weighted sum of the pathology at all other regions and the strength of outgoing projections arriving at those regions from region i, minus the sum of outgoing connections from region i times the amount of pathology at region i. Notably, as a property of all Laplacian matrices, L has a single eigenmode with an eigenvalue equal to 0, describing the steady state behavior of the system as t approaches ∞ ⁴⁹. Asymmetric graphs also have eigenmodes with complex eigenvalues, such that ${\widehat{\mathit{x}}}_i(t)$ oscillates, or in the case of our particular matrix A, exhibits a single, damped oscillation over time. Thus, the time constant c identifies where along the damped oscillation curve of the system $\widehat{\mathit{x}}(t)$ provides the best fit to the observed data, with large values of c indicating the best fit lies closer to the static end behavior. All computations were performed in R (R Core Team (2017). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. URL https://www.R-project.org/.) and MATLAB.

Model incorporating α-Synuclein expression

In addition to the spread of the misfolded protein along anatomical connections, we also hypothesized that the pathogenicity of misfolded synuclein would be dependent on the presence of endogenous α-synuclein at each brain region. We observed that the residuals of $\widehat{\mathit{x}}(t)$ as a linear predictor of x(t) were correlated with R, a vector of length N containing the estimated levels of α-Synuclein mRNA at each brain region (brain-map.org). Thus, we sought a way to explicitly incorporate R into our linear diffusion model as a measure of the intrinsic vulnerability of each region. To accomplish this, we modify A such that A = SA, where S is the diagonal matrix of R such that $\mathit{S}=\{\begin{array}{l}{\mathit{R}}_i\text{for}i=j\hfill \\ 0\text{otherwise}\hfill \end{array}$. This step weights the outgoing connections of each region in A by its level of synuclein expression, and can be viewed as an “update rate” in the context of linear systems theory⁴⁹. All subsequent steps, including generation of the Laplacian, fitting of the time constant c, and propagation of the model as a continuous linear system, were performed according to the procedures described above.

Code availability

All code is available at https://github.com/ejcorn/connectome_diffusion.

Statistical Analysis

Quantification of model specificity

After identifying that our connectome-based linear diffusion model could explain substantial variance in the spread of misfolded α-Synuclein from the iCPu over time, we next sought to test the specificity of this model to the use of iCPu as the seed site s, which defines the vector x₀. To test the model specificity, we fit the time constant c to the observed data as described above using every region as s except for iCPu, generating a distribution of non-specific fits for each time points. We assessed the specificity of iCPu as the seed region s by computing the number alternate seed regions yielding better fist than the fit obtained using iCPu as a seed.

While iCPu seed produced nearly the best possible fit at all time points, we observed that several models utilizing alternate seed regions still fit the observed data relatively well. We hypothesized that seed regions with similar connectivity profiles to that of iCPu would perform similarly in explaining the observed data. We computed the similarity of incoming connectivity to iCPu as the Pearson correlations between the column of A_ij where j is the iCPu, and the columns of A_ij where j is all other regions except iCPu. Conversely, we computed the similarity of outgoing connectivity to iCPu as the Pearson correlations between the row of A_ij where i is the iCPu, and the rows of A_ij where i is all other regions except iCPu.

Because the relationship between alternate seed model fit and similarity of incoming connectivity to iCPu appeared to have a non-linear form, we used a general additive model (GAM) to fit the relationship using the gam function from the mgcv package in R⁵⁰. A GAM is a generalized linear model in which the linear predictor is defined by unknown smooth functions of predictor variables^51,52. We fit the following non-linear model to predict the fit of the alternate seed model from a smooth function of the connection similarity:

$$y=s(C)+\epsilon ,$$

where y is the fit of the alternate seed model, C is the connection similarity of the respective seed region to iCPU (described above), and ε is an error term.

Evaluating split-reliability and generalizability of model fit

The data presented in the body of the paper utilize values for the time constant c derived from data from all mice at every time point (x_full(t)). To ensure that this approach did not result in overfitting, we randomly sampled without replacement the available mice at each time point to generate x_train (t) and x_test(t) for each time point. The time constant c was determined on x_train(t), and the model was evaluated based on its fit with x_test(t). This process was repeated 100 times, generating a distribution of out-of-sample fits for each time point. We computed a non-parametric p-value for the generalizability of the model as the number of times the fit generated using x_full(t) exceeded the fit generated by x_test(t), quantifying the difference between in-sample and out-of-sample performance.

Network null models

To ensure that our results were specific to the retrograde spread of misfolded synuclein along neuronal processes, we repeated our analyses using several network null models. To demonstrate a general specificity of the model for the topology of the synaptic connectome represented by A, we carried out a procedure that rewires the edges of G while exactly preserving the out-degree and in-degree sequence, i.e. ${\sum }_{j=1}^N{\mathit{B}}_{ij}$ and ${\sum }_{i=1}^N{\mathit{B}}_{ij}$, where ${\mathit{B}}_{ij}=\{\begin{array}{l}1\text{for}{\mathit{A}}_{ij}>0\hfill \\ 0\text{otherwise}\hfill \end{array}$. This rewiring approach tests whether the model fit is due to a relatively basic structural property of the graph, i.e. degree, as opposed to unique, higher order topological features of the synaptic connectome.

Next, we tested whether a model based on anterograde propagation of misfolded protein along axons might explain the observed spread of pathology. To test this model, we simply replaced A with its transpose A^T and repeated all subsequent steps as described above. Finally, we tested the null model that spread of misfolded protein occurs simply due to diffusion through tissue based on closeness in Euclidean space. To test this model, we reconstructed A = [A_ij] such that the edges represented the Euclidean distance between region i and region j. All subsequent steps were performed as described above.

Empirical Data

For α-Synuclein pathology data, a two-way ANOVA was run on each region, and the months were compared to each other using Tukey’s multiple comparison test, while the genotypes were compared to each other using Sidak’s multiple comparison test. For TH cell counts in the midbrain, the side ipsilateral to the injection was compared to the side contralateral to the injection and the genotypes were compared to each other using a two-way ANOVA with Sidak’s multiple comparison test. All behavioral data compared both non-injected mice to α-Synuclein PFF injection and NTG to G2019S cohorts using two-way ANOVA with Sidak’s multiple comparison test. Data distribution was assumed to be normal, but this was not formally tested. No statistical methods were used to pre-determine sample sizes but our sample sizes are similar to those reported in previous publications^8,15.

Reporting Summary

Further information on research design is available in the Life Sciences Reporting Summary linked to this article.

Data Availability

All primary pathology data are available in Supplementary Table 1 and on GitHub (https://github.com/eicorn/connectome_diffusion). Any other data used to generate the figures in this study are available from the corresponding authors upon reasonable request.