The promise of selecting individuals from the extremes of exposure in the analysis of gene-physical activity interactions

Abstract

Background:

Dichotomization using the lower quartile as cutoff is commonly used for harmonizing heterogeneous physical activity (PA) measures across studies. However, this may create misclassification and hinder discovery of new loci.

Objectives:

This study aimed to evaluate the performance of selecting individuals from the extremes of the exposure (SIEE) as an alternative approach to reduce such misclassification.

Method:

For systolic and diastolic blood pressure in the Framingham Heart Study, we performed genome-wide association study with gene-PA interaction analysis using three PA variables derived by SIEE and two other dichotomization approaches. We compared number of loci detected and overlap with loci found using a quantitative PA variable. In addition, we performed simulation studies to assess bias, false discovery rates (FDR), and power under synergistic/antagonistic genetic effects in exposure groups and presence/absence of measurement error.

Results:

In the empirical analysis, SIEE’s performance was neither the best nor the worst. In most simulation scenarios, SIEE was consistently outperformed in terms of FDR and power. Particularly, in a scenario characterized by antagonistic effects and measurement error, SIEE had the least bias and highest power.

Conclusion:

SIEE’s promise appears limited to detecting loci with antagonistic effects. Further study is needed to evaluate SIEE’s full advantage.

2. Introduction

Physical activity (PA) significantly reduces blood pressure (BP) in individuals with hypertension (high BP) and reduces the risk of incident hypertension in individuals with normal BP [1]. However, this influence has been shown to be modulated by genetic variants such that certain sub-populations do not experience the anti-hypertensive benefits of PA [2]. This underscores the importance of considering gene-PA interactions (GxPA) for characterizing the genetic architecture of hypertension. Candidate gene studies have identified specific genetic variants that modulate the effect of PA on BP, including the apolipoprotein E (APOE) and angiotensinogen (AGT) loci [3–6]. However, these studies are limited by sample size and the number of variants tested. Recent efforts like the Gene-Lifestyle Interaction Working Group of the Cohorts for Heart Aging Research in Genetic Epidemiology (CHARGE) consortium [7] have attempted to fill this gap. A recent study from this working group demonstrated enhanced power to detect novel loci by performing genome-wide meta-analysis combining a large number of cohorts [8].

However, a major challenge for such large multi-cohort studies is data harmonization. This is particularly true for PA, which is measured in various ways, ranging from subjective (e.g., selfreport) to objective (e.g., accelerometer-based) measures [9,10]. PA measures derived from self-reports/questionnaires in general have been shown to be subject to bias due to social stigma or recall bias and at best moderately correlated with objective measures of PA [11,12]. Furthermore, although the use of a quantitative PA variable such as hours spent in moderate and/or heavy PA increases power and would be preferred, this measure is not uniformly available across multiple studies.

Heterogeneous PA data in multi-cohort studies are often harmonized by splitting quantitative PA variables using a specified cutoff to distinguish physically active versus inactive individuals. This may create misclassification error because individuals with values close to but on opposite sides of the cutoff value may not differ substantially, but are categorized in different groups [13]. Further, dichotomizing a quantitative PA variable may result in a loss of distinctness in the exposure between groups and an increase in variability of individuals within groups [14]. Misclassification error and lack of exposure variability have been recognized as key factors reducing power to detect loci in GxE analysis [15–17].

In order to reduce misclassification arising from conventionally dichotomized PA variables, one can select individuals from the extremes of the exposure (SIEE). SIEE creates a dichotomous variable by assigning individuals in the extremes of the exposure distribution to distinct groups (e.g., active vs. inactive). It is based on the selective sampling approach of Boks et al. (2007), originally conceived as a cost-saving strategy to reduce the number of subjects being genotyped or sequenced by selecting individuals extremely discordant in the exposure variable (e.g. top and bottom 25%) [18]. Despite the sample size reduction, selective sampling markedly improved power of GxE studies under certain conditions [18].

Here, we explore the prospects of applying SIEE in GxPA studies to reduce exposure misclassification that results from conventional dichotomization. We considered three dichotomous PA variables: (i) created by the conventional approach [19], using the lower quartile as cutoff, (ii) created using the median as cutoff, and (iii) created by SIEE. For each dichotomous PA variable, we performed genome-wide association study (GWAS) of BP accounting for GxPA interactions. We also performed GWAS using the quantitative PA variable. These four GWAS results were compared in terms of number of loci detected and overlap in loci detected. In addition, we performed simulation studies to assess bias, false discovery rate (FDR), and power for the three dichotomous PA variables in the presence or absence of measurement error.

3. Materials and Methods

Study Individuals

Individuals of European ancestry between 18–80 years of age in Framingham Heart Study (FHS) were included in this study. The data was obtained from the Database of Genotypes and Phenotypes (dbGap) SNP Health Association Resource (SHARe). FHS is an ongoing longitudinal family-based study initiated by the National Heart, Lung, and Blood Institute and consisting of three cohorts; (i) the Original Cohort recruited in 1948; (ii) the Offspring Cohort, recruited in 1971 and composed of the biological descendants of the original cohort, their spouses and children; and (iii) the Third Generation Cohort recruited in 2002 and composed of the biological or adopted children of the offspring cohort. To create a cross-sectional data, we selected the 7^th visit for the Offspring Cohort and the 26^th visit for the Original Cohort, as these visits were contemporaneous. The methodology used for the FHS and SHARe data collection is described elsewhere [20].

Genotype data

From the FHS SHARe project, there were approximately 550,000 single nucleotide polymorphisms (SNPs) genotyped and ~ 2.5 million autosomal SNPs imputed with MACH using the Phase II (release 22) CEU reference panel from the International HapMap Project. Quality control procedures involved exclusion of genotyped SNPs with Hardy-Weinberg equilibrium P values < 10⁻⁶ or call rates < 90%, and imputed SNPs with imputation quality measure < 0.3. SNPs were also excluded if the minor allele frequency (MAF) was < 5%, or if the product of the number of copies of the minor allele and imputation quality was ≤ 20, to filter out unstable results of interaction analysis [21]. Approximately 2.1 million SNPs were used in our analysis (Table S1).

Phenotype data

Systolic (SBP) and diastolic BP (DBP) were measured following a consistent protocol using a standard mercury column sphygmomanometer in the clinic, as described in dbGap. SBP and DBP values for each individual represent the average of three blood pressure measurements; two were obtained by a physician and one by a nurse or technician. For individuals on anti-hypertensive medications, BP measures were adjusted by adding 15 mmHg to SBP and 10 mmHg to DBP [22].

PA variables

We derived four PA variables (Figure 1). The first was a quantitative variable, hereafter referred to as Quantitative. We calculated Quantitative as the sum of the hours spent in moderate PA per day and twice the hours spent in heavy PA per day; this information was self-reported. We then derived three dichotomous PA variables based on Quantitative: Lower Quartile Split (LQsplit); Median split (MEDsplit); and SIEE. LQsplit was derived by dichotomizing Quantitative using the lower quartile as a cutoff so that individuals in the lowest quartile (25%) are classified as inactive (exposed) and individuals above the lowest quartile are classified as active (unexposed). This is commonly used in GxPA studies [19]. MEDsplit was derived using the median (50%) as a cutoff such that individuals at or below the median are inactive, while individuals above the median are active. We considered this MEDsplit as it achieves equal prevalence of physically active and inactive participants. Equal-sized strata was shown to have the highest power in a simulation study investigating optimal conditions for detecting genetic risk score-PA interactions on obesity [23]. SIEE was derived by selecting individuals from the extremes of the distribution of Quantitative so that individuals in the lower quartile comprise the inactive group, while individuals in the upper quartile (top 25%) comprise the active group.

Figure 1.

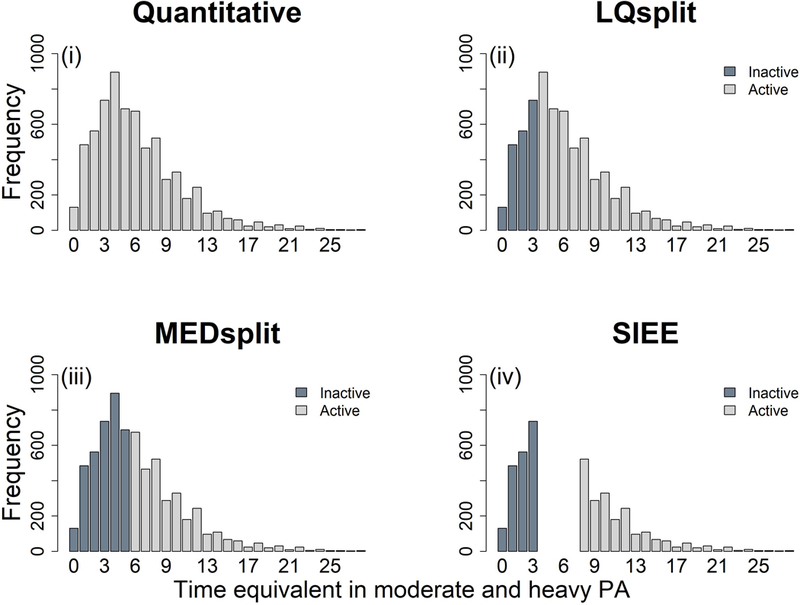
Distribution of four physical activity (PA) variables; (i) Quantitative, computed as the sum of hours spent in moderate PA and double the hours spent in heavy PA, (ii) LQsplit, a conventional dichotomous PA variable created by splitting Quantitative by the lower quartile of its distribution, (iii) MEDsplit, a dichotomous PA variable created by splitting Quantitative by the median of its distribution, and (iv) SIEE, a dichotomous PA variable created by selecting individuals with Quantitative values in the lower and upper quartiles and excluding individuals intermediate between the lower and upper quartile. Quartiles of Quantitative: lower quartile = 3, median=5, and upper quartile = 8.

Statistical analyses

We performed GWAS using a linear mixed effect model including SNP, PA exposure, and their interaction [24]:

$$y={\beta }_0+{\beta }_{cov}\ast X_{cov}+{\beta }_E\ast PA+{\beta }_G\ast G+{\beta }_{GE}\ast G\ast PA$$ (1)

where y is the phenotype (SBP or DBP), PA is the exposure variable (Quantitative, LQsplit, MEDsplit, or SIEE), G is the additively coded dosage of the genetic variant, X_cov are the covariates (age and sex), β_G is the genetic main effect, and β_GE is the interaction effect. To account for family relatedness in FHS data, we first obtained pedigree-adjusted residuals by running a polygenic model using the kinship matrix as a random component with GenABEL package [25]. Using ProbABEL package [26], we then performed GWAS by considering the resulting pedigree-adjusted residuals as the response in the regression model described above. From the model output, we calculated Wald test statistic for interaction effect β_GE that follows a χ² distribution with 1 degree of freedom (DF) (under H₀: β_GE = 0) and another one for jointly testing β_G and β_GE that follows a χ² distribution with 2 DF (under H₀: β_G = β_GE = 0) using EasyQC [27].

We considered a genome-wide threshold of P ≤ 5 × 10⁻⁸ for significant SNPs. In addition, we considered a less stringent threshold of P ≤ 1 × 10⁻⁵ as suggestive SNPs because this is an exploratory study evaluating multiple approaches (not novel loci discovery). For each significant/suggestive association, a locus was defined as a cluster of SNPs within ±500 kb of the index SNP (i.e., the SNP with the lowest P value in the region). We examined the extent of overlap in loci detected by GxE analyses for the three dichotomous PA variables, with Quantitative as a benchmark. To examine overlap, we used upSet plots created with the upSetR package [28] in R. A matrix layout is used by upSet plots to display intersections between sets. Overlap in loci detected equaled the sum of all intersections involving two particular sets.

Simulation studies

We performed simulation studies to assess bias, FDR, and power for the three dichotomous PA variables in R version 3.3.1 [29]. There were eight scenarios defined by the magnitude and direction of genetic effects in exposure groups, the cutoff used to define true PA status, and the presence/absence of measurement error in the dichotomized Quantitative (Table 2). The direction of simulated genetic effects was either synergistic, i.e., same direction in exposure groups (e.g., + in inactive and + in active), or antagonistic, i.e., opposite direction of effects in exposure groups (e.g., + in inactive and - in active). We varied the magnitude of genetic effect sizes to distinguish performance of PA variables.

Table 2.

Simulation scenarios defined by effect size differences between exposure groups and the cutoff for determining physical activity (PA) status.

Simulation scenario	Interaction effect direction	Effect sizes		True cutoff for defining PA status	Measurement error
		βactive	βinactive
LQ_SYN	Synergistic	0.4	0.8	Lower quartile	Absent
35%_SYN	Synergistic	0.4	0.8	35th percentile	Absent
MED_SYN	Synergistic	0.4	0.8	Median	Absent
MED_SYN+MEASUREMENT_ERROR	Synergistic	0.5	1.0	Median	Present
LQ_ANT	Antagonistic	−0.58	0.58	Lower quartile	Absent
35%_ANT	Antagonistic	−0.58	0.58	35th percentile	Absent
MED_ANT	Antagonistic	−0.58	0.58	Median	Absent
MED_ANT+MEASUREMENT_ERROR	Antagonistic	−1.4	1.4	Median	Present

Abbreviations: LQ, lower quartile; MED, median; 35%, 35^th percentile; SYN, synergistic (same effects direction); ANT, antagonistic (opposite effects direction); MEASUREMENT_ERROR, measurement error in Quantitative.

Each scenario had 500 replications. In each replication, we generated a population cohort with the same number of individuals and sex and age distributions as in FHS data (N=6,705). We simulated Quantitative from a normal distribution: Quantitative ~ N(μ=10, σ=3). Additionally, to introduce measurement error, we added error terms simulated from a normal distribution (~ N(μ=0, σ=4)) to the true Quantitative. Next, we derived the true PA status by dichotomizing Quantitative using a specified cutoff as defined in each scenario (Table 2). BP phenotype was simulated to be dependent on PA status and a randomly selected SNP dosage (> 0.05 MAF) from chromosome 22. Age and sex effects were kept similar to effects observed in FHS data (see Supporting Information S1 for details). We derived the three dichotomous PA variables (LQsplit, MEDsplit, and SIEE) based on the simulated Quantitative as described above in the PA variables section.

Next, we performed three sets of GxE analysis, one set for each dichotomous PA variable, while adjusting for kinship, age and sex. In each analysis set, single SNP regressions (i.e., the linear mixed effects model specified in (1) above) were run for 32,104 SNPs in chromosome 22. The combination of 8 scenarios, 3 PA variables, and 500 replications, resulted in 12,000 analysis sets in this simulation study. For each analysis set we tested for association between each SNP and the BP phenotype using the 2 DF joint test in EasyStrata [30].

For each PA variable in each scenario, we computed bias for a given genetic effect (e.g.,β_G or β_GE) as the deviation of the mean of estimated genetic effect sizes from the 500 replications from the simulated true effect size. We also calculated FDR as the proportion of total positive SNPs detected that are false positives. Lastly, we estimated power as the proportion of true positive SNPs found out of a total of 500 true positive SNPs.

4. Results

Real data analysis

Our analysis sample included 6,705 individuals for SBP and 6,704 for DBP. Basic characteristics of the study population by PA variables are shown in Table 1. The active group in SIEE included substantially fewer individuals than in the active group for LQsplit or MEDsplit. This was due to exclusion of 41% of the data, corresponding to individuals intermediate in the exposure distribution. There was also a larger percentage of males in the active relative to the inactive group (52.2 vs. 46.6%) for SIEE. For LQsplit, percentage of males was similar across groups (46.9 vs. 46.6%), while MEDsplit also had a higher percentage of males in the active group (48.8 vs. 45.0%).

Table 1.

Descriptive statistics of phenotypes and covariates considered by PA variables

Characteristics	Quantitative	LQsplit		MEDsplit		SIEE
		inactive	active	inactive	active	inactive	active
Sample size	6,705	1,913	4,792	3,495	3,210	1,913	2,071
Age (years)	49.1 ± 13.6	47.5 ± 12.7	49.7 ± 13.9	48.1±13.2	50.1±13.9	47.5 ± 12.7	50.1 ± 14.0
% Male	46.8	46.6	46.9	45.0	48.8	46.6	52.2
% Taking anti-	18.9	16.8	19.8	18.1	19.8	16.8	18.9
hypertensive medications
SBP (mmHg)	123.4 ± 19.2	121.9 ± 18	123.8 ± 19.6	122.4±19.5	124.1±18.8	121.9 ±18	124.0 ± 19.4
DBP (mmHg)	76.74 ± 10.4	77 ± 10.3	76.7 ± 10.4	76.8±10.4	76.6±10.4	77 ± 10.3	76.4 ±10.4

Abbreviations: %, percent; SBP, systolic blood pressure; DBP, diastolic blood pressure; LQsplit, created by splitting Quantitative by the lower quartile; MEDsplit, created by splitting Quantitative by the median; SIEE, created by selecting individuals with Quantitative values in the lower and upper quartiles and excluding individuals intermediate between the lower and upper quartile.

Sample size shown is for individuals with SBP data and is the basis for other descriptive statistics shown; descriptive statistics are very similar for DBP with sample size differing by a single individual (N=6,704).

Quantile-quantile (QQ) plots show no evidence of genomic inflation for any of the analyses (Figures S1 and S2). Observed genomic inflation factor (λ) values for SBP and DBP ranged from 0.965 to 1.047 and from 0.871 to 1.025, respectively. The observed –log₁₀P values for DBP exhibited moderate degree of deflation (λ = 0.871) for analysis involving LQsplit.

Significant/suggestive SNPs are presented in Tables S2 – S5 by phenotype and PA variable. Only one locus reached genome-wide significance for DBP using Quantitative and MEDsplit analyses (Tables 4S and S5). While SIEE detected it as a suggestive locus, LQsplit failed to detect the locus. The genome-wide significant SNP, rs13052701, is intronic within the gene MCM3AP (minichromosome maintenance complex component 3 associated protein). MCM3AP encodes a protein essential for the initiation of DNA replication and is associated with diseases such as peripheral neuropathy. Additionally, the genomic locus defined around this index SNP (± 500 MB) overlaps genes LSS, PCNT, YBEY, and C210rf58. Based on the MEDsplit analysis result, this genome-wide significant interaction is antagonistic in nature such that each copy of the risk allele results in a decrease in DBP by 1.038 mmHg in physically active individuals but an increase by 0.545 mmHg in physically inactive individuals. Although the Regulome DB variant classification scheme suggests that there is minimal evidence for disruption of transcription factor binding for rs13052701, this SNP may be in strong linkage disequilibrium with other yet to be discovered SNPs with functional consequences for BP.

In most cases, analysis using Quantitative provided the largest number of suggestive/significant loci, and conventional approach with LQsplit provided the smallest number of loci. Analysis with MEDsplit often provided almost equivalent number of loci as Quantitative, while SIEE analysis was intermediate. Using 1 DF test, Quantitative, LQsplit, MEDsplit, and SIEE provided 12, 3, 9, and 8 loci, respectively, for DBP (Table S6); this pattern was consistent for SBP (Table S6). Using 2 DF test, Quantitative, LQsplit, MEDsplit, and SIEE provided 13, 6, 15 and 10 loci, respectively, for SBP (Figure 2; panel i). For DBP, Quantitative, MEDsplit and SIEE equally found five suggestive/significant loci, while LQsplit found only three loci using the 2 DF joint test (Figure 2; panel ii).

Figure 2.

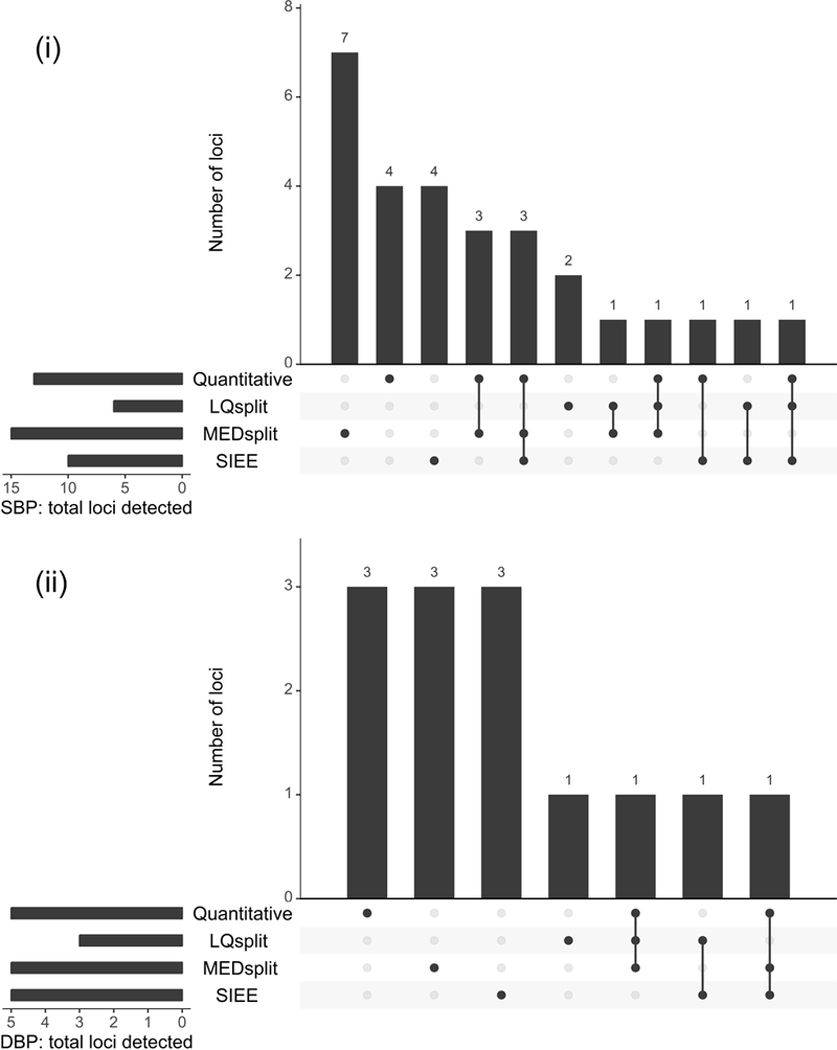
UpSet plot for (i) SBP, and (ii) DBP; showing in a matrix layout the overlap in loci detected through the 2 DF joint tests in different sets (GxPA analysis using a given PA variable), with the rows of the matrix representing the sets and the columns representing their intersections. The bars to the left of the matrix indicate the size of each set, i.e., the total number of loci detected by each analysis. Dark circles in the matrix indicate which sets are part of a given intersection. The bars above the matrix columns represent the number of elements in the intersection or overlap in loci detected. Overlap in loci detected equals the sum of all intersections involving two particular sets, e.g., for SBP in panel (i), overlap for SIEE and Quantitative equals the sum of 3, 1 and 1, which is 5. See Table 1 for definition of abbreviations.

Overlap in loci detected across analyses was moderate at best, as shown by intersections of sets in upSet plots in Figure 2. Using the 2 DF test, 39% (11 out of 28 loci) and 23% (three out of 13 loci) were found in common by at least two analyses for SBP and DBP, respectively. Using 1 DF interaction test, 32% (seven out of 22 loci) and 15% (four out of 27 loci) were detected in common by at least two analyses for SBP and DBP, respectively. The degree to which SIEE found loci in common with Quantitative was always more than LQsplit but either same or less than MEDsplit. This pattern was consistent for SBP and DBP using the 1 DF interaction (Table S6) and 2 DF joint tests (Figure 2). No locus was commonly found across all four GxPA analyses for SBP or DBP.

Simulation studies

Bias seemed to be more prominent in the antagonistic scenarios and in the presence of measurement error (Figure 3). In the six scenarios without measurement error, SIEE seemed to yield unbiased effect estimates (Figure 3). On the other hand, when not corresponding to the true cutoff in the absence of measurement error, the other two PA variables appeared to yield biased effect size estimates (Figure 3); LQsplit seemed to overestimate genetic main effect sizes and underestimate interaction effect sizes, while MEDsplit seemed to underestimate interaction effect sizes (Figure 3). However, in the presence of measurement error, all three PA variables appeared to overestimate genetic main effect sizes but underestimate interaction effect sizes, with the least bias shown by SIEE (Figure 3).

Figure 3.

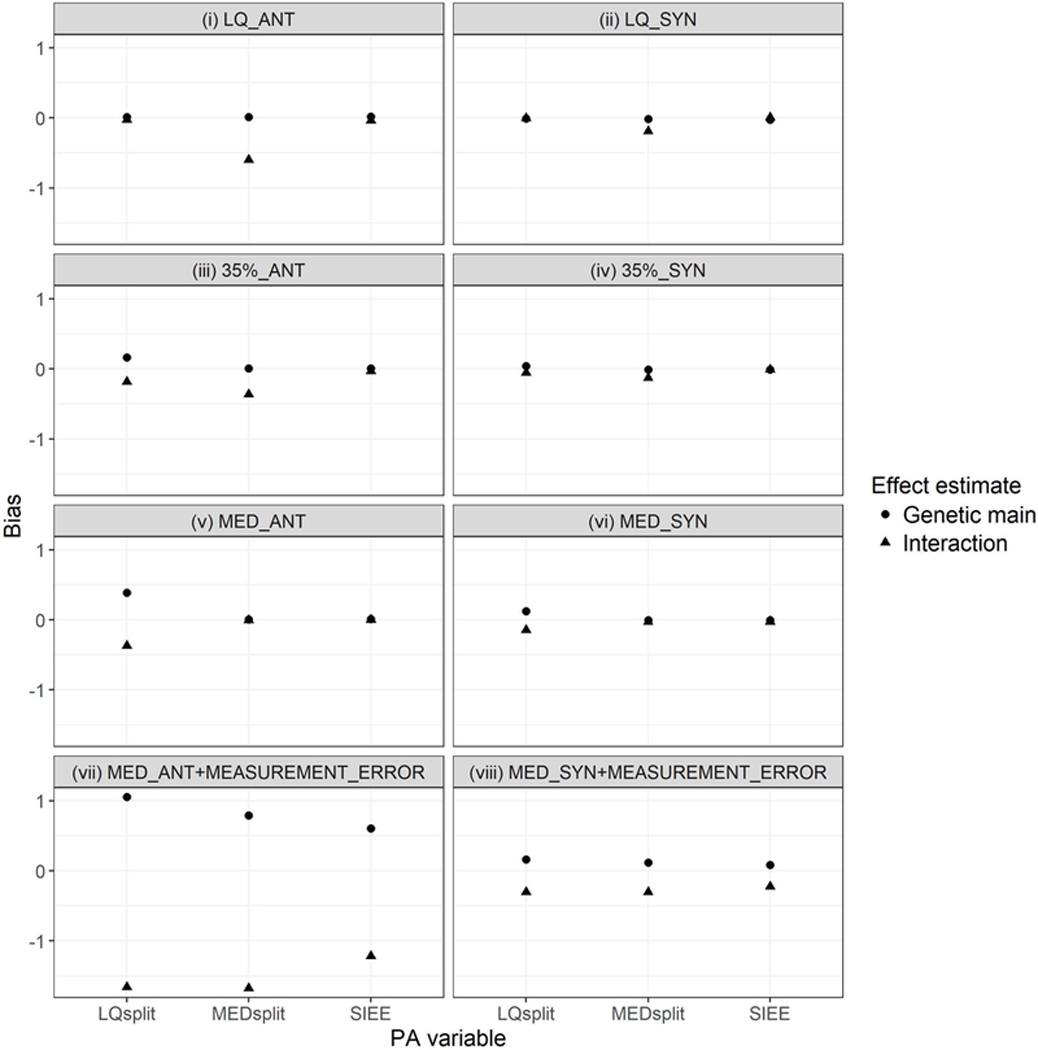
Bias comparison of three dichotomous physical activity (PA) variables in eight simulation scenarios, defined by the true cutoff and direction of interaction effects specified in the grey bar above each panel (35% = 35^th percentile, LQ = Lower quartile, MED = Median, ANT = Antagonistic, and SYN = Synergistic). In a given simulation scenario, bias was determined as the deviation of the average effect size estimate across all 500 replications from the true effect size estimate stipulated in the simulation scenario.

PA variables showed small differences in FDR at less stringent significance levels (≥ 5 × 10⁻⁶); in general, the PA variable with the least power, typically SIEE, correspondingly showed slightly higher FDR than the other PA variables. However, across scenarios at the genome-wide significance level, FDR was minimal (LQsplit 0 – 4.8%; MEDsplit 0 – 1.15%; SIEE 0 – 0.85%) for all three dichotomous PA variables (Figure 4). In the presence of measurement error, FDR was similar for all three PA variables across all significance levels considered (Figure 4; panels vii and viii).

Figure 4.

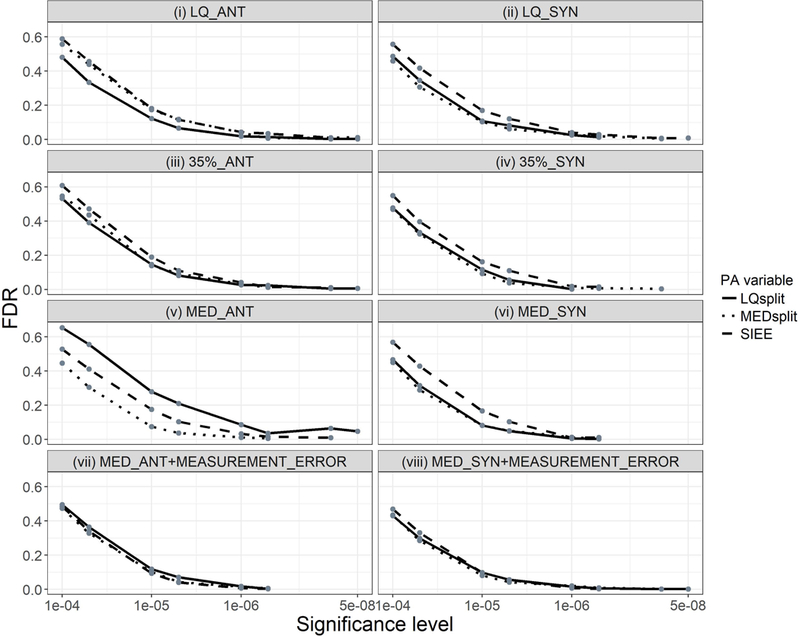
False discovery rate (FDR) comparison of three dichotomous physical activity (PA) variables in eight simulation scenarios, defined by the true cutoff and direction of interaction effects specified in the grey bar above each panel (35% = 35^th percentile, LQ = Lower quartile, MED = Median, ANT = Antagonistic, and SYN = Synergistic). In a given simulation scenario, FDR was determined as the fraction of total SNPs detected across all replications that were false positives. FDR was determined at seven significance levels, as indicated by the grey dots. LQsplit is represented by the solid line, MEDsplit by the dotted line, and SIEE by the long dashed line.

In all synergistic interaction scenarios, analyses with LQsplit and MEDsplit were more powerful than SIEE irrespective of the simulated true cutoff (Figure 5; panels ii, iv, vi, and viii). For the antagonistic interaction scenarios, SIEE outperformed the other two dichotomous PA variables only in the presence of measurement error (Figure 5; panel vii). In the absence of measurement error, SIEE’s performance was inferior to the PA variable that corresponded to the true cutoff. However, SIEE outperformed LQsplit when the median was the true cutoff and was similar to MEDsplit when the lower quartile was the true cutoff (Figure 5; panels i and v). When neither of the PA variables corresponded to the true cutoff, as in the 35^th percentile antagonistic scenarios, SIEE was slightly inferior in power to the other two dichotomous PA variables (Figure 5; panel iii).

Figure 5.

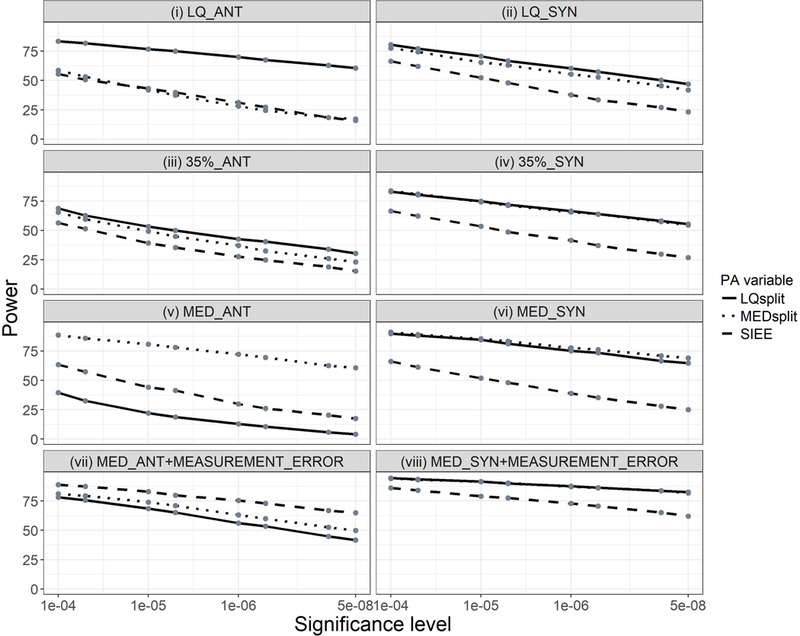
Power comparison of three dichotomous physical activity (PA) variables in eight simulation scenarios, defined by the true cutoff and direction of interaction effects specified in the grey bar above each panel (35% = 35^th percentile, LQ = Lower quartile, MED = Median, ANT = Antagonistic, and SYN = Synergistic). Power was determined as the proportion of true SNPs detected out of 500 true SNPs in all replications of a given simulation scenario. Power is expressed as a percentage, and was determined at seven significance levels, as indicated by the grey dots. LQsplit is represented by the solid line, MEDsplit by the dotted line, and SIEE by the long dashed line.

5. Discussion/Conclusion

We assessed several dichotomizing approaches for PA variables including SIEE using both empirical and simulation studies. From our empirical analysis, we found that SIEE’s performance was intermediate between MEDsplit and LQsplit in terms of number of loci found and overlap in loci detected with Quantitative. From simulation studies, with the exception of a single scenario, SIEE was consistently outperformed to varying degrees in terms of FDR and power. In terms of bias, in the absence of measurement error SIEE appeared to yield unbiased estimates of genetic main and interaction effects, but in the presence of measurement error showed relatively less bias than the other two dichotomous PA variables. Together, these results suggest some promise of SIEE as an alternative dichotomization strategy in GxE analysis.

Dichotomization-induced misclassification appeared to impact power more in antagonistic scenarios than in synergistic scenarios. Across all significance levels and across misclassification cases, power was consistently higher in synergistic scenarios than in antagonistic scenarios (despite genetic effect sizes being relatively more extreme, i.e., much smaller in active and much larger in inactive group, for the antagonistic scenarios). It has been previously recognized that genetic loci with antagonistic effects may be missed due to reduced power [31], justifying the call for more powerful approaches targeted at finding genetic loci with antagonistic effects depending on exposure [32].

The only scenario in which SIEE demonstrated relatively more power than the other two dichotomous PA variables was under an antagonistic interaction scenario in the presence of measurement error. SIEE’s performance may have been because of increased homogeneity within each group resulting from the exclusion of individuals with intermediate PA levels, some of whom may have been misclassified (up to 45% or more in simulations). Under synergistic scenarios, this benefit of increased homogeneity within each group did not appear to outweigh the reduction of ~ 50% sample size, as shown by the lower performance of SIEE. It has been previously demonstrated that smaller studies with more precise exposure variable are more powerful [33]. In the dichotomous exposure case, we found a similar pattern but specifically under the antagonistic case in the presence of measurement error.

On a practical note, this study provides some evidence that the use of lower quartile or median splits in dichotomizing quantitative exposure variables with random error would not compromise discovery of loci with synergistic effects in GxE analysis. For discovery of loci with antagonistic effects, the current study showed that SIEE reduced misclassification and improved loci discovery when measurement error was random. If the measurement error has a zero mean, we expect a superior performance for SIEE because there is a higher probability of misclassification near the splitting cutoff [13]. However, the results of the empirical analysis did not reflect the results of the simulation scenarios with measurement error. In empirical evaluation, SIEE did not find comparatively more loci overall, or more loci with opposite direction effects (Table 3), or more loci overlapping with loci detected by Quantitative. This may happen because self-reported PA is subject to non-random errors due to social stigma or recall bias [12]. In such case, SIEE’s exclusion of individuals intermediate in the exposure distribution would not necessarily translate to reduced misclassification, because individuals intermediate in the exposure distribution may not largely correspond to misclassified individuals.

Table 3.

Number of loci detected with antagonistic (ANT) effects, i.e., opposite effect direction effects, in GxE analysis using the different dichotomous PA variables. Percentage of total loci detected with ANT in parentheses.

		SBP		DBP
	Joint 2 DF	Interaction 1 DF	Joint 2 DF	Interaction 1 DF
LQsplit	3 (50%)	6 (100%)	1 (33%)	3 (100%)
MEDsplit	11 (73%)	9 (100%)	4 (80%)	9 (100%)
SIEE	0 (0%)	2 (25%)	4 (80%)	5 (62%)

Abbreviations: SBP, systolic blood pressure; DBP, diastolic blood pressure; LQsplit, created by splitting Quantitative by the lower quartile of its distribution; MEDsplit, created by splitting Quantitative by the median of its distribution; SIEE, created by selecting individuals with Quantitative values in the lower and upper quartiles and excluding individuals intermediate between the lower and upper quartile.

In summary, we found some promise of SIEE. In our empirical evaluation, performance of SIEE was somewhat inconclusive compared to the other two dichotomization approaches. However, in simulation studies, under the presence of random measurement error and antagonistic interactions in GxE analyses, SIEE provided higher power and less biased effect estimates despite sample size reduction. As discussed, the scope of our simulation study is limited because only random measurement error was considered. Further investigations should consider the presence of systematic or non-random errors to evaluate the performance of SIEE.