Magnetic resonance thermometry and its biological applications – Physical principles and practical considerations

Abstract

Most parameters that influence the magnetic resonance imaging (MRI) signal experience a temperature dependence. The fact that MRI can be used for non-invasive measurements of temperature and temperature change deep inside the human body has been known for over 30 years. Today, MR temperature imaging is widely used to monitor and evaluate thermal therapies such as radio frequency, microwave, laser, and focused ultrasound therapy. In this paper we cover the physical principles underlying the biological applications of MR temperature imaging and discuss practical considerations and remaining challenges. For biological tissue, the MR signal of interest comes mostly from hydrogen protons of water molecules but also from protons in, e.g., adipose tissue and various metabolites. Most of the discussed methods, such as those using the proton resonance frequency (PRF) shift, T₁, T₂, and diffusion only measure temperature change, but measurements of absolute temperatures are also possible using spectroscopic imaging methods (taking advantage of various metabolite signals as internal references) or various types of contrast agents. Currently, the PRF method is the most used clinically due to good sensitivity, excellent linearity with temperature, and because it is largely independent of tissue type. Because the PRF method does not work in adipose tissues, T₁- and T₂-based methods have recently gained interest for monitoring temperature change in areas with high fat content such as the breast and abdomen. Absolute temperature measurement methods using spectroscopic imaging and contrast agents often offer too low spatial and temporal resolution for accurate monitoring of ablative thermal procedures, but have shown great promise in monitoring the slower and usually less spatially localized temperature change observed during hyperthermia procedures. Much of the current research effort for ablative procedures is aimed at providing faster measurements, larger field-of-view coverage, simultaneous monitoring in aqueous and adipose tissues, and more motion-insensitive acquisitions for better precision measurements in organs such as the heart, liver, and kidneys. For hyperthermia applications, larger coverage, motion insensitivity, and simultaneous aqueous and adipose monitoring are also important, but great effort is also aimed at solving the problem of long-term field drift which gets interpreted as temperature change when using the PRF method.

1. Introduction

Interventional magnetic resonance (MR) guided applications are gaining interest, as minimally-invasive and non-invasive procedures enable shorter hospital stays, less risk of infections, and faster recovery times. Thermal therapies such as radio frequency, microwave, laser, and focused ultrasound therapy are integral drivers of this evolution. These thermal therapies can broadly be divided into two areas; hyperthermia and ablative procedures. In hyperthermia applications the target temperature is in the range of 41–45 °C; these temperatures are maintained in the target tissue for tens of minutes up to an hour, and have been utilized to directly kill cancer cells or to sensitize them to cytotoxic agents and/or radiation. In ablative procedures considerably higher temperature increases, reaching up to 60–90 °C, are applied over short time periods from a few seconds up to approximately a minute, to induce coagulative tissue necrosis.

In general, in-vivo tissue heating can be rather complex both in terms of energy application/delivery and in terms of the biological response to the heating [1]. The energy deposition in the target depends on the tissue’s ability to absorb the electromagnetic (in the case of radio frequency, microwave and laser) or acoustic (in the case of focused ultrasound) waves and is hence dependent both on tissue composition and its current state which may change with, for example, the tissue temperature. In ablative procedures, tissue coagulation may also significantly alter tissue parameters such as perfusion and heat conduction, and may result in a significant increase in the energy absorption. The conduction of the deposited heat through diffusion and perfusion will also vary locally depending, for example, on tissue composition, temperature, and physiological parameters. Further, physiological events, such as temperature-related changes in tissue perfusion, may also affect the induced heating both spatially and temporally.

It can be challenging to predict and model all these interacting effects of the local tissue temperature. Since the success of thermal therapies largely depends on the accuracy and precision with which temperature can be monitored and controlled, the in-vivo temperatures are ideally directly measured to ensure safe and efficient treatments. In the case of radio frequency-, microwave- and laser-based therapies the energy is most commonly delivered through a probe inserted into the body, where the probe often contains a thermometer. This does however just provide a point measurement and hence rather limited information. In the case of focused ultrasound where the energy delivering transducer is most commonly placed outside of the body (although, for example, transurethral and transrectal transducers are used) temperature probes can be inserted in the body. This does, however, reduce the non-invasiveness of the procedure and also just provides limited point measurements.

For these reasons many thermal therapies are currently performed under image guidance, and MRI is in many ways the ideal modality. MRI provides non-ionizing radiation imaging with excellent soft tissue contrast and high spatial resolution in any imaging orientation. This, together with the fact that many diseases and disorders can be visualized with the many different contrasts available, makes MRI a unique modality for treatment planning and targeting. For thermal treatment monitoring, MRI currently offers many of the most practical and widely available methods to accurately and non-invasively measure temperature inside the human body. Using MRI does require that the therapy equipment should not interact with the radio frequency (RF), gradient, and main magnetic fields of the MRI scanner, and that any magnetic or inducible parts be far from the MRI scanner [2–7]. Further, the presence of various biomedical implants and devices in the body may pose hazards for patients undergoing MR procedures, and thorough screening before any scan is important [8–10].

MR temperature imaging (MRTI) in biological tissue was first described in the early 1980s utilizing the temperature sensitivity of the T₁ relaxation time of the hydrogen protons in the water molecule [11,12]. Since then the temperature sensitivity of many other MR parameters such as the proton resonance frequency (PRF) shift, T₂, diffusion, and various contrast agents has been investigated. The PRF shift method is currently the most commonly used method due to its high sensitivity and excellent linearity for water protons over a relatively large temperature range, as well as its tissue-type independence, and because it can be performed with simple and widely available gradient recalled echo (GRE)-type MRI pulse sequences. Challenges with the PRF shift method include its lack of sensitivity in adipose tissues and its ability to measure only relative temperature changes. Therefore, recent research has investigated T₁- and T₂-based approaches for measuring temperature in adipose tissue, and spectroscopy and contrast agent-based methods, which utilize internal references, have been investigated for absolute temperature measurements.

As the scope of this paper is limited to biological applications of MRTI, the MR signals discussed will be assumed to come from biological tissue. As the human body is composed of approximately 50–60% water, the majority of the signal comes from water molecules, more specifically from the protons in the hydrogen nuclei of water. Examples of proton spectra from muscle and brain tissues are shown in Fig. 1. As can be seen, the water peak is the dominant signal in both tissue types. In muscle, which also contains adipose tissue, signal from protons in various fatty acids are also detected. The water peak is located at 4.7 ppm and the main fat peaks (methylene, CH₂) are shifted approximately 3.5 ppm downfield, at around 1.2 ppm. In brain tissue various metabolite signals, such as those of creatine-CH₃ (tCr) and N-acetylaspartate (NAA), can be detected, but their intensities are very small compared to the H₂O peak.

Fig. 1.

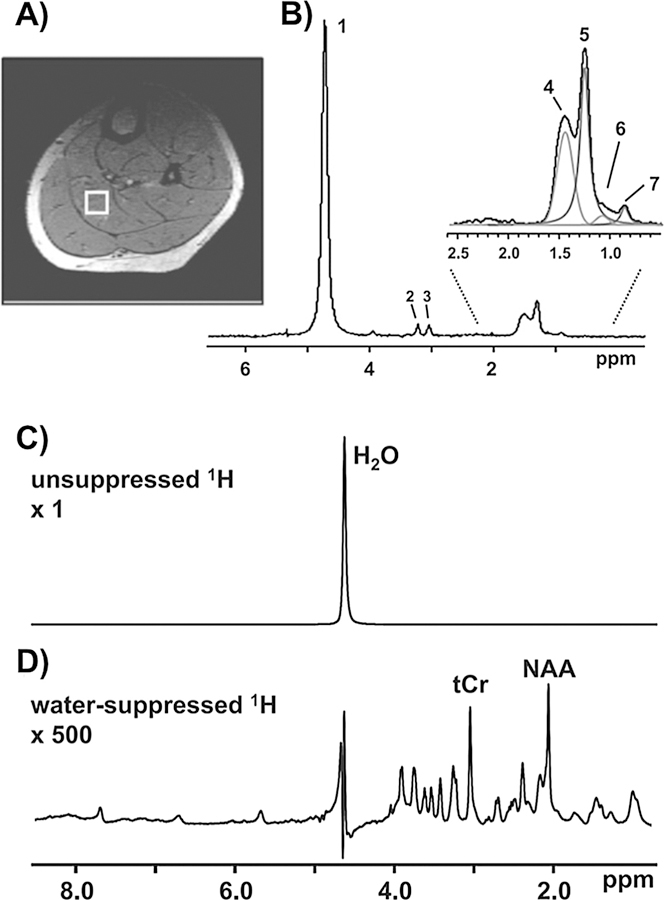
In vivo MR spectrum of muscle (A and B) and brain (C and D) tissues. (A) Localized muscle ¹H spectrum acquired from a specific region (voxel) within the soleus muscle. The selected voxel is outlined by a white box superimposed on a cross-sectional MRI image of the calf. (B) Multiple lipid peaks can be resolved enabling the quantification of intra- and extramyocellular lipid (IMCL and EMCL). Peak 1: water; peak 2: choline-CH₃; peak 3: creatine-CH₃; peak 4: EMCL-CH₂; peak 5: IMCL-CH₂; peak 6: EMCL-CH₃; and peak 7: IMCL-CH₃. (C) The ¹H spectrum of the brain features a prominent water peak that overwhelms the metabolite signals. Pulse sequences are available that selectively suppress or excite specific frequencies. (D) The inclusion of a water-suppression module selectively minimizes the ¹H₂O peak and enhances the detection of brain metabolites such as creatine-CH₃ (tCr). From Befroy DE and Shulman GI. Magnetic Resonance Spectroscopy Studies of Human Metabolism. Diabetes, 2011 May; 60(5): 1361–1369. Reprinted with permission.

This review discusses the physical principles of MRTI using PRF, T₁, T₂, diffusion, signal intensity (SI), magnetization transfer, spectroscopic approaches, various contrast agents, intermolecular quantum coherence, and the various combination methods (such as simultaneous PRF-T₁, PRF-T₂, and PRF-SI) which have been described. The scope of the review is limited to MR imaging approaches (i.e., where magnetic field gradients are applied to spatially encode the received signal so as to create images) as these are by far the most commonly used approaches in clinical applications. Practical considerations, such as what pulse sequences are used, and remaining clinical challenges and practical issues, such as potential artifacts and motion sensitivity, are further covered. Table 1 presents a general overview of the material that will be discussed in the review, including advantages and disadvantages of the different approaches.

Table 1.

General overview of physical principles and mechanisms of all methods covered below. The general advantages and disadvantages of each method are described, and if the method measures a relative or absolute temperature change. For each method, the linearity and sensitivity with respect to temperature change, the spatial and temporal resolution that can be achieved, and its sensitivity to motion, is further given using; ++ = Very good, + = Good, +/ = Average, − = Bad, −− = Very bad.

	Mechanism/principle	Advantages	Disadvantages	Absolute or Relative	Linearity	Sensitivity	Spatial resolution	Temporal resolution	Motion sensitivity	Pulse sequence	B0-field dependence
PRF	Hydrogen bondings are temperature dependent, resulting in increased electron screening and lower proton resonance frequencies at higher temperatures	High spatio-temporal resolution. Linear function of tissue temperature. Largely tissue type independent. Readily available imaging sequences	Does not work in adipose tissue.	Relative	++	+	++	++	+/−	GRE (Modified SE possible)	Linear increase; ω = γB0
T1	Energy exchange rate within and between water molecules increases with temperature	Readily available imaging sequences. Can be utilized in both aqueous and adipose tissues	Relatively low temperature sensitivity (a few %/C). Multiple factors can affect T1. Change becomes nonlinear at high temperatures	Relative	+ (below coagulation) − (above coagulation)	+/−	+	+	+/−	GRE and SE	T1 increases with B0, but the observed T1 contrast decreases, resulting in reduced sensitivity
T2	The de-phasing of spins within an image voxel depends on random thermal motion	Can be utilized in both aqueous and adipose tissues. Relatively high sensitivity, 3–6%/C	Can be time consuming to measure. dT2/dT is tissue type-dependent	Relative	+	+	+	+/−	+/−	SE	T2 largely unchanged with B0
Signal Intensity and Proton density	Proton (polarization) density is inversely related to the tissue temperature according to the Boltzmann distribution	Readily available imaging sequences. Relatively tissue type independent	Very low temperature sensitivity, 0.3%/C for PD. dSI/dT can change with amount of T1- and T2-weighting	Relative	+/−	–	+	+ (SI) −(PD)	+/−	GRE and SE	PD and SI increase linearly, but percentage change with temperature stays the same
Magnetization transfer	Exchange processes between macromoleculebound protons and pool of ‘‘free” protons are temperature dependent	None noted	Tissue-type dependent. Low sensitivity. Can be hard to measure	Relative	+/−	−	+/−	+/−	+/−	GRE and SE	Benefits from longer T1 at high B0
Diffusion	Temperature dependence of molecular diffusion obeys the Stokes-Einstein relation between viscosity and the translational self-diffusion coefficient, D	Readily available imaging sequences	Very sensitive to motion. Diffusion coefficient, D, depends on factors other than temperature. Slow imaging	Relative	−	+/−	+	−	−	SE	Negligible
Spectroscopic approaches	Separation of peaks from different tissue molecular components in a frequency spectrum depends on temperature	Can measure absolute temperature. Less motion sensitive	Low spatio-temporal resolution	Absolute	++	+/−	−	−	+	GRE and SE	Linear increase. High B0 needed to detect small metabolic signals
Contrast agents	TSL – transmembrane permeability increase at transition temperature. Paramagnetic lanthanide complexes experience PRFS	Can measure absolute temperature	Potentially nonuniform uptake and potentially toxic. Slow imaging	Absolute	−	++	+/−	+/−	+/−	SE	Benefits from higher SNR
Intermolecular quantum coherence	Resonance frequency difference of two spins can be measured and is temperature sensitive	Can measures absolute temperature. Low motion and drift sensitivity. Works in both aqueous and adipose tissues	Low spatio-temporal resolution. Low SNR. Needs fat and water in close proximity	Absolute	+	+/−	−	−	++	SE	Linear increase

2. Physical principles and practical considerations

In this section the physical principles of the various temperature-sensitive MR parameters that have been used to perform MRTI are described and discussed. For each method the pros and cons are listed, and example pulse sequences are described.

2.1. Proton resonance frequency (PRF) shift method

The temperature dependence of the PRF shift method can be described by the chemical shift effect. Due to temperature-dependent hydrogen bonding between protons and the surrounding oxygen atoms on water molecules, the local magnetic field a proton experiences, B_loc, will change with temperature. Because the proton resonance frequency is directly proportional to the local field that the proton experiences according to the resonance equation, ω₀ = γB_loc, the proton’s resonance frequency will also change with temperature. Here ω₀ is the Larmor frequency and γ is the gyromagnetic ratio. The fact that the resonance frequency of hydrogen protons in water molecules changes with temperature was first described in the 1950s and 1960s [13–15], and it was used to monitor temperatures in cell cultures [16] before being utilized in imaging and spectroscopic methods in the 1990s [17–22].

The local magnetic field in matter can be described by Maxwell’s equations and depends on the applied external main magnetic field of the MRI scanner, B₀, the volume magnetic susceptibility, χ₀, and the electronic screening constant, σ. For aqueous tissues the electronic screening constant is approximately an order of magnitude larger than the magnetic susceptibility [23], and a simplified equation describing the local magnetic field experienced by the protons can be written as

$$B_{loc}\cong B_0(1-\sigma (T))$$ (1)

The effects of this simplification are discussed in more detail below. The temperature dependence of σ arises from the shielding of the hydrogen nucleus (i.e., the protons being imaged in MRI) by the surrounding electron cloud, which is affected by temperature-dependent inter-molecular bondings between different water molecules (Fig. 2). The electron cloud of the hydrogen atoms interacts with the applied B₀-field. This interaction creates a current density at the site of the hydrogen nucleus according to Faraday’s law. Since the polarity of the induced current density creates a magnetic field that opposes the applied B₀-field, the electron cloud effectively shields the nucleus, resulting in a decreased B_loc. When the temperature increases, the inter-molecular hydrogen bonds start to rupture [13–15], bend [15,24], and break [13]. The result is that on average the water molecules spend less time in a hydrogen-bonded state, and the shielding from the electron cloud increases, resulting in a lower B_loc and hence a lower resonance frequency ω₀ with increased temperatures.

Fig. 2.

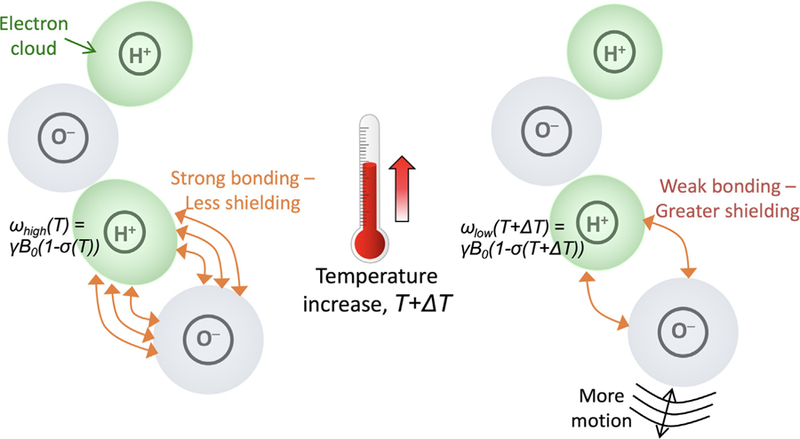
Schematic depicting the temperature dependence of the PRF. At lower temperatures strong hydrogen bondings exist between water molecules, resulting is weak shielding of the hydrogen proton. As temperature increases the molecular movements increase and the hydrogen bonds start to break, resulting in greater shielding from the electron cloud, and a lower resonance frequency. From Chapter 15 in Theory and Applications of Heat Transfer in Humans. Henrik Odéen and Dennis L Parker, Non-Invasive Thermometry with Magnetic Resonance Imaging. Devashish Shrivastava (Editor). John Wiley and Sons 2018. Reprinted with permission.

For aqueous tissue, the change of the electronic shielding constant with temperature is described by a linear relationship according to

$$\sigma (T)=\alpha T$$

where α is called the PRF coefficient and is measured in ppm/°C. For adipose tissues, which lack hydrogen bonds, the change in resonance frequency with temperature is dominated by susceptibility effects, as discussed below. Because of the unique properties of the PRF coefficient, the PRF method has become the most widely used method to monitor temperature in aqueous tissues. The PRF coefficient, α, has been found to be, to a large degree, tissue type independent and is constant over a wide temperature range, from −15 °C to close to 100 °C for pure water and from 20 °C to 80 °C for aqueous tissues [15,25]. The linear temperature range includes the temperatures usually targeted in both ablative- and hyperthermic-thermal therapies. The value of α is often assumed to be around –0.010 ppm/°C, but values between –0.007 and –0.011 have been reported depending on tissue type [26]. Some of the discrepancies in the reported values of α might be attributed to temperature-dependent changes in the tissue electrical properties and experimental parameters such as heat-source geometry and orientation, and partial volume effects encountered during calibration experiments, as discussed in more detail below [25,27–30]. α has further been shown to be consistent even after tissue ablation [25,31]. Although the reported values of α, which are on the order of fractions of ppm/°C, seem very small, they highlight the fact that very accurate phase measurements can be obtained with MRI. This is exemplified by the precise in-vivo temperature measurements which can be made by the PRF method, where precisions of 1–2 °C are routinely achieved [32–36].

The change in resonance frequency due to the PRF shift with temperature is observed in the phase of the complex MRI image. By subtracting a baseline reference phase image, acquired before the onset of temperature change, from phase images acquired while the temperature is changing, non-temperature related phases from, e.g., inhomogeneities in the B₀-field and due to difference in the phase of different RF-receive coils can be removed (Fig. 3). The resulting temperature-dependent phase can be written

$$\Delta \varphi =\varphi (T)-\varphi (T_{ref})=\gamma \alpha B_{0}TE\Delta T$$ (2)

where ∆ϕ is the measured phase change between temperatures T and T_ref TE is the echo time, and ΔT = T – T_ref. To improve the signal-to-noise ratio of the temperature measurements the noise in the reference image acquired at T_ref can be decreased by averaging multiple reference images acquired before the onset of temperature change [34]. To avoid phase discontinuities due to phase wrap, which occur when the phase change, Δϕ, exceeds ±π, a running complex subtraction between successive dynamic images can be performed according to

$$\Delta \varphi ={\varphi }_j-{\varphi }_{j+1}=angle\left(I_j\ast I_{j+1}^{\ast }\right)={\tan }^{-1}\left(\frac{Re(I_{j+1})Im(I_j)-Re(I_j)Im(I_{j+1})}{Re(I_j)Re(I_{j+1})+Im(I_j)Im(I_{j+1})}\right)$$ (3)

where Re and Im are the real and imaginary parts of images I₁ and I₂ [37], respectively. When all individual phase differences are calculated, they can be summed up to produce the final, total phase difference from which DT can be obtained. As can be seen, the PRF method only calculates temperature change compared to some reference temperature when the reference phase map was acquired. To convert to absolute temperatures the baseline temperature T_ref must be known and the absolute temperature can be calculated as T(t) = T_ref + ΔT(t).

Fig. 3.

Phase map subtraction to calculate PRF temperature maps. Two orthogonal views from a focused ultrasound heating in porcine muscle. By subtracting the reference phase map acquired before the start of the heating from the phase map of the current time frame and scaling according to ΔT = Δφ/ϒαB0TE the PRF temperature map can be calculated. It can be noted that by using complex subtraction, phase wraps occurring in the phase images (red arrows) get subtracted out and do not occur in the temperature map. From Chapter 15 in Theory and Applications of Heat Transfer in Humans. Henrik Odéen and Dennis L Parker, Non-Invasive Thermometry with Magnetic Resonance Imaging. Devashish Shrivastava (Editor). John Wiley and Sons 2018. Reprinted with permission.

2.1.1. Pulse sequences

The pulse sequences used in the PRF method must have a time interval, TE, between the time that all of the proton magnetic moments were in phase and the time when the zeroth gradient moment is zero. In spin echo (SE) pulse sequences, the dephasing magnetization is rephased by a refocusing (180°) RF pulse. If the time of spin refocusing occurs at the time of the gradients’ zero moment, the measured phase will be independent of magnetic field differences and hence independent of temperature. Since the 180° refocusing RF-pulse used to create the spin-echo refocuses all the spins at the time TE, no phase accrual due to PRF shift is normally seen in SE pulse sequences. To measure temperature-dependent phase change with a SE sequence a delay time (corresponding to the TE in GRE, see below) needs to be inserted between the time point where the spins refocus and the data acquisition so that phase accrual due to the PRF shift is created and can be measured [19,38,39].

For a gradient recalled echo (GRE) pulse sequence, TE is defined as the time from the excitation RF to the center of the frequency encoding (readout) gradient. Due to its simplicity and speed (there is no need for a refocusing RF-pulse and TR can be kept relatively short), GRE pulse sequences are currently the most used pulse sequences for PRF shift MRTI, and in principle any GRE-type pulse sequence can be utilized. Most commonly spoiled GRE pulse sequences, utilizing gradient and/or RF-spoiling, are used [40]. In the simplest form, and in what is currently the most used approach clinically, a single GRE-echo is sampled after each RF pulse, followed by the spoiling. To improve the temporal resolution and achieve faster imaging, echo planar imaging (EPI), where multiple lines of k-space are sampled after a single RF-excitation pulse using an echo-train, have been quite extensively utilized. Both segmented (multi-shot), where the full k-space is acquired in multiple segments after multiple RF-pulses, and single shot, where the full k-space is acquired in a single segment after a single RF-pulse, versions of GRE-EPI have been described [41–50].

As for any application using a spoiled GRE pulse sequence, the flip angle should be chosen to be the Ernst angle, which depends on the T₁ and TR according to ${\alpha }_E=arccos(e^{-TR/T_1})$ [51,52].

To achieve the optimal precision in PRF shift thermometry the phase difference SNR, SNR_∆Φ, should be maximized [37]. The phase difference SNR can be expressed in terms of the ‘‘signal”, corresponding to the phase difference ∆ϕ at the heating location, and the ‘‘noise”, corresponding to the standard deviation of the phase difference, σ_∆ϕ, in the background, according to

$$SN{R}_{\Delta \varphi }=\frac{\left|\Delta \varphi (\Delta T)\right|}{{\sigma }_{\Delta \varphi }}$$ (4)

Since ${\sigma }_{\Delta \varphi }$ is approximately equal to $\sqrt{2}\sigma /SI$ for high SNR, where σ is the Gaussian noise standard deviation of the real and imaginary parts of the MR image and SI is the spoiled-GRE signal intensity, $SN{R}_{\Delta \varphi }\propto \left|\Delta \varphi (\Delta T)\right|\cdot SI$. The signal intensity SI depends on both tissue parameters such as the T₁ and $T_2^{\ast }$ relaxation times and the proton density, as well as pulse sequence imaging parameters such as TR, TE, flip angle, voxel size and bandwidth. If the tissue parameters are assumed to be relatively constant as a first order approximation, SI will only depend on the imaging parameters. Since the GRE MR signal decays with the $T_2^{\ast }$ relaxation time according to $e^{-TE/T_2^{\ast }}$, and the phase accrues linearly with time from the time of excitation until the time of signal sampling at TE, $SN{R}_{\Delta \varphi }$ can be expressed as

$$SN{R}_{\Delta \varphi }\propto TE\cdot e^{-TE/T_2^{\ast }}$$ (5)

where differentiation with respect to TE gives the optimal echo time of $TE=T_2^{\ast }$. For most practical purposes the $T_2^{\ast }$ of the tissue is rather long, so obeying $TE=T_2^{\ast }$ would result in long TE and hence long TR and long scan times. In practice TE is therefore chosen as a trade-off between fast scan time (shorter TE and TR) and high precision in the phase difference measurement (long TE). Various approaches have successfully been described to both prolong TE by defocusing and storing successively excited 2D slices in k-space and later refocusing the slices with a longer than normal TE (MASTER, multiple adjacent slice thermometry with excitation refocusing), and to use echo-shifting to create TE > TR [45,53–55]. Although both approaches can lengthen TE, they are both subject to increased signal loss due to interactions with subsequent excitation pulses and the presence of signals from multiple pathways yielding a spread in actual TE of the received signal. Since the imaging SNR, and hence the PRF precision, is proportional to the square root of the total sampling/readout time, the precision can also be improved by increasing the sampling time. For PRF based MRTI, this has been done by acquiring multi-echo readouts, i.e., the same line of k-space is sampled multiple times with different echo times [36,56].

The GRE sequences described so far have utilized spoiled GRE readouts. It is also possible under certain circumstances to sample the higher SNR non-spoiled GRE signal utilizing so-called steady-state free precession pulse sequences, which can be both non-balanced (i.e., non-zero gradient area in any given TR) and balanced (i.e., zero gradient area in any given TR). Just as for spoiled GRE sequences, this can be done utilizing single-echo and multi-echo sampling to prolong the total sampling time [57,58]. For SSFP sequences multiple signal pathways can further be sampled, which again prolongs the total sampling time resulting in better PRF precision [46].

2.1.2. Challenges with the PRF method

This sub-section will discuss challenges including different tissue types (such as aqueous versus adipose tissues), magnetic susceptibility (which has been shown to have a large effect in adipose tissues, and the fact that it changes with the geometry and orientation of both the device delivering tissue heating and the pattern of the delivered temperature rise, relative to B₀), B₀ field drift (due to, e.g., gradient system heating), electrical properties (i.e., change in electrical properties with temperature resulting in constant incremental phase shift per unit change in temperature), perfusion (via the associated changes in the fractional regional blood volume of in-vivo tissue), and tissue motion (both intra- and inter-scan motion due to, e.g., respiration, cardiac pulsation, peristalsis, and bulk patient motion).

Tissue-type dependence

As discussed above, the PRF method has become the standard for MRTI in aqueous tissues because of the properties of α in these tissues. α is largely tissue type independent, linear over a large temperature range, and not significantly affected even after tissue ablation. One significant disadvantage of the PRF method is that adipose tissues do not have the same type of hydrogen bondings as aqueous tissues since the proton signal is from lipids rather than from water molecules (see also Fig. 1). The PRF change with temperature is therefore very small, on the order of −0.00018 ppm/°C [31,59]). This means that temperature changes in adipose tissues, such as commonly occurring in the breast and abdomen, cannot be monitored by the PRF method. In these tissues the temperature dependence is instead dominated by the temperature dependence of the magnetic susceptibility as discussed below. In voxels that contain a mixture of adipose and aqueous tissues, the measured change in the PRF with temperature will be reduced, resulting in an underestimation of the measured temperature change. It has, however, been shown that this effect can be reduced by utilizing a multi-echo approach if only small amounts of fat are present (<20%) [60]. When fat is present the temperature measured assuming ‘‘aqueous PRF” becomes dependent on TE, alternatively over- and under-estimating the temperature approximately every pi radians (Fig. 4). Using multiple echoes appropriately spaced and with a weighted echo-combination (based on how many echoes resulted in temperature over- versus under-estimations) the resulting error can be greatly reduced. To avoid the problem of multiple species, either suppression of the fat signal or selective excitation of the water signal is routinely employed and generally works well [31,44,45,61–64], especially at higher field strengths (>3 T) where the frequency separation of the fat and water peaks, which is on the order of 3.5 ppm depending on the fat composition, is larger. An alternative to suppressing the fat signal or selectively exciting the water signal is to image both species and perform fat-water separation using techniques such as Dixon or IDEAL [36,65–67]. If the fat is imaged, its signal can be utilized to correct the PRF measurements in aqueous tissues for errors from, e.g., B₀-field drifts and phase errors related to breathing and cardiac motion [65,68–72] (Fig. 5).

Fig. 4.

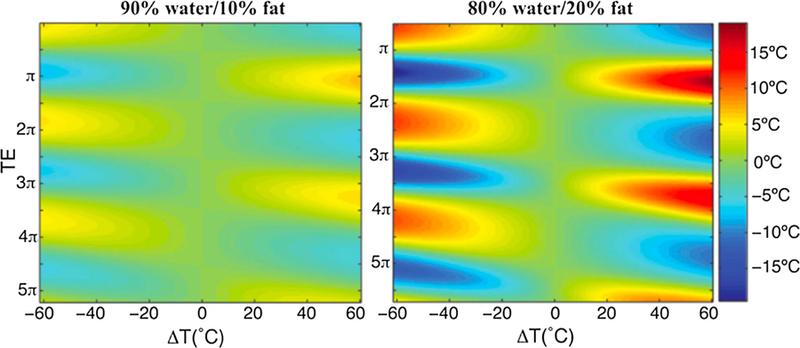
Temperature error for temperature changes from –60 to 60 °C as a function of echo time, expressed in terms of the phase angle between water and fat. Left image shows the absolute temperature error for a mixture of 90% water and 10% fat, and the right image for a mixture of 80% water and 20% fat. From ‘‘Echo Combination to Reduce Proton Resonance Frequency (PRF) Thermometry Errors From Fat” Viola Rieke and Kim Butts Pauly. Journal of Magnetic Resonance Imaging 27:673–677 (2008). Fig. 2. Reprinted with permission.

Fig. 5.

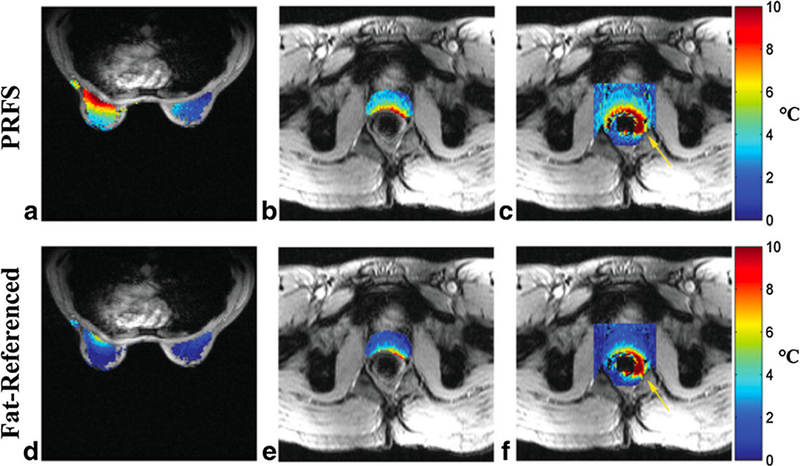
Temperature absolute error maps (°C) for conventional PRFS (a–c), and fat-referenced method (d–f). (a,b) depict error maps in breast, (b,e) depict error maps in prostate gland only, and (c,f) depict error maps in 41 × 41 pixel region surrounding the prostate gland. In the prostate gland for example, the RMSE reduced from 4.5 to 2.8 °C when the fat-referenced method was applied. Yellow arrows highlight measurement error near rectum. From ‘‘Fat-Referenced MR Thermometry in the Breast and Prostate Using IDEAL” Lorne W. Hofstetter, Desmond T.B. Yeo, W. Thomas Dixon, James G. Kempf, Cynthia E. Davis, and Thomas K. Foo. Journal of magnetic resonance imaging 36:722–732 (2012). Fig. 7. Reprinted with permission.

Magnetic susceptibility

Equation 1 does not consider the temperature dependence of the magnetic susceptibility, χ₀, as it has been shown to be on the order of 0.0016 ppm/°C for aqueous tissues over a temperature range of 30–45 °C - nearly an order of magnitude smaller than the effects from the electronic screening constant [23]. Based on this, many studies concerned with aqueous tissues such as muscle do not account for the temperature dependence of χ₀. It has been shown that for these tissues this results in temperature errors smaller than 10% [23]. It is possible to take into account the temperature dependence of χ₀ and Equation 1 becomes [23,59,73–75]

$$B_{loc}\cong B_{mac}-\left(\frac{2{\chi }_0(T)}{3}+\sigma (T)\right)B_0$$ (6)

where B_mac is the macroscopic magnetic flux density of an object with magnetic susceptibility χ₀ placed in the external field B₀. Higher order terms of χ₀ and σ have been neglected. B_mac depends on both B₀ and the geometry and the susceptibility distribution in and around the object being imaged.

Even though the effect of including χ₀ is rather small for aqueous tissues, the effect is substantially larger for adipose tissues where the temperature dependence of χ₀ has been found to be in the range of 0.0039–0.0094 ppm/°C [76,77] and can cause substantial distortions to both B₀ and B_mac. This has been shown to be a substantial source of errors in and around high fat content tissues [23,69,76–78]. It has further been shown that the local susceptibility changes, unlike chemical shift changes, are tissue type dependent [75]. Susceptibility effects can also depend on the geometry and orientation of both the device delivering the heating (e.g., the HIFU transducer) and the pattern of the delivered temperature rise, relative to B₀ [59,74]. Correction methods, based on, e.g., perturbation theory applied to the magneto-static Maxwell’s equations or based on 3D thermal modeling [78,79], have been presented. These approaches are not trivial since precise knowledge of, e.g., the local tissue susceptibility distribution and its temperature dependence, relative fat and water contents, and the shape of the heated region are needed. Hence, accurate PRF-based thermometry in high fat-content tissues remains challenging, and this is especially true for non-spherical heating patterns occurring perpendicular to B₀.

Lastly, the local microscopic susceptibility of tissues has been shown to depend on the concentrations of deoxyhaemoglobin and myoglobin which can change during therapy, as discussed in relation to changes in perfusion below.

B₀ field drift

Since the PRF method measures very small frequency changes, on the order of 0.010 ppm/°C, and the resonance frequency is ω = γB_loc, it is naturally very sensitive to time-varying changes in the local magnetic field. The fact that the temperature maps are calculated as a phase difference between the current and baseline phase maps further increases the sensitivity. A small change or drift in the B_loc-field will change the resonance frequency x and can result in substantial errors in the phase difference map, and hence in the calculated temperature maps. Modern clinical scanners have relatively stable B₀ fields with field drifts often quoted in the range of 0.1 ppm/hour. However, additional drift caused by, e.g., gradient system heating that occurs when applying large gradients [80,81], such as the readout gradients in echo-planar imaging pulse sequences, can add substantial amounts of field drift (Fig. 6). As an example, spatio-temporal B₀ phase drifts on the order of 0.01 to 0.06 ppm/minute (corresponding to 0.6 to 3.6 ppm/hour) have been reported for clinical horizontal bore scanners while scanning [25,80]. Assuming a PRF coefficient of −0.010 ppm/°C this results in temperature errors of up to 6 °C/ minute of scan time just from drift in B₀. The field drifts can result in both over- and under-estimation errors depending on the polarity of the induced field drift [21,80].

Fig. 6.

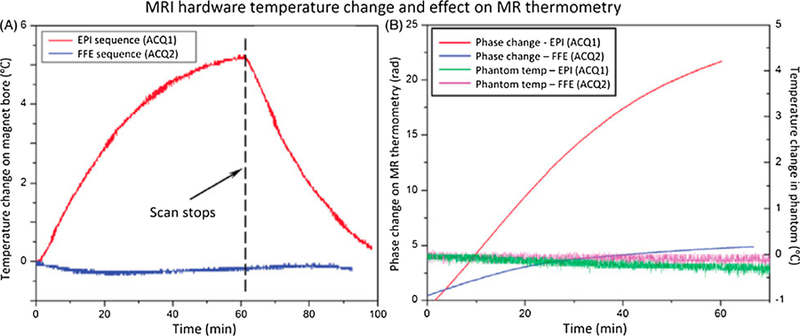
Scanner temperature and phase change under different thermometry sequences. (A) Temperature of the inner bore of the MRI increased at different rates during scanning depending on the gradient duty cycle of the sequence: echo-planar (EPI, upper curve) versus fast field echo (FFE, lower curve). The scan parameter and fan setting in the MR console were kept the same for two sequences. (B) Phase measurements acquired with MR thermometry (red and blue increasing curves) in an unheated phantom during scanning shows a monotonic change in phase. No significant temperature change was observed in the phantom (green and pink flat curves). The rate of change appears to be related to the gradient duty cycle and magnet heating. From ‘‘Drift correction for accurate PRF-shift MR thermometry during mild hyperthermia treatments with MR-HIFU” Chenchen Bing, Robert M. Staruch, Matti Tillander, Max O. Köhler, Charles Mougenot, Mika Ylihautala, Theodore W. Laetsch and Rajiv Chopra. Int J Hyperthermia. 2016 Sep;32(6):673–87. Fig. 4. Reprinted with permission.

Assuming the drift is slowly varying in space and time, it can be corrected for during image post-processing using either internal or external references. For internal references surrounding water-based tissues can be utilized assuming the reference-tissue does not change temperature [82–89]. This is commonly done in ablative therapies where the heated region is generally localized. For hyperthermia treatments where large tissue volumes are routinely heated, fat-based tissues can be used as a reference [65,68–70,90]. Using fat-based tissues has the added advantage that since their PRF change with temperature is small, the correction will work even if the tissue itself heats up. External references, such as the water bolus commonly used for RF hyperthermia treatments [91,92], or separate external vials or tubes [20,23,80], sometimes filled with lipids [93,94], have also been employed to monitor and correct for the field drift. For both internal or external references a polynomial fit is generally performed to the reference medium and then extrapolated over the heated region and used to subtract the effect of the field drift [82,83,91,94].

In an alternative approach so-called navigator echoes can be sampled and used to correct for the overall field drift either at the time of data acquisition (by adjusting the resonance frequency accordingly) or retrospectively (Fig. 7) [95]. It should be noted that this approach works best for localized heating, whereas for non-localized heating (such as certain hyperthermia treatments) the navigator correction could potentially cause an error by measuring and removing some of the temperature-induced phase change.

Fig. 7.

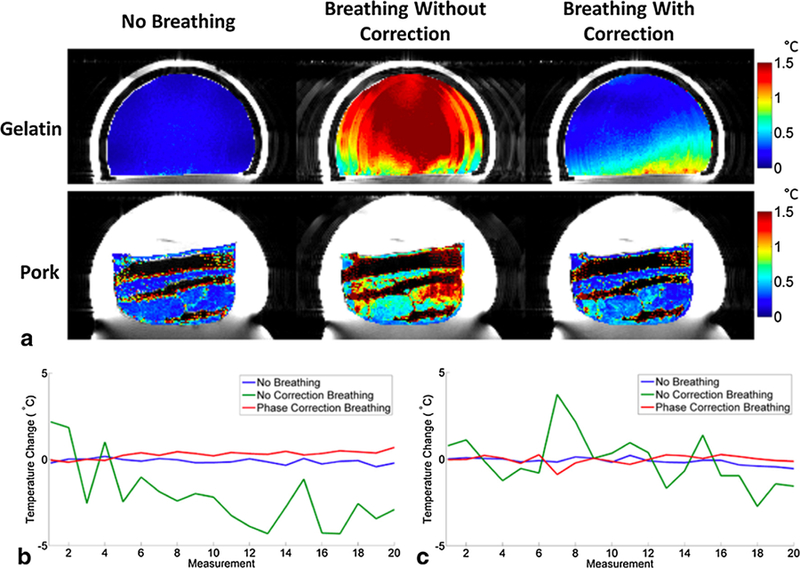
Phantoms under non-heating conditions. (a) PRF temperature precision images for gelatin and pork comparing the no breathing, breathing without correction, and breathing with correction cases without FUS heating. (b) PRF temperature change of a single voxel in gelatin phantom for all three cases. (c) PRF temperature change of a single voxel in pork phantom for all three cases. From ‘‘Respiration artifact correction in three-dimensional proton resonance frequency MR thermometry using phase navigators” Bryant T Svedin, Allison Payne, and Dennis L Parker. Magn Reson Med. 2016 Jul;76(1):206–13. Fig. 3. Reprinted with permission.

Electrical properties

Change in electrical properties with temperature can result in a constant incremental phase shift per unit change in temperature which is independent of TE [27–29]. A time-varying inductive field (such as the RF excitation-fields used in MRI) will undergo amplitude attenuation and phase retardation in electrically conductive materials [96]. In MRI this results in non-uniform flip-angle and phase of the transverse magnetization which depends on the depth of the imaged tissue. The spatial dependence of the phase retardation depends on the specific tissue properties and composition and the imaging RF coils used. Since both the electric conductivity, and to a lesser degree the electric permittivity, have temperature dependences (for conductivity 1.7%/°C for dog muscle, and for permittivity 0.5%/°C for pure water, have been reported [27,97]), the described phase retardation will increase with increasing temperature. When this happens the subtraction of a baseline image, as is usually done in the PRF method as described above, will not account for this additional phase retardation, resulting in a temperature measurement error. Since the retardation depends on the RF fields, and not on TE, as the PRF shift induced phase shift, it will only depend on the induced temperature change. The effect is further independent of field strength. Since the phase retardation varies with tissue depth, so will the severity of the induced phase error when large tissue volumes are heated [27,28]. The problem is hence likely to be more pronounced for, e.g., deep regional hyperthermia applications, which heat larger tissue volumes. For ablation procedures on the other hand, which generally ablate small tissue volumes, the problem is not likely to introduce substantial errors. However, many calibration experiments are performed on tissue samples in (large) water baths, and the resulting PRF-coefficient might therefore not be accurately estimated. This can possibly explain some of the variation seen in published PRF-coefficient values [25,26]. A method using dual-echo readouts (i.e., reading out the same k-space line with different TEs) has been presented and evaluated ex-vivo and in-vivo, and corrects for the temperature-dependent PRF coefficient [25,27,98,99].

Perfusion and blood volume

It has been showed that the fractional regional blood volume of in-vivo muscle increases with increased temperature and decreases with decreased temperatures (a 2.7 times increase for a temperature rise of 3.7 °C and a 3.5 times decrease for a temperature decrease of 8.8 °C have been reported) [100]. Increased regional blood volume associated, for example, with increased perfusion, will affect the local magnetic field due to the magnetism of hemoglobin. Increased volume will result in a reduced local field, decreasing the resonance frequency and therefore potentially resulting in an overestimation of the PRF temperatures [90]. A reduced blood volume will have the opposite effect on the local field, potentially resulting in an underestimation of the PRF temperatures. Since the susceptibility of blood is further dependent on its oxygenation level, not only changes in blood volume, but also change in the oxygenation level of the blood (the so-called blood oxygenation level dependent, BOLD, signal) will affect the PRF temperature measurements [101]. To date only anecdotal reports of the effect of perfusion changes on PRF temperatures have been reported [21,75,90], and the induced errors seem likely to be relatively small. For example, Gellermann et al. estimated a temperature error of 1 °C due to a measured perfusion increase of approximately 5 mL/100 g/min. The severity of the induced error due to perfusion changes is further likely to be very target- and patient-specific as it will depend on the local blood vessel size and orientation, and it has been shown that the blood flow direction affects the induced fields [102]. It can lastly be hypothesized that temperature overestimations will be most commonly seen in hyperthermia applications which heat large tissue volumes (and hence increase the perfusion), whereas temperature underestimations might be seen in ablation applications where potentially large non-perfused volumes of ablated tissue can be encountered.

Motion

The PRF method is sensitive to both intra-scan (i.e., during the acquisition of a single image) and inter-scan (i.e., between consecutive images) motion, and different approaches have been suggested to deal with each type of motion. In general, intra-scan motion is handled during the image acquisition step, whereas inter-scan motion is handled preferably during the post-processing of the PRF shift phase data. Depending on the target, a combination of both correction methods is often needed, e.g. when targeting abdominal organs or the heart which both exhibit fast motion in complex motion patterns. Motion of tissue in the form of deformations caused by, e.g., tissue swelling can also occur [103], and can be hard to correct for.

Just as in MR imaging in general, the PRF method is sensitive to intra-scan tissue and organ motion occurring during the image acquisition. Intra-scan motion results in blurring and ghosting artifacts across the phase-encoding direction in both the MR magnitude and phase images and will hence also degrade the PRF temperature maps. The most straightforward approach to alleviate problems with intra-scan motion is to reduce the acquisition time to attempt to freeze the motion. Fast GRE pulse sequences such as SSFP (which utilizes short TR values) and EPI (which samples multiple lines of k-space after each RF-excitation) have been utilized to speed up PRF acquisitions [32,41–50,57,58,104–106]. Most SSFP and EPI acquisitions have performed the k-space sampling on a Cartesian grid. As in other fields of MRI, the increased motion-robustness and more efficient sampling of k-space offered by non-Cartesian sampling patterns, such as radial and spiral, have also been utilized for the PRF method [36,50,53,56,107–110]. In, e.g., radial imaging where each view acquires the central points of k-space, these data can be used as a type of navigator to correct for motion [36,111]. Reconstruction time can be an issue for non-Cartesian approaches, as these routinely rely on post-processing steps such as density compensation and gridding onto a Cartesian grid, before standard Fourier transform and PRF calculations are performed. It can be challenging to perform all these post-processing steps in real-time (on the order of a few seconds), especially for volumetric acquisitions which contains many slices [35,36]. In addition to utilizing fast and more efficient pulse sequences, the image acquisition can be shortened by only sampling part of the k-space data and utilizing dedicated reconstruction methods to reconstruct artifact-free images. One popular and straightforward approach which is widely used in MRI in general, and also in PRF shift imaging, is parallel imaging, where the different spatial sensitivity from different RF-receive coils is used to reconstruct the images. Parallel imaging can be performed in both image space and k-space [112,113], and both approaches have been utilized in PRF shift imaging [50,71,114–117]. The speed-up factor that can be achieved depends on the number of available RF-coils, but acceleration factors between 2 and 6 have been reported in-vivo. In general, parallel imaging approaches are better tolerated at higher field strengths, taking advantage of the higher signal intensities with lower noise. Utilizing the different coil sensitivities, a recently developed method called simultaneous multi-slice (SMS) MRI has also been investigated for MRTI [54,118], achieving acceleration factors in the range of 3–4. In SMS MRI, multiple 2D slices are simultaneously excited and sampled, and the coil sensitivities are used to reconstruct artifact-free images. The theory of compressed sensing [119] has been utilized in PRF shift imaging to reconstruct subsampled k-space data [47,120,121] as well, and speed-up factors on the order of 3–10 are commonly achieved with these methods (Fig. 8). The largest challenge with these methods is that they are iterative in nature, and hence not well suited for real-time applications like MRTI where the temperature maps need to be available in very close to real time. Lastly, different filtering, modeling, and fitting approaches have been described to reconstruct subsampled data [122–129]. Kalman filters have been used to both reconstruct subsampled k-space data and to de-noise other fast PRF shift imaging acquisitions [125–128]. Todd et al. described a methods using The Pennes bioheat equation [130] to predict and fill in missing k-space data, and Gaur et al. described a method of direct k-space fitting [123,124]. In general, the filtering and fitting methods are non-iterative and less computationally heavy, and hence better suited for real-time applications.

Fig. 8.

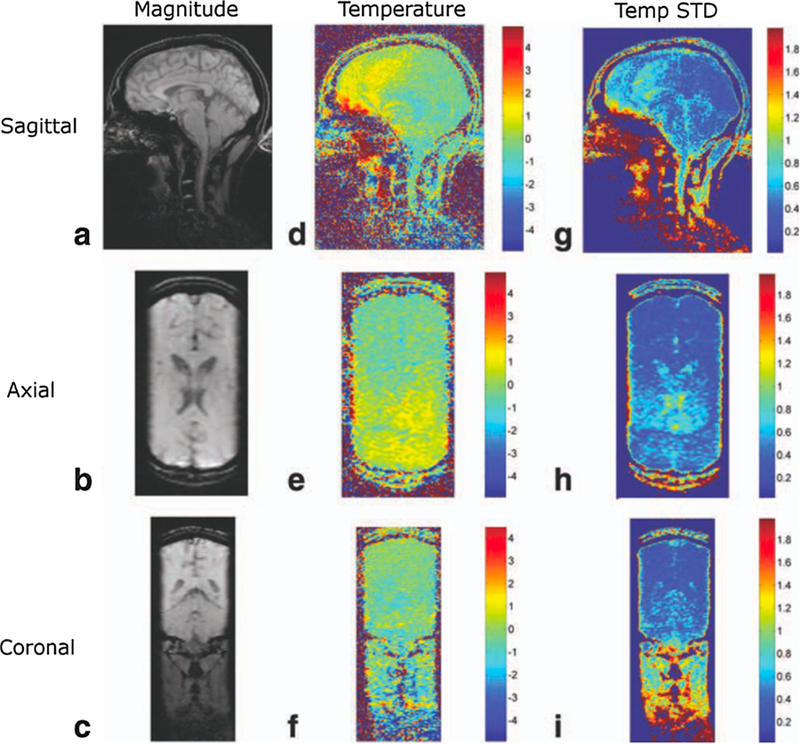
Temperature mapping for transcranial MRgHIFU. A compressed sensing method called temporally constrained reconstruction (TCR) is used to reconstruct 3D temperature maps during in-vivo brain imaging using k-space data subsampled with a factor of 6x. 1.5 mm × 2.0 mm × 3.0 mm resolution (zero-filled to 1.0 mm isotropic spacing), 288 mm × 216 mm × 108 mm FOV, and 1.8 s per time frame was achieved. The rows shown sagittal, axial, and coronal slices through the 3D imaging volume, and the columns show magnitude images, temperature maps, and temperature standard deviation maps. From ‘‘Reconstruction of Fully Three-Dimensional High Spatial and Temporal Resolution MR Temperature Maps for Retrospective Applications” Nick Todd, Urvi Vyas, Josh de Bever, Allison Payne, and Dennis L. Parker. Magnetic Resonance in Medicine 67:724–730 (2012). Fig. 4. Reprinted with permission.

The duration of most thermal therapies, ablation and hyperthermia alike, is too long to allow for breath-held imaging to eliminate respiratory motion, which is an otherwise popular approach in other MRI applications. Utilizing multiple breath-holds generally does not work either since it can be hard to get repeatable enough breath-holds for the phase-differencing needed to calculate the PRF temperature change. Gating methods, where the MRI acquisition is gated to either the cardiac or respiratory cycle and data are only sampled during (quasi-)calm periods of organ motion, have been utilized with more success. Gating has been described in both animal models and humans, under both ventilated and free breathing [131,132]. As in any gated acquisition, the methods can fail if the breathing is too irregular, resulting in errors in the temperature maps [114]. As an alternative or complement to gating, so-called navigator echoes can also be utilized [133]. The navigators monitor a specific tissue, such as the diaphragm, and trigger the data acquisition when the tissue is in a specific state. The use of navigators works well for rigid body motion but tends to fail for more complex motion patterns and tissue deformations, commonly seen in the abdomen and the heart. Another major drawback of gated acquisitions is the pro-longed scan time due to the low duty-cycle of the acquisition, and moreover the temporal resolution can vary and depends on the motion frequency.

The PRF method is not only sensitive to motion within the imaged field of view (FOV), but also to organ motion occurring outside. Motion of organs outside the FOV, such as filling of the lungs during breast imaging, will change the susceptibility inside the FOV, and hence affect the resonance frequency of the spins being imaged. One approach to correct this is to acquire field-navigator echoes before and after each readout, and to use the phase of the navigators to correct the field variation induced by the changing susceptibility due to the organ motion [95] (Fig. 7).

Inter-scan motion, caused by respiration, cardiac motion, peristalsis, and any other bulk patient motion can be a large problem because the pre-heating baseline image might have shifted compared to the images acquired during heating, causing problems with the phase differencing. New and additional baseline images cannot be acquired after the start of the heating, until the tissue has cooled back to its nominal temperature, as this would also introduce errors in the phase-differencing. Two different postprocessing/reconstruction approaches, and also combinations of the two methods, have been presented to solve the problem of inter-scan motion. In multibaseline reconstruction, a library containing multiple baseline images acquired before the start of the heating, each acquired during a different part of the organ motion/breathing cycle, is generated [49,68,134–136]. The images acquired during the heating are then compared to all the images in the library, and the baseline image (or some weighted combination of multiple baseline images) which is closest to the current image is used as the baseline for the phase difference calculation. The images can be compared using non-similarity or inter-correlation coefficients, or by means of evaluating the signal from a navigator echo [49,68,134,135]. Multibaseline methods correct for cyclic and repetitive motion such as cardiac and respiratory motion, but not for irregular motion such as bulk patient motion and peristalsis. Multibaseline approaches have been described and successfully implemented for brain [34,137], breast [36,138], cardiac [136], liver [32,135,136], kidney [32,49,139,140], and pancreas [141].

In referenceless PRF methods [82,89], the images acquired during the heating are themselves used to estimate the background phase which is subtracted to create the phase difference image. In its simplest form a polynomial is fitted to the unwrapped background phase (i.e., the background which does not experience any temperature rise). The polynomial fit is then extrapolated to cover the heated region, and a subtraction between the acquired image and the extrapolated polynomial is performed to achieve a phase difference image. Multiple extensions and improvements to the original method have been published, e.g. using complex polynomials, phase gradients, phase finite differences, or a magnitude-sorted list with multi-clustering approach to avoid the need for phase unwrapping [85,88,142,143], or the use of a regression algorithm to avoid the need to manually define an ROI [83]. Referenceless methods can compensate for both irregular (non-repetitive) physiological motion and B₀ field drifts. Since a region of unheated tissue is needed for the polynomial fit, referenceless methods usually work well in ablation procedures, but not always in hyperthermia applications where larger tissue regions can be heated. If adipose tissues are present in the image they should either be saturated or handled separately from the aqueous tissues since echo-time dependent phase discontinuities will appear at tissue interfaces between adipose and aqueous tissues. This can be done by, e.g., fat-water separation and separate polynomial fitting to each tissue type [144]).

Hybrid multibaseline-referenceless methods have also been described, which combine the immunity to repetitive motion of the multibaseline approach with the field-drift correction and immunity to irregular motion of the referenceless approach [128,129,136,139,140]. These methods have been shown to work well in brain, cardiac, kidney and liver applications (Fig. 9).

Fig. 9.

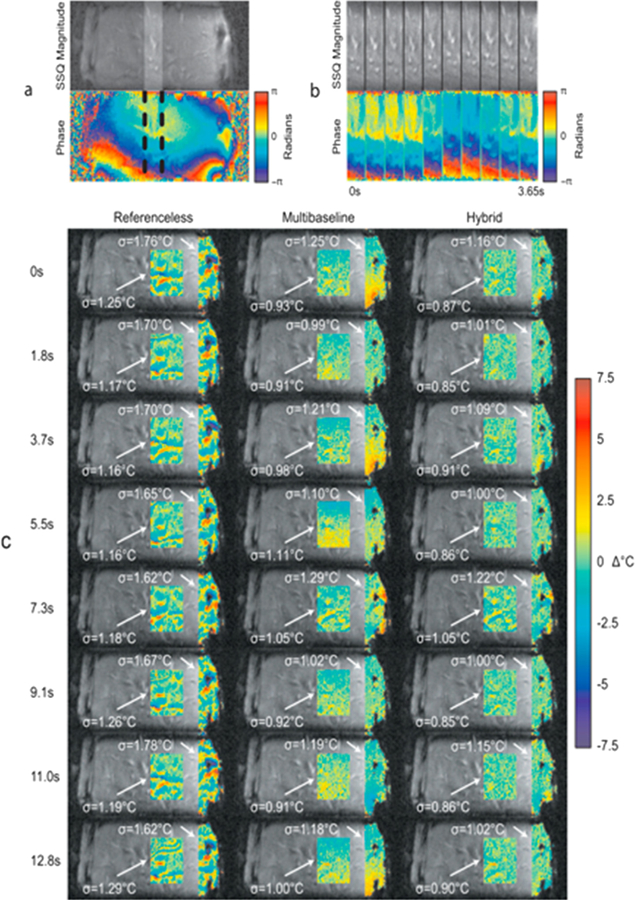
Comparison of modeling errors in sagittal liver images of a healthy volunteer. (a) (top) A library image (sum-of-squares across coils) and (bottom) image phase for a single coil. The phase is smooth in the liver center, but varies rapidly near the ribs. The highlighted region in (a) is shown across library images in (b) to illustrate the up-down motion of the liver. (c) shows residual temperature errors and standard deviations after estimation with the three methods in eight subsequently acquired images. The hybrid model is more accurate than the other two methods in both the inner liver and over the liver/rib interface region. From ‘‘Hybrid referenceless and multibaseline subtraction MR thermometry for monitoring thermal therapies in moving organs” William A. Grissom, Viola Rieke, Andrew B. Holbrook, Yoav Medan, Michael Lustig, Juan Santos, Michael V. McConnell, and Kim Butts Pauly. Med. Phys. 37, 9, September 2010. Fig. 2. Reprinted with permission.

2.2. Longitudinal (spin-lattice) relaxation time, T₁

Longitudinal (or spin-lattice) relaxation of water protons in biological tissue is mediated primarily by intra-molecular dipolar interactions (i.e., between hydrogen protons in the same water molecule), but also to a lesser degree by inter-molecular interactions (i.e., between protons in water and surrounding molecules). These interactions fluctuate as a result of the random thermal motion of molecules in the body. The interactions depend on the local magnetic field experienced by the protons and can be described by a frequency spectral density, J(ω), which is a measure of the number of interactions occurring at different frequencies, Fig. 10. For most effective relaxation of an excited spin system back to equilibrium, the fluctuations must occur at, or close to, the Larmor frequency, ω₀. Water in biological tissue experiences diverse local molecular environments and undergoes interactions with a wide range of other molecules of various sizes. As a result, extrapolation from the known theory of relaxation to a precise characterization of relaxation in biological tissue is fraught with problems. Nevertheless, as a first approximation, the relaxation time T₁ can be expressed in terms of τ_c, γ, ω₀; and the local field, B_loc [11,145,146] according to

$$\frac{1}{T_1}=\frac{2{\gamma }^2{B}_{loc}^2}{3}\frac{{\tau }_c}{1+{\omega }_0^2{\tau }_c^2}$$ (7)

where τ_c is the characteristic timescale of the magnetic fluctuations. The relationship between T₁ and τ_c is schematically shown in Fig. 11 and experimentally in, e.g., references [11,12,147]. For the field strengths and temperatures experienced in clinical MRI, it can be concluded that, as an approximation

$$\frac{1}{T_1}\propto {\tau }_c$$ (8)

Fig. 10.

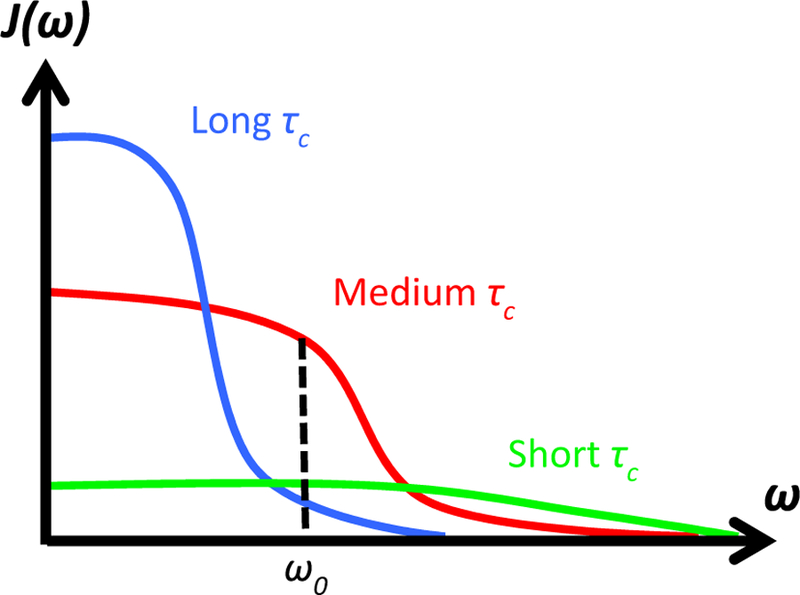
Frequency spectral density, J(ω), as a function of resonance frequency, ω, for different correlation times, τ_c. The longitudinal relaxation time T₁ is proportional to the number of protons that are tumbling at the Larmor frequency, ω₀. Pure water has a wide flat spectrum with relatively little energy around the Larmor frequency. This is also true for water molecules bound to large slow-moving macromolecules, which have a narrow spectrum. The largest contribution to T₁ come from water bound to intermediate-sized molecules. From Chapter 15 in Theory and Applications of Heat Transfer in Humans. Henrik Odéen and Dennis L Parker, Non-Invasive Thermometry with Magnetic Resonance Imaging. Devashish Shrivastava (Editor). John Wiley and Sons 2018. Reprinted with permission.

Fig. 11.

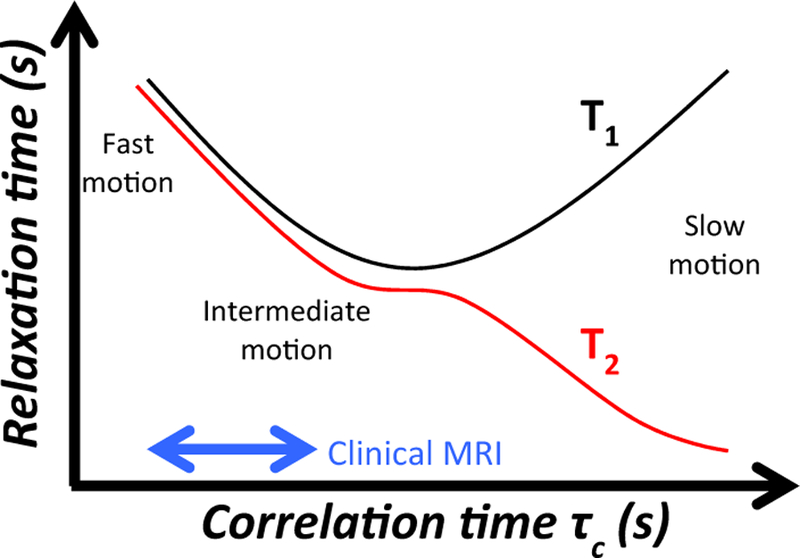
The T₁ and T₂ relaxation times as a function of correlation time, τ_c. The area of operation for modern MRI scanners is indicated by the blue arrow. Here both T₁ and T₂ increases as a function of decreased correlation time, and hence both T₁ and T₂ increase as a function of increased temperature. From Chapter 15 in Theory and Applications of Heat Transfer in Humans. Henrik Odéen and Dennis L Parker, Non-Invasive Thermometry with Magnetic Resonance Imaging. Devashish Shrivastava (Editor). John Wiley and Sons 2018. Reprinted with permission.

It can be shown that τ_c is also inversely proportional to temperature, and T₁ is hence directly proportional to temperature in most clinical MRI experiments. Temperature increases will hence result in longer T₁, which will in turn result in lower signal intensity in the MR image as discussed in more detail in the Signal intensity and proton density-section.

The temperature sensitivity of T₁ will be detected both in quantitative T₁-mapping methods and in the signal intensity magnitude of T₁-weighted images. In this section we will focus on temperature measurements utilizing quantitative T₁-mapping methods, and temperature measurements utilizing the effect of T₁ on the signal intensity will be discussed in the Signal intensity and Proton density-section, as there are many simultaneous effects contributing to the change in signal intensity with temperature.

T₁ measurements and T₁ mapping were among the first methods to be investigated for MR temperature imaging in the early 1980s [11,12,148,149]. Over a rather small range of temperatures the temperature dependence of T₁ has been shown to be nearly linear according to

$$T_1(T)=T_1(T_{ref})+m_1(T-T_{ref})$$ (9)

where T_ref is a known reference or starting temperature (e.g., body temperature, 37 °C) and m₁ = dT₁/dT (i.e., change in T₁ with temperature, measured in ms/°C or %/°C). This can be re-arranged into

$$T=\frac{T_1(T)-T_1(T_{ref})}{m_1}+T_{ref}$$ (10)

so that if m₁ and the baseline values of T_ref and T₁(T_ref) are known, and T₁(T) are being dynamically measured, the current temperature T can be calculated.

One challenge with utilizing T₁-based MRTI in biological tissues is that m₁ is tissue type dependent due to the difference in macromolecular content and microstructure for different soft tissue types. This means a separate m₁ needs to be estimated and used for each tissue type of interest. The temperature dependence of T₁ is rather high and has been shown to be on the order of 1–3%/°C, with slightly higher values reported for fat-based tissues than for water-based tissues [66,148,150–156]. For example, for bovine muscle values of 1.0–1.4%/°C has been reported [150,157], for liver 1–2%/°C [158], for cortical bone approximately 0.7–0.8%/°C [159], for breast fat 1.2–1.6%/°C [66,153], for porcine fat 2.0–2.5%/°C [152,157], for human brain approximately 0.5%/°C (white matter), 1.8%/°C (cortex) and 1.2%/°C (thalamus) [160], and for guinea pig brain between 1.7 and 4.5%/°C [161]. An example of change in T₁ with temperature in cortical bone is seen in Fig. 12. It has further been shown that m₁ can vary significantly between different fatty acids. In animal fat it was found that methylene (CH₂) and terminal methyl (CH₃) had m₁ of 1.79%/°C and 2.98%/°C, respectively [151]. These differences can make the ‘‘total” m₁ for fat depend greatly on its composition of different acids. A second challenge with utilizing T₁-based MRTI in the clinic is that T₁depends on the macromolecular and hydration state of the tissue, both of which can change as tissue is heated.

Fig. 12.

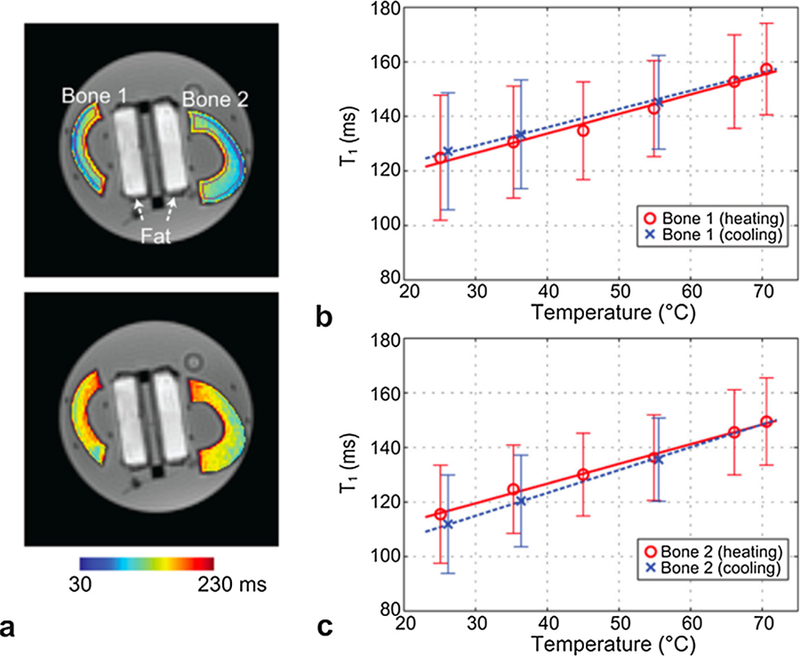
T₁ based temperature measurements. a: T₁ maps in ex-vivo bovine cortical femur bone at temperatures of 25 °C (top) and 70 °C (bottom), overlaid on UTE images with flip angle = 8°. ROIs used to determine T₁ in each bone sample are denoted in purple in the upper image. (b–c): The mean T₁ and error bar from the ROI is shown over different temperatures for each bone sample. Linear regression lines during the heating and cooling periods are plotted as well. An apparent linear increase of T1 with temperature is demonstrated. From ‘‘Quantifying Temperature-Dependent T1 Changes in Cortical Bone Using Ultrashort Echo-Time MRI” Misung Han, Viola Rieke, Serena J. Scott, Eugene Ozhinsky, Vasant A. Salgaonkar, Peter D. Jones, Peder E. Z. Larson, Chris J. Diederich, and Roland Krug. Magn Reson Med. 2015 Dec; 74(6):1548–55. Fig. 2. Reprinted with permission.

In terms of pulse sequences many of the conventional and more accurate T1-mapping methods, such as inversion- and saturation-recovery based methods, are very slow. This limits their usefulness for real-time applications such as MRTI in the clinic, especially for short ablative applications. These methods, which have scan times of ~4–8 minutes, have however been used for calibration studies to determine m₁ and for hyperthermia applications where scan times of a few minutes can be acceptable [148,154,157,162,163]. For ablative procedures, methods relying on just a few measurements, such as dual-TR spin echo or variable flip angle (VFA) gradient echo methods can be used [164–167]. In the VFA method, two or more magnitude images acquired at different flip-angles are acquired. By linearizing the signal equation, voxel-wise T₁ maps can be determined. The method is sensitive to B1-field inhomogeneities and corrections using flip angle mapping should be applied, which can be time-consuming. By combining the VFA method with fast EPI readout, scan times of 8–15 s for MRTI based on T₁ maps have been obtained [66,152,153,163,168].

Temperature monitoring using the T₁ technique has predominantly been utilized for temperature measurements in adipose tissues because the PRF method provides higher precision for water-based tissues. As mentioned above, the different m₁ values observed for different proton components of fat make T₁-based techniques potentially patient-dependent. However, Baron et al. found only a small variation in the inter-sample variability in m₁ from adipose breast tissue from 7 different patients [154], suggesting a small inter-patient variability in fat composition and that a ‘‘universal” m₁ can be found and used for all patients. This will greatly improve the usefulness of T₁-based thermometry in the clinic.

Just as for PRF and diffusion-based thermometry (see below), voxels with mixed water-fat content represent a problem in T₁- based thermometry due to the differences in m₁ in the different tissue types. If only one tissue type is of interest, selective excitation or saturation can be utilized to alleviate the problem. If measurements from both tissues are needed, fat-water separation methods, such as Dixon or IDEAL [169], can be employed to provide accurate measurements in both tissue types separately. When combining the two temperature maps, care must be taken to account for the bandwidth-dependent fat-water shift occurring due to the ~3.5 ppm frequency difference between fat and water protons.

Changes in T₁ with temperature have been found to be reversible and repeatable for low temperature increases, up to an absolute temperature of at least 43 °C, in both water- and fat-based tissues. For higher temperature increases, tissue coagulation can result in irreversible changes in aqueous tissues [148,157,162,163,170]. Adipose tissues, on the other hand, have shown repeatable behavior for temperature increases up to absolute temperatures of 65 °C [154,157], highlighting the promise of using T₁ for temperature monitoring in fat-based tissues.

The use of T₁ to non-invasively monitor temperature changes is still an area of active research. Apart from measurements in adipose tissue, recent approaches have attempted to monitor temperature changes in bone [159] as well as to combine PRF and T₁ temperature measurements for simultaneous temperature monitoring in both water- and fat-based tissues [152,153].

2.3. Transverse (spin-spin) relaxation time, T₂

The physical mechanism behind the T₂ relaxation time is de-correlation and de-phasing of spins within an imaging voxel. For water protons, the local magnetic field experienced by a spin depends both on the partner hydrogen-proton in its water molecule, but also on spins in neighboring molecules. The local field will vary in time due to the random thermal motions of the molecules. Since ω = γB_loc, the time varying B_loc will result in time-dependent variations in the spins’ precession rate, and hence result in a de-phasing of the spin coherence within an imaging voxel. Since this loss of spin coherence is due to random thermal motions, it cannot be reversed.

As is the case for T₁, T₂ also depends on the correlation time τ_c [12,145] but with a different relationship

$$\frac{1}{T_2}={\gamma }^2{B}_{loc}^2\left({\tau }_c+\frac{{\tau }_c}{1+{\omega }_0^2{\tau }_c^2}\right)$$ (11)

and so shorter τ_c results in longer T₂, as schematically shown in Fig. 11 and experimentally in, e.g., reference [12]. In environments with few macromolecules, such as free water, spins are moving fast and are unrestricted, and will have a short τ_c. They will therefore have longer T₂-values than water spins in tissue where the motion of the water molecules is restricted and the molecules move more slowly (i.e., longer τ_c resulting in shorter T₂-values).

MR temperature measurements using T₂ have been studied since the early 1980s [149]. Just as for T₁-based thermometry, T₂-based temperature measurements also utilize a calibration factor, m₂ = dT₂/dT, and known baseline values for T_ref and T₂(T_ref) to estimate the temperature, T, by dynamically acquiring maps of T₂(T), according to

$$T=\frac{T_2(T)-T_2(T_{ref})}{m_2}+T_{ref}$$ (12)

Historically T₂-based temperature measurements have not gained as much popularity as T₁-based measurements, partly because slower spin echo-based methods generally are needed to measure T₂. Gradient echo techniques (which are routinely used for PRF and T₁ based methods) measure $T_2^{\ast }$ rather than T₂, and $T_2^{\ast }$ depends on multiple additional effects such as field inhomogeneity, which might affect the value and repeatability of m₂ measurements. Recently more studies using T₂ for MRTI measurements in adipose tissues have been published. Kuroda showed that just as for T₁ different proton components can have different temperature dependence m₂, with CH₂ having values between 4 and 5%/°C, and CH₃ having values between 3 and 6%/°C, for bovine and porcine fat [151]. However, Baron et al. showed that just as for T₁ high subject-to-subject reproducibility in T₂ measurements could be achieved, highlighting the potential utility of T₂-based temperature measurements [171]. Multiple studies have further shown that T₂ increases linearly and reversibly with temperature in the range from 20 °C to approximately 50 °C of absolute temperature, and changes on the order of 5–7 ms/°C [154,171,172]. At higher absolute temperatures of 50 –70 °C Baron et al. observed a non-linear increase in T₂, however; still with a reversible change in T₂ as the tissue cooled back down to the initial temperature [171]. For accurate T₂ measurements it is important to saturate the signal from water protons that can be present interspersed with the fat. Since water and fat have different m₂, and the relative abundance of each might vary spatially throughout the sample, it does not appear possible to accurately measure the change in T₂ from a mixed fat-water signal without knowing their relative concentrations and m₂ for both tissues.

T₂-based thermometry has recently been used in-vivo to monitor the temperature in subcutaneous fat during MR-guided focused ultrasound treatments of uterine fibroids [171,172]. The temperature monitoring not only improves safety by making it possible to stop the treatment if the tissue gets too hot but can also make the treatments more efficient by helping to minimizing the cooling time required between consecutive ultrasound sonications. An example of T₂-based MRTI in the subcutaneous adipose tissue layer during a high intensity focused ultrasound uterine fibroid treatment is shown in Fig. 13.

Fig. 13.

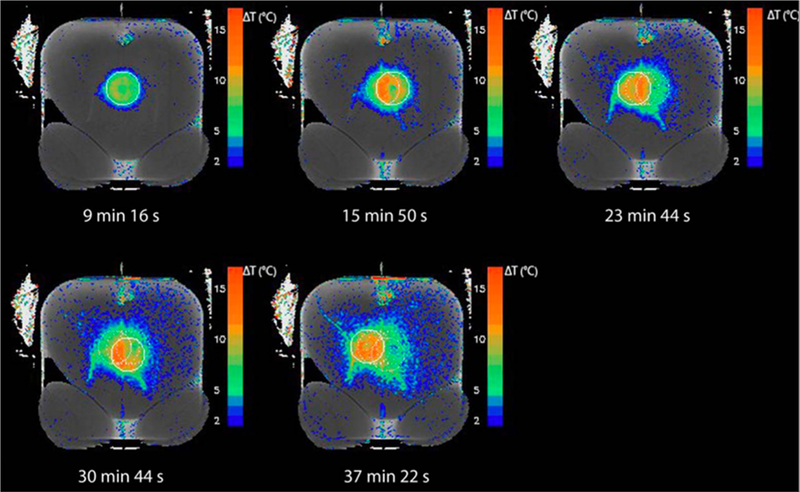
T₂-based temperature measurements. Example of a T₂ reference map with T₂ difference-based temperature overlay showing near-field heating in the subcutaneous adipose tissue layer after five consecutive volumetric sonications during a uterine fibroid treatment in a human patient. The intersection of the beam cone with the imaging slice during the latest sonication is shown as a solid circle. The sonications before that are shown as dotted circles. The time difference between the new T2 measurement and the reference T2 map is given. From ‘‘In Vivo T2-Based MR Thermometry in Adipose Tissue Layers for High-Intensity Focused Ultrasound Near-Field Monitoring” Paul Baron, Mario Ries, Roel Deckers, Martijn de Greef, Jukka Tanttu, Max Köhler, Max A. Viergever, Chrit T. W. Moonen, and Lambertus W. Bartels. Magnetic Resonance in Medicine 72:1057–1064 (2014). Fig. 7. Reprinted with permission.

In terms of pulse sequences, most T₂-based approaches utilize multi-echo spin echo type pulse sequences to measure the signal decay at multiple echo times. This is traditionally a rather slow technique with scan times in the order of minutes [154], but by combining the acquisition of just two echoes with fast turbo-spin echo readouts scan times of 15–16 s per image can be achieved [171,172]. T₂-based MRTI is still an area of active research, and the higher temperature sensitivity of T₂ compared to T₁ makes it a promising candidate for temperature measurements in fat-based tissues.

2.4. Signal intensity and proton density

The equilibrium magnetization in MRI, M₀, is determined by the Boltzmann distribution, which exhibits a temperature dependence. M₀ depends on the sample temperature according to [173–175]

$$M_0\approx n\frac{{\gamma }^2{\hslash }^2\left|B\right|}{4kT}$$ (13)

where n is the number of spins, $\hslash$ is the reduced Planck constant, k is the Boltzmann constant, and T is the absolute temperature of the sample. The temperature dependence is rather small and the fractional change in M₀ is

$$\frac{\Delta M_0}{\Delta T}\approx -n\frac{{\gamma }^2{\hslash }^2\left|B\right|}{4k{T}^2}$$ (14)

such that

$$\frac{\Delta M_0}{M_0}\approx -\frac{\Delta T}{T}$$ (15)

At room temperature of approximately 300 K a one-degree change in temperature will hence corresponds to ~0.3% fractional change in the magnetization M₀ [175].

The proton density (PD) in MRI can be estimated from the magnitude images by accounting for all confounding T₁- and T₂-effects. For example, long TRs of at least 5*T₁ should be utilized to minimize any T₁-effects, resulting in long scan times. Using a shorter TR to speed up the acquisition can make it difficult to separate changes in PD from changes in T₁. T₂-effects can be eliminated by using, e.g., double-echo methods and estimating the signal at a TE of 0 ms [176]. It should be noted that the actual density of protons in the tissue does not change but it is rather the magnetic susceptibility, which reflects the ratio of spins parallel to spins antiparallel to the external field, which changes with temperature. The PD is further directly proportional to the magnetization M₀ and will hence experience the same temperature dependence of ~0.3%/°C as M₀. Only a few studies have attempted to monitor temperature change using PD [175–177]. Kamimura et al. only performed studies on CuSO₄ solutions, and Young et al. performed in-vivo studies on human muscles, and therefore over relatively small temperature ranges. Chen et al. performed experiments in ex-vivo porcine muscle and abdominal fat. In the adipose tissue the apparent proton density (APD) was shown to change linearly at a rate of 0.29%/°C between 30 and 75 °C, in good agreement with theory according to the temperature dependence of the Boltzmann distribution. In muscle the change in APD was shown to be linear but non-reversible, with a larger APD observed during heating (approximately 0.40%/°C) than during cooling (approximately 0.28%/°C). In general APD measurements are very sensitive to low SNR, with a SNR of 100 needed for a precision of 3 °C [176].

Rather than attempting to control for all contributing temperature-dependent effects in measuring the (A)PD, MRI signal intensity, SI, can be measured. Measuring SI is more straightforward since accurate SI measurements can be performed without accounting for T₁ and T₂ effects, and instead SNR is usually the limiting factor. The measured SI depends on M₀ (and hence PD), but also on parameters such as the diffusion of protons and the T₁ and T₂ relaxation times. All these parameters have a temperature dependence of their own, which all contribute to the total temperature dependence of the SI. The SI further depends on imaging parameters such as the TR, TE, and flip angle. For a spoiled GRE sequence, e.g., the SI can be expressed as [52]

$$SI=M_0(T)sin(\alpha )\frac{1-E_1}{1-\cos (\alpha )E_1}{E}_2$$ (16)

where α is the flip angle, $E_1=e^{-\frac{TR}{T_1(T)}}$, $E_2=e^{-\frac{TE}{T_2(T)}}$, and T₁(T) and T₂(t) are the relaxation times at temperature T. This highlights the more complicated temperature dependence of the measured SI. An example of the change in SI with temperature during a focused ultrasound heating in a gelatin phantom can be seen in Fig. 14. Further, depending on the chosen values for TR, TE, and α, the acquired image is said to be, e.g., T₁-weighted (T₁w) or T₂- weighted (T₂w), both of which have been used to monitor thermal therapies. As described above the exact temperature dependence of the SI, dSI/dT, can be complicated since it depends on the amount of the different weightings which in turn depends on multiple parameters with their own temperature dependence. The temperature dependence of each of these parameters can also change depending on tissue state; e.g., T₁ of liver has been described to initially increase with temperature, but to decrease after thermal coagulation occurs [178]. It has also been shown that the magnitude of dSI=dT depends on the amount of weighting in the acquired image. In T₁w images, for example, Gellermann et al. observed a change of ~1%/°C when using a TE = 5 ms, but in images with less T₁w (using TE = 20 ms) only a change of ~0.75%/°C was observed [99]. Both T₁ and T₁ change per °C increase with increasing B₀ field strengths but the observed T₁ contrast decreases [149,179], resulting in the reduced temperature sensitivity [99]. Because of these challenges, temperature mapping based on T₁w images may be more suitable at low B₀ field strengths which has higher contrast and sensitivity. Non-linear effects in dSI/dT in T₁w images have also been observed, particularly in conjunction with tissue coagulation [170,178,180,181]. This is likely explained by temperature-dependent changes in exchange processes and effective tumbling rates of water. Both T₁w and T₂w images have been used for quantitative and qualitative MRTI measurements [150,158,170,178,181–185]. In quantitative studies values of dSI/dT have been reported in the range of 0.7–1.0 %/°C in liver, 0.97%/°C in fat, 0.7–1.0%/°C in cortical bone, and 1.0%/°C in muscle.

Fig. 14.

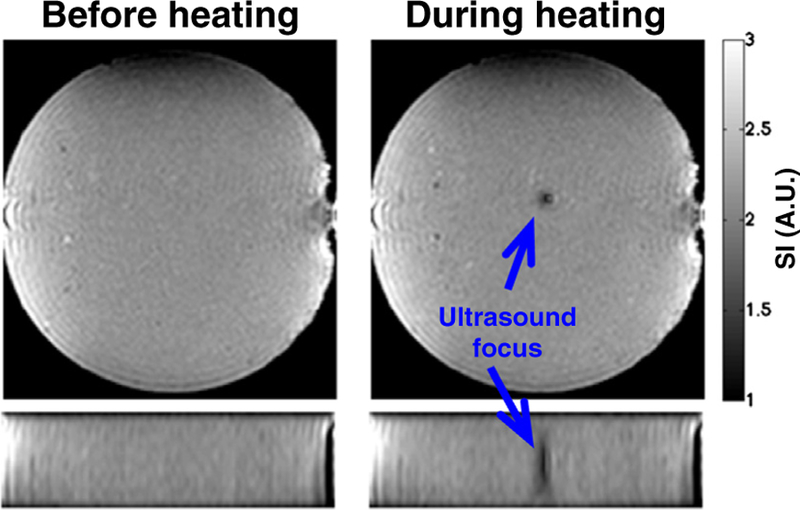
Two orthogonal views of a cylindrical gelatin phantom showing decreased signal intensity in the magnitude image during focused ultrasound heating. The signal intensity decreases with approximately dSI/dT = −1.1%/°C due to decrease in the magnetization and changes in the T₁ and T₂ relaxation times. From Chapter 15 in Theory and Applications of Heat Transfer in Humans. Henrik Odéen and Dennis L Parker, Non-Invasive Thermometry with Magnetic Resonance Imaging. Devashish Shrivastava (Editor). John Wiley and Sons 2018. Reprinted with permission.

2.5. Magnetization transfer

Protons bound to macromolecules are in general hard to image with MRI due to their very short T₂ and ${\text{T}}_2^{*}$ relaxation times. There do, however, exist exchange processes between protons bound to macromolecules and those in the ‘‘free” proton pool, mainly water. These exchanges can happen in two different ways; first the magnetization from the macromolecule-bound protons can be transferred to protons in the ‘‘free” proton pool. Second, the protons themselves can enter the ‘‘free” pool of protons [186]. In magnetization transfer methods off-resonance spectrally selective RF pulses are utilized to selectively excite and saturate the magnetization which is associated with large macromolecules. If a spectrally selective RF pulse is applied, saturating the macromolecules, the exchange of saturated magnetization from the macromolecules with unsaturated free water causes a decrease in the detectable MR signal [170,175,180]. Although these exchange processes are temperature-dependent and can potentially be used for relative temperature measurements, the sensitivity is rather low, and has been shown to be fairly tissue type dependent. For example, fat, liver, and white matter have been shown not to display any change in MT-weighted signal with temperature, whereas prostate, heart, and muscle showed increases in MT-weighted signal above approximately 50 °C [170]. Due to the low sensitivity and tissue type dependent signal change, magnetization transfer based methods have not gained much popularity as a temperature measurement technique.

2.6. Diffusion

The temperature dependence of molecular diffusion can be derived from the basis of the Stokes-Einstein relation between viscosity and the translational self-diffusion coefficient, D, as

$$D\approx e^{-E_a(D)/kT}$$ (17)

where E_a is the activation energy for translational molecular diffusion, k is the Boltzmann constant, and T is the absolute tissue temperature [187,188]. In general the un-restricted random thermal molecular motion is a stochastic thermal phenomenon described by Brownian motion, and results in a Gaussian distribution of displacements. However, the diffusion of water molecules in biological tissues is influenced by macromolecules, cell membranes and other cellular and subcellular structures resulting in restricted diffusion. These structures can greatly affect the diffusion of water molecules, and, for example, water in the intracellular space, which has a higher concentration of macromolecules, experiences less diffusion than water molecules in the extracellular space. In general, in the presence of macromolecules and tissue structures such as muscle fibers and white matter tracks, water diffusion is not symmetric but can vary greatly with directionality, resulting in what is known as diffusion anisotropy. However, because the diffusion tensor is symmetric, there are in fact only 6 independent coefficients.

Diffusion imaging in MRI is based on the application of strong, usually dual-lobe, diffusion gradients. Spins moving along the direction of the applied gradient experience a net phase-dispersion, resulting in signal attenuation, whereas stationary spins do not. This phase dispersion results in signal attenuation. The amount of signal loss is related to the displacement distribution of the spins and the applied gradients and can be described as e^‒bD. b is called the b-value and describes the magnitude and duration of the applied diffusion gradients according to $b=-{\gamma }^2{G}^2{\delta }^2(\Delta -\delta /3)$, where G is the gradient amplitude, δ the gradient duration, and Δ the separation of the two gradient lobes [52]. The application of higher amplitude and/or longer duration diffusion gradients results in more phase dispersal and signal loss.

There are several different approaches to diffusion imaging, of varying complexity. In simple diffusion weighted imaging (DWI) a single b-value is usually used and the image intensity of each voxel is weighted by the average diffusion coefficient in that voxel. Quantitative diffusion coefficient mapping is based on acquiring at least 2 DWI images with different b-values, and post-processing yields a quantitative map of diffusion coefficients. Since the measured diffusion may be affected by a number of factors, including cellular structures and boundaries, as well as tissue perfusion, this is often called the apparent diffusion coefficient (ADC). The effects of perfusion can to some degree be compensated for by the choice of b-values [102]. Lastly, diffusion tensor imaging (DTI) measures the diffusion anisotropy and requires at least a set of 6 independent DW-images. Apart from SNR advantages at high field strengths, MRTI based on diffusion is independent of the field strength.

Temperature changes will result in viscosity and diffusion changes which can be investigated by differentiating the above equation. Differentiation and normalization gives

$$\frac{dD}{DdT}=\frac{E_a(D)}{k{T}^2}$$ (18)

which can be re-arranged as

$$\Delta T=T-T_{ref}=\frac{k{T}_{ref}^2}{E_a(D)}\left(\frac{D-D_{ref}}{D_{ref}}\right)$$ (19)

Here D_ref is the diffusion constant measured at some known reference temperature T_ref, and D is the dynamically acquired diffusion constant at the current tissue temperature T. In this expression it is assumed that the temperature dependence of the activation energy E_a is small (i.e., that it is approximately constant with temperature) and that the total change in tissue temperature is also limited, i.e., ΔT ≪ T_ref.

The in-vivo temperature sensitivity of diffusion has been shown to be relatively high. With an activation energy of approximately 0.2 eV at 20 °C [188], a sensitivity in the range of 2.0–2.5 %/°C is achieved from equation 19 [20,189,190]. However, temperature measurements using the diffusion method have not gained substantial popularity due to various practical difficulties in its application. First and foremost, diffusion imaging is very sensitive to both physiological and bulk patient motion. This can be realized since the diffusion distances which are encoded are on the order of tens of µm [52]. In general diffusion imaging is rather slow, on the order of minutes, and hence not well suited for real-time applications. However, faster imaging using, e.g., EPI readout have been described to speed up the acquisitions, resulting in scan times down to 2 s for a single 2D DWI slice [100,191,192]. These faster imaging protocols are also inherently less sensitive to motion.

Diffusion imaging is sensitive to tissue changes such as altered membrane permeability, treatment induced edema, irreversible tissue necrosis and coagulation, and reversible ischemia [170]. These effects can alter the diffusion pathways, which in turn can greatly affect the measured diffusion values. This can further result in competing effects on the diffusion. For example, diffusion increases due to change in temperature but has also been shown to decrease by up to 40% due to ischemia [193], in part due to cell swelling. Just as in PRF phase mapping, adipose tissues are a concern in diffusion imaging. Diffusion in adipose tissues is very low and hence hard to measure. The adipose tissues should therefore be suppressed to avoid partial volume effects, resulting in underestimation of the measured diffusion from the water signal. Temperature imaging based on diffusion can also be affected by temperature gradients in a voxel, which results in spatially varying PRF inside the voxel. This will cause phase dispersion, which can be interpreted as a diffusion change, and the effect can be exaggerated due to the usually long TE values used in diffusion imaging. This effect can be reduced using high spatial resolution in gradient echo imaging or the effect can be avoided using spin echo pulse sequences. Despite these challenges both DWI and ADC have been used to monitor relative temperature change [20,100,156,170,189–192,194,195]. It should be noted that methods relying on basic DWI, where changes in the DW signal intensity are utilized, will depend on signal changes due to other effects such changes in T₁ and T₂ as described in the Signal Intensity and Proton Density-section.

Absolute temperature measurements of in-vivo cerebrospinal fluid (CSF) have recently been described using DWI [196–199]. A reference image, S₀, with b-value 0 s/mm², as well as multiple diffusion weighted images, S₁, with between 12 and 32 independent diffusion directions and b-values between 700 and 1000 s/mm² were used. Using single-shot EPI pulse sequences scan times between 2 and 6 min were achieved. The diffusion coefficient D_i was calculated as

$$D_i=\frac{\ln (S_0/S_1)}{b}$$ (20)

and the corresponding temperature was calculated as [198,200]

$$T_i=\frac{2256.74}{\ln \left(\frac{4.39221}{D_i}\right)}-273.15$$ (21)

where T_i is the temperature in °C. An example of CSF temperature measurements in the lateral ventricles of a human volunteer is shown in Fig. 15. The absolute temperature measurements work because of the similarity of CSF macromolecular content between subjects and the resulting relative subject independence of the activation energy in CSF.

Fig. 15.

Estimating CSF temperature in the lateral ventricles of a human volunteer using. (a) Uncorrected temperature map showing artificially high temperatures within the lateral ventricles because of outliers and artificially low temperature estimates for brain tissue due to restricted diffusion. (b) Display of all the 32 diffusion constant estimates from six representative voxels (marked with white squares in (a). The asterisks represent the nine directions found to be least prone to artefacts. (c) Temperature map where only the directions marked on panel (b) were averaged for each voxel within the lateral ventricles. The mean estimated temperature within the lateral ventricles is 37.9 °C in this slice. From ‘‘Using diffusion MRI for measuring the temperature of cerebrospinal fluid within the lateral ventricles” LR Kozak, M Bango, M Szabo, et al. Acta Paediatrica 2010 99, pp. 237–243. Fig. 2. Reprinted with permission.

2.7. Spectroscopic approaches

MR spectroscopy-based temperature measurement methods are based on the concept that the separation of peaks from different tissue components in a frequency spectrum is a function of temperature. As opposed to the previously described methods which measure relative temperature (i.e., a temperature change), spectroscopic temperature measurement methods measure absolute temperature. In proton spectroscopy, which just like PRF phase mapping utilizes the temperature induced water proton chemical shift, the water resonance peak changes with temperature while a reference peak (e.g., lipid or N-acetyl-aspartate in the brain [93,201]) does not. Having an internal reference removes the need to compare to a reference image, and hence makes spectroscopic imaging measurements inherently less sensitive to motion and drift in the magnetic field [201,202]. When lipids and water are uniformly distributed within a voxel, their frequency peak separation is proportional to the absolute temperature. Because spectroscopic imaging adds another dimension to the image, it is generally slow and relatively low resolution is achieved. Multiple different spectroscopy approaches have been utilized for thermometry, such as single voxel spectroscopy [201,203,204], magnetic resonance spectroscopic imaging (MRSI) [22,205–207], echo planar spectroscopic imaging (EPSI) [206], and line scan echo planar spectroscopic imaging (LSEPSI) [207,208]. Spatial resolution on the order of 3–4 mm and temporal resolution of about 1 min have been demonstrated [206–209]. This makes spectroscopic imaging too slow for real time temperature control except for treatments with slow temperature changes. It does, however, provide a unique tool for potentially absolute temperature measurements, which is not possible with previously mentioned methods. It should be noted that spectroscopic methods can be sensitive to intravoxel field inhomogeneities, which can affect the spectral widths and make it difficult to determine the peak positions. This effect can be alleviated by increasing the spatial resolution (acquiring smaller voxels), at the cost of SNR and/or scan time. High field scanners (>1.5 T) with good temporal stability and spatial homogeneity may be needed to reliably detect some of the small metabolic signals used for the internal references. Complex post-processing steps are also usually necessary and can include modeling of the induced eddy currents and peak fitting using dedicated functions. Also, although the internal reference technique removes the need for subtraction of a reference image the methods still need to be calibrated, since the absolute value of chemical shift difference between the water signal and the reference signal may depend on tissue location and parameters such as pH and ion concentration. In two in-vivo studies measuring the absolute temperature in the human brain, for example, calibrations were performed using invasive probes in porcine brains and using tympanic temperature readings [201,210].

2.8. Temperature sensitive contrast agents

One major challenge with the majority of the previously described methods is that they only measure a relative temperature change, as opposed to the absolute tissue temperature. Alleviating this limitation is one of the main advantages with using various types of temperature sensitive contrast agents, and this approach has been investigated since the mid- to late-1990s. The described methods make use of various paramagnetic thermosensitive liposomes, paramagnetic lanthanide complexes, and spin transition molecular materials.

Thermosensitive liposomes (TSL) were first introduced by Yatvin et al. in the late 1970s. They showed that locally a 100:1 increase in drug release could be achieved during hyperthermia conditions in-vitro by increasing the temperature from 37 to 44 °C [211]. TSL contains a phospholipid membrane which exhibits a distinct gel-to-liquid crystalline phase transition temperature, T_m. Below T_m the liposomes do not allow water exchange through the membrane. At the phase transition temperature, the phospholipid membrane exhibits a phase-change from a gel phase to a liquid crystalline phase, which results in greatly increased transmembrane permeability. For MRTI, TSLs with entrapped paramagnetic molecules, such as manganese- (Mn) or gadolinium (Gd)- based compounds, are usually used. Below T_m the paramagnetic agents do not affect the tissue relaxation times due to the low water exchange rate through the membrane. When the tissue temperature rises above T_m the tissue water relaxation is affected both by the release of the entrapped paramagnetic materials across the membrane and due to increased water exchange (similar to magnetization transfer effects described above). The effect on T₁ relaxation by the paramagnetic TSL depends on concentration and intrinsic relaxivity of the entrapped paramagnetic agent, composition of the membrane, size of the liposome (where smaller liposomes can cause shorter T₁ due to the greater ratio of surface area to volume which increases the water flux across the liposomal membrane [212]), if the paramagnetic molecules are located in the lipid membrane or in the aqueous space, and the binding probability [213,214]. Increased T₁ relaxivities have been shown by membrane surface modifications using polyethyleneglycol (PEG) [215,216]. Trubetskoy et al. showed an approximately twice as high T₁ relaxivity of PEG-modified Gd-labelled liposomes [215]. One major limitation of TSL is that they do not allow continuous temperature measurement, but rather just an absolute measurement at the specific T_m. T_m can be adjusted by altering the length and amount of saturation of the hydrocarbon chain, where increasing the length results in increased transition temperature due to the increase of Van der Waal’s forces. Gd-based paramagnetic TSL have been demonstrated both in-vitro and in-vivo. Fossheim et al. utilized liposomally-entrapped Gd-HP-DO3A and demonstrated significantly increased T₁ relaxivity at T_m values of 41 and 50 °C [217]. In gel phantoms it was further shown that inducing a heating from 22 to 65 °C resulted in a 1.4–3.0-fold increase in T₁ relaxivity after the temperature exceeded the T_m, which was ~42 °C. McDannold et al. further investigated Gd-based TSL in-vivo in rabbit liver and kidney [218]. The TSL had a T_m of 57 °C to monitor focused ultrasound induced ablations. In liver tissue signal intensity increases were seen in all sonication locations (except in necrotic and poorly perfused tumor centers) and agreed well with 57 °C isotherms. In kidneys the enhanced zones were smaller than expected and surrounded by hypo-intense signal – this was explained by wash out of the contrast agent due to the persisting blood flow in the kidney. TSL encapsulating free manganese ions (Mn²⁺), in addition to doxorubicin (DOX), with a T_m of 39.5–40.0 °C have also been investigated and show promising results [219,220]. In general, further (in-vivo) studies investigating dose, pharmacokinetics and toxicity are needed before TSL can be used clinically.

Various paramagnetic lanthanide complexes have been shown to experience a considerably higher temperature sensitivity than protons imaged in the standard phase-mapping PRF technique discussed above [221]. The chemical shifts observed in the paramagnetic lanthanide complexes exhibit strong temperature dependence because of large hyperfine paramagnetic interactions [222], and the chemical shift has been shown to be up to 300 times larger than for protons in H₂O. These approaches are of particular interest for applications where small temperature changes are measured, such as in hyperthermia or when monitoring heating induced by the MRI RF coils [223], where high accuracy and resolution are needed. In general, the ideal lanthanide complex should have a highly temperature sensitive chemical shift, rather short T₁ relaxation so that it can be imaged efficiently, chemically inert in-vivo, and capable of providing absolute temperature measurements.

Some early studies used MR spectroscopy together with Pr-MOE-DO3A, exploiting the temperature sensitivity influence of Pr of the ¹H spectrum [224,225]. A temperature sensitivity of approximately 0.12–0.13 ppm/°C was found. Other early studies investigated the thulium-based complex TmDOTP⁵⁻ which was shown to have a chemical shift of 0.89 ppm/°C for ¹H and 2.18 ppm/°C for ³¹P (corresponding to frequency shifts of ~57 Hz/°C for both at 1.5 T, compared to ~0.7 Hz/°C for the ¹H in water used in standard PRF), and be stable over a temperature range of 4 to 50 °C [222,226]. It was further shown that in-vivo toxicity was low and that high enough concentrations can be safely used [227–229], and that short T₁ values due to dipolar interactions between ¹H and ³¹P enabled relatively fast scans. The main drawback of TmDOTP⁵⁻ is that it was shown to produces a slight drop in blood pressure in animal studies, making it ill-suited for in-vivo human studies [229,230]. It was further shown that the chemical shift depended strongly on pH [231] and Ca²⁺ [222,226]. Despite these challenges in-vivo results in rat brains have been shown [231].

To resolve the problems with drop in blood pressure, and the pH and Ca²⁺ sensitivity of TmDOTP^5–, alternative lanthanide complexes have been investigated. To take advantage of the large temperature sensitivity of Tm³⁺, and proven safety of the commonly used MRI contrast GdDOTA^‒ (which itself is unsuitable for MRTI since Gd³⁺ is a very efficient relaxation agent and signals from its complexes are hence challenging to image), TmDOTA⁻ has been investigated [232,233]. Because of its similarity in molecular structure to GdDOTA⁻, TmDOTA⁻ is believed to have a similar toxicity. The temperature sensitivity of TmDOTA⁻ has been shown to be approximately 100 times that of water protons. The chemical shifts of its protons are hundreds of ppm away from that of water protons, and it is insensitive to pH and Ca²⁺. However, all the proton signals show very short T₂ values, which is challenging because it broadens the linewidth and reduces the accuracy in measuring chemical shifts. Pulse sequences with short TE values are also needed to sample the signal. In animal studies doses of approximately 1–2 mmoL/kg have normally been used [233].

To achieve narrower line widths Hekmatyar et al. investigated Pr³⁺, Yb³⁺, Tb³⁺, Dy³⁺, and Tm³⁺ complexes of DOTMA⁴⁻ (i.e., the methyl-substituted analogue of DOTA⁴⁻) since it has 12 magnetically equivalent methyl protons, which provide an intense and sharper resonance compared to corresponding DOTA⁻ complexes [234]. The narrower linewidth also results in longer T₂ values, so it is easier to image, and a four-fold increase in SNR compared to DOTA⁴⁻ was observed [234]. It was found that TmDOTMA⁻, which is ~60 times more sensitive to temperature than the water ¹H shift and is insensitive to changes in pH and Ca²⁺, was the most favorable option. The chemical shifts are approximately 100 ppm away from the water signal, so selective imaging free of water signal can be relatively easily achieved with frequency selective RF pulses. TmDOTMA⁻ has also been shown to be insensitive to complex concentration and to a large extent to inhomogeneities in the main magnetic field [234,235]. Absolute MRTI using TmDOTMA⁻ has been demonstrated in-vivo in rats and in a mouse tumor model [234–236]. Spatial resolution up to 1 mm isotropic was achieved in a 3 min scan time, with temperature precision of approximately 0.1–0.3 °C [235,236], as shown in Fig. 16.

Fig. 16.

In-vivo thermometry in rat using TmDORMA^‒. Representative coronal slices from 3D ¹H MRI of water (a). Heart and liver labeled H and L, respectively. Methyl signal from TmDOTMA⁻ (b) and temperature change maps computed from the phase shift in TmDOTMA⁻ images as the rectal temperature changed from 35.7 to 36.4 (c), 37.1 (d), 37.6 (e) and 38.1 (f) °C. The TmDOTMA⁻ dose was 0.61 mmol/kg body weight and the total imaging time was ~3 min. From ‘‘Non-invasive temperature imaging with thulium 1,4,7, 10-tetraazacyclododecane-1,4,7,10-tetramethyl-1,4,7, 10-tetraacetic acid (TmDOTMA-)’’ Sait Kubilay Pakin, S. K. Hekmatyar, Paige Hopewell, Andriy Babsky and Navin Bansal. NMR Biomed. 2006;19:116–124. Fig. 4. Reprinted with permission.

Overall, MRTI methods based on hyperfine-shifted MR signals from paramagnetic lanthanide complexes appear promising and have been shown in-vivo for animal experiments. Further studies relating to toxicity, acceptable dose and signal-to-noise ratio are necessary before human clinical use.

Instead of directly measure the signal from the paramagnetic lanthanide complex, the change in water signal intensity as a results of chemical exchange saturation transfer (CEST) can be measured. Since paramagnetic agents are used the method is often referred to as PARACEST. Due to the large chemical shift between water and the complex used, the signal from the complex can easily be saturated by frequency selected RF pulses. Because the exchange rate between the saturated complex and the water is directly proportional to temperature via the Arrhenius-equation, $k=e^{-E_a/R_{g}T}$ where k is the rate coefficient, E_a is the activation energy, R_g is the universal gas constant, and T is the temperature, the temperature can be determined if the agent concentration is known. However, this is not usually the case for in-vivo applications, and CEST-based methods have not gained much popularity. Zhang et al. described a method acquiring a series of images with different frequency-selective saturation pulses covering the resonance frequency of the complex, and using the frequency offset which caused the lowest signal to determine the temperature change [237]. This removes the constraint on knowing the concentration of the complex, but it is rather slow (on the order of minutes).

Spin transition molecular materials are based on a direct temperature-sensitive transition from a diamagnetic spin S = 0 state to a paramagnetic S = 2 state, where the transition temperature is determined by the chemical composition of the molecular complex. These methods have so far only been demonstrated in-vitro [238]. For further in-vivo use, non-toxicity needs to be evaluated and the transition temperature has to be adjustable and evaluated for individual applications.

2.9. Intermolecular multiple quantum coherences

As discussed in the PRF section above, MRTI in fat-based tissues is challenging because of the very small chemical shift dependence of fat protons (0.00018 ppm/°C [59]) as well as the relatively large susceptibility change with temperature (0.0094 ppm/°C [76,77]) which can affect the resonance frequency of the nearby water spins. To address these challenges MRTI based on intermolecular multiple quantum coherence (iMQC) was developed [239–241]. iMQC is a lesser known type of MR signal which arises from the simultaneous transition of two spins on separate molecules. The two most commonly used types of iMQC are intermolecular zero quantum coherences (iZQCs) and intermolecular double quantum coherences (iDQCs), which both can be utilized for MRTI. In iZQC two or more spins are simultaneously flipped in opposite directions, whereas in iDQC two spins are flipped in the same direction. The resonance frequency of concern in iZQC is the difference in the resonance frequency between the spins, which in the case of MRTI is a fat spin and a water spin. The two spins are separated by a tunable distance, often called the ‘‘correlation distance”, which is on the order of 10–100 µm. The iZQC peaks are therefore narrow because contributions from magnetic susceptibility and field inhomogeneities act on a scale which is at least an order of magnitude smaller than the typical MRI voxel size.

While the iMQC method of MRTI can seem similar to the PRF methods, it should be noted that rather than looking at changes in the absolute resonance frequency, the iMQC method relies on changes in the difference between the chemical shift of a water spin and a nearby fat spin, as stated above. This is what makes the method insensitive to the effects of magnetic field inhomogeneities, susceptibility gradients and magnetic field drift. The method is further less sensitive to physiological motion than, e.g., the phase-mapping PRF method because the resonance frequency difference is more likely to remain constant as the two spins are in close proximity and move together. By looking at changes in the difference between the chemical shift of a water spin and a nearby fat spin, the iMQC method can also produces absolute temperature maps.

The pulse sequence commonly used for iMQC MRTI is named HOT, and is based on the previously described HOMOGENIZED sequence [242]. It uses a combination of iZQCs and iDQCs, and suppresses unwanted coherence pathways from unwanted temperature-insensitive same-spin iMQCs and inter-molecular single quantum coherences (iSQCs). The HOT sequence acquires two separate echoes where the phase difference gives the absolute measure of temperature.

Challenges with the iMQC methods involve the need for both water and fat to be present in close proximity, something that is not always the case in-vivo. The signal from the HOT sequence scales as the product of the water and fat magnetization, so it is highest when there are comparable amounts of both species within the correlation distance. For anatomies with compartmentalized fat and water the iMQC method will only be able to detect temperature in the interfaces between the compartments, which greatly diminishes its usefulness. The SNR of iMQC pulse sequences in general, and also the HOT sequence, is further only about 10% of the SNR observed in standard imaging sequences. However, a multi-spin echo spatial encoding scheme has been presented which partly alleviates this constraint, improving the SNR by up to a factor of three [243]. The HOT sequence also includes more RF pulses (to selectively only preserve the iZQC and iDQC used for the MRTI) than other iMQC pulse sequences, making it sensitive to flip angle errors and pulse imperfections, which in turn can further reduce the signal intensity. Since the frequency measured by the HOT pulse sequence is the difference between the water and fat resonances, and fat is made up of many different resonance frequencies, the detected HOT signal will be a (weighted) average of the difference in resonance frequency between the water and the different fat components. This will potentially result in different frequency shifts between different tissues, since they can have different fat compositions.

Despite these challenges promising ex-vivo results in porcine red bone marrow [243,244] and in-vivo results in an obese mouse model have been shown [239]. Accurate absolute temperature maps were achieved over rather small FOV (3–4 cm) with a scan time on the order of minutes. While the low spatial and temporal resolution currently limits the usefulness of iMQC MRTI for ablative therapies, its resiliency to magnetic susceptibility, field drift and inhomogeneities, and ability to measure absolute temperatures makes it an intriguing approach for hyperthermia therapies.

2.10. Combined methods

Various combination methods where multiple temperature sensitive MR parameters are measured simultaneously or inter-leaved have been described. Most commonly has been to combine PRF with T₁ measurements, but combinations of PRF with diffusion, T₂(*), and SI has also been described.

Das et al. were among the first to present a combination method, combining PRF and ADC imaging [245]. The PRF images provide high spatial resolution and low-noise characteristics, whereas the water ADC images provide phase-drift correction. The method was demonstrated in tissue mimicking gel where PRF and ADC imaging were interleaved with a combined scan time of approximately 33 s (9 s for PRF and 24 s for ADC). The relatively long scan time makes the approach most interesting for slower heating such as in hyperthermia applications.

Multiple recent studies have combined PRF and T₁ measurements. Bos et al. simultaneously measured PRF and T₁ using a segmented Look-Locker EPI-sequence, where the relaxivity values were obtained from the magnitude image and PRF measurements were derived from the phase information from all signal samples [246]. The method was demonstrated in RF-heating of a phantom with thermosensitive liposomes containing a paramagnetic contrast agent. An increase of liposome permeability close to the phase transition temperature was demonstrated by the relaxivity measurements at the same time as the temperature change was measured using PRF. An interleaved approach to PRF-T₁ measurements where an Inversion Recovery Look-Locker sequence for T₁ measurements was interleaved with standard GRE PRF measurements was recently demonstrated in-vivo in a rat model during HIFU-induced hyperthermia by Kneepkens et al. [247]. T₁ maps (single slice, used to determine doxorubicin concentration which was co-encapsulated with a paramagnetic MR contrast agent inside TSL), were achieved every 2 min and PRF measurements (two orthogonal slices) were achieved every 8.6 s. Multiple studies have also combined the VFA method for fast, dynamic T₁ mapping with regular PRF to simultaneously monitor temperature in adipose (using T₁) and aqueous (using PRF) tissues [66,78,152,153, 163,168]. The method has been demonstrated using both single- and multi-echo GRE (where the multiple echoes are combined for improved temperature measurement precision) [153,168] and EPI approaches for faster or volumetric 3D measurements [66,152]. An example using DFA GRE for simultaneous temperature mapping in a pork-breast fat sample during HIFU heating is shown in Fig. 17. In ex-vivo tissues Hey et al. reported temperature accuracies of 2.5 °C for T₁-based thermometry in fat and 1.2 °C for PRF in muscle with scan times of 4.6 and 1.2 s for fat and muscle, respectively [152]. In-vivo, Todd et al. reported PRF temperature precision of 1.0 °C (with 1.3 × 1.3 × 3.5 mm spatial resolution and 1.9 s temporal resolution), and T₁ measurements with 2.5– 4.8% precision (with 3.8 × 3.8 × 3.5 mm resolution and 3.8 s temporal resolution) [168]. Challenges with combined PRF-T₁ measurements include the validity of the assumed signal equation when using short TRs or if the acquisition is not adequately spoiled, non-uniform flip angle over the sample due to B₁ inhomogeneities, and the fact that the VFA approach assumes that T₁, ${\text{T}}_2^{\ast }$, and M₀ remains constant over the measurement [153,248]. The effect of these various sources of error was investigated in detail by Todd et al. [153].

Fig. 17.

Simultaneous MRTI during HIFU heating in a pork and breast fat sample. (a) and (b) Three-point Dixon images showing the water and fat contents of the pork and breast tissue samples. (c) PRF temperature map showing temperature changes in the pork muscle but not in the breast fat, as expected. (d) Combined PRF/T₁ temperature map overlaid on the magnitude image where the calculated T₁ change has been converted to temperature using 1.4%/°C. From Hybrid proton resonance frequency/T1 technique for simultaneous temperature monitoring in adipose and aqueous tissues. Todd N, Diakite M, Payne A, Parker DL. Magn Reson Med. 2013 Jan;69(1):62–70. Fig. 6. Reprinted with permission.

Recent studies have also demonstrated that PRF can be measured either simultaneously with ${\text{T}}_2^{\ast }$ or interleaved with T₂ measurements. Svedin et al. presented a GRE multi-echo radial stack-of-stars approach where each individual echo gives a PRF measurement, and the ${\text{T}}_2^{\ast }$ decay curve can be fitted from the multiple echoes [36]. Keupp et al. used the same interleaving-framework as Kneepkens et al. [247] to achieve GRE-based PRF measurements and dual spin-echo-based T₂ measurements, for simultaneous thermometry in muscle and fat [249]. Finally, Ramsey et al. have presented an approach where PRF is used to measure temperature change in soft tissue simultaneously with SI-based thermometry in cortical bone from ex-vivo beef shanks, using a dual-echo GRE pulse sequence [185]. The first echo with TE of 1.04 ms was used to detect SI-changes in the bone, whereas the second echo with a longer TE of 6–15 ms was used for better PRF precision in soft tissue.

3. Discussion and conclusions

MR thermometry is in general mature and widely available, and is one of the factors contributing to the wider availability of many thermal therapies. The most used MR thermometry method is the PRF method thanks to its excellent linearity with tissue temperature, high sensitivity, relative tissue type independence, and because it can be performed with simple and very widely available spoiled GRE pulse sequences. Fast imaging approaches, such as EPI and parallel imaging, and dedicated reconstruction approaches, such as referenceless and multi-baseline methods, have alleviated many of the issues with motion. Challenges still remain in terms of providing real time availability of the measurements when more advanced acquisition (such as non-Cartesian) and reconstruction (such as compressed sensing and model-based approaches) are used. Another challenge with the PRF method is its insensitivity to temperature changes in adipose tissues, and the related susceptibility changes that occur when adipose tissues change temperature. For environments with lower B₀-field homogeneity, such as around invasive devices, spin echo pulse sequences might be better suited. In these cases, T₁-, T₂-, or diffusion-based MRTI can offer viable and attractive approaches. If strong gradients are available diffusion-based approaches can offer high sensitivity, but if tissue motion is a concern T₁- or T₂-based methods are likely better options. The various contrast agent-based approaches which have been investigated are interesting if absolute temperatures are needed, but often just provide an indication for when a specific pre-determined temperature is reached. An alternative for absolute temperature measurements is spectroscopic approaches, but due to generally low spatial and temporal resolution these methods are likely best suited for slow and diffuse heating such as commonly seen in hyperthermia. It should be noted that absolute temperature measurements are potentially a very powerful diagnostic tool to, for example, detect increased temperatures associated with increased tissue metabolism. Finally, unresolved general challenges with MRTI includes fast and reliable measurements in adipose tissues, although promising results using T₁- and T₂-based methods have recently been presented. The susceptibility effects related to temperature change in adipose tissue affecting measurement accuracy in aqueous tissues pose an additional challenge for treatments in, for example, the breast and abdominal regions. Reliable measurements in moving organs, such as liver, kidney and the heart, are still challenging, especially when volumetric information is desirable. In general, real time reconstruction of large volumetric measurements, for example, covering the full head in transcranial FUS applications, is not currently available.

Glossary

ADC

Apparent diffusion coefficient

BOLD

Blood oxygenation level dependent

CEST

Chemical exchange saturation transfer

CSF

Cerebrospinal fluid

DOX

Doxorubicin

DTI

Diffusion tensor imaging

DWI

Diffusion weighted image

EPI

Echo planar imaging

EPSI

Echo planar spectroscopic imaging

FOV

Field of view

GRE

Gradient recalled echo

HIFU

High intensity focused ultrasound

IDEAL

Iterative decomposition of water and fat with echo asymmetry and least-squares estimation

iDQC

Intermolecular double quantum coherences

iMQC

Intermolecular multiple quantum coherence

iZQC

Intermolecular zero quantum coherences

LSEPSI

Line scan echo planar spectroscopic imaging

MASTER

Multiple adjacent slice thermometry with excitation refocusing

MR

Magnetic resonance

MRI

Magnetic resonance imaging

MRSI

Magnetic resonance spectroscopic imaging

MRTI

Magnetic resonance temperature imaging

PD

Proton density

PEG

Polyethyleneglycol

PRF

Proton resonance frequency

RF

Radiofrequency

ROI

Region of interest

SE

Spin echo

SI

Signal intensity

SMS

Simultaneous multi-slice

SNR

Signal to noise ratio

SSFP

Steady state free precession

TE

Echo time

TR

Repetition time

TSL

Thermosensitive liposomes

VFA

Variable flip-angle