Sampling and Sampling Frames in Big Data Epidemiology

Abstract

Purpose of Review:

The ‘big data’ revolution affords the opportunity to reuse administrative datasets for public health research. While such datasets offer dramatically increased statistical power compared with conventional primary data collection, typically at much lower cost, their use also raises substantial inferential challenges. In particular, it can be difficult to make population inferences because the sampling frames for many administrative datasets are undefined. We reviewed options for accounting for sampling in big data epidemiology.

Recent Findings:

We identified three common strategies for accounting for sampling when the data available were not collected from a deliberately constructed sample: 1) explicitly reconstruct the sampling frame, 2) test the potential impacts of sampling using sensitivity analyses, and 3) limit inference to sample.

Summary:

Inference from big data can be challenging because the impacts of sampling are unclear. Attention to sampling frames can minimize risks of bias.

Introduction

As technological developments have rendered collection, storage, and sharing of vast quantities of data trivial, a social and cultural push toward re-using open (i.e. freely shared) ‘Big Data’ [1–5] for social good, including for epidemiologic studies, has emerged. However, many of these big datasets were crowd-sourced (i.e. volunteers donated their own data) or compiled for administrative rather than research purposes (e.g. the primary purpose of electronic health records is to record what clinical and billing staff need to deliver effective patient care, not to perform population-based research). Thus, survey methodologies were typically not used to define the population from which the data arose. Moreover, crowd-sourced and administrative datasets can be quite large, minimizing random error in parameter estimates. This combination raises concerns greater than those previously articulated in reference to secondary analysis alone (e.g. in [6]), because highly precise but biased estimates can easily be over-interpreted.

In this paper, we review the potential role of sampling in inference from big data in order to provide a framework for deciding whether it is necessary to account for sampling, and if so, how. First, we review the principles that underlie the link between sampling and statistical inference on populations. Next, we consider how re-using data collected for non-research purposes inverts the paradigm under which inferential principles were developed. Third, we suggest several options for working with big secondary datasets and illustrate them in several case studies. Finally, we make suggestions for future directions for research and practice.

The Importance of Sampling for Population Inference

Epidemiologic data analysis is typically performed only after outcomes have occurred in some study participants. Therefore, these estimates are typically useful only to the extent that we believe they represent the effect we would see in people for whom the outcome has not yet occurred, either in the remainder of the present population or another population. That is, consequence in research depends on generalizability of results [7], which typically must be treated as an assumption in observational data analysis [8] – that is, researchers cannot simply take generalizability for granted.

Consider a policymaker interpreting results from the Moving to Opportunity study, a randomized trial of residents of a federally subsidized housing project in which some families received vouchers to pay for housing in other locations, some families received these vouchers and counseling about moving, and some received nothing. Results indicated that girls whose parents had received vouchers and counseling had improved mental health in adolescence as compared to girls whose parents had not received vouchers and counseling [9]. Policymakers considering whether to implement a housing voucher program might wonder whether these results would apply in populations other than the precise population that was randomized: would other disadvantaged girls benefit from housing vouchers and counseling? Would disadvantaged boys benefit? Would effects be different in rural areas? What about outside the United States? Answering these questions requires understanding the characteristics of the population that the estimate represents. How were families chosen to participate in Moving to Opportunity? Were they like other families in ways that make us believe the intervention would work in other families as well? The theory of survey sampling helps link a study population to the target population it aims to represent.

Sampling Frames

In an idealized survey, researchers interested in estimating the prevalence of some condition in a population would first formally define the population of interest, e.g. adults living in New York City at the start of 2018. Next, the research team would enumerate that population, typically leveraging contact information, e.g. a list of phone numbers for a phone survey or a list of home addresses for a door-to-door survey. That population enumeration (ideally a full census of the population of interest, but typically a subset) is called the sampling frame because it frames the sample selection process. Next, the study team selects subjects (ideally randomly) from the sampling frame. If selection from the sampling frame (and willingness to participate after contact) is truly random, then the observed prevalence of the condition in the sample estimates the true prevalence of the condition in the population of the sampling frame [10].

In real-world surveys, of course, non-random inability to contact subjects and non-random subject refusals typically preclude such simple interpretation. Formal enumeration of the sampling frame allows the study team to assess differences (according to variables available in the sampling frame) between subjects who were included in the sample and subjects who could not be contacted or who refused to participate. Under the assumption that differences enumerable from the sampling frame account for differences in participation, the study team can use weighting or other techniques to estimate the prevalence of a condition or a causal effect in the sampling frame [11].

For example, suppose we are studying the cross-sectional association between cycling over 15 minutes per day and self-reported life satisfaction, and suppose further that this association is stronger in adults. The population data might then look as shown in Table 1.

Table 1.

Underlying cross-tabulation of cycling, age, and life satisfaction in a hypothetical population

Population	Satisfied	Not Satisfied	Total
Children who cycle	5,000	5,000	10,000
Adults who cycle	7,500	2,500	10,000
Total for cyclists	12,500	7,500	20,000
Children who don’t cycle	2,500	7,500	10,000
Adults who don’t cycle	2,500	7,500	10,000
Total for non-cyclists	5,000	15,000	20,000
Population Total	17,500	22,500	40,000

Risk Difference = 12,500/20,000–5,000/20,000 = 0.375

Now suppose researchers were able to contact a random 1% of children and a random 10% of adults from this population and were able to assess their life satisfaction accurately. The observed data from such a study might look as shown in Table 2

Table 2.

Data regarding cycling, age, and life satisfaction observed in a sample of a random 1% of children and random 10% of adults from the population shown in Table 1.

Population	Satisfied	Not Satisfied	Total
Children who cycle	50	50	100
Adults who cycle	750	250	1000
Total for cyclists	800	300	1100
Children who don’t cycle	25	75	100
Adults who don’t cycle	250	750	1000
Total for non-cyclists	300	800	1100
Total	1100	1100	2200

Risk Difference = 800/1100 – 300/1100 = 0.454

If the researchers proceed without accounting for the sampling frame, then, they would estimate the risk difference calculated below Table 2, which is 21% higher than the true population risk difference calculated below Table 1.

However, if the researchers have access to the number of children and adults in the population (i.e. the sampling frame) and a reason to believe inclusion in the study was random conditional on age category, they can invert the probabilities of being included in the sample such that each observed child represents 100 children in the population whereas each observed adult represents only 10 adults in the population. Multiplying the estimates in the cells of Table 2 by these sampling fractions results in reconstructing the data in Table 1, so the sample-weighted risk difference the researchers would calculate is an unbiased estimate of the population risk difference.

Secondary Data and Sampling Frames

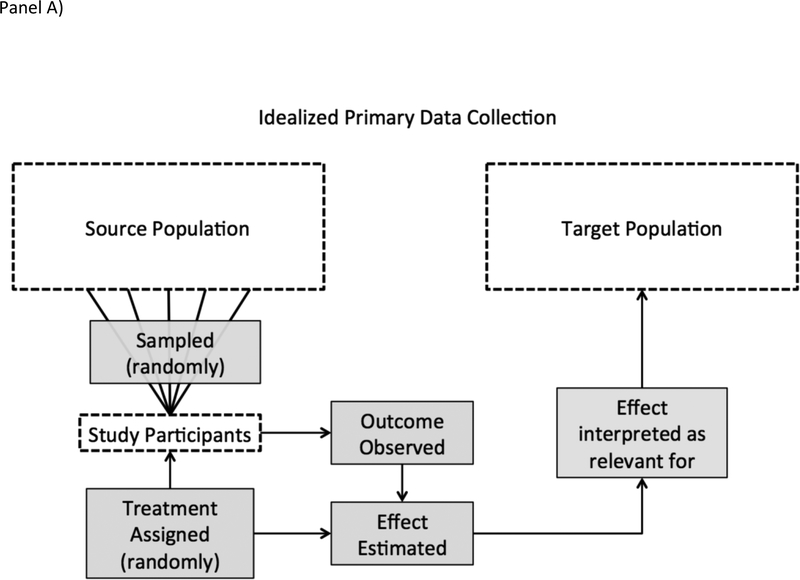
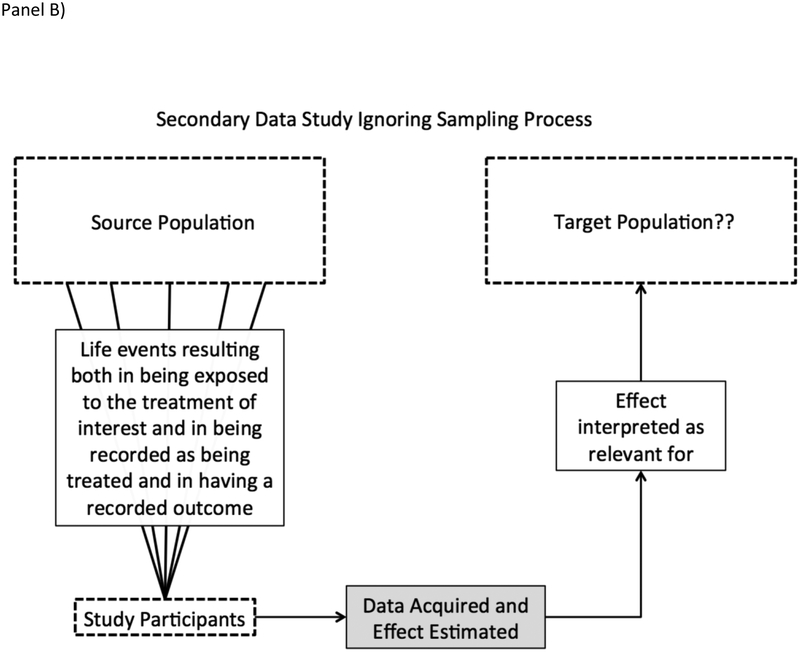
In analysis of big secondary data, however, a study team leverages data that someone else – often an algorithm or administrative process such as a hospital billing system – has collected. Secondary data use turns the selection process on its head: whether a subject was in the dataset was not under researcher control, and therefore, a research team would typically need to reconstruct a sampling frame to identify the population from which study results were taken [12]. Figure 1 depicts the differences between an idealized study and how analysis of secondary administrative data is often performed in practice.

Figure 1.

Panel A shows the process of inference, including sampling, in an idealized study design. Shaded rectangles indicate the processes under researcher control. If the study participants are a simple random sample of the source population, treatment is assigned randomly, and the target population is the source population, the effect observed in the study participants estimates the effect that would have been observed had treatment been assigned to the target population.

Panel B shows the de facto process of inference in a typical ‘Big Data’ study. In such a study, researchers are only involved after treatment and outcome have both occurred and been observed. As a result, even if treatment were plausibly considered quasi-random and all treatments and outcomes were measured without error, it can be unclear which populations the estimated effect may be relevant for.

Note that secondary data analysis does not necessarily imply lack of population-based sampling. For example, secondary use of the National Health and Nutrition Examination Survey (NHANES) can (and often should!) leverage the sampling frame and sampling weights defined by the study team. However, the administrative datasets used in big data analyses typically do not include a deliberate sample.

Best Practices for Big Data Epidemiology

Given that understanding the sampling process is a necessary component of population inference, what can researchers who endeavor to use big data to make consequential epidemiologic inference do? We have three specific recommendations:

Recommendation 1: Reconstruct a Sampling Frame explicitly and correct for sampling

In some cases, the process by which the population is selected into the dataset of interest can itself be studied quantitatively. This information may be available in existing validation studies or may require an internal validation study on the part of the investigators. For example, Hargittai investigated social network service use reported by a nationally representative sample of United States adults to determine that demographics strongly predict participation in various social network services [13]. Using these data, an investigator could construct and use Horvitz-Thompson-style sampling weights [11,14] to compute results using social-network-service data that would generalize to a general US adult population. The key intuition around this process, commonly called inverse-probability-of-observation weighting (raking in the statistical literature [15]), is that each observation is weighted such that the observation accounts not only for itself but also for those like it (i.e. with the same demographic values, in this example) in the target population who were not selected in to the dataset.

Etiologic analyses using sampling weights to estimate population effects require two key assumptions: 1) that demographics fully explained differences between those who participated in a given social network and those who did not (i.e. the sampled population is exchangeable with its target conditional on these demographics [16]) and 2) after accounting for demographics, participating in a social network was not associated with both the exposure and the outcome of interest [17]. Because these are strong assumptions, researchers will need to consider carefully whether the threats to inference due to correcting for sampling using inaccurate sampling weights may be greater than the threats due to sampling bias. Indeed, in some cases quantitative analysis using population weights may be more appropriate for sensitivity analyses than for main results [18].

Recommendation 2: Reconstruct a Sampling Frame conceptually for sensitivity analysis

Unfortunately, in many administrative datasets, it may be impossible to fully reconstruct a sampling frame. The sampling assumptions may be too strong, or joint distributions of sampling-relevant covariates may be unavailable, or the association between covariates and selection into the dataset may be unknown. Many big data sources, particularly personal-monitoring data or effluent data sources (Table 3), are made available to researchers only after being anonymized or aggregated such that each observation carries limited information along with it. In such cases, researchers may still consider what the selection factors might be in order to create a conceptual sampling frame, even if one cannot be constructed quantitatively. For example, a researcher using Google Search data to assess whether opinion polls underestimate the prevalence of racial animus (e.g. [19]) does not have access to the demographics of each search user to construct a formal sampling frame, but can use what is known about Internet usage to estimate what differences there might be between the population using Google Search and the general population. Researchers might use such logic in conjunction with targeted bias analyses to determine how extreme selection bias would need to be to draw qualitatively incorrect inference to the population [20,21].

Table 3.

Taxonomy of big public health data, with reference to how sampling challenges might affect inference from these datasets

Form	Example	Sampling Challenges
-omic/biological	Whole exome sequencing	What populations do biological samples represent?
Geospatial	Neighborhood profile	What places do sampled places represent?
Electronic Health Records	Records of all patients visits with trauma billing codes	Are people within the health system systematically different from the target population?
Personal monitoring	Fitbit readings	What populations do the people contributing personal data represent? Do times for which minute-by-minute data are available represent times when data are unavailable?
Effluent data	Google search results	Which real-world populations actions are represented by actions logged on web servers?

Recommendation 3: Acknowledge data limitations for population inference

Finally, some data are generated from processes that preclude identifying a sampling frame, even conceptually. While this precludes inference to a specific population, it does not preclude results being a component of a broader etiologic inference. There is an ongoing debate in epidemiology about the relative merits of a formal focus on conditions necessary to estimate valid causal effects as compared with a focus on integration of evidence from multiple sources [22–26]. Without wading into that debate, we observe that most commentators agree that ultimately, decision-making should draw on multiple sources of evidence [23]. In accordance with this view, big data for which a sampling frame cannot be reconstructed might most appropriately be used to test and generate hypotheses where no specific population-based effect estimate is of interest (e.g. in a ‘causal identification’ scenario wherein establishing that any non-null effect of an exposure exists in any population is an interesting outcome [25].).

Three Case Studies

Which recommendation a researcher should take depends on the data at hand, but the types of datasets considered to be big data vary widely. Table 3 provides a brief taxonomy of types of big public health data (adapted from [27]), and we further illustrate how researchers may interpret study findings in light of sampling in three case studies below.

Case Study 1: Group Practice Medical Data

First, consider a study using electronic health records (EHR) of children and adolescents to determine how built environments affect children’s BMI trajectory as they age [28]. This study’s investigators selected records from a large database of physician group practice in Eastern Massachusetts, requiring participants to have a) an address in Massachusetts, b) at least two BMI measures between January 2008 and August 2012, and c) no known medical conditions that would affect BMI.

While this contact in this study was triggered by clinic visits rather than investigators, a sometimes vexing problem in EHR studies [29, 30], it may still be possible to make population inferences from this dataset. We can view participants as a non-random sample of children aged between 4 and 19 in 2008 in Eastern Massachusetts, and so inferring to that population requires reversing the sampling process. Given that American Community Survey includes a good estimate of the population of children in Eastern Massachusetts on factors that may be available in the study data (e.g. race, ZIP code, potentially parental employment), computing population weights should be possible.

Case Study 2: Crowdsourced Data

Next, consider an effort to understand the distribution and determinants of foodborne illness using crowdsourced data from restaurant review platforms, such as Yelp® (e.g. available at: https://www.yelp.com/dataset/; accessed 9/20/18). Government health departments have begun to use crowdsourced data, including Yelp, to identify previously unreported cases of foodborne illness [31–33]. As foodborne illness is under-reported [34], using crowdsourced information holds promise for improving the coverage of existing surveillance systems. However, Henly and colleagues found that higher county-level affluence, such as higher median income and fraction of the population with a bachelor’s degree, was associated with greater use of the online review platform.[35]

Without considering these socioeconomic correlates, a study relying on Yelp data may erroneously find that incidence of foodborne illness is higher in wealthier counties, despite evidence that lower-SES communities may have a higher burden of foodborne illness. [36] To address this bias, researchers might conduct a validation study in which individuals with a foodborne illness are identified and asked whether they reported information about their case in an online-review site. The proportion responding yes, analogous to a sampling fraction, could be stratified by socioeconomic characteristics and could then be used to weight estimates from Yelp accordingly.

Case Study 3: Civic Administration Data

Finally, consider an ‘effluent data’ study that used archived traffic camera imagery in order to assess the impact of adding cycling infrastructure to a street in Washington, DC on prevalence of cycling on that street [38].

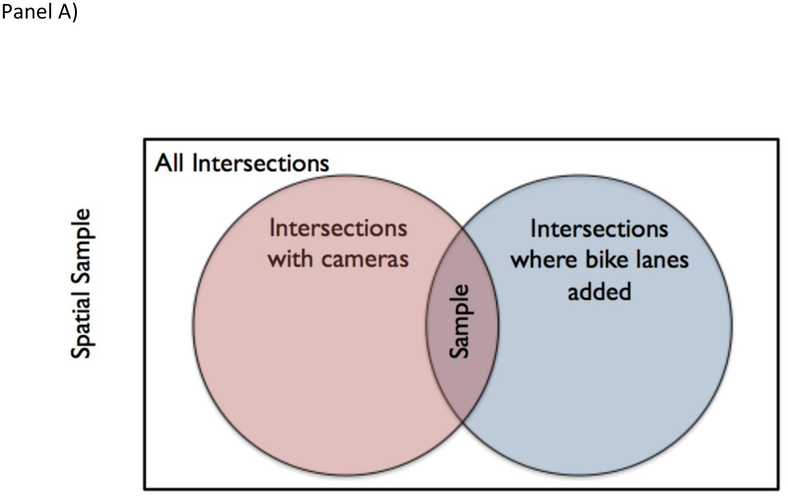
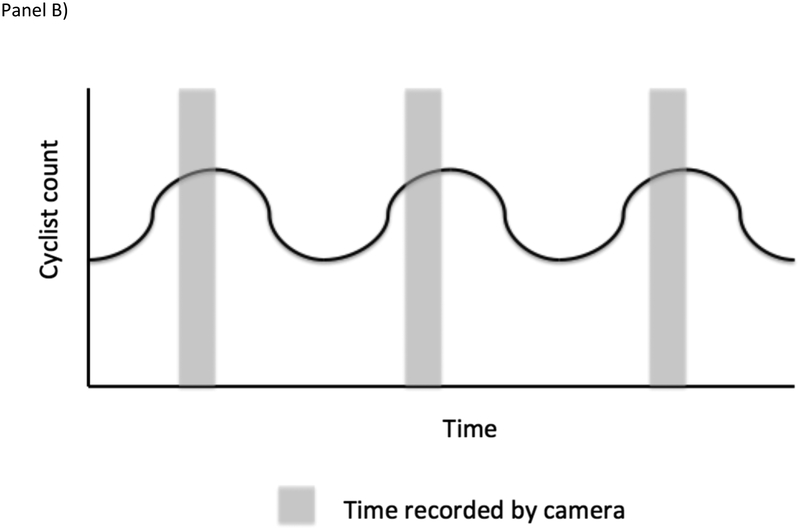
The selection process leading to data collection was, briefly: First, from all locations in Washington, DC, the department of transportation selected a subset to add traffic cameras to. That selection was likely driven by a number of factors, not all of which may be available to the study team, including traffic network delay, alternate route availability, access to a location for a camera, and so on. Second, from all traffic cameras available in the world, this one was added to the Archive of Many Outdoor Scenes, a dataset with millions of images gathered from publicly available outdoor webcams [39]. This was not random in the true stochastic sense, but it is unlikely selection was related to exposure or outcome. Third, from all streets in Washington, DC, the department of transportation chose this one to add a bike lane, a process likely related to available street space, local politics, and several of the same factors as resulted in the selection of this intersection to receive a traffic camera. Fourth, from all images recorded by this camera, AMOS chose every 30 minutes to archive. Figure 2 illustrates these sampling steps schematically.

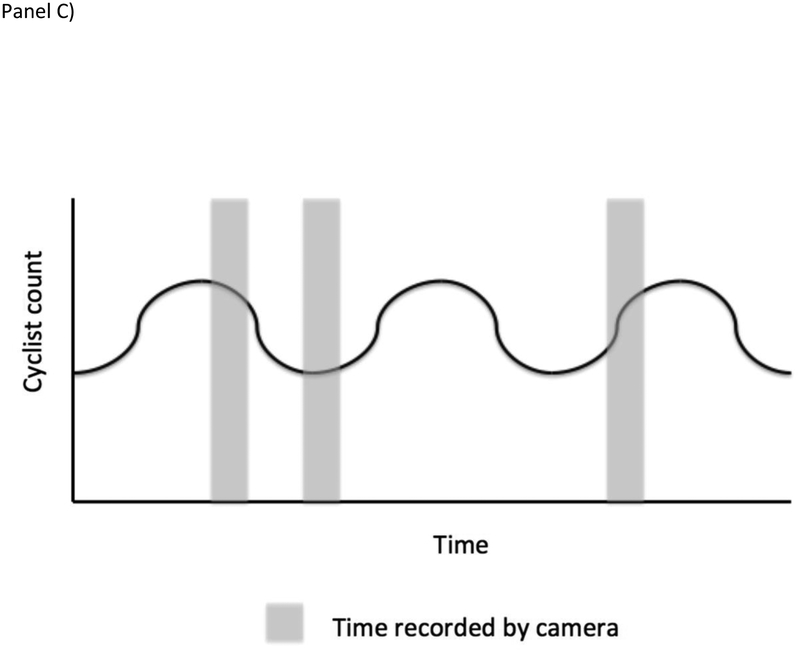
Figure 2.

Spatial and temporal sampling issues that can arise in administrative data (as in Case Study #3). Panel A is a Venn Diagram displaying conceptually how intersections were selected to be included in data collection. As discussed in the main text, treating the target population as only intersections where bike lanes were added is both conceptually appropriate and minimizes the need to account for a sampling process that cannot easily be reverse engineered. Panels B and C illustrates the potential impacts of temporal sampling in one location with a periodic change in cyclist counts. In Panel B, time sampling is systematic and synchronized with the period change in cyclist count resulting in an overestimate of the count of cyclists over time. In Panel C, sampling is random, avoiding the systematic over-count.

Unfortunately, though the sampling process can be described, it cannot easily be reversed into a sampling frame that treats whether a given intersection was observed as random conditional on observed factors – the factors that might lead to selecting a given street for improvement are not readily available for the source population of streets. However, by defining the target population as subject to the same criteria as the source population, we can simplify generalizability. In particular, stakeholder interest will typically focus on other roads where transportation departments might improve cycling infrastructure, so accounting the selection process by which these roads are selected for improvements or cameras may be unnecessary.

However, the temporal selection problem is somewhat more problematic. Because camera images were taken at 30 minute intervals, there may be systematic error if what is shown in the image every 30 minutes is different from what we would see if we were able to look at all images. For example, if the traffic light cycle takes 2 minutes to complete, then every image shown will be at the same phase in the light cycle (i.e. if it aligns with a red light for bicycles, we may see them queuing, whereas if it aligns with a green light, we may see only an empty queue). This potential artifact is a systematic sampling bias and can be acknowledged but not repaired. In such a scenario, modifying future data collection (e.g. so some the image recording interval is not fixed) could allow researchers to assess the risk of systematic bias due to the systematic time sampling.

Further Considerations for Transportability of Effects

A final consideration regarding the role of sampling in big data epidemiology is that constructing a causal effect estimate for the study population is only a part of the problem. Researcher intent is typically focused on identifying an effect that could inform future decisions or interventions targeting different populations [7]. While the formal requirements for transporting a causal effect estimate are out of scope here, we observe that estimating transported effects requires impacts of covariates that modify the causal effect and the prevalence of such variables in the target population [16,40]. In general, then, it will be easier to assess transportability using the big datasets that include enough covariates to assess potential sampling artifacts (e.g. full Electronic Health Record databases) and more challenging with more restricted datasets, including most effluent data or stripped-down public use datasets.

Conclusion

Big Data holds substantial potential for epidemiology, including low data acquisition costs and ample statistical power to avoid Type II error [29]. Big data also holds many well-understood and frequently articulated threats, including difficulties identifying and accounting for systematic error and challenges properly integrating development of theory into analysis [3]. The risk of incorrect inference due to failure to account for sampling should be added to the list of potential threats to Big Data epidemiology. When reconstructing a sampling frame is possible, researchers may minimize this threat by explicitly selecting a target population and, where feasible, weighting study results accordingly. When no sampling frame can be identified, results should be treated with appropriate caution.