Soluble klotho regulates TRPC6 calcium signaling via lipid rafts, independent of the FGFR-FGF23 pathway

Abstract

Soluble klotho (sKlotho), the shed ectodomain of α-klotho, protects the heart by down-regulating transient receptor potential canonical isoform 6 (TRPC6)–mediated calcium signaling. Binding to α2-3-sialyllactose moiety of gangliosides in lipid rafts and inhibition of raft-dependent signaling underlies the mechanism. A recent 3-Å X-ray structure of sKlotho in complex with fibroblast growth factor receptor (FGFR) and fibroblast growth factor 23 (FGF23) indicates that its β6α6 loop might block access to the proposed binding site for α2-3-sialyllactose. It was concluded that sKlotho only functions in complex with FGFR and FGF23 and that sKlotho’s pleiotropic effects all depend on FGF23. Here, we report that sKlotho can inhibit TRPC6 channels expressed in cells lacking endogenous FGFRs. Structural modeling and molecular docking show that a repositioned β6α6 loop allows sKlotho to bind α2-3-sialyllactose. Molecular dynamic simulations further show the α2-3-sialyllactose–bound sKlotho complex to be stable. Domains mimicking sKlotho’s sialic acid–recognizing activity inhibit TRPC6. The results strongly support the hypothesis that sKlotho can exert effects independent of FGF23 and FGFR.—Wright, J. D., An, S.-W., Xie, J., Lim, C., Huang, C.-L. Soluble klotho regulates TRPC6 calcium signaling via lipid rafts, independent of the FGFR-FGF23 pathway.

α-Klotho is a type-1 membrane protein with a large ectodomain. Its loss of function in mice results in phenotypes resembling premature human aging (1). Membrane-bound α-klotho (mKlotho) is a coreceptor with fibroblast growth factor receptor (FGFR) for the ligand fibroblast growth factor 23 (FGF23) (2). Binding of FGF23 to the mKlotho and FGFR coreceptor is important for vitamin D biosynthesis as well as calcium and phosphate homeostasis (3). The ectodomain of mKlotho is shed extracellularly [soluble klotho (sKlotho)] and functions as an endocrine or autocrine-paracrine hormone. sKlotho exerts pleiotropic effects acting in multiple tissues (4). Among these, sKlotho inhibits insulin and IGF-stimulated PI3K signaling (5). We had shown that sKlotho protects against stress-induced cardiac injury by down-regulating transient receptor potential canonical isoform 6 (TRPC6) calcium signaling in the heart (6, 7) and identified its target, viz., α2-3-sialyllactose moiety of gangliosides in lipid rafts (8). sKlotho consists of 2 homologous domains, KL1 and KL2, at residues 57–506 (αKL1) and residues 515–953 (αKL2), respectively. Using homology modeling and molecular docking, we had elucidated residues within αKL1 domain for α2-3-sialyllactose recognition and confirmed the predictions by mutagenesis and functional studies (9). These studies reveal that binding to α2-3-sialyllactose of gangliosides in lipid rafts and inhibition of growth factor–stimulated PI3K-dependent TRPC6 channel exocytosis underlies the mechanism of cardioprotection by sKlotho.

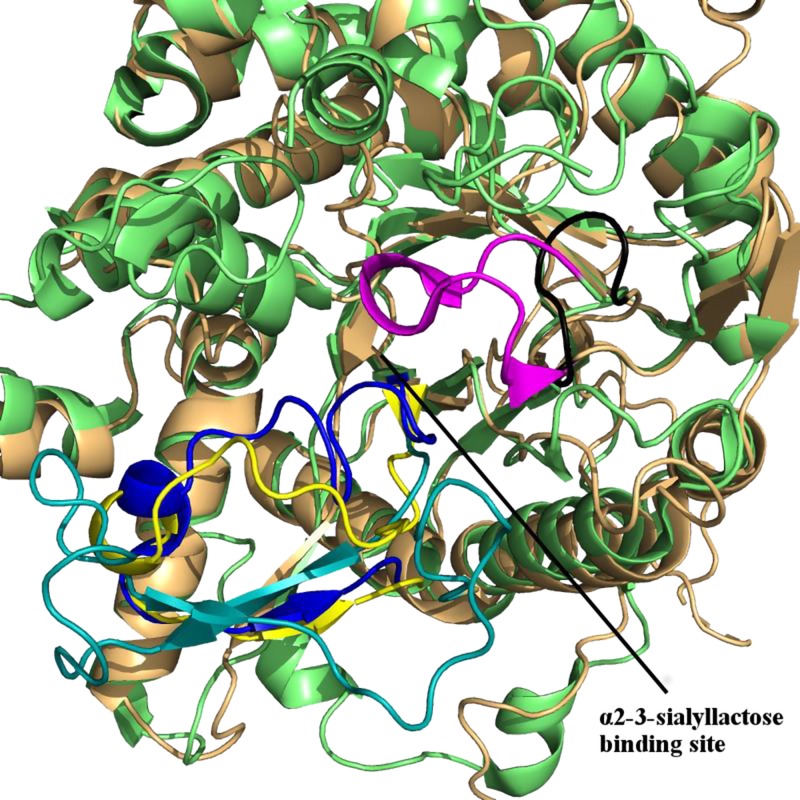
Recently, Chen et al. (10) published a 3.0 Å crystal structure [Protein Data Bank (PDB) 5w21] of αKL1 and αKL2 in complex with the ectodomain of FGFR1 isoform c (FGFR1c) and FGF23. The αKL1 and αKL2 domain each adopts a triosephosphate isomerase barrel fold, comprising a central core formed by β-strands stabilized by α-helices on the surface. α2-3-Sialyllactose is predicted to bind in this central core (9), in accord with its binding in β-strand cores seen in crystal structures of α2-3-sialyllactose–bound proteins such as hemagglutinin-neuraminidase (PDB entries 5b2d, 1z4x) (11, 12) and Trypanosoma cruzi trans-sialidase (PDB 1s0i) (13). Our αKL1 homology model structure shows high structural similarity with the respective X-ray structure (PDB 5w21), as evidenced by a root-mean-square deviation (RMSD) over the 1784 comparable backbone atoms of only ∼0.6 Å. However, it shows the αKL1 β6α6 loop (residues 370−393) in an open conformation, allowing α2-3-sialyllactose to enter the proposed binding site, whereas the crystal structure shows the same loop in an occluded conformation, blocking access to the binding pocket.

Partly on the basis of the occluded β6α6 loop conformation, Chen et al. (10) concluded that sKlotho cannot bind ligands and that sKlotho only functions in complexes with FGFR and FGF23. This conclusion disagrees with functional studies showing that sKlotho elicits multiple actions independent of FGFR and FGF23 (5, 6, 14–17). Furthermore, different ligands with different net charges could induce different loop conformations, as seen in crystal structures of the same protein bound to different ligands. Whereas α2-3-sialyllactose has a net charge of −1, FGF23 is neutral, but the FGF23 residues (Glu182, Asp184, Ser185, Pro189, and Leu190) within 5 Å of the αKL1 β6α6 loop have a net charge of −3. Here, we address the critical questions of whether sKlotho can exert actions independent of FGFR and FGF23 and whether the β6α6 loop could relocate to a nonoccluding position that would allow α2-3-sialyllactose to bind to αKL1.

MATERIALS AND METHODS

Electrophysiological recordings of TRPC6 currents

TRPC6 currents were recorded from human embryonic kidney 293 (HEK293) cells or L6 cells expressing recombinant TRPC6 with or without sKlotho proteins as previously described (6, 7). Cells expressing TRPC6 were treated with or without sKlotho or recombinant carbohydrate-binding module (CBM) (at indicated concentration) in serum-containing medium overnight. Bacterial fusion protein of CBM containing aa 121–305 of Streptococcus pneumoniae neuraminidase A (NanA) sialidase was prepared and purified as previously described (18). Currents were recorded by voltage-clamp in ruptured whole-cell mode with an Axopatch 200B patch-clamp amplifier and Pulse software (Molecular Devices, Sunnyvale, CA, USA). Cells were held at 0 mV membrane potential and stimulated with repetitive ascending ramp pulse from −100 mV to +100 mV for 400 ms every 10 s. The pipette and bath solution for recording HEK293 cells contained (in mM) 140 CsCl, 1 MgCl₂ 1.5 CaCl₂, 2 ATP-Mg, 5 EGTA, 10 HEPES (pH 7.2 with CsOH) and 140 NaCl, 0.5 EGTA, 10 HEPES, 10 glucose, 10 mannitol (pH 7.4 with NaOH), respectively. The resistance of electrodes containing pipette solution was 1.5–3 MΩ. TRPC6 currents were activated by bath application of oleoyl-acetyl-glycerol (OAG; 100 μM), low pass filtered, at 2 kHz and sampled every 0.1 ms (10 kHz). At the end of experiments, the bath solution was replaced by a solution containing nonpermeant cation N-methyl-d-glucamine to assess TRPC6-mediated inward currents. Data acquisition and analysis were performed using the pClamp v.9.2 program (Molecular Devices) and Prism v.3.0 software (GraphPad Software, La Jolla, CA, USA). Results shown are repeated at least 3 times with similar results.

Preparation of the α2-3-sialyllactose ligand and αKL1 and αKL2 receptors for docking

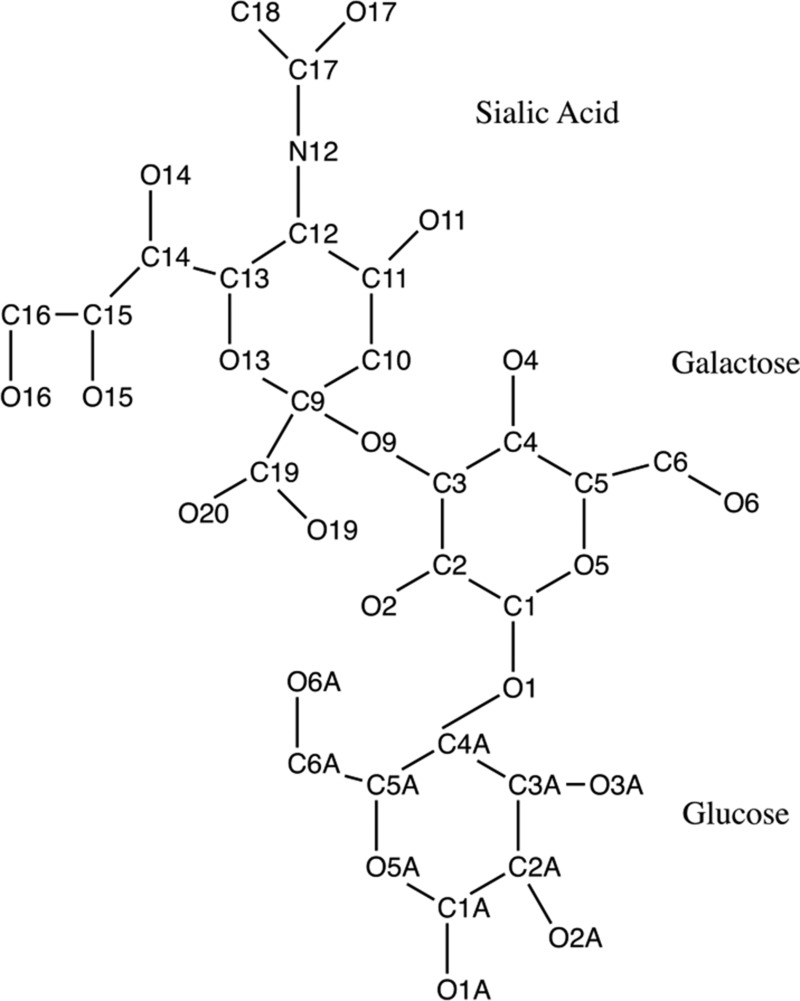
The α2-3-sialyllactose was taken from the 1.60 Å structure of T. cruzi trans-sialidase (PDB 1s0i) (13), and hydrogen atoms were added using the Chimera program (12, 13, 18–21). Its geometry was then optimized at the RHF/6-31G* level using Gaussian09 (22), and the charges were derived at the MP2/6-31+G* level using the Natural Bond Orbital v.5.9 program (23). The numbering scheme for the α2-3-sialyllactose is given in Fig. 1.

Figure 1.

Schematic diagram of α2-3-sialyllactose showing PDB numbering.

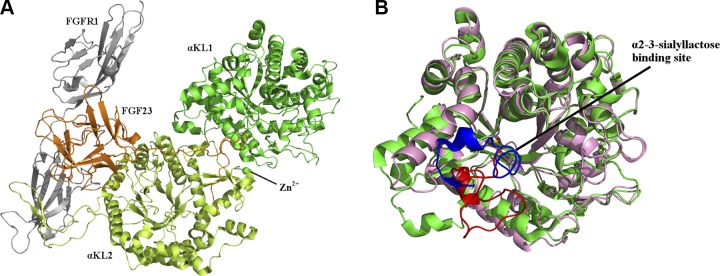
The αKL1 and αKL2 domains were taken from the 3.0 Å crystal structure of the sKlotho-FGF23-FGFR1c ternary complex (PDB 5w21) (Fig. 2A) , and the missing residues between positions 98–115 and 957–960 were modeled using the Modeler program (24–26). The 2 domains were then separated and treated as 2 independent receptors for docking because each is a separate domain. For the αKL1, 20 new models of the β6α6 loop (residues 370−393) was produced as follows: The first 3 loop residues, ³⁷⁰CFG³⁷², were realigned to follow the analogous loop from the klotho-related protein structure to direct the loop into a conformation away from the occluded position. The following 16 residues, ³⁷³PTLSFQLLDPHMKFRQ³⁸⁸, were de novo modeled using Modeler with the constraints that ³⁸³HMK³⁸⁵ retained an α-helix seen in the X-ray structure (PDB 5w21), whereas the remaining loop residues, ³⁸⁹LESPN³⁹³, retained the crystal structure because they formed an antiparallel β-sheet with other non–β6α6-loop residues. Each of the new structures was ranked by the Modeler score, and the lowest-energy one was checked to determine if the proposed binding site was available. During this process, the His467 sidechain was found to impinge on the proposed binding site. Testing different rotamers of His467 using PyMOL (Schrodinger, New York, NY, USA) showed that the His rotamer in the 5w21 crystal structure was the fifth most common (27), whereas the 3 most common rotamers would have steric clashes with Leu253. However, the fourth most common His rotamer (28) would have no clashes, making the binding site available; hence it was chosen to replace the His467 sidechain in the 5w21 crystal structure.

Figure 2.

The sKlotho, FGF23, FGFR1 complex showing the blocking of the proposed α2-3-sialyllactose–binding site. A) 3.0-Å crystal structure (PDB 5w21) of αKL1 (light green) and αKL2 (lemon) bound to Zn²⁺ (green sphere) in complex with FGF23 (orange) and the FGFR1c ectodomain (gray). B) Superposition of the αKL1 backbones in the homology model structure (9) (pink) and in the 5w21 X-ray structure (light green) showing similar overall structure. The αKL1 β6α6 loop from the 5w21 X-ray structure (blue) blocks the proposed α2-3-sialyllactose–binding site, whereas that from the previous homology model (red) is in an open conformation.

The αKL1 and αKL2 receptors were prepared using the Dock Prep module (29) of Chimera (19) and the Amber FF14SB force field (30). Spheres representing potential atoms that could bind into cavities on the αKL1 and αKL2 were mapped onto the protein surface using the Sphgen from the Dock 6 suite of programs (31–34). Grid-based electrostatic and van der Waals (vdW) potentials were then calculated for a box containing the chosen sphere cluster with an additional 12 Å in each direction using the grid program (35, 36).

Docking protocol

The α2-3-sialyllactose was docked, as a flexible ligand, into the αKL1 or αKL2 binding site (described as spheres) using the anchor-and-grow methodology in the Dock 6 program. For each configuration, an anchor of 5 atoms from one of the ligand rings was aligned with 5 spheres to locate the initial docked structure of that ring; then the rest of the ligand was grown out from this anchor. Electrostatic and vdW grid-based scoring was used to score the docked configuration with simplex energy minimization to optimize each configuration. The 500 best scoring conformations were clustered using a 2.0-Å RMSD cutoff over all atoms such that in a given cluster, the RMSD of the backbone atoms of any 2 structures differed by ≤1 Å.

Docking of α2-3-sialyllactose into the binding site of the αKL1 yielded 137,410 initial orientations; after energy minimization followed by clustering, 86 unique orientations remained. The resulting top scoring clusters were analyzed for hydrogen bonds and vdW contacts using the ViewDock module from Chimera (http://www.cgl.ucsf.edu/chimera/). A klotho residue was deemed to be in vdW contact with the α2-3-sialyllactose if one of the atoms was within 0.4 Å of the sum of the vdW radii of the residue and ligand atoms. Hydrogen bonds were defined by the reference values given in Mills and Dean, 1996 (37), but with the criteria relaxed by 0.4 Å and 20°.

Molecular dynamics simulations of klotho complexes

Starting structure

The 3.0 Å crystal structure of sKlotho-FGF23-FGFR1c ternary complex (PDB 5w21) was used to calibrate the simulation force field and protocol before applying it to assess the stability of the docked αKL1–α2-3-sialyllactose complex. Missing residues in the 5w21 crystal structure (at positions 98–115 and 957–960) were modeled using the Modeler program. All Asp and Glu residues were assumed to be deprotonated, and Lys and Arg residues were assumed to be protonated, whereas the His residues were protonated or deprotonated according to the Reduce program (38).

Simulation protocol

The complete sKlotho-FGF23-FGFR1c complex (including Zn²⁺) was used as the starting point for 4 simulations using the Chemistry at Harvard Macromolecular Mechanics (CHARMM) graphical user interface website (http://www.charmm-gui.org) with the CHARMM36 all-atom force field (39–43). The system was neutralized with potassium counterions with the constraints that each counterion was ≥6 Å from the protein surface. The resultant system was solvated in a truncated octahedron of TIP3P water molecules (44) and subjected to rounds of minimization with constraints on the protein heavy atoms to relieve any bad contacts in the solvated complex structure. vdW interactions were switched to zero between 10 and 12 Å, whereas electrostatic interactions were treated using the particle mesh Ewald summation method (45). The resulting solvated system consisting of 304,663 atoms was subjected to molecular dynamics (MD) at a mean temperature of 300 K using a 2-fs timestep, periodic boundary conditions, for 27 ns using NAMD v.2.12 (46). Coordinates from the final 10 ns were saved every 4 ps giving a total of 2500 coordinate sets. The RMSD of the backbone atoms over the entire complex, consisting of 5353 atoms, was found to plateau at around 3.5 Å, indicating that the MD simulations could maintain the structural integrity of the sKlotho-FGF23-FGFR1c X-ray structure (PDB 5w21). MD simulations of the αKL1 and αKL2 in complex with α2-3-sialyllactose using the CHARMM all-atom carbohydrate force field for α2-3-sialyllactose (47, 48) were performed in a similar way except that Cl^– and Na⁺ counterions were added to neutralize the αKL1 and αKL2 complexes, respectively.

Computing the binding free energy

The free energy of klotho (denoted by KL) binding to FGF23 or FGFR1c or α2-3-sialyllactose (denoted by X) in solution was calculated according to the thermodynamic cycle in Scheme 1:

In Scheme 1, the gas-phase binding free energy, ΔG_gas, was approximated as a sum of the changes in the vdW (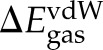) and electrostatic () energies upon binding, which were computed using the CHARMM program and force field with a dielectric constant of 1 and a nonbond cutoff of 999 Å. The gas-phase electrostatic interaction energy (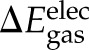) between klotho and ligand X was calculated for each of the 2500 conformations from a single MD simulation using a 14-Å cutoff and sorted into 25 evenly distributed 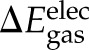clusters using CHARMM41. Within each cluster, the conformation whose gas-phase electrostatic interaction energy was closest to the mean of the cluster was chosen as the representative one. The solvation free energy, ΔG_solv, of each molecule was estimated as a sum of the nonelectrostatic (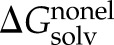) and electrostatic (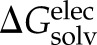) contributions, with 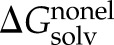∼ γ × solvent accessible surface area (SASA) [γ = 8 cal/mol/Ų (49, 50)] and 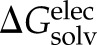estimated by finite-difference solution to the linearized Poisson-Boltzmann equation implemented by the Adaptive Poisson-Boltzmann Solver program (51–53). Thus, the binding free energy in aqueous solution, ΔG_sln, is given by

Because the different clusters contain different numbers of conformations, the ΔG_sln free energies derived from the 25 representative conformations were weighted according to the number of coordinate sets in each cluster to give a final weighted mean binding free energy for that individual simulation.

RESULTS

sKlotho regulates TRPC6 in the absence of FGFR and FGF23

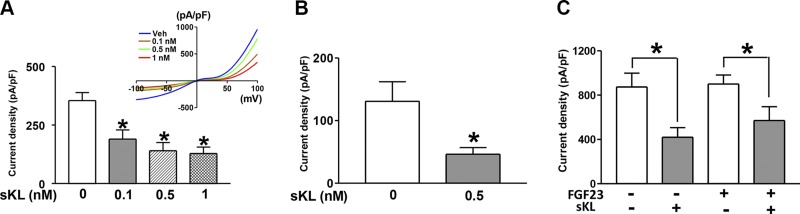
sKlotho down-regulates TRPC6-mediated calcium signaling by inhibiting PI3K-dependent exocytosis of channels (6). This effect is due to sKlotho binding to α2-3-sialyllactose of sialogangliosides in lipid rafts and inhibiting raft-dependent PI3K signaling cascades (8). To investigate whether sKlotho can elicit cellular actions without FGF23 and FGFR, we expressed recombinant TRPC6 channels in a myoblast cell line L6 lacking endogenous FGFRs (5) and examined the effects of sKlotho on TRPC6 channels. Diacylglycerol (DAG)-stimulated currents through TRPC6 channels were recorded by ruptured whole-cell patch-clamp recording. In TRPC6 channels expressed in HEK293 cells, sKlotho inhibited TRPC6-mediated currents (Fig. 3A). DAG-stimulated TRPC6 currents were authenticated by the characteristic current-voltage (I-V) relationship curves and their absence in mock-transfected cells (12 ± 5 pA/pF in mock vs. 357 ± 25 pA/pF TRPC6-expressing cells; P < 0.001). Without DAG, currents through TRPC6-transfected cells were not different from mock-transfected cells. Importantly, sKlotho also inhibited currents in TRPC6 expressed in L6 cells (Fig. 3B). The dose-response relationship for sKlotho regulation of TRPC6 in L6 cells is similar to that in HEK293 cells. We further examined the effect of FGF23 and its effects on sKlotho regulation of TRPC6. FGF23 had no effects on TRPC6 and did not affect regulation of TRPC6 by sKlotho (Fig. 3C). Thus, sKlotho regulates TRPC6-mediated calcium signaling independent of FGF23 and FGFR.

Figure 3.

sKlotho inhibits TRPC6 currents independent of FGFR and FGF23. A, B) sKlotho inhibits DAG-activated TRPC6 expressed in HEK cells (A) and in L6 cell line lacking endogenous FGFRs (B). Inset is I-V relationship curves for DAG-stimulated currents. OAG (a membrane-permeant analog of DAG, 100 μM) was used to activate TRPC6. Bar graph shows means ± sem of maximal DAG-stimulated inward TRPC6 current density (∆ current ± DAG in picoamperes at −100 mV divided by cell capacitance in picofarads). C) FGF23 has no effect on TRPC6, nor does it affect sKlotho regulation of TRPC6. FGF23 (400 pM) and sKlotho (100 pM) were used. sKL, sKlotho; n = 7–10 each group. *P < 0.05 vs. control (first bar from left, no sKL).

Relatively small movement of the αKL1 β6α6 loop can accommodate α2-3-sialyllactose

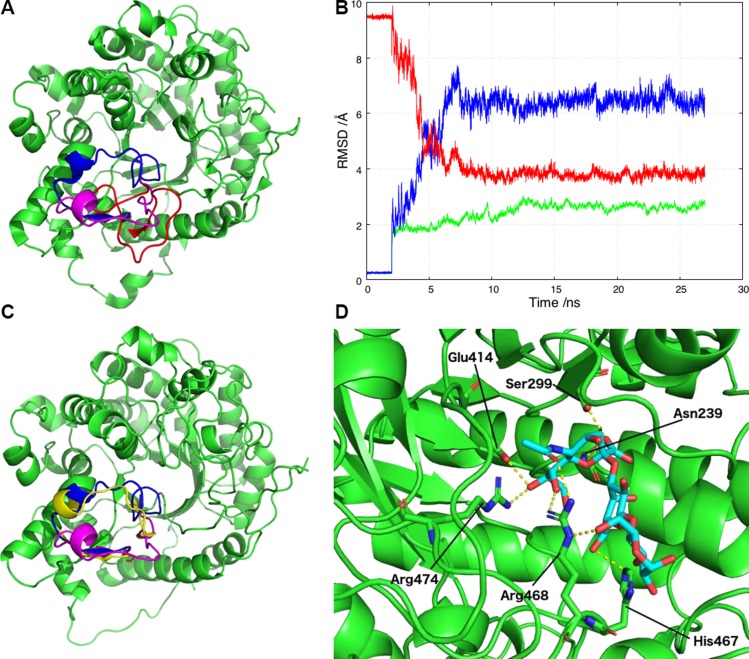
In the X-ray structure of sKlotho-FGFR1c-FGF23 ternary complex, the β6α6 loop in αKL1 adopted an occluded conformation (Fig. 2B). It is possible that in solution and in the absence of FGF23-FGFR, the β6α6 loop may move to a nonoccluding position that allows α2-3-sialyllactose to bind to αKL1. Assuming that the β6α6 loop is not totally rigid and locked in an occluded conformation, alternative possible conformations were modeled, as described in the Materials and Methods section, retaining the crystallographic coordinates from PDB 5w21 for the rest of the αKL1. This yielded a αKL1 structure with a nonoccluding β6α6 loop conformation, as depicted in Fig. 4A. α2-3-Sialyllactose was docked into the proposed binding site of this structure, and the top 5 scoring orientations were analyzed for hydrogen bonds and vdW contacts. The second-highest ranked docked orientation of α2-3-sialyllactose with αKL1 displayed the most potential hydrogen bonds between the ligand and receptor (5 from the sialic acid group and 1 from the glucose). To assess whether this docked αKL1–α2-3-sialyllactose complex is stable, it was subjected to 4 27-ns MD simulations in explicit water. The final 10 ns of each simulation were analyzed for the presence of hydrogen bonds, which were deemed to be stable if they were found in at least 2 of the simulations for more than 50% of the time.

Figure 4.

αKL1 binds to α2-3-sialyllactose and allows the open conformation of the β6α6 loop to relocate to one closer to the X-ray structure during the MD simulation. A) Three β6α6 loop configurations in αKL1: the X-ray configuration (blue), the revised conformation (magenta), and the previous homology model conformation (red). B) RMSD plot against the initial starting model for the αKL1 non-β6α6 loop backbone atoms (green) and the β6α6 loop backbone atoms (blue) during the simulations. Superimposed (red) is the RMSD of the β6α6 loop backbone atoms against the X-ray structure. C) During the simulations, the β6α6 loop changes conformation from the starting homology model open conformation used for docking (magenta) to the final conformation (yellow) that is closer to the X-ray conformation (blue). D) A snapshot from the simulations of αKL1 (light green) and α2-3-sialyllactose (cyan with O atoms in red) showing their potential hydrogen bonds. The sialic acid carboxylate group moves closer to the Asn239 and Ser299 sidechains to accept a hydrogen atom from each. The sialic acid hydroxyl group serves as a hydrogen bond donor to Glu414 and a hydrogen bond receptor from Arg474. Arg468 participates in multiple hydrogen bonds with the glucose and the sialic acid, whereas His467 forms a hydrogen bond with galactose O⁶.

The simulations show a stable αKL1–α2-3-sialyllactose complex: the RMSD of the αKL1 backbone atoms (excluding the β6α6 loop) from those in the starting structure was found to plateau at around 3.0 Å (Fig. 4B, green curve). On the other hand, the β6α6 loop backbone of the starting structure underwent larger movement than the rest of the αKL1 backbone, but it also attained a stable conformation after ∼10 ns (Fig. 4B, blue curve). During the simulation, the β6α6 loop backbone reoriented and adopted a conformation closer to the occluded conformation observed in the X-ray structure (PDB 5w21): the mean RMSD of the β6α6 loop backbone atoms decreased from 9.5 Å over the first 8 ns of MD simulation and plateaued at ∼4.0 Å (Fig. 4B, red curve). Figure 4C shows the 3 different β6α6 loop conformations in the X-ray structure (blue), in the starting structure before MD simulations (magenta), and after MD simulations (yellow). The movement of the αKL1 β6α6 loop needed to accommodate the binding of α2-3-sialyllactose is relatively small and can be restricted to N-terminal loop segment, ³⁷⁰CFGPTLSFQLL³⁸⁰. The α2-3-sialyllactose was stabilized by hydrogen bonding interactions with 6 residues, viz., Asn239, Ser299, Glu414, His467, Arg468, and Arg474, as shown in Fig. 4D. As shown in our previous work, single-point mutation of Ser299 and Arg468 to Ala each resulted in a significant loss of inhibition of TRPC6 channel function relative to the wild-type sKlotho (9).

α2-3-Sialyllactose binds preferentially to αKL1 rather than αKL2

In the X-ray structure, αKL2 adopts a fold similar to αKL1 (10), but unlike αKL1, its central core is wider and shallower and its β6α6 loop is in a nonoccluding conformation (Fig. 5). To see if the αKL2 domain can be a potential α2-3-sialyllactose–binding site, α2-3-sialyllactose was docked to αKL2 using the same protocol as employed in docking to αKL1. Among the 72,942 initial orientations of α2-3-sialyllactose bound to αKL2, 137 unique orientations remained after energy minimization and clustering. The top scoring 3 docked orientations were each subjected to four 27-ns simulations yielding a total of 12 27-ns simulations. From the final 10 ns of each trajectory, the αKL2–α2-3-sialyllactose interaction energy and hydrogen bonds were calculated and compared with those from αKL1–α2-3-sialyllactose simulations. As compared with αKL1, α2-3-sialyllactose interacts with αKL2 much less favorably by ∼10 kcal/mol and forms only 2 stable hydrogen bonds in the simulations, whereas it forms 8 hydrogen bonds on average in the αKL1–α2-3-sialyllactose simulations (Tables 1 and 2). The lower interaction energy and fewer stable hydrogen bonds indicate that α2-3-sialyllactose binds preferentially to αKL1 rather than αKL2. This could be related to differences in a 12-residue loop (⁴⁶³GFEWHRGYSIRR⁴⁷⁴) that forms the putative α2-3-sialyllactose–binding site, where the underlined αKL1 loop residues interact favorably with α2-3-sialyllactose in the docked structure. The equivalent loop in αKL2 comprises only 7 residues (⁹¹⁹DRTAPRF⁹²⁵) and adopts a conformation that is oriented away from the potential binding site; thus this loop does not participate in binding to α2-3-sialyllactose (Fig. 5). Therefore, α2-3-sialyllactose is more likely to bind the αKL1 than the αKL2. This conclusion is supported by our previous studies reporting that mutation of Glu465 and Arg468 of sKlotho disrupts the regulation of TRPC6 by sKlotho, indicating that αKL1 is essential for binding α2-3-sialyllactose (9).

Figure 5.

The crystal structure of sKlotho (PDB 5w21) shows that αKL2 (orange) provides a less favorable binding site for α2-3-sialyllactose than αKL1 (green). A 12-residue loop in αKL1 (residues 463–474, magenta) has multiple interactions with the bound α2-3-sialyllactose. The equivalent loop in αKL2 contains only 7 residues (residues 919–925, black) and is oriented away from the proposed binding site. Its orientation renders the central αKL2 core wider and less favorable for binding α2-3-sialyllactose. The αKL1 β6α6 loop (residues 370–393) from the X-ray structure is shown in blue, whereas its location from the MD simulations is in yellow and the equivalent β6α6 loop from αKL2 is in teal. Note that the β6α6 loop of αKL2 is in a nonoccluding conformation.

TABLE 1.

Interface residue binding energy contributions and hydrogen bonds observed between αKL1 and α2-3-sialyllactose during the simulations^a

Residue	ΔGbinding (kcal/mol)b	Hydrogen bond partner	Residue	ΔGbinding (kcal/mol)b	Hydrogen bond partner
Ser115	−0.3 ± 0.3		Glu414	0.7 ± 0.4	Sialic acid
Leu117	−0.4 ± 0.5		Gly416	−0.1 ± 0.1
Trp194	−1.0 ± 0.4		Trp417	−0.5 ± 0.4
Asn239	−0.8 ± 0.2	Sialic acid	Phe418	−1.2 ± 0.6
Tyr241	−0.6 ± 0.3		Trp458	−0.3 ± 0.3
Val242	−1.3 ± 0.5		Glu465	0.4 ± 0.3
His246	−1.4 ± 0.2		His467	−1.9 ± 1.1	Galactose
Leu253	−0.6 ± 0.4		Arg468	−2.9 ± 1.1	Glucose, sialic acid
Ser299	−0.1 ± 0.5	Sialic acid	Arg474	−1.6 ± 0.7	Sialic Acid
Gly372	−0.5 ± 0.3		Total	−18.1 ± 2.0
Pro373	−0.5 ± 0.2
Thr374	−0.2 ± 0.5		Glucose*	−7.3 ± 1.4*	Arg468*
Leu375	−0.7 ± 0.6		Galactose*	−3.7 ± 0.6*	His467*
Phe377	−1.4 ± 0.9		Sialic acid*	−13.9 ± 1.6	Asn239*, Ser299*, Glu414*, Arg468*, Arg474*
Leu379	−0.6 ± 0.8		Total*	−25.0 ± 2.8*

^aThe binding energy contribution of the interface residues between αKL1 and α2-3-sialyllactose; hydrogen bonds are reported if present in at least 2 simulations for ≥50% of the analyzed trajectory. The interface residues are defined as those that had a mean heavy-heavy atom distance of <5 Å in at least 3 of the 4 simulations.

^bThe binding free energy was decomposed in 2 ways. One is per amino acid residue, which gives rise to a total ΔG_binding = −18.1 ± 2.0 kcal/mol. The other (*) is per sugar unit, which gives rise to a total ΔG_binding = −25 ± 2.8 kcal/mol. Note that the 2 totals are not identical because the electrostatic salvation energies cannot be equally divided between the receptor and ligand and only the interface residues within 5 Å were included in the first calculation (some long-range electrostatic interactions were not included). Arg468 makes [³H] bonds with α2-3-sialyllactose (2 with sialic acid, 1 with glucose), and contributes to the largest single residue binding energy (−2.9 ± 1.1 kcal/mol). Mutation of this residue disrupts sKlotho regulation of TRPC6 (9).

TABLE 2.

Interface residue binding energy contributions and hydrogen bonds observed between αKL2 and α2-3-sialyllactose during the MD simulation for the top ranked docked configuration^a

Residue	ΔGbinding kcal/mol	Hydrogen bond partner	Residue	ΔGbinding kcal/mol	Hydrogen bond partner
Thr692	−0.2 ± 0.1		Tyr827	−3.4 ± 1.4
Arg693	−3.0 ± 1.4		Leu828	−0.7 ± 0.4
Asn694	−1.0 ± 0.4		Total	−12.4 ± 3.1
Tyr697	−0.1 ± 2.3	Galactose
Phe755	−0.5 ± 0.3		Glucose*	−4.5 ± 0.4*
Asn783	−0.5 ± 0.3		Galactose*	−6.4 ± 1.3*	Tyr697*, Asn825*
Leu785	−0.8 ± 0.2		Sialic acid*	−4.6 ± 2.4*
Tyr824	−0.4 ± 0.3		Total*	−15.5 ± 3.2*
Asn825	−1.8 ± 1.2	Galactose

^aSee footnote for Table 1.

α2-3-Sialyllactose cannot outcompete sKlotho binding to FGF23-FGFR1c

Because a relatively small movement of the αKL1 β6α6 loop could allow α2-3-sialyllactose access to the proposed binding site, can α2-3-sialyllactose displace the FGF23-FGFR1c complex from sKlotho? To answer this question, four 27-ns simulations of the sKlotho-FGF23-FGFR1c ternary complex were performed, and the final 10 ns of each trajectory was analyzed for the free energy contributions of each molecule most toward binding. Interestingly, although αKL2 binds weakly, if at all, to α2-3-sialyllactose, it is the sole contributor toward binding FGFR1c (ΔG_sln = −63.5 ± 1.8 kcal/mol) and makes the major contribution to the free energy for binding FGF23 (ΔG_sln = −70.5 ± 4.0 kcal/mol vs. −29.1 ± 3.3 kcal/mol with αKL1) (Table 3). There is very little interaction between the αKL1 β6α6 loop and the FGF23-FGFR1c complex energetically. However, even if the β6α6 loop of the αKL1 can relocate to a nonoccluding conformation, α2-3-sialyllactose would not be able to displace FGF23-FGFR1c from sKlotho: the free energy contribution of sKlotho toward binding the FGF23-FGFR1c complex is much greater than that toward binding α2-3-sialyllactose (ΔG_sln = −163.1 ± 3.0 kcal/mol vs. −24.5 ± 3.8 kcal/mol, Table 3).

TABLE 3.

Free energy of αKL1, αKL2, or both binding to targets^a

Receptor	Ligand	ΔGbinding (kcal/mol)
αKL1	FGF23	−29.1 ± 3.3
αKL1	FGFR1c	0 ± 0
αKL1	α2-3-sialyllactose	−24.5 ± 3.8
αKL2	FGF23	−70.5 ± 4.0
αKL2	FGFR1c	−63.5 ± 1.8
sKlotho (αKL1 + αKL2)	FGF23 + FGFR1c	−163.1 ± 3.0

^aFree energy of αKL2, αKL1, or both binding to FGF23, FGFR1c, both, or α2-3-sialyllactose calculated from the MD simulations, as described in the Materials and Methods section.

Domains with sialic acid–binding activity inhibit TRPC6 in the absence of FGFR

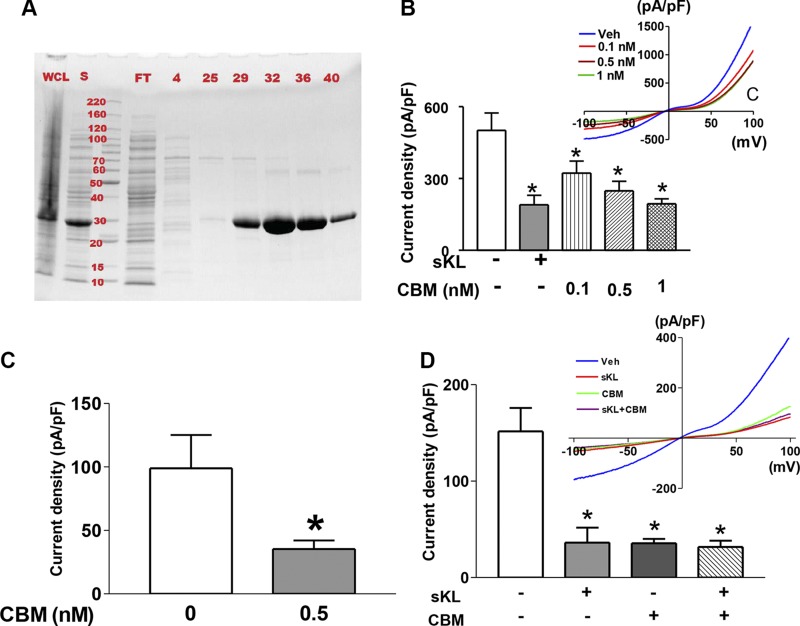
Some bacteria including S. pneumoniae produce sialidase targeting the sialic acid–containing lipids in host cell membrane. The binding affinity of the CBM of S. pneumoniae NanA sialidase to α2-3-sialyllactose has been well characterized (18). The CBM has no sequence homology with sKlotho. We employed the CBM as a tool to further test the hypothesis that α2-3-sialyllactose binding is the mechanism for sKlotho regulation of TRPC6 channels. We produced recombinant fusion protein containing CBM and examined the effects on regulation of TRPC6 channels. HEK293 and L6 cells expressing TRPC6 channels were incubated with CBM. TRPC6-mediated currents were measured by whole-cell patch-clamp recordings. As shown, incubation with CBM resulted in inhibition of TRPC6 channel currents expressed in HEK cells as well as in FGFR-null L6 cells (Fig. 6A–C). Th effects of sKlotho and CBM were not additive (Fig. 6D), indicating the same mechanism of action by sKlotho and CBM. The finding that CBM reproduces the effects of sKlotho in both HEK293 and L6 cells further supports FGFR-independent mechanism of action of sKlotho in the regulation of TRPC6 channels.

Figure 6.

Sialic acid–recognizing CBM can inhibit TRPC6 like sKlotho. A) Production and purification of CBM. His-tagged CBM was subcloned in pEHISTEVb vector, expressed in bacteria, and purified with a Ni–nitrilotriacetic acid column. Coomassie blue gel of proteins in whole-cell lysate (WCL), supernatant of lysate after centrifugation (S), flow-through of after loading on to the column (FT), and fractions 4, 25, 29, 32, 36, 40. MW markers are in kilodaltons. B) Incubation with CBM resulted in inhibition of TRPC6 channel currents expressed in HEK cells dose dependently. The effect of sKlotho (sKL; 1 nM) is shown for comparison. Bars are means ± sem of inward current density at −100 mV. Inset shows I-V relationship curves. Veh, vehicle. C) Incubation with CBM-inhibited TRPC6 in FGFR-null L6 cells. D) No additivity between sKL (1 nM) and CBM (1 nM) on TRPC6 currents in L6 cells. n = 7–10 each group. *P < 0.05 vs. control (first bar from left, no sKL, no CBM).

Sialic acid–binding and lipid rafts are important for inhibition of TRPC6 by CBM

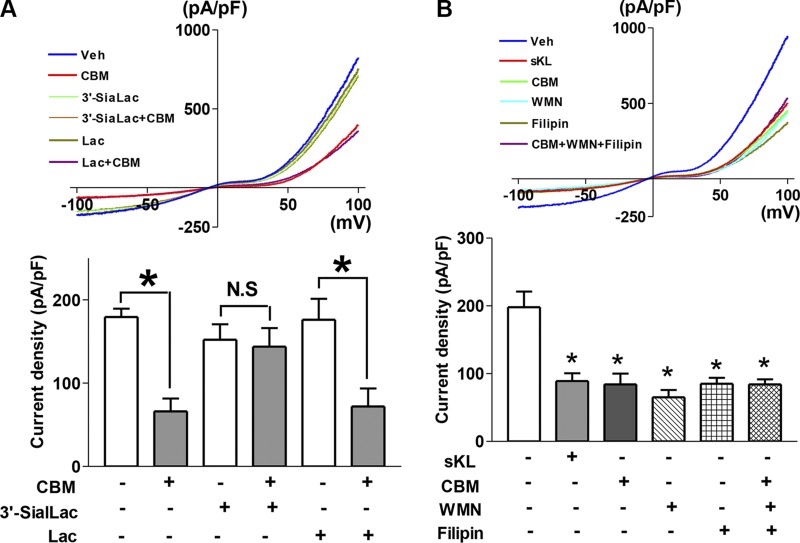
To further support the notion that the effect of CBM is mediated by its sialic acid–binding activity, we performed competition experiments preincubating CBM with α2-3-sialyllactose or control molecule lactose, which lacks the α2-3–linked sialic acid. In support of the notion, preincubation with α2-3-sialyllactose, but not with lactose, neutralized the ability of CBM to inhibit DAG-stimulated TRPC6 currents (Fig. 7A).

Figure 7.

Evidence for CBM regulating TRPC6 via binding sialic acid, involving lipid rafts. A) Preincubation with α2-3-sialyllactose (3′-SiaLac), but not with lactose (Lac), prevents inhibition of TRPC6 by CBM. 3′-SiaLac, Lac, and CBM were premixed with 100 μl of conditioned media and incubated for 1 h, then added into cells and incubated for 3 h. n = 6–8 each group. *P < 0.05 between indicated groups. Veh, vehicle; N.S., statistically not significant. B) No additivity of inhibitory effects among CBM, PI3K inhibitor WMN, and filipin (cholesterol sequester–lipid raft inhibitor). Where indicated, cells were treated with sKL, CBM, WMN, filipin, or a combination for ∼3 h prior to recording the current. *P < 0.01 vs. control (first bar from left); n = 9–12 each group.

We have shown that sKlotho inhibits TRPC6 currents by down-regulating lipid raft–dependent PI3K signaling cascade and DAG-stimulated, PI3K-dependent exocytosis of TRPC6 channels (8). This is due to sKlotho binding to α2-3-sialyllactose of sialogangliosides in lipid rafts. To further support that CBM inhibits TRPC6 by the same mechanism, we examined the effects of CBM in the presence or absence of perturbations of lipid rafts, PI3K signaling cascades, or both. We have previously shown that TRPC6 channel is activated by DAG via dual mechanisms—direct activation of channel gating and stimulation of channel exocytosis—and that sKlotho partially inhibits TRPC6 because it interferes with DAG-stimulated, PI3K-dependent TRPC6 channel exocytosis but does not affect direct channel activation by DAG (8). Cholesterol sequester filipin was used to disrupt lipid raft and wortmannin (WMN) to inhibit PI3K signaling cascade. We have previously demonstrated that the effects of sKlotho, WMN, and filipin on TRPC6 are nonadditive, supporting a lipid raft–dependent PI3K-mediated mechanism (8). Here, we found that sKlotho, CBM, filipin, and WMN each cause similar inhibition of TRPC6 and that the inhibition by CBM is not additive to the effects by filipin and WMN (Fig. 7B). The results provide compelling support for the notion that CBM acts via the same mechanism as sKlotho to regulate TRPC6.

DISCUSSION

mKlotho is thought to function as a coreceptor for circulating FGF23 such that the action of FGF23 is restricted to klotho-expressing cells. sKlotho, the shed ectodomain of α-klotho, is a circulating endocrine hormone that exerts pleiotropic effects in distant organs or acts locally as an autocrine-paracrine factor (4). The notion of FGFR- and FGF23-independent function of sKlotho, however, has recently been challenged (10). The main goal of the present study is to address this critical question. We have previously shown that sKlotho protects the heart against stress-induced injury by down-regulating TRPC6-mediated calcium signaling. Loss of cardioprotection by sKlotho is believed to contribute to cardiomyopathy in patients of chronic kidney disease (6, 7). Here, we show that sKlotho can inhibit TRPC6 channels in the absence of FGFR. In silico studies indicate that in the absence of FGF23 and FGFR1c, the αKL1 β6α6 loop can relocate slightly to allow α2-3-sialyllactose access to the αKL1 core. That binding to α2-3-sialyllactose is the underlying mechanism for regulation of TRPC6 by sKlotho is further supported by experimental evidence that sequence-unrelated sialic acid–recognizing domains reproduce the effect of sKlotho in the regulation of TRPC6. Altogether, our results provide compelling support for the hypothesis that sKlotho can function independently of FGFR and FGF23.

Activation of mKlotho and FGFR coreceptors by FGF23 plays a critical role in vitamin D and phosphate homeostasis, and its disturbances are pivotal in the pathogenesis of many diseases (3). The X-ray structure of the sKlotho in complex with FGFR and FGF23 provides deep insight into the molecular interactions of the ternary complex on the cell surface membrane. Furthermore, it provides invaluable information on how to design specific modulators of the complex. The potential significance of circulating sKlotho to substitute for mKlotho on the cell surface remains unclear. The physiologic circulating levels of sKlotho and FGF23 are ∼30 and ∼2 pM, respectively. The concentrations of sKlotho and FGF23 required for crystallization of sKlotho-FGFR1c-FGF23 are supraphysiological. The same caution applies to in vitro cell proliferation assays based on the ability of sKlotho to substitute for mKlotho to form ternary complexes with FGF23 and FGFR. A 300-fold higher sKlotho (10 nM) and 1000-fold higher FGF23 (2 nM) than their respective physiologic circulating levels were used in these assays (10). For comparison, the FGFR-independent regulation of TRPC6 by sKlotho occurs at physiologic concentrations (100 pM) (see Fig. 3). Thus, unless a mechanism or mechanisms exist to concentrate sKlotho locally (such as in cells expressing mKlotho), it is unlikely that physiologic circulating sKlotho can substitute for mKlotho in the formation of ternary complexes.

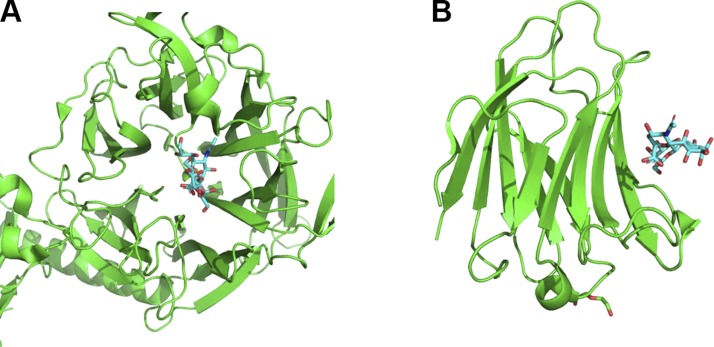
Structures from the PDB archive containing α2-3-sialyllactose reveal 2 common binding modes of α2-3-sialyllactose. It can bind to loops formed by 1 end of a β-sheet core, as in our proposed model of α2-3-sialyllactose binding to αKL1 and found in the structures of T. cruzi trans-sialidase (PDB 1s0i), parainfluenza virus 5 hemagglutinin-neuraminidase (PDB 1z4x), and the mumps virus hemagglutinin-neuraminidase (PDB 5b2d) (Fig. 8). Alternatively, α2-3-sialyllactose can bind to a raft of 4 β-sheets on the protein surface, as seen in S. pneumoniae NanA sialidase (PDB 4c1w and 4yz5) (18, 21), galectin-8 (PDB 4wvw) (20), and galectin-1 (PDB 4y20). The protein structures corresponding to the second α2-3-sialyllactose–binding mode differ from the sKlotho structure. Despite differences in the amino acid sequence and in the structural features for recognition of α2-3-sialyllactose, we find that S. pneumoniae CBM recapitulates the effect of sKlotho. This fact strongly supports the conclusion that α2-3-sialyllactose is the target for sKlotho regulation of TRPC6.

Figure 8.

α2-3-Sialyllactose exhibits 2 different binding modes to proteins. A) α2-3-Sialyllactose binds to loops formed from a β-sheet core in T. cruzi trans-sialidase (PDB 1s0i). B) α2-3-Sialyllactose binds to a raft of antiparallel β-sheets on the galectin-8 protein surface (PDB 4wvw).

In summary, computational studies reveal that in the absence of FGF23 and FGFR1c, the β6α6 loop of the αKL1 can relocate slightly to allow α2-3-sialyllactose access to the αKL1 core for binding. This notion is supported by results of functional studies. Thus, α-klotho has 2 distinctly separate functions. mKlotho interacts with FGFR to form coreceptor for FGF23 in cells expressing α-klotho. sKlotho functions as a hormone that can elicit actions in distant organs or locally independent of FGFR and FGF23.

Glossary

αKL1

residues 57–506 of sKlotho

αKL2

residues 515–953 of sKlotho

CBM

carbohydrate-binding module

CHARMM

Chemistry at Harvard Macromolecular Mechanics

DAG

diacylglycerol

FGF23

fibroblast growth factor 23

FGFR

fibroblast growth factor receptor

FGFR1c

FGFR1 isoform c

HEK293

human embryonic kidney 293

I-V

current-voltage

MD

molecular dynamic

mKlotho

membrane-bound α-klotho

NanA

neuraminidase A

PDB

Protein Data Bank

RMSD

root-mean-square deviation

sKlotho

soluble klotho

TRPC6

transient receptor potential canonical isoform 6

vdW

van der Waals

WMN

wortmannin

AUTHOR CONTRIBUTIONS

J. D. Wright performed the modeling, docking, and molecular dynamics simulations, prepared figures, and wrote the first draft; S.-W. An performed electrophysiological recording, prepared figures, and participated in writing of manuscript; J. Xie generated and purified CBM proteins and participated in writing of manuscript; and C. Lim and C.-L. Huang conceived and supervised the project, analyzed the data, and edited the manuscript and figures.