Summary:
Copy number variation (CNV) of DNA plays an important role in the development of many diseases. However, due to the irregularity and sparsity of the CNVs, studying the association between CNVs and a disease outcome or a trait can be challenging. Up to now, not many methods have been proposed in the literature for this problem. Most of the current researchers reply on an ad hoc two-stage procedure by first identifying CNVs in each individual genome and then performing an association test using these identified CNVs. This potentially leads to information loss and as a result a lower power to identify disease associated CNVs. In this paper, we describe a new method that combines the two steps into a single coherent model to identify the common CNV across patients that are associated with certain diseases. We use a double penalty model to capture CNVs’ association with both the intensities and the disease trait. We validate its performance in simulated datasets and a data example on platinum resistance and CNV in ovarian cancer genome.
Keywords: Association study, Copy number variation, Ovarian cancer, Penalized regression model
1. Introduction
Segments of DNA have copy number variation (CNV) if there are more (gains) or fewer (losses) than two copies of DNA at a particular location in the genome. It is an important aspect of genomic structural changes that has been shown to be associated with many complex diseases. Based on the type of DNA that harbors CNVs, they can be categorized into germline CNV and tumor (or somatic) CNV. For germline CNVs, their locations are typically well defined and the boundaries of a CNV are consistent across individuals (McCarroll et al., 2008), while the occurrences and locations for somatic CNVs are much more variable. CNVs carry much information with regards to the human’s health status, for example germline CNVs have been reported to be associated with several diseases (Elia et al., 2011, Dajani et al., 2015). Somatic CNVs are a main characteristic of tumor growth, associated with various aspects of cancer, including progression and treatment response (Shlien and Malkin, 2009, Walker, Wiggins, and Pearson, 2015).
Methods for analysis of genome-wide arrays and sequencing data with respect to CNVs can be summarized into two categories. One group of methods focus on applying association tests to identify the relationship between a phenotype (disease trait) and known CNVs (such as well-defined germline CNVs). In such case, the focus is on developing association tests using these known CNVs. As a result, many known CNVs have been reported to be associated with diseases such as neuroblastoma, prostate cancer, breast cancer, and other cancer types (Kuiper et al., 2010, Krepischi et al., 2012, Park et al., 2015).
Another group of methods focus on identification of CNVs that are associated with the disease. In many cases, the CNVs are not known beforehand and need to be identified from intensity data (from a SNP array or sequencing data). For example, many somatic CNVs fall into this category. The identification of somatic CNVs is an active research topic. The main complication of the identification of somatic CNVs is tumor heterogeneity (Cheng et al., 2017). Because of this heterogeneity, the actual number of copies of the DNA can be between 0 and 6 (or even more). As a result, many times an arbitrary small value (for example, 0.2) is used as the cut off value to identify a CNV. Any segment with a copy number greater than the predefined cut off value is classified as a CNV. Another complication that makes the identification of CNV association more difficult is that CNVs happen irregularly: they do not happen at the exact same location across individuals. So summarization of the CNV pattern among all individuals can be challenging. Inefficient use of such information might lead to loss of power, especially when the percentage of subjects with a particular CNV is small.
Because of the difficulties mentioned above, many researchers employ an ad hoc, twostage procedure to identify recurrent CNVs among samples: At the first stage, a CNV calling algorithm is used to identify CNV segments in each individual genome, using CNV calling algorithms such as PennCNV (Wang et al., 2007), PSCBS (Olshen et al., 2011), Control-FREEC (Boeva et al., 2012). At the second stage, the inferred CNVs are considered for downstream analyses, often ignoring the uncertainty in the CNV identification. The follow-up statistical tests are performed based on either the frequency of CNVs at each location in the genome (STAC, Diskin et al., 2006) or the (SNP array or sequencing) inferred intensities of the segmented CNVs (GISTIC, Mermel et al., 2011; JISTIC, Sanchez-Garcia et al., 2010). As a result, the uncertainty in the CNV calling is carried over to the testing stage, thus diminishing the statistical power of the test. Also, different choices of parameters (such as the cut off value) might leads to very different results because the uncertainty from the first stage is not taken into consideration in the second stage. This could lead to serious information loss especially when the intensity of the individual CNVs is small. Related to CNV association testing, methods for identifying recurrent CNVs have also been proposed recently. For example, Recurrent Aberrations from Interval Graphs (RAIG, Wu, Hajirasouliha, and Raphael, 2014) identifies recurrent CNVs using interval graphs. Cancer driving pathways using mutual exclusivity of genomic alterations are identified in Babur et al., 2015. A random effect model to model the association between disease and CNVs is used in Tzeng et al., 2015. CNVtools (Barnes et al., 2008) tests for known CNV regions using Gaussian mixture models.
Interestingly, most of the existing methods focus on identifying recurrent CNVs and cannot be readily applied to an association test with both cases and controls (or with cases of two different types of cancer). To the best of our knowledge, there are only a few of methods that aim to identify the association between a disease trait and the CNVs using both cases and controls. For example, VTET (Shi et al., 2014) and CNVtest (Jeng, Wu, and Li, 2015) identify trait associated CNVs by testing for all regions with length less than a pre-defined threshold.
In light of the significance of CNV association tests and the limitations with existing methods, we propose a method called double penalized CNV association test (DPtest) that uses a penalized regression model for CNV association testing for CNVs in somatic DNA. As such, unless we explicitly refer to CNVs as germline, all references to CNV are to somatic CNVs in the remainder of this paper.
A unique aspect of our model is that we minimize a cost function with two penalty terms to prioritize the identification of the disease associated CNVs. The first penalty term is designed to encourage the selection of CNVs that are shared across multiple individuals. The second penalty term is to encourage the selection of those CNVs that are associated with a disease outcome, that, for example, is occurring more frequently in cases than controls. Using this novel approach, we combine the two tasks (CNV detection and association testing) in a single step. As such, efficient usage of information is achieved, as well as a great improvement of the detection power compared to the existing two-step procedures. One salient feature of the proposed method is that, through a unified regression model, we are able to leverage CNV signals from different individuals and compare the differences between cases and controls. Therefore, our method is advantageous to other method when the signal of CNVs from each individual is weak but there is concordance between individuals. In what follows, the newly proposed method is compared to existing methods using simulated data, and is applied to a genomic study of ovarian cancer aiming to identify CNVs that are associated with platinum resistance.
2. Methods
In this section, we provide details of the DPtest method. The testing of the CNV association with a (binary) phenotype can be viewed as a combination of two problems: The first is a regression or dimension reduction problem for the log ratio (LR), where LR is defined as log2(observed copy number/2). It helps us to identify the CNVs with their locations and intensities. The second problem is a regression problem for the phenotype and the CNVs. This helps us to understand whether the CNV is associated with the phenotype.
2.1. Description of CNV data
Let z1 be a vector of LR for a subject. Suppose for the moment, copy number data are collected from normal human samples. Then the observed copy numbers should be close to for all locations in the entire genome and the LRs should be close to 0. Similarly, positive LR values for a specific region suggest a copy number gain (copy number greater than 2) and negative LR values for a region suggest a copy number loss (copy number less than 2) for that region.
If we plot the LR values (as y-axis) along the locations on a chromosome (as x-axis), then for samples with chromosome regions of gains or losses, we should observe that the LRs for those regions are away from 0. Thus, the CNV detection or change point detection problem can be formulated as a change point detection problem using linear regression. We introduce a covariate matrix , where is a p by p lower triangular matrix with all 1’s for the lower triangle (Harchaoui and Lévy-Leduc, 2008). Each column of can be viewed as a covariate, with the first column corresponding to the intercept and the jth column corresponding to a change in copy number at location j. Let’s assume there is a copy number gain (copy number 3 for example) for a region starting from the 100th location to the 200th location. Then, in our formulation the coefficients for and are log2(3/2) and −log2(3/2) respectively, and 0 for all the remaining coefficients. This provides a natural way of incorporating spatial continuity of the LRs.
An alternative approach to perform the CNV detection is to simply set to be an identity matrix. However, in order to enforce the continuous nature of the LRs, an extra fused penalty term will be needed to penalize the difference between neighboring coefficients. Thus, this alternative approach will create an extra penalty term in the regression model and increase the computational cost. Due to this reason, we will follow the set up of as in Harchaoui and Lévy-Leduc (2008).
2.2. A double penalized linear regression problem
Let Z = (z1,…,zn) be the matrix with the LR data for n subjects; i.e. Z is a p by n matrix with each column representing a subject and each row representing a location on the genome. Usually p is of the order of 106 or even higher, a much larger number than the sample size n, which will typically be of the order of 10 to 1000. We use the same linear regression set up as introduced in the previous subsection. Let B = (β·1,··· ,β·n) be a p by n matrix with the ith column being the coefficient for regressing zi on . The first part of the regression problem treats Z as the outcome or response variable and treats as the covariates.
Let {ỹ1,… , ỹn} be a 0–1 vector of phenotypes. We assume the first n1 subjects are cases (ỹ1,…, ỹn1 = 1) and the last n2 subjects are controls (ỹn1+1,…, ỹn = 0, n1 +n2 = n). Let y be a mean and variance standardized version of ỹ such that and Let X be a column-wise mean standardized version of , so that each column of X has mean 0. Note that the first column of is all 0’s and can thus be dropped.
Denote the jth row of B as βj·, then βj· is a vector of length n, with the ith element corresponding to the copy number change (shift) at location j for individual i. The association between the shift at location j and the phenotype can be modeled as:
| (1) |
where y = (y1,…,yn), θ = (θ1,…,θn) and η = (η1,…,ηn). If a shift at location j is truly associated with the phenotype, then we should have ηj ≠ 0. We can decompose bj as
| (2) |
where βji is the ith element of βj··
Motivated by the model above, we propose to identify the non-zero ηjs by minimizing
| (3) |
where ‖βj·‖p = (Σ|βji|p)1/p. The first term measures the difference between the observed LR and the estimated LR. Heuristically, the second term can be rewritten as which helps to select the non-zero associations between copy number and phenotype. The third term encourages the non-zero element of B to be at the same location across all samples. This helps to construct a common boundary for CNVs that occur across n individuals. Here α is a parameter between 0 and 1. It can be viewed as a weight that leverages the importance of the last two terms. Some additional factors are included for the second term and the third term so that all terms are on the same scale. In particular, for each location so an n is included as a scale for the third term along with λα. Each βj· is a vector of length n, denoting the shift of the LR at location j for all individuals. Therefore, we standardize this vector by dividing its l2 norm by √n. Finally, 1 is added to ‖βj·‖2/√n to make sure that the logarithm of it is always larger or equal than 0.
One potential issue with having X as the covariate is that neighboring columns are strongly correlated. So if an l1 norm were to be used as the penalty term for βj·, j = 1,…,p, then the true shift location and it’s neighboring locations would tend to be selected together because of the collinearity of the columns of X. An l0 penalty would appear to be a good option to deal with this problem, but it introduces computational difficulties at the same time. Instead, we employ a log−l2 penalty, whose linear approximation is identical to that of an l0 penalty, but results in a more straightforward computation. Thus the log−l2 penalty can be viewed as an approximation of an l0 penalty with a computational benefit.
We apply a group version of the coordinate descent method to solve the problem (3). Given , we estimate βj· by minimizing
| (4) |
where with X(−j) = (x1,…,xj−1,xj+1,…,xp−1). Using the subgradient method, we get that when βj· ≠ 0, it satisfies the equation
| (5) |
for some t ∈ [−1,1].
Let , where Then the solution is with dj being a positive number that solves
| (6) |
where
| (7) |
After some algebra, we get that βj· ≠ 0 if and only if lies in the intervals given in Table 1.
Table 1.
Intervals for such that bj ≠ 0, where , a* satisfies
|
|
|||
|
|
|
For given λ and α, we will obtain and . is a p × n matrix, with the (j,i) element being the copy number shift at location j for subject i. Because of the penalty terms, will be a sparse matrix. Let S be the collection of the index for non-zero rows of , then S provides the collection of all copy number shift locations. Since copy number variation occurs over regions, we expect the size of S to be much smaller than p. Similarly, is a vector of length p. It measures the change in association strength at each location. If the jth row of is all zero, then the corresponding jth element in will be zero. Thus, S also denote the non-zero element in .
2.3. Choice of λ and α
N-fold cross validation can be used to select the combination of λ and α that produces the smallest prediction error. However, a direct application of cross validation can be time consuming because there are two tuning parameters. Empirical evidence shows that the model selected usually has a good performance in terms of prediction error when α ∈ (0.2,0.5) (See Appendix). So throughout this paper, we fix α to be 0.4 and set λ to take a series of value between λmax and λmin, where λmax is the value when the first variable enters the model and λmin can be a very small number, for example, 0.001. Usually λ can be set to take values equally spaced between λmax and λmin on a logarithmic scale. More details on the choices of α are given in Web Appendix A.
2.4. Identification of disease associated regions and false discovery rate
In order to determine which CNVs are associated with the disease status, we use ζˆ1,…,ζˆp as candidate associations, the selection of which can be controlled by the false discovery rate. Similar to the estimation procedure described in Tibshirani, and Wang, 2008, we propose to estimate the false discovery rate by
| (8) |
Although the observations are not independent, the above expression still serves as a valid estimator as discussed in Benjamini, and Hochberg (1995), Storey (2002), Efron, and Tibshirani (2002).
While the null distribution is unknown, we can use permutations to approximate it. For the mth permutation, we randomly permute the response y → y(m). Then can be obtained using the algorithm introduced in this paper. Thus, by combining the results from M permutations, provides an approximation of the ζ.
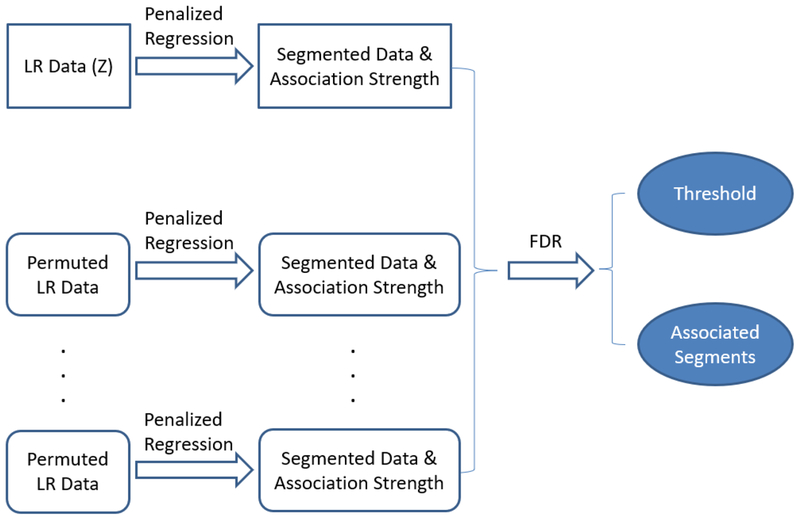
To summarize the steps used for the identification of the disease associated CNVs, Figure 1 shows a diagram that explains the processes of the proposed method. To be specific, the proposed method consists of three steps. The first step is to use penalized regression to obtain the segmented data and the corresponding association strength of each segment. Note here, that if a segment range from location j1 to j2, then the disease association strength for locations j1 to j2 are all the same, that is . In the second step, the same procedure is used for the M permuted datasets, and the association measure are obtained. In the the third step, a threshold ζ0 is obtained by controlling the FDR; all segments with are labeled as disease associated CNVs.
Figure 1.
Diagram for the process to identify the disease associated CNVs.
3. Simulations
We conducted two sets of simulation studies to answer the following questions: What are the advantages of our method? What is the effect of different choices of algorithm parameters on the results? Empirical results show that our method is not very sensitive to the choices of the parameters. So we will focus on answering the first question in this section. More illustrations on the effect of the algorithm parameters are given in the Appendix.
We compare the performance of the proposed method (DPtest) with existing methods including CNVtest (Jeng et al., 2015) and a procedure inspired by GISTIC (Mermel et al., 2011) which uses CBS for segmentation and then applies the two sample t-test to the segmented data).
First, we give a brief overview of these methods. CNVtest scans the whole genome by computing the “length-standardized sum” for each candidate interval. This sum is coded into a 0–1 indicator (Z) by comparing it with a pre-defined cut-off value (ν). The cut-off value ν is a function of the interval length as well as the total number of markers in the data. Then the Z for the same region across samples are tested using a GLM model. The resulting p-value shows the significance of the association between the disease trait and the genomic region. The authors showed that CNVtest controls the genome-wide error rate with a probability close to 1 (Jeng et al., 2015). However, because the cutoff value is gauged towards reducing the overall rate of falsely discovering a CNV, the cutoff value is usually set to a large number which decreases the power of identifying true (disease associated) CNVs.
GISTIC is a multi-stage method developed to identify recurrent CNVs among cases. At the first stage, CNVs are identified using the Circular Binary Segmentation (CBS) algorithm (Olshen et al., 2004). Then a reconstruction method is used to further decompose the identified CNVs into independent CNV events to recover the most likely history of the CNV developments. A G-score is assigned to each CNV as the sum of all the intensities higher than a threshold. Finally a permutation test is used to access the significance of each CNV by comparing the G-score with the permuted G-scores. To adapt GISTIC for our purpose, we modify GISTIC by applying a two-sample t-test to test the association between the individual G-scores and their disease status. Also, we did not include the deconstruction step of the original GISTIC as the code to do so was not available to us. We refer to this approach as CBS-Ttest.
The goal of this simulation study is to learn the advantage and disadvantage of DPtest relative to existing approaches. For CNVtest, we use the R code available at the authors’ website. Direct application of CNVtest provides extremely conservative results. Instead, we fine-tuned this method by varying the cut-off values (ν) and select the ν that provides the largest number of correctly identified CNVs. For CBS-Ttest, we first use the “segmentByCBS” function from the “PSCBS” package in R to obtain segments. Then, we apply the two-sample t-test on the segmented data to obtain T scores as the association strength measurements. Disease associated segments are identified by controlling the false discovery rate (FDR) at 0.05.
We simulate data sets with n = 500 individuals, of whom 250 are cases and 250 are controls. We generate the LRs for m = 5000 markers and randomly select 5 regions with length S = 20 or S = 30 as the candidate CNV regions. The LRs are generated in two steps to mimic the observed correlation between nearby locations. Step 1: we generate 5000 independent N(0,1) values for each individual. Step 2: we randomly split the 5000 markers into 100 segments, then for each segment extra additive noise with distribution N(0,0.3) is added. This extra noise can be thought of as an experimental artifact that induces correlation between nearby locations in the genome, as often observed in actual genomic data.
For each of the 5 candidate CNV regions for each individual, we randomly decide whether to add a CNV to that region. We consider several combinations for the parameters of the CNVs as listed below.
For each candidate CNV region, the probability of adding a CNV is set to be p0 = 0.2 for the controls and p1 = 0.2,0.3,0.4,0.5 for the cases. So for an individual without a disease, the expected number of CNVs is 5 × 0.2 = 1. And for an individual with a disease, the expected number of CNVs is 1,1.5,2,2.5 for different p1 values, respectively. Note that if p1 = 0.2 there is no difference between cases and controls for this CNV.
The first model assumes that each disease associated CNV occurs at the same genomic locations across all samples and the length of the region S is 20. The second model assumes each disease associated CNV occurs within a range with length of the region set to S = 30, the starting position is selected uniform over a segment of length 30.
For the region with a CNV, the average LR is set to be μ = 0.5,0.75,1.0,1.25, such that the corresponding copy numbers CN ≈ 2.8,3.4,4,4.8, by noting that CN = 2 × 2LR.
For each combination of p1, S, and μ, we simulate 10 data sets and compare the number of correctly and falsely identified CNVs as well as the “recovery rate”. To calculate the false discovery rate, the null distribution is generated using 100 permuted data sets. The false discovery rate is controlled at level 0.05. For any CNV identified, if more than 50% of the region overlaps with the region where the CNV was generated, we call it is a correct identification. If it does not overlap with a known CNV or if the overlap is less than 50% of the length of the region, we refer to it as a false identification. The “recovery rate” refers to the ability to correctly recover the regions where CNVs occur. It is calculated as the ratio between the total length of the identified true CNVs and the total length of the CNVs (i.e. 100 if S = 20 and 150 if S = 30).
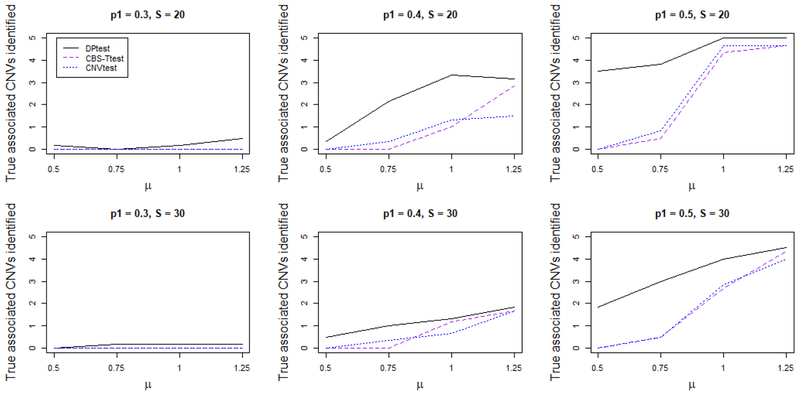
In Figure 2, we report the average number of true disease associated CNVs identified for each method for p1 = 0.3, p1 = 0.4, and p1 = 0.5, respectively. Any CNV region is classified as correctly identified by a method if at least 50% of the region is identified to be disease associated. For the first row of the figures, a CNV happens at exactly the same location across all samples (S = 20, model one). For the second row of the figures, a CNV happens randomly within a region (S = 30, model two). As expected, as the percentage of CNV carried among the cases increases, the power for all the methods increases as well. Similarly, the power increases when the LR (μ) of the CNVs increases. Among all methods, DPtest has the highest power: when the signal is strong (p1 = 0.5, μ = 1.0 or 1.25), it always correctly identifies all CNV regions, while other methods only identify a portion of the 5 disease associated CNV regions. When the signal is moderate (p1 = 0.4), DPtest still consistently performs better than the other methods. It is worth mentioning the difference between the performance of DPtest and the other methods is the largest when the LR is low (μ = 0.5 or μ = 0.75) while the percentage of CNV carriers is reasonably higher in the cases (p1 = 0.4 or p1 = 0.5) than in the controls (p1 = 0.5). This is largely due to the fact that DPtest does not depend on identifying CNV regions individually for each subject. Rather, DPtest looks at all samples and picks the regions with a large difference in LR between cases and controls. In other words, DPtest is most powerful when the signal of CNVs from each individual is weak but there is joint signal from all samples.
Figure 2.
Averaged number of true disease associated CNVs identified by each method. For the top row the CNV occurs at the same genomic location for all subjects carrying the CNV, which has length 20 (S = 20). For the bottom row the CNV occurs at slightly shifted genomic locations for each subject carrying the CNV, which has length 30 (S = 30). DPtest performs the best among all competitors, especially when the LR (μ) of the CNVs is small. This figure appears in color in the electronic version of this article.
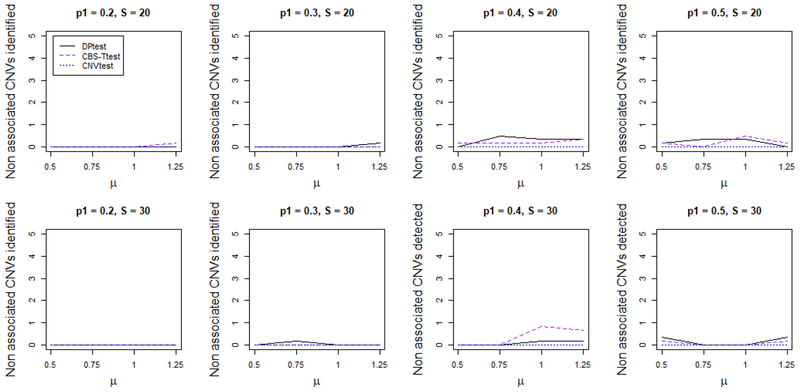
In Figure 3, we report the average number of false CNVs identified for each method. DPtest produces on average less than 0.1 false CNV, which corresponds to about a 0.05 false discovery rate. While CNVtest is a little conservative, it does not identify any false CNV regions. CBS-Ttest identifies the most number of false CNVs. This is partially because we summarize the results by counting the number of segments. Since the segmentation for CBS is performed at the individual level, we might have several falsely identified segments but each only contains a small number of loci.
Figure 3.
Average number of false disease associated CNV regions identified by each method. For the top row the CNV occurs at the same genomic location for all subjects carrying the CNV, which has length 20 (S = 20). For the bottom row the CNV occurs at slightly shifted genomic locations for each subject carrying the CNV, which has length 30 (S = 30). Overall, the number of false discoveries is low for DPtest and CNVtest, but the number of false discoveries for CBS-Ttest is higher. This figure appears in color in the electronic version of this article.
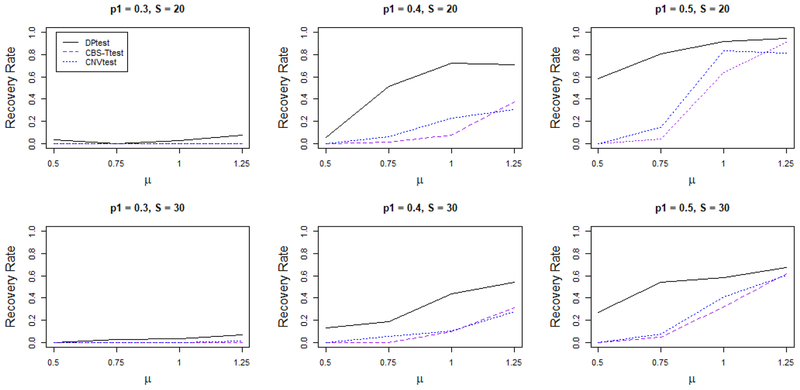
In Figure 4, we report the “recovery rate”. For example, when there are 5 such disease related CNVs, each with S = 20 loci, there are in total 100 disease associated loci. We summarize the percentage of the loci correctly identified, to assess the ability to recover the disease associated region in terms of coverage. The first row of the figures corresponds to the model with fixed CNV locations and S = 20 and the second row of the figures correspond to model with variable CNV locations and S = 30. Overall, DPtest has the best coverage rate, followed by CNVtest and CBS-Ttest. DPtest shows the largest advantage when the signal is weak to moderate, since it has the ability to group the signal across subject. When the CNV location is not exactly the same across subjects, DPtest still gives reasonably good recovery rate, while there is a dramatic decrease for other methods. CNVtest has a much smaller identification rate. The reason for that is two-fold: First, the signal strength for each subject is attenuated, so it becomes harder for any region to be identified as a CNV at the individual level. Second, in order to identify a wider spread CNV region, CNVtest needs to test for more candidate regions, and as it needs to adjust for more multiple testing, a smaller p-value is needed to claim any region significant.
Figure 4.
Average percentage of markes within true disease associated CNVs identified by each method. For the top row the CNV occurs at the same genomic location for all subjects carrying the CNV, which has length 20 (S = 20). For the bottom row the CNV occurs at slightly shifted genomic locations for each subject carrying the CNV, which has length 30 (S = 30). DPtest performs the best among all competitors, especially then the LR μ of the CNVs is small. When the averaged true LR of the CNVs (μ) is high, DPtest, CNVtest and CBS-Ttest perform equally well: they are all able to capture a large fraction of the true CNV. However, when the μ value is low, DPtest is still able to capture a big portion of the true CNV regions while the other methods do not perform as well. This figure appears in color in the electronic version of this article.
4. Case study: identification of driver CNVs for platinum-resistant ovarian cancer patients
Ovarian cancer is one of the most common cancers among women. It is diagnosed in over 20,000 women in the US each year (TCGA, 2011). The most commonly used first-line chemotherapy agents after surgery are taxanes (paclitaxel or docetaxel) and platinum (carboplatin or cisplatin). There is, however, a proportion of the ovarian cancer patients (20–30%) who will not respond to such treatment, and they are referred to as the platinum-resistant patients (Davis, Tinker, and Friedlander, 2014). Predicting chemo-resistance using genomic features in resected tumor samples at surgery will facilitate selection of alternative treatment regimens.
In this section, we apply DPtest to identify the CNVs that are associated with platinumresistant status, using whole exome sequencing (WES) and SNP array data from the TCGA for our analysis. Detailed description of the data sets can be found in the original paper (TCGA, 2011). The TCGA data were downloaded from NCI/GDC data portal under project 11179. There are in total 470 patients and we have the platinum sensitive/resistant status available among 299 of them. Among these 299 patients included in our analysis, 91 patients were platinum-resistant and the remaining patients were platinum-sensitive.
Exome sequencing data for each patient for both tumor samples and blood (normal) samples were obtained using Illumina GAIIx and ABI SOLiD at the Broad Institute, Washington University School of Medicine, and Baylor College of Medicine. We obtain the sequencing data and calculated the LR of the read count for tumor/normal pairs over windows of size 10kb. The SNP array copy number data for tumor/normal sample pairs were obtained using multiple array platforms including Illumina 1MDUO and Affymetrix SNP6, processed at the Broad Institute and the Hudson Alpha Institute for Biotechnology. We obtained copy number data and calculated the LR using the tumor/normal pairs. For the follow up analysis, the LRs are used as the input of DPtest. We fix α at 0.4. To evaluate the false discovery rate, we run the analysis 10 times with permuted y values to approximate the distribution of the association under the null.
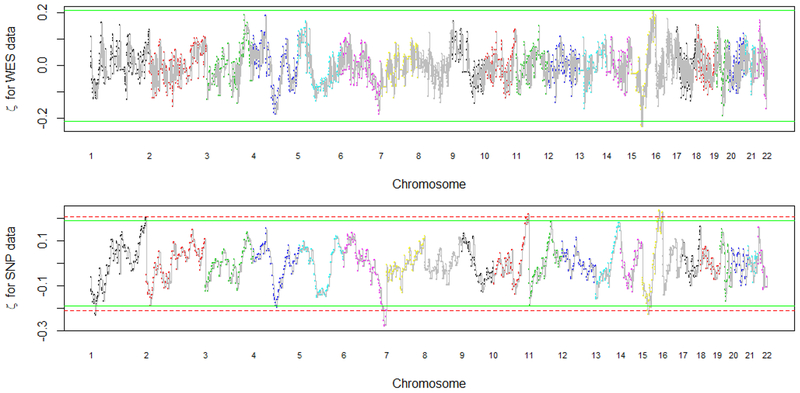
In Figure 5, we plot the estimated association strength by genomic location. The top figure contains the results obtained using the whole exome sequencing data. The bottom figure contains the results obtained using the SNP array data. The solid line is the cutoff value by controlling the false discovery rate at 20%. The dashed line is the cutoff value by controlling the false discovery rate at 10%. Multiple regions of CNVs are identified to be associated with platinum resistant status. For example, CNVs in 4q23, 6q26 and 15q21 are identified. We observe that more regions are identified using the SNP array data for the same set of patients, and the signal from the SNP array data is stronger than the signal from the WES data. This is possibly because the CNVs are interrogated in high density by SNP arrays while exome-sequencing is concentrated in the exome, and thus non-exome regions were omitted in the WES data. Other than the difference in signal strength, the overall pattern of the results is similar for both types of data.
Figure 5.
The estimated η values using the WES data and the SNP data. The dashed and solid line are the cutoff values for controlling the false discovery rate at 10% and 20%, respectively. Multiple locations of CNVs are identified to be associated with the platinum resistant status, with more locations being identified using the SNP data. For example, the regions at 4q22, 6q26, and 15q26 are significant at a false discovery level of 20% for both WES and SNP data. This figure appears in color in the electronic version of this article.
In Table 2, we list the regions that are identified to be associated with platinum-resistant status using our method by controlling the FDR at 0.2. For each identified region, we list the chromosome, and starting and ending base-pair (bp) locations. We also indicate whether CNVs or genes in those regions have been previously reported in the literature. Genomic locations are based on human genome build 37. We line up the regions that are identified to be associated with the platinum-resistant phenotype, as identified by DPtest for the SNP array and WES data, with bold font being regions identified by both the SNP array and WES data. We note that many of the genes and regions that DPtest identifies have been previously associated with ovarian cancer. Using our method, we successfully identified regions containing genes such as AKT3, HTRA1, IGF1R, and RCCD1 that have been reported in the literature to be linked to ovarian cancer (references listed in Table 2). It should be noted that gene CCPG1 has been found to be predictive of chemo-response (Bosquet et al., 2016).
Table 2.
CNV regions identified to be associated with the platinum-resistant phenotype, as identified by DPtest using the SNP array and WES data, with an FDR controlled at 0.2. If a region is identified by both SNP array and WES data, we mark the region with bold font. Locations are from human genome build 37. The genes are those that have been reported in the literature as being associated with ovarian cancer or cancer drug resistance in or near the interval.
| Chrom | Start | End | Selected Gene & Literature |
|---|---|---|---|
| 1 | 18,029, 434 | 21,576, 796 | 1p36 Alvarez et al., 2001 |
| 1 | 244,183, 432 | 249,222,471 | AKT3 TCGA, 2011 |
| 4 | 96,324,052 | 99, 069, 827 | 4q23 TCGA, 2011 |
| 6 | 155,184, 273 | 171,050, 993 | RPS6KA2 Bignone et al., 2007 |
| 10 | 124,671, 655 | 129,282, 460 | HTRA1 Chien et al., 2004 |
| 10 | 133, 326, 776 | 135,424,083 | |
| 15 | 42, 373, 631 | 49,408, 050 | 15q21 TCGA, 2011 |
| 15 | 55,311,786 | 56,928, 535 | CCPG1 Bosquet et al., 2016 |
| 15 | 87,201,931 | 93,590,130 | RCCD1 Kar et al., 2016 |
| 15 | 99,797,210 | 102,429,113 | IGF1R Denduluria et al., 2015 |
5. Discussion
CNVs play an important role in disease etiology. Understanding the association of CNVs with diseases will help early detection and outcome prediction of those diseases. In some cases, it may also help in identifying the most effective patient dependent treatment strategies. Despite the scientific significance, only a few methods have been developed to identify CNV-disease association. Most of the current research on CNVs focus on (recurrent) CNV identification, or ad-hoc two-stage procedures to identify disease-associated CNVs. In light of methodological challenges, we proposed a novel method, DPtest, to address the limitations of existing methods. Compared to two-step procedures that identify CNVs in the first step and conduct association test in the second step, the penalized regression model we propose combines these two steps in one cohesive model. The advantage of this novel approach is supported by both simulation and real data analysis.
In simulated data, we show that under different scenarios our method can outperform competitors in terms of power to identify disease-associated CNVs, while maintaining correct control of false discovery rates. The advantage stems from the fact that our method uses a unified algorithm for the association test based on the original LR data. Thus there is no information loss in the modeling process. Also, the double penalty term helps us to leverage the information across individuals. In contrast, for the two-step process, there are uncertainties in determining whether a CNV occurred at a given region, and that information is lost when only the CNV identification results are passed to the second stage of the algorithm. In the two-stage procedures, the segmentation in the first stage is usually performed separately for each subject while no cross subject information is utilized in this process. The partial utilization of the information in the two-step procedure might lead to potential power loss. As shown in Figure 2, the largest power gain occurs when the CNV from any single individual is weak but there are multiple cases or controls who carry the CNV. This is because our method is capable of leveraging the potential CNV signal occurring at similar locations across samples.
We applied DPtest to discover CNVs that are associated with platinum-resistance status among ovarian cancer patients. This is a serious clinical problem: about 30% of the ovarian cancer patients that will not respond to the platinum-based chemotherapy and the expected survival time for resistant patients is less than one year. If the platinum-resistance status could be predicted successfully before treatment is assigned, an alternative treatment regime could be offered to resistant patients, which would potentially improve the patients survival. We have successfully identified a list of CNVs and many of the findings are potentially relevant based on a literature search on genes that were previously linked to ovarian cancer. Interestingly, we were able to identify genes that are reported to be predictive of the chemoresponse status (such as the gene CCPG1 on 15q21 and THBS1 on 15q15, Bosquet et al., 2016). These findings could help to predict platinum resistant patients and help physicians assign alternative treatment regimens. Naturally, our findings would need to be replicated in independent data sets.
We have illustrated the power of our method in the case-control setting where the outcome variable is binary. However, our method can be readily extended to the situation where the outcome variable is continuous. Such extension can be useful if people are interested in identifying CNVs that are associated with continuous disease trait.
6. Supplementary Materials
Web Appendices referenced in Section 2.3 are available with this paper at the Biometrics website on Wiley Online Library. Accompanied R codes are also available and are described in detail in Web Appendices.
Supplementary Material
References
- Alvarez AA, Lambers AR, Lancaster JM, Maxwell GL, Ali S, Gumbs C, et al. (2001). Allele Loss on Chromosome 1p36 in Epithelial Ovarian Cancers. Gynecologic Oncology 82, 94–98. [DOI] [PubMed] [Google Scholar]
- Babur O, Gonen M, Aksoy BA, Schultz N, Ciriello C Sander G, and Demir E (2015). Systematic identification of cancer driving signaling pathways based on mutual exclusivity of genomic alterations. Genome Biology 16, 45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barnes C, Plagnol V, Fitzgerald T, Redon R, Marchini J, Clayton D, and Hurles ME (2008). A robust statistical method for case-control association testing with copy number variation. Nature Genetics 40, 1245–1252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bast RC Jr. (2011). Molecular approaches to personalizing management of ovarian cancer. Annals of Oncology 22, viii5–viii15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini Y, and Hochberg Y (1995). Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society: Series B 57 289–300. [Google Scholar]
- Bignone PA, Lee KY, Liu Y, Emilion G, Finch J, Soosay AE, et al. (2007). RPS6KA2, a putative tumour suppressor gene at 6q27 in sporadic epithelial ovarian cancer. Oncogene 26, 683–700. [DOI] [PubMed] [Google Scholar]
- Boeva V, Popova T, Bleakley K, Chiche P, Cappo J, Schleiermacher G, et al. (2012). Control-FREEC: a tool for assessing copy number and allelic content using next generation sequencing data. Bioinformatics 28, 423–425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bosquet JG, Newtson AM, Chung RK, Thiel KW, Ginader T, Goodheart MJ, et al. (2016). Prediction of chemo-response in serous ovarian cancer. Molecular Cancer 15, 66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng Y, Dai JY, Paulson TG, Wang X, Li X, Reid BJ, et al. (2017). Quantification of multiple tumor clones using gene array and sequencing data. The annals of applied statistics 11, 967–991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chien J, Staub J, Hu SI, Erickson-Johnson MR, Couch FJ, Smith DI, et al. (2004). A candidate tumor suppressor HtrA1 is downregulated in ovarian cancer. Oncogene 26, 1636–1644. [DOI] [PubMed] [Google Scholar]
- Dajani R, Li J, Wei A, Glessner JT, Chang X, Cardinale CJ, et al. (2015). CNV analysis associates AKNAD1 with Type-2 diabetes in jordan subpopulations. Scientific Reports 5, 13391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis A, Tinker AV, and Friedlander M (2014). “Platinum resistant” ovarian cancer: what is it, who to treat and how to measure benefit?. Gynecologic Oncology 133, 624–631. [DOI] [PubMed] [Google Scholar]
- Denduluria SK, Idowua O, Wang Z, Liao Z, Yan Z, Mohammed MK, et al. (2015). Insulin-like growth factor (IGF) signaling in tumorigenesis and the development of cancer drug resistance. Genes and Diseases 2, 13–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diskin SJ, Eck T, Greshock J, Mosse YP, Naylor T, Stoeckert CJ, et al. (2006). STAC: A method for testing the significance of DNA copy number aberrations across multiple array-CGH experiments. Genome Research 16, 1149–1158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efron B, and Tibshirani R (2002). Empirical Bayes methods and false discoery rates for microarrays. Genetic Epidemiology 64 479–498. [DOI] [PubMed] [Google Scholar]
- Etemadmoghadam E, deFazio A, Beroukhim R, Mermel C, George J, Getz G, et al. (2009). Integrated Genome-Wide DNA Copy Number and Expression Analysis Identifies Distinct Mechanisms of Primary Chemoresistance in Ovarian Carcinomas. Clinical Cancer Research 15 1417–1427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elia J, Glessner JT, Wang K, Takahashi N, Shtir CJ, Hadley D, et al. (2011). Genome-wide copy number variation study associates metabotropic glutamate receptor gene networks with attention deficit hyperactivity disorder. Nature Genetics 44, 78–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harchaoui Z, and Lévy-Leduc C (2008). Catching change-points with lasso. Advances in Neural Information Processing Systems 9 18–29. [Google Scholar]
- Huang RY, Chen GB, Matsumura N, Lai HC, Mori S, Li J, et al. (2012). Histotypespecific copy-number alterations in ovarian cancer. BMC Medical Genomics 5, 47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeng J, Wu Q, and Li H (2015). A statistical method for identifying trait-associated copy number variants. Human Heredity 79, 147–156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kar SP, Beesley J, Al Olama AA, Michailidou K, Tyrer J, Kote-Jarai Z, et al. (2016). Genome-wide meta-analyses of breast, ovarian and prostate cancer association studies identify multiple new susceptibility loci shared by at least two cancer types. Cancer Discovery 6, 1052–1067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krepischi AC, Achatz MI, Santos EM, Costa SS, Lisboa BC, and Brentani H, et al. (2012). Germline DNA copy number variation in familial and early-onset breast cancer. Breast Cancer Research 14, R24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuiper RP, Ligtenberg MJ, Hoogerbrugge N, and Geurts van Kessel A (2010). Germline copy number variation and cancer risk. Current Opinion in Genetics and Development 20, 282–289. [DOI] [PubMed] [Google Scholar]
- Kudoh K, Takano M, Koshikawa T, Hirai M, Yoshida S, Mano Y, et al. (1999). Gains of 1q21-q22 and 13q12-q14 are potential indicators for resistance to cisplatin-based chemotherapy in ovarian cancer patients. Clinical Cancer Research 5, 2526–2531. [PubMed] [Google Scholar]
- Loveday C, Turnbull C, Ramsay E, Hughes D, Ruark E, Frankum JR, et al. (2011). Germline mutations in RAD51D confer susceptibility to ovarian cancer. Nature Genetics 43, 879–882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCarroll SA, Kuruvilla FG, Korn JM, Cawley S, Nemesh J, Wysoker A, et al. (2008). Integrated detection and population-genetic analysis of SNPs and copy number variation. Nature Genetics 40, 1166–1174. [DOI] [PubMed] [Google Scholar]
- Mermel CH, Schumacher SE, Hill B, Meyerson ML, Beroukhim R, and Getz G (2011). GISTIC2.0 facilitates sensitive and confident localization of the targets of focal somatic copy-number alteration in human cancers. Genome Biology 12, R41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olshen AB, Bengtsson H, Neuvial P, Spellman P, Olshen RA, and Seshan VE (2011). Parent-specific copy number in paired tumor-normal studies using circular binary segmentation. Bioinformatics 27, 2038–2046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olshen AB, Venkatraman ES, Lucito R, and Wigler M (2010). Circular binary segmentation for the analysis of array-based DNA copy number data. Biostatistics 5, 557–572. [DOI] [PubMed] [Google Scholar]
- Park RW, Kim TM, Kasif S, Park PJ (2015). Identification of rare germline copy number variations over-represented in five human cancer types. Molecular Cancer 14, 25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanchez-Garcia F, Akavia UD, Mozes E, and Pe’er D (2010). JISTIC: Identification of Significant Targets in Cancer. BMC Bioinformatics 11, 189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi J, Yang XR, Caporaso NE, Landi MR, and Li P (2014). VTET: a variable threshold exact test for identifying disease-associated copy number variations enriched in short genomic regions. Frontiers in Genetics 5, 53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shlien A, and Malkin D (2009). Copy number variations and cancer. Genome Medicine 1, 62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storey JD (2002). A direct approach to false discoery rate. Journal of the Royal Statistical Society: Series B 64, 479–498. [Google Scholar]
- The Cancer Genome Atlas Research Network. (2011). Integrated genomic analyses of ovarian carcinoma. Nature 474, 609–615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani R, and Wang P (2010). Spatial smoothing and hot spot detection of CGH data using the fused lasso. Biostatistics 9, 18–29. [DOI] [PubMed] [Google Scholar]
- Tzeng JY, Magnusson PKE, Sullivan PF, The Swedish Schizophrenia Consortium, and Szatkiewicz, J.P. (2015). A New Method for Detecting Associations with Rare CopyNumber Variants. PLoS Genetics 11, e1005403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker LC, Wiggins GAR, and Pearson JF (2015). The role of constitutional copy number variants in breast cancer. Microarrays (Basel) 4, 207–223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang K, Li M, Hadley D, Liu R, Glessner J, Grant S, et al. (2007). PennCNV: an integrated hidden Markov model designed for high-resolution copy number variation detection in whole-genome SNP genotyping data. Genome Research 17, 1665–1674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu H, Hajirasouliha I, and Raphael BJ (2014). Detecting independent and recurrent copy number aberrations using interval graphs. Bioinformatics 30, i195–203. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.