Modelling and estimation of nonlinear quantile regression with clustered data

Abstract

In regression applications, the presence of nonlinearity and correlation among observations offer computational challenges not only in traditional settings such as least squares regression, but also (and especially) when the objective function is nonsmooth as in the case of quantile regression. Methods are developed for the modelling and estimation of nonlinear conditional quantile functions when data are clustered within two-level nested designs. The proposed estimation algorithm is a blend of a smoothing algorithm for quantile regression and a second order Laplacian approximation for nonlinear mixed models. This optimization approach has the appealing advantage of reducing the original nonsmooth problem to an approximated L₂ problem. While the estimation algorithm is iterative, the objective function to be optimized has a simple analytic form. The proposed methods are assessed through a simulation study and two applications, one in pharmacokinetics and one related to growth curve modelling in agriculture.

1. Introduction

Quantile regression (QR) (Koenker and Bassett, 1978) is a flexible statistical tool with a vast number of applications that complements mean regression. QR has become a successful analytic method in many fields of science because of its ability to draw inferences about individuals that rank below or above the population conditional mean. The ranking within the conditional distribution of the outcome can be considered as a natural index of individual latent characteristics which cause heterogeneity at the population level (Koenker and Geling, 2001). There is an increasingly wider acknowledgement of the importance of investigating sources of heterogeneity to quantify more accurately costs, benefits, and effectiveness of interventions or medical treatments, whether it be an after-school physical activity program, a health care reform, or a thrombolytic therapy (see, for example, Austin et al., 2005; Beets et al., 2016; Beyerlein, 2014; Ding et al., 2010; Rehkopf, 2012; Wei and Terry, 2015; Winkelmann, 2006). QR is particularly suitable for this purpose as it yields inferences that are valid regardless of the true underlying distribution. Also, quantiles enjoy a number of properties (Gilchrist, 2000), including equivariance to monotone transformations and robustness to outliers.

Here, we are interested in data from cluster samples that are commonly found, for example, in biomedical and agricultural research. QR analysis of clustered data is a very active area of research. Since the seminal work of Koenker and Bassett (1978) on methods for cross-sectional observations, there have been a number of proposals on how to accommodate for the dependency induced by cluster designs (e.g., longitudinal). As outlined by Geraci and Bottai (2014) and then extensively reviewed by Marino and Farcomeni (2015), approaches to linear QR with clustered data can be classified into distribution-free and likelihood-based approaches. The former include fixed effects (Koenker, 2004; Lamarche, 2010; Galvao and Montes-Rojas, 2010; Galvao, 2011) and weighted (Lipsitz et al., 1997; Fu and Wang, 2012) approaches. The latter are mainly based on the asymmetric Laplace (AL) density (Geraci and Bottai, 2007,2014; Yuan and Yin, 2010; Farcomeni, 2012) or other, usually flexible, parametric distributions (for example, Reich et al., 2010; Noufaily and Jones, 2013). A different classification can be made into approaches that include cluster-specific effects (e.g., Koenker, 2004; Geraci and Bottai, 2014) and those that ignore or remove them (Lipsitz et al., 1997; Canay, 2011; Párente and Santos Silva, 2016).

In some applications, the assumption of linearity may not be appropriate. This is often the case in, for example, pharmacokinetics (Lindsey, 2001) and growth curve modelling (Panik, 2014). Broadly speaking, one can consider two strategies to nonlinear regression modelling: parametric nonlinear modelling and nonparametric modelling. We now review parametric nonlinear methods, which are of direct relevance to the present study. An account of nonparametric quantile regression methods is given elsewhere (Mizera, 2018; Geraci, 2018). COntributions to statistical methods for nonlinear mean regression when data are clustered can be found in the literature of mixed-effects modelling (Lindstrom and Bates, 1990; Pinheiro and Bates, 1995, 2000) as well as generalized estimating equations (Davidian and Giltinan, 1995, 2003; COntreras and Ryan, 2000; Vonesh et al., 2002). In contrast, the statistical literature on parametric nonlinear QR functions with clustered data is somewhat sparse. To our knowledge, there seem to be only a handful of published articles. Karlsson (2008) considered nonlinear longitudinal data and proposed weighting the standard QR estimator (Koenker and Bassett, 1978) with pre-specified weights. Wang (2012), taking her cue from Geraci and Bottai (2007), used the AL distribution to define the likelihood of a Bayesian nonlinear QR model. Huang and Chen (2016) proposed a Bayesian joint model for time-to-event and longitudinal data using Wang’s (2012) model for the nonlinear longitudinal QR component. An approach based on copulas is developed by Chen et al. (2009). Finally, Oberhofer and Haupt (2016) established the consistency of the Li-norm nonlinear quantile estimator under weak dependency.

Here, we propose an extension of Geraci and Bottai’s (2014) linear quantile mixed model (LQMM) to the nonlinear case and, as in LQMM, we use the AL distribution as pseudo-likelihood for the error which provides the quantile regression interpretation of its location parameter. Our proposal is novel in terms of modelling and estimation. We develop an approach to nonlinear QR with random effects in a frequentist setting that makes use of a modelling framework akin to that of Pinheiro and Bates (2000), familiar to many researchers. None of the papers cited above provides an approach to modelling and estimation of nonlinear quantile functions with random effects in a frequentist framework. Such an approach is desirable when the correlation between measurements is modelled by means of random effects, but the parameters of interest are assumed to be fixed. As compared to the Bayesian approach, ours avoids having to introduce prior distributions on the fixed effects. Putting ‘philosophical’ considerations aside, this has practical consequences in terms of estimation since lack of a closed form for AL-based posterior distributions leads to the application of some form of sampling algorithms that are computationally demanding (Wang, 2012). In contrast, we will provide an analytic form of the objective function to be optimized. What is more important, in the proposal by Wang (2012) there is no mention of how to assess uncertainty and this represents a serious limitation. In our approach, we propose using bootstrap which provides good coverage in LQMMs (Geraci and Bottai, 2014). On the other hand, while Karlsson’s (2008) approach is frequentist, it does not allow for inference at the cluster level. Moreover, our model has the ‘quantile’ interpretation conditionally on the random effects, whereas Karlsson’s (2008) model gives a (weighted) estimate of the marginal (with respect to the clusters) quantiles.

Estimation represents another element of novelty. This is carried out using an algorithm which is a combination of a smoothing algorithm for QR and a second order Laplacian approximation for nonlinear mixed models. The advantages of this approach as compared to numerical integration (Geraci and Bottai, 2014; Geraci, 2014) are discussed further on.

In Section 2, we briefly introduce the standard linear QR model and outline the LQMM approach. In Section 3, we introduce the nonlinear quantile mixed-effects model, or nonlinear quantile mixed model (NLQMM) for short, and related inference. In Section 4, we carry out a simulation study to assess the statistical and computational performance of the proposed methods. Since there are no alternative models that can be placed in a direct comparison with ours for the reasons given above, we consider nonlinear QR for cross-sectional data to investigate potential gains in efficiency when intra-cluster correlation is accounted for. In Section 5, we consider an application of NLQMM to pharmacokinetics and growth curves modelling. We conclude with some remarks in Section 6.

2. Linear quantile mixed models

First, let us introduce the classical QR model for cross-sectional data (Koenker and Bassett, 1978). Let y be a continuous random variable and x a p × 1 vector of known covariates. The distribution of y conditional on x is denoted by F_y(t) = Pr (y ≤ t|x), while for a given τ ∊ (0, 1) its inverse $Q_y(\tau )\equiv F_y^{-1}(\tau )$ gives the τ th quantile of y conditional on x. The linear specification of the QR model for a sample of n independent observations $\left(x_i^{\top },y_i\right)$ is given by

$$Q_{y_i}(\tau )=x_i^{\top }{\beta }_{\tau },i=1,\dots ,n.$$

The τ-specific regression parameter β_τ is interpreted as the ‘quantile treatment effect’ of x on Y (Koenker, 2005). An estimate is obtained by solving the L₁-norm regression problem

$$\underset{\beta }{\text{min}}\sum _{i=1}^n{\rho }_{\tau }\left(y_i-x_i^{\top }\beta \right),$$

where pτ(r) = r {τ — I(r < 0)} is the ‘check’ function and I denotes the indicator function.

COnsider now data from a two-level nested design in the form $\left(x_{ij}^{\top },z_{ij}^{\top },y_{ij}\right)$, for j = 1, ni and i = 1,…,M, $N=\sum _i{n}_i$, where $x_{ij}^{\top }$ is the jth row of a known ni × p matrix X_i, $Z_{ij}^{\top }$ is the jth row of a known ni × q matrix Zi and y_ij, is the jth observation of the response vector (yi1, …, yini)^⊤ for the ith cluster. Throughout the paper, the covariates x and z are assumed to be given. The n × 1 vectors of ones and zeros will be denoted by l_n and 0_n, respectively, the n x n identity matrix by I_n, and the m m×n matrix of zeros by O_{m ×n}

In a distribution-free approach, the linear QR model for clustered (or panel) data (e.g., Koenker, 2004; Abrevaya and Dahl, 2008; Bache et al., 2013) can be specified as

$$Q_{y_{ij}}(\tau )=x_{ij}^{\top }{\beta }_{\tau }+z_{ij}^{\top }{\delta }_{\tau ,i},$$ (1)

where 0 <τ < 1 is the given quantile level, is a β_τ is a p × 1 vector of coefficients common to all clusters, while the q × 1 vector δ_{τ, i} may vary with cluster. All the parameters in model (1) are τ-specific, although the cluster-specific effects are often specified simply as pure location-shift effects (Koenker, 2004; Lamarche, 2010). Fitting can be achieved by solving

$$\underset{{}_{\beta ,\delta }}{\text{min}}\sum _{i=1}^M\sum _{j=1}^{n_i}{\rho }_{\tau }\left(y_{ij}-x_{ij}^{\top }\beta -z_{ij}^{\top }{\delta }_i\right)+\sum _{i=1}^M\mathcal{P}\left({\delta }_i\right).$$ (2)

The penalty P on the cluster-specific effects controls the variability introduced by a large number of parameters δi and is usually based on the Li-norm (Koenker, 2004; Lamarche, 2010; Bache et al., 2013).

To mimic the minimization problem (2) in a likelihood framework, Geraci and Bottai (2014) introduced the convenient assumption that the responses y_ij, j = 1, …, ni, i = 1, …,M conditionally on a q × 1 vector of random effects u_i, independently follow the asymmetric Laplace (AL) density

$$p\left(y_{ij}|u_i\right)=\frac{\tau (1-\tau )}{{\sigma }_{\tau }}\text{exp}\left\{-\frac{1}{{\sigma }_{\tau }}{\rho }_{\tau }\left(y_{ij}-{\mu }_{\tau ,ij}\right)\right\},$$

with location and scale parameters given ${\mu }_{\tau ,ij}=x_{ij}^{\top }{\beta }_{\tau }+z_{ij}^{\top }{u}_i$ and a_r, respectively, which we write as $y_{ij}~\mathcal{A}\mathcal{L}\left({\mu }_{\tau ,ij},{\sigma }_{\tau }\right)$ (The third parameter of the AL is the skew parameter τ ∊(0,1) which, in this model, is fixed and defines the quantile level of interest.) Also, they assumed that u_i = (u_i1,…, u_iq)^⊤, for i = 1,…, M, is a random vector independent from the model’s error term with mean zero and q × q variance-covariance matrix ${\Sigma }_{\tau }$. Note that all the parameters are τ-dependent. The random effects vectors depend on τ through the variance-covariance matrix. If we let $u={\left(u_1^{\top },\dots ,u_M^{\top }\right)}^{\top }$ and $y={\left(y_1^{\top },\dots ,y_M^{\top }\right)}^{\top }$, the joint density of (y, u) based on M clusters for the rth linear quantile mixed model (LQMM) is given by Geraci and Bottai (2014)

$$p(y,u)\equiv p(y|u)p(u)={\left\{\frac{\tau (1-\tau )}{{\sigma }_{\tau }}\right\}}^N\prod _{i=1}^M\text{exp}\left\{-\frac{1}{{\sigma }_{\tau }}\sum _{j=1}^{n_i}{\rho }_{\tau }\left(y_{ij}-{\mu }_{\tau ,ij}\right)\right\}p\left(u_i\right).$$

Geraci and Bottai (2014) proposed estimating LQMMs through a combination of Gaussian quadrature and nonsmooth optimization. They approximated the marginal (over the random effects) log-likelihood using the rule

$${\mathcal{l}}_{\text{GQ}}\left({\beta }_{\tau },{\Sigma }_{\tau },{\sigma }_{\tau }|y\right)=\sum _i^M\text{log}\left\{\sum _{k_1=1}^K\cdots \sum _{k_q=1}^{K}p\left(y_i|v_{k_1,\dots ,k_q}\right)\prod _{l=1}^q{w}_{k_l}\right\},$$ (3)

With v_k1,…,kq = (v_k1,…,v_kq)^⊤, where v_kl and w_kl, k_l = 1, …, K, l = 1, …, q, denote, respectively, the abscissas and weights of the (one-dimensional) Gaussian quadrature. In principle, one can consider different distributions for the random effects, which may be naturally linked to different quadrature rules (or penalties). For example, it is immediate to verify that the double exponential distribution confers robustness to the model and is akin to a Gauss-Laguerre quadrature. Prediction of the random effects was carried out via best linear prediction (BLP) (Geraci and Bottai, 2014).

We depart from Geraci and Bottai’s (2014) estimation approach to avoid its disadvantages in a nonlinear modelling framework. First, the product rule entails a ‘curse of dimensionality’, an exponential increase of the number of evaluations of the integrand function, which may aggravate the typical fragility of nonlinear estimation algorithms. Second, it would not be possible to resort to BLP for random effects prediction.

Throughout this paper, we assume that the random effects are normally distributed. Some studies have investigated the impact of incorrect specification of the random effects’ distribution in mixed models and, in general, there is some disagreement as to whether such parametric assumptions are harmless or have important consequences on inference (McCulloch and Neuhaus, 2011). The answer partly lies in the specific model and type of variables involved, as well as the target of the inference. In the context of QR with random effects, Geraci and Bottai (2014) found that parameter estimation in LQMMs was relatively robust to random effects with a heavy-tailed distribution or a distribution contaminated with outliers, although bias resulted when random effects followed a skewed distribution. We also note that distributions other than normal could be considered, although possibly at the cost of more involved technical developments. Alternatively, parametric assumptions on the random effects can be avoided following, for example, the approach by Alfo et al. (2016).

Assessing the impact of misspecification of the random effects’ distribution in nonlinear quantile regression is particularly complicated due to the nature of the models and the difficulty of calculating analytically the ‘true’ quantiles (see further comments in Section 4). We do not explore this issue here but our recommendation is to exercise caution if there is reason to believe that random effects are non-normal, especially if skewed.

3. Nonlinear quantile mixed models

3.1. The model

We consider the nonlinear quantile regression function

$$Q_{y_{ij}|u_i}(\tau )=f\left({\varphi }_{\tau ,ij},x_{ij}\right),j=1,\dots ,n_i,i=1,\dots ,M,$$ (4)

Where f is a nonlinear, smooth function of the s × 1 random parameter ϕ_τ,ij = F_ijβ_τ + G_iju_i,F_ij and G_ij are two given design matrices of dimensions s × p and s × q, respectively, which in general contain elements of the covariates X_ij.

To stress the functional dependence of the quantiles on the p × 1 fixed parameter βτ and on the q × 1 random parameter u_i, we write f (ϕ_τ,ij, x_ij) ≡ f_ij (β_τ,u_i). For estimation purposes, model (4) can be equivalently written as

$$y_{ij}=f_{ij}\left({\beta }_{\tau },u_i\right)+{ϵ}_{\tau ,ij},$$ (5)

conditionally on u_i, where ${ϵ}_{\tau ,ij}~\mathcal{A}\mathcal{L}\left(0,{\sigma }_{\tau }\right)$ Moreover, we assume $u_i~\mathcal{N}\left(0_q,{\Sigma }_{\tau }\right)$ independently from e#.

Note the similarities and dissimilarities between the proposed model (5) and the traditional nonlinear mixed-effects (NLME) model

$$y_{ij}=f_{ij}\left(\beta ,u_i\right)+{ϵ}_{ij},$$

with $u_i~\mathcal{N}\left(0_q,\Sigma \right)$ and ${ϵ}_{ij}~\mathcal{N}\left(0,{\sigma }^2\right)$. First of all, conditionally on the random effects, both models impose a restriction on the error term (Powell, 1994). However, the NLME model requires E (ϵ_ij | x_ij, u_i) = 0, while the AL-based specification of the error given in (5) leads to $Q_{{ϵ}_{\tau ,ij}|x_{ij},u_i}(\tau )=0$ or, equivalently, Pr (ϵ_τ,ij < 0|x_ij, u_i) = τ. Secondly, the fixed effects can be interpreted as the average value of the cluster-specific parameters, i.e. ${\text{E}}_{u_i}\left({\varphi }_{ij}\right)$, or as the regression parameters of the ‘zero-median’ cluster, i.e. a cluster with a zero random-effect vector. However, the parameter is allowed to vary with the quantile level τ, while β in the NLME model is not (except for a location shift). Finally, in both approaches the variance-covariance matrix of the random effects gives a measure of the variability of u_i around ${\text{E}}_{u_i}\left({\varphi }_{ij}\right)$ but, again, estimates are allowed to differ by τ only for the quantile mixed-effects model.

In general, neither model (5) nor the NLME model provides fixed parameters that can be interpreted as, respectively, regression quantiles or regression means for the population. This is because random effects are allowed to enter nonlinearly in the model. (Similarly, several generalized linear mixed models with nonlinear link functions lack marginal interpretabil-ity (Ritz and Spiegelman, 2004; Gory et al., 2016).) In contrast, the fixed effects of a linear (normal) mixed model remain the same after the random effects are integrated out, whereas, in general, this is not true for the fixed effects of the LQMMs of Geraci and Bottai (2014).

3.2. Inference

In this section, we discuss NLQMM estimation and other inferential procedures.

Let ${\Psi }_{\tau }={\Sigma }_{\tau }/{\sigma }_{\tau }$ be the scaled variance-covariance matrix of the random effects and define ${\theta }_{\tau }={\left({\beta }_{\tau }^{\top },{\xi }_{\tau }^{\top }\right)}^{\top }$, where §_r is an unrestricted m-dimensional vector, 1 ≤ m ≤ q(q + 1)/2, of non-redundant parameters in Ψ_τ. Our goal is to maximize the marginal log-likelihood

$$\mathcal{l}\left({\theta }_{\tau };y\right)=N\text{ log}\left\{\frac{\tau (1-\tau )}{{\sigma }_{\tau }}\right\}-\frac{M}{2}\text{log}\left|{\Psi }_{\tau }\right|-\frac{Mq}{2}\text{log}{\sigma }_{\tau }-Mq\text{log}\sqrt{2\pi }+\sum _{i=1}^M\text{log}\underset{{ℝ}^q}{\int }\text{exp}\left\{-\frac{1}{{\sigma }_{\tau }}\sum _{j=1}^{n_i}{\rho }_{\tau }\left(y_{ij}-{\mu }_{\tau ,ij}\right)-\frac{1}{2{\sigma }_{\tau }}{u}_i^{\top }{\Psi }_{\tau }^{-1}{u}_i\right\}\text{d}{u}_i,$$ (6)

where μ_τ,ij = f_ij (β_τ, u_i).

First of all, we consider the following smooth approximation of p_τ (Madsen and Nielsen, 1993; Chen, 2007):

$${\kappa }_{\omega ,\tau }(r)=\{\begin{array}{ll}r(\tau -1)-\frac{1}{2}{(\tau -1)}^2\omega \hfill & \text{ if }r\le (\tau -1)\omega ,\hfill \\ \frac{1}{2\omega }{r}^2\hfill & \text{ if }(\tau -1)\omega \le r\le \tau \omega ,\hfill \\ r\tau -\frac{1}{2}{\tau }^2\omega \hfill & \text{ if }r\ge \tau \omega ,\hfill \end{array}$$

where $r\in ℝ$ and ω > 0 is a scalar “tuning” parameter. ω→ 0we have that ${\kappa }_{\omega ,\tau }(r)\to {\rho }_{\tau }(r)$. A similar approximation is given by Muggeo et al. (2012) who claimed that their method provides a better approximation than Chen’s (2007) algorithm. However, no analytical evidence was provided in their paper to support such claim. This point might offer scope for additional investigation but, here, it represents a secondary issue and will not be discussed any further.

Let $r_i={\left(r_{i1},\dots ,r_{i{n}_i}\right)}^{\top }$ be the vector of residuals r_ij = y_ij − f (ϕ_τ,ij, x_ij), j = 1,…,n_i, for the ith cluster, and define the corresponding sign vector $s_i={\left(s_{i1},\dots ,s_{i{n}_i}\right)}^{\top }$ with

$$s_{ij}=\{\begin{array}{ll}-1\hfill & \text{ if }{r}_{ij}\le (\tau -1)\omega ,\hfill \\ 0\hfill & \text{ if }(\tau -1)\omega <r_{ij}<\tau \omega ,\hfill \\ 1\hfill & \text{ if }{r}_{ij}\ge \tau \omega .\hfill \end{array}$$ (7)

(Note that the notation above has been simplified since the r_ij’s as well as the s_ij’s should be written as functions of the ϕ_τ,ij’s.) Then, we have

$$\sum _{j=1}^{n_i}{\kappa }_{\omega ,\tau }\left(r_{ij}\right)=\frac{1}{2}\left(r_i^{\top }{A}_i{r}_i+b_i^{\top }{r}_i+c_i^{\top }{1}_{n_i}\right),$$ (8)

where Ai is an ni × n diagonal matrix with diagonal elements ${\left\{A_i\right\}}_{jj}=\left(1-s_{ij}^2\right)/\omega$ b_i and c_i q are two ni x 1 vectors with elements

$$b_{ij}=s_{ij}\left((2\tau -1)s_{ij}+1\right)$$

And

$$c_{ij}=\frac{1}{2}\left\{(1-2\tau )\omega s_{ij}-\left(1-2\tau +2{\tau }^2\right)\omega s_{ij}^2\right\},$$

respectively.

We now define the function

$$h\left({\theta }_{\tau },y_i,u_i\right)=r_i^{\top }{A}_i{r}_i+b_i^{\top }{r}_i+c_i^{\top }{1}_{n_i}+u_i^{\top }{\Psi }_{\tau }^{-1}{u}_i,$$ (9)

which is akin to a regularized, nonlinear, weighted least-squares loss function. The gradient of h with respect to u_i is given

$$h^{\prime }\left({\theta }_{\tau },y_i,u_i\right)=-J_i{\left(u_i\right)}^{\top }\left[2A_i\left\{y_i-f_i\left({\beta }_{\tau },u_i\right)\right\}+b_i\right]+2{\Psi }_{\tau }^{-1}{u}_i,$$ (10)

Where $f_i={\left(f_{i1}\left({\beta }_{\tau },u_i\right),\dots ,f_{i{n}_i}\left({\beta }_{\tau },u_i\right)\right)}^{\top }$ and $J_i\left(u_i\right)=\partial f_i\left({\beta }_{\tau },u_i\right)/\partial u_i^{\top }$, while the Hessian is given by

$$h^{″}\left({\theta }_{\tau },y_i,u_i\right)=\sum _{j=1}^{n_i}\left\{-\frac{2}{\omega }\left(1-s_{ij}^2\right)r_{ij}-b_{ij}\right\}\frac{{\partial }^2{f}_{ij}\left({\beta }_{\tau },u_i\right)}{\partial u_i\partial u_i^{\top }}+\sum _{j=1}^{n_i}\frac{\partial f_{ij}\left({\beta }_{\tau },u_i\right)}{\partial u_i}\frac{\partial f_{ij}\left({\beta }_{\tau },u_i\right)}{\partial u_i^{\top }}+2{\Psi }_{\tau }^{-1},$$ (11)

Moreover, let

$${\widehat{u}}_i=\underset{u_i}{\text{arg min}}h\left({\theta }_{\tau },y_i,u_i\right)$$ (12)

be the conditional mode of u_i. For a given value of ω, this can be obtained by means of penalized least-squares. A second-order approximation of h around ${\widehat{u}}_i$ is given by

$$h\left({\theta }_{\tau },y_i,u_i\right)\simeq h_i+{\stackrel{.}{h}}_i^{\top }\left(u_i-{\widehat{u}}_i\right)+{\left(u_i-{\widehat{u}}_i\right)}^{\top }{\stackrel{\mathrm{..}}{H}}_i\left(u_i-{\widehat{u}}_i\right),$$

where $h_i\equiv h\left({\theta }_{\tau },y_i,{\widehat{u}}_i\right)$, ${\stackrel{.}{h}}_i\equiv h^{\prime }\left({\theta }_{\tau },y_i,{\widehat{u}}_i\right)$ and ${\stackrel{\mathrm{..}}{H}}_i\equiv h^{″}\left({\theta }_{\tau },y_i,{\widehat{u}}_i\right)/2$. Since h_i is zero at $u_i={\widehat{u}}_i$ we have the following Laplacian approximation of the log-likelihood

$${\mathcal{l}}_{\text{LA}}\left({\theta }_{\tau };y\right)=N\text{log}\left\{\frac{\tau (1-\tau )}{{\sigma }_{\tau }}\right\}-\frac{M}{2}\text{log}\left|{\Psi }_{\tau }\right|-\frac{1}{2{\sigma }_{\tau }}\sum _{i=1}^M{h}_i+\sum _{i=1}^M\text{log}{\int }_{{ℝ}^q}{\left(2\pi {\sigma }_{\tau }\right)}^{-q/2}\times \text{exp}\left\{-\frac{1}{2{\sigma }_{\tau }}{\left(u_i-{\widehat{u}}_i\right)}^{\top }{\stackrel{\mathrm{..}}{H}}_i\left(u_i-{\widehat{u}}_i\right)\right\}\text{d}{u}_i=N\text{log}\left\{\frac{\tau (1-\tau )}{{\sigma }_{\tau }}\right\}-\frac{1}{2}\left\{\sum _{i=1}^M\text{log}\left|{\Psi }_{\tau }{\stackrel{\mathrm{..}}{H}}_i\right|+{\sigma }_{\tau }^{-1}\sum _{i=1}^M{h}_i\right\}.$$ (13)

If we ignore the negligible contribution of the first term in expression (11) (Pinheiro and Bates, 1995), then only the first-order partial derivatives of f are required to compute (13). Note the slimmer form of (13) as compared to a numerically integrated likelihood as in (3).

Since ${\widehat{u}}_i$ does not depend on σ, the log-likelihood ℓ_La can be profiled on σ leading to

$${\mathcal{l}}_{\text{LA}p}\left({\theta }_{\tau };y\right)=N\left[\text{log}\left\{\frac{\tau (1-\tau )}{{\widehat{\sigma }}_{\tau }}\right\}-1\right]-\frac{1}{2}\sum _{i=1}^M\text{log}\left|{\Psi }_{\tau }{\stackrel{\mathrm{..}}{H}}_i\right|,$$ (14)

where ${\widehat{\sigma }}_{\tau }={(2N)}^{-1}{\sum }_i^M{h}_i$.

Estimation of the parameters is carried out iteratively as described in the pseudo-code in Appendix A. The algorithm requires setting the starting value of θτ, στ, and the tuning parameter ω, the tolerance for the change in the log-likelihood, and the maximum number of iterations, as well as obtaining an initial estimate of the random effects (see further below). At each iteration, the parameter ω is reduced by a factor 0 < γ < 1. Hence, γ controls the speed at which the smoothing parameter ω approaches zero. At convergence, the value of co should be small, ideally, since the approximation of k_ω,x to the loss function p_τ improves with decreasing ω.

The modes of the random effects can be obtained by minimizing the objective function of the penalized least-squares problem using a Gauss-Newton method. Let Δτ be the relative precision factor such that ${\Psi }_{\tau }^{-1}={\Delta }_{\tau }^{\top }{\Delta }_{\tau }$ (Pinheiro and Bates, 2000). Then the function in (9) can be rewritten as

$$\begin{gathered} h\left({\theta }_{\tau },y_i,u_i\right)=\Vert A_i^{1/2}{r}_i{\Vert }^2+b_i^{\top }{r}_i+c_i^{\top }{1}_{n_i}+\Vert {\Delta }_{\tau }{u}_i{\Vert }^2 \\ =\Vert {\tilde{y}}_i-{\tilde{f}}_i{\Vert }^2+b_i^{\top }\left(y_i-f_i\right)+c_i^{\top }{1}_{n_i}, \end{gathered}$$ (15)

where

$${\tilde{y}}_i=\left[\begin{array}{c}{\tilde{A}}_i{y}_i\\ 0\end{array}\right],{\tilde{f}}_i=\left[\begin{array}{c}{\tilde{A}}_i{f}_i\\ {\Delta }_{\tau }{u}_i\end{array}\right],{\tilde{A}}_i=A_i^{1/2}.$$

Note that, in contrast to an approach based on numerical quadrature (Geraci and Bottai, 2014), the predicted random effects are a by-product of the estimation procedure.

When using the asymmetric Laplace as pseudo-likelihood, inference must be restricted to point estimation since the distribution is misspecified (see for example Reich et al., 2010; Yang et al., 2016). Standard errors for non-random parameters can be calculated using block bootstrap, although this increases the computational cost. Bootstrap confidence intervals have been shown to have good coverage in LQMMs (Geraci and Bottai, 2014).

We conclude this section by introducing additional statistics of interest that can be obtained from the fitted model. We define ${\widehat{Q}}_{y_{ij}|u_i=0}^{(0)}(\tau )=f_{ij}\left({\widehat{\beta }}_{\tau },0_q\right)$ as the NLQMM prediction of the rth quantile of yij at level 0. Similarly, we define ${\widehat{Q}}_{y_{ij}|u_i}^{(1)}(\tau )=f_{ij}\left({\widehat{\beta }}_{\tau },{\widehat{u}}_i\right)$ as the NLQMM prediction of the rth quantile of j/j, at level 1 (i.e., at the cluster level). Since model (4) is conditional on the random effects, only predictions at level 1 can be interpreted as sample quantiles. As a consequence, if the model is correctly specified, the proportion of negative residuals (PNR) at level 1 should be approximately r. In contrast, predictions at level 0 can be seen as sample quantiles of the ‘zero-median’ cluster.

4. Simulation study

In this section, we perform a simulation study to evaluate statistical and computational characteristics of the proposed methods. We start from a setting similar to the one used in Pinheiro and Bates (1995), which is ideal for normal NLME models, and then investigate scenarios more apposite for NLQMM.

In the first scenario, we simulated the data from the following logistic model

$$y_{ij}=\frac{{\beta }_1-{\beta }_4+u_{1i}}{1+\text{exp}\left\{\left({\beta }_2+u_{2i}-x_{ij}\right)/{\beta }_3\right\}}+\left({\beta }_4+{ϵ}_{ij}\right),$$ (16)

where β = (70, 10, 3, 10)^⊤, $u_i={\left(u_{1i},u_{2i}\right)}^{\top }~\mathcal{N}\left(0_2,\Sigma \right)$,$x_{ij}~\mathcal{U}(0,20)$, and ${ϵ}_{ij}~\mathcal{N}(0,1)$. The random effects are thus associated with the asymptotes (β₁ and β₄) and the sigmoid’s midpoint (β₂). Their variance-covariance matrix was defined as

$$\Sigma =\left[\begin{array}{cc}4& -2\\ -2& 5\end{array}\right].$$

In the second scenario, we used the same model (16), but we sampled the errors from a standardized chi-squared distribution with 3 degrees of freedom, i.e ${ϵ}_{ij}~{\chi }_3^2/\sqrt{6}$.

In the third scenario, we slightly changed model (16) and used

$$y_{ij}=\frac{\left({\beta }_1-{\beta }_4\right)}{1+\text{exp}\left\{\left({\beta }_2+u_i-x_{ij}-0.5x_{ij}{ϵ}_{ij}\right)/{\beta }_3\right\}}+{\beta }_4,$$ (17)

where β = (1, 4, 1, 0)^⊤, $x_{ij}~\mathcal{U}(0,5)$, $u_i~\mathcal{N}(0,0.1)$, and ${ϵ}_{ij}~{\chi }_3^2/\sqrt{60}$. Note that the error is skewed as in the second scenario but now operates within the exponential function. In this heteroscedastic model, there is only one random effect associated with the sigmoid’s midpoint.

In the fourth and last scenario, we used the biexponential model

$$y_{ij}=\left({\beta }_1+u_{1i}\right)\text{exp}\left\{-\text{exp}\left({\beta }_2+u_{2i}\right)x_{ij}\right\}+\left({\beta }_3+u_{3i}\right)\text{exp}\left\{-\text{exp}\left({\beta }_4+u_{4i}\right)x_{ij}\right\}+\left(1-x_{ij}/8\right){ϵ}_{ij},$$ (18)

where $u_i={\left(u_{1i},u_{2i},u_{3i},u_{4i}\right)}^{\top }~\mathcal{N}\left(0_4,\Sigma \right)$, $x_{ij}~\mathcal{U}(0,8)$, and ${ϵ}_{ij}~\mathcal{N}(0,0.1)$, with parameters β = (2, 0.8, 0.4, −1.5)^T and $\Sigma =0.1I_4$.

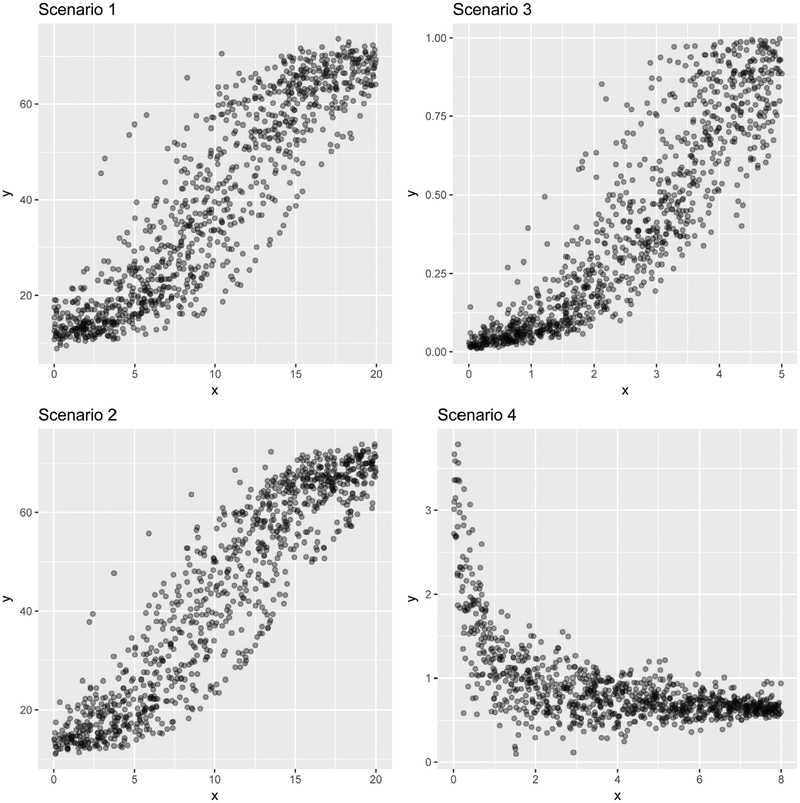
In all scenarios, we used a balanced design (ni = n, i = 1, … ,M)with three sample sizes: (M = 50, n = 5), (M = 100, n = 5), and (M = 100, n = 10). Instances of replications are shown in Fig. 1. For data sampled from models (16) and (17), we fitted mixed-effects logistic quantile functions with parameter ϕ_τ,ij = F_ijβ_τ + G_iju_i, where

$$F_{ij}=\left[\begin{array}{cccc}1& 0& 0& -1\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$

in the first 3 scenarios,

$$G_{ij}=\left[\begin{array}{l}{I}_2\hfill \\ O_{2\times 2}\hfill \end{array}\right]$$

in the first and second scenarios, and G_ij = (0, 1, 0, 0)^T in the third scenario. For data sampled from model (18), we fitted mixed-effects biexponential quantile functions with parameter ϕ_τ,ij = F_ijβ_τ + G_iju_i, where F_ij = G_ij = I₄.

Fig. 1.

Examples of data generated from the logistic (scenarios 1–3) and the biexponential (scenario 4) models.

For each scenario, we replicated R = 500 datasets and fitted NLQMMs at three quantile levels using r τ ∊ {0.1, 0.5, 0.9}. Estimation was carried out by following the algorithm as described in Appendix A. An attempt to maximize the approximated Laplacian log-likelihood (13) was made by using the Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm (optim) in the first instance. Upon failure of the BFGS algorithm during any iteration of the main estimation algorithm, the latter was started again and a new attempt to maximize (13) was made by using the Nelder-Mead algorithm. The maximum number of iterations was set to 500, while the tolerance for the relative change in the log-likelihood was set to 10⁻⁴.

We now provide details on starting values for the algorithm (further discussion on this point is given at the end of this section) and other computational aspects. Starting values for β_τ were taken from nonlinear quantile regression (NLRQ) for independent data (Koenker and Park, 1996), while the mean NLRQ deviance was used to calculate the starting value for στ. The parameter §_r was initialized using the estimate from NLME. It should be noted that both NLRQand NLME are nonlinear models whose estimation algorithms may too, in general, need starting values. These were obtained from a ‘crude’ minimization of $\sum _i\left|y_i-f_i(\beta )\right|$ Nelder-Mead. The Newton-type optimization algorithm (nlm) to estimate the random effects was initialized with the predictions from NLME. The starting value for the tuning parameter ω was set equal to max_i=1,…,N {|r_i(β_NLRQ)|/τ, |r_i(β_NLRQ)|/(1−τ)}/2, where r_i(β_NLRQ) denotes the NLRQ residuals, along the lines of the approach suggested in Chen (2007, p. 143). Between two successive iterations, ω was multiplied by the factor γ = 0.2. All the parameters of the optimization algorithms in optim and nlm were set at their default values. COmputations were performed using the R environment for statistical computing and graphics (R COre Team, 2016) version 3.3.2 on a desktop computer with a 3.60 GHz quad core i7–4790 processor and 16 GB of RAM.

Before we proceed with the analysis of the results, it is important to note that, in general, the nonlinearity of the models along with the presence of the random effects poses a difficulty for establishing the ‘true’ value of β_τfor quantiles other than the median (see for example the simulation study in Karlsson, 2008), even when the errors are normal. For example, in the logistic model not only the asymptotes β_τ and β_τ,4 but also the midpoint β_τ,2 and the scale β_τ,3 change with r in a rather complicated way. (An exception is given by model (17) for which the lower and upper asymptotes (β_τ,4 and β_τ,1, respectively) do not change with r.) We find solace in observing that such limitation brings out one of the advantages of quantile-based over moment-based modelling, since direct estimation of conditional quantiles does not require nontrivial manipulation of nonlinear relationships (Demidenko, 2013, p. 435). As a reference, we can consider the corresponding results from NLRQ under the assumption of independent observations. Similarity of the magnitude and direction of the estimates would support the interpretation of β_τ as regression parameters of the ‘zero-median’ cluster, while comparing the variability of the estimates from NLQMM and NLRQ would inform us on whether accounting for clustering provides a gain in efficiency. Additionally, we determined the proportion of negative level-1 residuals (PNR)

$$\frac{1}{N}\sum _{i=1}^M\sum _{j=1}^{n}I\left\{y_{ij}-{\widehat{Q}}_{y_{ij}|u_i}^{(1)}(\tau )<0\right\},$$

which is expected to be approximately equal to r. All summary measures were averaged over the replications.

The average estimates τ and standard deviations of the estimates are reported in Tables 1–4. In summary, NLQMM estimates were close to NLRQ estimates in all scenarios. The variability of the estimates from NLQMM was either lower or close to that of the estimates from NLQR, and the standard errors decreased with increasing M and n. Of all the results, perhaps those related to the quantile 0.9 in the third scenario (Table 3) deserve more discussion. Both NLQMM and NLRQ clearly failed to provide meaningful estimates of the parameters. This is due to the fact that the range of the simulated values for x was not wide enough to correctly estimate the upper asymptote at upper quantiles. This observation may have a particular relevance when modelling reference growth curves. Further, the estimated variance-covariance parameters and the predicted random effects obtained from (12) were, in general, consistent with the parameters of the true distribution of the random effects, although, as noted before, direct comparisons are not straightforward (additional results are reported in supplementary material).

Table 1.

Estimates of the fixed effects from nonlinear quantile mixed-effects regression (NLQMM) and from nonlinear quantile regression (NLRQ) with τ.∊{0.1, 0.5, 0.9} for the first scenario. The estimates are averaged over 500 replications and the standard deviations are reported in brackets. Data were generated using the model’s parameter β (70, 10, 3, 10)^⊤.

	β1	β2	β3	β4	PNR
NLQMM (M = 50, n = 5)
τ = 0.1	69.28 (6.52)	12.85 (0.91)	3.10 (0.59)	9.20 (2.15)	0.09
τ = 0.5	70.40 (0.82)	9.99 (0.45)	3.06 (0.15)	9.55 (0.63)	0.50
τ = 0.9	73.09 (1.40)	7.20 (0.65)	3.16 (0.37)	9.12 (2.42)	0.91
NLRQ(M = 50, n = 5)
τ = 0.1	69.22 (7.98)	12.84 (1.19)	3.07 (0.67)	9.44 (1.27)	0.10
τ = 0.5	69.81 (1.84)	9.99 (0.55)	2.99 (0.39)	10.09 (1.61)	0.50
τ = 0.9	72.13 (1.63)	7.38 (0.81)	2.98 (0.56)	10.82 (5.06)	0.90
NLQMM (M = 100, n = 5)
τ = 0.1	69.04 (2.08)	12.79 (0.54)	3.10 (0.25)	8.93 (0.63)	0.09
τ = 0.5	70.44 (0.57)	10.00 (0.31)	3.06 (0.11)	9.55 (0.42)	0.50
τ = 0.9	73.16 (0.87)	7.20 (0.48)	3.17 (0.22)	9.10 (1.49)	0.91
NLRQ(M = 100, n = 5)
τ = 0.1	68.65 (4.12)	12.80 (0.72)	3.04 (0.41)	9.54 (0.78)	0.10
τ = 0.5	69.84 (1.37)	10.00 (0.37)	3.00 (0.29)	10.12 (1.13)	0.50
τ = 0.9	72.11 (1.17)	7.29 (0.77)	3.02 (0.45)	10.40 (5.05)	0.90
NLQMM (M = 100, n = 10)
τ = 0.1	68.00 (0.73)	12.66 (0.40)	3.06 (0.10)	8.79 (0.34)	0.09
τ = 0.5	70.23 (0.38)	9.99 (0.28)	3.04 (0.05)	9.70 (0.22)	0.50
τ = 0.9	73.47 (0.56)	7.28 (0.38)	3.15 (0.10)	9.76 (0.52)	0.92
NLRQ(M = 100, n = 10)
τ = 0.1	68.47 (2.76)	12.77 (0.58)	3.04 (0.27)	9.54 (0.53)	0.10
τ = 0.5	69.79 (0.92)	9.99 (0.33)	3.00 (0.18)	10.11 (0.71)	0.50
τ = 0.9	72.26 (0.85)	7.19 (0.53)	3.11 (0.32)	9.53 (2.75)	0.90

Table 4.

Estimates of the fixed effects from nonlinear quantile mixed-effects regression (NLQMM) and from nonlinear quantile regression (NLRQ) with τ ∊{0.1, 0.5, 0.9} for the fourth scenario. The estimates are averaged over 500 replications and the standard deviations are reported in brackets. Data were generated using the model’s parameter β (2, 0.8, 0.4, −1.5)^⊤.

	β1	β2	β3	β4	PNR
NLQMM (M = 50, n = 5)
τ = 0.1	2.11 (0.63)	1.02 (0.55)	0.30 (0.13)	−∞ (∞)	0.04
τ = 0.5	2.06 (0.28)	0.72 (0.22)	0.88 (0.13)	−3.06 (0.31)	0.50
τ = 0.9	2.09 (0.40)	0.71 (0.31)	1.65 (0.16)	−2.40 (0.18)	0.94
NLRQ(M = 50, n = 5)
τ = 0.1	2.00 (0.60)	0.96 (0.37)	0.46 (0.15)	−∞ (∞)	0.09
τ = 0.5	2.07 (0.38)	0.71 (0.30)	0.87 (0.15)	−3.24 (1.52)	0.50
τ = 0.9	2.24 (0.73)	0.63 (0.42)	1.40 (0.24)	−0.92 (24.07)	0.88
NLQMM (M = 100, n = 5)
τ = 0.1	1.99 (0.26)	0.99 (0.16)	0.37 (0.11)	−∞ (∞)	0.04
τ = 0.5	2.04 (0.19)	0.69 (0.16)	0.94 (0.11)	−3.15 (0.25)	0.50
τ = 0.9	2.05 (0.24)	0.66 (0.19)	1.71 (0.12)	−2.46 (0.14)	0.94
NLRQ(M = 100, n = 5)
τ = 0.1	1.91 (0.37)	0.98 (0.25)	0.54 (0.13)	−∞ (∞)	0.09
τ = 0.5	2.05 (0.23)	0.68 (0.20)	0.93 (0.13)	−3.23 (0.47)	0.50
τ = 0.9	2.17 (0.31)	0.59 (0.27)	1.46 (0.16)	−1.80 (3.46)	0.88
NLQMM (M = 100, n = 10)
τ = 0.1	1.93 (0.19)	1.06 (0.12)	0.46 (0.13)	−∞ (∞)	0.06
τ = 0.5	2.04 (0.15)	0.72 (0.10)	1.03 (0.11)	−3.19 (0.17)	0.50
τ = 0.9	2.05 (0.17)	0.61 (0.15)	1.82 (0.12)	−2.48 (0.11)	0.94
NLRQ(M = 100, n = 10)
τ = 0.1	1.86 (0.26)	0.98 (0.19)	0.61 (0.14)	−∞ (∞)	0.09
τ = 0.5	2.04 (0.18)	0.70 (0.14)	1.01 (0.13)	−3.27 (0.24)	0.50
τ = 0.9	2.17 (0.21)	0.61 (0.19)	1.55 (0.14)	−2.32 (1.89)	0.90

Table 3.

Estimates of the fixed effects from nonlinear quantile mixed-effects regression (NLQMM) and from nonlinear quantile regression (NLRQ) with τ ∊ {0.1, 0.5, 0.9} for the third scenario. The estimates are averaged over 500 replications and the standard deviations are reported in brackets. Data were generated using the model’s parameter β (1, 4, 1, 0)^⊤.

	β1	β2	β3	β4	PNR
NLQMM (M = 50, n = 5)
τ = 0.1	1.03 (0.20)	4.05 (0.32)	0.96 (0.14)	0.00 (0.01)	0.08
τ = 0.5	0.99 (0.06)	3.19 (0.16)	0.83 (0.10)	0.01 (0.01)	0.49
τ = 0.9	−0.13 (0.86)	2.13 (1.18)	−1.51 (2.13)	1.11 (0.66)	0.91
NLRQ(M = 50, n = 5)
τ = 0.1	1.17 (0.93)	4.08 (0.68)	1.01 (0.16)	−0.00 (0.01)	0.12
τ = 0.5	1.02 (0.10)	3.20 (0.23)	0.88 (0.14)	−0.00 (0.02)	0.50
τ = 0.9	−0.33 (1.60)	−0.47 (3.64)	−2.06 (2.22)	0.46 (0.44)	0.89
NLQMM (M = 100, n = 5)
τ = 0.1	1.00 (0.08)	4.00 (0.14)	0.98 (0.09)	0.00 (0.00)	0.10
τ = 0.5	0.99 (0.04)	3.18 (0.11)	0.82 (0.07)	0.01 (0.01)	0.49
τ = 0.9	−0.20 (0.73)	2.10 (1.09)	−1.36 (1.62)	1.15 (0.45)	0.88
NLRQ(M = 100, n = 5)
τ = 0.1	1.04 (0.15)	3.99 (0.24)	1.01 (0.08)	−0.00 (0.01)	0.12
τ = 0.5	1.01 (0.06)	3.18 (0.15)	0.87 (0.09)	−0.00 (0.01)	0.50
τ = 0.9	−0.36 (0.69)	−0.76 (1.88)	−2.11 (1.22)	0.43 (0.27)	0.90
NLQMM (M = 100, n = 10)
τ = 0.1	0.95 (0.06)	4.18 (0.20)	0.92 (0.08)	0.00 (0.00)	0.08
τ = 0.5	1.00 (0.03)	3.19 (0.08)	0.85 (0.05)	0.00 (0.01)	0.49
τ = 0.9	−0.25 (0.93)	2.09 (1.34)	−1.16 (1.40)	1.11 (0.36)	0.92
NLRQ(M = 100, n = 10)
τ = 0.1	1.01 (0.03)	3.96 (0.06)	1.01 (0.02)	−0.00 (0.00)	0.13
τ = 0.5	1.00 (0.04)	3.18 (0.10)	0.87 (0.06)	−0.00 (0.01)	0.50
τ = 0.9	−0.48 (0.57)	−1.24 (1.65)	−2.19 (0.98)	0.40 (0.22)	0.90

In general, PNR rates for NLQMM were equal to the expected nominal r or within binomial variability, i.e. $\tau \pm 1.96\sqrt{N^{-1}\tau (1-\tau )}$. However, in the fourth scenario PNRs were somewhat below (τ = 0.1) or above (τ = 0.9) the expected proportion. The PNRs for NLRQwere in general closer to the nominal r. This is explained by the different models’ setups and estimation procedures. While NLQR provides quantiles of the ‘marginal’ distribution of y_ij, NLQMM seeks a balance between random effects and errors. Given the approximated nature of (13), some inaccuracies in NLQMM are inevitable, especially at smaller sample sizes.

We now provide basic details about the algorithm’s performance at the larger sample size (M = 100, n = 10) and a few recommendations. On average, it took about 7 iterations (approximately 35 s) to fit one model for the quantile 0.1 or 0.9, and about 6 iterations (approximately 20 s) for the median in the first two scenarios. In the third scenario it took between 2 and 7 iterations (approximately 20 s on average) to fit one model for any of the three quantile levels. In the fourth scenario, the algorithm needed a similar number of iterations as in the first two scenarios but the time to convergence was, on average, twice as long. This means that, within each iteration, the number of function evaluations required by optim to fit the more complex biexponential model was greater than that needed to fit the logistic model. In the first two scenarios, the median value of the smoothing parameter co at the last iteration was about 2.0 × 10−³ for all considered quantiles. In the third scenario, it was less than 4.5 × 10⁻⁵ for the tail quantiles and 0.5 for the median. In the fourth scenario, it was less than 4.5 × 10⁻⁵ for all considered quantiles.

In a separate analysis with M = 100 and n = 10 (results not shown), the average number of iterations to convergence increased to at least 10 when γ was increased to 0.5. In contrast, the algorithm converged too q_uickly to smaller values of the log-likelihood when setting γ to less than 0.2. We recommend using γ between 0.2 and 0.5 in most situations.

Further, in the first three scenarios the average number of iterations and the values of the estimates were not particularly sensitive to the specific algorithm used for optimizing the log-likelihood, although the BFGS algorithm did fail to converge in about 20% of the replications, more often when estimating tail quantiles (28%) rather than when estimating the median (12%). In contrast, BFGS never failed to converge in the fourth scenario. We then ran a separate analysis (results not shown) in which biexponential models were fitted exclusively using Nelder-Mead. For τ = 0.1, estimates were unreasonable. We recommend using BFGS as default optimization algorithm.

Finally, we comment on the sensitivity of the algorithm to different starting values. We simulated data from the first scenario with M = 100 and n = 10 and we fitted NLQMMs for three quantile levels τ ∊ {0.1, 0.5, 0.9}. In one case, we used the starting values as defined above. Let us denote the resulting estimate by ${\widehat{\theta }}_1$. In another, we initialized β_τ using a nonlinear least squares (NLS) estimate (Bates and Watts, 1988), while the square root of the mean NLS deviance was used to calculate the starting value for στ. The parameter §_r was initialized using the NLME estimate as before. Let us denote the resulting estimate by ${\widehat{\theta }}_2$. The relative absolute difference of the norms $\Vert {\widehat{\theta }}_1\Vert$ and $\Vert {\widehat{\theta }}_2\Vert$ was always less than 3%.

In summary, we conclude that the proposed algorithm gives similar estimates as long as starting values are obtained from analogous models, i.e., NLS or NLRQ, for initializing and β_r, and NLME for initializing β_τ and the random effects. In turn, starting values for NLS, NLRQ, and NLME can be obtained from a crude estimate as those provided by a self-starting nonlinear function (R COre Team, 2016). For details on nonlinear algorithms in NLS, NLRQ, and NLME, we refer the reader to the relevant publications (Bates and Watts, 1988; Koenker and Park, 1996; Pinheiro and Bates, 1995, 2000).

5. Applications

5.1. Pharmacokinetics

We begin with the analysis of a dataset taken from an old pharmacokinetics study (Kwan et al., 1976), often used as a toy example in nonlinear regression modelling (Davidian and Giltinan, 1995; Pinheiro and Bates, 2000). The data consists of 11 measurements of plasma concentrations of indomethacin which was injected intravenously in 6 subjects. In this study, the goal is to model the distribution and elimination of the drug. By using NLME, one is able to describe how the average drug concentration changes (nonlinearly) over time while taking into account the heterogeneity among subjects. It might also be of interest to model change on the tails of the distribution to establish, for example, percentile reference limits for drug concentration at specific times after injection or to compare rates of change across quantiles. The advantage of NLQMM is, first of all, its ability to model the quantiles of interest directly. The importance of this advantage becomes apparent if we consider that the marginal distribution in NLME generally lacks a closed form (Demidenko, 2013). Another advantage of NLQMM is its flexibility when assessing the impact of covariates on the location, scale, and shape of the conditional distribution of the response (Geraci, 2016). In contrast, NLME’s scope is limited to the modelling of location-and location-scale-shift effects, always within the bounds of a normal shape of the errors.

To analyse the Indomethacin Data, we used the biexponential model

$$Q_{y_{ij}|u_i}(\tau )=\left({\beta }_{\tau ,1}+u_{1i}\right)\text{exp}\left\{-\text{exp}\left({\beta }_{\tau ,2}+u_{2i}\right)t_j\right\}+\left({\beta }_{\tau ,3}+u_{3i}\right)\text{exp}\left\{-\text{exp}\left({\beta }_{\tau ,4}\right)t_j\right\},$$

where y_ij denotes the jth measurement of drug concentration (mcg/ml), j = i,…, 1, on the ith subject, i = 1,…, 6, and tj is the time (hr) of the measurement since injection (given that the design is common to all subjects and the dataset is balanced, t does not depend on i). We modelled the variance-covariance of the random effects using the diagonal matrix ${\Sigma }_{\tau }={\oplus }_{k=1}^3{\sigma }_{\tau ,k}^2$ (variance components). Note that the regression model above includes 3 random effects, one for each of the first 3 fixed effects. In a separate analysis (results not shown), we found that the random effect associated with β_τ,4, τ ∊ {0.1, 0.5, 0.9}, had near-zero variance (see also Pinheiro and Bates, 2000, p. 283).

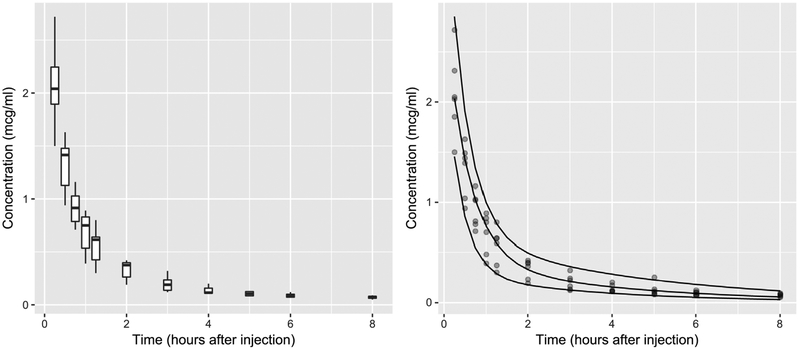
In this two-compartment model, the first exponential term determines the initial, rapidly declining distribution phase of the drug. The elimination of the drug is the predominant process during the second phase and is primarily determined by the second exponential term. Besides the average rates at which the drug is distributed and then eliminated, it might be of interest to assess the change over time of concentrations that are higher or lower than the mean. The left plot of Fig. 2 shows the boxplots of indomethacin concentration at each measurement occasion. It appears that the scale and possibly even the shape of the distribution are changing over time. This would mean that the rates are not similar across the quantiles of the conditional distribution.

Fig. 2.

Boxplots of indomethacin concentration by measurement occasion (left) and fitted biexponential curves at the 10th, 50th and 90th centiles of drug concentration conditional on time since injection (right) using the Indomethacin Data.

The fitted biexponential curves for τ ∊{0.1, 0.5, 0.9} are given in the right plot of Fig. 2, while estimates of the fixed effects and their standard errors are reported in Table 5. The average rate (NLME) at which the drug decreases during the distribution phase was comparable to that of the 90th centile. However, the decrease was about 20 % faster at the lower 10th centile but about 20% slower at the median as compared to the mean. During the second phase, the rate of decrease was, again, greatest at the 10th centile. However, the average rate was similar to that of the median and greater than that of the 90th centile. One implication is that the distribution of the response becomes increasingly right-skewed as time passes. This is an advantage of NLQMM over NLME as the latter cannot obviously model changes in the shape of the distribution.

Table 5.

Estimates of the fixed effects (standard errors) from three biexponential quantile mixed-effects models with τ ∊ {0.1, 0.5, 0.9} and from the normal nonlinear mixed-effects model (NLME) using the Indomethacin Data. Standard errors for quantile regression estimates are based on 200 bootstrap replications. Bold denotes statistically significant at the 5% level.

	β1	β2	β3	β4
τ = 0.1	2.31 (0.48)	0.99 (0.16)	0.30 (0.13)	−1.19 (0.57)
τ = 0.5	2.55 (0.28)	0.58 (0.19)	0.44 (0.17)	−1.33 (0.23)
τ = 0.9	3.73 (0.52)	0.75 (0.35)	0.69 (0.34)	−1.49 (0.37)
NLME	2.83 (0.26)	0.77 (0.11)	0.46 (0.11)	−1.35 (0.23)

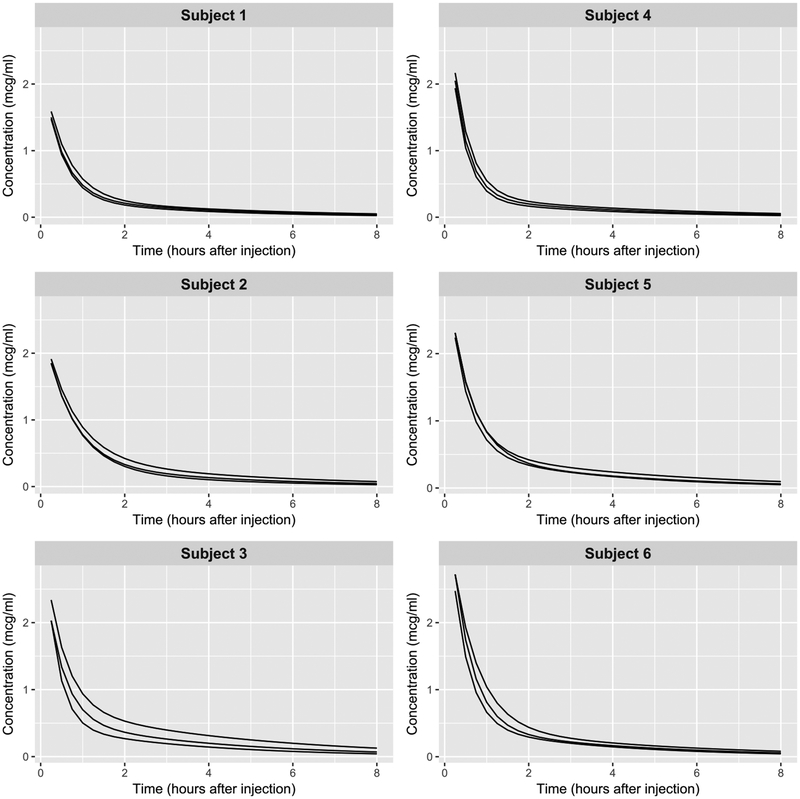
Finally, there was substantial heterogeneity among subjects regarding starting concentration levels during the distribution phase, especially at the 90th centile (Table 6). The predicted biexponential individual curves for each of the 6 subjects are given in Fig. 3. This kind of plot provides potentially useful information at the individual level. For example, the estimated drug concentration over time for the individual labelled as ‘Subject 3’ clearly shows a wider spread as compared to the other individuals.

Table 6.

Estimates of the variance components from three biexponential quantile mixed-effects models with tτ ∊{0.1, 0.5, 0.9} and from the normal nonlinear mixed-effects model (NLME) using the Indomethacin Data.

	${\sigma }_1^2$	${\sigma }_2^2$	${\sigma }_3^2$
τ = 0.1	0.78	0.06	0.02
τ = 0.5	0.59	0.08	0.02
τ = 0.9	1.34	0.05	0.06
NLME	0.33	0.03	0.01

Fig. 3.

Fitted biexponential curves at the 10th, 50th and 90th centiles of drug concentration conditional on time since injection for individual subjects in the Indomethacin Data.

5.2. Growth curves

In this section, we analyse data on growth patterns of two genotypes of soybeans: Plant Introduction #416937 (P), an experimental strain, and Forrest (F), a commercial variety (Davidian and Giltinan, 1995). The response variable is the average leaf weight of 6 plants chosen at random from each experimental plot and measured at approximately weekly intervals, between two and eleven weeks after planting. The experiment was carried out over three different planting years: 1988, 1989, and 1990. Eight plots were planted with each genotype in each planting year, giving a total of 48 plots in the study (Pinheiro and Bates, 2000).

Here, the goal is to compare growth of the plants in the two genotypic groups, P and F. We consider the application of NLQMM for reasons analogous to those given in the preceding example. From previous analyses of these data (Davidian and Giltinan, 1995; Pinheiro and Bates, 2000), we know that the experimental strain yielded on average heavier plants than the commercial variety in one particular year. Two questions of interest here are how the two genotypes compare at different quantiles of leaf weight and whether quantile treatment effects depend on planting year.

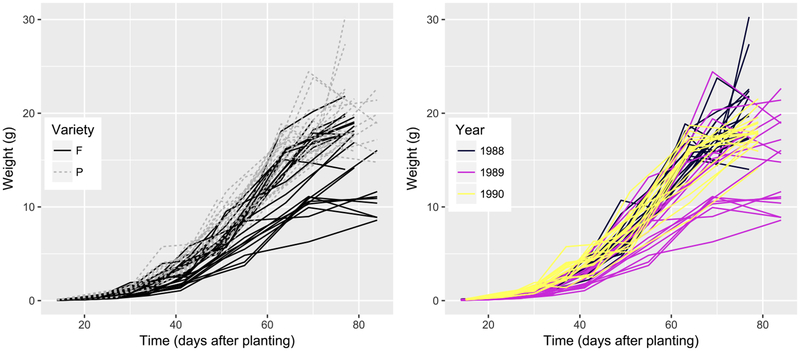
Fig. 4 shows the temporal trajectories of the average leaf weight for individual plots. It is apparent that the experimental strain yielded heavier leaves than the F variety, at least on average. There also seem to be differences between planting years, with a wider spread of the curves in 1989. Given that previous analyses of these data focused on the average growth curves, we set out to investigate growth in the tails of the distribution. For our analysis, we used the same logistic model as that in Pinheiro and Bates (2000, p. 293) which was selected over a number of alternative models, that is

$$Q_{y_{ij}|u_i}(\tau )=\frac{{\varphi }_{\tau ,1ij}}{1+\text{exp}\left\{\left({\varphi }_{\tau ,2ij}-t_{ij}\right)/{\varphi }_{\tau ,3ij}\right\}},$$

where y_ij denotes the average leaf weight (g) observed on occasion j, j = 1,…, n_i, in the ith plot, i = 1,…, 48, and t_ij is the time (days) of the measurement after planting. The number of measurements per plot ranged between 8 and 10. The design matrices of the 3 × 1 parameter ϕ_τ,ij = F_ijβ_τ + G_iju_i were given by

$$F_{ij}=\left[\begin{array}{lllllllllllll}1\hfill & {\chi }_{ij}^{(89)}\hfill & {\chi }_{ij}^{(90)}\hfill & {\chi }_{ij}^{(P)}\hfill & {\chi }_{ij}^{(89)}\cdot {\chi }_{ij}^{(P)}\hfill & {\chi }_{ij}^{(90)}\cdot {\chi }_{ij}^{(P)}\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & {\chi }_{ij}^{(89)}\hfill & {\chi }_{ij}^{(90)}\hfill & {\chi }_{ij}^{(P)}\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 1\hfill & {\chi }_{ij}^{(89)}\hfill & {\chi }_{ij}^{(90)}\hfill \end{array}\right]$$

and $G_{ij}={\left[\begin{array}{lll}1\hfill & 0\hfill & 0\hfill \end{array}\right]}^{\top }$. Thus,β_τ is a 13 × 1 vector. The covariates in the F matrix are dummy variables for year of planting, x⁽⁸⁹⁾ and x⁽⁹⁰⁾, and genotype, x^(p). The baseline is represented by year 1988 and variety F. The only random effect included in the model was associated with the asymptote.

Fig. 4.

Observed growth curves of soybean plants. Each line represents the average leaf weight per plant in each experimental plot. Curves are grouped by variety (left) or by year (right).

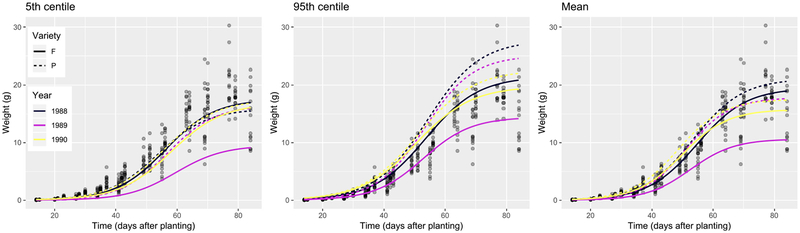
The three plots in Fig. 5 show the 5th centile, 95th centile, and mean predicted growth curves by variety and planting year, while the estimates and standard errors of the fixed effects are reported in Table 7. For the sake of brevity, we confine our discussion to the genotypic effect on the asymptote. In 1988, the experimental strain had an advantage over the commercial variety but only at the 95th centile of the leaf weight distribution, with an estimated asymptote difference of 6.31 g (as given by ${\widehat{\beta }}_{\tau ,4}$)in following year, the overall effect of variety P on the asymptote (calculated as ${\widehat{\beta }}_{\tau ,4}+{\widehat{\beta }}_{\tau ,5}$) was equal to 6.95 g at the 5th centile and 10.67 g at the 95th centile. In comparison, the mean effect was 7.19 g, closer to the 5th than to the 95th centile. However, the interaction between variety and year 1989 was not statistically significant at the 95th centile. Finally, in 1990 the overall effect of variety P on the asymptote (calculated as ${\widehat{\beta }}_{\tau ,4}+{\widehat{\beta }}_{\tau ,6}$) was relatively small at both the 5 th (0.58 g) and 95th (2.81 g) centiles. In summary, the experimental strain did yield heavier leaves than the F variety, not only in 1989 as estimated by NLME, but also in 1988, and the magnitude of the genotypic effect was dependent on the quantile level.

Fig. 5.

Fitted logistic growth curves of soybean plants at the 5th centile (left), 95th centile (centre), and at the mean (right).

Table 7.

Estimates of the fixed effects (standard errors) from two logistic quantile mixed-effects models with τ ∊{0.05, 0.95} and from the normal nonlinear mixed-effects model (NLME) using the Soybean Data. Standard errors for quantile regression estimates are based on 200 bootstrap replications. Bold denotes statistically significant at the 5% level.

	τ = 0.05	τ = 0.95	NLME
β1	17.49 (1.47)	21.43 (2.34)	19.43 (0.95)
β2	−7.99 (1.53)	−7.02 (2.30)	−8.84 (1.07)
β3	−0.66 (2.06)	−1.67 (2.49)	−3.71 (1.18)
β4	−1.64 (2.01)	6.31 (1.99)	1.62 (1.04)
β5	8.59 (1.93)	4.36 (2.41)	5.57 (1.17)
β6	2.22 (2.05)	−3.50 (2.01)	0.15 (1.18)
β7	56.16 (1.13)	53.71 (2.57)	54.81 (0.75)
β8	3.30 (2.11)	−0.86 (2.85)	−2.24 (0.97)
β9	1.94 (2.48)	−3.14 (2.79)	−4.97 (0.97)
β10	−2.50 (1.70)	0.51 (0.97)	−1.30 (0.41)
β11	8.11 (0.32)	8.63 (0.79)	8.06 (0.15)
β12	−0.29 (0.51)	−0.76 (0.85)	−0.90 (0.20)
β13	0.40 (0.49)	0.44 (0.91)	−0.67 (0.21)

6. Final remarks

Mixed-effects modelling has a long tradition in statistical applications. There is a vast number of applications of mixed models to the analysis of clustered data in the social, life and physical sciences (Pinheiro and Bates, 2000; Demidenko, 2013). Linear quantile mixed models (Geraci and Bottai, 2007,2014) have too been used in a wide range of research areas, including marine biology (Muir et al., 2015; Duffy et al., 2015; Barneche et al., 2016), environmental science (Fornaroli et al., 2015), cardiovascular disease (Degerud et al., 2014; Blankenberg et al., 2016), physical activity (Ng et al., 2014; Beets et al., 2016), and ophthalmology (Patel et al., 2015,2016). The present paper provides a novel and valuable contribution to the modelling of nonlinear quantile functions which broadens the applicability of quantile regression for clustered data.

NLQMMs represent a flexible alternative to nonlinear mixed models for the mean as they allow direct estimation of conditional quantile functions without imposing normal assumptions on the errors. As shown in two real data examples, NLQMMs reveal nonlinear relationships that may be quantitatively and qualitatively different at different quantiles. Also, changes in location, scale, and shape of the response distribution determined by the covariates are naturally brought into light by examining central and tail quantiles (Geraci, 2016).

As compared to NLRQ, which is based on the assumption of independent data, the proposed models provide additional information about the heterogeneity among clusters and allow for inference at the cluster level. The results of a simulation study show that NLQMM predictions at the cluster level have approximately the correct quantile level. The results also support the interpretation of the predictions at level 0 as sample quantiles of the ‘zero-median’ cluster.

The performance of the novel algorithm, a blend of a smoothing algorithm for quantile regression and a second order Laplacian approximation for nonlinear mixed models, was satisfactory overall. The average number of iterations to convergence (5 to 7) and average time needed (20 to 30 s with the larger sample size, and 5 to 15 s with the smaller sample size) were acceptable. An important advantage of the proposed algorithm relative to, say, numerical quadrature (Geraci and Bottai, 2014) is the availability of estimated random effects at convergence. However, it is precisely the estimation of the random effects that takes up most of the running time. We believe that there is scope for further improvement and this is part of future research.

Table 2.

Estimates of the fixed effects from nonlinear quantile mixed-effects regression (NLQMM) and from nonlinear quantile regression (NLRQ) with τ ∊ {0.1, 0.5, 0.9} for the second scenario. The estimates are averaged over 500 replications and the standard deviations are reported in brackets. Data were generated using the model’s parameter β = (70, 10, 3, 10)^⊤.

	β1	β2	β3	β4	PNR
NLQMM (M = 50, n = 5)
τ = 0.1	71.06 (5.86)	12.90 (1.00)	3.13 (0.51)	10.27 (1.20)	0.09
τ = 0.5	71.54 (0.80)	9.96 (0.43)	3.06 (0.14)	10.58 (0.53)	0.50
τ = 0.9	74.32 (1.45)	7.11 (0.77)	3.21 (0.44)	9.72 (3.56)	0.92
NLRQ (M = 50, n = 5)
τ = 0.1	70.25 (5.89)	12.82 (1.01)	3.06 (0.56)	10.71 (1.03)	0.10
τ = 0.5	70.98 (1.75)	9.98 (0.53)	2.98 (0.37)	11.26 (1.53)	0.50
τ = 0.9	73.51 (1.65)	7.19 (0.94)	3.09 (0.63)	10.77 (5.75)	0.90
NLQMM (M = 100, n = 5)
τ = 0.1	70.25 (1.65)	12.80 (0.49)	3.09 (0.21)	10.32 (0.45)	0.09
τ = 0.5	71.62 (0.50)	9.97 (0.29)	3.07 (0.09)	10.55 (0.36)	0.50
τ = 0.9	74.45 (0.90)	7.19 (0.46)	3.19 (0.22)	10.18 (1.41)	0.92
NLRQ (M = 100, n = 5)
τ = 0.1	69.86 (3.53)	12.79 (0.67)	3.03 (0.36)	10.81 (0.65)	0.10
τ = 0.5	71.06 (1.23)	10.00 (0.35)	3.00 (0.27)	11.30 (1.07)	0.50
τ = 0.9	73.41 (1.13)	7.19 (0.68)	3.08 (0.45)	10.85 (4.14)	0.90
NLQMM (M = 100, n = 10)
τ = 0.1	69.28 (0.68)	12.70 (0.40)	3.05 (0.08)	10.25 (0.22)	0.09
τ = 0.5	71.39 (0.35)	9.97 (0.27)	3.05 (0.05)	10.64 (0.19)	0.50
τ = 0.9	74.67 (0.55)	7.26 (0.38)	3.15 (0.10)	10.98 (0.58)	0.91
NLRQ (M = 100, n = 10)
τ = 0.1	69.67 (2.53)	12.77 (0.55)	3.03 (0.24)	10.80 (0.46)	0.10
τ = 0.5	71.03 (0.90)	9.98 (0.31)	3.01 (0.18)	11.25 (0.72)	0.50
τ = 0.9	73.49 (0.82)	7.17 (0.54)	3.11 (0.32)	10.73 (2.86)	0.90

Appendix A. NLQMM estimation

The estimation algorithm for NLQMM is based on a set of decreasing values of ω. This optimization approach has the appealing advantage of reducing the original nonsmooth problem to an approximated L₂ problem. The pseudo-code is given below.

Smoothing Algorithm with Laplacian Approximation for Nonlinear Quantile Mixed Models.

1. Set the maximum number of iterations T; the factor 0 < γ < 1 for reducing the tuning parameter ω the tolerance for the change in the log-likelihood; and t = 0. Estimate the starting values as follows:

   1. obtain an estimate for ${\beta }_{\tau }^{(0)}$ 1using nonlinear quantile regression (Koenker and Park, 1996). See, for example, the function nlrq in the R package quantreg (Koenker, 2016) which supports self-starting models such as SSlogis. If the nonlinear quantile regression algorithm fails, consider the estimate of the fixed effects from the NLME model in step (l.b) below or, if the latter fails too, a standard NLS estimate (Bates and Watts, 1988);
   2. obtain an estimate for ${\xi }_{\tau }^{(0)}$ from an NLME model. See, for example, the function nlme in the R package (Pinheiro et al., 2014). This function too supports self-starting models. If the NLME algorithm fails, provide an arbitrary value ${\xi }_{\tau }^{(0)}$;
   3. obtain an estimate for ${\sigma }_{\tau }^{(0)}$ For example, this can be estimated as the mean of the absolute residuals from step (1.a) above;
   4. provide a starting value ω⁽⁰⁾ (see, for example, Chen, 2007, p. 143);
   5. using ${\beta }_{\tau }^{(0)}$, ${\xi }_{\tau }^{(0)}$, and ${\sigma }_{\tau }^{(0)}$ solve the penalized least-squares problem (12) to obtain $u_i^{(0)}$, i = 1, M. See, for example, the R function nlm.
2. While t < T

   1. Update ${\theta }_{\tau }^{(t)}$ by minimizing (13) (or (14)). See, for example, the R function optim.
   2. If the change in the log-likelihood is smaller than a given tolerance

      1. then return ${\theta }_{\tau }^{(t+1)}$;
      2. else set ${\theta }_{\tau }^{(t+1)}={\theta }_{\tau }^{(t)}$; ω^(t+1) = γ ∙ ω^(t); t = t + 1; go to step (2.a).

3. Update ${\sigma }_{\tau }^{(t)}$ and $u_i^{(t)}$, i = 1,…,M.